서 론
ANN에 의한 RMR분류
텐서 플로우(Tensor flow)
ANN RMR 분류시스템
학습코드
학습과 평가
학습결과
RMR 평가
학습결과의 고찰
학습결과의 튜닝
학습자료 분석
튜닝(Tuning)
결 론
서 론
암반의 공학적 분류는 Q-System과 같이 암반의 복잡한 특성을 세분화하여 점수를 산정하는 방법과 암반의 특성을 세분화하기보다 육안조사 및 실험 등에 의하여 비교적 간단하게 평가할 수 있는 RMR방법 등이 있다.
RMR 분류는 RMR을 구성하는 요소들을 여러 단계로 이산화하여 점수 구간을 설정해 놓음으로써 실용성을 높이고자 한 것으로 RMR 요소들의 구간별 경곗값을 효율적으로 배분하기 위하여 현지 암반의 강도, RQD, 불연속면의 간격 등은 적합(curve fitting)에 의하여 정량적으로 점수를 산정하기도 한다. 이러한 암반분류를 좀더 쉽고 간편하게 하기 위한 연구들이 Butler and Franklin(1990), Yang et al.(1995), Bae and cho(2001) 등에 의하여 수행된 바 있으나 이들은 현장 조사방법의 개선이나 현장조사 자료를 토대로 특정 분야에서 이루어졌다.
본 연구에서는 현장에서부터 RMR 요소의 수준별 분류코드의 체크리스트(check list)를 적용하여 기계적으로 RMR 요소들의 점수를 산정하고자 인공신경망(Artificial Neural Network, ANN) 기술을 이용하였다. RMR분류 ANN 시스템의 학습자료 선정을 위하여 적은 수의 실험으로 많은 수의 인자들에 대한 연구가 가능한 강건설계(Robust design)를 적용하였다.
이러한 RMR 분류시스템은 RMR 조사 수가 많을 때 번거로운 작업을 간편하게 하고 다양한 포맷으로 출력할 수가 있어서 통계처리도 쉽다. RMR 분류 ANN 시스템의 완벽한 예측을 위하여 1차 예측값들에 대하여 주어진 수준 범위내에서 튜닝을 실시하였다. 그 결과 강건설계에 의한 25개의 학습자료로 3125개의 RMR을 완벽하게 예측하는 RMR분류 ANN 시스템이 가능하였다.
ANN에 의한 RMR분류
텐서 플로우(Tensor flow)
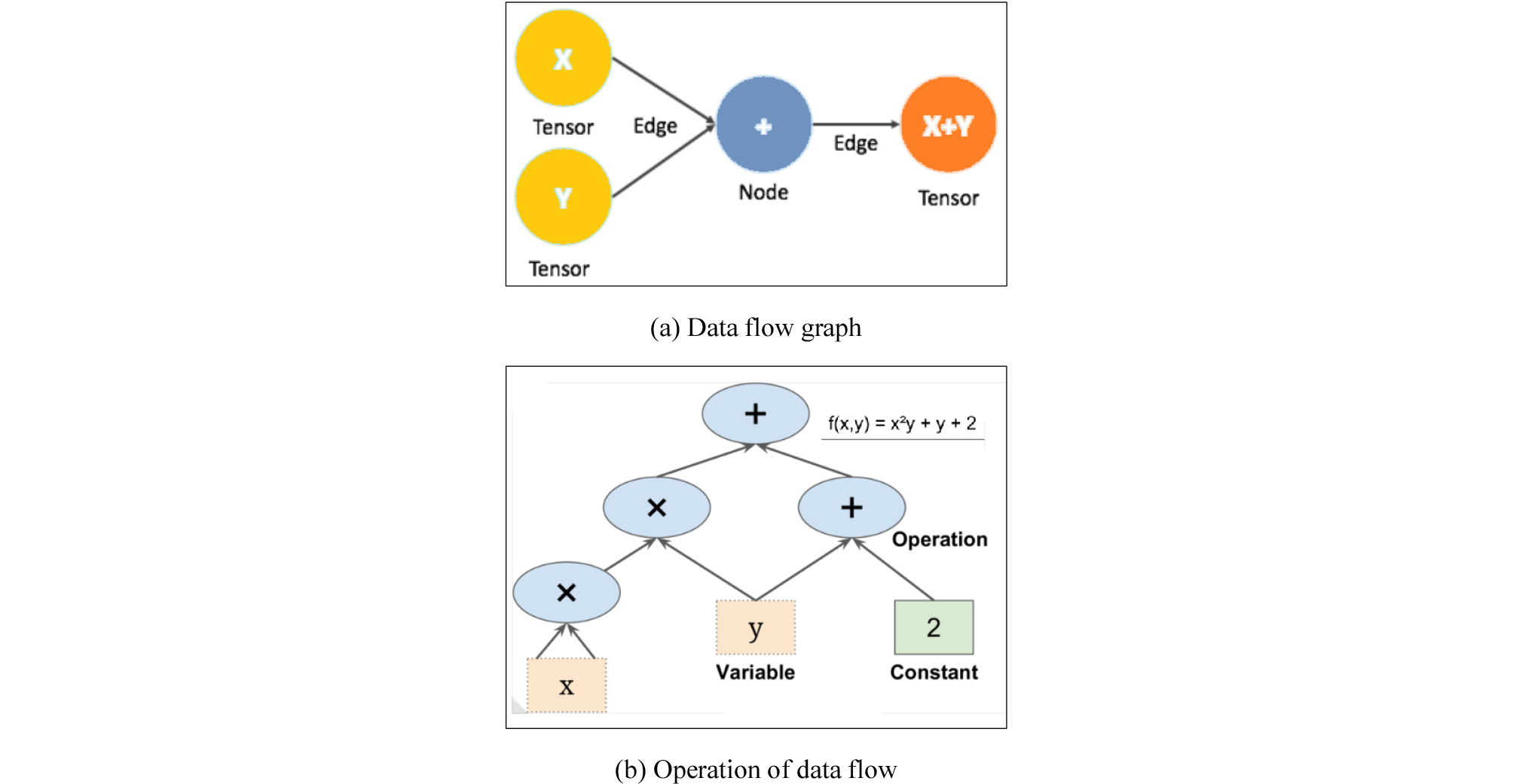
텐서 플로우는 머신러닝(machine learning)과 딥 뉴럴 네트워크(deep neural network) 연구를 목적으로 구글에서 개발한 데이터 플로우 그래프(data flow graph)를 사용하여 수치 연산을 하는 오픈소스 라이브러리이다. Fig. 1은 텐서 플로우에서 데이터 플로우 그래프를 나타낸 것이다. Fig. 1(a)와 같이 그래프의 노드(node)는 수치 연산을 나타내고 엣지(edge)는 노드 사이를 이동하는 다차원 데이터 배열(tensor)을 나타낸 것이다(Tensorflow, 2019).
텐서 플로우에서는 Fig. 1(b)와 같이 복잡한 수식을 간단하게 쪼개어서 단순화 할 수 있고, 단순화된 그래프들은 미분을 쉽게 할 수 있으므로 복잡한 문제들을 단순하게 처리할 수 있다.
ANN RMR 분류시스템
ANN에 의한 기계적인 RMR 분류를 위하여 공개 프로그램인 파이썬(Python) 기반의 텐서 플로우를 이용 하였으며 주요함수는 학습모델을 구성하는 Hypothesis(H(x))와 학습모델의 학습결과를 평가하는 Cost function(cost(W))으로 다음과 같이 간단하게 표현할 수 있다.
| $$H(x)=Wx+b$$ | (1) |
| $$\cos t(W,b)=\alpha\frac1m\sum_{i=1}^m(H(x^{(i)})-y^{(i)})^2$$ | (2) |
위 식에서 W는 가중치(weight)이고 b는 상수(bias)로서 학습이 끝난 인공지능에 해당되며 평가모델에서 W, b를 입력받아 테스트를 수행하게 된다. Cost function에서 는 학습률, 는 학습자료이고 학습과정은 아래로 볼록한 2차 함수 형태의 기저(0)에 수렴하는 것으로 학습결과를 평가한다.
Fig. 2는 ANN에 의한 RMR 분류시스템의 학습모델과 평가모델의 개념도로써 평가모델은 학습모델의 학습결과(W, b)를 토대로 RMR을 평가할 수 있도록 하였다. 비즈니스 모델로 발전시킨다면 학습모델은 원천기술이 되며 평가모델은 원천기술의 학습결과를 활용하기 때문에 이용자는 다수가 될 수 있다.
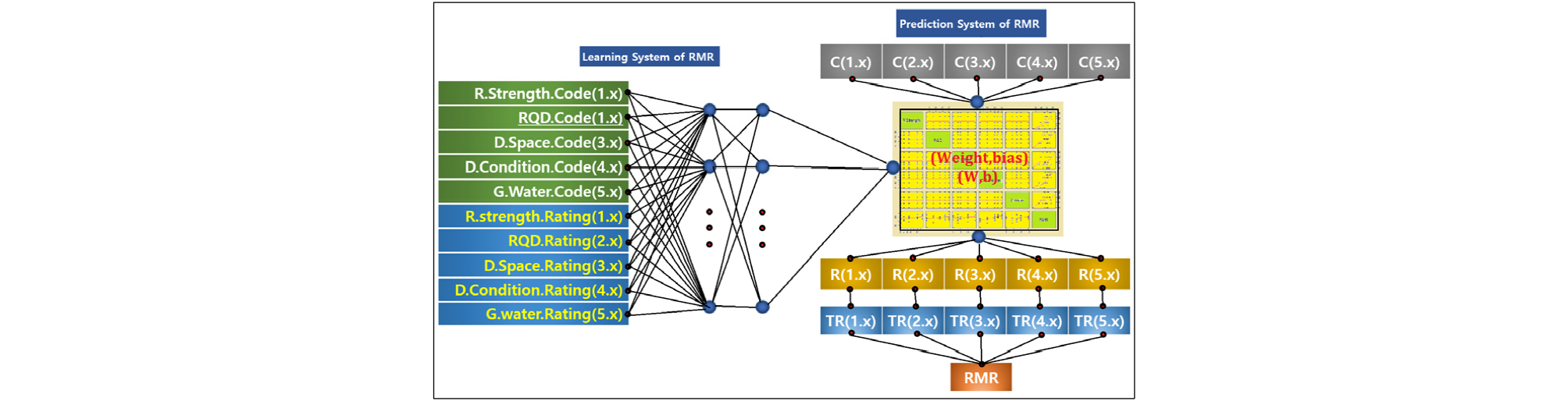
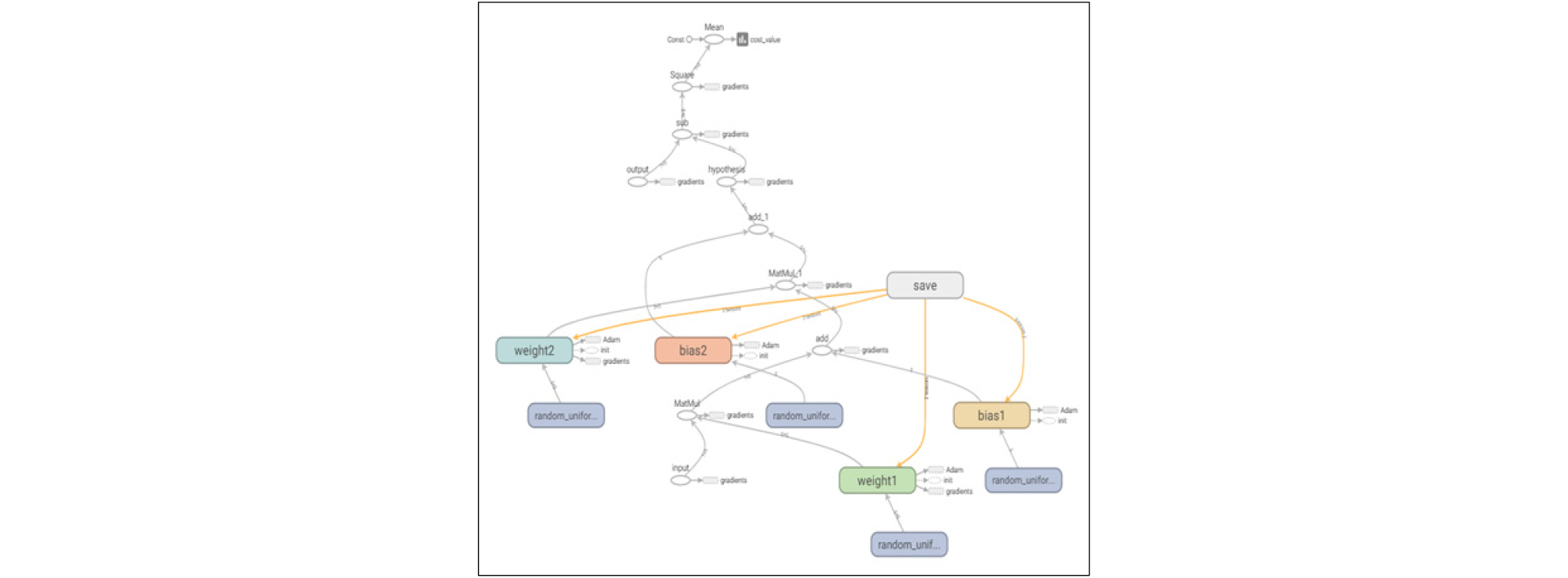
Fig. 3은 ANN에 의한 기계적인 RMR 분류시스템의 세부 개념도로서 학습자료의 변수들에 대한 의미와 평가방법은 Table 1과 같으며 학습모델에 대한 텐서 플로우는 Fig. 4와 같다.
Table 1. Meaning of learning and prediction code
ANN에 의한 RMR 분류는 현장 조사단계에서 간단한 RMR 인자별 분류코드를 결정하여 RMR의 인자별 점수를 기계적으로 산출하고 RMR 인자들의 경곗값 내에서 대푯값으로 튜닝하여 인자별 점수를 합산하는 방식으로써 최종 RMR이 산정된다.
학습코드
ANN에서 가장 중요한 것은 작성된 시스템을 학습시킬 수 있는 학습자료의 유무이다. RMR에 의한 암반분류는 정량분석으로 일축압축강도, RQD, 불연속면의 간격, 정량/정성분석으로 불연속면의 상태, 지하수 조건 등 5개의 인자에 대한 점수를 산정하고 합산하는 비교적 단순한 작업이다.
본 연구에서는 Bieniawski(1973)의 RMR 분류표를 이용하여 RMR 인자들에 임의의 학습코드를 부여하여 이에 대응하는 인자별 점수를 학습시켜 주어진 분류코드에 따라 RMR을 기계적으로 분류하는 개념을 도입하였다.
암석의 일축 압축강도에 대한 수준별 점수는 1~5 MPa 1점, 5~25 MPa은 2점으로 두 수준간의 점수 차는 1점으로 전체 RMR 점수에서 1% 정도로 특별한 경우에만 해당함으로 효율적 학습자료 작성을 위하여 25 MPa 이하 수준을 1개의 수준으로 단순화시켰다. Table 2는 RMR 요소들의 학습코드와 이에 대응하는 점수를 나타낸 것이다. Table 3은 Table 2의 RMR 요소들의 학습코드와 점수를 종합한 것으로 학습코드는 어떤 가중치나 물리적인 의미는 없다.
Table 2. Code and rating of RMR's factors
 |
Table 3. Code and rating of RMR
학습과 평가
일반적으로 ANN은 선정된 학습자료의 학습결과를 토대로 향후 발생할 수 있는 조건에 관한 결과를 예측하거나 평가할 수 있다. 따라서 ANN에서 주어진 문제에 적합한 학습자료를 설계하는 것은 ANN에 의한 시스템개발에 중요한 요소가 된다.
Table 3으로부터 학습코드와 이에 대응하는 점수에 대한 경우의 수는 각각 =3125개이다. 1개의 RMR 분류를 한다는 것은 주어진 3125개의 RMR 값 중에서 1개를 선택하는 것과 같다. 이것을 간단한 육안적인 현장조사와 ANN에 의하여 기계적으로 RMR 값을 평가하는 것이 본 연구의 목적이기도 하다.
본 연구에서는 학습자료의 배열과 학습자료 수가 학습결과와 평가에 어떤 영향을 미치는가를 분석하기 위하여 Table 3의 RMR 5개 인자(일축 압축강도, RQD, 불연속면의 간격, 불연속면의 상태, 지하수 상태)들의 학습코드(code)와 점수(rating)를 이용하여 Table 4과 같이 학습자료를 작성하였다.
Table 4. Learning and test data by RMR factors
Table 4에서 [1] RMR factor는 Bieniawski(1973)의 RMR 표를 변형하여 이용하는 것으로써 학습자료 수는 5개이고, [2] Select cases는 3125개의 경우의 수를 전개한 후 RMR을 5의 간격으로 이에 대응하는 RMR 요소들의 학습코드와 점수를 선정한 것으로써 학습자료 수는 19개이다. [3] Robust design은 RMR의 요소와 수준에 맞는 직교행렬을 이용하여 25개의 학습자료를 추출한 것으로써 비교적 단순하게 학습자료를 습득할 수 있다. [4] Total cases는 전체 3125개의 경우의 수에 대한 RMR 요소들의 학습코드와 점수를 배열하여 학습자료를 선정한 것이다. 따라서 학습자료 준비에 [2]과 [3]은 많은 시간과 노력이 필요하나, [3]번의 방법은 비교적 간단하게 학습자료를 만들 수 있다.
학습결과
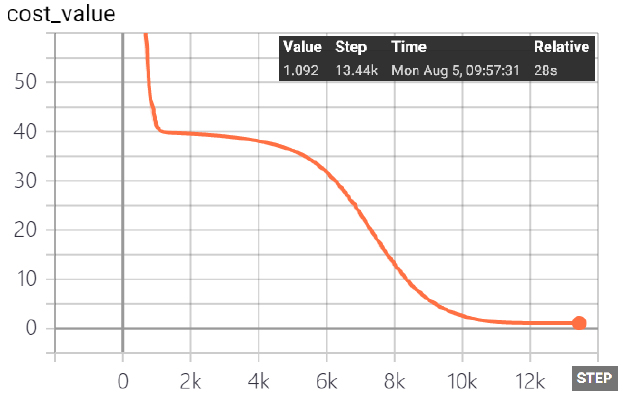
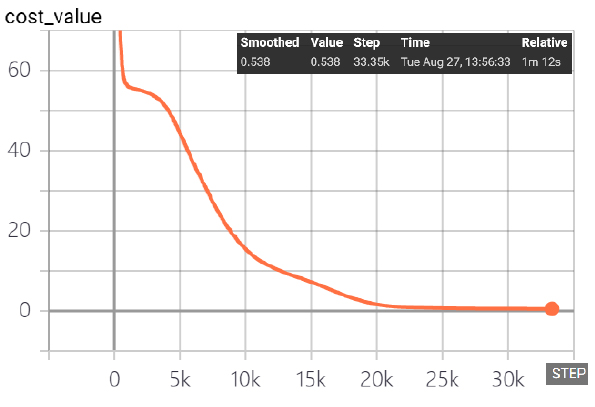
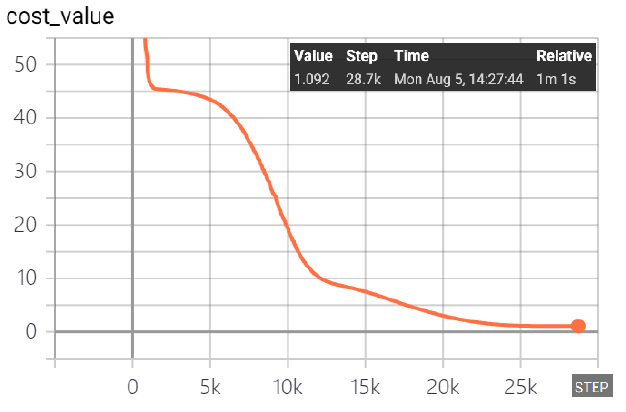
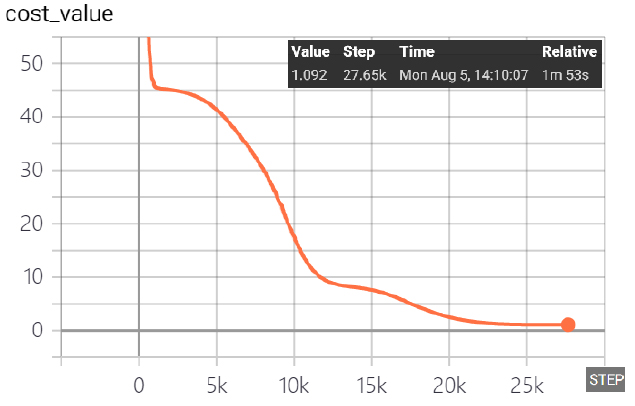
학습성과는 Cost function이 0에 도달하면 잘된 학습결과로 평가가 되지만 대부분 0에 가깝게 수렴되는 일정한 값에 도달하면 무한 루프에 빠지게 된다. 본 연구에서는 학습자료별 Cost function이 일정한 값에 수렴하면 학습을 종료하도록 하였다. 그 결과 Table 5와 같이 Cost function이 모두 급격한 기울기로 비교적 빨리 일정한 값으로 수렴되었으며 학습패턴도 유사하였다.
Table 5. Cost function and learning results by learning data
Cost function은 [1], [3], [4]번 학습자료의 경우 1.092의 일정한 값으로 수렴되었으며 [2]번 학습자료의 경우는 0.538로써 가장 작은 값으로 수렴되었다.
RMR 평가
[1] RMR 인자(RMR factor)
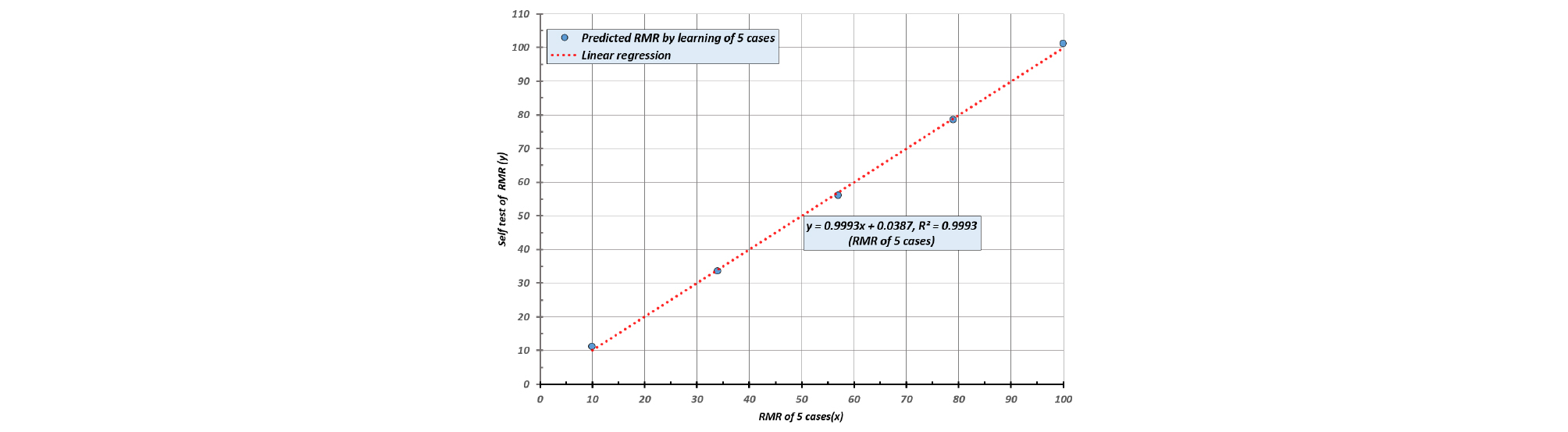
Table 3의 RMR 점수표를 적용한 것으로써 학습자료 수는 5개이다. 학습결과 Cost function은 1.092에 수렴되었으며, 자가 테스트(학습자료를 테스트 자료로 사용) 결과 Fig. 5와 같이 선형회귀분석 상관관계(r2)가 0.9993으로 매우 높았으나 주어진 RMR 값과 완전히 일치하지 않았다.
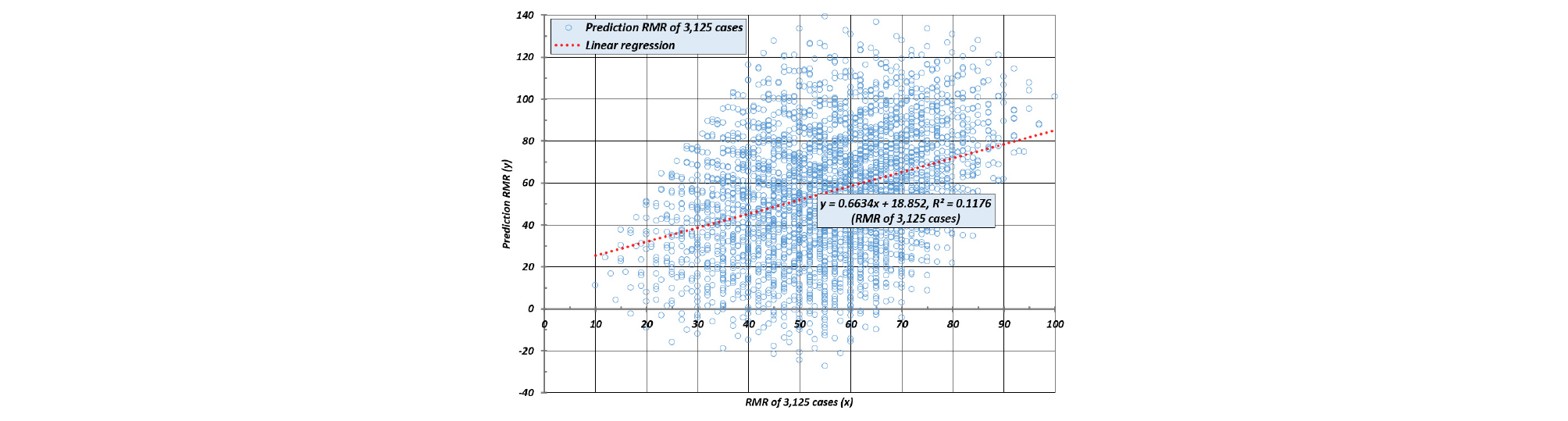
Fig. 6은 3125개의 RMR 점수에 대하여 평가한 것으로 선형회귀분석 상관관계(r2)는 0.1176으로 자가 테스트 결과와 비교하여 아주 낮았다. 따라서 적은 수의 학습자료는 자가 테스트에서는 좋은 결과를 보였지만 전체자료에 대한 테스트에서는 전혀 맞지 않은 평가결과를 보여 주었다.
[2] 선정자료(Select data)
Table 6은 Table 3의 3125개의 RMR을 오름차순으로 정렬하고 RMR 점수를 10~100까지 +5씩 증가시켜 RMR 점수에 대응하는 RMR 인자의 학습코드와 점수에 대한 19개의 학습자료를 추출한 것이다. 학습결과 Cost function은 0.538에 수렴되었으며 4가지 학습자료 중 가장 우수한 학습결과를 보여 주었다.
Table 6. Learning data by select data of RMR total cases
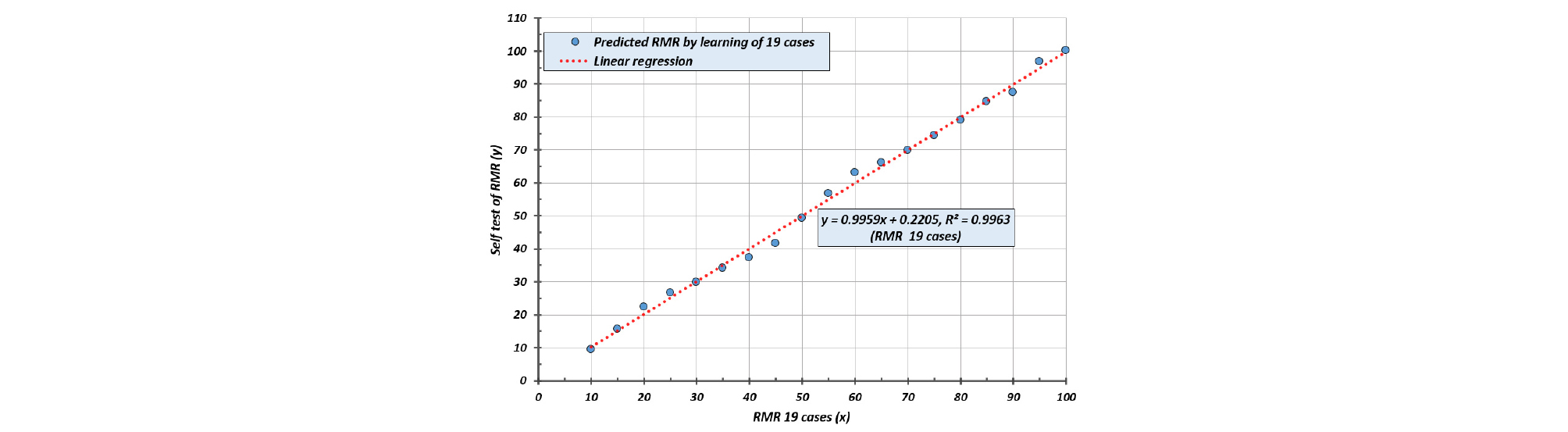
Fig. 7은 19개의 학습자료에 대한 자가 테스트 결과 선형회귀분석 상관관계(r2)가 0.9963으로 비교적 높았으나 학습자료와 정확하게 일치하지 않았다.
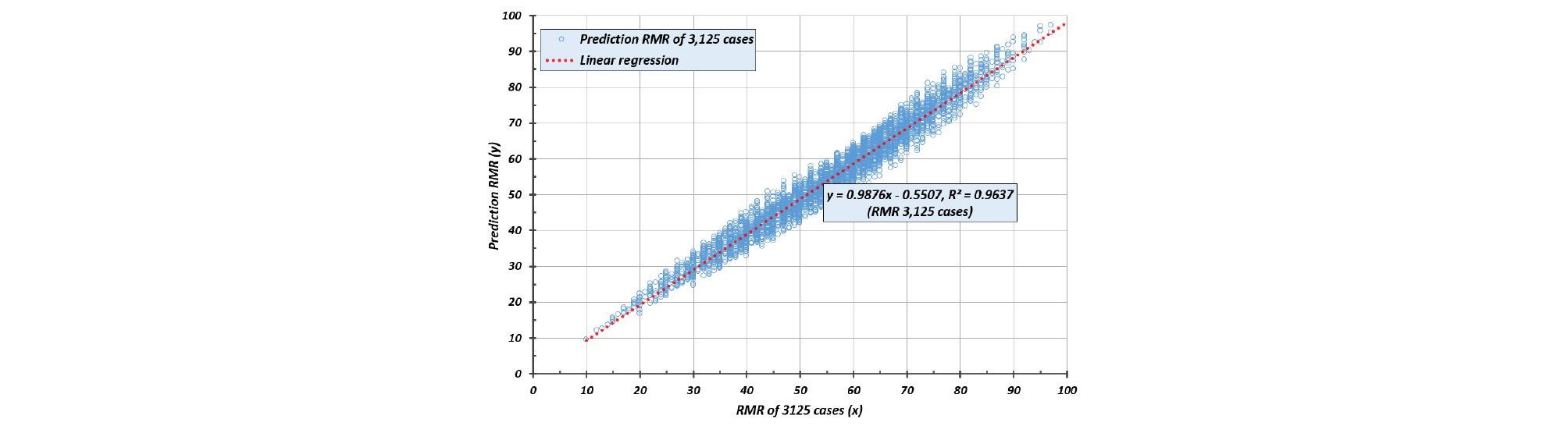
Fig. 8은 본 학습결과의 평가를 위하여 3125개의 RMR 점수에 대하여 평가결과로서 선형회귀분석 상관관계(r2)는 0.9637로 자가 테스트 결과보다 다소 낮았다.
[3] 강건설계(Robust design)
강건설계는 적은 수의 실험으로 많은 인자를 연구하기 위하여 직교배열(orthogonal arrays)이라는 수학적 방법을 사용한다. 직교배열표는 형태로 표시하는데, n은 필요한 실험의 수이고 a는 실험에 사용되는 인자(factor)의 수, 그리고 b는 인자가 변화하는 수준(level)의 수로써 n회 실험으로 회 만큼의 실험효과를 얻을 수 있다(Madhav, 1989). 강건설계는 광산관련 분야의 다양한 분야에 적용 가능한 것으로써(Jang, 2018), 직교 배열표는 표본으로 만들어진 것을 사용해도 되고 해석에 알맞은 것이 없을 때는 실험 목적에 맞게 만들어도 된다.
본 연구에서는 Table 3의 5개 RMR 인자에 대하여 각각 5개 수준으로 발생할 수 있는 최소의 수준을 강건설계에 의하여 의 직교배열로 Table 7과 같은 학습자료를 추출하였다.
Table 7. Learning data by robust design of RMR factors
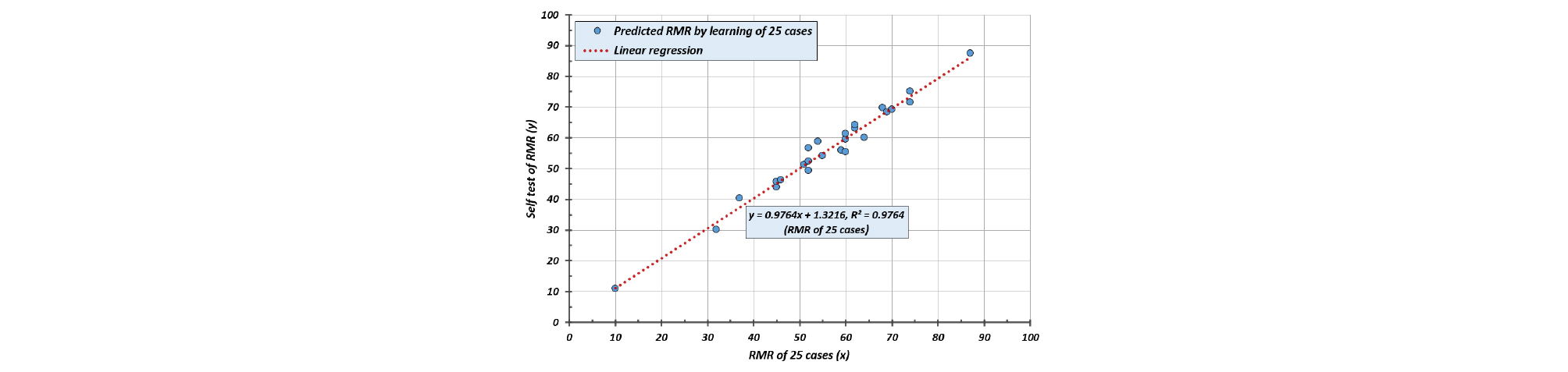
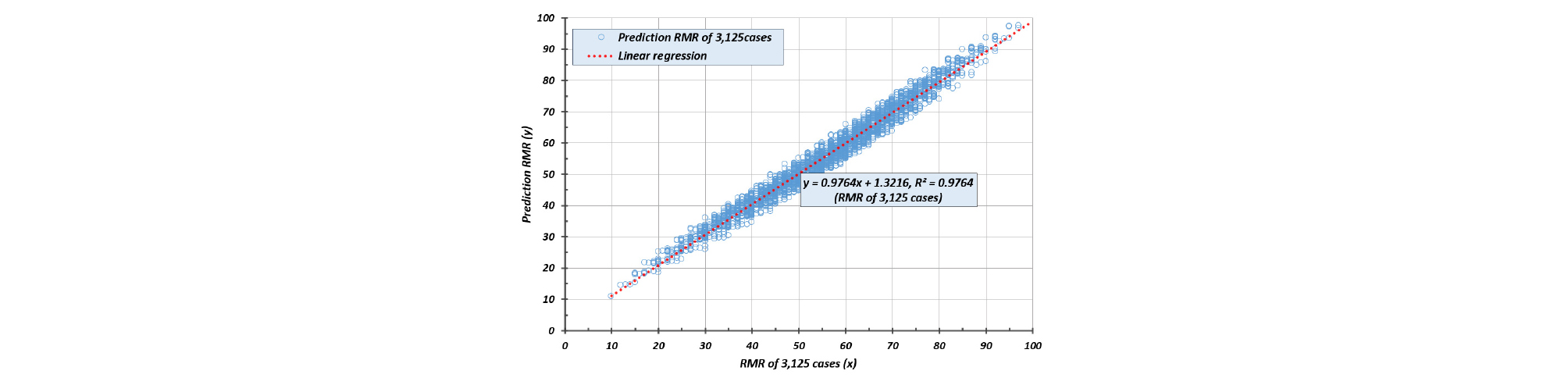
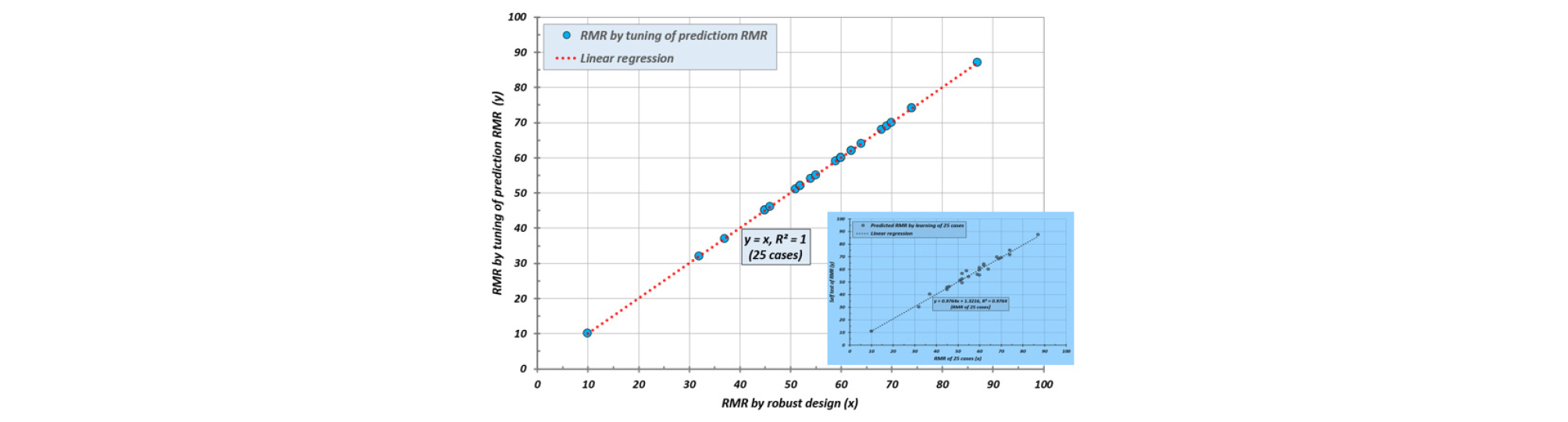
Table 6과 Table 7을 비교하였을 때 Table 6은 RMR 점수가 중복되지 않았으나, Table 7은 RMR 인자들의 학습코드와 점수는 다르지만 일부 구간에서 RMR 점수가 중복되는 특성이 있다. Fig. 9는 25개 학습자료에 의한 자가 테스트 결과를 선형 회귀분석 상관관계(r2)는 0.9764로서 [2]번 방법의 학습결과 보다 다소 낮았다.
Fig. 10은 3125개의 RMR 평가결과를 보여 준 것으로 선형 회귀분석 상관관계(r2)는 0.9764로서 자가 테스트 결과와 같았고 [2]번 방법의 상관관계 r2=0.9637 보다 더 높았다.
[4] 전체 경우의 수(Total cases)
본 연구에서는 Table 4의 [1]~[3]의 3가지 방법의 학습효과를 평가하기 위하여 [4]번과 같은 전체 경우의 수인 3125개의 RMR 인자들의 학습코드와 점수를 학습자료로 사용하였다. 학습결과 Cost function은 1.092에 수렴되었으며 자가 테스트 결과 상관관계(r2)는 0.9764로서 강건설계에 의한 학습결과로 예측한 3125개의 RMR 값들을 도시한 Fig. 8과 완벽하게 일치하였다.
학습결과의 고찰
ANN에 의한 기계적인 RMR 분류를 위하여 4가지 학습자료로 학습시킨 학습결과와 예측값들을 Table 8에 정리하였다. 표에서 예측값(prediction)은 전체 경우의 수인 3125개의 RMR 값을 의미한다. 표에서 자료 수가 아주 작은 경우의 자가 테스트 결과는 아주 양호하였으나 전체 경우의 수에 대한 예측결과는 아주 낮은 상관관계를 보여 주었다.
Table 8. Learning and prediction by code and rating of RMR 5 factors
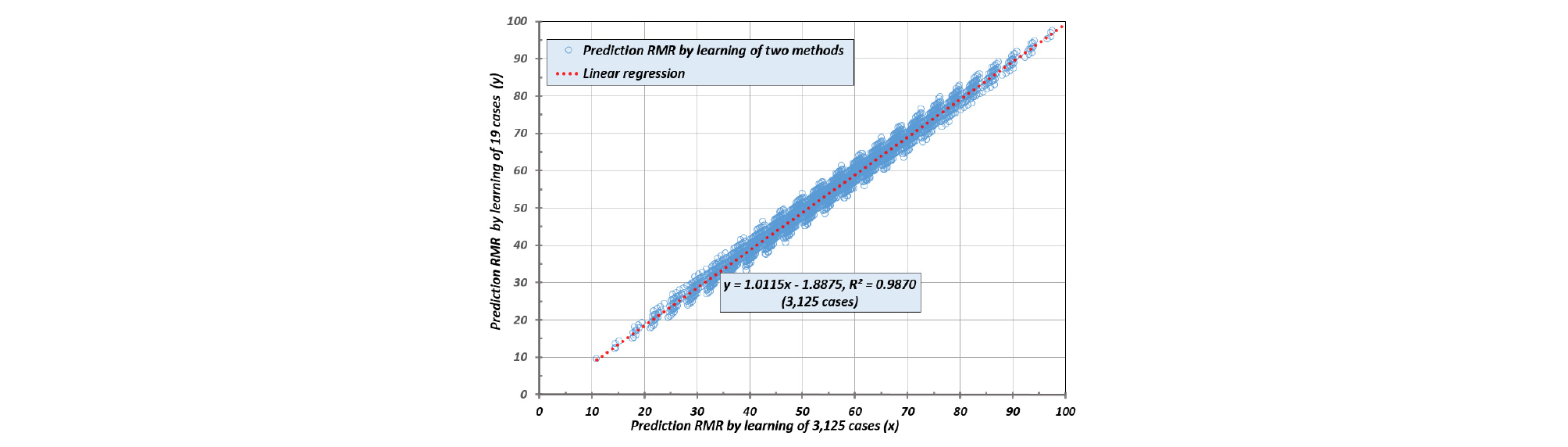
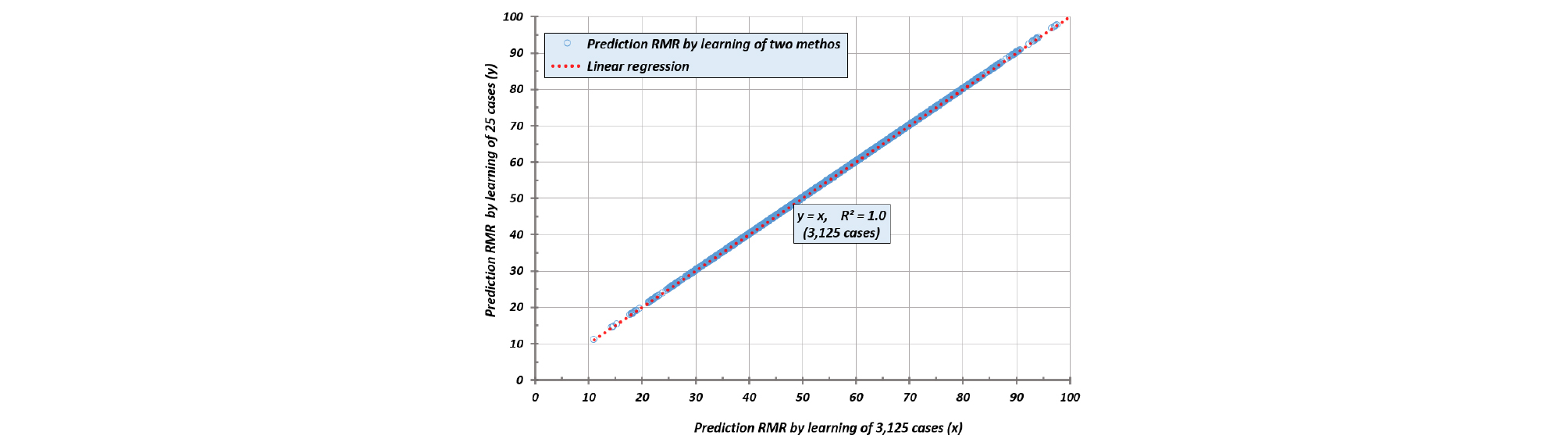
[2]번 학습자료의 경우 학습효과(cost function)는 0.538로 가장 양호하였으나 3125개의 예측값에 대한 선형회귀분석 상관관계(r2)는 0.9637로 강건설계에 의한 0.9764보다 다소 낮았으며, Fig. 11과 같이 전체 경우의 수에 의한 학습결과와도 서로 일치하지 않았다. [3]번 강건설계에 의한 학습효과는 자가 테스트에서 다른 방법보다는 다소 낮았지만 3125개의 예측값에 대한 선형회귀분석 상관관계(r2)는 0.9764로서 제일 높았다. 이 방법은 전체 3125개의 학습자료로 학습시켜 자가테스트한 [4]번의 결과와 완벽하게 일치하였다. Fig. 12는 [3]번의 학습결과로 [4]번을 예측한 것을 나타낸 것으로써 서로 완벽하게 일치하고 하였다.
따라서 ANN에서 학습자료를 정형적인 표로 만들 수 있다면 강건설계에 의하여 간편하게 학습자료를 전체의 1% 이하로 축소 시켜서 동일한 학습효과를 얻을 수 있다. 이는 강건설계에 의한 학습자료가 전체자료를 학습자료로 사용하는 것과 같은 결과를 나타내는 것으로써 시간과 비용이 들어가는 분석에서 강건설계에 의한 학습자료 추출은 의미가 있을 것으로 사료된다.
학습결과의 튜닝
학습자료 분석
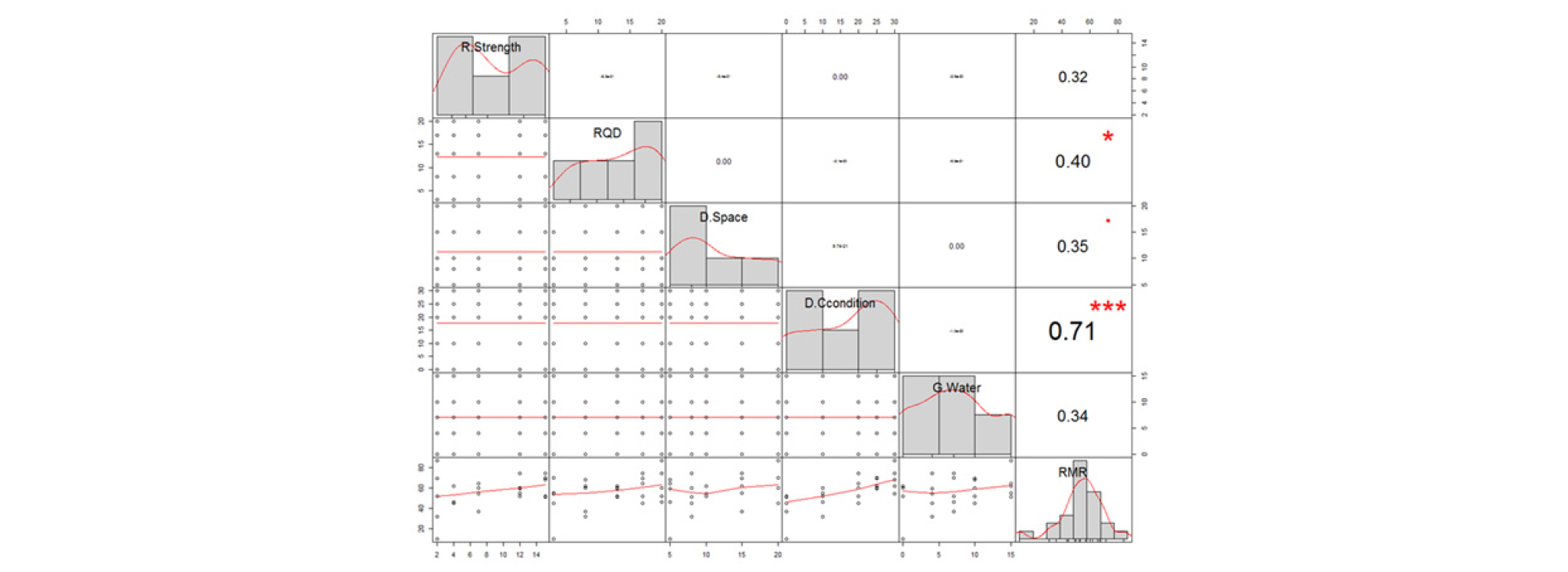
ANN RMR 분류시스템의 학습자료는 4장에서 분석한 바와 같이 강건설계에 의한 25개의 학습자료를 선정하였다. Fig. 13은 각 RMR 인자별 25개 수준에 대하여 다중회귀분석을 실시한 결과로 RMR 인자들 간의 상관성은 거의 없는 자료구조로 분석되었다. 그러나 RMR과 RMR 인자 간의 상관관계는 불연속면의 조건이 0.71, RQD가 0.40이었고 암석의 일축압축강도, 불연속면의 간격, 지하수 조건은 거의 비슷한 상관관계를 갖는 학습자료 구조로 분석되었다.
본 학습자료에 의한 학습결과로 1차 RMR 평가를 하고 RMR 인자별 수준별 최적값으로 튜닝을 실시하였다.
튜닝(Tuning)
ANN에 의한 기계적인 RMR 분류의 예측이 100% 완벽하게 이루어져야 한다. 즉 완벽한 시스템이 되려면 학습결과에 의한 예측이 3125개의 RMR 값들을 100% 완벽하게 예측을 할 수 있어야 한다.
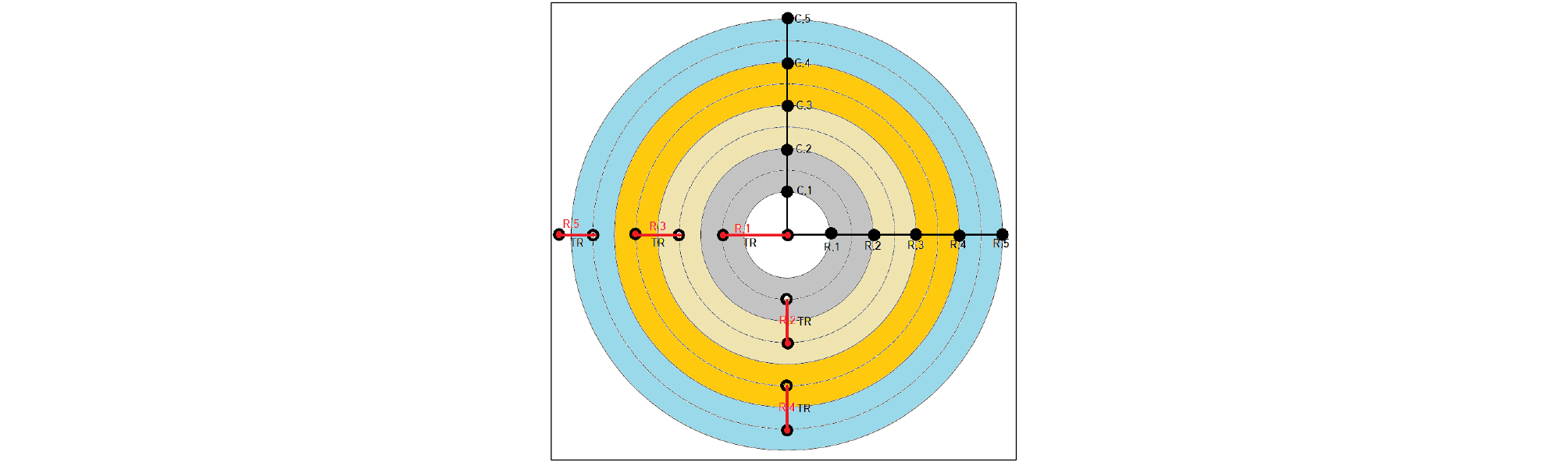
그러나 다양한 학습자료를 만들어 학습시킨 결과로 예측한 결과 100% 일치되지 않았다. 이러면 기계적인 RMR 분류를 시스템적으로 할 수 없다. 따라서 이러한 문제를 해결하기 위하여 ANN에 의한 1차 예측값들에 대하여 튜닝(tuning range,TR)을 Fig. 14와 같은 방법으로 실시하였다.
Fig. 14에서 그림은 좌표계가 아닌 그룹화를 위한 개념도로써 Rx(x=1~5)는 RMR 요소들의 수준별 점수이고, Cx(x=1~5)은 RMR 요소들의 수준별 학습코드로서 모두 상대적 크기와 무관하며 물리적인 의미는 없다. R3에 대한 튜닝 값은 TR(R3)로써 다음식과 같이 이루어진다.
| $$\mathrm C3-\mathrm>=((\mathrm R3-(\mathrm R3-\mathrm R2)/2))\sim(\mathrm R3+(\mathrm R4-\mathrm R3)/2))=\mathrm{TR}(\mathrm R3)$$ | (3) |
식에서 C3는 특정 RMR 인자의 3번째 수준의 학습코드로써 시스템에 의한 예측결과가 ±R3라면 R3로 튜닝할 필요가 있다. 따라서 R3의 범위는 다음식과 같다.
| $$\mathrm((R3-\mathrm(\mathrm R3-\mathrm R2)/2))\sim < R3≦\mathrm(\mathrm R3+\mathrm (\mathrm R4-\mathrm R3)\mathrm/\mathrm2))$$ | (4) |
(4)식에서 튜닝 범위로 수준별 경곗값은 낮은 단계의 수준에 포함 시켰다. 실제로 학습이 잘 이루어지면 (4)식의 범위내에 예측값들이 분포함으로 경곗값에 의한 튜닝 문제는 발생하지 않는다.
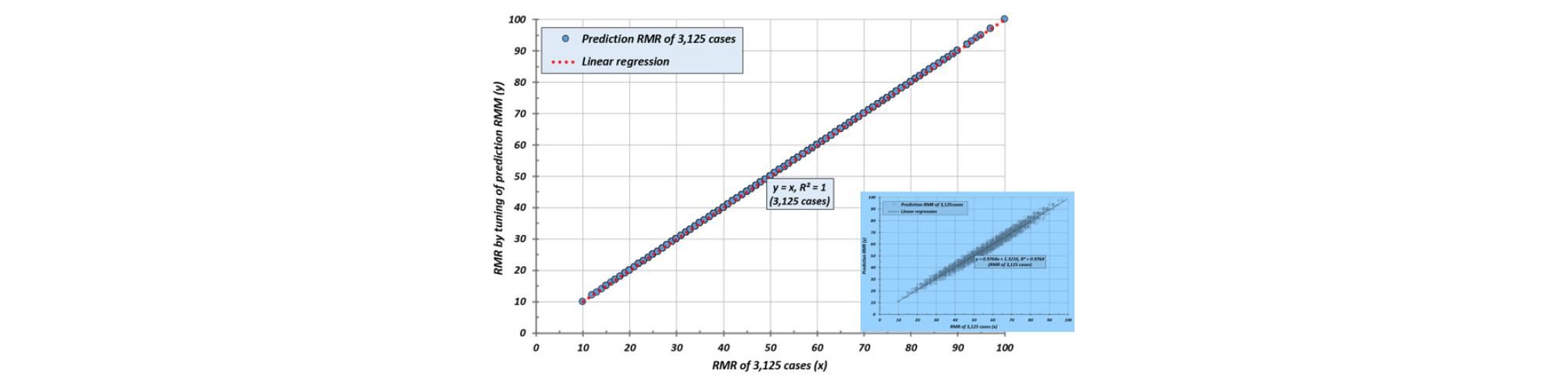
Fig. 15는 학습자료에 의한 예측값들의 튜닝을 실시한 것으로써 학습자료와 예측값이 완전히 일치되었으며, Fig. 16은 [3]번 강건설계의 학습결과로 3125개 RMR자료에 대한 예측값을 튜닝한 것으로써 실제값과 완전하게 일치하였다. 그림에서 작은 도표는 튜닝전의 예측값들이다.
따라서 ANN에 의한 RMR의 기계적 분류는 강건설계에 의한 학습자료로 학습을 시키고 학습결과로 예측한 RMR 인자들의 수준별 점수를 튜닝함으로서 100% 예측 가능한 시스템 구현이 가능하였다.
결 론
강건설계에 의하여 학습자료를 추출하고 학습결과에 따라 예측한 RMR 값을 튜닝함으로써 완벽한 ANN RMR 분류시스템을 구현하였으며 그 결과는 다음과 같다.
(1) ANN에 의한 RMR 분류시스템을 학습모델과 평가모델로 작성하였으며 평가모델은 학습모델의 학습결과를 토대로 RMR을 평가할 수 있도록 하였다. 비즈니스 모델로 발전시킨다면 학습모델은 원천기술이 되며 평가모델은 원천기술의 학습결과를 활용하기 때문에 이용자는 다수가 될 수 있다.
(2) 학습자료 수가 작은 경우 학습에 의한 자가 테스트는 양호하였으나 실전평가에서는 아주 낮은 예측결과를 보여 주었다. 강건설계에 의한 학습자료는 자가 테스트에서 RMR을 일정한 간격으로 작성한 학습자료보다 상관관계가 낮았지만 실전 테스트에서의 예측결과는 제일 양호하였다.
(3) 강건설계에 의하여 전체 경우의 수를 1% 이하로 축소한 학습자료로 전체자료와 동일한 학습효과를 얻었다는 것은 학습자료 습득에 드는 노력과 비용을 크게 절감할 수 있을 것으로 사료된다.
(4) 강건설계에 의한 25개의 학습자료에 대한 다중회귀분석결과 RMR 인자들 간의 상관성은 거의 없는 학습자료구조로 분석되었다.
(5) ANN을 이용한 기계적 RMR 분류에 대한 예측치의 선형 회귀분석결과 상관관계가 높았으나 완전하게 일치되지는 않았다. 예측값들에 대한 수준별 튜닝을 실시함으로써 3125개의 테스트에서 실제값과 완전하게 일치하는 기계적 RMR 분류를 구현할 수 있었다.
(6) 본 연구를 통하여 ANN을 효율적이고 경제적으로 학습시킬 수 있는 학습자료 추출방법으로 학습자료가 정형화되어 있다면 강건설계를 매우 유용하게 적용할 수 있을 것으로 판단되었다.