서 론
급속히 확대되고 있는 태양광 발전이 향후 성장 안정단계에 접어들기 위해서는 전력 계통연계가 보강되어야 한다. 하지만 계통연계를 위해서는 기반 시설에 대한 투자가 수반되어야 한다. 일반적으로 이러한 계통연계를 위한 비용을 계통비용(grid cost)으로 규정하고 있으나, 계통비용에 대한 명확하게 합의된 정의는 없으며 연구마다 상이한 개념을 적용하고 있다(KEEI, 2019).
본 연구에서는 계통비용을 ‘재생에너지의 경제성을 확보하는데 필요한 송배전의 평균투자비’로 정의하였으며, 이는 다른 의미로 ‘재생에너지의 경제성을 확보할 수 있는 수준으로의 계통보강비용’을 의미한다. KEEI(2019)에 따르면 계통비용은 크게 ‘밸런싱비용(balancing cost), 그리드비용(grid cost), 그리고 프로파일비용(profile cost) 등 세 가지 항목’으로 구성되는데, 본 논문에서 정의한 계통비용은 이 중 ‘그리드 비용’에 부합한다. 그렇기에 이하 본 논문에서 명시하고 있는 계통비용은 KEEI(2019)의 그리드비용을 의미한다. 재생에너지 발전사의 입장에서는 계통연계가 되어 있지 않거나 계통용량이 부족하여 전력판매수입이 현실화되지 않으면 경제성이 확보되지 않는다. 이때 계통비용은 계통연계의 부족으로 실현되지 못한 태양광 발전 투자에 대한 전력판매수입을 ‘적정’ 수준까지 증가시키는데 필요한 계통투자비용을 이용하여 평균계통비용을 구하는 방식을 취한다.
기존의 계통비용 관련 선행연구도 본 논문의 접근 방식과 유사하게 송배전 설비투자비와 계통연계된 재생에너지의 전력판매량을 기준으로 추산하였다(Mills et al., 2012). 하지만, 본 연구는 이에 더하여 위험중립(risk-neutral)의 태양광 발전 사업자가 경제성을 확보할 수 있는 최소한 수준의 전력판매량을 기준으로 계통비용을 추산하였다.
본 논문에서는 경제성 평가를 위한 방법론으로는 SMP와 REC 가격의 불확실성을 반영할 수 있는 실물옵션(real options) 모형을 택하였다(Lee et al., 2012; Park, 2012, Nam and Kang, 2017). 최근 일부 발전소의 경제성 평가가 한국개발연구원(KDI, Korea Development Institute)의 공공기관 사업 예비타당성조사로 시행된 바가 있는데, 이들 연구는 주요 경제변수의 불확실성을 배제한 순현재가치(NPV, Net Present Value) 기법에 기초하고 있다. 본 연구에서는 NPV와는 달리 발전 사업자가 노출되어 있는 불확실성 요인을 반영할 수 있는 경제성 평가기법을 제시하는데 기여하고자 한다.
일반적으로 재생에너지 투자에 있어 전력가격, 연료비, 투자비용 등 다양한 불확실성 요인이 있겠지만, 본 연구에서는 태양광 발전사업자가 수취하는 SMP와 REC의 통합가격(이하 ‘SMP+REC 가격’)을 불확실한 확률과정으로 규정하였다.
대부분의 실물옵션 연구에서는 분석의 편의상 기하학적 브라운 (geometric Brownian motion, gBm) 확률과정을 가정하나, 본 연구에서는 SMP+REC의 장기평균회귀성향까지도 반영할 수 있는 평균회귀성향의 Ornstein-Uhlenbeck (이하 ‘OU’) 확률과정도 따름을 가정하여 분석하였다.
gBm 확률과정 및 OU 확률과정을 연료전환 관점에서 분석한 대표적인 연구로는 Detert and Kotani(2013)가 있는데, 해당 연구는 석탄과 재생에너지의 관계 속에서 석탄가격의 시계열 추세가 gBm과 OU의 확률과정을 분석한 바 있다. 국내에서도 OU 과정을 다루는 연구가 차츰 이루어지고 있는데, 주로 발전사업에 대해 실물옵션 방법론을 적용하여 분석하고 있으며, 주요 연구로는 Park and Jang(2007) 및 Park and Nam(2018)이 있다. 진화 프로그래밍(evolutionary programming) 기법의 알고리즘을 이용한 El-Sharkh et al.(2010)은 연료전지 발전의 경제성을 보장하는 수준의 최소 운영비용을 계산하는데 실물옵션을 적용하였다. Tsui (2005)는 이항옵션 모형과 고전적인 블랙-숄즈 모형으로 전기차 투자옵션을 분석한 바 있으며, 이와 유사하게 Li et al.(2016)는 전기차를 실물옵션 관점에서 분석하였다.
이하 논문의 구성은 다음과 같다. 다음 장에서는 실물옵션 방법론을 활용하여 OU 확률과정 및 gBm 확률과정에서 태양광 발전 투자모형을 개발하였으며, 태양광 발전소의 사례를 바탕으로 전력가격 불확실성하에서의 계통비용을 추정하였다. 마지막으로 계통비용 추정 결과와 연계한 정책적 시사점을 제시하였다.
실물옵션 모형
OU 확률과정
우선 본 논문에서 제시한 실물옵션 모형은 기본적으로 Park(2018)에서 소개하고 있는 ‘평균회귀 모형’이다. 여기서 전력가격은 평균회귀 성향의 OU 확률과정으로서 아래와 같이 정의된다1).
1) 이하 파라미터의 하첨자 는 OU 확률과정에서의 파라미터를 의미하며, 하첨자 은 gBm 확률과정에서의 파라미터를 의미한다.
| $$dp(t)=\eta(\overline p-p(t))dt+\sigma_{OU}dw(t)$$ | (1) |
위 식에서 는 전력의 장기평균 가격이며, 는 시계열이 평균 추세에서 벗어날 경우 장기적으로 평균수준으로 다시 회귀하는 평균회귀율(mean-reverting rate)을 나타내며, 평균 회귀속도(speed of mean reverting)로 칭하기도 한다.
OU 확률과정에서 시간 및 일 때 평균과 분산은 다음과 같다.
| $$E(p(t))= {\bar{p}} + \left ( p- {\bar{p}} \right ) e ^{- \eta t}$$ | (2) |
| $$Var(p(t)-\overline p)=\frac{\sigma_{OU}^2}{2\eta}\left(1-e^{-2\eta t}\right)$$ | (3) |
한편, OU 확률과정의 모수인 는 아래 식 (4)의 로그우도함수를 활용하여 추정할 수 있다(Park, 2018).
사업의 기대연한이 로 주어져 있으며 할인율이 일 때, gBm을 따르는 하에서 발전소의 가치함수 는 다음과 같다.
| $$V(p)=q \int _{0} ^{T} {} (pe ^{\alpha t} )e ^{- \rho t} dt$$ | (5) |
여기서 전력판매량 는 계통연계 정도에 의해 결정되는데, 만일 계통연계가 개선된다면 판매량도 증가하게 된다. 전력가격이 OU 확률과정을 따를 때, 가 되므로 위의 가치함수 는 다음과 같이 전개될 수 있다.
| $$V _{OU} (p)=q \left [ \frac {p- {\bar{p}}} {r+ \eta } \left ( 1-e ^{-(r+ \eta )T} \right ) + \frac {{\bar{p}}} {r} \left ( 1-e ^{-rT} \right ) \right ]$$ | (6) |
그 다음 태양광 발전의 투자옵션 을 구하도록 한다. OU 확률과정에서의 투자옵션 는 아래와 같은 HJB(Hamilton-Jacobi-Bellman) 방정식을 갖는다.
| $$\rho F _{OU} \left ( p \right ) = \eta ( {\bar{p}} -p)F _{OU,p} (p)+ \frac {1} {2} \sigma _{OU}^{2} F _{OU,pp} (p)$$ | (7) |
위 식 (7)은 의 2계 미분방정식의 형태를 취하고 있다. 그렇기에 로 가정 한 후 미정계수법으로 미지수를 도출해야 한다. 여기에서 , 및 는 미정계수법으로 도출해야 하는 상수항과 함수이다. 를 상태변수 로 1계 및 2계 미분한 및 를 식 (7)의 동차방정식에 대입하면 다음의 식 (8)을 얻을 수 있다.
우선 위 식의 우변을 와 로 정리한 후 동류항을 제거하여 정리하면 를 구할 수 있다. 변수변환을 위하여 로 정의한 후, 커머(Kummer) 방정식을 이용하여 아래 식을 정의할 수 있다(Park, 2018).
| $$\Phi(x;\theta,b)=\sum_{k=0}^{+\infty}\frac{(\theta)_k}{(b)_k}\frac{x^k}{k!}$$ | (9) |
여기서 이며, 는 인 감마함수(단, . 일 경우에는 가 됨)를 나타낸다. 위 관계를 통해 투자옵션 를 구하면 다음과 같다(Park, 2018).
| $$F_{OU}(p)=A_{OU}p^\theta\Phi\left(\frac{2\eta p}{\sigma_{OU}};\theta,b\right)$$ | (10) |
전력가격 불확실성하에서의 최적투자분기점 는 아래의 등가조건(value matching condition)과 한계조건(smooth-pasting condition)을 바탕으로 도출할 수 있다.
등가조건 및 한계조건은 각각 아래의 식 (11) 및 식 (12)과 같다. 아래 식에서 는 태양광 발전사업 초기의 비가역적 투자비용으로서, 매몰비용을 의미한다.
| $$F_{OU}(p)=q\left[\frac{p-\overline p}{r+\eta}\left(1-e^{-(r+\eta)T}\right)+\frac{\overline p}\rho\left(1-e^{-rT}\right)\right]-I$$ | (11) |
| $$F_{OU,p}(p)=\frac q{\rho+\eta}\left(1-e^{-(r+\eta)T}\right)$$ | (12) |
위 식에서 는 를 나타내며, 는 태양광 발전사업 초기의 비가역적 투자비용으로서 매몰비용을 의미한다. 위 식 (11)과 식 (12)를 만족하는 와 옵션상수 는 비선형 수치해석 방법으로 구할 수 있다.
gBm 확률과정
다음으로 전력가격이 gBm 확률과정을 따를 경우의 최적투자분기점을 분석하겠다.
우선 일반적인 gBm 확률과정은 아래의 식 (13)과 같이 정의된다.
| $$dp(t)=\alpha_{gBm}p(t)dt+\sigma_{gBm}dw(t)$$ | (13) |
위 식에서 는 gBm 확률과정에서의 의 증가율(drift rate), 는 gBm 확률과정에서의 변동률(volatility rate)을 뜻하며, 는 위너프로세스(Wiener’s process)의 증분을 의미한다.
gBm 확률과정의 모수인 증가율과 변동률은 아래 방법에 의해 추정한다. 우선 가 로그정규분포(log normal distribution)를 따른다.
| $$x(t)=\frac{lnX(t)}{lnX_0}\sim N\left(\left(\alpha_{gBm}-\frac12\sigma_{gBm}^2\right)(t-t_0),\;\sigma_{gBm}^2(t-t_0)\right)$$ | (14) |
평균()과 표준편차()는 아래 공식을 이용하여 계산한다.
| $$\overline x=\left(\alpha_{gBm}-\frac12\sigma_{gBm}^2\right)\Delta t=\frac{\sum_{}^{}x_t}n$$ | (15) |
| $$s _{gBm} = \sigma _{gBm} \sqrt {\Delta t} = \sqrt {\sum _{} ^{} \left ( x _{t} - {\bar{x}} \right ) ^{2} /(n-1)}$$ | (16) |
위 식 (15)와 식 (16)를 와 로 정리하면 gBm 확률과정의 변동률()과 증가율()을 다음 식을 바탕으로 추정할 수 있다.
| $$\widehat{\sigma_{gBm}}=\frac s{\sqrt{\Delta t}},\widehat{\;\alpha_{gBm}}=\frac{\overline x}{\Delta t}+\frac12\widehat{\sigma_{gBm}}^2$$ | (17) |
만약 전력가격이 gBm 확률과정을 따르고, 태양광 발전소의 기대연한이 이면 gBm 확률과정에서의 가치함수 는 아래와 같이 정의할 수 있다.
| $$V_{gBm}(p)=q\int_0^T(pe^{\alpha t})e^{-rt}dt=q\left[\frac p{r-\alpha}\left(1-e^{-(r-\alpha)T}\right)\right]$$ | (18) |
위 식에서 는 전력판매량을 의미하는데, 만일 해당 발전소의 계통연계가 부족하게되면 해당발전소의 전력 판매율도 낮아지게 된다. 그리고 는 할인율을 나타낸다.
만약 Dixit and Pindyck(1994)에서 잘 알려진 바와 같이 발전사의 투자옵션을 로 표기하면, 이는 의 동차방정식을 통해 구할 수 있다. 일반적으로 의 일반해는 의 형태로 주어지며, 여기에서 는 동차방정식에서 도출하는 특성방정식(characteristic equation)의 근으로 식 (19)를 의미한다(Park, 2015).
| $$\beta=\frac12-\frac{\alpha_{gBm}}{\sigma_{gBm}^2}+\sqrt{(\frac12-\frac{\alpha_{gBm}}{\sigma_{gBm}^2})+\frac{2r}{\sigma_{gBm}^2}}>1$$ | (19) |
| $$\beta=\frac12-\frac{\alpha_{gBm}}{\sigma_{gBm}^2}+\sqrt{(\frac12-\frac{\alpha_{gBm}}{\sigma_{gBm}^2})+\frac{2r}{\sigma_{gBm}^2}}>1$$ | (19) |
한편, gBm 확률과정에서의 최적투자분기점 는 투자옵션를 이용하여 닫힌 해(closed form solution)를 구할 수 있다. 이는 기본적인 만기유한의 실물옵션 모형으로서 Park(2018)에서 소개하고 있는 ‘M1-2. 사업연한 존재’ 모형의 풀이법을 따른다. 여기서는 자세한 도출 과정은 생략하고 그 결과만 제시하면 다음과 같다.
| $$p _{gBm}^{*} = \left ( \frac {\beta } {\beta -1} \right ) \left ( \frac {r- \alpha } {q(1-e ^{-(r- \alpha )T} )} \right ) I$$ | (20) |
계통비용 추정
본 절에서는 앞서 개발한 모형을 이용하여 태양광 발전의 계통비용 도출하였다. 전술한 바와 같이 본 논문에서는 계통비용을 ‘태양광의 경제성을 확보하는데 필요한 송배전의 평균투자비’를 계통비용으로 정의하였다. 그리고 계통비용은 계통연계의 부족으로 실현되지 못한 태양광 발전 투자에 대한 전력판매수입을 ‘적정’ 수준까지 증가시키는데 필요한 계통투자비용을 이용하여 평균계통비용을 구하는 방식을 취한다.
투자비용은 다음과 같이 도출하였다. 한국전력공사의 ‘송배전용 전기설비 이용규정’의 ‘[별표4] 배전용 전기설비 성능기준’에 따르면 배전용 전기설비는 1회선 당 운전용량은 10,000 kw를 따르도록 되어있다. 그리고 1회선 당 투자비용은 18억 원2)을 가정하였다. 결론적으로 1회선 당 투자비가 18억 원이 소요되고, 한 회선에서 10,000 kw의 태양광이 접속될 경우의 투자비용은 18만 원/kw로 가정할 수 있을 것이다.
2) 한국전력공사 내부자료(2019)
아래 Table 1은 본 논문에서 실증분석을 위해 사용한 각 발전소의 설비용량 규모를 나타낸다(KEEI, 2019). 아래 표에서 보는 바와 같이 A발전소의 경우 시설용량이 492 kw이며, 투자비용은 136만 원/kw가 소모된다. 그리고 B발전소의 경우 시설용량이 98.55 kw이며, 투자비용은 141만 원/kw가 소모된다. 반면 시설용량이 3 kw 밖에 되지 않는 C발전소의 경우에는 187만 원/kw로 큰 값을 갖는 것으로 나타났다.
Table 1. Investment Cost by Solar Power Plant Size
| Power Plant A | Power Plant B | Power Plant C | |
| Total Investment Cost (Won) | 670,000,000 | 139,000,000 | 5,600,000 |
| Capacity (KW) | 492 | 98.55 | 3 |
| Unit Investment Cost (Won/kw) | 1,361,789 | 1,410,452 | 1,866,667 |
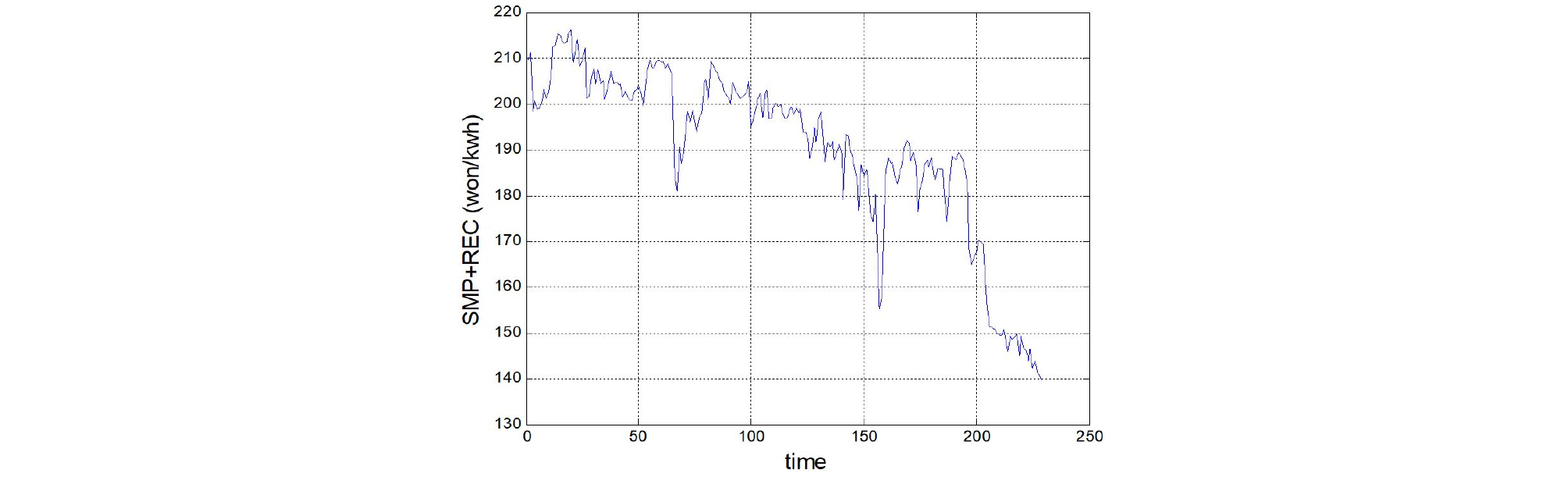
다음으로 2017년 3월의 부터 2019년 7월까지의 SMP+ REC 가격을 살펴보겠다. 아래 Fig. 1에서 보는 바와 같이 2017년 3월 SMP+REC 가격의 약 210원/kwh 수준이었는데, 2019년 7월의 경우 약 140원/kwh 정도로 지속 하락하였으며, 최근 들어서는 더욱 가파르게 하락했음을 알 수 있다. SMP와 REC의 하락요인은 상이한데, 일반적으로 SMP는 최근 들어 전력 예비율 상승에 따라 가격기준이 크게 내려갔기 때문이며, REC는 재생에너지의 가파른 공급 증대가 주요인으로 작용하고 있다. 이에 따라 SMP+REC 가격은 더욱 가파른 속도로 하락하고 있다.
식 (17)을 이용하여 gBm 확률과정에서의 증가율(drift rate)과 분산율(volatility rate)을 도출하였다. 그 결과 및 로 추정되었다. 그리고 SMP+ REC 가격을 식 (1)의 OU 확률과정을 적용하면 및 으로 추정되었다. 여기에서 가 의미하는 바는 OU 확률과정에서 SMP+REC 가격이 장기적으로 166.4원/kwh선으로 평균회귀됨을 의미한다.
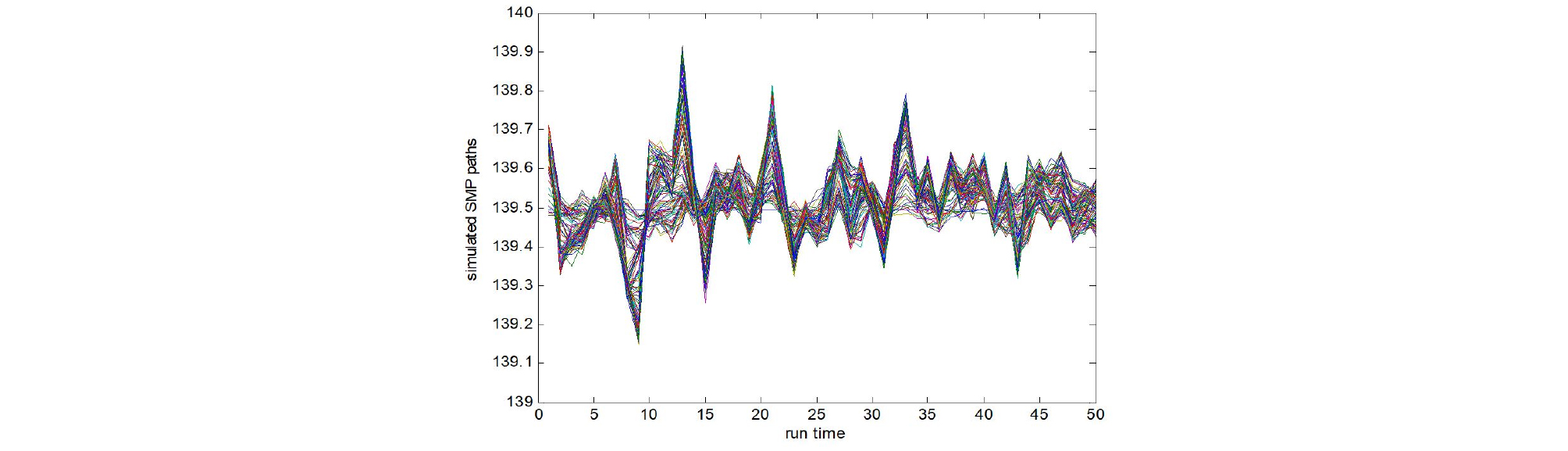
Fig. 2는 OU 확률과정을 따르는 SMP 가격을 시뮬레이션 한 결과이다.
계통비용을 구하기 위해서는 경제성을 확보할 수 있는 SMP+REC 가격수준과 이에 대응되는 전럭판매율(발전량 대비 계통연계를 통해 판매할 수 있는 판매량)을 확보해야 한다. 이때 비교기준이 필요한데, 본 논문에서는 ‘RPS 고정가격계약 경쟁입찰 제도(이하 ‘고정가격제도’)’ 거래방식을 비교기준으로 설정하였다. 고정가격제도의 경우 100 kw 미만의 발전사업자에 대해 ‘우선순위’를 두고 있으며, 100 kw 이상 1MW미만의 경우 ‘일반선정A’로 입찰을 하고 있다. 본 논문에서 실증분석을 한 3개의 발전소의 경우도 3~492 kw규모의 중소사업자이고, 이들은 고정가격제도에 참여하였을 경우 SMP+REC 가격의 불확실성에 노출되어 있다. 그렇기에 SMP+REC 가격 불확실성에 따른 모형을 설정하였으며, 불확실성에 노출되지 않고 안정적으로 전력판매수입을 거둘 수 있는 고정가격제도 계약과 비교해서, 태양광 현물시장에서 ‘태양광 발전으로 수익을 거두기 위해서는 어느 정도의 전력판매율(이윤보장 최소전력판매율)’이 보장되어야 하는지를 파악하였다. 그 다음으로 이윤보장 최소전력판매율을 달성하기 위한 계통투자비를 도출한 후, 이를 발전량 비중으로 나누어 kwh당 계통투자비를 산출하였다.
우선 평균회귀과정인 OU 확률과정에서 계통비용을 구하는 알고리즘은 다음과 같다(Park, 2018).
Ornstein-Uhlenbeck 과정 pseudo-code
1. find using numerical analysis (with 100% sales rate)
2. simulate to identify until to reach the max of SMP+REC
3. 165.94KRW/kwh is 2019 average price
4. identify → = 165.94
5. check with the property
6. calculate
7. grid cost = 205.94
Table 2는 위 알고리즘에 따라 OU 확률과정에서 산출된 평균계통비용(average grid cost), 즉 계통비용을 보여주는데 A발전소는 0.5561원/kwh 및 B발전소는 0.5544원/kwh로 도출되었다.
Table 2. Estimating the Average Grid Cost under OU Process (10% efficiency)
이윤보장 최소판매율(sales rate) 값은 A발전소는 현물시장에서 33.76%, 고정가격제도 시장에서는 31.02%로 나타났다. 그리고 B발전소는 현물시장에서는 34.96%, 고정가격제도 시장에서는 32.13%로 나타났다. 이렇게 이윤보장 최소판매율이 31~34% 수준으로 나온 까닭은 OU 확률과정의 경우에는 기본적으로 높은 수준의 SMP+REC 가격을 보장해주기 때문이다.
다음으로 동일한 파라미터로 gBm 확률과정 하에서 A발전사 및 B발전사의 평균계통비용 및 이윤보장 최소판매율을 도출하였다.
2019년 기준 고정가격제도에서 SMP+REC 상한가는 180.56원/kwh였는데, 동 가격 기준에서 A발전사가 경제성을 확보할 수 있는 최소전력판매율은 88.72%인 것으로 나타났다. 마찬가지로 SMP+REC 현물시장에서의 이윤보장 최소판매율을 구하였는데, 2019년의 SMP+REC 현물 평균가격이 165.93원/kwh인 상황에서 A발전사가 경제성을 확보할 수 있는 이윤보장 최소판매율이 96.54% 정도로 요구되는 것으로 나타났다. 이상의 결과를 이용하여 평균계통투자비를 구하면 약 0.56원/kwh 추정되었으며, SMP 가격과 비교할 경우 동 투자비는 SMP 가격의 약 0.6%에 해당하는 것으로 나타났다.3)
3) 2019년 1월부터 7월까지의 SMP 평균가격 95.95원/kwh을 기준으로 하였다.
Table 3에서 보는 바와 같이 B발전소를 대상으로 동일한 과정을 거쳐 계통비용을 구하여도 A발전소와 동일한 0.56원/kwh으로 추정되었다.
Table 3. Estimating the Average Grid Cost under gBm Process (10% efficiency)
여기에서 OU 확률과정과 비교하여 이윤보장 최소판매율이 높아짐에도 불구하고 계통비용이 거의 불변인 이유는 결국 고정가격제도 가격 대비 현물시장에서 경제성을 확보해주기 위한 최소판매율의 증가율이 OU 확률과정이나 gBm 확률과정에서 유사하기 때문이다.
다음으로 Table 4는 다른 조건이 동일한 상황에서 태양광 발전 효율만이 10%에서 20%로의 10%포인트 상승을 가정하여 gBm 확률과정의 평균계통비용을 추산한 결과이다. 그 결과 이윤보장 최소판매율이 하락한 것 외에는 계통비용 자체는 거의 변화가 없는 것으로 나타났다.
Table 4. Estimating the Average Grid Cost under gBm Process (20% efficiency)
이상의 결과를 정리하면, 태양광 발전의 계통비용은 그 시설규모 또는 시계열 가격의 프로세스(OU 확률과정 또는 gBm 확률과정), 이용효율 등에 거의 영향을 받지 않으며, 평균적으로 0.55~0.56원/kwh인 것으로 나타났다.
KEEI(2019)에서는 전술한 바와 같이 계통비용을 ‘밸런싱비용, 그리드비용, 프로파일비용’의 합으로 정의하였으며, 여기에서 본 논문에서 도출한 계통비용(0.55~0.56원/kwh)은 KEEI(2019)에서의 그리드비용을 의미함을 설명하였다. KEEI(2019) 메타회귀분석을 위해 태양광 발전 그리드비용 관련 선행연구의 추정치를 확보하였는데, 추정치의 평균은 5.14원/kwh4)로 나타났다. 이는 본 연구에서 도출한 결과와 차이가 있는데, 이러한 결과는 계통비용이 태양광 발전 시설이 위한 국가, 전력수요패턴, 날씨, 전원믹스 및 인접국가들의 계통연계에 따라 다르게 결정되기 때문이다(KEEI, 2019).
4) KEEI(2019)에서 총 3개의 선행연구에서 21개의 그리드비용 추정치를 확보하였다. 확보한 그리드비용 평균값은 4.36$/Mwh이며, 이에 환율 1,180원/$을 곱하여 동 값을 도출하였다.
다음으로는 본 논문에서 개발한 모형의 주요 파라미터를 바탕으로 민감도 분석을 시행하였다. 민감도 분석은 OU 확률과정에서의 A발전사의 파라미터로 분석하였다.
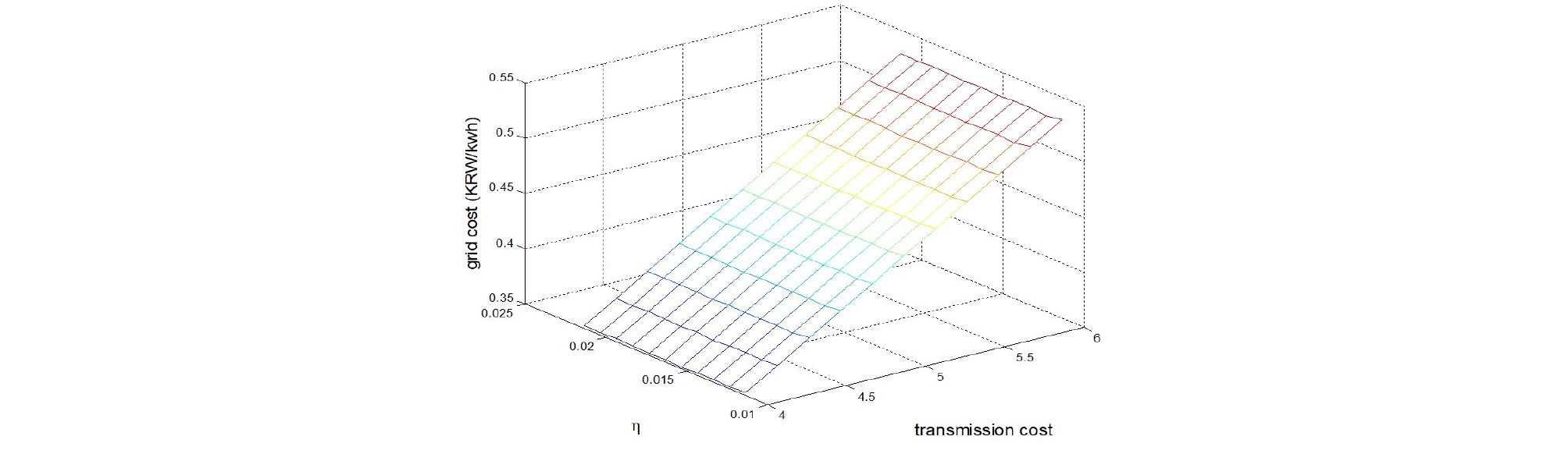
우선 Fig. 3과 같이 OU 확률과정에서의 송전설비투자비(transmission cost)와 수렴계수 와의 민감도 분석을 시행하였다. 그 결과 계통비용은 송전설비투자비에는 민감하게 반응하는 것에 비하여 수렴계수에는 불변인 것으로 나타났다.
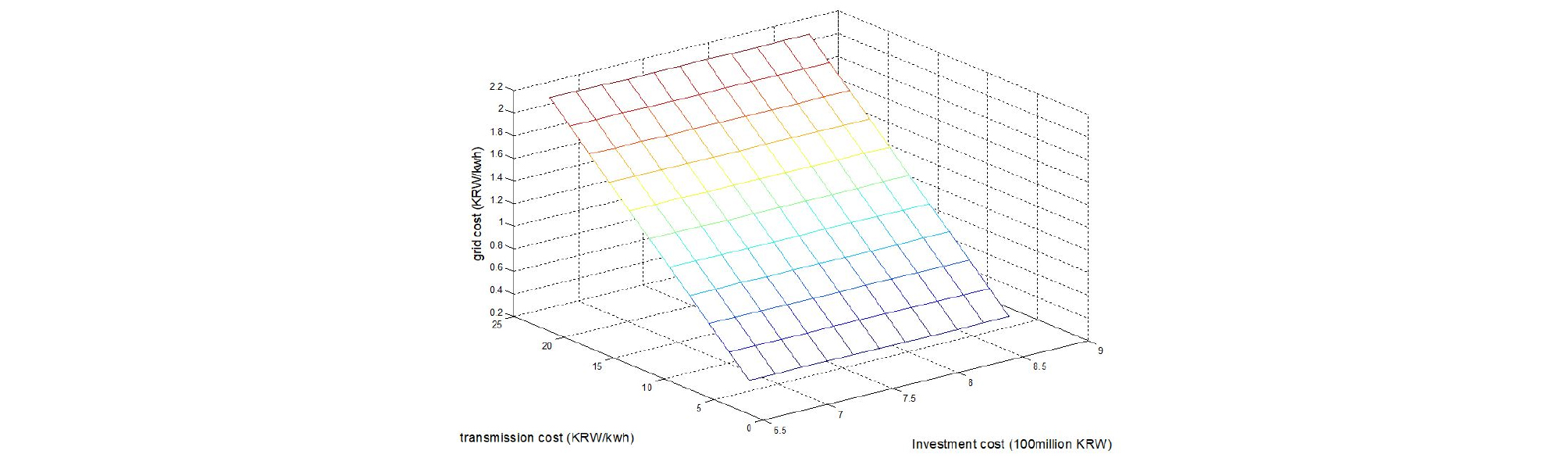
Fig. 4는 OU 확률과정에서의 송전설비투자비와 태양광 투자비의 민감도 분석결과를 나타낸다. Fig. 3과 마찬가지로 계통비용은 송전설비투자비에는 민감하게 반응하는 것에 비하여 태양광 투자비에는 불변인 것으로 나타났다.
이를 종합하면 OU 확률과정에서의 수렴계수 및 태양광 투자비는 계통비용에 영향을 주지 않는 반면, 송전설비투자비는 계통비용에 크게 영향을 주는 것으로 나타났다. 이 결과는 계통연계비용이 반영된 계통비용을 특성을 고려할 경우 직관적으로 부합하는 결론으로 판단된다.
결 론
본 논문에서는 태양광 발전 사업자가 계통연계의 경제성을 확보할 수 있는 수준의 계통보강비용 도출을 위해 실물옵션 방법론을 사용하였다. 전력가격이 불확실한 상황을 가정하였으며, 전력가격은 OU 확률과정 및 gBm 확률과정을 따름을 가정하였다. 그리고 개발된 모형에 태양광 발전소의 파라미터를 대입하여 전력가격 불확실성하에서의 계통비용을 추정하였다.
우선 이윤보장 최소판매율은 OU 확률과정에서 현물시장의 경우 31~32%, 고정가격제도의 경우 33~34%로 나타났다. 그리고 gBm 확률과정에서 현물시장의 이윤보장 최소판매율은 96~99%, 고정가격제도의 이윤보장 최소판매율은 88~91%로 나타났다.
계통비용의 경우 OU 확률과정 및 gBm 확률과정 모두에서 0.56원/kwh로 산출되었다. 이렇게 gBm 확률과정과 비교하여 이윤보장 최소판매율이 높아짐에도 불구하고 계통비용이 거의 불변인 이유는 결국 고정가격제도 가격 대비 현물시장에서 경제성을 확보해주기 위한 최소판매율의 증가율이 OU 확률과정 및 gBm 확률과정에서 유사하기 때문이다.
마지막으로 다른 조건이 동일하게 하고 gBm 확률과정에서 태양광 발전 효율만 20%로 상승시켜 평균계통비용을 추산한 결과 이윤보장 최소판매율이 하락한 것 외에는 계통비용 자체는 거의 변화가 없는 것으로 나타났다.
이상의 결과를 정리하면, 태양광 발전의 계통비용은 시설규모, 전력 가격의 프로세스(OU 확률과정 또는 gBm 확률과정), 이용효율 등에 거의 영향을 받지 않으며, 평균적으로 0.55~0.56원/kwh인 것으로 나타났다.
본 논문에서는 ‘SMP+REC 가격’의 불확실한 확률과정으로 규정하였으며, SMP+REC 가격이 OU 확률과정 및 gBm 확률과정에 따를 때의 재생에너지 계통비용을 추정하였다. 하지만 향후에는 계통비용을 추정함에 있어서 SMP+REC 가격의 불확실성 뿐 아니라, SMP 가격 또는 REC 가격을 분리하여 계통비용 분리하여 추정하고 이의 비교를 통해 계통비용에 영향을 미치는 요소에 대한 체계적인 연구가 필요할 것으로 판단한다.