서 론
선진국을 중심으로 전력시장은 독점시장에서 규제 완화와 구조개편을 통해 점점 경쟁적인 시장으로 바뀌고 있다. 우리나라도 이에 발맞춰 전력시장에 경쟁을 도입했다. 제한적이긴 하지만 1999~2002년에 한국전력 발전부문을 6개사로 분리하여 전력생산부문에서 경쟁을 도입했다. 이에 따라 전력시장의 발전부문에서 각발전사들이 얼마나 발전해야 할지는 중요한 문제가 되었다. 따라서 시장원리에 따라 시장참여자들은 더 많은 이익을 얻기 위해 전략을 세워야할 필요성이 생겼다. 입찰전략은 날씨, 온도 등 다양한 요소들의 영향을 받지만 단기가격에 큰 영향을 받는다. 따라서 계통한계가격(System Marginal Price, SMP)의 예측은 시장참여자들에게 전략을 세우는데 중요한 요소라고 할 수 있다. 또한 시장운영자 입장에서도 안정적인 전력시장을 원하기 때문에 이는 중요한 요소이다.
우리나라의 경우 구조개편 초기에 공급전원구성에서 기저발전설비가 상대적으로 부족했다. 또한 구조개편을 하기 전에 발전부문의 독점과정에서 시장균형을 벗어난 상태였기 때문에 기저발전에서 초과이윤이 발생하는 문제점이 있었다. 현재 우리나라 전력시장은 비용반영시장(Cost-Based Pool, CBP) 시장이며, 우리나라 전력시장의 비효율성을 지적한 보고서와 논문들이 존재한다(KEEI, 2013; KIET, 2007; Kim, 2015). 이에 따라 정부는 시장을 안정화하기 위해 기저발전부문에서 초과이윤의 문제를 해결하고자 하였다. 이에 대한 대책으로 기저발전 부문의 정산규칙을 인위적으로 조정하여 가격 안정을 시키려고 했다. 하지만 이러한 규칙은 가격 안정화의 문제점을 개선하지 못하고 있다. 게다가 발전회사는 비용 절감을 통해 향상된 수익성을 추구하더라도 바로 정산조정계수의 조정을 통해 비교적 낮은 보상가격을 적용받음으로써 단기적인 발전설비운영 비용 절감 유인도 이끌어내지 못했다. 따라서 발전사업자의 장기적 투자의사결정을 방해하지 않고 발전회사의 단기적인 운영 효율성을 이끌어낼 수 있는 가격 안정화 방식이 필요하다. 또한 안정적인 가격예측을 할 수 있다면 발전시장의 효율성을 높일 수 있다. 현재 전력거래시장에서 시장참여자와 시장운영자가 효율성을 극대화하지 못하고 있고 발전부문의 불균형한 구조 때문에 시장균형에 벗어나 있는 상태이다. 이러한 제한된 시장에서는 발전사가 능동적으로 얼마나 발전을 할지 한계가 존재한다. 따라서 계통한계가격의 예측력을 높이는 것은 향후 신규 발전소의 진입 여부와 신규설비에 대한 투자여부를 결정하는 중요한 요소일 뿐만 아니라 전력시장의 효율성 측면에서도 중요하다.
본 연구에서는 이에 근거하여 전력거래 과정에서 가격예측이 중요하다고 생각했고 예상치 못한 시장참여자들의 행동에 의해 이상패턴이 나타날 수 있다고 생각했다. 따라서, 정확한 예측을 하기 위해서는 선형모형으로 한계가 있을 수 있다. 이에 근거하여, 기존 경제학에서 일반적으로 사용되는 선형 형태의 경제모형과 달리 비선형 모형중 하나인 인공신경망(Artificial Neural Network, ANN)기반 모델을 사용하는 것을 제안한다.
국내 SMP 예측에 다양한 분석 방법론이 연구 되어왔다. 가격은 시장참여자들의 행태를 집약적으로 보여준다고 생각하고 접근한 게임이론적 접근방법(KEEI, 2003), SMP 변동성에 초점을 맞춰 다중주기의 관점에서 연구한 MSM (Markov Switching Multifractal)모형(Lee, 2016), 구조충격을 식별하고 이를 SMP 증가율에 대해 표현한 후 구조변화 분석방법으로 SMP의 변동성 변화를 분석한 SVAR (Structural Vector Autoregressive)모형(Shin and Kim, 2015), 예측력에 초점을 맞춘 ARIMA(Autoregressive Integrated Moving Average)모형(Kim et al., 2005; Kim et al., 2006), 인공신경망 등이 있다(Lee et al., 2005; Jeong et al., 2005; Jeong, 2006; Kim, 2019; Shin et al., 2018). 그러나 ARIMA 모형은 단기 예측의 정확성이 매우 높지만 새로운 자료가 투입될 때 마다 모형에 적합한 모수를 선정해야 하는 단점이 있다. 선행연구에서도 2004년 8월 어느 한 시점만 예측한 것이기 때문에 연속성이 보장되지 않는다는 한계점이 존재한다. 그에 반해, 인공신경망은 복잡하지만 스스로 데이터를 학습하는 알고리즘을 통해 다양한 문제에 대해 적용이 가능하다는 장점이 있다.
Lee et al.(2005)은 역전파 인공신경망을 통해 전력수요와 과거 SMP를 사용해 SMP예측을 시도했다. 특히, 시간별 SMP와 일별 SMP를 모두 이용하여 시장 정보를 최대한 반영하여 정확도를 높이고자 했다. Jeong et al.(2005)은 입력자료를 유사한 패턴별로 분류하는 코호넨 자기조직화 네트워크를 이용하여 역전파 인공신경망과 SMP 예측력을 비교했다. 역전파 인공신경망 보다 평균 오차율이 약 1.1% 정도 더 높은 결과를 보여주었다. Jeong(2006)은 역전파 인공신경망을 통해 전력수요와 요일별 특성을 고려하기 위해 동일 요일의 과거 자료들을 이용해 학습하고 요일별 예측을 실시했다. Kim(2019)은 시계열 데이터인 SMP의 특성을 고려해 시계열 데이터를 학습하고 예측하는데 유용한 LSTM (Long Short-Term Memory) 알고리즘을 활용하여 SMP 예측을 시도했다. Shin et al.(2018) 또한 시계열 데이터를 학습하고 예측하는데 유용한 NARX(Nonlinear Autoregressive exogenous) 모형을 이용하여 SMP예측을 시도했다.
본 논문에서는 이러한 다양한 문제에 유연하게 적용할 수 있는 인공신경망을 선택하였으며, 2가지의 인공신경망을 제안한다. 첫 번째는 MLP(Multi-Layer Perceptron), 두 번째는 NARX(Nonlinear Autoregressive exogenous)이다. LSTM 모형은 은닉층에 셀을 추가한 형태로 과적합하기 쉽다는 단점이 있다. 그러나 MLP와 NARX는 입력층, 은닉층, 출력층으로 이루어져 있어 비슷한 구조를 가졌기 때문에 서로 비교하기 용이하다. 마지막으로, 전통적인 시계열 모형과 예측력의 정확도를 비교하는 것이 그렇게 중요하지 않지만 ARIMA를 통해 비교를 실시했다. MLP와 NARX는 MLP는 전방향 인공신경망 중에서 가장 일반적으로 쓰이는 모형으로 모형의 이름에서 알 수 있듯이 다층의 퍼셉트론으로 구성되어 있다. 반면, NARX는 순환신경망의 일종으로 시계열 데이터를 모델링 하는데 적합하다. 더 자세한 설명은 뒷장에서 설명하고자 한다.
분석 방법론
컴퓨터는 사칙연산을 시작으로 계속해서 발전해 왔고 단순한 정보 처리 기능을 넘어서 현대에 들어 인간의 뇌를 모방한 인공지능까지 발전해 왔다. 최근에는 인간의 두뇌를 넘어서 머신러닝, 딥러닝 수준까지 발전해왔고 다양한 분야에서 패턴인식, 음성분석, 로봇학 등에 사용되고 있다.
인공신경망은 인간의 두뇌와 비슷한 형식으로 이루어져 있다. 인간의 두뇌는 감각 기관을 통해 받아들여진 정보가 뉴런을 통해 뇌로 전달되고 뇌는 다시 명령을 내리는 형식으로 이루어져 있다. 인공신경망도 기본적으로 입력층, 은닉층, 출력층으로 이루어져 있으며 인간의 두뇌와 감각기관이 행동하는 것과 마찬가지로 받아들인 정보를 전달하고 출력하는 뉴런과 같은 형식으로 되어 있다. 입력층은 처음 데이터를 입력하는 뉴런층을 의미하며, 은닉층은 입력층과 출력층 사이에 있으며, 입력층에서 입력된 데이터가 출력층에 도달하기 전에 가중치를 통해 출력값이 정확히 도출될 수 있도록 도와주는 역할을 한다. 출력층은 결과적으로 얻고자 하는 데이터가 출력되는 뉴런층이다. 처리하는 문제가 복잡할수록 은닉층은 더 많아지고, 이러한 기본적인 형태를 전방형 인공신경망이라고 하며 더 나아가 역전파 인공신경망을 볼 수 있다. 역전파 인공신경망의 알고리즘은 기본적으로 각각의 입력층에 변수를 넣으면 은닉층에 전달되고 마지막으로 출력층까지 도달한다. 이에 끝나지 않고 각 층을 연결하는 가중치가 존재하며 최종적으로 출력층에서 은닉층, 은닉층에서 입력층을 거쳐 역방향으로 출력값과 실제값을 비교하며 가중치를 조정한다. 즉, 상위층에서 다시 역전파하여 하위층에서는 이를 토대로 다시 가중치를 수정해나가는 과정을 거친다.
MLP(Multi-Layer Perceptron)
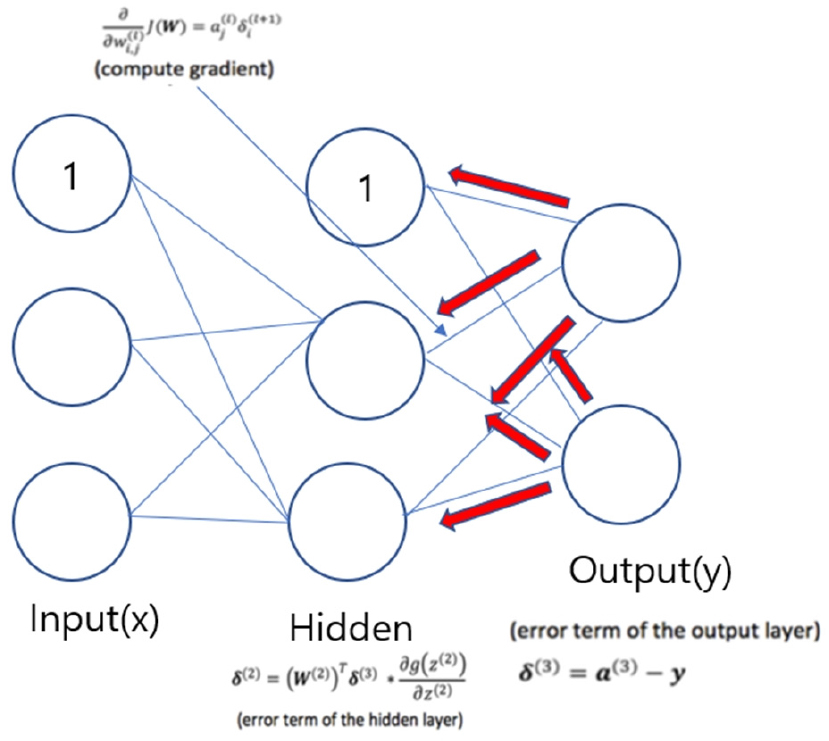
MLP(Multi-Layer Perceptron)는 전방향(feedforward) 인공신경망 중에서 가장 일반적으로 쓰이는 모형이다. MLP모형은 입력층, 은닉층, 출력층으로 이루어진 다층 모형이며, Fig. 1과 같이 역방향으로 출력값과 실제값을 비교하며 가중치를 조정하는 역전파 기법을 사용하기도 한다.
MLP의 기본구조는 다음과 같은 식으로 나타낼 수 있다.
여기서 k는 측정값, n은 은닉층의 수, 는 편의 값, 는 가중치, 는 입력값이다.
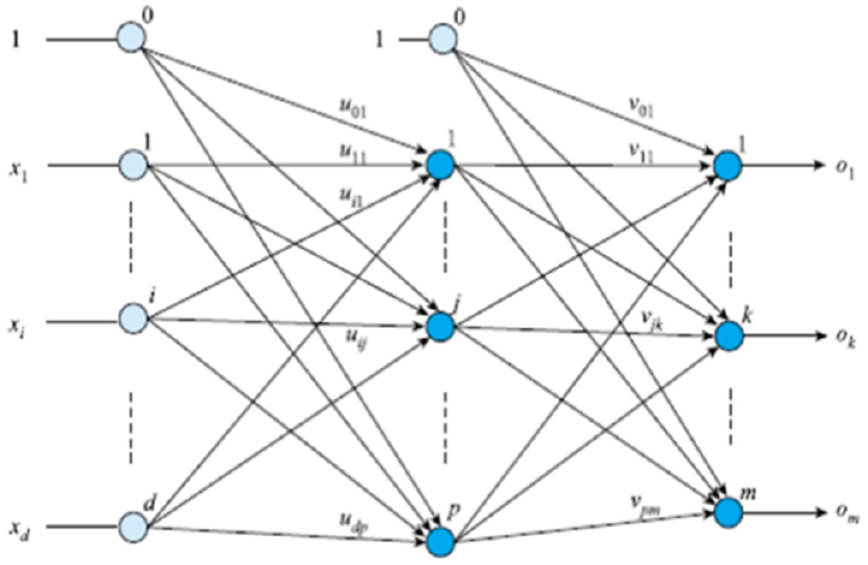
가중치를 다시 나타내면 Fig. 2와 같이 입력층과 은닉층 사이의 가중치는 로 표기하며 i의 값은 0부터 d까지, j의 값은 1부터 p까지로 나타낸다. 이는 입력층의 i번째 노드와 은닉층의 j번째 노드를 연결하는 연결선의 가중치를 의미하고 은닉층 노드는 1번부터 p번까지 순서대로 정한다(1). 은닉층과 출력층 공간의 가중치는 로 표현하는데 j의 값은 0부터 p까지, k의 값은 1부터 m까지로 나타내고 은닉층의 j번째 노드와 출력층의 k번째 노드를 연결하는 연결선의 가중치를 의미한다(1)(SPRI, 2017).
NARX(Nonlinear Autoregressive exogenous)
순환신경망(Recurrent Neural Network, RNN)의 일종으로 순환신경망은 특정 노드의 출력이 해당 노드에 다시 입력되는 구조를 갖는 신경망이다. 즉, 현재 입력된 입력데이터와 과거에 입력받았던 데이터를 동시에 고려하여 결과값을 도출하는 방식이다. NARX(Nonlinear Autoregressive exogenous)또한 이러한 특징을 가지고 있으며, 외부변수를 갖는 비선형 자기회귀 모형이다. 다음과 같은 식으로 나타낼 수 있다.
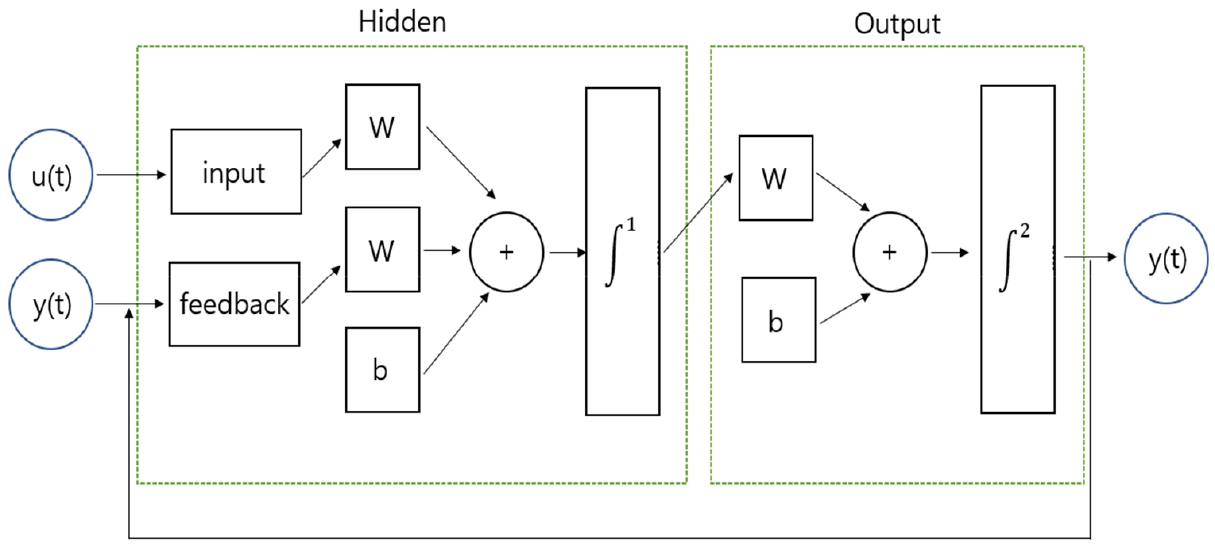
y는 관심변수(종속변수), u는 외부변수로서 u에 대한 정보가 y를 예측하는데 도움을 준다는 개념이다. 즉, y의 이전값들과 u값이 y를 예측한다. 이러한 특징을 갖기 때문에 시계열 패턴을 가지고 있는 데이터를 예측하는데 장점을 가지고 있다. NARX의 기본구조는 Fig. 3과 같다.
NARX는 전기의 자기 자신의 값()과 외부변수()의 현재값이 각각 가중치를 갖고 입력되고 그 후에 출력값()이 다시 입력신호로 돌아가는 순환 과정을 거친다. 이러한 순환 과정을 위해서 닫힌 경로가 필요하다. 닫힌 경로를 통해 데이터가 끊임없이 순환하고 업데이트 하면서 최신의 데이터로 갱신 할 수 있다. 그러나 은닉층이 복잡해지고 순환의 깊이가 깊어질수록 가중치를 계속 개선하면서 기울기 소멸(vanishing gradient)1)이 발생하게 되어 학습이 제대로 이루어지지 않는 문제가 발생한다. 따라서 적절한 학습 강도와 횟수가 중요하다(SPRI, 2017).
1) 활성화 함수의 미분 값들이 여러 차례 곱해지게 되고 이 값에 의존하는 gradient 값들이 0으로 수렴하는 현상
실증 분석
본 장에서는 계통한계가격(SMP)예측을 위해 우선 데이터 전처리 과정을 거친 다음 예측을 위해 두 가지 모델을 제안한다. 첫 번째로 인공신경망의 전방형 모델 중 기본이라고 볼 수 있는 MLP 모델과 두 번째로 시계열 데이터에 적합한 NARX 모델이다. 마지막으로 계통한계가격(SMP)을 예측한 후 이를 평가한다. 또한 전통적인 시계열 모형중 하나인 ARIMA와 비교를 실시했다. 본 연구는 인공신경망 모형중 MLP와 NARX가 SMP 예측에 사용될 수 있는지 확인하고 그에 맞는 최적의 모형을 제시하는 것에 목적이 있으므로 비교는 ARIMA에 한정하기로 한다.
실증분석자료
우선 데이터 선정은 전력수요와 공급에 따라 결정되는 계통한계가격(SMP)결정 원리에 근거했다. 이에 근거해 전력수요를 외부요인으로 설정한 Jeong(2006)에 따라 현재 계통한계가격에 영향을 미치는 요소로 과거 계통한계가격과 과거 전력수요를 사용했다. 기간은 구할 수 있는 전력수요와 계통한계가격 기간을 동일하게 하여 최대 데이터인 2005. 1~2020. 7월까지의 일별데이터를 사용했으며 각데이터들은 몇몇 특징을 보인다. 우선, 계통한계가격(SMP)은 점점 증가하다가 최근들어 다시 감소하는 모습을 보인다. 또한 변동성이 컸다가 최근들어 다시 줄어든 것을 보인다. 전력수요는 점점 증가하는 모습을 보이고 최근 코로나 바이러스의 영향으로 조금 줄어든 모습을 보이며 매년 일정한 규칙을 보이면서 움직인다. 기초통계량은 Table 1에 제시했다. 계통한계가격(SMP) 데이터들의 분포는 중앙값보다 평균이 더 크고, 데이터의 분포가 왼쪽으로 치우쳐진 것을 알 수 있다. 반면, 전력수요는 대체로 정규분포 하다.
Table 1.
Summary Statistics
|
SMP (Won/kWh) |
Electricity Demand (MW) | |
| Mean | 104.44 | 60844 |
| Standard Deviation | 32.9615 | 10268.12 |
| Min | 19.19 | 31214 |
| Max | 225.17 | 92478 |
| Median | 94.97 | 60745 |
다음으로 데이터 범위의 편차가 상이하여 0과 1사이에서 나타낼 수 있도록 정규화 과정을 거쳐 분석을 진행했다. 정규화 식은 다음과 같다.
분석결과
이 예측을 평가하기 위해 RMSE(Root Mean Square Error)와 MAPE(Mean of Absolute Percentage Error)를 제안한다. RMSE는 잔차의 제곱합을 평균한 값의 제곱근으로서 관측값들간의 편차를 의미한다. 즉, 실제값과 예측값과의 차이가 얼마인가를 나타낸다. 다시 말해서 개별 예측값이 얼마나 멀리 중심으로부터 떨어져 있는지를 나타낸다. 다음과 같은 식으로 나타낼 수 있다.
RMSE는 절대적인 예측오차에 기반하여 예측오차의 크기를 나타낸다. 따라서 상대적인 예측오차를 비교하는 지표가 필요하다. 예를 들어 실제값 100에 대한 예측오차 10과 실제값 1000에 대한 예측오차 10의 경우, 같은 예측오차가 10이라도 상대적인 의미의 오차 크기는 다르다. 따라서 예측오차의 전체적인 크기를 알기위해 MAPE를 사용한다. MAPE는 다음과 같이 나타낼 수 있다.
본 연구에서는 시계열 분석에 대표적으로 사용되는 RMSE를 중심으로 MAPE를 제시했다.
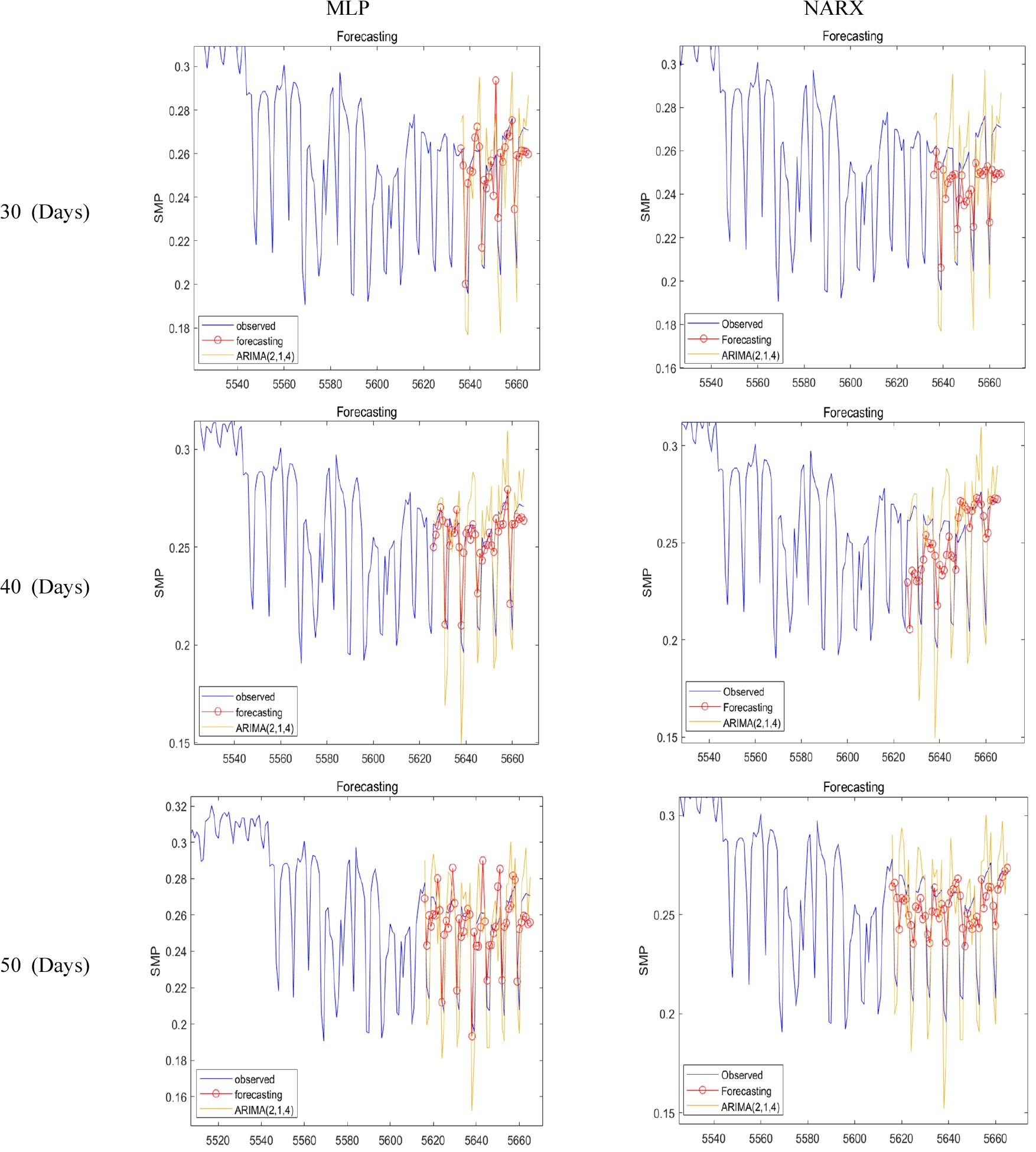
Table 2는 MLP와 NARX 각각 30일, 40일, 50일을 예측한 결과를 보여준다. 약 5000개의 데이터를 훈련시켰으며, 은닉층은 50개부터 100개까지 총 11개의 은닉층을 설정하여 최적화 과정을 나타냈다. Fig. 4에서는 그 결과를 ARIMA 모형과 비교하여 그래프로 나타냈다. ARIMA 모형은 최적의 모형을 찾기 위해 Akaike 정보 기준(information criterion)을 통해 차수를 ARIMA(2, 1, 4)로 결정하고 30일, 40일, 50일을 예측했다.
Table 2.
Accuracy of daily forecasting using MLP & NARX (MAPEs are in the parenthesis)
| Hidden layer units | MLP | NARX | ||||
| 30 (Days) | 40 (Days) | 50 (Days) | 30 (Days) | 40 (Days) | 50 (Days) | |
| 50 |
0.0210 (0.0659) |
0.0209 (0.0603) |
0.0215 (0.0653) |
0.0284 (0.0898) |
0.0273 (0.0900) |
0.0243 (0.0888) |
| 55 |
0.0229 (0.0776) |
0.0215 (0.0608) |
0.0209 (0.0662) |
0.0400 (0.1398) |
0.0336 (0.1171) |
0.0249 (0.0878) |
| 60 |
0.0222 (0.0661) |
0.0212 (0.0628) |
0.0201 (0.0596) |
0.0270 (0.0930) |
0.0309 (0.1069) |
0.0309 (0.1012) |
| 65 |
0.0209 (0.0658) |
0.0199 (0.0621) |
0.0204 (0.0575) |
0.0373 (0.1309) |
0.0328 (0.1147) |
0.0292 (0.1006) |
| 70 |
0.0201 (0.0616) |
0.0202 (0.0671) |
0.0219 (0.0696) |
0.0342 (0.1178) |
0.0296 (0.0973) | 0.0218* (0.0726) |
| 75 |
0.0229 (0.0729) |
0.0201 (0.0602) |
0.0210 (0.0621) |
0.0318 (0.1034) |
0.0251 (0.0813) |
0.0320 (0.1069) |
| 80 |
0.0207 (0.0641) |
0.0212 (0.0644) | 0.0192* (0.0569) |
0.0243 (0.0838) | 0.0236* (0.0773) |
0.0238 (0.0787) |
| 85 |
0.0213 (0.0685) | 0.0194* (0.0576) |
0.0199 (0.0607) |
0.0326 (0.1100) |
0.0341 (0.1174) |
0.0368 (0.1291) |
| 90 | 0.0189* (0.0579) |
0.0215 (0.0678) |
0.0208 (0.0691) |
0.0251 (0.0762) |
0.0299 (0.0957) |
0.0284 (0.0900) |
| 95 |
0.0212 (0.0694) |
0.0199 (0.0641) |
0.0207 (0.0662) | 0.0212* (0.0639) |
0.0256 (0.0851) |
0.0246 (0.0794) |
| 100 |
0.0209 (0.0632) |
0.0204 (0.0627) |
0.0213 (0.0674) |
0.0349 (0.1170) |
0.0257 (0.0815) |
0.0274 (0.0895) |
30일 예측에서는 MLP의 경우 은닉층이 90개일 때 RMSE가 0.0189로 최적이었고, NARX의 경우 은닉층이 95개일 때 RMSE가 0.0212로 최적이었다. 40일 예측에서는 MLP의 경우 은닉층이 85개일 때 RMSE가 0.0194로 최적이었고, NARX의 경우 은닉층이 80개일 때 RMSE가 0.0236으로 최적이었다. 50일 예측에서는 MLP의 경우 은닉층이 80개일 때 RMSE가 0.0192로 최적이었고, NARX의 경우 은닉층이 70개일 때 RMSE가 0.0218로 최적을 보여주었다.
대체로 MLP 보다 NARX가 RMSE가 더 높았으며, ARIMA모형의 30일, 40일, 50일 RMSE는 각각, 0.0154, 0.0185, 0.0174로 MLP보다도 더 낮은 RMSE를 보여주었다. 기존 선행연구들의 오차율이 3%~10%사이에 있는 것을 보았을 때, 본 연구의 인공신경망을 이용한 예측 오차율은 기준 내에 있는 것으로 보인다.
NARX가 MLP보다 더 낮은 예측력을 갖는 이유는 코로나 바이러스가 발생한 극단적인 상황이 발생해 더 낮은 예측력을 보인다고 생각했다. 시간 종속적인 특징을 가지고 있는 NARX의 특성상 코로나 바이러스와 같은 외부충격이 발생했을 때, 외부충격의 효과를 상대적으로 반영하지 못하기 때문이다. 그러나 이러한 해석은 결과만을 바탕으로 했고, 경제적인 과정을 설명할 수 없기 때문에 한계점이라 볼 수 있다.
결 론
본 논문에서는 전력통계정보시스템에서 제공되는 데이터로 MLP와 NARX를 사용하여 SMP예측을 시도했다. 우리나라 전력시장은 발전시장을 제외한 송전, 배전 부문은 한국전력이 독점하고 있는 전력시장의 제한적 개방으로 비효율이 나타나고 있다. 발전 부문에서도 SMP의 변동성이 커질수록 발전사업자들에게는 손익의 불확실성이 더 커지게 된다. 따라서 이러한 비효율을 줄일 수 있는 기술적인 방법중 하나로 SMP의 정확성을 높이는 것이다. SMP 예측을 위한 방법으로 많은 방법들이 있지만 본 논문에서는 비선형 모형으로 예측할 수 있는 인공신경망을 사용했다. 그 중에서도 전방향 인공신경망중 많이 사용되는 MLP 모형과 시계열 데이터에 유용하게 사용되는 NARX 모형을 사용했고 ARIMA(2,1,4)와 성능을 비교해 보았다. MLP와 NARX 두 모형 각각 30일, 40일, 50일을 예측했다.
동일하게 두 모형에서 일별 데이터를 이용하여 2005년 1월부터 2020년 7월까지 약 5700개의 데이터를 사용했으며 그 성능을 평가해 보았다. 그 결과, 30일 예측에서는 MLP와 NARX의 경우 각각, 은닉층이 90개, 95개일 때 최적이었다. 40일 예측에서는 MLP와 NARX의 경우 각각, 은닉층이 85개, 80개일 때 최적이었다. 50일 예측에서는 MLP와 NARX의 경우 각각, 은닉층이 80개, 70개일 때 최적이었다. ARIMA의 경우 전반적으로 30일, 40일, 50일 예측 모두 MLP와 NARX보다 더 낮은 RMSE를 보여주었다.
결론적으로 본 연구는 경제변수를 고려하여 외부변수로 전력수요를 고려했고 보다 적합한 모형을 찾기 위해 역전파 기법을 이용한 MLP모형, 시계열 특징을 이용한 NARX모형을 이용하여 30, 40, 50일을 예측하여 비교 분석했다. 적은 변수로 예측을 한다는 것은 예측력만 봤을 때 인공신경망의 장점으로 볼 수 있다. 그러나 일반적으로 경제적인 변수를 가지고 함수관계를 형성하는 경제모형과 달리 해석에 있어 어려움이 있다는 한계점을 가지고 있다.
정확한 SMP 예측은 우리나라 전력시장의 비효율성을 개선하는데 도움을 줄 것으로 예상된다. 또한 향후 전력파생상품시장시장이 생길 경우 SMP 예측의 중요성은 더욱 커질 것이다. 더불어, 우리나라 신재생 에너지 발전시장은 더욱 커질 것이라 예상된다. 따라서 전력시장 구성도 변화할 것이며 이에 대한 미래 전력시장에서의 가격예측도 중요해질 것이다. 향후, 이에 따른 적합한 예측 모델을 연구한다면 우리나라 전력시장의 SMP 예측에 있어 도움이 될 것이다.