서 론
탄성파 이방성
사방정계 이방성의 형성 원인
사방정계 이방성 매질에 대한 탄성 파동방정식
사방정계 이방성 매질에서의 탄성파의 거동
사방정계 이방성을 고려한 병렬 탄성파 모델링 알고리듬
엇격자 유한차분법(Staggered grid finite difference method)
영역 분할법(Domain decomposition)
수치 예제
모델링 알고리듬의 정확성 및 효율성 검증
3차원 SEG/EAGE 오버스러스트 모델에 대한 적용
결 론
서 론
유가스전 탐사를 위한 탄성파 탐사 자료 처리의 목적은 구조보정을 이용하여 지층의 정확한 깊이를 추정하는 데 있다. 대표적인 구조보정 기술인 역시간 구조보정(Reverse Time Migration, RTM)은 주어진 속도 모델에서 수치모델링을 통하여 계산된 송신원 파동장과 수진기 파동장을 상호상관함으로써 수행되는데(Zhou et al., 2018), 지층의 정확한 속도를 이용하고 파동의 정확한 전파시간을 계산하는 것이 필수적이다. 지층의 속도 추정을 위한 한 방법으로 최근 탄성파 완전파형역산(Full Waveform Inversion, FWI) 기술 개발이 활발하며, 이는 실제 현장 자료와 수치모델링 통해 획득된 모델링 자료의 오차를 최소화시키는 방향으로 속도 구조를 갱신하면서 지하의 속도 모델을 추정하는 방법이다(Virieux and Operto, 2009). 완전파형역산 기술도 수치모델링을 기반으로 모델링 자료를 생성하기 때문에, 주어진 속도 모델에서 파동의 정확한 전파 거동을 구현하는 것이 중요하다. 하지만 실제 지구는 이방성을 갖는 매질이기 때문에 이방성을 고려한 수치모델링 기술이 요구된다.
탄성파 탐사 규모에서 탄성파 이방성은 퇴적분지에서 흔하게 나타나는 물리적인 현상으로 파동이 이방성 매질을 통과할 때 전파 방향에 따라 속도의 차이가 발생한다(Tsvankin, 1997; Lee et al., 2008). 이방성의 형태와 정도에 따라 파동의 전파 양상은 매우 복잡하게 나타나기 때문에 이방성이 강한 지역에서 획득된 탄성파 탐사 자료를 처리할 때에는 탄성파 이방성이 반드시 고려되어야 한다. 이를 위하여 이방성을 고려한 파동방정식을 이용한 역시간 구조보정 및 완전파형역산 기술의 개발이 활발하게 진행되고 있다(Fletcher et al., 2009; Operto et al., 2013; Gholami et al., 2013; Alkhalifah and Plessix, 2014; Oh and Alkhalifah, 2018).
사방정계 형태의 이방성 매질은 횡등방성(Vertically Transverse Isotropy, VTI)과 종등방성(Horizontally Transverse Isotropy, HTI)이 결합된 매질로 세 방향에 따른 탄성파의 속도가 다른 매질이다. 따라서 사방정계 이방성을 고려한 3차원 탄성파 모델링은 3차원 가정이 필수적이며, 시간영역과 주파수영역 모델링을 통한 접근이 가능하다. 주파수 영역 3차원 모델링은 주로 음향파동방정식을 계산하는 데 많이 활용되고 있다(Operto et al., 2007; Operto et al., 2014; Amestoy et al., 2016).
하지만 일반적으로 128 GB~256 GB의 RAM(Random Access Memory)을 가지는 현재의 컴퓨터로는, 효율적인 행렬 계산 프로그램(예, Intel MKL PARDISO)을 사용하더라도 메모리의 한계로 탐사 규모(일반적인 탐사 영역 10 km × 10 km × 5 km, 송신원 주파수 20 Hz)에서 탄성파동방정식을 계산하는 것이 어렵다. 따라서 현재의 컴퓨터 기술 수준에서는 3차원 탄성파동방정식을 수치해석적으로 계산하기 위한 시간영역 모델링 알고리듬이 활발하게 개발되고 있다(Min et al., 2006).
Madariaga(1976)이 시간영역 탄성 파동방정식을 풀기 위해 엇격자 유한차분법(staggered grid finite difference method)을 처음 제안하였으며, 이 후 대표적인 시간영역 모델링 방법으로 널리 활용되고 있다. Levander(1988)는 엇격자 유한차분법을 공간 4차 정확도로 확장하였고, Graves(1996)는 지진파 모델링을 위한 3차원 탄성 파동방정식을 계산하는 데 적용하였다. 고성능 컴퓨팅(High Performance Computing, HPC)을 위하여 Bohlen(2002)은 점탄성 파동방정식에 대하여 영역 분할법(domain decomposition)을 이용한 병렬 모델링 기술을 적용하였고, Komatitsch et al.(2010)은 GPU(Graphic Processing Unit)를 이용하여 탄성 파동방정식에 유한요소법을 적용한 병렬 모델링을 연구하였으며, Weiss and Shragge(2013)은 GPU를 이용한 병렬 이방성 유한차분법 모델링 알고리듬을 제안하였다. 이처럼 방대한 계산량이 요구되는 사방정계 이방성을 고려한 역시간 구조보정과 완전파형역산 기술에서 3차원 탄성파 모델링 알고리듬의 병렬화는 필수적인 요소이다.
이 연구에서는 먼저 탄성파의 이방성을 유발하는 세 가지 지질학적 이유에 대해서 논의한다. 다음으로 사방정계 형태의 이방성 매질을 고려한 탄성 파동방정식을 소개하며, 사방정계 이방성 매질에서의 이방성 변수의 의미와 P파, SV파, SH파의 위상속도 분석을 통해 이방성 변수의 영향을 논의한다. 그리고 사방정계 이방성 매질에 대한 수치모델링 알고리듬의 효율성을 증대시키기 위한 영역 분할법의 원리를 소개하고, 균질한 사방정계 이방성 모델에 대한 적용을 통하여 알고리듬의 정확성과 효율성을 검증한다. 마지막으로 3차원 SEG/EAGE 오버스러스트 모델에 대한 적용을 통하여 복잡한 사방정계 이방성 매질에 대한 알고리듬의 적용성을 검토한다.
탄성파 이방성
사방정계 이방성의 형성 원인
탄성파의 이방성은 한 매질에서 전파 방향에 따라 탄성파의 속도가 달라지는 현상으로 퇴적분지에서 탄성파 탐사를 수행할 때 흔하게 나타나는 물리적인 현상이다. 퇴적분지에서 탄성파의 이방성을 유발하는 대표적인 세 가지 원인은 다음과 같다(Fig. 1). 첫 번째로 대표적인 덮개암 중 하나인 셰일이 갖는 고유의 이방성(Hornby et al., 1994; Cholach and Schmitt, 2003), 두 번째로 서로 다른 속도를 갖는 지층이 얇게 교호할 때 발생하는 겉보기 이방성, 마지막으로 수직으로 균열망이 나란히 발달할 때 균열을 통과하는 방향과 균열에 평행한 방향의 속도차이로부터 발생하는 이방성을 들 수 있다.

Fig. 1.
Three reasons of seismic anisotropy in the sedimentary basin. Left one is SEM (Scanning Electron Microscope) image of a shale (Cholach and Schmitt, 2003) and the middle one is an example of thin layering from Grand Canyon. The right one shows an example of vertically aligned fractures from Dongjeom Formation in Joseon Supergroup.
퇴적분지에서 흔하게 발견되는 셰일은 풍화의 산물인 스멕타이트(smectite)나 일라이트(illite)와 같은 점토광물이 퇴적되고 오랜 속성작용(diagenesis)을 받을 경우 형성된다. 점토광물은 대부분 Fig. 2와 같이 판상 규산염 광물(sheet silicate mineral)로 규산염 사면체(silicate tetrahedron)가 판상으로 잘 결합된 것이 특징이며, 각각의 판은 양이온에 의해 연결된 결정구조를 가지고 있다. 이 때 규산염 사면체끼리 연결된 판에 평행한 방향으로의 결합은 양이온에 의해 연결된 수직방향으로 결합에 비해 강하며, 이는 판에 평행한 방향으로의 에너지 전달을 쉽게 하여 탄성파 속도를 더 빠르게 한다. 이러한 고유의 이방성을 갖는 점토광물이 퇴적분지에서 속성작용을 거쳐 매몰압을 받게 되면 압력에 평행한 방향으로 배열되는 경향이 나타나기 때문에 셰일에서는 Fig. 1과 같이 수평적인 층상구조가 흔하게 나타나며, 일반적으로 수평방향의 속도가 수직방향의 속도에 비해 빠른 횡등방성(VTI)을 갖는다.
두 번째 원인은 탄성파의 수직 분해능과 관련되어 있다. 탄성파의 수직분해능 한계는 중심 파장의 1/4에 해당하는데, 탄성파 탐사에서 이보다 작은 규모의 수직적인 변화는 감지하기 어렵다. 따라서 수직분해능보다 작은 규모에서 얇은 지층이 교호할 경우, 탄성파는 이를 하나의 유효매질(effective medium 또는 equivalent medium)로 인식하게 되고 지층에 평행한 방향은 페르마 원리에 따라 가장 빠른 층의 속도로 전파하기 때문에 수직방향 속도보다 빠른 횡등방성을 갖는다(Hornby et al., 1994; Ikelle and Amundsen, 2005). 특별한 지각변동이 없는 퇴적분지에서는 단주기(예, 조석간만의 차)에서 장주기(예, 간빙기-빙하기)를 갖는 해수면 변동에 의해 입자가 큰 퇴적층과 입자가 작은 퇴적층이 교호하기 때문에 탄성파 탐사의 주파수 대역(3 Hz~ 200 Hz)에서 이러한 겉보기 횡등방성은 쉽게 관찰된다. 주파수 대역에 따른 겉보기 횡등방성은 Backus 평균화(Backus averaging; Backus, 1962)에 의해 표현될 수 있다.
마지막 원인은 탄성파의 수평 분해능과 관련이 있으며, 프레넬 영역(Fresnel zone)내에서 일정한 방향성을 갖는 균열망이 수직적으로 잘 발달될 경우 이방성이 나타날 수 있다. 탄성파는 수평 분해능 내의 변화를 감지하기 어렵기 때문에 균열망이 존재하는 매질을 하나의 유효매질로 인식하게 되는데, 균열망을 통과하는 방향의 속도가 균열망에 평행한 방향보다 느린 종등방성(HTI)을 갖게 된다. 이러한 종등방성 매질에서 균열을 통과하는 방향의 속도 감소는 균열의 밀도와 유체포화도와 같은 균열망 변수(fracture parameters)에 의해 결정된다(Bakulin et al., 2000).
사방정계 형태의 이방성 매질(Fig. 3)은 횡등방성과 종등방성이 결합된 매질로, 퇴적분지에서 셰일이나 연속된 얇은 교호층이 수직적으로 배열된 균열망과 함께 존재할 때 나타나는 현실적인 이방성 모델이다(Tsvankin, 1997; Oh and Alkhalifah, 2016). 사방정계 형태의 이방성 매질에서는 종등방성에 의해 균열에 평행한 방향과 균열에 수직인 방향의 탄성파 속도가, 횡등방성에 의해 균열에 평행한 방향과 지층에 수직인 방향의 속도가 달라지기 때문에, 최종적으로 세 방향의 탄성파 속도가 모두 다른 복잡한 특징을 갖는다. 따라서 복잡한 지질학적 구조를 갖는 사방정계 형태의 이방성 매질에서의 파동을 정확하게 구현하기 위해서는 수치모델링을 통한 접근이 요구된다. 또한 사방정계 형태의 이방성을 고려한 탐사자료 처리시 3차원 가정이 필수적이며 역시간 구조보정(RTM)이나 완전파형역산(FWI)의 적용을 위해서는 멀티코어 환경에서 모델링 알고리듬을 병렬화하는 것이 요구된다.
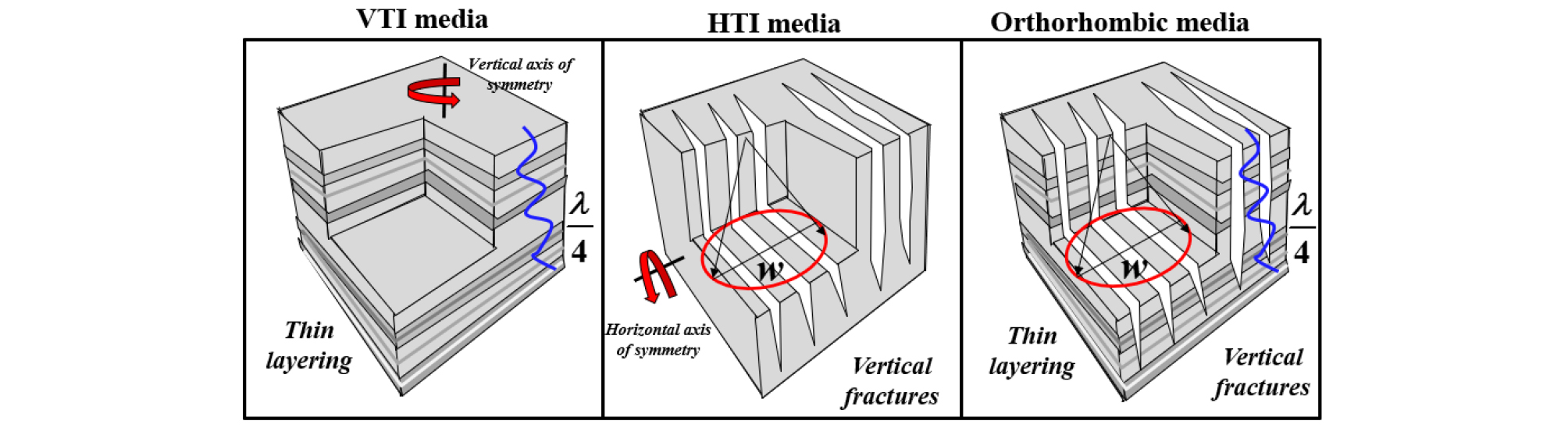
Fig. 3.
The VTI, HTI and orthorhombic models. Blue lines show the dominant wavelength of seismic waves related to the vertical resolution (a quarter of wavelength) and red circles show the horizontal resolution limit related to the Fresnel zone. The parameters, λ and w, indicate the wavelength and width of the Fresnel zone.
사방정계 이방성 매질에 대한 탄성 파동방정식
사방정계 형태의 이방성 매질에 대한 3차원 탄성파동방정식은 응력-변형률 관계와 뉴턴의 운동방정식에 의해 다음과 같이 표현된다(Graves, 1996).
| $$\rho\frac{\partial^2u_x}{\partial t^2}=\frac{\partial\tau_{xx}}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}+\frac{\partial\tau_{xz}}{\partial z}+f_x$$ | (2) |
| $$\rho\frac{\partial^2u_y}{\partial t^2}=\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\tau_{yy}}{\partial y}+\frac{\partial\tau_{yz}}{\partial z}+f_y$$ | (3) |
| $$\rho\frac{\partial^2u_z}{\partial t^2}=\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}+\frac{\partial\tau_{zz}}{\partial z}+f_z$$ | (4) |
Cij는 탄성계수, ρ는 밀도, (τxx, τyy, τzz)은 각각 X, Y, Z 방향의 수직응력, (τyz, τxz, τxy)은 각각 YZ, XZ, XY 단면상에서의 전단응력을 의미하며, (ux, uy, uz)는 각각 X, Y, Z 방향에 따른 입자 변위이다. (fx, fy, fz)는 방향에 따른 체적력 형태의 탄성파 송신원이다. 사방정계 형태의 이방성 매질에서는 식 (1)과 같이 탄성계수 C11, C22, C33가 다르기 때문에 X, Y, Z 세 방향에 따른 P파 속도가 다르며, YZ, XZ, XY 단면상에서의 전단계수인 C44, C55, C66가 다르기 때문에 전파방향에 따라 SV파, SH의 속도가 다르다.
이 때 수직방향의 P파 속도(VP0)와 XZ단면을 따라 전파하는 SV파의 속도(VS0)는 다음과 같이 표현된다.
| $$V_{P0}=\sqrt{\frac{C_{33}}\rho}$$ | (5) |
| $$V_{S0}=\sqrt{\frac{C_{55}}\rho}$$ | (6) |
사방정계 매질에서의 방향에 따른 탄성파 속도의 변화는 Thomsen의 이방성 변수(ε, δ, γ)에 의해 정의될 수 있으며 탄성계수(Cij)와는 다음과 같은 관계를 갖는다(Thomsen, 1986; Tsvankin, 1997).
| $$\varepsilon_1=\frac{C_{11}-C_{33}}{2C_{33}}$$ | (7) |
| $$\varepsilon_2=\frac{C_{22}-C_{33}}{2C_{33}}$$ | (8) |
| $$\gamma_1=\frac{C_{66}-C_{55}}{2C_{55}}$$ | (9) |
| $$\gamma_2=\frac{C_{66}-C_{44}}{2C_{44}}$$ | (10) |
| $$\delta_1=\frac{{(C_{13}-C_{55})}^2-{(C_{33}-C_{55})}^2}{2C_{33}(C_{33}-C_{55})}$$ | (11) |
| $$\delta_2=\frac{{(C_{23}-C_{44})}^2-{(C_{33}-C_{44})}^2}{2C_{33}(C_{33}-C_{44})}$$ | (12) |
| $$\delta_3=\frac{{(C_{12}-C_{66})}^2-{(C_{11}-C_{66})}^2}{2C_{11}(C_{11}-C_{66})}$$ | (13) |
이방성 변수 ε과 δ는 방향에 따른 P파와 SV파의 속도를 결정짓는 변수로 ε1과 δ1은 XZ 단면 상에서의 전파 방향에 따른 속도 차이를, ε2와 δ2는 YZ 단면 상에서의 전파 방향에 따른 속도 차이를 유발한다. γ1과 γ2는 각각 YZ, XZ 단면 상에서 SH파의 전파방향에 따른 속도 변화를, δ3는 방위각에 따른 이방성의 변화를 결정짓는 변수이다. 이 연구에는 사방정계 이방성에 따른 방위각 방향의 변화를 정의하는 편차 변수(deviation parameters; Oh and Alkhalifah, 2016)를 이용하여 사방정계 이방성 모델의 물성을 정의하였다.
| $$\varepsilon_D=\frac{\varepsilon_2-\varepsilon_1}{1+2\varepsilon_1}$$ | (14) |
| $$\delta_D=\frac{\delta_2-\delta_1}{1+2\delta_1}$$ | (15) |
| $$\gamma_D=\frac{\gamma_1-\gamma_2}{1+2\gamma_2}$$ | (16) |
사방정계 이방성 매질에서의 탄성파의 거동
사방정계 형태의 이방성 매질을 고려한 모델링 알고리듬의 정확성 검증을 위해서는 이론적인 해와의 비교가 필수적이다. 이를 위하여 사방정계 매질에서의 P, SV, SH파의 거동을 위상속도 식을 이용하여 이론적으로 계산할 수 있다(Tsvankin, 1997). 먼저 사방정계 이방성 매질에서 입사각(θ)와 방위각(ϕ)에 따른 P파의 위상 속도는 다음과 같다.
| $$V_p(\theta,\;\phi)=V_{p0}\lbrack1+\delta(\phi)\sin^2\theta\cos^2\theta+\varepsilon(\phi)\sin^4\theta$$ | (17) |
이 때, ε(ϕ)와 δ(ϕ)는 방위각에 따른 이방성 변수 ε과 δ의 변화로 다음과 같이 표현될 수 있다.
| $$\varepsilon(\phi)=\varepsilon_2\sin^4\phi+\varepsilon_1\cos^4\phi+(2\varepsilon_1+\delta_3)\sin^2\phi\cos^2\phi$$ | (18) |
| $$\delta(\phi)=\delta_1\sin^2\phi+\delta_2\cos^2\phi$$ | (19) |
식 (14)에서 확인할 수 있듯이, 이방성 변수 ε은 수평방향의 P파 속도에 주로 영향을 주며(θ = 90°), 이방성 변수 δ는 주로 대각방향의 P파 속도에 영향을 준다(θ = 45°). 이방성 변수 ε과 δ가 같을 때 P파의 파면은 정확히 타원형을 가지게 된다(elliptical anisotropy; Helbig, 1983). 식 (15)와 같이 δ3는 수평 대각방향의 전파에 영향을 주는 변수이다.
사방정계 이방성 매질에서 SV파는 XZ, YZ 단면에서 다른 속도를 가지게 되는데, 각 단면 상에서의 입사각에 따른 위상속도는 다음과 같다.
| $$V_{SV}^{x-z}(\theta)=V_{S0}\left(1+\left(\frac{V_{P0}}{V_{S0}}\right)^2\left(\varepsilon_1-\delta_1\right)\sin^2\theta\cos^2\theta\right)$$ | (20) |
| $$V_{SV}^{x-z}(\theta)=V_{S0}\left(1+\left(\frac{V_{P0}}{V_{S0}}\right)^2\left(\varepsilon_2-\delta_2\right)\sin^2\theta\cos^2\theta\right)$$ | (21) |
SH파에 의한 입자의 운동방향은 XZ, YZ 단면 상에서 각각 Y방향, X방향이며, 각 단면상에서의 위상속도는 다음과 같다.
| $$V_{SV}^{x-z}(\theta)=V_{S0}\sqrt{\frac{1+2\gamma_1}{1+2\gamma_2}}\sqrt{1+2\gamma_2\sin^2\theta}$$ | (22) |
| $$V_{SH}^{y-z}(\theta)=V_{S0}\sqrt{1+2\gamma_1\sin^2\theta}$$ | (23) |
사방정계 이방성을 고려한 병렬 탄성파 모델링 알고리듬
엇격자 유한차분법(Staggered grid finite difference method)
3차원 탄성 파동방정식을 수치해석적으로 모델링하기 위하여 가장 널리 사용되는 방법은 식 (1)~식 (4)의 공간 1차 미분을 정확하게 계산할 수 있는 엇격자 유한차분법을 이용하는 것이다(Graves, 1996). 엇격자 유한차분법에서 수직응력과 매질의 물성은 같은 격자점에 정의되며, 전단응력(τyz, τxz, τxy)은 각각 Y, Z 방향, X, Z 방향, X, Y 방향으로 반 격자 씩, 입자 변위(ux, uy, uz)는 각각 X, Y, Z 방향으로 반 격자 씩 떨어져 있다(Fig. 4). 사방정계 이방성 탄성 파동방정식에 대한 엇격자 유한차분법은 등방성 탄성 파동방정식에 대한 유한차분법과 구조적으로 같으며(Graves, 1996), 탄성계수(Cij)를 사방정계에 맞게 변경함으로써 동일하게 수행될 수 있다. 이 연구에서는 모델 경계에서 발생하는 반사파를 제거하기 위하여 CPML(Convolutional Perfectly Matched Layer) 경계조건을 사용하였다(Komatitsch and Martin, 2007; Cho and Lee, 2009).
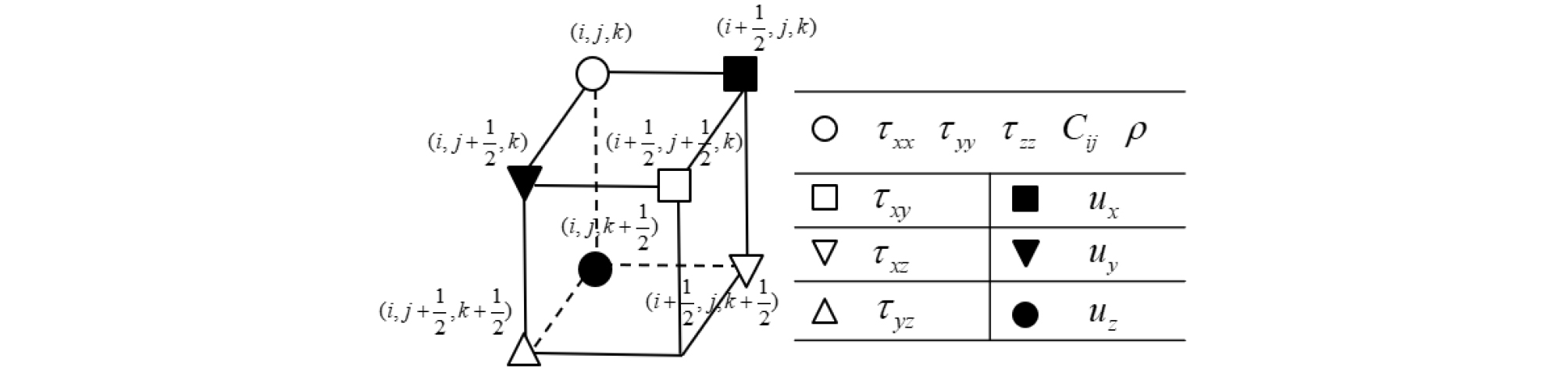
Fig. 4.
Grid layout for a standard staggered-grid formulation (modified from Graves, 1996). A unit cell consists of particle displacements, normal and shear stresses. The elastic coefficients (Cij) and the density are located on the same grid as the normal stresses.
영역 분할법(Domain decomposition)
앞서 언급된 것과 같이 사방정계 형태의 이방성 매질을 고려한 모델링은 필수적으로 3차원 가정이 필요하기 때문에 멀티코어 환경에서 모델링 알고리듬을 병렬화하는 것이 요구된다. 이 연구에서는 MPI(Message Passing Interface)를 이용한 영역분할법(Domain decomposition)을 적용하여 모델링 알고리듬의 병렬화를 수행하였다. Fig. 5는 공간 2차 정확도 유한차분법에서 3차원 탄성 파동방정식의 병렬화를 이용한 영역 분할법 원리를 보여준다. 설명의 편의를 위하여 전체 모델 영역(global domain)을 X방향과 Y방향으로 각각 2개씩, 총 4개의 소 영역(sub domain)으로 나누었으며, 각각의 프로세서(예, 코어)는 각 소 영역의 파동방정식을 동시에 계산하게 된다. 이 때 각 소 영역의 경계에서 유한차분법을 수행하기 위해서는 인접 프로세서의 파동장 값이 필요하므로 MPI_Send와 MPI_Recv 명령어를 이용하여 주변 프로세서와 이전 시간의 파동장 값을 교환해야 한다. 교환된 이전 시간의 파동장 값을 패딩영역(padding area)에 저장하면 현재 시간의 파동장 값을 마치 각 소 영역이 연속적으로 연결된 것처럼 계산할 수 있다. 이 연구에서는 수치 분산 효과를 줄이기 위하여 공간 4차 정확도 유한차분법(4th-order finite difference method)을 이용하였으며, Fig. 5의 공간 2차 미분 유한차분법과 비교할 때, 인접 두 격자점의 파동장 값이 필요하기 때문에 두 줄의 패딩영역이 필요하다.
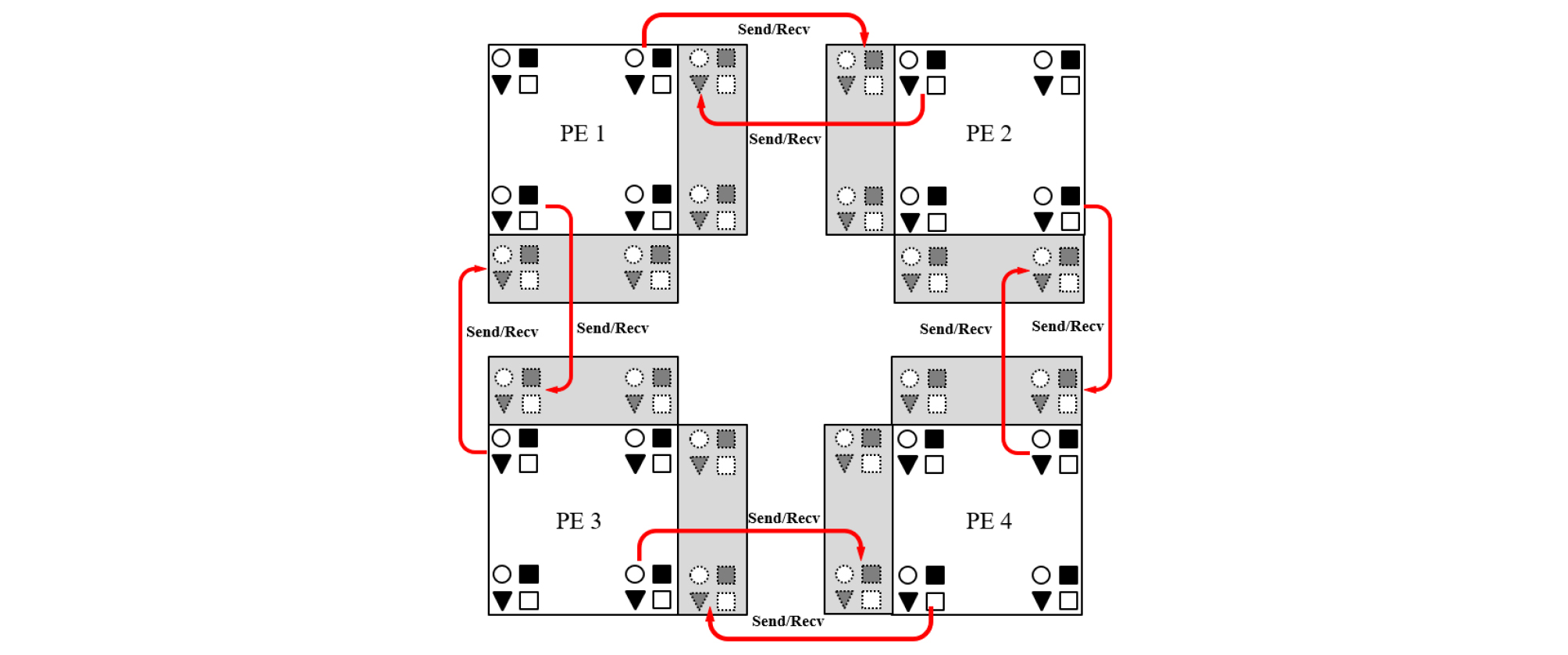
Fig. 5.
Decomposition of the global domain into subdomain computed by a different processing element (PE). Red arrows illustrate MPI communication between subdomains to share wavefields at the boundaries of the subdomains (modified from Bohlen, 2002). Gray areas indicate the padding area to store boundary values and to calculate wavefields continuously.
수치 예제
모델링 알고리듬의 정확성 및 효율성 검증
이 연구에서 개발된 사방정계 형태의 이방성을 고려한 병렬 탄성파 모델링 알고리듬의 정확성과 효율성을 검증하기 위하여, 균질한 사방정계 이방성 모델에 대한 수치모델링을 수행하였다(Table 1). 밀도는 1 g/cm3으로 가정하였고 모델은 10 m 간격으로 X, Y, Z 방향으로 각각 400개의 격자를 가지며, 모델 경계에서 20장의 CPML 층을 추가하였고 총 2초 동안의 파동 전파를 모델링하였다. 송신원은 모델의 정중앙에 위치하며, 송신원 함수는 최대주파수가 10 Hz인 리커함수(Ricker wavelet)를 이용하였다.
Table 1. Homogeneous orthorhombic model parameters
| Parameter | VP0 | VS0 | $$\varepsilon_1$$ | $$\delta_1$$ | $$\gamma_1$$ | $$\varepsilon_D$$ | $$\delta_D$$ | $$\gamma_D$$ | $$\delta_3$$ |
| Value | 1.5 km/s | 0.866 km/s | 0 | 0.2 | 0.2 | 0.2 | 0 | 0.2 | 0.05 |
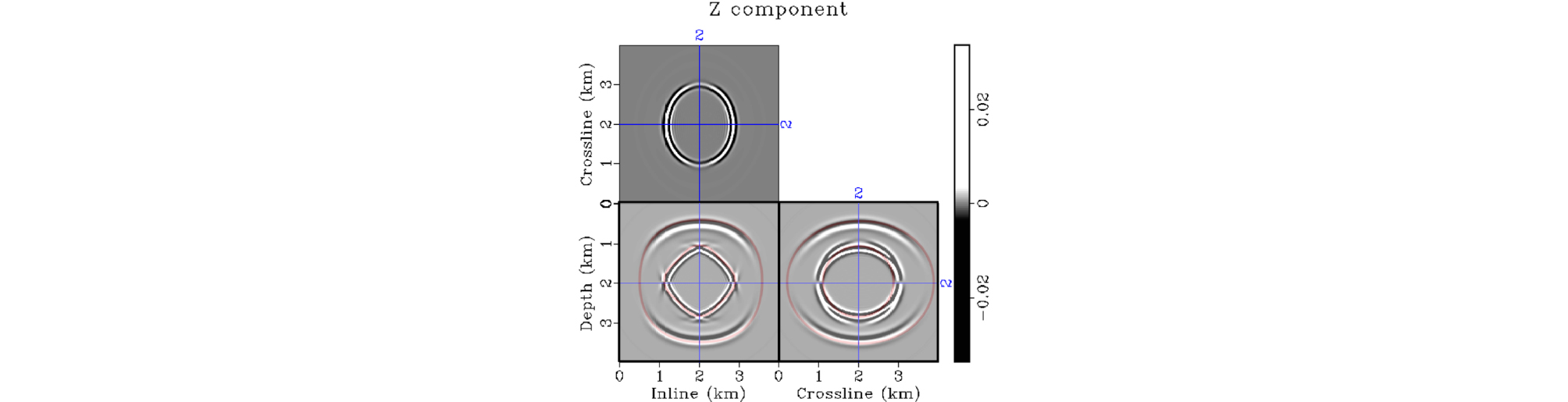
Figs. 6, 7, 8은 각각 모델링 결과 계산된 Z방향, X방향, Y방향 입자변위의 순간포착영상(snapshot)이다. 알고리듬의 검증을 위하여 먼저 각 파동의 위상속도를 이용해 계산된 이론해와 비교하였다. 먼저 Z방향 입자 변위(Fig. 6)에서 P파와 SV파의 움직임이 뚜렷하게 관찰되며, 수평적인 입자운동을 하는 SH파는 수직 변위에서 관측되지 않는다. XZ(ϕ = 0°)와 YZ(ϕ = 90°) 단면 상에서 나타나는 P파의 파면은 식 (17)에 의해 계산된 이론해와 잘 일치한다. XZ 단면상에서 P파는 이방성 변수 ε1이 0이기 때문에 수평 X 방향과 수직방향의 속도는 동일하지만 δ1에 의해 대각방향의 속도가 빨라져서 사각형 형태의 파면을 가지는 것이 특징이다. 반면 YZ 단면 상에서는 ε2가 0.2로 Y 방향으로의 수평방향 속도가 빨라졌고, δ2도 마찬가지로 0.2의 값을 가지기 때문에 타원형의 파면을 갖는 것이 특징이다. XZ 단면과 YZ 단면 상에서의 SV파의 이론해는 각각 식 (20)과 식 (21)에 의해 계산되었으며, XZ 단면 상에서는 대각 방향의 속도가 감소하여(ε1 -δ1 < 0) 마름모 형태의 파면을, YZ 단면 상에서는 등방향성을 갖는 것이 관찰된다(ε2 -δ2 = 0).
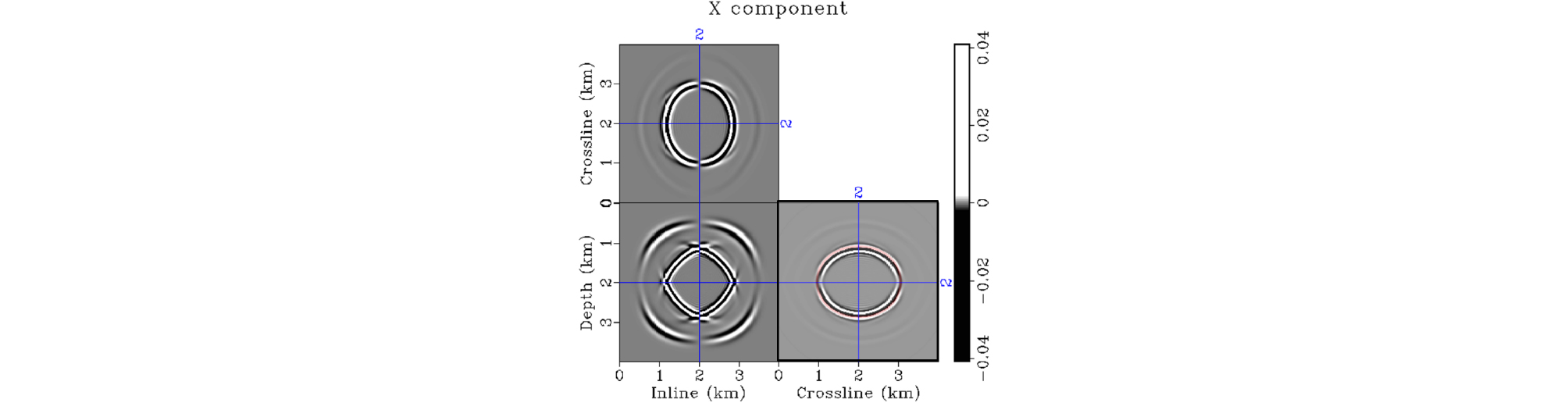
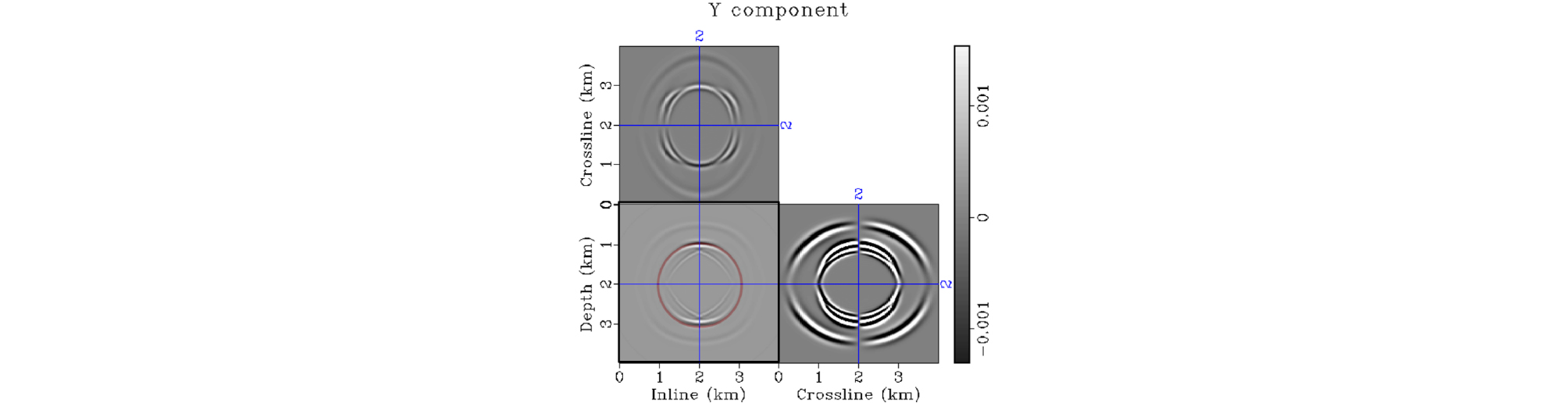
Fig. 7과 Fig. 8의 수평방향 변위를 보면, SV파의 X 방향 성분은 XZ 단면에서, Y 방향 성분은 YZ 단면에서 뚜렷하게 관찰된다. 반면에 SH파는 YZ 단면상에서는 X 방향으로 진동을, XZ 단면상에서는 Y 방향으로 진동하기 때문에, Fig. 7의 YZ 단면과 Fig. 8의 XZ 단면에서만 관찰된다. 각 수직단면에서의 SH파의 파면을 식 (22)와 식 (23)에 의해 계산된 이론해와 비교하였다. 먼저 YZ 단면상에서 나타나는 SH파의 X 성분을 보면(Fig. 7), 식 (20)에서 예측할 수 있듯이 γ1에 의해 수평방향 속도가 빠른 것이 특징이다. 반면 XZ 단면상에서 SH파는 γ2가 0이기 때문에 식 (19)와 같이 등방향성을 갖는다.
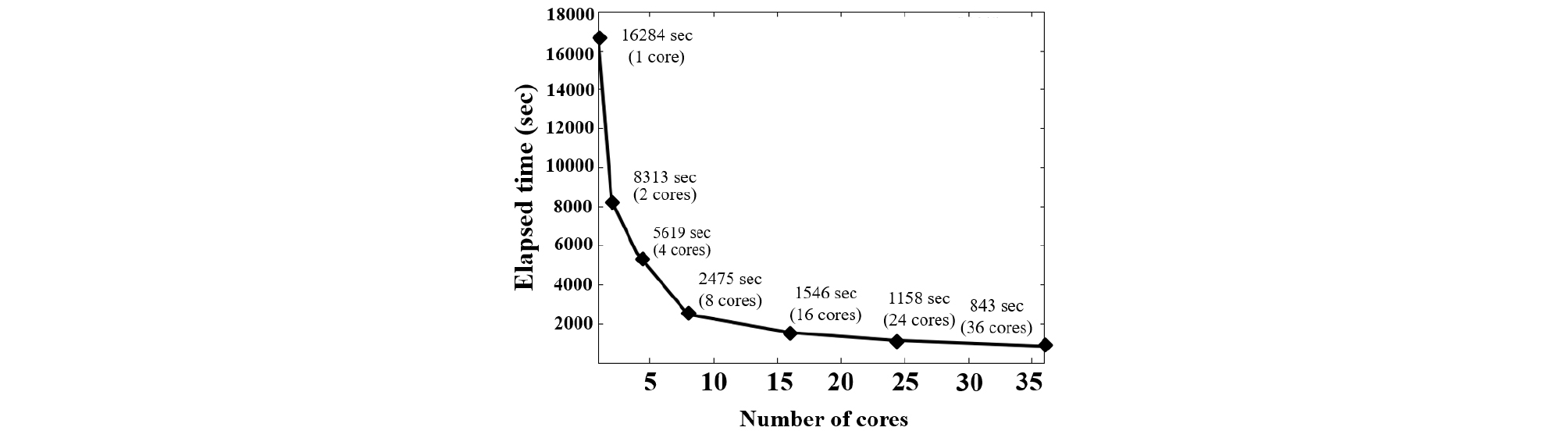
다음으로 MPI를 이용한 병렬 모델링 알고리듬의 효율성을 검증하기 위하여 확장성 실험(Scalability test)을 수행하였다. 이 연구에서 사용한 클러스터는 각각 192 GB의 RAM을 갖는 2대의 노드(node)로 구성되어 있으며, 각 노드 당 18개의 코어를 갖는 인텔 Xeon Gold 6150 CPU(Central Processing Unit)가 2개씩 설치되어 있어 한 노드에서 총 36개 코어로 병렬계산이 가능하다. 확장성 실험을 위하여 CPML 층을 포함하여 480 × 480 × 240인 모델을 X, Y 방향으로 (1 × 1), (2 × 1), (2 × 2), (4 × 2), (4 × 4), (6 × 4), (6 × 6)의 소 영역으로 분할하였고, 각각 1개, 2개, 4개, 8개, 16개, 24개, 36개의 코어를 동시에 활용하여 병렬계산을 수행하였다. Fig. 9와 같이 소 영역을 작게 분할할수록 계산속도가 단축되는 것을 확인할 수 있다.
영역 분할법은 MPI를 기반으로 하기 때문에 openmp를 이용한 병렬화와 다르게 두 노드를 모두 활용하여 72개의 소 영역으로 나누는 것이 가능하다. 하지만 다른 노드에 있는 코어와의 자료 교환은 동일 노드 내에서의 교환 속도보다 현저히 떨어지기 때문에, 효율성을 위해서는 한 노드 안에서 사용가능한 36개의 코어로 영역을 분할하는 것이 바람직하다. 하지만 한 대의 노드가 가진 메모리보다 큰 규모의 광범위한 3차원 모델링에서는 다수의 노드를 동시에 활용한 영역 분할법이 필수적이다. 또한 많은 송신원 자료를 처리해야 하는 RTM이나 FWI에서는 충분한 규모의 클러스터가 이용 가능하다면, 한 노드 당 하나의 송신원에 대한 모델링을 수행하면서 한 노드 안에서는 영역분할법을 이용하여 각 코어가 각 소 영역의 파동방정식을 계산하는 이중 병렬화를 수행할 수 있다(Oh et al., 2018).
3차원 SEG/EAGE 오버스러스트 모델에 대한 적용
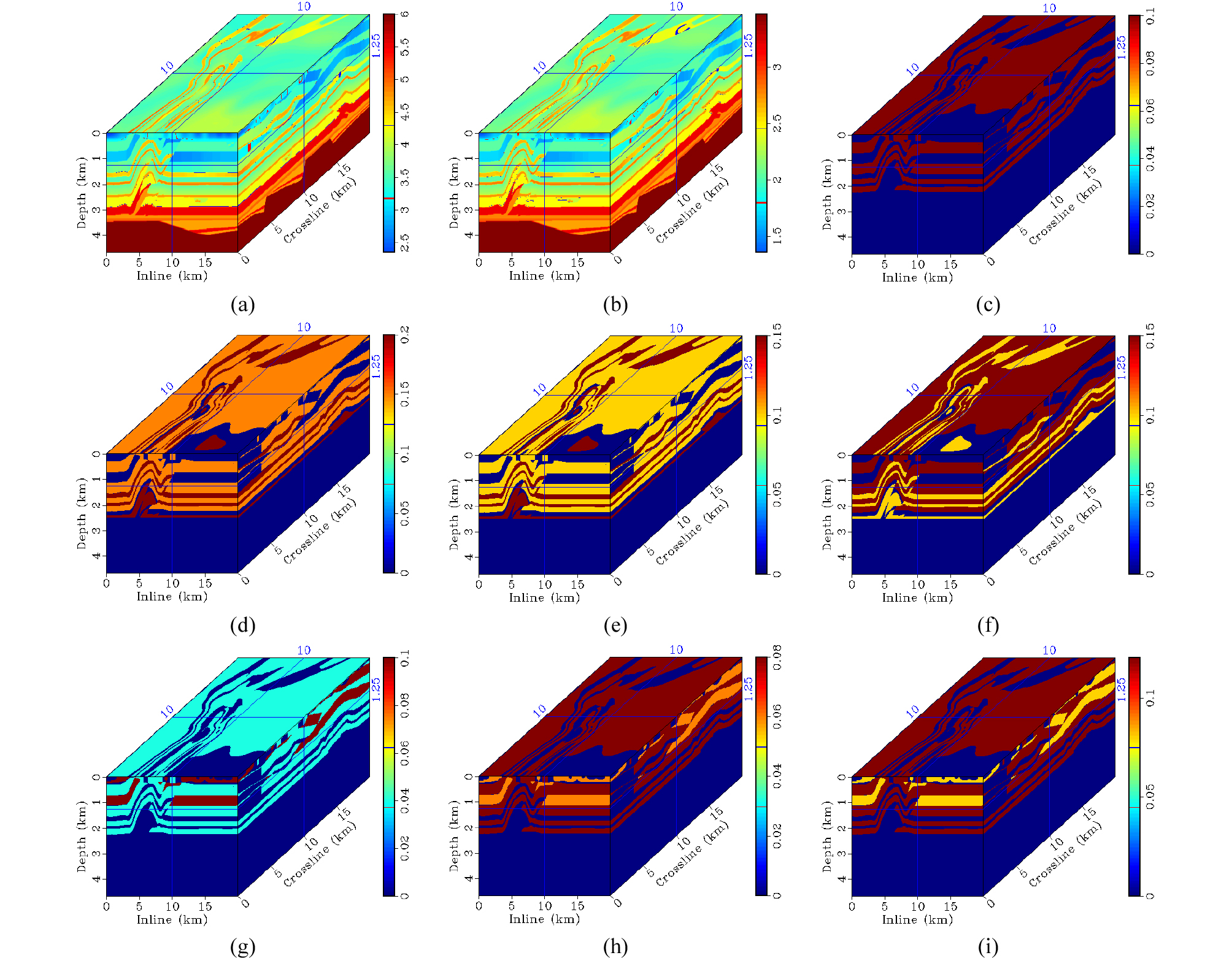
마지막으로 복잡한 사방정계 이방성 지질모델에 대한 병렬 탄성파 모델링 알고리듬의 적용성 검토를 위하여 3차원 SEG/EAGE 오버스러스트 모델(Aminzadeh et al., 1997)에 대한 수치 모델링을 수행하였다. SEG/EAGE 오버스러스트 모델은 P파 속도 모델로 25 m 간격으로 800 × 800 × 187개의 격자를 가진 큰 규모의 3차원 모델이다. 20장의 CPML 층을 추가하였으며, 최대주파수가 15 Hz인 리커함수를 모델 표면의 중앙에 적용하여 총 3초 동안의 파동 전파를 모델링하였다. 탄성 사방정계 이방성 매질을 만들기 위하여, 포아송비를 0.25로 하여 S파 속도 모델을 구축하였고, 이방성 변수는 Fig. 10과 같이 상부에 강한 이방성을 가지도록 설정하고 밀도는 1 g/cm3으로 가정하였다. Fig. 11에서는 사방정계 이방성을 고려한 파동방정식을 계산하여 얻은 수직 변위, Fig. 12에서는 주어진 P파 속도와 S파 속도만을 이용한 등방성 파동방정식을 계산하여 얻은 수직 변위를 확인할 수 있다. 상부의 지층들이 강한 사방정계 이방성을 가지고 있기 때문에 등방성 매질에서의 결과와 비교하여 전파 양상이 복잡하여, 전반적으로 수평방향으로 속도가 빠른 것을 확인할 수 있다.
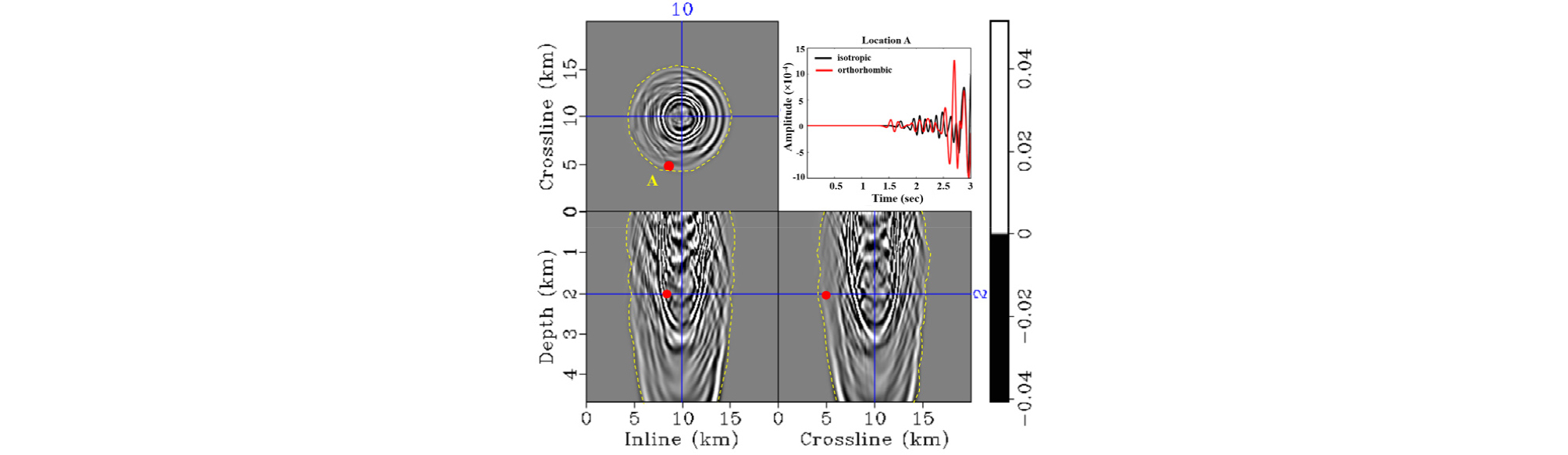
Fig. 11.
The snapshots of the particle displacement along Z direction on the orthorhombic model at 1.5 sec (Fig. 10). A seismic trace is recorded at location A (red dot) and shows the differences between orthorhombic modeling and isotropic modeling result (Fig. 12). Yellow dashed lines indicate approximated first arrivals on each snapshot.
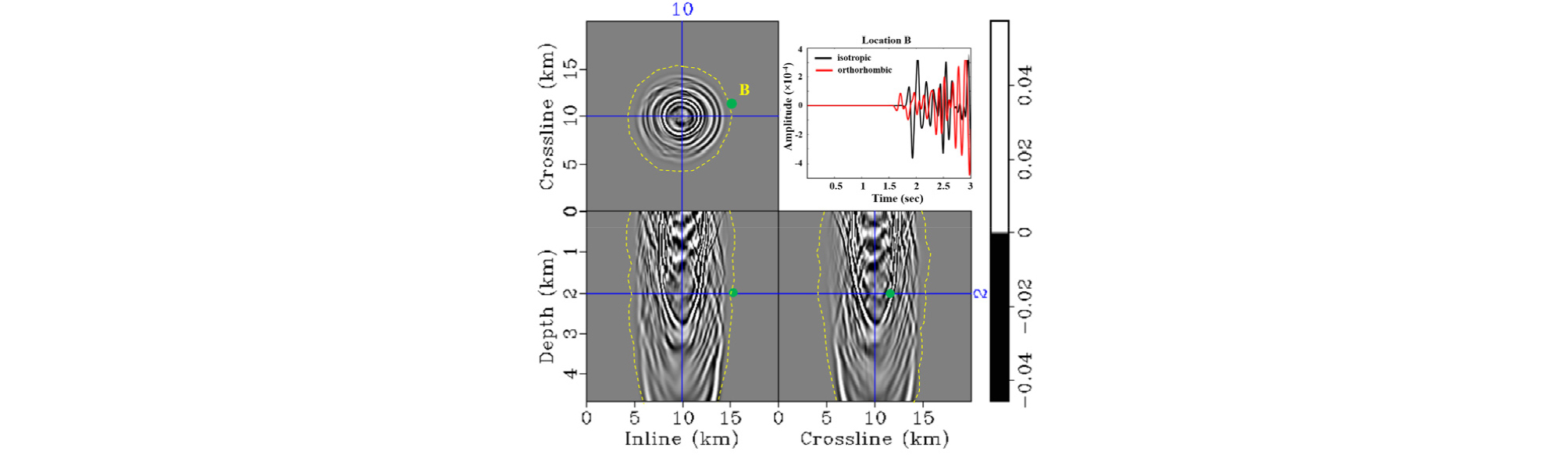
Fig. 12.
The snapshots of the particle displacement along Z direction on the isotropic model at 1.5 sec (only Fig. 10a and 10b). A seismic trace is recorded at location B (green dot) and shows the differences between orthorhombic modeling (Fig. 11) and isotropic modeling result. Yellow dashed lines from Fig. 11 are overlaid on each snapshot.
결 론
이 연구에서는 사방정계 형태의 이방성 매질을 고려한 탄성파 모델링 알고리듬을 제안하였다. 먼저 탄성파 이방성의 세 가지 주요한 원인을 지질학적인 관점에서 설명하고자 하였다. 퇴적분지에서는 셰일층의 이방성, 파장에 비해 얇은 지층의 교호, 수직적으로 배열된 방향성을 갖는 균열망에 의해 방향에 따른 탄성파 속도가 다를 수 있으며, 이를 반영할 수 있는 가장 현실적인 모델이 사방정계 형태의 이방성 매질이다. 사방정계 형태의 이방성 매질에서의 탄성 파동방정식을 엇격자 유한차분법을 이용하여 수치해석적으로 계산하였으며, 3차원 모델링 알고리듬의 효율성을 증가시키기 위하여 영역 분할법을 이용하여 알고리듬을 병렬화하였다. 균질한 사방정계 이방성 모델에 대한 수치모델링 결과를 P, SV, SH파의 위상속도에 대한 이론해와 비교한 결과, 사방정계 이방성에 의한 각 파동의 파면이 일치하였다. 또한 확장성 실험을 통해 멀티코어 환경에서의 효율성을 검토한 결과, 영역 분할을 많이 할수록 확장성은 다소 떨어지나 계산속도가 빨라지는 것을 확인하였다. 마지막으로 3차원 SEG/EAGE 오버스러스트 모델에 대해 개발된 알고리듬을 적용함으로써, 복잡한 지질모델에 대한 적용성을 검토하였다.