서 론
본 론
DEM 개요
DEM에 의한 분쇄기 내 에너지 분포 도출
다양한 분쇄 장비 운전 모사에 DEM의 활용 사례
PBM-DEM 연계 해석 및 ANN의 활용
미립자에 대한 이산요소의 적용 및 해결 과제
결 론
서 론
원광으로부터 유용광물과 맥석을 분리, 정광을 선별하는 선광 분야 연구는 오랜 기간 경험적, 현상학적 접근법에 의존해 왔다. 선광 분야 대부분의 분쇄 장비와 분리 장비들은 블랙박스 형태로 가동되며 장비 거동에 따른 시료 특성의 변화에 대한 직접적 접근이 용이하지 않다. 이에 장비 내에서의 매질과 광물의 거동은 일반적으로 단순화된 가정 하에서의 이론적 모델을 바탕으로 수립된 가설을 통해서, 혹은 경험적 데이터에 의존하여 분석될 수밖에 없는 한계를 가진다.
이에 선광 공정에 대한 모델링 연구는, 개별 분쇄 장비에 투입된 시료특성과 처리 결과물 간의 상관 관계를 실험적으로 분석, 시료 특성, 운전 조건, 장비 설계 조건 등에 따른 단위 분쇄 공정의 성능 지수를 후시적으로 규명하여 경험적 모델을 도출하는 방식으로 진행되어 왔다. 이러한 형태의 모델들은 지금까지도 분쇄 분야 연구의 주류를 이루고 있으며 산업 현장에서는 이러한 경험적 모델들에 의존하여 공정 설계 및 장비 설계가 이루어지고 있다. 예를 들어 분쇄 장비의 운전 조건 결정은 에너지-입도 관계 모델(Rittinger, 1867; Kick, 1885; Bond, 1952)을 바탕으로 목적 입도에 따른 투입 에너지를 결정하거나, 1970-1980년대 물질수지모델(population balance model, PBM)(Austin and Luckie., 1972; Austin et al., 1984; Herbst and Fuerstenau, 1980; Whiten, 1974)을 활용하여 장비 운전 및 설계 조건을 결정해 왔다.
이러한 경험론적, 현상학적 모델들은 모두 장비 내부의 거동 혹은 분쇄 기작에 대해 단순화된 가정에 근거하며, 일반론적 관점에서 엔지니어링을 위한 기초 정보를 제공해 주는 역할을 수행하지만, 실제 공정에 보다 적절한 장비를 선택하거나 새로운 기작의 장비를 설계하는 등 공정 최적화에의 적극적 대응성을 저하시킨다는 단점이 있다. 장비 설계 및 운전 조건 변경에 따른 성능 향상은 일반적으로 성공적 사례에 대해서만 보고되고 있으나, 실제 현장에서는 경험적 근거를 바탕으로 한 개별 공정의 최적화에 일반적으로 수년의 시간이 소요된다(Mackey and Nessett, 2003).
이와 같은 과정을 거쳐 검증, 개선된 설계는 사실상 해당 공정의 대상이 되는 광석에 대해서만 유효하며 다른 광체에 대해서는 다시 최적화 작업을 거쳐야 한다. 또한 개별 광물에 대한 모델이 성공적으로 수립된 경우에도, 광석 내 혼합비를 이용하여 모델을 확장 적용할 때 정확도와 신뢰도가 심각하게 저하되게 된다. 경험론적, 현상학적 모델은 대상 광석 변화에의 확장성, 회로 변화에의 확장성 양쪽 측면에서 모두 심각한 취약성을 내포하고 있다.
현상학적, 경험적 모델의 이러한 한계로 인해 기계론적 해석 모델을 활용한 기작 분석 및 설계의 필요성은 날이 갈수록 증가하는 추세이며, 이 과정에서 입자를 다루는 선광 공정의 특성상 기존 유한요소법(finite element method, FEM), 유한차분법(finite difference method, FDM), 유한체적법(finite vloume method, FVM)적 접근과 차별화되는 입자 해석법(particle method)은 선광 분야 및 입자 산업 분야에서 그 활용도를 점차 높여 왔다. 입자를 매개체로 시스템을 해석하는 입자 해석법은 실체적 입자를 다루는 이산요소법(discrete element method, DEM), 분자동역학(molecular dynamics, MD)에서부터 연속체 방정식 해석을 위한 수학적 도구로서의 입자를 다루는 완화입자유체동역학(smoothed particle hydrodynamics, SPH), 반음해이동입자법(moving particle semi-implicit, MPS), 격자볼츠만법(lattice boltzmann method, LBM) 등에 이르기까지 광역의 방법론들을 포괄한다. 특히 DEM은 입자 패킹(Yen and Chaki, 1992; Yu et al., 2006), 분리(Knight et al., 1993; Mishra and Tripathy, 2010; Kwon et al., 2017), 교반(Stewart et al., 2001; Basinskas and Sakai, 2016) 등 선광 및 입자 산업 분야 전반에서 널리 활용되고 있다.
파분쇄 분야에서 DEM은 최근 20여년간 분쇄 기작 연구에 중요한 역할을 수행해 왔다. 초기 장비 내 에너지 스펙트럼 분석 중심으로 활용되던 DEM은 입자내 균열의 발생 및 전파, 파쇄, 장비 마모에 이르기까지 다양한 현상을 입자 스케일의 정보를 활용하여 분석하는 도구로 활용되어 왔으며, 물질수지모델과의 연계 해석을 통해 공정 스케일 연구의 폭을 확장시키는 데도 기여해 왔다. 본 연구에서는 최근 DEM을 이용한 분쇄 연구 동향의 변화, 활용 사례, 추후 전망 및 해결 과제 등에 대해 세부적으로 살펴보았다.
본 론
DEM 개요
DEM은 입자의 운동 및 충돌을 역학적으로 계산, 입자 및 입상 흐름을 기계론적으로 모사하는 수치 해석 기법으로, 비연속, 과립계 거동 해석에서 효과적인 방법으로 그 적용성을 확대하고 있다. 전체 시스템을 연속체로 가정하고, 연속 방정식에 대한 적분해를 구하는 FEM, FVM 등과 달리, DEM은 개별 요소들을 이산적으로 존재하는 개체로 취급, 개별 요소간의 상호작용이 독립적으로 일어난다는 가정 하에 각 시간구간마다 개별의 입자가 받는 힘을 계산, 과립계를 구성하는 모든 개별 입자의 운동을 추적한다.
DEM에서 접촉 역학에 기반한 접촉힘은 입자 간 상호작용의 핵심 요소로 작용하며 입자 재료의 시간응답 이력 및 에너지 손실은 접촉 힘의 시간 적분에 의해 결정된다. 접촉 힘 모델은 일반적으로 Hertz 모델에 의한 비선형 모델과 Mindlin 의 전단 모델의 조합, 혹은 선형 스프링 형태로 단순화된 모델이 사용된다. 보존힘과 비보존힘은 Kelvin-Voight 점탄성 충돌모델로 표현될 수 있으며, 선형 스프링 모델 기반으로 충돌힘을 계산할 경우 다음과 같이 표현될 수 있다.
| $${\mathbf f}_{\mathbf n}(t)=K_n\delta_n(t)\widehat{\mathbf n}+C_n{\mathbf u}_{\mathbf n}(t)$$ | (1) |
여기서, 는 적용된 스프링의 수직 방향 강성 계수이며, 는 시간 에서 입자-입자 사이 혹은 입자-벽 사이에 발생한 수직 방향의 변형 성분의 크기, 는 수직 방향 단위 벡터이다. 은 완충 계수이며 는 충돌 상대 속도의 수직 방향 성분,. 이때 첫 번째 항 는 충돌 시 보존되는 탄성력이며 두 번째 항 는 충돌 시 비보존력으로 충돌 이력 중에 두 번째 항의 적분 값이 충돌에 의한 역학적 에너지의 소실 항이 된다. 전단 방향의 접촉 힘은 다음과 같다.
| $${\mathbf f}_{\mathbf s}(t)=\min(\vert K_s\delta_s(t)+C_su_s(t)\vert,\vert\mu f_n\vert)\widehat{\mathbf s}$$ | (2) |
는 전단 방향 단위 벡터이다. 전단 방향 접촉 힘을 계산하는 식 (2)는 (1)과 유사한 형태를 띄나 크게 두 가지 점에서 구별된다. 첫 번째로 전단방향의 변형 는 기하적 조건 뿐 아니라 하중 이력(loading history)에서 결정되는 값으로 가 중심 간의 단순 거리 계산을 통해 도출될 수 있는 것과 달리 증분(incremental) 형태로 결정되어야 한다. 두 번째로 단 방향의 최대 작용 힘은 Coulomb 마찰 법칙에 의해 수직 항력에 비례하는 임계 마찰력 로 제약된다.
는 전단 방향 단위 벡터이다. 전단 방향 접촉 힘을 계산하는 식 (2)는 (1)과 유사한 형태를 띄나 크게 두 가지 점에서 구별된다. 첫 번째로 전단방향의 변형 는 기하적 조건 뿐 아니라 하중 이력(loading history)에서 결정되는 값으로 가 중심 간의 단순 거리 계산을 통해 도출될 수 있는 것과 달리 증분(incremental) 형태로 결정되어야 한다. 두 번째로 단 방향의 최대 작용 힘은 Coulomb 마찰 법칙에 의해 수직 항력에 비례하는 임계 마찰력 로 제약된다.
DEM에서 시뮬레이션의 안정성을 위한 타임스텝은, 개별 입자의 질량, 속도 및 스프링 계수 등에 의해 영향을 받는다. 예를 들어 선형 스프링 모델의 경우 완전 탄성 충돌 시 입자의 충돌 시간은 로 특성화할 수 있다. 이 때 전체 충돌 시간은 스프링 계수가 증가할수록, 입자의 질량이 감소할수록 증가하며, 시뮬레이션의 타임스텝 또한 전체 충돌 시간에 비례하여 설정될 필요가 있다.
DEM에 의한 분쇄기 내 에너지 분포 도출
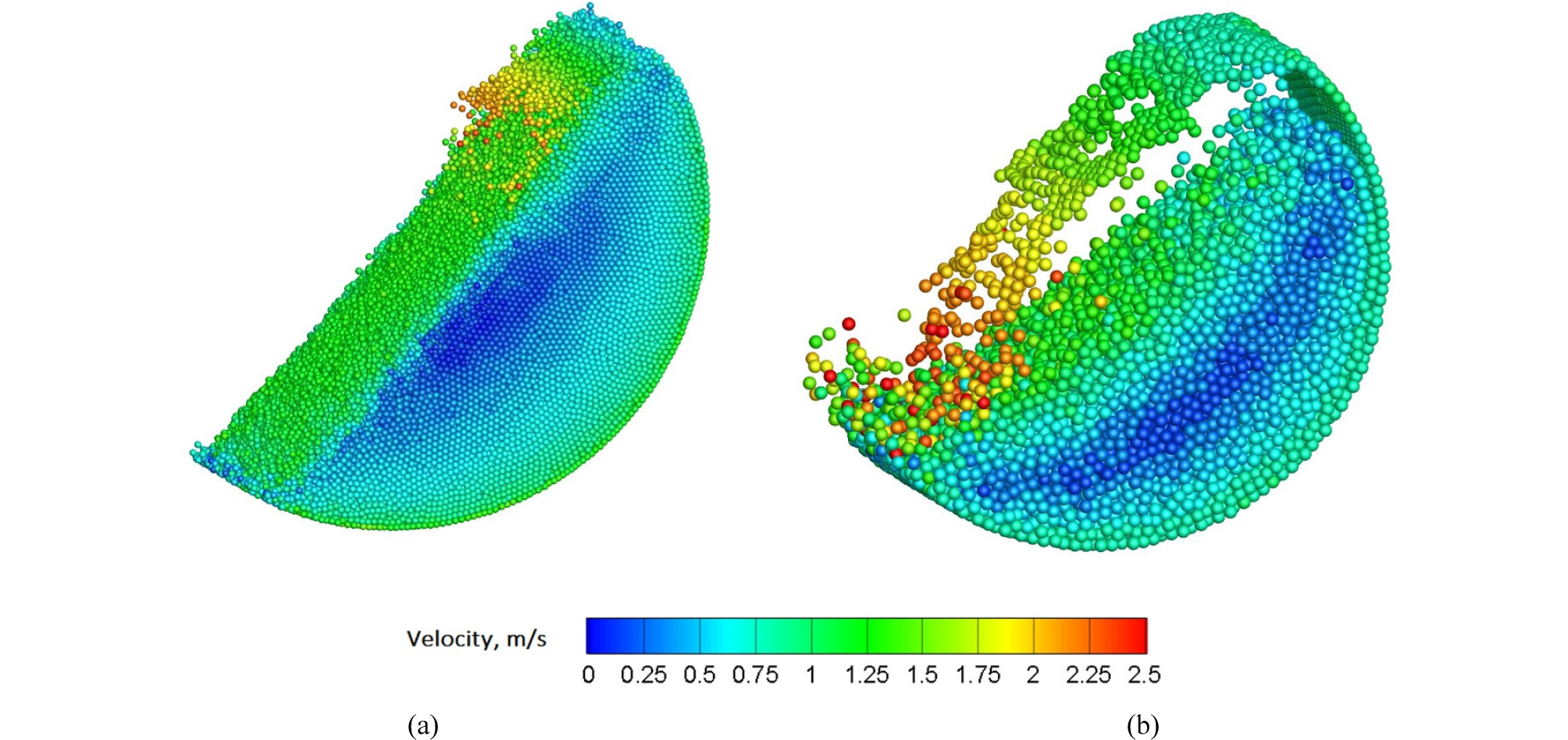
대표적 분쇄 장비인 볼밀에의 DEM 적용은 선광 분야에서의 첫 적용 사례로 1990년대 초반에 이루어졌다(Mishra and Rajamani, 1992; Mishra and Rajamani, 1994). 볼밀은 선광 분야의 대표적인 블랙박스 장비 중 하나로 운전 및 설계 조건에 따른 분쇄 에너지의 발생 양상은 데이터를 이용한 경험식 혹은 단순화된 해석적 모델을 통해서만 접근이 가능했다. Mishra and Rajamani는 DEM을 이용하여 볼밀 내 발생하는 충돌 에너지 스펙트럼을 분석하고자 하였으며, 카메라를 이용하여 실험 장치와 장비 내 볼의 움직임 등을 비교 검증하고자 하였다. 유사한 방식의 접근법들이 1990년대 및 2000년대에 선광 분야에서 활발히 진행되었으며, 장비 설계 인자 및 운전 조건에 따른 볼밀 거동 특성 변화를 DEM 기반으로 정량적으로 규명하고자 하였다 (Misra and Cheung, 1999; Datta et al., 1999; Nierop et al., 1999; Mishra and Thornton, 2001; Mishra and Thornton, 2002; Powell and McBride, 2004; Djordjevic, 2005; Monama and Moys, 2002).
DEM 기반의 볼밀 연구의 주 관심 분야는 밀 내 분쇄 매체에 의한 충돌 에너지 발생 양상인데 이 때 충돌에너지는 그 정의 방식에 따라 세 가지로 분류할 수 있다. 첫 번째는 충돌 힘의 적분에 의한 역학적 에너지의 손실분을 계산하는 방식으로 대시포트와 마찰력 항에 의해 발생하며, 수식으로 표현하면 다음과 같다.
| $$E_{diss}=\int_{t=t_0}^{t=t_1}\left[\int_{\boldsymbol r=\boldsymbol r(t_0)}^{\boldsymbol r=\boldsymbol r(t_1)}{\mathbf f}_{\mathbf c}(t)\bullet\mathbf{dr}\right]dt$$ | (3) |
여기서, 은 입자의 위치 벡터, 와 은 각각 충돌 시작 및 종료 시간이며, 는 접촉힘으로 수직방향 및 전단방향 성분의 합, 즉 이다. 이 때 소실 에너지는 마찰계수 및 반발계수 값에 직접적으로 영향을 받는다. 가장 많이 활용되고 있는 충돌 에너지 계산 방식 중 하나이나 (Mishra and Rajamani, 1992; Mishra and Rajamani, 1994; Datta et al., 1999; Hlungwani et al., 2003) 개별 충돌에 대한 소실 에너지의 적분이 시간에 따른 증분 형태로 계산되기 때문에 대용량 시뮬레이션 및 SIMD(single instruction multiple data) 기반의 GPU 병렬 프로세싱에 최적화되기 어려운 단점이 있다.
보다 단순화된 형태로 새로운 충돌 감지 시에 입자 간 상대 속도를 이용한 에너지 계산 방식이 있으며(Mori et al., 2004; Iwasaki et al., 2010), 이는 충돌 시작 시점에 즉각적으로 에너지를 계산하는 방식이다. 수식으로는 다음과 같이 표현된다.
| $$E_{cont}=\frac12\overline m\vert\mathbf u\vert^2$$ | (4) |
여기서, 은 충돌하는 두 입자의 평균 질량, 는 두 입자의 상대속도이다. 세 번째로 밀의 운전의 측면에서 동일 RPM을 유지하기 위해 필요한 전력 강하를 계산하는 방식으로 이는 밀에 작용하는 토크와 회전각속도의 내적으로 나타낼 수 있다 있다(Nierop et al., 1999; Nierop et al., 2001; Cleary., 1998).
| $$P_{draw}(t)=-\boldsymbol\omega\bullet\overset{}{\underset{\mathbf i}{\boldsymbol\sum}}{\mathbf T}_{\mathbf i}\boldsymbol(\boldsymbol t\boldsymbol)$$ | (5) |
여기서, 는 토크, 는 회전 각속도이다. 이 때 충돌에너지는 개별 충돌 에너지가 아닌 전력 강하로 도출된다. 이는 개별 충돌의 디테일한 분포보다 실제 밀 구동에서의 측정값과 동일한 정보의 도출이 더 중요할 때 활용될 수 있다.
물질수지 분쇄모델에서 볼밀의 분쇄율은 밀 크기, 볼 크기, 회전속도 등의 스케일업 인자에 영향을 받는다. 볼밀의 DEM 연구에서는 밀 내 충돌 에너지의 발생 추이와 이러한 설계 인자 간의 상관성을 분석하는 연구들이 이루어졌다 (Fig. 1). 이때 분쇄매체 및 밀 챔버의 물성 인자 값은 분석 결과의 신뢰도에 중요한 영향을 끼치는데 특히 기존 보고된 결과에 따르면 볼-벽 간 마찰 계수는 볼 궤적을 결정짓는 요소로 신중하게 결정될 필요가 있다(Nierop et al., 2001; Cleary, 2001).
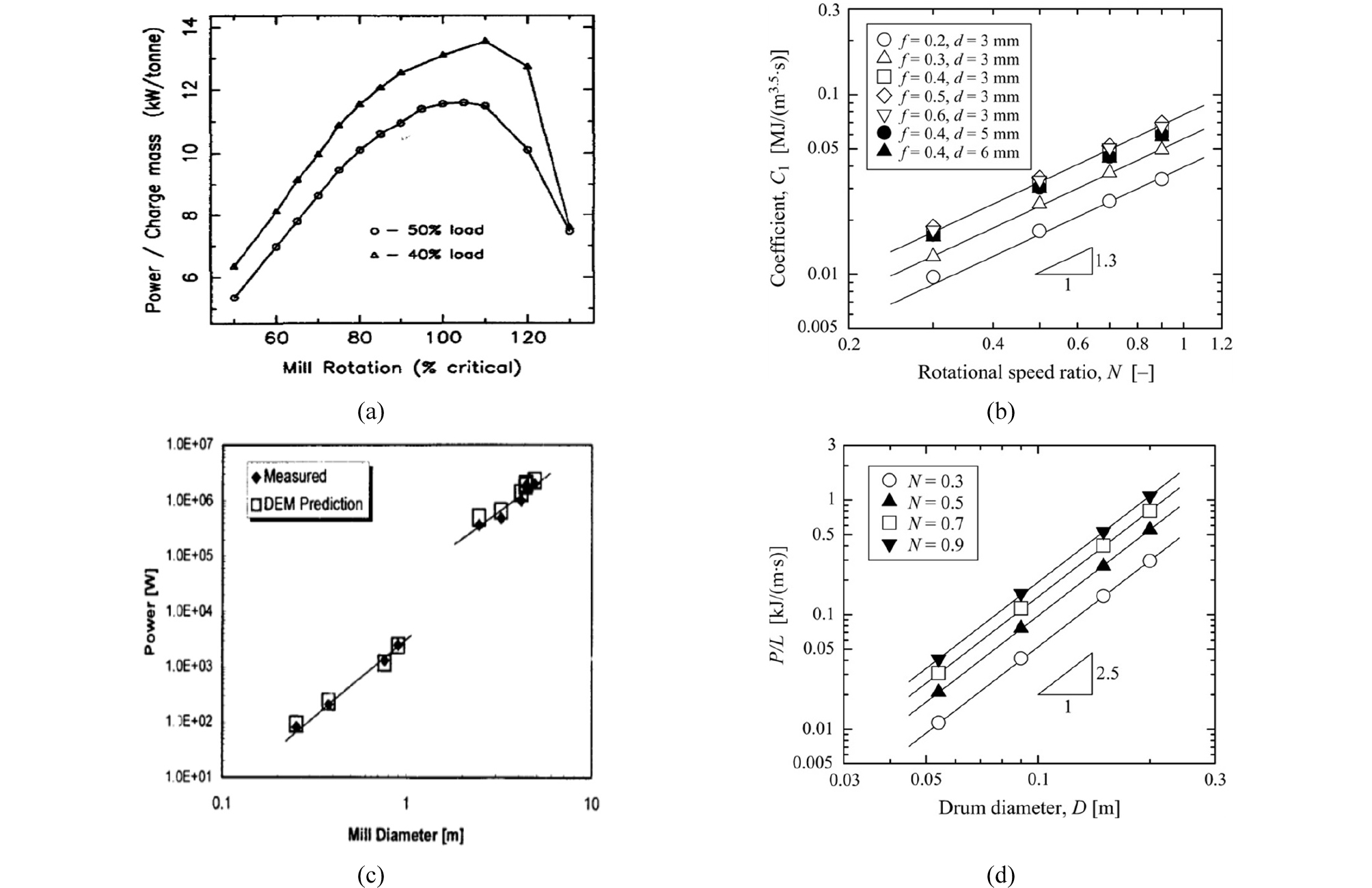
Fig. 1.
Relationship between mill scale-up factors and comminution energy using DEM. (a) rotational speed (Cleary, 1998) (b) rotational speed (Iwasaki et al., 2010) (c) mill diameter (Abd El-Rahman et al., 2001) and (d) mill diameter (Iwasaki et al., 2010).
다양한 분쇄 장비 운전 모사에 DEM의 활용 사례
분쇄 분야에서 DEM은 전통적인 볼밀 뿐 아니라 유성밀(Dallimore and McCormick, 1996; Hoyer, 1999), 원심밀(Inoue and Okaya, 1996), 교반밀(Sinnott et al., 2006; Sato et al., 2010) 등의 초미분쇄 장비에서부터 원광의 파쇄기에 이르기까지 다양하게 확장 적용되었다(Fig. 2). 유체 에너지를 이용하는 제트밀의 경우, DEM과 전산유체해석(computational fluid dynamics, CFD)의 연성해석 접근법들이 활용되었으며 몇몇 연구 사례가 보고된 바 있다(Brosh et al., 2014; Bnà et al., 2020). 그러나 미분체의 거동 해석의 경우 입자 수 증가에 의한 연산 부하 외에도 타임 스텝의 감소로 인한 연산 부하 등의 문제가 존재하며, 이러한 이유로 제트밀에의 DEM 적용 연구는 분쇄 에너지 분석 측면보다 입자의 분급 효과 및 거동 특성 규명에 주로 연구 초점이 맞춰져 있다.
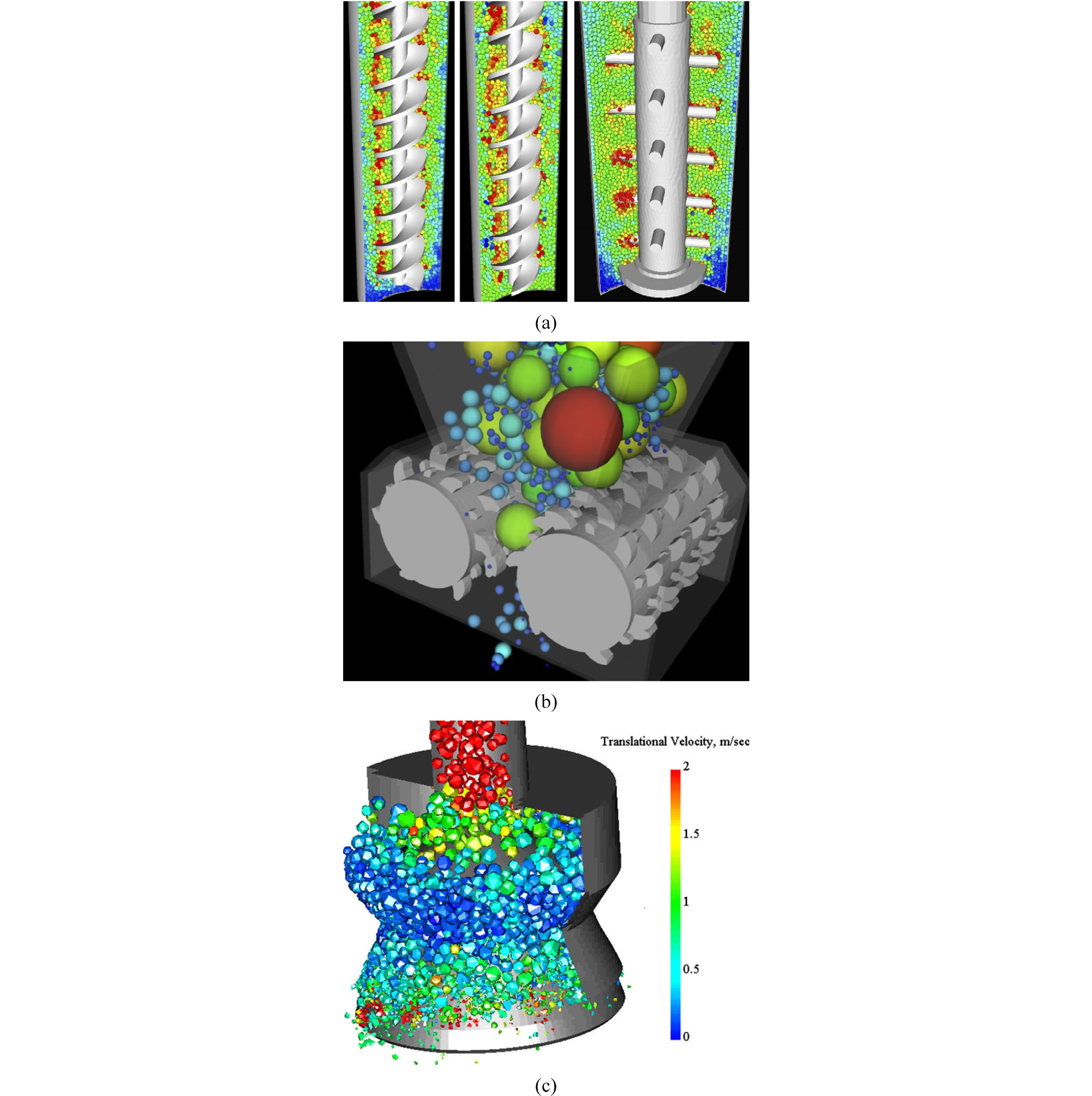
Fig. 2.
Application case of discrete element method in various grinding devices: (a) stirred mill (Sinnott et al., 2006) (b) double roll crusher (Cleary and Sinnot., 2015) (c) cone crusher (Lichter et al., 2009).
투입되는 입자의 수가 장비 시뮬레이션 스케일 대비 상대적으로 작은 파쇄 장비의 경우, 실제 결합입자모델(bonded particle model, BPM)을 활용한 분쇄 모사 접근법이 효과적으로 작용할 수 있다. 결합입자모델은 보다 미시적 관점에서 단일 입자를 알갱이(grain)와 알갱이 간의 교결(cementation)의 집합으로 표현하는 기법으로, Potyondy and Cundall (2004)에 의해 처음 고안되었다. 결합입자모델에서 입자간의 결합은 압축(인장)응력, 전단 응력, 비틀림 모멘트 및 휨 모멘트에 대한 저항력을 행사하며(Fig. 3), 임계 강도 이상의 수직 응력이 적용되었을 때 결합은 파괴된다. 결합입자모델은 단일 입자에서 초기 균열의 발생, 균열의 전파 및 파괴 양상을 미시적 관점에서 관찰할 수 있는 접근법으로, 취성 파괴에서의 크랙 발생 및 전파 양상을 분석하기 위한 도구로 고안 되었다. 분쇄 기작 및 분쇄 현상 모사의 측면에서 BPM은 응력 기작에 따른 1차 분쇄 분포의 형성 양상들을 분석하는 데에 활용될 수 있다. 이 때 단축 압축 파괴 테스트 등을 통해 결합강도 계수 및 신뢰도 있는 모델 인자들의 산정 과정이 필요하며, 특히 개별 결합에서 임계 전단 응력과 임계 인장/압축 응력의 비율은 외부 응력에 따른 입자의 파괴 양상에 중요한 영향을 끼치므로 신중하게 결정되어야 한다.
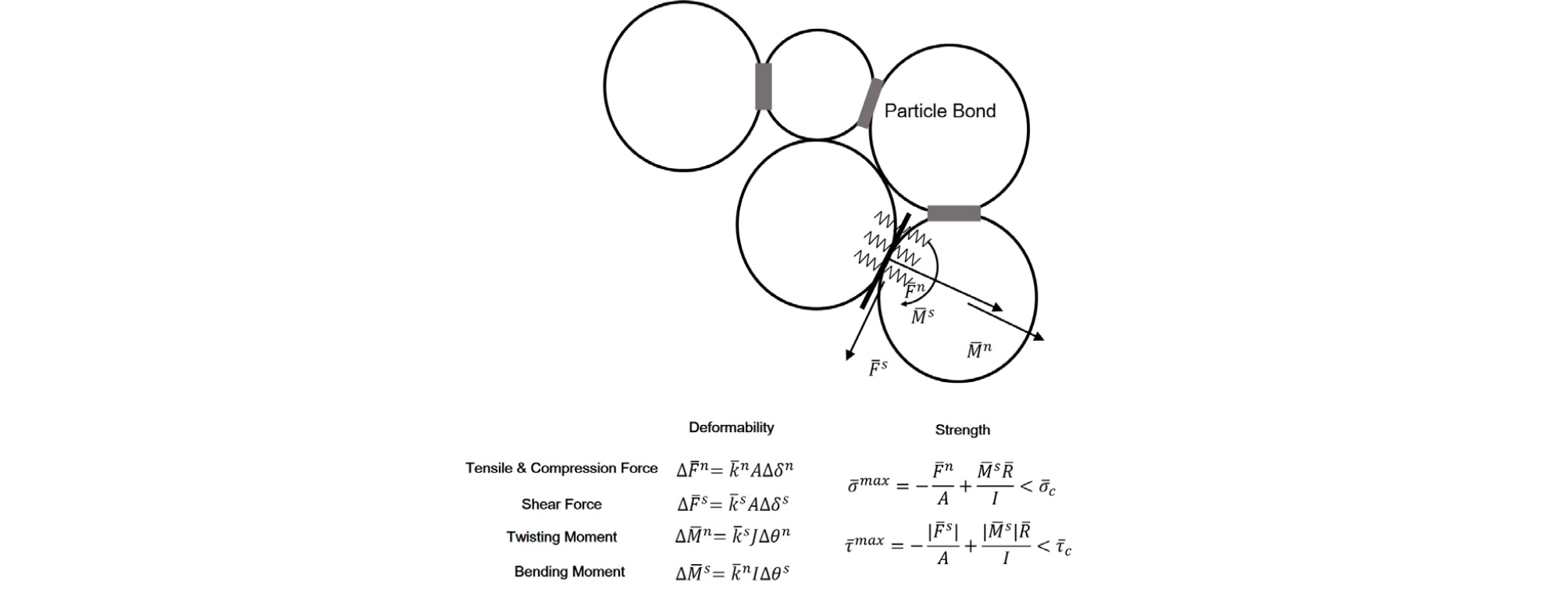
Fig. 3.
Force-displace behavior in a particle bond model. The schematic is modified from Potyondy and Cundall (2004) and Cho et al. (2007). A, I, and J are the area, moment of inertia and polar moment of inertia of the parallel bond cross-section, respectively. The bond breaks if the maximum normal or shear stress (, ) exceeds the normal or shear strength (, ), respectively.
입자 내부에 초기에 존재하는 미세 균열 양상들이 파괴 양상에 영향을 끼칠 수 있으며(Kou et al., 2019; Patel and Martin, 2020), 이는 BPM이 고안된 본래의 취지라 할 수 있다. 다만, 마이크로 크랙에 대한 연구는 일반적으로 단일 공시체를 통해 분석하며, 모델 복잡도의 증가로 인해 이전의 DEM 파분쇄 연구에서는 일반적으로 이를 고려하지는 않았다.
파쇄기의 경우 DEM 모사는 분쇄매체가 아닌 시료 자체에 대해 이루어지며, 일반적으로 파쇄 현상에 의해 발생하는 입도의 기하학적 크기 감소가 시료의 흐름 과정에 영향을 미치는 관계로 시료의 파쇄를 기계론적으로 모델 내에서 표현하는 것이 필수적으로 요구된다. BPM의 경우 단일입자들을 알갱이의 집합체로 표현하는 과정에서 일반적 DEM 모델에 비해 막대한 연산 부하를 초래한다. 이를 단순화하여 단일 DEM 입자에 대한 접촉 임계 힘을 설정, 임계값을 초과할 경우 조각 입자를 모입자 주변으로 생성시키는 모델들이 적용되었다. 이를 입자치환법(particle replacement method, PRM) 혹은 빠른 분쇄(fast breakage, FB) 모델이라 칭하며, 이러한 기법은 주로 분쇄기보다는 파쇄기 모사 과정에서 많이 활용되어 왔다(Cleary, 2004; Lichter et al., 2009; Cunha et al., 2013).
Djordjevic(2003)과 Schubert and Jeschke(2005)는 수평형 해머밀의 분쇄 기작을 모사 분석하기 위해 BPM을 활용한 바 있다. 콘크러셔, 조크러셔와 같은 파쇄기에서 주요 파쇄 기작으로 발생하는 압축 파쇄에 의한 양상은 BPM 에서의 단축 압축 강도 실험 등과 연계, 개별 시료의 물성을 DEM 모델 인자 형태로 도출하고 이를 적용하여 조 크러셔, 임팩트 크러셔, 콘크러셔 등과 같은 파쇄 장비에 활용할 수 있다(Khanal, 2005; Lichter et al., 2009)
PBM-DEM 연계 해석 및 ANN의 활용
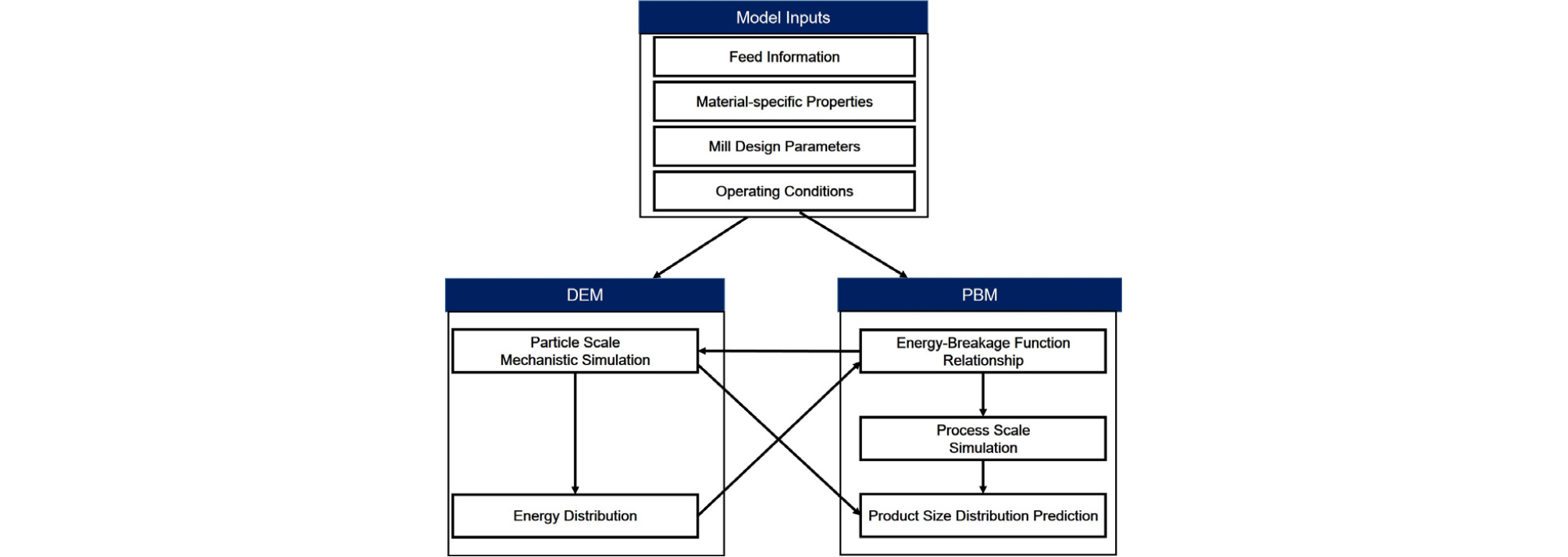
PBM과 DEM 간의 다중스케일 연구는 DEM 시뮬레이션을 통해 획득한 입자 레벨의 에너지, 충돌 정보를 PBM 모델의 인자에 통합, 시간에 따른 분쇄산물의 입도를 예측하려는 형태로 주로 활용될 수 있다(Chaudhury et al., 2014; Capece et al., 2018; Metta et al., 2018; Cleary et al., 2020; Wang et al., 2012).
스케일업 인자 연결 관계 외에 물질수지모델에서의 분쇄율과 DEM 분석 결과 간의 상관관계 규명 연구는 다양하게 진행되어 왔다. Vogel and Peukert는 물성 기반으로 분쇄 확률 모델 기반을 수립하고 이를 이용하여 시간에 따른 분쇄율과 1차분쇄에 의한 분쇄 분포를 결정하는 모델 연구를 수행하였으며(Vogel and Peukert, 2002; Vogel and Peukert, 2003; Vogel and Peukert, 2004), Morrison et al.(2007)은 이 모델을 적용, DEM 연구에서 분쇄 현상 모사를 위한 하부 모델로 활용하였다. 해당 모델은 임계에너지와 입자 강도에 대한 2가지의 모델 인자로 분쇄에 대한 물성 특성을 분쇄 장비 운전 조건과 분리, 취급할 수 있도록 했다는 점에서 의의를 가지나 이는 분쇄 기작의 변화에 따른 입자 분쇄 양상 변화 특성을 고려하지 못한다는 한계를 지닌다.
일반적인 PBM-DEM 연계 모델링 연구의 프레임워크를 Fig. 4에 도시하였다. 실제 DEM 기반의 충돌 에너지 및 소산 에너지 정보는 실제 분쇄에 활용되는 임계에너지의 선택, 충돌 계수 등의 물성치 설정 등 다양한 요인에 의해서 영향을 받을 수 있다. 이 때 충돌 에너지 정보는 분쇄 매체 간에 발생하는 것으로, 발생한 충돌에너지가 충돌된 입자층에 있는 입자들에 배분되는 방식에 대한 하부 모델을 설정함으로써 밀 내의 시료와 충돌 에너지 간 연결성을 보다 명확히 모델 내에 반영할 수 있다(Tavares et al., 2009; Carvalho, 2009).
분쇄산물의 입도 분포를 DEM과 PBM간 다중 스케일 해석 모델을 통해 도출하는 경우, DEM을 통한 에너지 분포 결정 부분에 많은 연산 부하 및 시간이 소요가 되며 이는 DEM의 분쇄 분야 활용의 난제 중에 하나이다. 최근에는 DEM 시뮬레이션에서의 에너지 획득 과정을 대리 모델(surrogate model, SM)을 통해 단순화시키려는 시도들이 이루어지고 있는데(Barasso et al., 2015; Metta et al., 2019), 이는 DEM 모델의 결과 도출 과정을 인공신경망(artifical neural network, ANN)을 활용한 데이터 기반 모델로 치환, 해석에 소요되는 부하를 줄이고자 하는데 그 초점이 맞추어져 있다.
DEM의 많은 모델링 인자들은 물성 테스트를 통해 결정될 필요가 있는데 이는 매우 큰 실험적 부하를 가져오는 작업으로. 일반적으로 안식각 실험 등을 통해 거시 물성치를 검증하는 방식으로 이루어진다. Benvenuti et al.(2016)은 DEM 인자와 거시 물성 간 관계를 ANN 기반 대리 모델을 이용하여 예측하고자 하였다. 인공 지능 분야의 급속한 발전과 함께 이러한 시도는 다양한 수치 해석 모델 분야에서 이루어지고 있는데, 다른 분야에서와 마찬가지로 시스템 복잡도로 인한 특성공학(feature engineering)적 설계의 어려움을 극복하는 것이 이러한 접근법의 성공 여부를 결정짓는 중요한 요인으로 작용할 수 있다.
미립자에 대한 이산요소의 적용 및 해결 과제
분쇄 장비 내에서 분쇄 매체가 아닌 시료를 모사할 경우 겪게 되는 어려움은 입자의 수에 따른 연산 부하 문제이다. 컴퓨터 하드웨어의 발전과 병렬 연산 처리 알고리듬의 진화로 시뮬레이션의 스케일은 2000년 이후 크게 증가하였으나, 실제 파분쇄기 내 입자들을 모사하는 것은 여전히 연산 부하의 측면에서 매우 어려운 일이다. 특히 분쇄기의 경우 랩 스케일의 장비 운전에도 수십억 개 이상의 입자들이 발생하고, 산업 스케일의 분쇄 장비를 그대로 모사하는 것은 사실상 불가능하다고 할 수 있다. 또한 타임스텝 크기의 측면에 있어서도, 해석 안정성(stability criteria) 확보를 위해 타임스텝은 입경의 감소에 따라 줄어들어야 하며, 이는 미립자 모사를 더욱 어렵게 만드는 요인으로 작용한다. 연속체를 가정하는 기존의 FEM, FVM 방식 접근은 입자 레벨의 불연속성에서 발생하는 현상들에 대한 모사가 어려워, 입자 단위의 거동이 지배적으로 작동하는 분쇄기를 모사하기에 적절치 못하다.
이러한 문제를 해결하기 위해서 DEM에서는 조립화(coarse graining, CG)라고 불리우는 업스케일링 방식의 접근법들이 제안된다. 분자동역학에서 처음 시도된 조립화는, 원래 입자 스케일에서의 정보들의 디테일을 줄이고 더 조립화된 입자의 형태로 해상도를 감소, 시뮬레이션의 속도를 증가시키는 것을 목적으로 한다.
이 때 조립화 과정에서 원 시스템과 동일한 에너지 밀도를 유지할 있도록 스케일링이 이루어져야 하나, DEM의 경우 입자 간 충돌 에너지 밀도를 유지하는 것이 난제로 작용한다. Kuwagi et al.(2004), Sakai and Koshizuka(2009)이 유동층 등의 공정에 조립화 기법을 적용하였으나, 이러한 에너지 측면에서 상사성 문제에 대해 심도 있는 해답을 제시하지는 못했다.
Feng et al.(Feng et al., 2009; Feng et al., 2014)은 역학적 거동에 대한 정확한 스케일링이 이루어질 수 있는 조건들에 대해 차원해석의 측면에서 분석, 여러 물리량에 대한 스케일링 방법론은 제안하였다. 그 과정에서 스케일링 과정을 통해 에너지 밀도가 보존될 수 있음을 보였으나, 차원해석에 의한 상사성이 입자 간 충돌 스케일에서 만족되는지 여부는 여전히 명확하게 주장되기 어려우며, 개별 문제에 대해서 현상학적으로 검증하는 과정이 필요하다. 이는 조립화 모델과 실제 모델을 짧은 시간에 걸쳐 적용, 물리량의 보존 여부를 직접 도출된 결과를 통해 판단할 수 있음을 의미한다.
원 시스템의 특성길이와 조립화된 입자 입경의 비율은 조립화 과정에서의 상사성 만족을 위해 중요한 요소이며, 성공적인 조립화 과정은 입자간 힘에 의한 유변학적 특성의 보존, 경계 조건의 길이 스케일과 입경의 비율에 따른 결과 값의 변화 등이 종합적으로 검증되어야 한다. 예를 들어, 조립화가 적용된 시스템에서 벽면 근처에서의 전단응력 전파는, 원 시스템과 동일한 속도로 이루어져야 하며(Fig. 5) 이를 위해서는 입자 간의 전단 마찰력 계수의 스케일링이 정확히 이루어져야 한다.
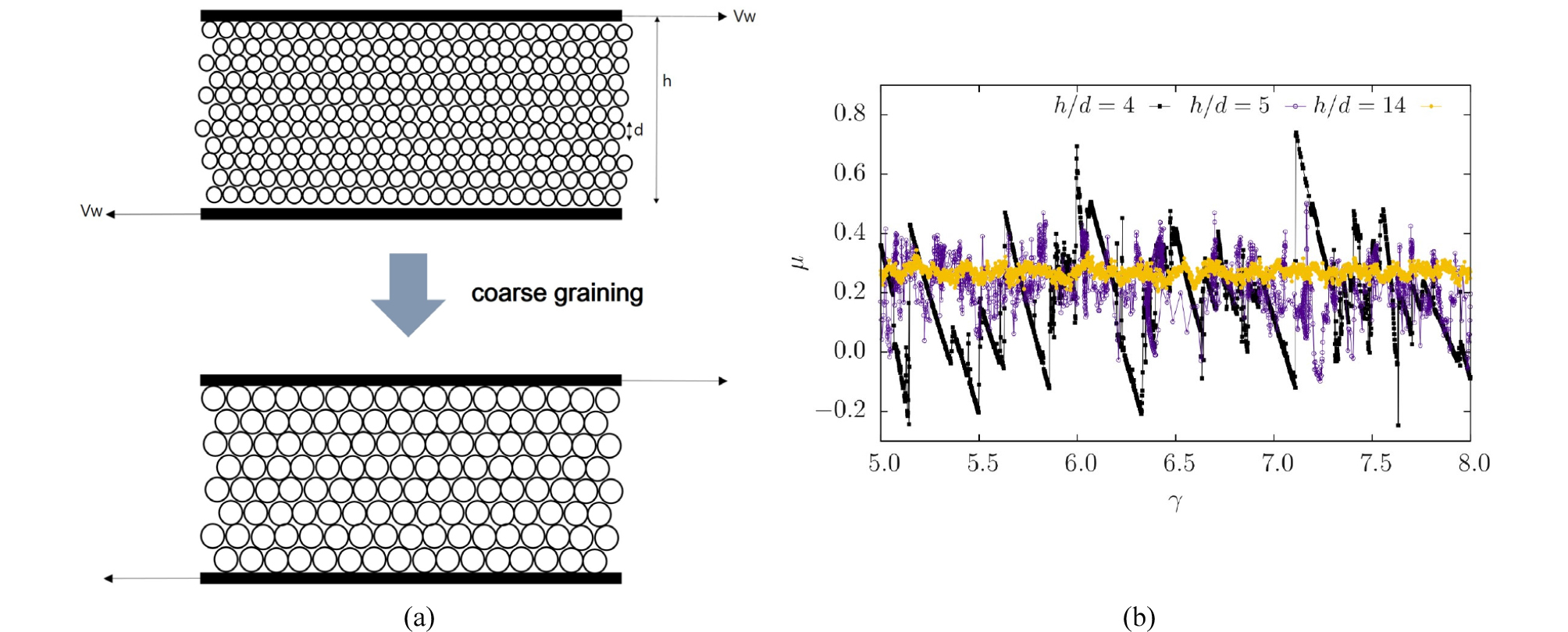
Fig. 5.
Coarse graining in granular shear flow (a) schematic of CG and (b) DEM investigation of dynamic viscosity (μ) with various h/d ratio(γ: shear rate) by Schumacher and Radjai (2015).
일례로, 볼밀 내부의 분쇄 매체 거동을 모사하려 할 때, 볼 직경이 밀 직경의 일정 비율 이상이 될 경우 볼의 거동은 캐스케이딩(cascading)에서 낙하 운동의 형태로 변한다(Fig. 6). 조립화 모형에 의해 발생하는 천이는 두 모델 사이에 상사성을 만족시키지 못함을 의미한다. 차원 해석을 통해 중력, 회전 속도 등을 조정하여 상사성을 보완할 수 있으나 이 경우 실제 밀내 거동과는 다른 양상을 띠게 된다. 이와 같이 조립화 천이가 일어날 경우 조립화 모델은 더 이상 유용하지 않게 되며, 이는 조립화의 허용 범위를 결정하는 중요한 요소가 될 수 있다. 이는 개별 장비의 거동 기작에 따라 변하며 미립자 모형의 업스케일링에서 매번 고려되어야 한다는 것이 범용적 CG모델의 적용을 어렵게 한다.
결 론
선광의 많은 분야 중 특히 파분쇄 분야에서 DEM은 분쇄 장비의 블랙박스적 특성을 극복하고 에너지 스펙트럼에 대한 정보를 제공해 줌으로써, 분쇄 기작, 밀 설계 및 운전조건 도출에 활용되어 왔다. 최근 수 십년동안 컴퓨터 하드웨어 및 병렬처리 알고리듬의 급격한 발전에 힘입어 DEM 시뮬레이션의 입자 스케일은 급격히 증가해 왔으며 이 추세는 향후에도 지속될 것으로 보인다. 이는 에너지 스펙트럼 기반의 정보 뿐 아니라 FB 및 BPM 등을 활용하여 입자의 파괴에 대해 직접적으로 정보를 획득하는 접근법의 활용도를 높일 것으로 판단된다.
PBM과 DEM의 결합을 통해 입자 스케일에서의 정보를 공정 스케일로 확대하는 시도는 지속적으로 이루어지고 있으며, DEM 기반의 충돌 에너지 및 소산 에너지 정보는 다양한 요인에 의해서 영향을 받을 수 있다. 인공지능 기반의 대리 모델을 활용하는 접근법도 시작 단계에 있으며, 인공지능의 특성공학 설계가 성공 여부를 결정짓는 중요한 요인으로 작용할 것으로 판단된다.
현재 DEM은 조립자 혹은 분쇄 매체의 경우 거의 모든 장비에 적용 가능하다고 판단할 수 있으나, 분쇄기 내의 미립자들을 모사하기 위해서는 업스케일링 방식의 접근이 불가피하다. 조립화 모델은 실제 파일럿 스케일의 공정 시뮬레이션을 가능하게 하는 접근법으로 많은 관심을 받고 있으나, 상사성의 만족을 위한 신중한 접근이 요구된다. DEM을 이용한 예측의 신뢰도를 보여 주는 많은 검증 사례들이 있으나, 현존하는 모든 DEM 기반 접근법 및 상업용 DEM 소프트웨어는 개별 장비별로 충분한 검증이 필요한 단계이다.