서 론
파라핀 생성 원리
파라핀 결정화(Paraffin Crystallization)
왁스 침전(Paraffin Wax Deposition)
유동관 매설 깊이에 따른 온도 변화와 파라핀 침전 간의 상관성
연구대상지역
생산정의 채유 시스템 운영 조건과 파라핀 침전 간의 상관성
생산시설 모델링
수치해석 조건
수치해석 결과
수치해석 결과기반 파라핀 침전 예측
결 론
서 론
인공채유법(artificial lift)은 유정에 펌프 등을 설치하여 원유를 인위적으로 생산하는 방법이다. 생산 초기에는 저류층 자연압력에 의한 원유회수를 수행하며, 압력감소로 인해 생산량이 일정량으로 감소하게 되면 인공채유법을 실시하게 된다. 일반적으로 인공채유 방식으로 원유를 생산하기 위해 사용되는 용적형 펌프는 Sucker-rod pump와 PCP가 있다. PCP 시스템은 1920년대 후반 처음 개발되어 현재는 가장 일반적인 인공채유법으로 자리 잡았으며(Clegg et al., 2007), 본 연구의 현장실증 연구대상지역인 카자흐스탄 A광구에서도 사용 중이다. PCP는 설치 깊이와 주변 온도에 제한을 받지만, 이물질이 함유된 유체에도 막힐 염려가 적고 펌프 수명이 길어 모래생산(sand production) 문제가 발생하는 유정에 비교적 적합한 것으로 알려져 있다(Sanks et al., 1998).
그럼에도 파라핀 침전 문제들은 여전히 발생하여 해결해야만 하는 문제 중 하나다(Sousa et al., 2019). 파라핀 자체의 주요 침전 원인은 온도감소에 의한 원유 내 파라핀 결정의 석출(precipitation)이다. 파라핀 결정의 석출에 의해 발생한 침전물은 유동관 내벽에서부터 침전되어 유동 가능 면적과 유량을 감소시킨다(Singh et al., 2000). 석출된 파라핀 결정은 분자확산(molecular diffusion) 전단 응력, 브라운 확산, 중력 침전과 같은 메커니즘에 의해 생산시스템의 각 구성 요소에 침전된다. 파라핀 침전을 억제하기 위한 다양한 연구가 진행되고 있음에도(Mandal et al., 2019), 실제 생산시설에서의 파라핀 침전은 설비구성, 운영조건, 환경조건 등 다양한 요소를 고려해야 하므로 각 요인별 파라핀 침전에 미치는 영향 분석을 위한 상관성 검토가 필수적이다.
따라서 본 연구에서는 석유생산설비 내 생산정과 유동관의 실제 환경/운영조건과 파라핀 침전 간의 상관관계를 검토하였다. 유동관의 경우 계절 변화에 따른 심도별 온도 편차를 평가하여 파라핀 침전 억제를 위한 적정 지하 매설 심도에 대하여 논의하였다. 생산정의 경우 인공채유설비 운영에 따른 관내 유동을 수치해석적으로 예측하고, 운영 조건에 따른 유동 패턴과 파라핀 침전에 영향을 주는 요인을 분석하였다.
파라핀 생성 원리
파라핀 결정화(Paraffin Crystallization)
파라핀은 원유에 용해되어 액체상으로 존재한다. 유동관 주위 저온환경으로 인해 유동관 내벽의 온도가 낮아지면, 유동관 중심과 내벽 사이에서 온도 구배가 발생한다. 지속적인 온도감소로 인하여 원유의 용해도가 과포화되면 원유 내 액체상으로 용해되어있던 임계 탄소수 이상의 고분자 탄화수소(파라핀)가 고체상으로 분리된다. 이러한 메커니즘을 파라핀 석출 혹은 결정화(crystallization)라 한다.
파라핀 결정화는 파라핀 결정의 핵생성(nucleation)과 성장(growth) 단계로 이루어진다. 원유의 온도가 감소하면 파라핀 입자의 운동에너지가 줄어들면서 입자 간 거리가 줄어든다. 이로 인해, 파라핀 분자들이 서로 뒤엉키며 무리(cluster)를 형성하고, 임계크기(critical size)에 도달하여 안정화 될 때까지 성장한다. 임계크기에 도달하지 못한 무리들은 재용해 되는 등 불안정한 상태로 존재하게 되는데 이를 세포핵(nuclei)이라 한다. 임계크기에 도달한 세포핵은 결정화 환경이 유지되는 동안 파라핀 분자들이 달라붙으며 크기가 점점 증가한다. 이러한 일련의 과정을 통해 파라핀 결정이 생성되고 침전된다.
왁스 침전(Paraffin Wax Deposition)
왁스 침전은 파라핀 결정화 과정을 통해 원유로부터 석출된 파라핀 결정들이 전단확산(shear dispersion), 중력 침강(gravity settling), 브라운 운동(Brownian motion)을 통해 발생하거나 용해되어있는 파라핀 분자들의 분자확산 작용에 의해 발생한다(Bern et al., 1980; Burger et al., 1981). 왁스 침전은 왁스 젤 형성(wax gel formation) 후, 침전된 왁스 젤이 경화(aging)되는 두 단계를 거쳐 발생한다(Singh et al., 2001). 유동관 중심과 내벽 사이에 존재하는 온도 구배에 의해, 원유에서 석출된 파라핀 입자가 유동관 내벽에서부터 생성되고 침전된다.
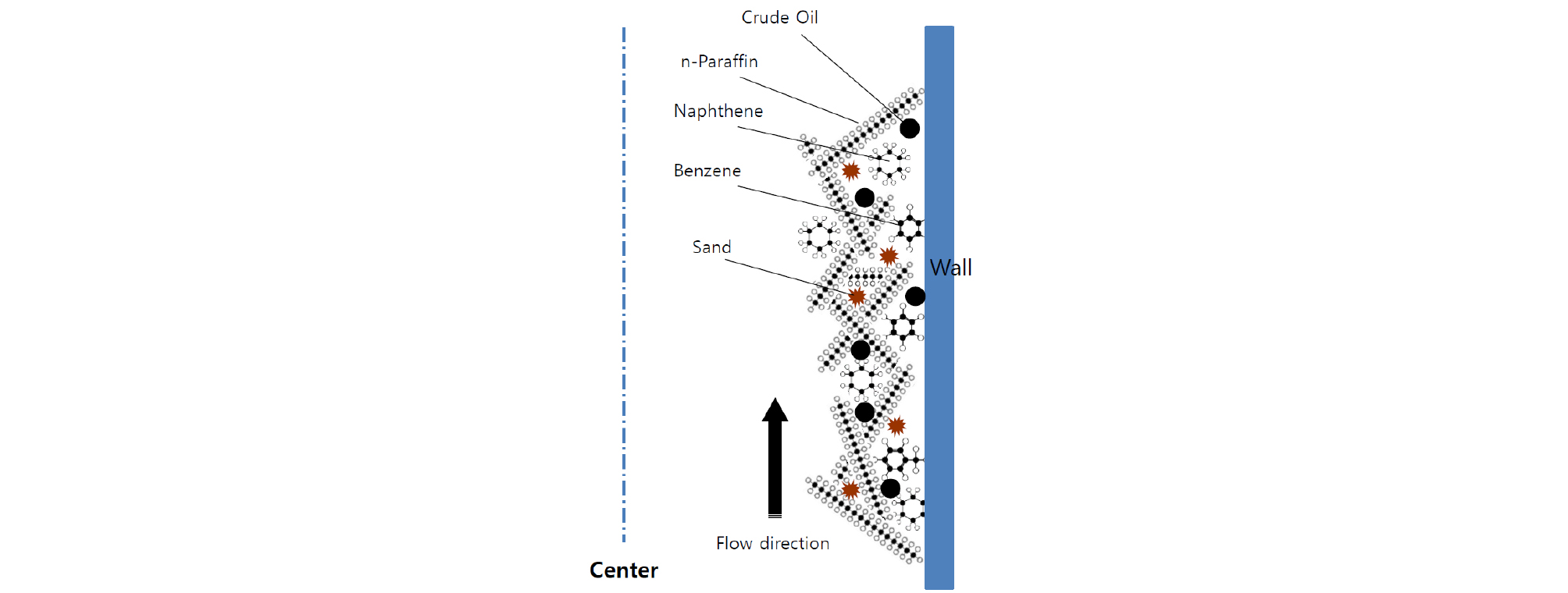
파라핀 결정화 및 침전 과정 중 원유(crude oil), 수분(water), 고무(gums), 수지(resins), 모래(sand), 아스팔텐(asphaltenes) 등 성분들이 Fig. 1과 같이 파라핀(n-paraffin) 안에 갇히게(entrapped) 된다(Holder and Winkler, 1965). 갇힌 원유는 분자확산을 야기하여 파라핀 성분이 젤 침전물로 이동하게 하고, 동시에 상호확산(counter-diffusion)을 통해 원유 성분이 젤 침전물로부터 빠져나오게 된다. 이 일련의 과정은 해당 원유의 임계 탄소수에 의해 결정되며 임계 탄소수는 각 왁스성 원유(waxy crude oil) 마다 다르고 각 현장의 운영조건에도 영향을 받는다. 이러한 상호확산 과정이 반복되면서 젤 침전물 내부의 왁스 성분의 함량이 증가하고, 왁스 젤의 크기와 굳기가 증가한다.
유동관 매설 깊이에 따른 온도 변화와 파라핀 침전 간의 상관성
생산현장에서 저류층 유체를 운반하는 유동관은 지상이나 지하에 설치되어 유동관 내벽의 온도 변화에 영향을 미친다. 온도 변화는 파라핀 침전에 있어 가장 중요한 인자로, 유체온도를 최대한 파라핀 생성온도 이상으로 유지하기 위해 유동관에 절연체를 설치하는 단열법, 유동관을 가열하는 가열법 등이 사용되고 있다(Lim et al., 2013). 이와 같은 생산시설에 대한 최적 솔루션을 수립하기 위해서는 명확한 온도구배 파악이 중요하며, 이를 위해 주변온도(ambient temperature)에 대한 분석이 필요하다.
지상에 노출되어있는 유동관의 경우 대기 온도의 직접적인 영향을 받아 온도 계측 및 파라핀 침전 예측에 유리하지만, 지하에 매설되어있는 유동관은 온도 계측과 온도 변화 추이를 파악하기 어려워 파라핀 침전 시기 및 위치 예측 정확성을 높이기 위해서는 토양온도(soil temperature) 변화 양상에 대한 분석이 선행되어야 한다.
토양온도는 지역 및 토질 유형에 따라 다르다. 토양은 다공성 매질이기 때문에, 가볍고 건조한 토양보다 젖은 토양은 높은 수분 함량으로 열전도도가 높아 연중 열 전달량이 증가한다. 지표면에서부터 심도가 깊어질수록, 대기의 대류열전달로 인한 토양의 온도 변화에 미치는 영향이 점차 감소하기 때문에 연중 온도차가 점점 줄어든다. 특정 깊이에 도달한 후, 대기 온도가 미치는 영향은 무시할 정도로 미미하여 연중 온도 차가 일정한 지층 구간을 토양 일정 온도층이라고 한다(Cheng et al., 2017).
시간과 깊이에 따른 토양온도의 주기적인 변화에 대한 계산식은 식 (1)과 같다(Marquez et al., 2016).
| $$T_{soil}(z,t)=T_m-T_pe^{-z\sqrt{\frac\omega{2\alpha}}}\cos(\omega t-z\sqrt{\frac\omega2\alpha})$$ | (1) |
이때, 는 심도 및 시간에 따른 토양온도, 는 심도, 는 시간, 은 연중 평균온도, 는 연간 월평균 일교차, 는 각진동수, 는 토양 열 확산률을 의미한다.
연구대상지역
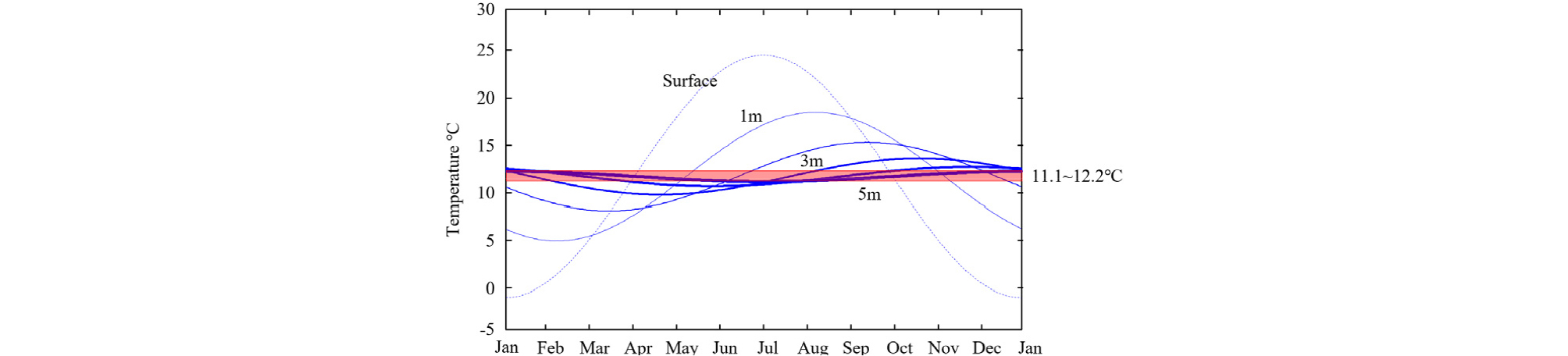
본 연구의 주요 타깃인 카자흐스탄 A 광구의 2018년 기온데이터를 바탕으로 심도별(0 m, 1 m, 2 m, 3 m, 4 m, 5 m) 토양온도를 산출한 결과는 Fig. 2와 같다. 결과 그래프에 따르면 지표면의 최저, 최고 온도는 각각 1월, 7월이지만 지표면으로부터 5 m 심도에서의 최저, 최고 온도는 각각 7월, 1월에 도달함으로써 최저, 최고 온도에 도달하는 시간이 지표면과 상이함을 확인하였다. 이때 지표면에서 최대 온도 차는 26.5°C이며, 5 m 심도에서의 최대 온도 차는 약 1.1°C로 나타났다. 즉, 심도가 증가함에 따라, 대기의 주기적인 온도 변화가 토양온도에 미치는 영향은 점차 미미해졌다.
Table 1과 같이 심도별 지표면 대비 최대 온도차 비율을 분석한 결과 5 m에 도달했을 때, 5% 이하로 감소하게 된다. 따라서 본 연구에서 활용된 카자흐스탄 A 광구의 경우, 해당 심도를 토양 일정 온도층으로 설정하였다. 동토지역의 왁스발생을 억제하기 위해 단열재나 발열재를 설치할 시 최소한의 비용으로 목적달성하기 위해서는 외부온도 변화를 차단할 수 있는 최소 매설 심도에 대한 고려가 필요하며, 본 연구 현장의 경우 해당 심도를 5 m로 제시하였다.
Table 1. Soil temperature difference and ratio by depth
생산정의 채유 시스템 운영 조건과 파라핀 침전 간의 상관성
생산시설 모델링
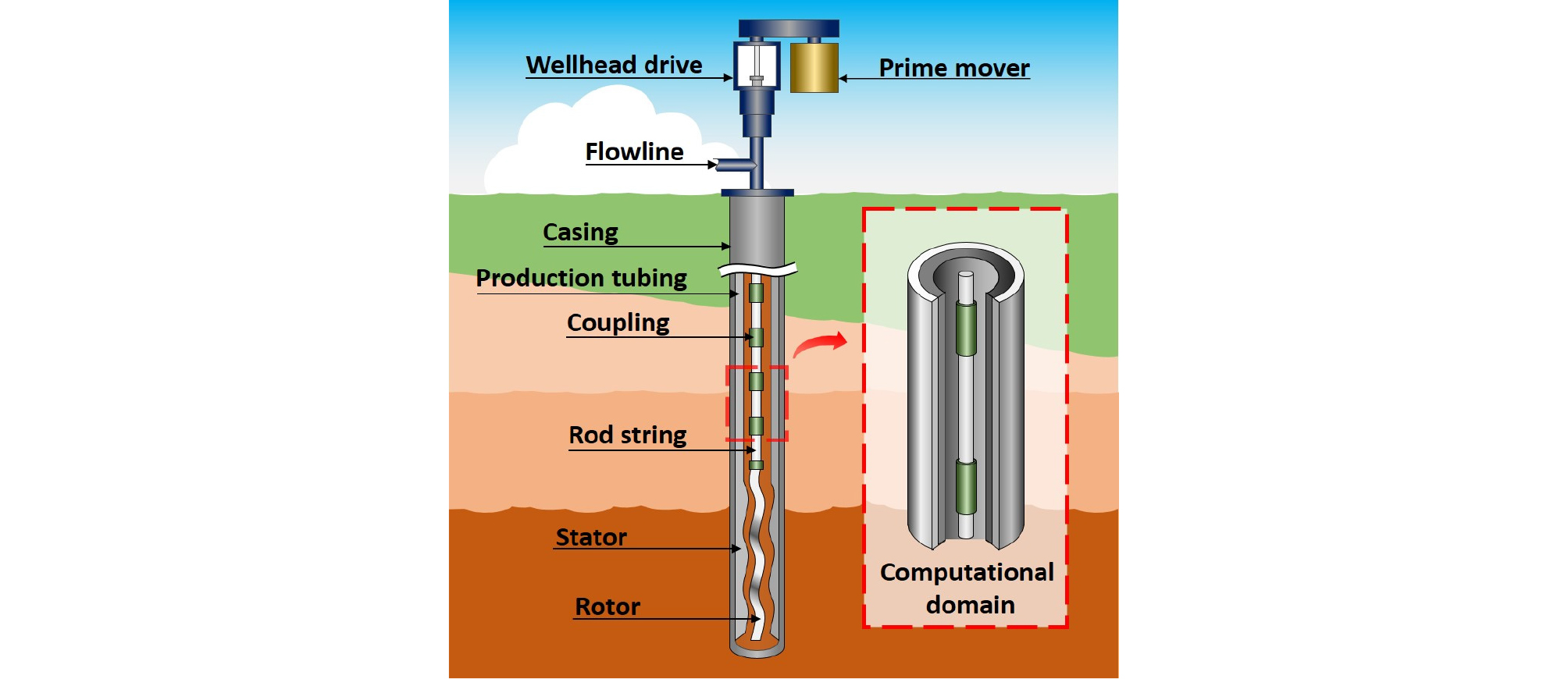
PCP 시스템은 Fig. 3과 같이 지상에 설치된 모터로부터 rod string구간을 지나 지하 유전에 삽입된 stator구간으로 동력을 전달한다. Stator 구간의 경우, rotor의 헬리컬(helical)한 형상 특성으로 이물질이 함유되어있어도 지속적으로 채유할 수 있을 정도로 파라핀이 침전될 확률이 낮다. 그럼에도 수직 생산정에서 유동관 내 파라핀 침전 문제는 계속해서 보고되고 있다(El-Dalatony et al., 2019). 다시말해, PCP 시스템 내 파라핀 침전 문제는 stator 구간이 아닌 rod string구간에서 발생 가능성이 높다. 따라서, rod string구간의 환경 및 운영조건이 파라핀 침전에 미치는 영향에 대한 연구가 필요하다. 또한 rod string구간은 PCP 시스템 전체 길이의 90% 이상을 차지하는 대표 영역이므로 파라핀 침전을 연구하기 위해서는 이 구간의 유동 패턴 파악이 필요하다. 하지만 실제 현장과 동일한 조건으로 실험 장비를 구축하고 계측하는 데에는 시간 및 금전적인 비용에 한계가 있다. 또한, 복잡한 관내 유동을 가시화하기에도 많은 어려움이 있기 때문에 수치해석적 방법을 통해 관내 유동패턴을 예측하였다. Fig. 3의 확대도를 보면 rod string구간은 외벽인 공벽보호관(casing), 내벽인 튜빙(tubing), 동력전달을 위한 rod string으로 크게 나뉜다. 본 논문에서는 원유의 유로를 구성하는 튜빙과 rod string만을 고려하였으며, 운영조건에 따라 rod string의 회전에 의해 발생하는 스월 유동을 고려하여 관내 유동 패턴을 구현하였다.
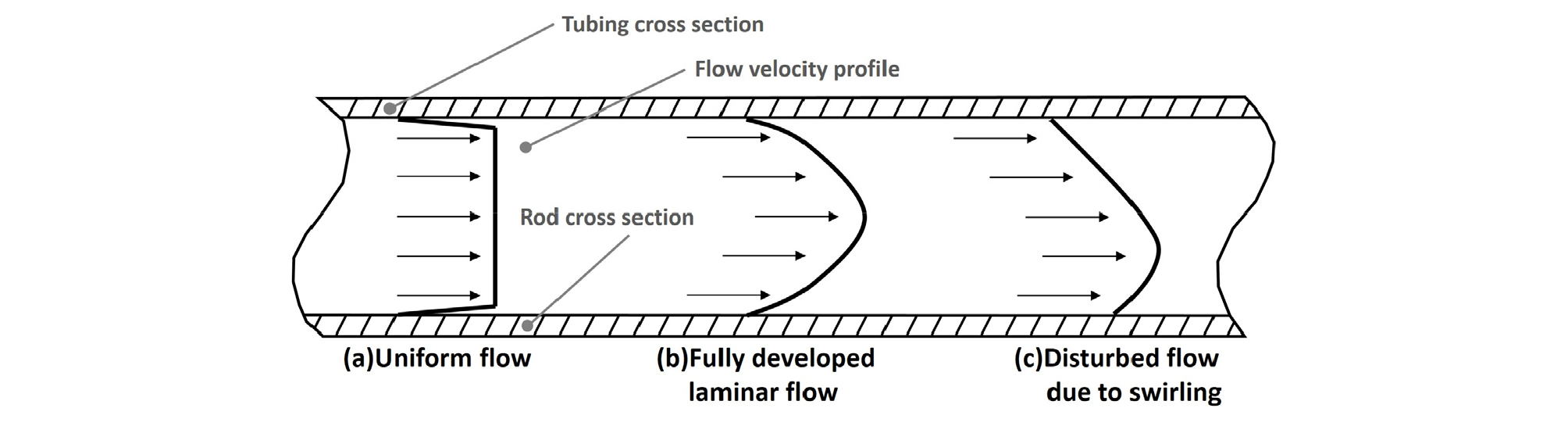
일반적으로 관내 유동은 Fig. 4(a)와 같이 균일하게 주입되어 점착조건(no-slip)에 의해 양쪽 벽면에서 속도가 0이 되어 Fig. 4(b)와 같은 완전발달유동(fully developed flow)이 발생한다. 그러나 PCP 내부에 위치한 rod string이 일정 속도로 회전하며 스월 유동을 발생시켜 Fig. 4(c)와 같이 비대칭적인 유속이 발생한다. 또한, 이 비대칭적인 스월 유동은 원유 유동 속도와 rod 회전속도의 상관관계에 의해 결정되며, 스월 유동을 구현하기 위해서는 3차원으로 해석을 진행해야 한다. 스월 유동이 벽-근접 유동에 미치는 영향을 분석하면 파라핀 침전을 물리적으로 억제하는 데에 도움을 줄 수 있다. 따라서, 관내 유동과 파라핀 침전의 상관성 검토를 위해 전산유체역학 상용프로그램인 ANSYS Fluent를 사용하여 수치해석을 수행하였다(ANSYS Inc., 2011).
수치해석 조건
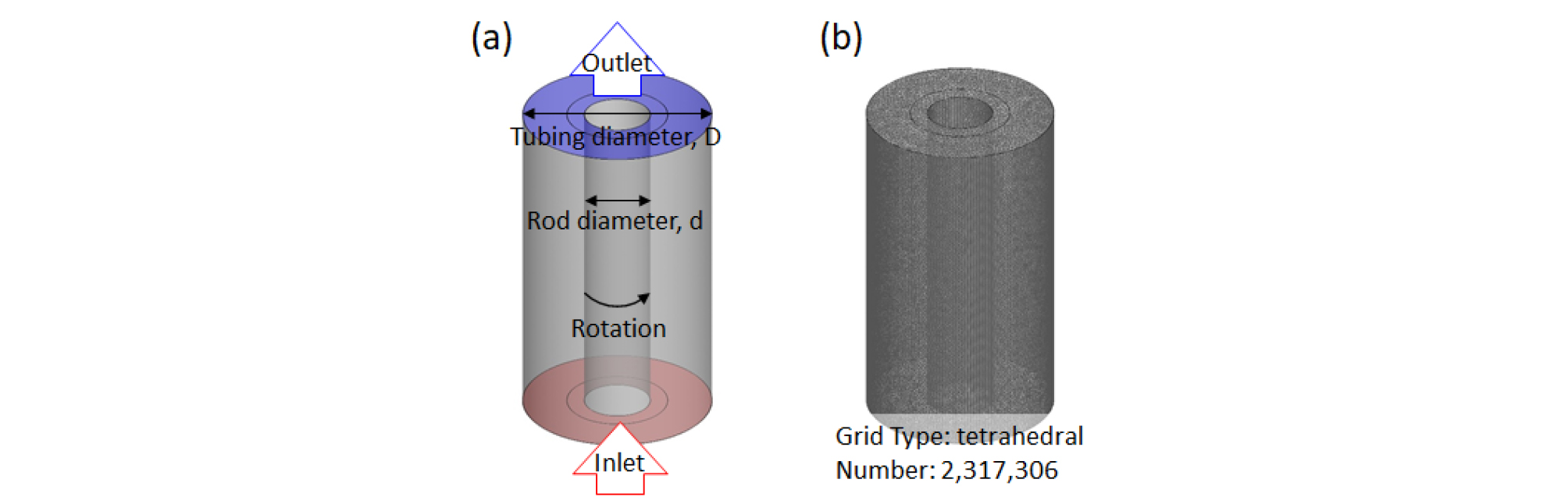
생산시설 모델링은 카자흐스탄 A광구의 현장자료에 기반하여 생성하였다. 실린더 모양의 생산 튜빙 내부에 rod string이 있는 형태로, 생산 튜빙 내부직경은 62.0 mm, rod string 외부 직경은 22.0 mm이다. 길이 방향으로는 튜빙 직경의 10배로 충분히 길게 설정하여 관내 유동에 미치는 입·출구 경계조건의 영향을 최소화하였다. Fig. 5(a)는 해석에 사용한 3차원 모델링을, Fig. 5(b)는 생성한 격자를 나타낸다. 파라핀의 침전 메커니즘은 튜빙 벽면에서 발생하므로, 벽에서 유동에 초점을 맞춰 벽면의 격자를 특히 조밀하게 작성하였다. 격자 독립성 테스트를 수행한 결과, 관의 중간지점에서 반경 방향으로 속도를 비교하여 비교 오차 1% 미만이 되도록 2,317,306개의 4면체(tetrahedral) 격자로 결정하였다.
본 연구에서는 원유의 유동 패턴이 파라핀의 침전 특성에 미치는 영향을 분석하기 위해 연속방정식, 운동량 방정식을 사용하였다(ANSYS Inc., 2011). 생산정 내 원유는 단상(single-phase) 액체로 가정하였으며, 원유의 점성값은 문헌을 참고하여 shear-thinning 특성을 반영하였다(Dong et al., 2013). 관내 유동이기는 하나, 원유의 점성이 크고 유속이 매우 작아 레이놀즈 수는 989( 989 ≪ 2100)로 계산되어 층류 모델을 사용하였다. 또한, 원유는 non-Newtonian 특성을 보여 유체의 점성모델에 반영하였다(Liyana Nadirah, 2014). 해석 영역은 심도에 상관없이 관내 유동이므로 중력의 영향은 무시하였다. 관내 유동 특성 분석을 위해 정상상태(steady state)로 해석을 진행하였고 rod string의 회전속도가 일정하기 때문에, 회전 영역에 코리올리 힘(Coriolis force)과 원심력(centrifugal force)을 반영한 후 상대속도를 계산하여 회전유동을 모사하는 MRF(Multiple Reference Frame) 해석기법을 사용하였다(Deglon and Meyer, 2006). 또한, 상대적으로 축방향 길이가 매우 길어 생산정 전체 구간 중 일부 구간만을 모델링 하여 주기 경계조건(periodic condition)을 적용하였다. 온도 변화에 따른 물성치 변화는 고려하지 않았으며 자세한 수치해석 조건들은 Table 2에 요약하였다.
Table 2. Numerical conditions
수치해석 결과
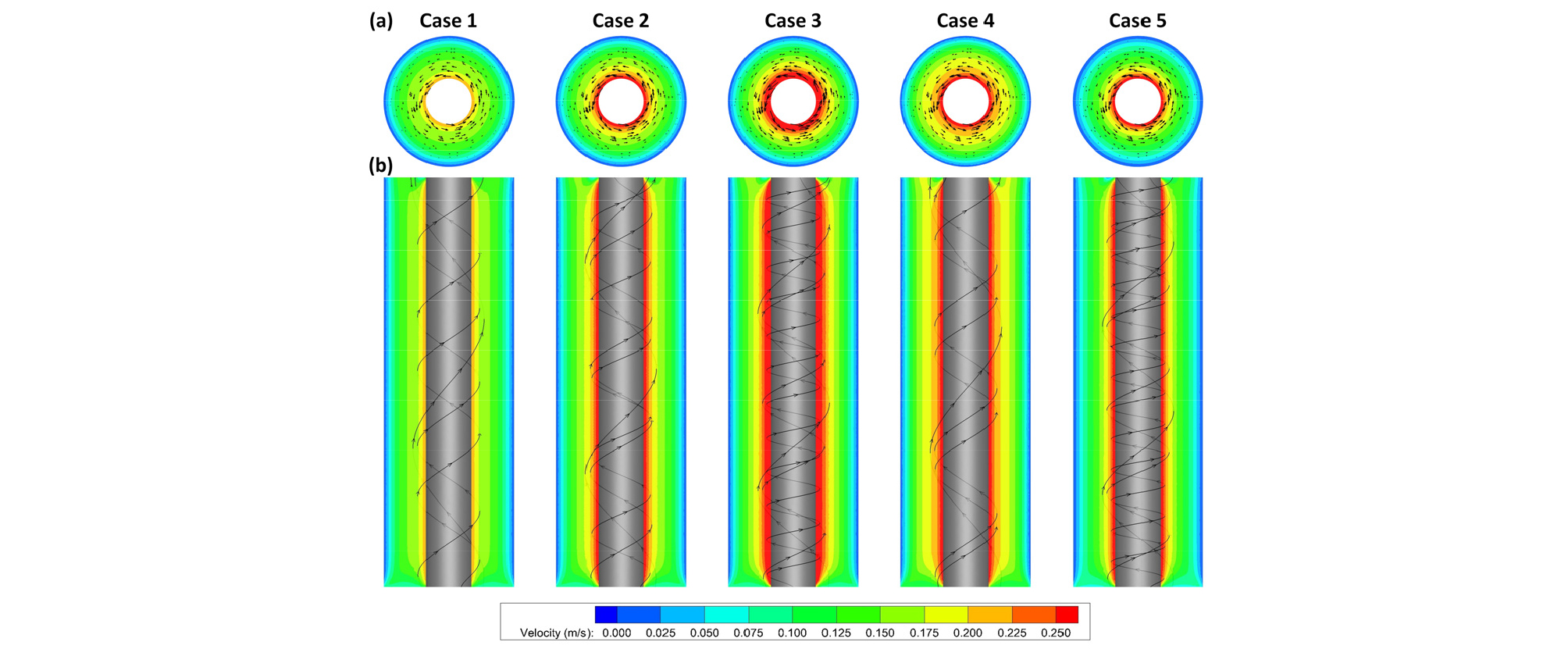
수치해석은 총 5가지 Case(시나리오)에 대하여 수행하였다. 원유가 주입되는 속도와 rod string의 회전속도에 대하여 각각 실 운영조건의 80%, 100%, 120%로 변화시키며 경향을 분석하였다. 이 경우 회전으로 인한 rod string의 접선속도(v=rω=dω/2)는 각 0.230 m/s, 0.288 m/s, 0.346 m/s로 계산되었으며 주입속도보다 2배 이상 빠르다. Case 2를 기준으로 설정하였고, 수치해석 Case별 운영조건들을 자세하게 Table 3에 정리했다. 수치해석 결과는 Fig. 6과 같이 속도장으로 도출하였으며, Fig. 6(a)는 상면도에 벡터를 나타냈고, Fig. 6(b)는 정면도에 유선을 나타냈다. Case 1, 2, 3을 보면 rod string의 회전속도가 증가함에 따라 rod string 주변으로 더 강한 유동이 발생하는 것을 볼 수 있다. 또한, 원유 주입 속도는 일정하지만 회전속도 증가로 인해 rod string에서 속도합벡터의 방향이 변경되어 유선이 변형된다. 원유 유동 속도보다 rod string의 회전속도가 더 빠르기 때문에 해석영역 내 최고속도는 rod string에서 발생하였다. Case 2, 4, 5를 보면 원유 주입 속도 변화에 따라서 rod string과 튜빙 벽면에서 속도는 일정하고 관내 유속만 변화가 발생한다. 이는 rod string의 회전속도와 튜빙 벽면에서 점착조건이 경계조건으로 결정되어있어 내부 유동에만 영향을 주는 것으로 판단된다.
Table 3. Simulation Cases
| Case | Rotational speed ω (RPM) | Tangential speed v (m/s) | Inlet velocity u (m/s) |
| 1 | 200 | 0.230 | 0.0896 |
| 2 | 250 | 0.288 | 0.0896 |
| 3 | 300 | 0.346 | 0.0896 |
| 4 | 250 | 0.288 | 0.1075 |
| 5 | 250 | 0.288 | 0.0717 |
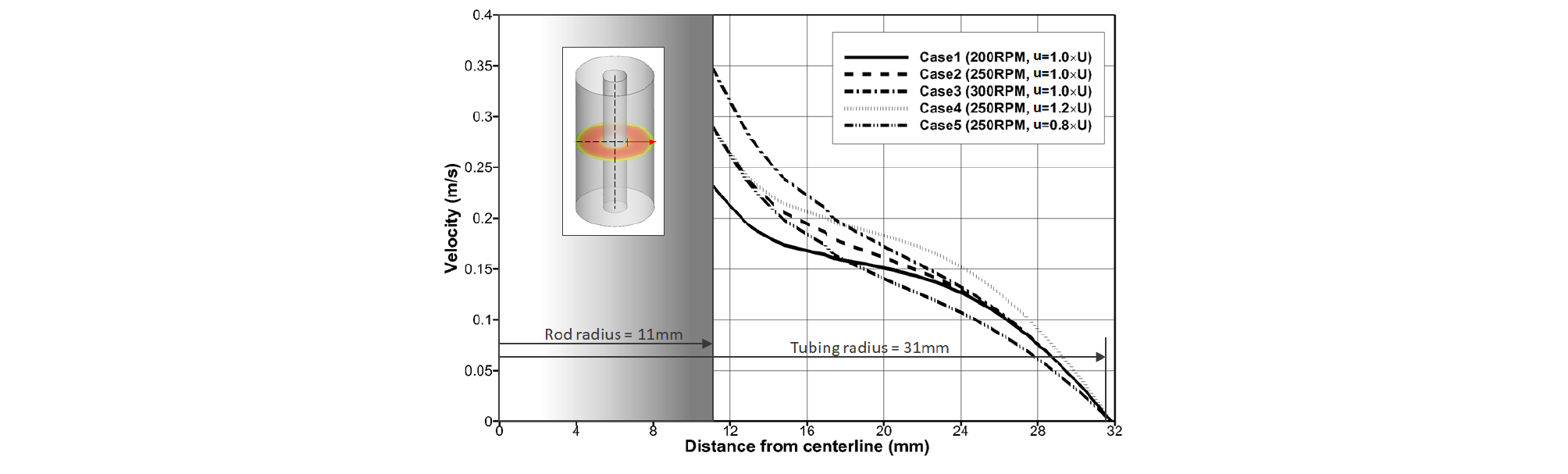
관내 유속을 자세히 분석하기 위해 Fig. 7과 같이 각 Case별로 관의 중심선에서부터 반경 방향으로 속도 선도를 나타냈다. Rod string의 외벽에 해당하는 11 mm 지점에서는 rod string의 회전속도에 따라 속도 값이 결정된다. 반면 튜빙의 내벽에 해당하는 31 mm 지점에서는 점착조건으로 속도가 0이 된다. 관내 유동으로 완전발달유동을 보이지만 좌우 경계조건이 달라 비대칭한 유속을 보인다. 특히 원유 유동 속도보다 rod string의 회전으로 발생한 접선속도가 더 빨라 포물선 모양의 속도 선도가 나타나지는 않았다. 회전속도에 의한 영향을 보기 위해 Case 1, 2, 3을 비교하면, rod string에서 서로 다른 속도로 시작하여 감소하다가 튜빙에 점점 가까워지면서 약 27 mm 이후부터 속도값이 수렴하는 것으로 나타난다. 즉 rod string의 회전속도가 튜빙 벽-근접 유동까지는 영향을 미치지는 못하는 것으로 판단된다. 일반적으로 rod string은 회전축으로 사용되어 부드러운 표면을 갖기 때문이며 물리적인 표면처리를 통해 회전 시, 표면에서 와류(vortex)를 만들어 영향 범위를 넓힐 수도 있다. 주입속도의 영향을 보기 위해 Case 2, 4, 5를 보면, 양쪽 경계에서는 각각 같은 속도 값을 갖지만, 원유 유동 속도의 변화로 관내 유속 전체에 영향을 준다. 이로 인해 튜빙 벽-근접 유동 속도에도 영향을 주는 것으로 나타났다. 위와 같이 운영조건에 따른 내부 유동의 변화를 고려하여 벽-근접 유동이 파라핀 침전에 미치는 영향을 분석하였다.
수치해석 결과기반 파라핀 침전 예측
파라핀 침전을 예측하기 위해 메커니즘을 연구하고 다양한 모델이 개발되고 있다. 그 중 RRR(Ryhh, Rydahl and Rønningsen) model에서는 벽면에서 발생하는 점성하위층(viscous sub-layer)을 고려하여 층류전단속도를 계산하여 파라핀의 침전을 예측한다(Giancarlo et al., 2019). RRR model은 유정과 운송관에서 파라핀 침전에 지배적인 분자확산과 전단확산 메커니즘을 고려한 모델이다. 점성하위층이란 벽면 유동을 결정할 때에 유체의 점성이 지배적인 역할을 하는 구간으로 일반적으로 가 5 이하인 영역을 말하며 식 (2)와 식 (3)으로 나타낼 수 있다(Munson et al., 2013).
| $$y^+=(y\times u_\tau)/\nu$$ | (2) |
| $$u_\tau=\sqrt{\tau_w/\rho}$$ | (3) |
여기서 는 벽좌표, 는 벽으로부터 거리, uτ는 마찰속도, ν는 유체의 동점성, τw는 벽면의 전단응력, ρ는 유체의 밀도를 의미한다. 이러한 관계식을 통해 수치해석결과로 계산된 벽면의 전단응력으로 점성하위층 두께를 추산하였으며 결과는 Table 4에 요약했다. Rod string의 회전속도 변화에 따라서 튜빙 벽면에 작용하는 전단응력의 변화량이 적었고, 점성하위층 두께에 미치는 영향 역시 미미하였다. 즉 rod string의 회전속도 변화가 내부 유동 패턴을 변화시키기는 하지만 튜빙 벽에 근접한 영역까지는 영향을 주지 못했다. 변화량은 Case 2를 기준으로 비교하였으며 1% 미만이었다. 이와 달리 원유의 주입 속도에 따라서는 최대 12%까지 변화하며 매우 큰 영향을 나타냈다. 점성하위층의 두께 증가는 튜빙 벽면에 파라핀 침전 가능 영역을 증가시키고, 유동면적 감소로 이어져 파라핀 침전 속도가 증가할 수 있음을 나타낸다. 비록 수치해석 결과의 점성하위층의 두께가 절대적으로는 작은 값이기는 하나 파라핀의 침전은 분자 단위로 발생하는 현상이기 때문에 이 결과는 충분히 유의미한 값으로 사료된다. 또한, 파라핀의 침전은 단발적인 현상이 아니라 지속적으로 누적되기 때문에 운영 시간이 지남에 따라 점차 격차가 증가할 것으로 예상된다. 반면, rod string 표면에서는 회전으로 인한 스월 유동이 발생하고 빠른 회전속도 때문에 점성하위층이 나타나지 않았다. 따라서 rod string 표면에서는 파라핀 침전이 발생하기 어려울 것으로 사료된다.
Table 4. Prediction for paraffin deposition thickness
| Case | Wall shear stress (kg/m·s2) | Laminar sub-layer thickness (mm) | Thickness ratio (%) |
| 1 | 287.19 | 0.0573 | 0.78 |
| 2 | 291.68 | 0.0569 | 0.00 |
| 3 | 292.39 | 0.0568 | -0.12 |
| 4 | 350.75 | 0.0518 | -8.81 |
| 5 | 231.99 | 0.0637 | 12.13 |
결 론
생산유전 시설에서 파라핀 침전을 억제하기 위해서는 우선 파라핀 침전에 영향을 미치는 원유의 조성, 환경조건, 지상 및 지하 시설설비, 운영조건 등 다양한 요소가 종합적으로 고려되어야 한다. 그 중 환경조건과 운영조건에 대한 영향 요인을 분석하고 연구대상지역 현장실증을 위한 기초연구를 수행하였으며 결론은 다음과 같다.
카자흐스탄 A광구의 환경조건을 적용한 결과, 연간 계절 변화가 뚜렷하고 연중 최고-최저 온도차가 크다는 특성이 있어 매설 심도에 따른 온도 분포 변화를 분석하였다. 심도가 깊어질수록 연간 최대 온도차는 감소하며, 연간 최대 온도차가 1.1°C로 계절에 따라 균일하게 유지되는 심도 5 m를 적정 매설 심도로 제안하였다. 온도 분포가 균일한 경우 효과적으로 파라핀 침전을 관리할 수 있으며, 각 현장별 환경 조건에 따른 연간 최대 온도차 허용 범위와 매설 심도 대비 경제성 등을 고려하여 최적 매설 심도를 결정해야 한다.
PCP 시스템의 운영조건에 따른 물리적 영향 요인 분석 결과, rod string의 회전력은 원유의 유동에 접선(tangent)방향으로 작용하여 유속 증가 및 스월 유동을 발생시켜 rod string 인근으로는 강한 회전 유동이 나타난다. 특히, 연구대상지역 현장의 경우 원유 채유에 따른 완전발달유동 속도보다 회전에 의한 접선속도가 더 빨라 rod string 인근으로는 파라핀 침전 가능성이 매우 낮을 것으로 사료된다. 하지만 rod string에 의한 회전 유동이 튜빙 벽-근접 유동까지는 영향을 미치지 못하였다. 따라서, 생산정의 운영조건에 따라 파라핀의 침전 양상이 달리 나타나기 때문에, 현장 운영조건을 조절함으로써 파라핀의 침전을 억제하는 효과를 얻을 수 있을 것으로 판단된다.
원유 주입 속도의 경우, 파라핀 침전 예측 모델에서 활용되는 주요 인자인 점성하위층 두께에 영향이 큰 것으로 분석되었다. 점성하위층 두께 변화는 파라핀 침전량 차이를 의미하며, 이 차이는 파라핀 침전이 누적될수록 원유의 유동 가능 면적 감소에 큰 영향을 줄 것이다. 따라서, 튜빙 벽면의 파라핀 침전 예측을 위해서는 관내 유동을 분석하여 점성하위층의 발달을 필수적으로 고려해야 한다.
본 연구에서 고려한 영향 요인들은 파라핀 억제 가능성를 위해 연구한 결과로써 의의가 있으며, 해당 인자들을 추가 고려한다면 생산시설에서의 파라핀 침전에 대해 더욱 정밀한 평가가 가능할 것으로 기대된다. 향후, 본 연구에서 도출한 인자들의 영향을 반영하여 온도변화와 침전 메커니즘을 고려한 비정상 상태(transient) 해석을 통해 파라핀의 침전 현상에 대한 심도있는 이해와 침전 억제 기술 발전에 기여할 계획이다.