서 론
다양한 회수증진기법(EOR, enhanced oil recovery) 중 CO2 주입기법은 새로운 관점에서 다시 주목을 받고 있다. 주입된 CO2는 오일에 용해되어 오일을 팽창시켜 점성도를 낮추며, 고압 주입에 따른 혼화 상태(miscible state)가 만족되면 단상유동(single phase flow)이 가능하여 추가적인 회수율 증진 효과를 볼 수 있다(Perera et al., 2016). 또한 주입된 CO2와 저류층 오일과의 밀도차에 의한 낮은 접촉효율(sweep efficiency)를 증가시키기 위한 WAG(water alternating gas) 공법 등이 고안되어 세계적으로 상업적인 개발에 적용되고 있는 실정이다(Godec et al., 2011).
현재까지 대다수의 CO2-EOR 프로젝트는 고가의 CO2 소비를 최소화하면서 최대의 오일 생산 효과를 보기 위한 공법 설계가 수행되었다. 그러나 최근들어 온실가스 저감에 대한 필요성이 증가하면서, CO2 처분에 따른 수익창출이 가능할 수 있게 되어 CO2 저장량 및 오일 회수율을 동시에 고려하는 광구운영 설계(CCS-EOR operation optimization)가 제안되고 있다(Kovscek and Cakici, 2005).
성공적인 CCS-EOR 공법 적용을 위해서는 저류층 특성을 고려한 다양한 형태의 운영조건을 고려하여야 한다. 특히 저류층 특성에 대한 불확실성이 클 경우, 고려해야 할 인자의 수는 기하급수적으로 증가한다. CCS-EOR 최적화 과정은 크게 운영 인자(오일 생산량 거동, CO2 활용도: 단위 오일 생산량에 대한 CO2 저장량, CO2 재활용도: CO2 주입량에 대한 CO2 생산량 등)과 경제성 인자(유가, CO2 가격, 세제혜택 등) 등을 고려해 수행된다(Ettehadtavakkol et el., 2014). 경제성 인자는 외부환경에 좌우되므로 인위적인 조절이 어렵지만, 광구 운영 인자는 운영 목적에 따라 적절한 범위의 값을 선정하게 된다.
CCS-EOR 광구 운영 최적화를 위해 우선 민감도 분석을 통해 각 인자에 대한 영향 정도를 결정한다. 대표적인 설계인자로는 CO2 주입량, WAG비, 주입패턴(flooding pattern), 유정완결형태(completion) 등이 있으며, 치밀 또는 비전통 저류층을 대상으로 할 경우 수압파쇄 형태(파쇄균열 거리, 간극 등) 및 자연균열과의 연결성 등이 추가로 고려되어야 한다(Ghaderi et al., 2012).
인자에 대한 민감도 분석을 위해 우선적으로 대상 저류층에 대한 정적모델(지질모델) 및 동적 모델을 구축하고 인자의 범위에 따른 경우의 수를 선정하여 시뮬레이션을 수행한다. 각 인자들의 민감도는 목적함수에 따라 그 영향 정도가 다를 수 있기 때문에 최적화 목적함수(최대 오일 회수율, 최대 CO2 저장량 또는 최대 NPV 등)에 따른 분석이 각각 수행되어야 한다. 이 과정에서 현실적인 문제에 직면하게 된다. CO2-EOR 뿐 아니라 CCS-EOR 분석을 위해서는 조성시뮬레이터를 활용하게 되는데, 일반적으로 5에서 10개 정도의 유사 조성(pseudo-component)으로 구성된 유체, 현장 규모 격자 체계 및 다수 정호에 대한 설정 등으로 인해 상당한 계산량이 요구된다. 일반적인 개인용 워크스테이션 기준으로 1회 시뮬레이션 수행을 위해 최소 수 시간이 소요되며, 여러 인자들의 민감도 분석 및 최적화 경우를 선정하기 위해서는 적게는 수백 회, 많게는 수천 회 시뮬레이션 수행이 필요하므로 모든 경우에 대한 시뮬레이션 수행은 현실적으로 불가능하다. 예를 들어, 8개 인자에 대한 경우의 수(2개 인자는 2개 파라미터, 6개 인자는 3개 파라미터)는 2,916(=22×36)에 이르며, 인자의 범위가 연속적일 경우 그 경우의 수는 무한대로 증가하게 된다. 이러한 문제를 해결하기 위해 계산의 효율을 위해 대표성을 갖는 경우를 찾기 위한 DOE(design of experiment; Montgomery, 2013) 방법 등이 적용되고 있다.
최근 들어 석유개발 분야에도 머신러닝(또는 인공지능) 기술 접목이 활발히 이루어지고 있다. 프록시 모델 구성, 히스토리 매칭, 프로젝트 디자인, 그리고 최적화 분야에 활발한 적용사례가 발표되고 있다(Min et al., 2020; Kim et al., 2017). 머신러닝 기술 접목을 통해 저류층 특성화 및 유체 거동 파악을 위한 원시자료 처리, 가공 시간 감축 및 시뮬레이션 연산에 소요되는 시간 감축 등이 가능할 것으로 판단되나, 아직까지 전통적인 분석 절차를 대체할 수준은 아니고 분석의 효율을 높이기 위한 보조적인 수단으로 활용되고 있다(Ertekin and Sun, 2019).
이 연구에서는 CCS-EOR 최적 해를 도출하기 위한 머신러닝 기법 적용 가능성을 검토하고자 하였다. 대상 저류층은 캐나다 알버타주에 위치하는 Pembina Cardium 필드이며, 기 발표된 시뮬레이션 결과를 활용하였다. 전체 경우의 수를 대표할 수 있는 방법(design of experiment)을 통해 도출된 105개 경우에 대한 시뮬레이션 결과를 활용하여 프록시 모델링을 수행한 결과, 총 경우의 수(2,916)에 대한 예측값을 도출하였으며, 이를 발표된 결과와 비교하여 최적화 분야에서의 머신러닝 기법의 적용성 및 활용가능성을 검토하였다.
본 론
대상 광구 개요
문헌 검토를 통해 CCS-EOR 최적화 분석이 수행된 저류층을 선정하였다. 대상 저류층은 캐나다 알버타주에 위치한 Pembina Cardium 필드로써, 낮은 투과도로 인해 회수율이 낮아 수압파쇄를 계획 중에 있다(Clarkson and Pedersen, 2011). Ghaderi et al.(2012)은 대상 저류층에 대한 유체 및 저류층 모델을 구축하여 상업모델(CMG GEM)을 활용한 시뮬레이션을 수행하였으며, 8개의 인자를 선정하여 이에 대한 민감도 및 최적화 분석을 수행하였다. 이를 개략적으로 요약하면 다음과 같다.
저류층 특성
저류층 유체 비중은 38 °API의 경질유이며, 초기 압력은 5,279 ft 기준으로 2,520 psi, 기포점 압력은 127℉에서 약 1,620 psi이다. 저류 유체 및 암석, 그리고 시뮬레이션 구동 관련한 주요 특성은 Table 1과 같다. CO2를 포함한 7개의 유사조성으로 유체성분을 구성한 후 PVT 실험자료(swelling test 및 MMP 측정실험)와 매칭하여 PVT 입력자료를 구성하였으며, Peng-Robinson 상태방정식을 사용하였다.
당초 코어 및 로깅자료를 활용한 3차원 지질모델이 구축되었으나, 다양한 인자들의 영향을 관측하기 위해 저류층의 일부분(640 acre)을 대상으로 분석하였다(Fig. 1). 특히 균열 특성(fracture spacing 및 fracture half length 등)은 저류층 지질특성에 영향을 받을 수 있으므로 고도차를 배제한 모델을 사용하였다.
Table 1.
Reservoir fluids and rock properties
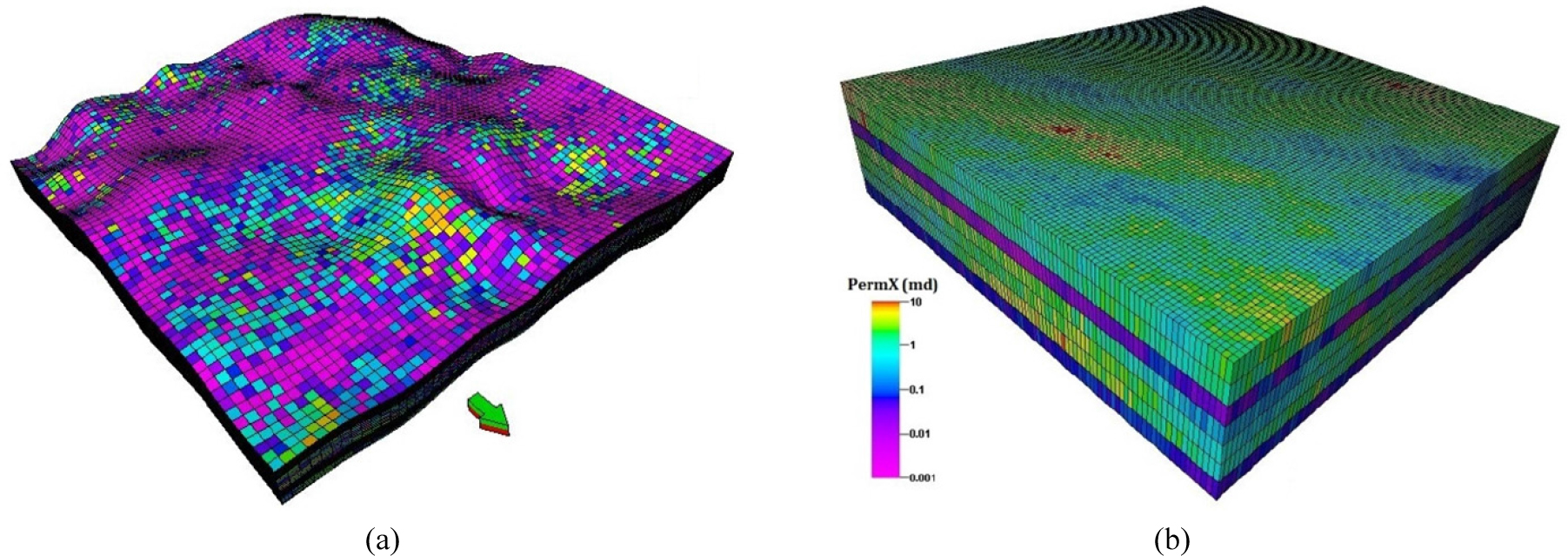
Fig. 1
(a) One section of Pembina Cardium reservoir considered as the study area, (b) the flattened version of reservoir model used in reservoir simulation (Ghaderi et al., 2012).
시뮬레이션을 위해 대상 지역은 외곽이 단절된 것으로 가정하였으며, 하부 대수층의 영향은 고려하지 않았다.
생산정 및 CO2 주입정은 모두 수평정으로 설계되었으며, 모두 4,650 ft의 길이를 갖는다. 수압파쇄에 의한 균열 전도도(fracture conductivity=)는 균열 간극()을 0.1ft로 가정하여, 약 200 md-ft 내외인 것으로 가정하였다.
시뮬레이션 수행 결과
Ghaderi et al.(2012)은 시뮬레이션 수행을 통해 CCS-EOR 최적화에 영향을 미치는 인자를 선정하였다. 최대 오일 회수율과 최대 CO2 저장량을 목적함수로 할 경우 영향을 미치는 인자 8개가 선정되었으며, 이에 대한 설명은 Table 2와 같다. 동시에 경제적 효과에 대한 최적화를 동시에 고려하기 위해 NPV(net present value)를 목적함수로 분석을 수행하였다. NPV 계산을 위해 사용된 가정은 Table 3과 같다. OPEX 뿐 아니라 CAPEX 비용 또한 고려하여 분석되었으며, cemented 정호 비용을 open-hole에 비해 1.5배로 가정하였다. 그러나 그 이상의 자세한 내용은 문헌에 수록되지 않았다.
Table 2.
Different factors and the associated parameters for sensitivity runs
Table 3.
Input parameters for NPV calculations
|
Oil price, $/bbl *Royalty, % CO2 price, $/mscf CO2 recycle cost, $/mscf Oil lifting cost, $/well/year Operating cost of producers, $/well/year Operating cost of injectors, $/well/year Operating cost cut-off, $/boe |
80 variable 1.0 0.52 15 24,000 30,000 60 |
8개 인자 중 A와 B는 2개의 파라미터를, C에서 H는 3개의 파라미터를 고려하였으며, 이에 대한 모든 경우의 수는 2,916(=22×36)에 이른다. 이에 대한 각각의 시뮬레이션은 현실적으로 불가능하기 때문에 Ghaderi et al.(2012)은 DOE(design of experiment) 방법(Montgomery, 2013)을 도입하여 대표성을 가지는 105가지 경우를 선정하여 결과를 도출하였다. DOE 방법은 1개 이상의 인자에 대한 상관성을 파악하는데 활용되며, 목적함수에 대한 인자의 영향을 반응표면(response surfaces) 형태로 표현할 수 있다는 장점을 가지고 있다.
105개 경우에 대한 시뮬레이션 수행 결과는 Table 4와 같다. 목적함수에 따른 결과를 살펴보면, 회수율은 37.0%에서 60.6% 사이의 값을 보이며, 오일 생산량 증가비율은 OOIP 기준 0.4~17.1%이다. 또한 CO2 저장량은 0.2~3.6 bcf, 그리고 NPV는 8.6~38.1 mm$의 범위를 갖는다. 위에서 산출된 목적함수별 최소, 최대 범위는 105개 경우에 대한 범위이며, 전체 조합의 수가 2,916이므로 보다 다양한 조합을 통해 이 범위 이상의 목적함수 최소, 최대값들이 산출될 수 있다.
Table 4.
Sensitivity factors and response values for the selected runs
이를 위해 Ghaderi et al.(2012)은 “half-normal probability” 도시법을 통해 목적함수에 따라 영향이 큰 인자들을 선정한 후, 반응표면 도시법을 통해 상호 연관성이 있는 인자들에 대한 영향 정도를 파악하였다. 즉, 불연속적인 값을 가지는 인자(D1/D2, cemented/open-hole 등)들은 영향 정도를 고려해 미리 고정한 후, 연속적인 값을 가지는 나머지 인자들은 반응표면의 값을 활용하여 추가적인 시뮬레이션 수행없이 내삽법을 활용해 Table 5와 같은 조합의 최적해를 산출하였다.
Table 5.
The proposed optimal values of factors
제시된 방법 및 결과는 과도한 시뮬레이션 횟수를 줄이기 위해 일반적으로 시도되는 타당한 방법이나, 저류층 특성 및 유동(주입) 거동에 영향을 미치는 인자들에 대한 고려가 추가적으로 필요할 경우, 이러한 과정도 매우 복잡하고 과도한 계산량을 요구하기 때문에 한계를 가질 것으로 판단된다.
머신러닝 기법 적용
CCS-EOR 최적화 분석에서 머신러닝 기법의 적용성을 검토해 보기 위해 먼저, 최적화 모델을 개발하였으며, 다음으로 위에서 설명된 저류층 분석 자료를 활용하여 최적화 과정 및 결과를 비교하였다. 각각의 과정 및 결과는 다음과 같다.
프록시 모델 개발 및 적용
위와 같은 형태의 최적화 문제는 머신러닝 기법에서 지도학습(supervised learning)의 분류(classification)에 해당된다. 즉, 학습 데이터로 주어진 테이터의 피처(feature)와 레이블(label) 값을 머신러닝 알고리즘으로 학습해 모델을 생성하고, 이렇게 생성된 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측하는 과정이다(Géron, 2019). 관련된 분석을 위해 다양한 패키지 활용이 가능한 파이썬 언어를 이용하였으며, 기본적으로 활용된 패키지는 pandas, numpy 및 scikit-learn이다. 최적화 모델로는 트리기반(decision tree) 앙상블 학습에서 가장 각광받고 있는 XGBoost 알고리즘을 사용하였다. 또한 결과 도시 및 엑셀 파일, PDF 형식 출력을 위한 matplotlib, openpyxl 등의 패키지가 활용되었다.
프록시 모델 적용결과 및 분석
먼저 Table 4의 105개 자료를 범주형(categorical) 자료로 변환하였다. 즉, Table 2와 같은 8개의 변수 중 A(well pattern)와 같이 2개의 파라미터를 갖는 변수들은 0과 1의 자료형으로, C(fracture spacing)와 같이 3개의 파라미터를 갖는 변수들은 0, 1, 2의 자료형으로 변환하였다. 변환된 105개의 세트 자료를 scikit-learn 패키지의 train_test_split 함수를 활용하여 학습 및 테스트 자료를 분리하였다. 이때 활용된 최적화 모델은 XGBoost 패키지의 XGBRegressor 함수이며, 파라미터를 순차적으로 입력하여 최적의 파라미터를 선정하는 GridSearchCV 방법을 적용하였다. 여기서 테스트 사이즈는 0.25이며(학습에 활용된 자료 비율은 0.75), 학습자료에 대한 무작위 선택에 따른 오류를 최소화하기 위해 100회의 실험을 수행하여 이를 평균한 값을 대표값으로 선정하였다. 50회 이상의 실험 수행 시 평균값이 수렴되는 현상을 발견할 수 있었으나, 평균 및 표준편차 값의 대표성을 확보하기 위해 실험 횟수를 충분히 크게 설정하였다.
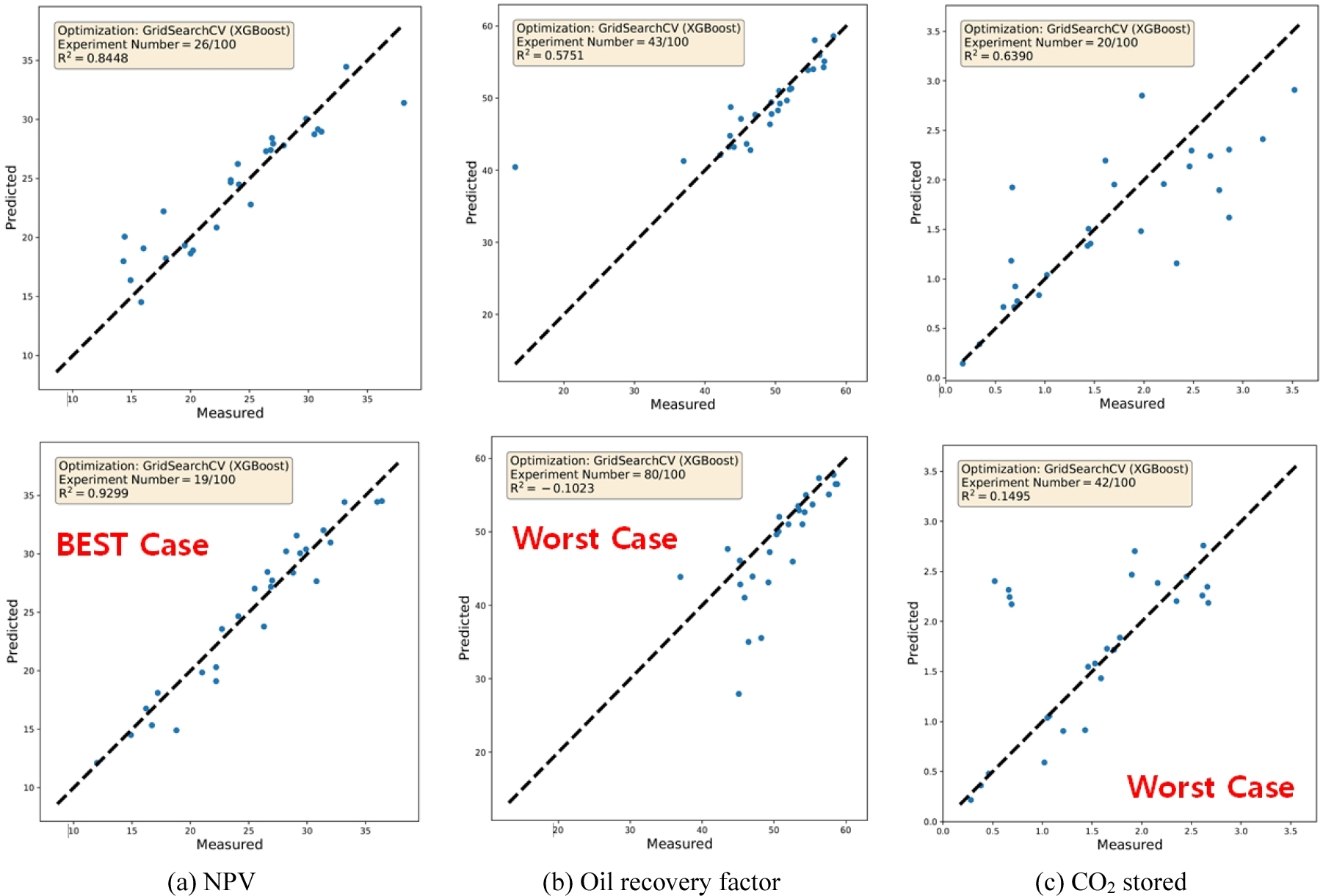
위의 방법으로 수행된 학습 및 테스트 결과는 Table 6과 같다. 목적함수가 NPV일 경우 100회 실험의 평균 정확도는 0.8485이며, 최소 0.6865, 최대 0.9299의 수치를 나타내었다. 이에 반해 오일 회수율과 CO2 저장량 항목은 평균 0.5860 및 0.6227을 보였으며, 특히 음의 값을 갖는 적합도(R-square)를 보이기도 하였다. Fig. 2는 각 100번의 실험 중 적합 특성을 나타내는 예를 보여주는 것으로, 그림의 상부는 평균치에 가장 가까운 경우를 예로 보여주고 있으며, 하부는 적합도가 가장 높은 경우와 가장 낮은 경우를 나타내었다. 여기서, 평균값이 대표값을 갖지 못할 경우 적합도는 음의 값을 보이기도 하며, 특히 사용된 자료 중 이상치(outlier)의 영향이 클 경우 이와 같은 현상이 발생할 수 있다(Scikit-learn, 2020). NPV의 경우 어느정도 만족스러운 수준이나, 오일 회수율과 CO2 저장량의 경우 적합도가 떨어짐을 알 수 있으며, 이를 활용한 적절한 예측이 어려울 것으로 판단되어 학습 및 테스트 수행을 위한 초매개변수(hyper-parameter) 선정 방식을 다음과 같이 수정하였다.
Table 6.
The averaged accuracy in test procedure by GridSearchCV method
| Accuracy | Standard Deviation | |||
| Mean | Min. | Max | ||
| NPV | 0.8485 | 0.6864 | 0.9299 | 0.0505 |
| Oil Recovery Factor | 0.5860 | -0.1177 | 0.8881 | 0.2048 |
| CO2 Stored | 0.6227 | 0.1495 | 0.8448 | 0.1317 |
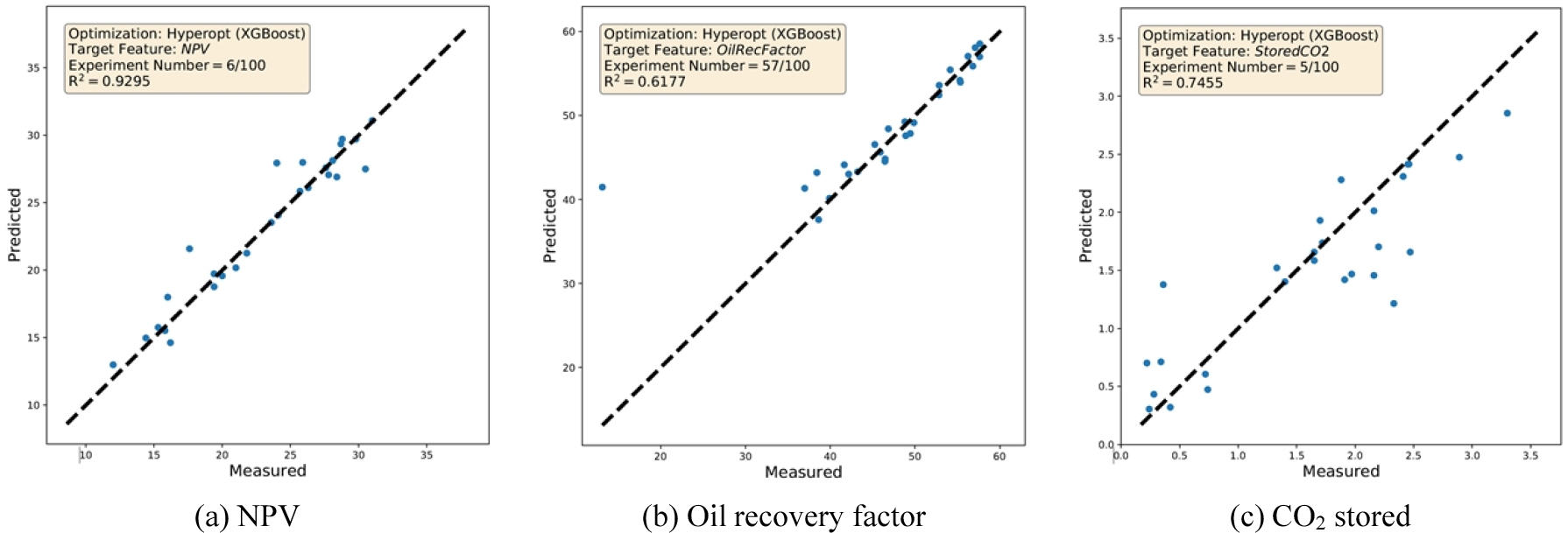
앞서 수행한 GridSearchCV 함수의 초매개변수는 4개를 선정하였으며, 일정 범위 내에서 최적의 값을 탐색하는 방식이었기 때문에 최적값 도출에 한계가 있는 것으로 판단되었다. 이를 개선하기 위해 Hyperopt 함수를 활용하여 초매개변수의 범위를 확장하고 보다 많은 수의 초매개변수를 고려하였다. Hyperopt 함수의 튜닝(tuning) 알고리즘 중 Baysian 방법을 사용하였으며, 이 방법은 격자탐색(grid search)이나 무작위탐색(random search) 방법에 비해, 사전 지식을 충분히 반영하면서 동시에 전체적인 탐색 과정을 체계적으로 수행할 수 있다는 장점을 가진다(Brochu et al., 2010). Hyperopt 함수를 활용한 테스트 자료 정확도는 Table 7과 같다. 마찬가지로 100회의 실험을 통한 평균값은 NPV, 오일 회수율, CO2 저장량의 경우 각각 0.9279, 0.7651, 0.7396으로 산출되었다. 앞서 수행한 GridSearchCV 방법에 비해 정확도가 모두 증가한 것을 확인할 수 있으며, 각 목적함수에 대한 대표적인 자료 적합 특성을 Fig. 3에 도시하였다. 각 그림은 평균에 가장 근사한 경우를 도시한 것으로, 그림에서와 같이 NPV의 경우 테스트 자료에 대한 적합이 매우 고르게 분포하고 있음을 알 수 있다. 그러나 오일 회수율의 경우 대부분의 테스트 자료가 고르게 적합되나 간헐적으로 이상치가 관측되는 특징을 보이기도 하였다. CO2 저장량의 경우 앞선 두가지 목적함수의 적합 분포에 비해 전체적으로 자료가 분산되어 있는 특징을 보인다.
Table 7.
The averaged accuracy in test procedure by Hyperopt method
| Accuracy | Standard Deviation | |||
| Mean | Min. | Max | ||
| NPV | 0.9279 | 0.8256 | 0.9779 | 0.0314 |
| Oil Recovery Factor | 0.7651 | 0.4431 | 0.9470 | 0.1496 |
| CO2 Stored | 0.7396 | 0.3492 | 0.8942 | 0.1084 |
위에서 관측된 특성을 토대로 추가적인 분석을 수행하였다. 즉, 각 목적함수에 대한 최적화는 동일한 8개의 인자가 활용되었으나, 인자의 특성을 살펴보면 각 목적함수에 미치는 영향정도가 상이한 것으로 판단된다. 목적함수를 최적화하기 위해 민감도가 큰 인자를 선별하는 과정이 필수적이므로, 우선 각 목적함수에 대한 인자들의 영향 정도를 파악하였다. NPV의 경우 학습/테스트 결과가 만족스럽기 때문에 오일 회수율 및 CO2 저장량 목적함수에 대한 인자들의 영향만을 파악하였다. 먼저 오일 회수율 학습에 기여한 인자들의 정도를 알아보았으며, 이를 위해 내장 함수인 “feature importance”를 활용한 결과는 Table 8과 같다. 상대적으로 영향 정도가 낮은 B, E, F, 및 G 인자 중에서 E와 F를 제외하였는데, 이는 Ghaderi et al.(2012)이 제시한 반응표면(response surface) 분석 결과를 동시에 참고하여 결정하였다. 반응표면 분석에 의하면 오일 회수율 목적함수에 대한 인자들의 영향 정도는 H, A, D, C, G 순으로 낮아진다. 두 개의 인자를 제외한 학습 및 테스트 결과, 적합도는 0.9251, 표준편차는 0.0246으로 계산되었으며, NPV와 유사한 수준으로 적합도가 산출되었으며 약 20%의 적합도 향상이 가능하였다. 위의 과정과 동일하게 CO2 저장량 목적함수에 대한 분석을 수행하였으나, 유의미한 적합도 향상 결과를 획득하지 못하였다. 이는 CO2 저장량 목적함수 최적화를 위해 선정된 인자들의 재선정 및 민감도 분석과정이 추가적으로 필요함을 보여준다.
Table 8.
The averaged feature importance values in Oil Recocery Factor calculation
최적 목적함수 예측
먼저 입력자료로 활용된 105개의 시뮬레이션 결과를 살펴보면, Table 4에서와 같이 NPV의 경우 28번의 38.1 MM$, 오일 회수율 및 CO2 저장량의 경우 각각 102번인 60.6%, 3.6 bcf를 보이고 있다. 앞선 과정을 통해 선정된 초매개변수를 기준으로 각 파라미터에 대한 목적함수를 예측하였다. 먼저 NPV의 경우, 8개 파라미터에 대한 2,916가지 경우의 NPV를 산출하여, 최대 NPV를 보이는 3가지 파라미터 조합을 Table 9에 정리하였다. 입력자료로 활용한 38.1 MM$ 대비 약 5% 증가한 39.9 MM$의 최대 NPV 산출이 가능함을 알 수 있으며, 파라미터 C, G를 제외한 나머지 파라미터는 최대 목적함수를 나타내는 3가지 경우에서 모두 고정된 양상을 보이기 때문에 영향인자에 대한 보다 명확한 분석 방향을 제시하고 있다.
Table 9.
Maximum NPV cases and parameter combination
| Cases | A | B | C | D | E | F | G | H | NPV |
| 1961 | D2 | Open-Hole | 300 | 100 | 1300 | 0.5 | 0.50 | 1 | 39.91 |
| 1493 | D2 | Open-Hole | 200 | 100 | 1300 | 0.5 | 0.50 | 1 | 39.88 |
| 1496 | D2 | Open-Hole | 200 | 100 | 1300 | 0.5 | 0.25 | 1 | 39.47 |
다음으로 오일 회수율의 경우 E, F 파라미터를 제외한 6개 파라미터에 대한 최대값은 Table 10과 같다. 최대값은 60.62%로써 입력자료에 비해 향상된 값을 보이지 못하고 있으며, 이러한 현상은 CO2 저장량 경우에서도 유사한 양상을 나타낸다. 목적함수 오일 회수율의 경우 6개 인자를 활용한 최적화가 만족할 만한 수준이나, CO2 저장량 목적함수 최적화는 상대적으로 신뢰성이 떨어짐을 알 수 있다. 이는 목적함수에 따른 영향 인자 선정이 개별적으로 이루지거나, 보다 추가적인 영향인자 선정이 필요함을 보여준다.
Table 10.
Maximum Recovery Factor cases and parameter combination
| Cases | A | B | C | D | G | H | Recovery Factor |
| 320 | D2 | Cemented | 300 | 300 | 0.50 | 1 | 60.62 |
| 29 | D1 | Open-Hole | 400 | 100 | 0.75 | 2 | 59.61 |
| 26 | D1 | Open-Hole | 400 | 100 | 0.50 | 2 | 59.49 |
기존 문헌 결과를 활용한 머신러닝 최적화 분석의 한계로 인해, 예측된 목적함수 최대값이 실제 시뮬레이션 결과와 어느정도 일치하는지에 대한 비교분석을 수행하지 못하였으나, 이 연구에서 제시된 값들은 기존 문헌의 최적화 방법을 통해 제시된 결과와 유사한 수준의 값을 보이고 있으므로, 신뢰성은 확보된 것으로 판단할 수 있다.
결 론
이 연구에서는 CCS-EOR 최적화 분석에서 머신러닝 기법의 적용성을 검토해 보기 위해, 문헌 검토를 통한 기존 최적화 분석 필드 검토, 머신러닝 기반 저류층 최적화 모델 개발 및 적용성 검토 분석을 수행하였으며, 이를 통해 도출된 결론은 다음과 같다.
최근들어 다양하고 복잡한 형태의 저류층 운영방식이 고안되어 적용되는 시점에서 저류층 특성, 현장 운영 조건, 외부 환경 등을 동시에 고려한 효과적인 최적화 방안이 요구되고 있는 실정이며, 수반되는 과도한 계산량 문제를 해결하기 위해 시뮬레이션 수행 횟수를 최소화하고자 하는 노력들이 다양하게 진행되고 있다.
이 연구에서 제안한 머신러닝 최적화 과정은 학습에 필요한 최소한의 시뮬레이션 결과를 활용하여, 모든 경우의 시뮬레이션 결과를 예측할 수 있는 프록시 모델 개발 및 적용 과정을 제안하였다. 학습에 필요한 시뮬레이션 경우 수 및 영향인자 선정 등에 따라 머신러닝 학습 적합도는 차이를 보였으나, 목적함수에 대한 적절한 영향인자 선정 및 학습자료가 확보될 경우, 머신러닝 최적화 기법은 기존 기존의 최적화 과정을 대체할 수준의 매우 효과적인 방법임을 보여주고 있다.
목적함수 NPV에서와 같이 학습 및 테스트 과정은 매우 높은 적합도를 보여주었으며, 추가적인 시뮬레이션 수행 없이 가능한 모든 경우에 대한 결과 예측이 가능함을 알 수 있다. 또한 영향인자가 추가되어 경우의 수가 증가하더라도 비교적 쉽게 이에 대한 고려가 가능하므로, 다양하고 복잡한 저류층 운영조건에 대한 최적화 과정에 효과적으로 이용될 수 있을 것으로 판단된다.