서 론
지열냉난방시스템은 땅 속 매질이나 지하수의 온도가 연중 거의 일정한 것을 이용하여 냉난방에 필요한 에너지를 기존의 공기열냉난방시스템에 비해 감소시킨 기술이다. 공기의 열물성이나 분포가 어느 곳에서나 거의 동일한 것과는 다르게 땅 속 매질의 열물성이나 지하수의 분포 및 흐름특성은 지역에 따라 상당한 차이가 있고 이는 지열냉난방시스템의 성능에 유의미한 영향을 줄 수 있다. 그러므로 지열냉난방시스템의 설계는 이러한 불균질성을 잘 반영하는 것이 중요하다. 불균질성의 반영을 위해서는 설치하는 곳의 열적 특성이나 수리지질학적 특성을 잘 조사해야 하고 또한 그것을 제대로 해석할 수 있는 툴이 필요하다.
과거에는 주로 Line source model(Ingersoll and Plass, 1948; Ingersoll et al., 1950; Penrod, 1954)이나 Cylindrical source model(Kavanaugh and Rafferty, 1997)과 같은 해석해(analytical solution)를 이용하여 간단하게 계산하는 툴이 주를 이루었지만 최근에 들어서는 3차원 수치모델이 지열냉난방시스템의 성능 계산과 설계에 이용되고 있다(Signorelli, 2004, Kim et al., 2010). 3차원 수치모델은 다양한 물성, 실제에 가까운 지오메트리, 복잡한 가동조건 등을 모두 반영할 수 있으므로 해석해로는 알 수 없는 다양한 결과를 얻을 수 있다.
TOUGH2(Pruess et al., 1999)는 (현재는 판올림으로 TOUGH3(Jung et al., 2017)) 미국 Lawrence Berkeley Lab.에서 개발된 지하수의 흐름과 열 및 용질의 이동을 3차원으로 계산할 수 있는 시뮬레이션 코드로 세계적으로 널리 사용되고 있다. 특히 이산화탄소 지중 저장 시뮬레이션, 방사성폐기물 처분장 설계 등과 같이 소위 난이도가 높은 문제를 계산하기 위해 많이 활용되고 있다. 또한 연구용으로 사용한다면 가격이 저렴한 편이고 소스 코드도 공개되어 있어서 필요하다면 모듈을 추가할 수도 있다. TOUGH2는 IFDM(Integrated finite difference method)을 사용하여 지배방정식을 계산한다. 계산 방식은 일반적인 FDM(finite difference method)과 유사하여 FEM(finite element method)보다 상대적으로 빠르고 수렴이 잘 되며 직육면체가 아닌 다면체 메쉬를 사용할 수 있어서 FDM에 비해 훨씬 적은 수의 메쉬로 원하는 형태의 반영이 가능하다(Narasimhan and Witherspoon, 1976).
해석해는 그 해석해를 만들 때 사용된 가정이 문제의 상황과 맞는다면 항상 정확한 계산 결과를 보장한다. 그러나 수치모델은 메쉬의 형태, 시간간격(time step)의 설정, 경계조건 및 초기조건, 방정식을 풀기 위해 역행렬을 구하는 방법 등에 따라 계산 오차가 발생할 여지가 존재한다. TOUGH2에서는 특히 메쉬의 형태에 주의를 기울여야 한다. IFDM은 인접한 두 셀 사이의 물질이나 에너지 흐름을 계산할 때 두 셀의 중점을 연결한 직선과 셀의 경계가 직교해야 한다는 규칙을 가지고 있다. 또한 지중냉난방시스템의 시뮬레이션을 위한 메쉬는 관정과 파이프의 형태를 반영해야 하는데 관정이나 파이프의 크기는 수 mm에서 수십 cm의 크기이고 여기에 영향을 줄 수 있는 범위는 수평적으로 수백 m에서 수 km에 이르므로 TOUGH2에 내장된 기능으로 메쉬를 만드는 것은 쉽지 않다.
이러한 제약 사항을 극복하고 지중냉난방시스템을 위한 관정이나 파이프의 형태를 실제와 가깝게 만드는 방법이 지난 연구를 통해 보로노이 테셀레이션을 이용하여 진행되었다(Kim et al., 2015). 보로노이 테셀레이션을 통해 형성된 셀은 Fig. 1과 같이 IFDM의 메쉬 요구 조건을 정확하게 만족시키기 때문이다.
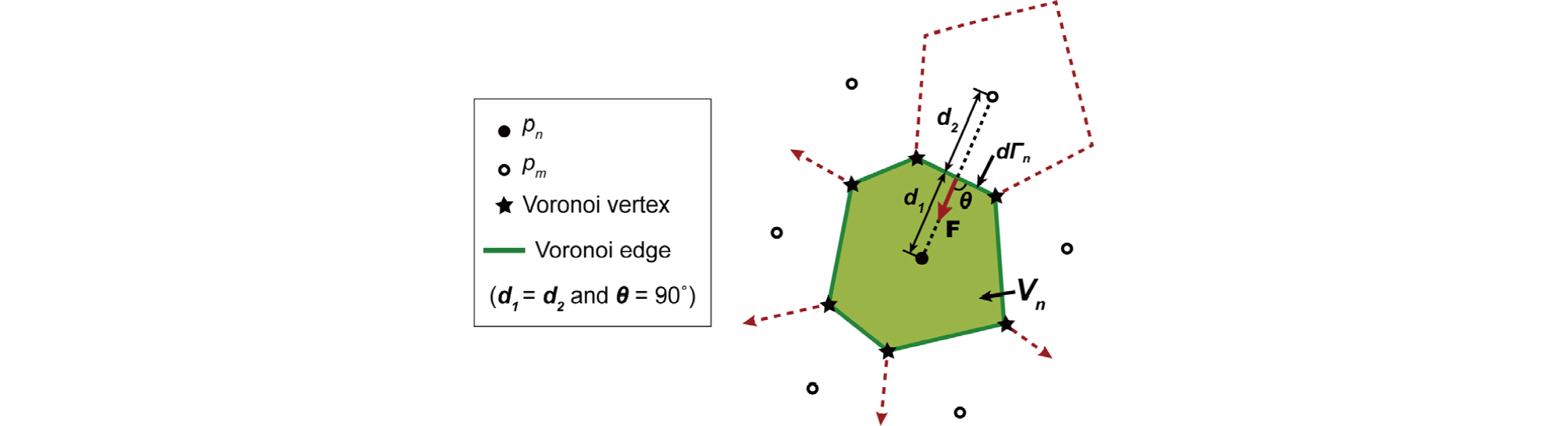
Fig. 1.
Space discretization and geometric parameters in the integrated finite difference method and Voronoi tessellation. The connections between two adjacent cells are always orthogonal to their connection interface (Kim et al., 2015).
이 연구에서는 이전 연구를 좀 더 발전시켜서 무게중심 보로노이 테셀레이션 기법을 이용하여 지열냉난방시스템의 시뮬레이션은 물론이고 2차원 단면을 길이 방향으로 확장시켜서 표현할 수 있는 관정이나 파이프가 존재하는 도메인을 시뮬레이션 해야 하는 상황에서 사용 가능한 메쉬를 만드는 방법을 개발했다. 이전 연구에서 부족했던 부분은 셀의 중점의 위치가 그 셀의 무게중심의 위치와 차이가 클 수 있다는 점이었다. 보로노이 셀의 중점이 셀의 무게중심과 멀어진다는 것은 인접한 보로노이 셀과의 크기 차이가 많이 발생한다는 뜻이다. 지배방정식을 원래의 해(exact solution)에 가장 가깝게 풀기 위해서는 일관성 있는 공간 분할이 필요하다(Tu et al., 2018). 즉 급격한 메쉬 사이즈의 증감을 피할수록 일관성 있는 공간 분할이 가능하다. 또한 셀의 중점은 그 셀의 물성을 대표하는 점이므로 무게중심에 위치하는 것이 가장 이상적이다. 그러므로 무게중심 보로노이 테셀레이션 기법 도입을 통해 계산 오차를 줄이고 계산 효율을 향상시킬 수 있다(Du et al., 2003, Ringler et al., 2008).
이 론
보로노이 테셀레이션은 평면을 다각형으로 빈틈없이 채우는 기법으로 Dirichlet(1850)과 Voronoi(1908)에 의해 제안되었고 식 (1)과 같이 정의된다.
| $$V_n=p:\parallel p-p_n\parallel < \parallel p-p_m\parallel,\forall m\neq n$$ | (1) |
보로노이 테셀레이션은 보로노이 생성점 p(generator 혹은 seed)로부터 보로노이 영역 Vn(region 혹은 cell)을 형성하면서 진행된다. Vn은 pn과 가장 가까이에 있는 영역으로 점 pm의 영역과 중첩되지 않는다. 즉 Vn 내부에 있는 임의의 점은 모든 생성점 중 pn과 가장 가까워야 한다. 보로노이 모서리(edge)는 두 보로노이 영역의 경계로 보로노이 생성점을 연결한 직선의 수직이등분선이다. 그러므로 이는 IFDM이 요구하는 메쉬의 조건을 만족시킨다.
무게중심 보로노이 테셀레이션(Centroidal Voronoi tessellation, CVT)은 보로노이 생성점의 위치가 보로노이 영역의 무게중심과 일치하도록 다각형을 생성하는 것이다. CVT를 생성하기 위해 다양한 알고리즘이 개발되어 있고 대표적으로 Lloyd’s algorithm과 Quasi-Newton method 등이 있다(Nocedal and Wright, 2006).
이 연구에서는 Lloyd's algorithm을 기반으로 하여 무게중심 보로노이를 계산했다. Lloyd's algorithm은 다음과 같은 방법으로 무게중심 보로노이 테셀레이션을 수행한다(Du et al., 1999).
1. 주어진 도메인에서 초기 생성점 집합 X=(x1, …, xn)을 만든다.
2. 생성점 집합 X로부터 보로노이 영역 V=(V1, …, Vn)을 식 1과 같이 계산한다.
3. 각 보로노이 영역의 무게중심 T(X)를 밀도함수 ρ(x)를 사용하여 식 (2)와 같이 계산하고 그 무게중심을 새로운 생성점 집합으로 사용한다.
4. 새로운 생성점 집합이 수렴 조건을 만족하면 종료하고 만족하지 않으면 2번으로 돌아가 반복계산을 한다.
| $$T_i(X)=\frac{\int_{V_i(X)}{x\rho(x)dx}}{\int_{V_i(X)}{\rho(x)dx}},\;\;\;\;i=1,\cdots,n$$ | (2) |
수렴 조건은 식 (3)의 에너지함수 E가 최소값을 가지는 조건이다. 반복계산을 통해 수렴이 수학적으로 가능한지 실제로 최소값을 찾을 수 있는지 수렴 속도를 어떻게 하면 빠르게 할 수 있는지에 대한 연구는 현재에도 활발하게 진행 중이다(Gersho and Gray, 1992; Kanungo et al., 2002; Du et al., 2010; Hateley et al., 2015). Lloyd's algorithm은 최소값을 찾는 문제를 풀기 위해 변수를 대체하는 알고리듬 중의 하나로(Du and Emelianenko, 2006)) 수렴을 할 수 있는지의 여부는 Felischer(1964)와 Kieffer(1983)에 의해 대부분 연구되었다.
| $$E=\sum_{i=1}^n\int_{V_i(X)}{\rho(x)\;\left\|x-x_i\right\|^2\;dx}$$ | (3) |
전 도메인에 걸쳐서 밀도가 일정하다면(ρ(x)=1) 반복계산을 진행했을 때 생성점이 도메인 전체에 골고루 퍼지게 된다. 하지만 정확하고 효율적인 시뮬레이션 수행을 위해서는 변화가 큰 곳의 메쉬를 조밀하게 생성해야 하고 변화가 적은 곳의 메쉬는 상대적으로 성기게 생성해야 한다. 이를 위해 밀도함수를 사용할 수 있다.
관정이나 파이프의 모양 반영을 위해서는 다음과 같은 특수한 조건을 만족해야 한다는 것을 이전 연구를 통해 알아냈다(Kim et al., 2015). 원형의 다각형을 생성하기 위해서는 Fig. 2와 같이 두 개의 동심원 모양으로 생성점을 배치하면 된다. 내부의 원과 외부의 원을 구성하는 한 쌍의 점을 지나는 직선은 두 동심원의 중심을 향해야 한다. 이러한 한 쌍의 점들은 Fig. 2a와 같이 동일한 간격으로 배치되어도 되지만 Fig. 2b와 같이 다른 간격으로 배치되어도 무방하다. 이러한 점의 개수가 많을수록 그리고 점의 간격이 일정할수록 원에 가까운 모양이 생성된다. 만약 이 점 집합과 너무 가까운 거리에 다른 점이 위치한다면 원의 모양이 변형될 수도 있으므로 그러한 점의 생성은 억제해야 한다.

Fig. 2.
Circular-shaped polygons (Py) bounded by Voronoi edges obtained with two sets of concyclic generators, which lie on two concentric circles (C1 and C2): (a) Circular-shaped polygons with generators lain uniformly on the circle and (b) generators lain nonuniformly on the circle (Kim et al., 2015).
이 연구에서는 다음과 같은 과정을 통해 지열냉난방시스템의 시뮬레이션을 위한 무게중심 보로노이 테셀레이션을 수행하는 일련의 코드를 FORTRAN 90을 사용하여 개발했다.
1. 관정 형태의 보로노이 영역이 형성되도록 보로노이 생성점을 만든다. 생성점을 만드는 방식은 이전 연구에서의 방식을 사용한다.
2. 보로노이 영역을 찾는 계산을 수행한다. 이 계산을 위해 AMESH(Haukwa, 1998)를 사용한다. Python 등을 사용하여 계산할 수도 있지만 AMESH는 TOUGH2를 위해 개발된 보로노이 테셀레이션 계산 프로그램이므로 나중에 TOUGH2의 입력 파일을 만들 때 편리하다는 장점이 있다.
3. 각 보로노이 영역의 무게중심과 에너지함수를 계산한다. 밀도함수는 생성점의 위치에 따라 다르게 적용하여 사용한다.
4. 수렴 조건을 만족할 때까지 반복계산을 한다.
관정 외부에 위치한 생성점에 대한 밀도함수는 가장 가까운 관정까지의 거리에 대한 함수로, 관정 내부에 위치한 생섬점에 대한 밀도함수는 가장 가까운 파이프 혹은 관정벽까지의 거리에 대한 함수로 설정했다. 관정이나 파이프의 형태를 유지하는데 필요한 생성점의 경우 무게중심을 새로운 생성점으로 할 경우 형태 유지가 불가능하기 때문에 생성점의 좌표를 관정이나 파이프의 중심까지의 거리 r과 x축을 기준으로 했을 때의 각도 θ로 치환한 후 r은 그대로 유지하고 무게중심 방향으로 θ만 변하도록 설정했다. 즉 Fig. 2a와 같은 최초의 생성점이 무게중심의 이동에 따라 Fig. 2b와 같은 형태로는 변할 수 있다. 하지만 이렇게 이동한 위치는 무게중심은 아니다.
결 과
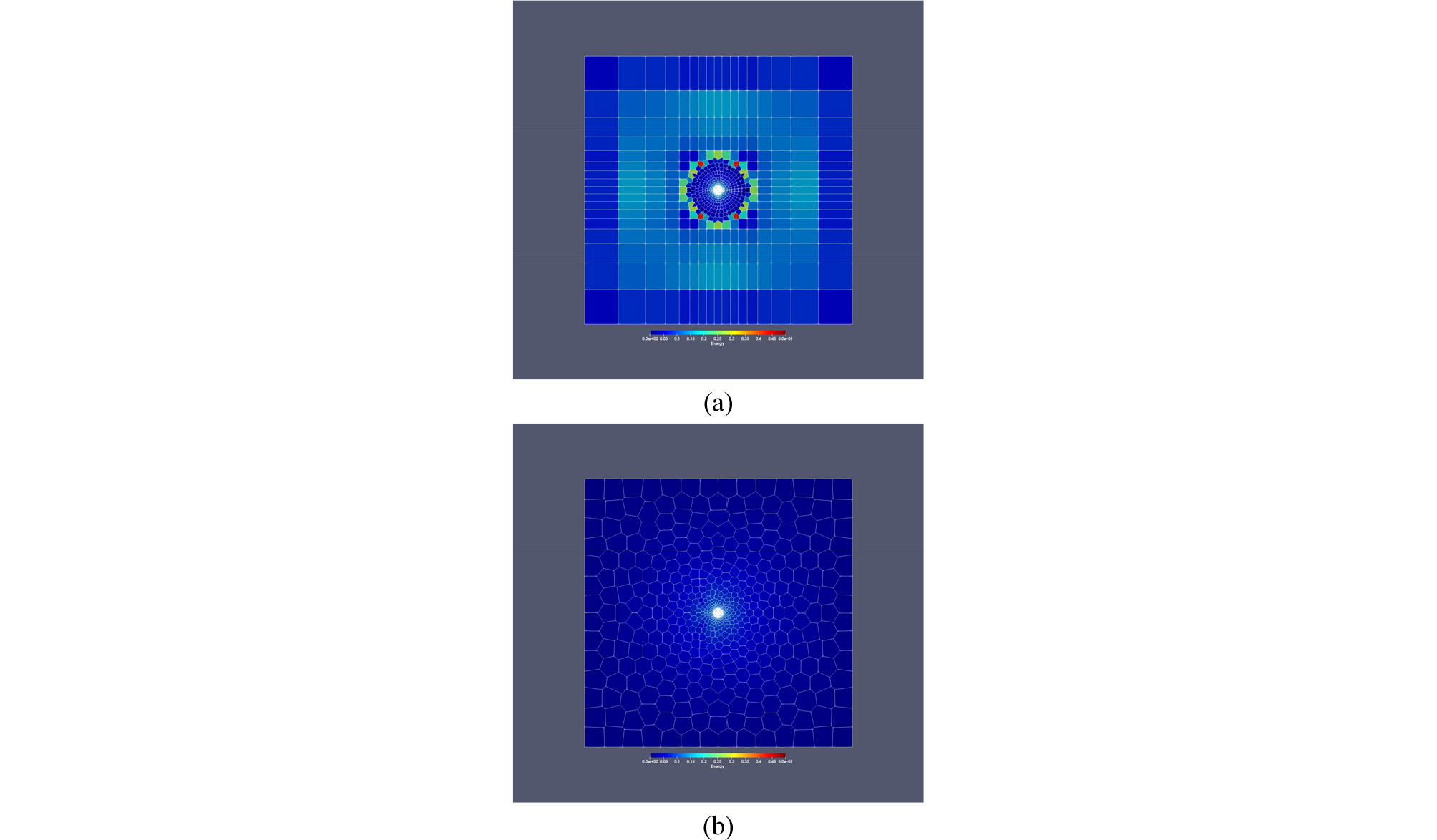
4개의 파이프(2개의 double U-tube)가 설치된 관정이 중심에 위치해 있는 도메인을 대상으로 무게중심 보로노이 테셀레이션 반복계산을 통한 에너지와 메쉬 형태의 변화를 살펴보았다. 이 도메인은 1,579개의 보로노이 영역으로 구성되어 있고 중심으로 갈수록 생성점이 촘촘하게 배치되어 보로노이 영역도 중심으로 갈수록 크기가 작아진다. 그림과 같이 사각형 형태의 보로노이 영역에서 육각형 형태의 보로노이 영역으로 바뀌는 지점에서의 보로노이 영역 에너지값이 크다. 또한 파이프 외부 그리고 관정 외부를 형성하는 보로노이 영역의 에너지값도 상대적으로 큰 편이다. 무게중심 보로노이 테셀레이션을 찾는 100번의 반복계산을 통해 얻어진 도메인의 모습은 Fig. 3과 같다. 이 연구에서 사용된 수렴 조건은 반복 계산의 횟수를 충분히 크게(100회) 하는 것이다. 20번 정도의 반복계산을 거치면 에너지 함수와 가장 에너지가 큰 셀의 에너지값은 거의 변하지 않았다.
도메인 상에 관정이 있을 경우 가장 큰 지하수위나 온도의 변화는 보통 관정 주위에서 발생하므로 관정 주위의 메쉬를 촘촘하게 만든다. 즉, 밀도함수는 관정에서의 거리에 따라 생성점의 밀도가 달라지는 함수가 될 것이다. 임의의 생성점에서 가장 가까운 관정 중심까지의 거리를 구한 후 밀도함수에 따른 가중치를 계산하면 관정과 가까운 곳에서는 생성점의 밀도가 높고 먼 곳에서는 생성점의 밀도가 낮은 도메인이 생성된다. Fig. 3b에서 셀의 변화된 분포를 보면 밀도함수의 특성이 잘 반영된 것을 확인할 수 있다. 각 셀의 에너지 감소도 색깔의 변화를 통해서 확인이 가능하다. 붉은색일수록 상대적으로 에너지가 높은 셀인데 초기에는 관정 주변의 동심원 형태의 셀들과 그 외부의 직사각 형태의 셀들이 만나는 부분에서 큰 에너지를 가지는 셀들이 다수 분포한다. 무게중심 보로노이 테셀레이션을 거치면 셀들의 형태가 5각형이나 6각형으로 바뀌면서 크기가 자연스럽게 증가하고 에너지도 0에 가까운 값을 가지게 된다.
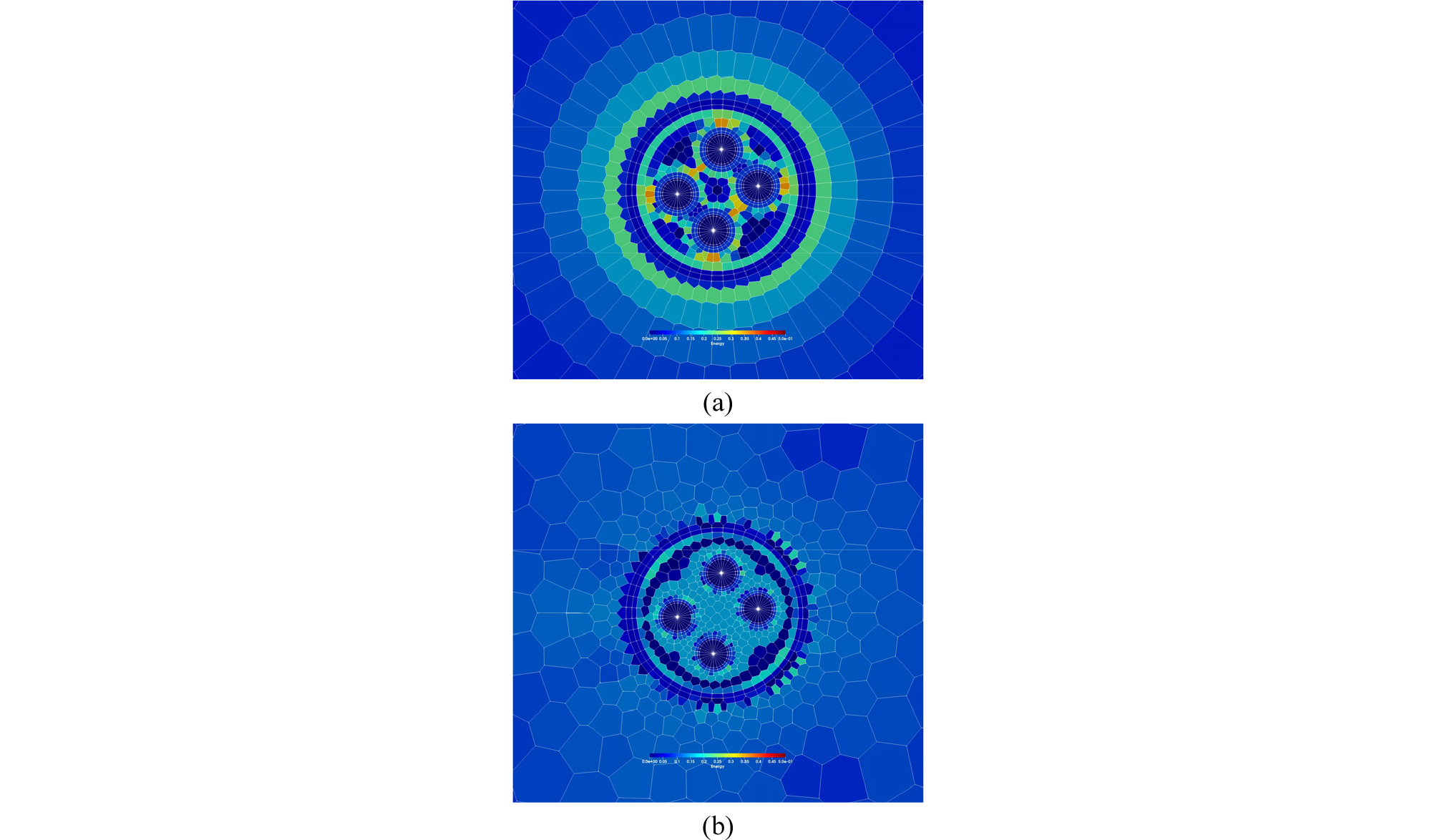
하지만 앞서 언급했듯이 이 연구에서는 관정 및 파이프의 형태를 유지해야 하므로 도메인 전체에 걸쳐 같은 밀도함수를 사용할 수는 없었다. 대신에 관정 내부와 관정 외부로 도메인을 구분하여 다른 밀도함수를 적용하고 관정이나 파이프의 형태를 유지하기 위해 필요한 생성점은 그 밀도함수의 영향을 받지 않도록 설정했다. 관정 내부의 밀도함수는 파이프까지의 거리 혹은 관정벽까지의 거리에 따라 생성점의 밀도가 달라지도록 하였다. 관정과 파이프 형태 유지를 위해 에너지가 완전히 0에 가깝게 수렴하지는 않았지만 에너지의 감소 및 셀 형태의 개선은 Fig. 4를 통해 확인할 수 있다.
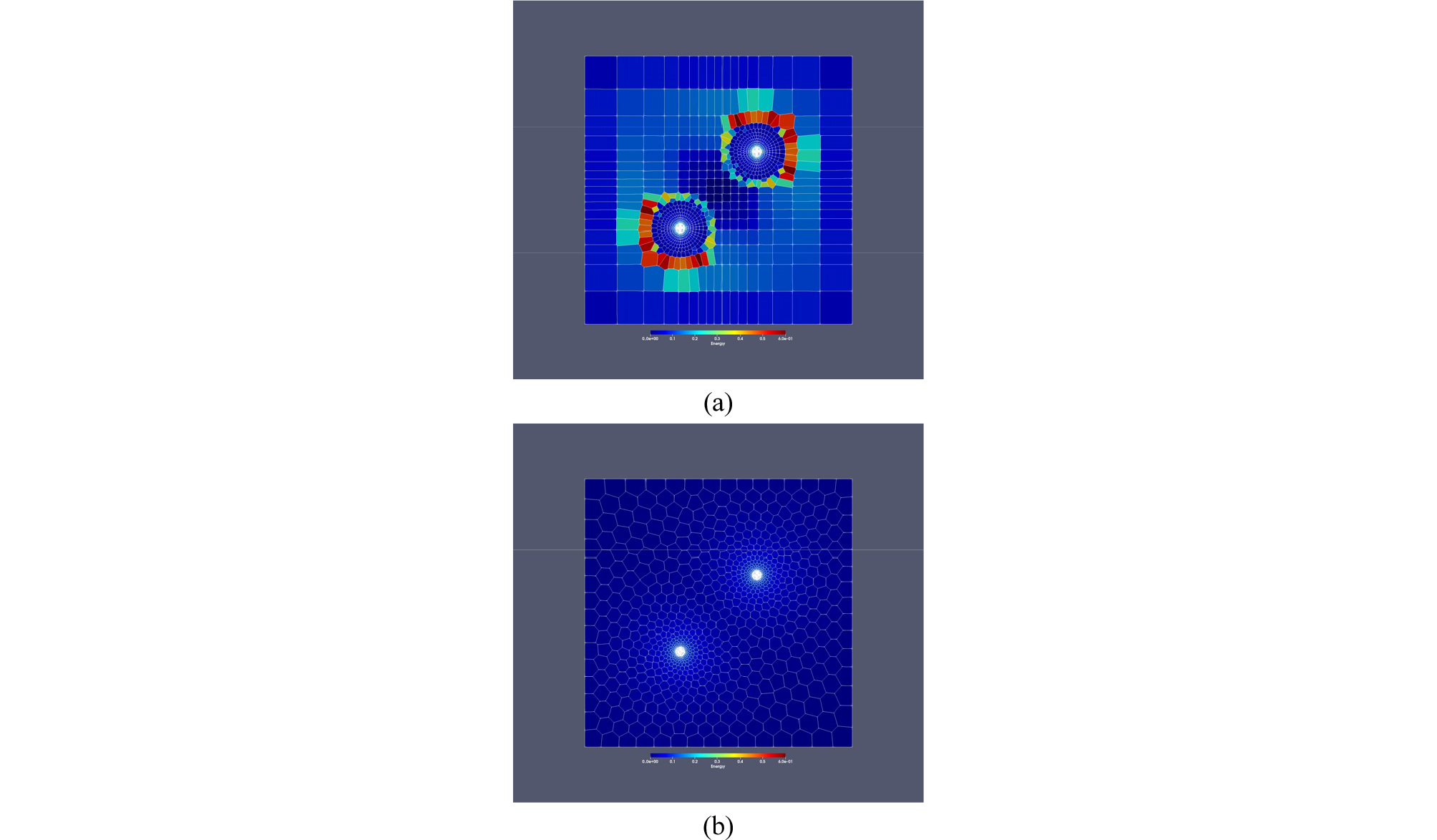
관정 하나가 중심에 위치한 첫 번째 예시의 도메인에서 관정 외곽의 직사각 형태의 메쉬는 중심으로 갈수록 직사각형의 크기가 조밀해지도록 구성했다. 즉 관정이 중심에 위치할 경우를 생각하여 디자인 된 메쉬라 할 수 있다. 그것과 동일한 직사각 형태의 메쉬 위에 2개의 관정을 Fig. 5a와 같이 만들고 무게중심 보로노이 테셀레이션 반복계산을 수행했다. 이 경우는 관정이 2개인 경우를 생각하지 않았으므로 초기 에너지가 관정이 하나인 경우에 비해 더 큰 셀들이 많이 분포하고 있다. 그러나 반복계산 결과 관정 둘 중 가까운 관정과의 거리에 따라 셀의 크기가 자연스럽게 달라지고 에너지도 0에 가까운 값을 가지는 결과를 얻을 수 있었다.
결 론
이전 연구의 보로노이 테셀레이션을 이용하여 지중냉난방시스템의 시뮬레이션을 위해 필요한 관정과 파이프 형태의 TOUGH2용 메쉬를 만드는 연구를 발전시켜 무게중심 보로노이 테셀레이션을 이용하여 메쉬를 만드는 방법을 개발했다. 새로운 방법으로 만들어진 메쉬는 기존 메쉬에 비해 더 낮은 에너지를 가져서 셀의 형태 및 상대적 크기 차이에 의한 계산오차를 감소시킬 수 있을 것으로 기대된다. TOUGH2에서 FEM에서 사용하는 삼각형이나 사각형 메쉬를 그대로 가져와서 사용해도 그럴듯해 보이는 결과를 얻을 수는 있다. 어쩌면 시뮬레이션을 통해 알고자하는 결과를 얻는데 큰 문제가 없을 수도 있다. 그러나 정량적인 값을 얻기 위해 수행하는 복잡한 3차원 시뮬레이션에서 메쉬에 의한 알 수 없는 오차가 누적된 결과를 얻는다는 것은 반드시 지양해야 할 일이다. 이전 연구의 보로노이 테셀레이션을 이용한 메쉬는 적어도 IFDM을 사용하여 방정식을 계산할 때 필요한 가정은 지키기 때문에 매질의 물성이 동일하거나 급격한 수위차이나 온도차이가 발생하지 않는 경우에 있어서는 정확한 결과를 얻을 수 있다. 무게중심 보로노이 테셀레이션을 이용한 메쉬에서는 매질의 물성이 위치에 따라 달라도 급격한 수위차이나 온도차이가 발생하는 경우에 있어서도 언제나 정확한 결과를 얻을 수 있고 지배방정식을 계산하는 과정에서 역행렬 계산의 수렴성을 높여 전체 계산 효율성도 향상된다. 관정이나 파이프의 형태 유지를 위해 고정된 생성점으로 인한 셀의 에너지 증가는 앞으로 해결해나가야 할 과제 중 하나이다. 또한 밀도함수를 관정 내외부에 통합적으로 적용하여 좀 더 에너지가 낮고 자연스러운 형태의 메쉬를 만들기 위한 추가적인 연구가 필요하다.