서 론
이론적 배경
연구대상
다상유동 모델 구축 및 검증
해저배관 내 최소유동가스량 및 유동특성 추정
Case 1(8, 7, 6 mmscfd)
Case 2(5, 4 mmscfd)
Case 3(3, 2, 1 mmscfd)
결과 및 분석
결 론
서 론
해상플랫폼에서 생산된 가스/컨덴세이트는 해저배관(pipeline, 파이프라인)을 따라 육상으로 이송된다. 해상플랫폼을 운영함에 있어서, 해저배관 내 최소유동가스량 추정과 관내 유동특성 변화는 안정적인 광구 운영을 위해 파악해야하는 중요한 요소 중 하나이다. 해저배관 내의 다상유동은, 관내에 존재하는 잔류액체, 가스 등의 가스유량, 그리고 경사각 등의 지형정보 등에 영향을 받고, 또한 시간에 따른 유동조건 변화와 그에 따른 패턴변화는 순차적으로 향후 유동특성을 결정짓는 요소가 된다.
해저배관 내 다상유동을 분석하기 위한 기법으로는 주로 정상 다상유동 모델(steady state multiphase flow model)과 천이 다상유동 모델(transient multiphase flow model)이 사용된다. 정상 다상유동 모델은 관내 다상유동을 정상유동으로 가정함으로써 분석을 빠르고 쉽게 수행할 수 있는 장점이 있다. 반면에, 특정 시점에서의 주어진 조건에 한해서만 분석을 수행할 수 있으며, 시간에 따른 변화를 고려하기 위해서는 시간별 입력조건을 독립적으로 산정하여야 한다는 한계가 있다. 이에 비해 천이 다상유동 모델은 특정시점에서의 유동이 다음 시점에 입력값으로 적용되어 순차적으로 이산적인(discrete) 시간에 따른 변화를 모사할 수 있다(Norris and Rydahl, 2003). 이 과정에서, 연속방정식, 모멘텀방정식, 에너지방정식을 결합한 지배방정식(Irfansyah, 2005)을 순차적으로 풀기 때문에 막대한 연산시간이 소요된다는 단점이 있다. 본 연구에서는, 현장 플랫폼 운영 관련하여, 막대한 비용이 들어가는 파이프 유지보수, 피깅(pigging) 여부 결정, 슬러깅(slugging) 발생여부 예측, 최소유동가스량 예측 등의 천이 다상유동 모델 개발 및 관련 정밀분석이 요구된다.
연구 대상인 해상플랫폼 및 관련 시스템은 현재 약 30 mmscfd 이하의 가스/컨덴세이트를 생산하는 상황이며, 최고생산량 대비 50%이상 생산량이 감소한 상황이다. 따라서, 생산량 연장을 위해서 다양한 노력들이 필요한 시점이며, 그 일환으로 최근 플랫폼에서 파이프라인으로의 송출압력을 105 barg에서 90 barg로 감소시키는 작업을 수행하였다. 이러한 공정개선 작업을 통해, 동일유량을 생산하더라도 저류층 압력의 15 barg의 추가감소가 가능하며 해당량 만큼 가스/컨덴세이트 추가생산이 가능하다. 또한 관련하여, 파이프라인에서 육상으로의 인입압력도 90 barg에서 80 barg로 감소하여 운영하도록 시스템이 개선되었다. 따라서, 현 시점에서 파이프라인의 운영압력조건 변화에 따른 유동안정성에 대한 분석이 필요하며, 나아가 생산종료를 고려할 시, 생산하는 가스와 부산물인 컨덴세이트의 파이프라인 내 최소유동량에 대한 분석이 필요하다. 본 연구에서는, 유동환경변화에 따른 유동안정성을 분석하기 위해, 천이 다상유동 모델을 구축하였으며, 다양한 유량에서의 유동특성들을 규명하여 최소유동가스량을 추정하고자 한다.
이론적 배경
관내 다상유동에서 각 상(phase)들의 속도, 즉 점착 속도(no-slip velocity)와 실제 속도(actual velocity)는 차지하는 면적에 따라, 아래의 식 (1), (2), (3)로 결정된다(Beggs, 1973).
여기서 과 는 각각 액체점유율(liquid hold-up)과 기체점유율을 의미한다. 가스와 액체 유량 , 에 대해서, 각 실제 속도는 식 (2)와 같이 정의되고, 각 상의 선속도(superficial velocity)는 식 (3)과 같이 정의된다. 여기서, 액체와 가스의 관내충진 비율, 즉 , 은 1보다 작은 값이므로, 각 상의 선속도는 실제 속도에 비해 작은 값을 갖게 된다. 는 관내 단면적을 의미한다.
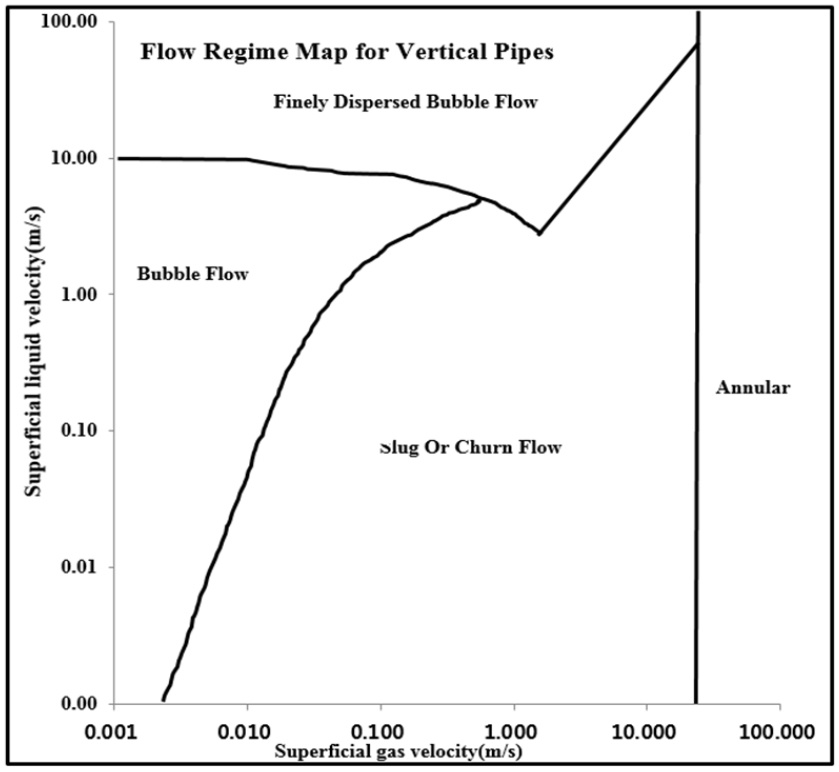
Fig. 1은 수직 관내를 기체-액체의 다상유동에서 선속도에 따른 유동패턴변화의 전형적인 모습을 보여주고 있다. 이로부터 식 (2), (3)을 이용하여 대상 해저배관의 복잡한 지형(geometry) 중 수직유동을 하는 구간에 대해서 각 구간별 선속도를 계산하여 유동패턴과 가스유량에 따른 변화를 추정할 수 있다.
다상유동이 해저배관을 따라서 발생하는 압력손실, 즉 은 아래의 식 (4)로부터 계산할 수 있다. 각각의 항은 순서대로, 수두손실(elevation loss), 마찰손실(friction loss), 가속손실(acceleration loss)이며 식 (5), (6), (7)과 같이 정의된다. 여기서 각각 , , , , ,는 각각, 중력가속도(gravitational acceleration), 변환계수(conversion factor), 마찰계수(friction factor), 속도(velocity), 밀도(density)를 뜻한다. 변환계수는 단위변환으로 인해 발생하는 상수이고, 마찰계수는 유동특성과 파이프 재질에 따라 결정되는 상수이다. 속도 의 경우는 유량에 따라 결정되며 식 (6)과 (7)의 는 유동패턴과 압력손실에 따라 각각 결정되고, 는 로 결정된다(Beggs, 1973). 본 연구에서는 이러한 압력손실을 전체 해저배관시스템에서 계산하기 위해, Schlumberger 社의 OLGA 프로그램을 활용하여 모델을 구축하였다.
연구대상
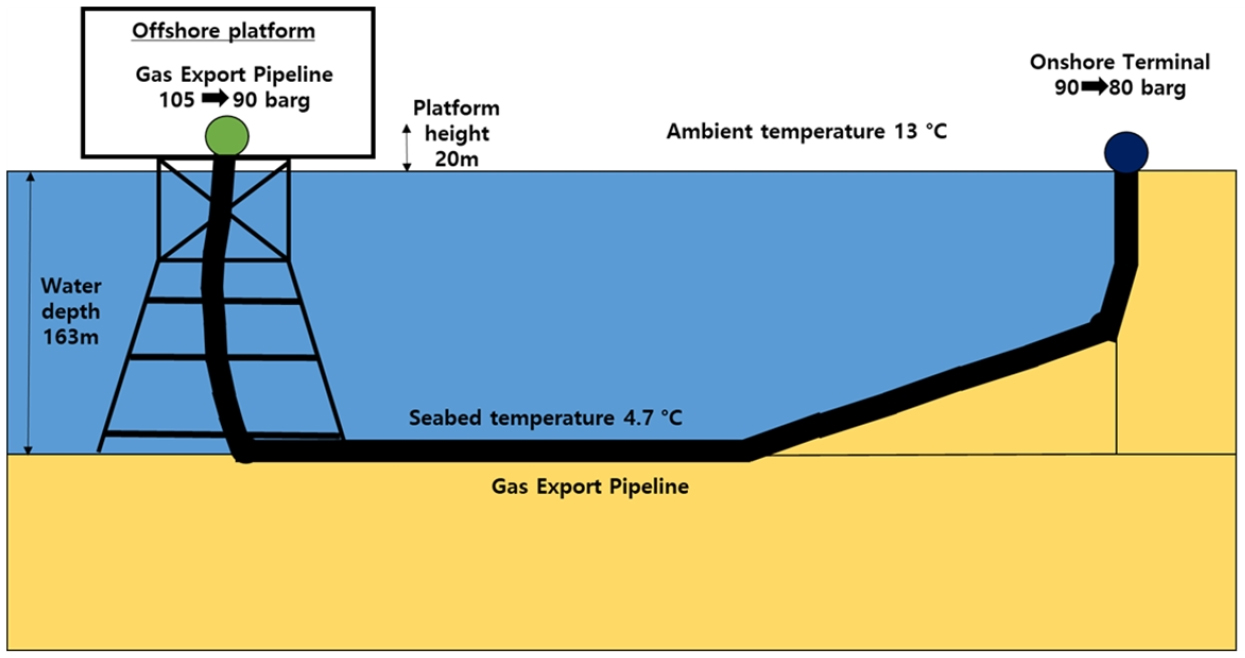
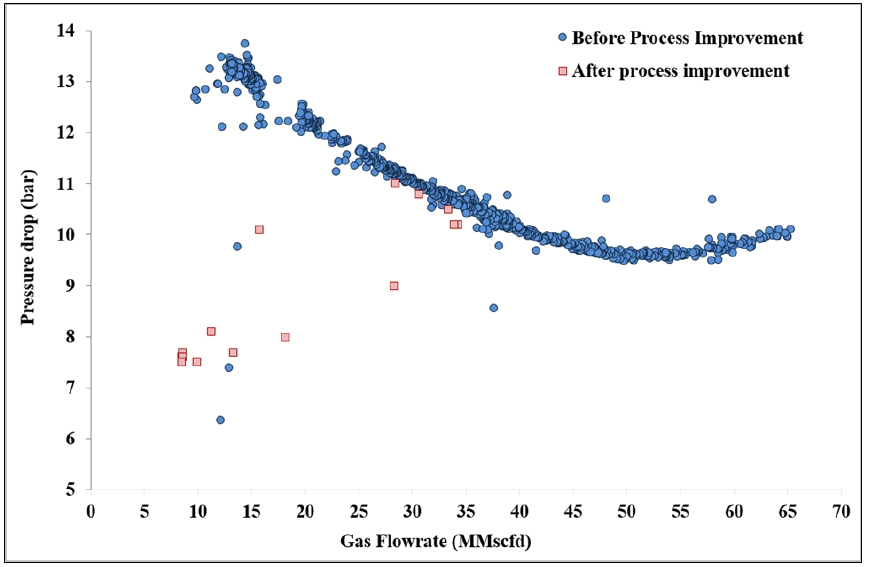
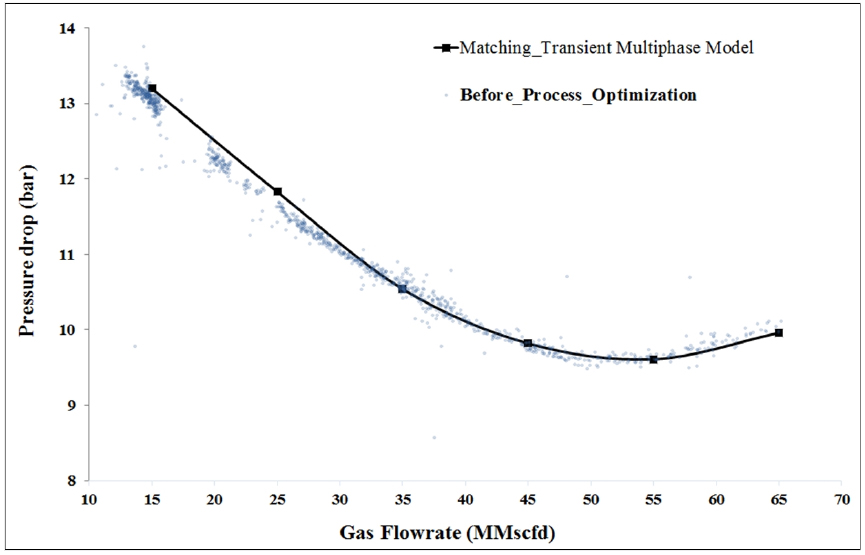
연구대상 해상플랫폼은 해수면에서 고정식 형태로 설치되어 저류층에서의 탄화수소를 생산·처리·저장하고 육상이나 셔틀탱커 등으로 이송하는데 필요한 해상설비를 탑재하고 있다(Moon et al., 2018). 현재 해상플랫폼에서 105 barg인 고압으로 가스/컨덴세이트를 해저배관으로 송출 후 육상공정에서 90 barg로 취득하여 운영하였으나, 최근 공정개선 작업으로 송출·취득 운영조건이 육·해상 각각 90 barg에서 80 barg로 완화시키는 작업을 실시하였다(Fig. 2). Fig. 3은 공정개선 작업 전·후에 대해 실제 필드에서 취득한 가스유량과 압력차를 도시한 그래프이다. 공정개선 전 가스유량 대비 압력차(푸른색)에서는 고유량에서는 압력손실이 적어지나, 약 55 mmscfd를 기준으로 저유량으로 갈수록 압력손실이 커지는 경향이 나타난다. 반면 공정개선 작업이후에는 아직 충분한 데이터를 확보하지 못한 상황이다. 또한, 가스유량 대비 압력차에서는 붉은색 점들이 산재되어 있는 현상을 보이므로 현 단계에서 해저배관 내 최소유동가스량과 유동특성을 경험적으로 분석하기란 매우 어려운 실정이다.
다상유동 모델 구축 및 검증
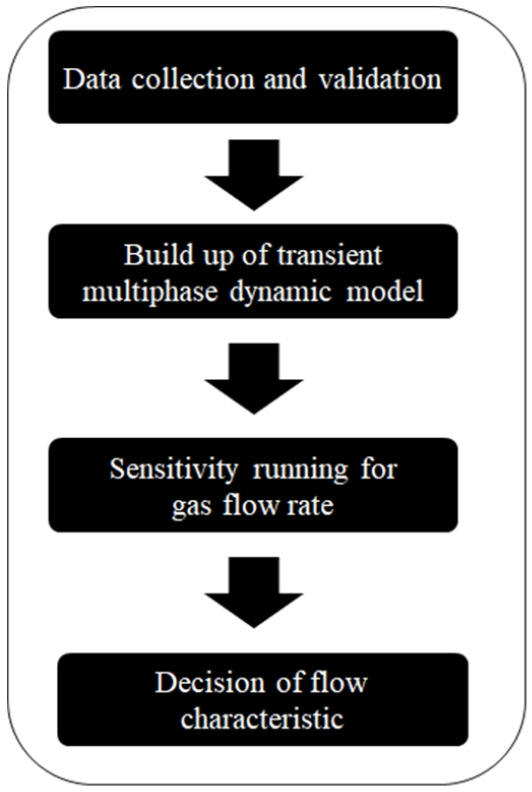
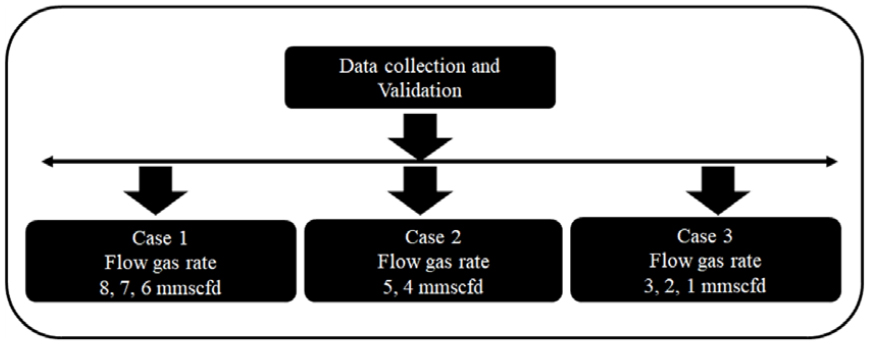
본 연구에서 천이 관내 다상유동 특성을 분석하는 방법은 Fig. 4와 같다. 우선 자료 취득과 검증과정을 거쳐 자료의 사용여부를 검토한다. 다음 단계에서는 천이 관내 다상유동 모델을 구축한 뒤 현장과의 교차검증을 수행한다. 이후 분석하고자 하는 생산가스량에 따라 민감도 분석을 수행하여 그 결과를 통해 최소유동가스량을 추정하고 그 뒤 육·해상 압력차, 유동패턴, 액체점유율, 가스유량 안정화 여부 등의 분석을 수행한다. 그리고 실제 안정적인 유동을 가장 위협하는 지형이 급격하게 수직으로 변하는 구간에 대해서 정밀 분석을 수행하였다.
또한, 본 모델을 구축하기 위해서는 해저배관 내 가스 이송 유량 및 취득압력, 관내 길이, 경사 각, 유체조성, 시간에 따른 현장자료 등이 필요하다. 여기서 사용한 자료들은 아래 Table 1과 같이 해저배관의 등고 정보, Table 2는 해저배관에서 가스/컨덴세이트가 같이 관내로 생산되는 상황에서 조성이 혼합된 상태를 보여준다.
Table 1.
Gas export pipeline geometry
| Length [km] | Elevation [m] |
| 0 | 30 |
| 5 | -169 |
| 10 | -144 |
| 15 | -145 |
| 20 | -144 |
| 25 | -139 |
| 30 | -131 |
| 35 | -124 |
| 40 | -118 |
| 45 | -105 |
| 50 | -88 |
| 55 | -66 |
| 60 | -29 |
| 65 | 8 |
| 68 | 43 |
Table 2.
Fluid component (mol %)
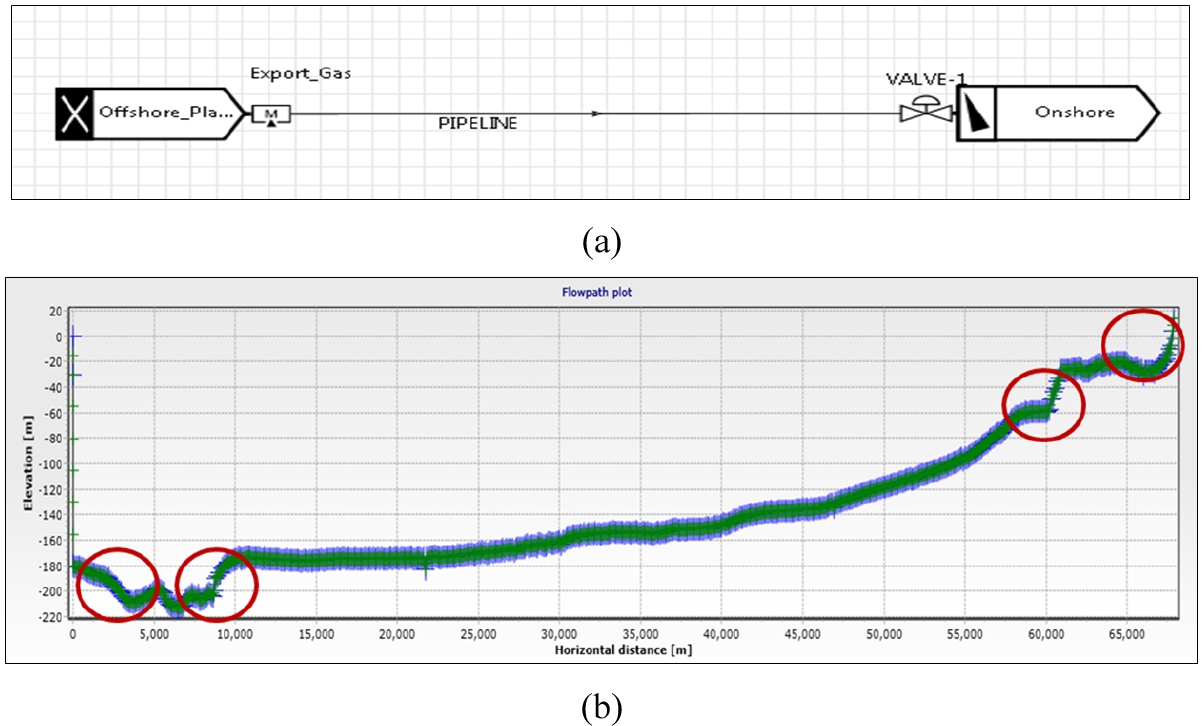
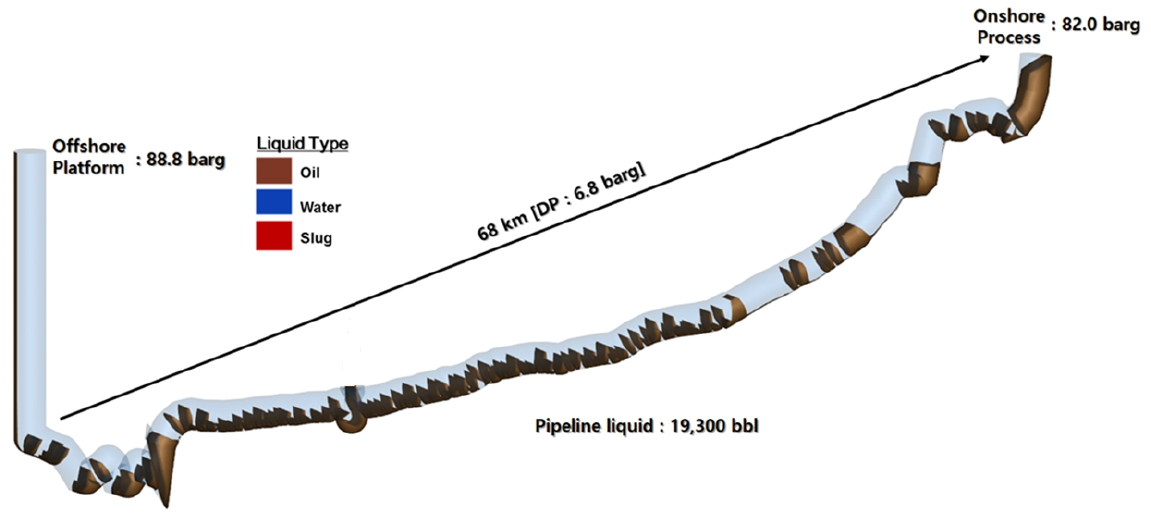
본 연구의 대상 해저배관에 대한 분석을 위해 다상유동 모델을 구축하였고, 모식도는 Fig. 5(a)와 같이 구성은 해상플랫폼에서 시작하는 bottom node, 육상지점의 pressure node, 육해상을 이송하는 파이프라인과 기체-액체를 파이프라인으로 주입하는 source를 설정하여 운영조건을 모사하였다. 지형정보는 Fig. 5(b)와 같다. 해상플랫폼에서 육상공정시설까지 거리는 약 68 km (해저배관 : 61 km, 육상매설배관 : 7 km)이고, 육·해상 모두 배관이 1 - 4 m 깊이로 매설되어 있으므로, 전 구간 외부온도 변화에 대한 불확실성은 크지 않다. 해저면의 온도는 가장 보수적인 운영조건에서의 연구를 수행하기 위해 동절기 해저면 최저 온도(약 4.7°C)를 가정하였다. 수심은 최대 169 m이며, 해상플랫폼 송출지점은 해수면으로부터 약 20 m 높이, 육상공정 도달지점은 약 40 m 높이에 있다. 이러한 전체시스템에서의 해저배관의 지형변화가 심한 지점은 그림과 같이 네 곳이 존재한다.
개발한 모델은 변화된 조건에서 취득된 현장테스트 결과를 통해 검증하였다. 이 과정에서 초기조건 즉, 해저배관 내 축적되어 있는 액체의 분포를 구현하는 것이 필요하다. 여기서, 생산초기부터 십여년에 가까운 기간의 시뮬레이션을 통해서 관내 액체 분포를 추론하는 것은 불가능하므로, 본 연구에서는, 초기에 관내에 컨덴세이트를 채워놓고 가스/컨덴세이트를 주입하여 유동이 안정화되는 시점을 추론하였다. 이후에, 모델에서의 압력강하 예측값과 실제 필드에서의 취득값의 비교를 통해서 모델을 검증하고자 하였다.
Fig. 6은 실제 필드에서 다양한 유량에 따른 압력강하 측정값들을 보여주고 있다. 본 연구에서는, Table 3의 유량 즉, 65, 55, 45, 35, 25, 15 mmscfd의 가스 유량에 대해서 모델의 검증을 수행하였다. 개발한 모델은 표에서 실제와 거의 유사한 값들을 모사하고 있으며, 저유량에서 압력강하가 크고, 유량이 증가할수록 감소하며, 특정 유량(약 55 mmscfd)이상에서 압력강하가 증가하는 경향을 정확하게 모사하고 있음을 알 수 있다.
Table 3.
Model validation with field data (before process improvement)
| Gas rate (mmscfd) | P_loss (Field) | P_loss (Model) |
| 65 | 9.9 | 9.9 |
| 55 | 9.6 | 9.5 |
| 45 | 9.8 | 9.8 |
| 35 | 10.5 | 10.6 |
| 25 | 11.8 | 11.7 |
| 15 | 13.2 | 13.2 |
다음으로는 공정개선 이후의 저유량에 대해서 관측값과 모델의 예측값을 검증하고자 하였다. 공정개선 이후 현장에서 8.5 mmscfd 유량에 대한 실험결과, Table 4와 같이 7.6 bar의 압력강하가 관측되었고, 이에 대한 모델의 결과는 육상에서 8.8 mmscfd의 유량을 취득, 압력강하는 8 bar로 예측되었다. 여기서, +0.3 mmscfd, +0.4 barg의 오차는 현장의 데이터 취득의 정확성을 고려하였을 경우 충분히 작은 값으로 판단된다.
해저배관 내 최소유동가스량 및 유동특성 추정
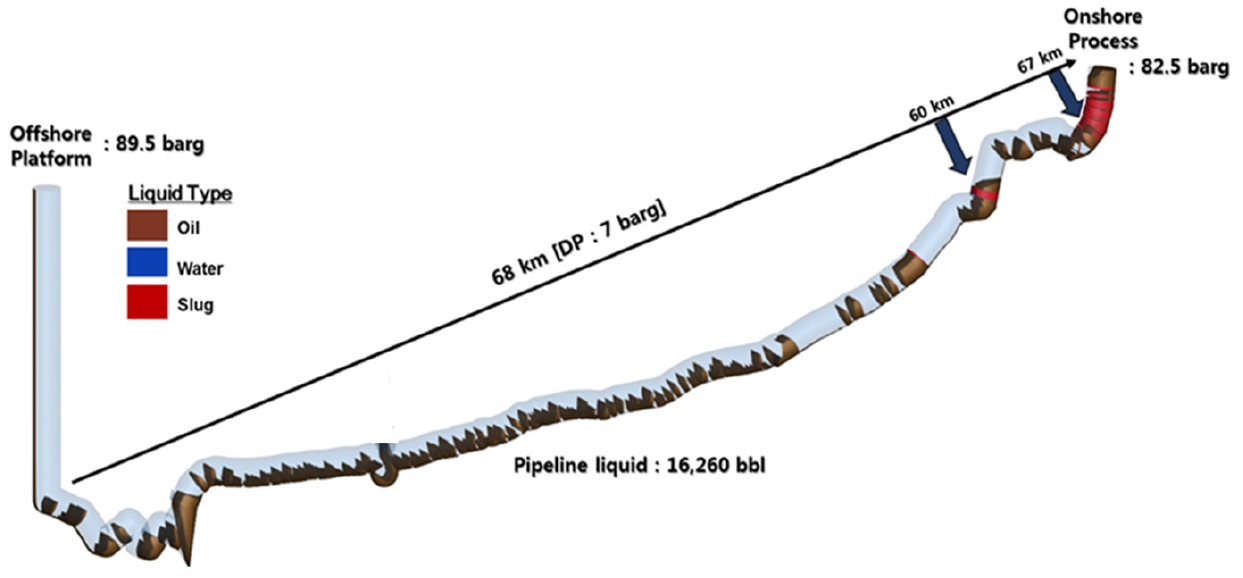
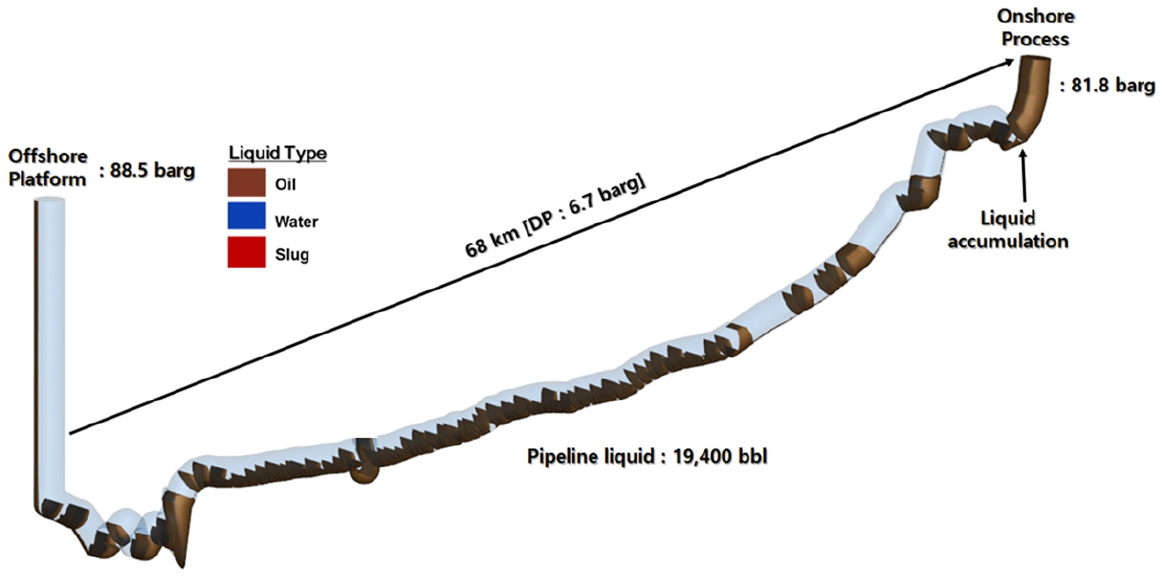
이 연구에서는 해저배관 내 저유량의 가스가 해저배관을 유동할 때 관내 유동특성을 분석하고, 이를 바탕으로 최소유동가스량을 추정하고자 한다(Fig. 7). 즉, 초기상태의 관내 컨덴세이트를 가스가 밀어낼 때, 안정적인 유동이 성립되는지 여부를 판단하고자 하였다. 생산말기에, 저유량을 송출할때의 관내 유동안정성 분석이 목적이고, 이를 위해 공정개선 작업을 한 것이므로, Table 4보다 낮은 유량, 즉, 1 - 8 mmscfd의 유량에 대해서 압력강하와 유동특성을 분석하였다. 앞서 설명한 구축/검증한 모델을 바탕으로 파이프라인 내 유동특성을 모사한 결과, 유동특성이 각각 case 1(8, 7, 6 mmscfd), case 2(5, 4 mmscfd), case 3(3, 2, 1 mmscfd)로 구분되어짐을 알 수 있었다. 특히, 관내 지형이 급격하게 변하여 유동안정성에 위협이 될 것으로 예측되는 지점, 즉 Fig. 5의 송출지점으로부터 60 km, 67 km인 경사각 70도 이상인 지점에서의 유동변화를 모사하였다. 이에 대한 구체적인 결과는 다음과 같다.
Case 1(8, 7, 6 mmscfd)
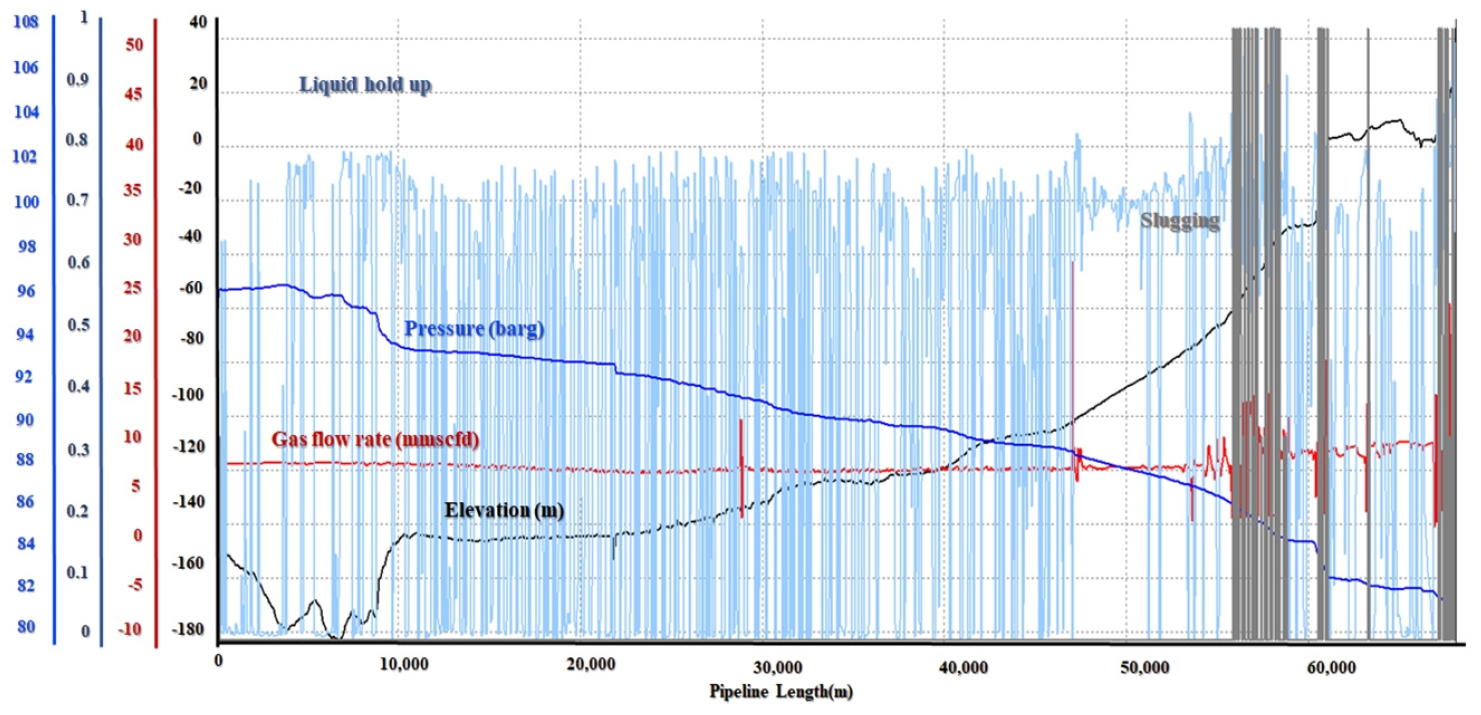
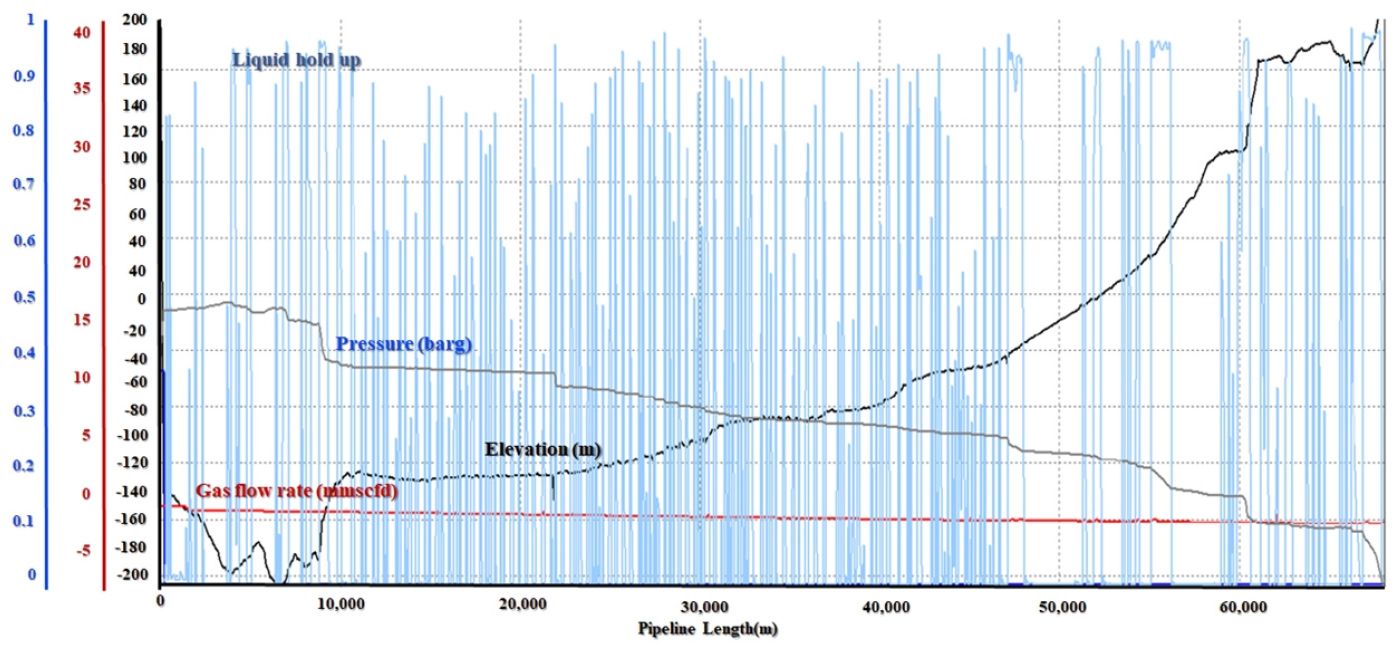
유량 8, 7, 6 mmscfd의 경우에 대해서 시뮬레이션 기간은 50일을 적용하였다. 모사결과, 세 유량 모두 공통적으로 60 km, 67 km 지점에서 슬러깅이 발생하는 것을 확인하였다(Fig. 8). 초기에 컨덴세이트로 가득찬 관내를 주입한 가스/컨덴세이트가 치환하였으나, 언급한 두 지점에서는 관내 경사각이 약 70°로 급격히 증가하여 이러한 치환이 효과적으로 이뤄지지 못하고 있다. 또한 Fig. 9에서와 같이, 파이프라인 모든 구간에 걸쳐서 액체점유율이 0.8 내외로 나타나며, 특히 60 km, 67 km 지점은 액체점유율이 0.9이상으로 높게 나타나고 있다. 또한 55 km 지점 이후로는 해저배관 경사각 증가로 인해 유동패턴도 슬러깅으로 유동하고 있다.
즉, 주어진 지형 조건에서 액체 대비 유동성이 큰 가스가 이 지점들에서 액체를 불연속적으로 운반하는 현상이 발생하고 있다. 이러한 불연속적인 유동은 육상공정에서의 진동현상을 야기하고 육상공정에서의 슬러그 캐쳐 설치, 피깅작업 등의 추가비용을 발생시킬 가능성이 있다.
Case 2(5, 4 mmscfd)
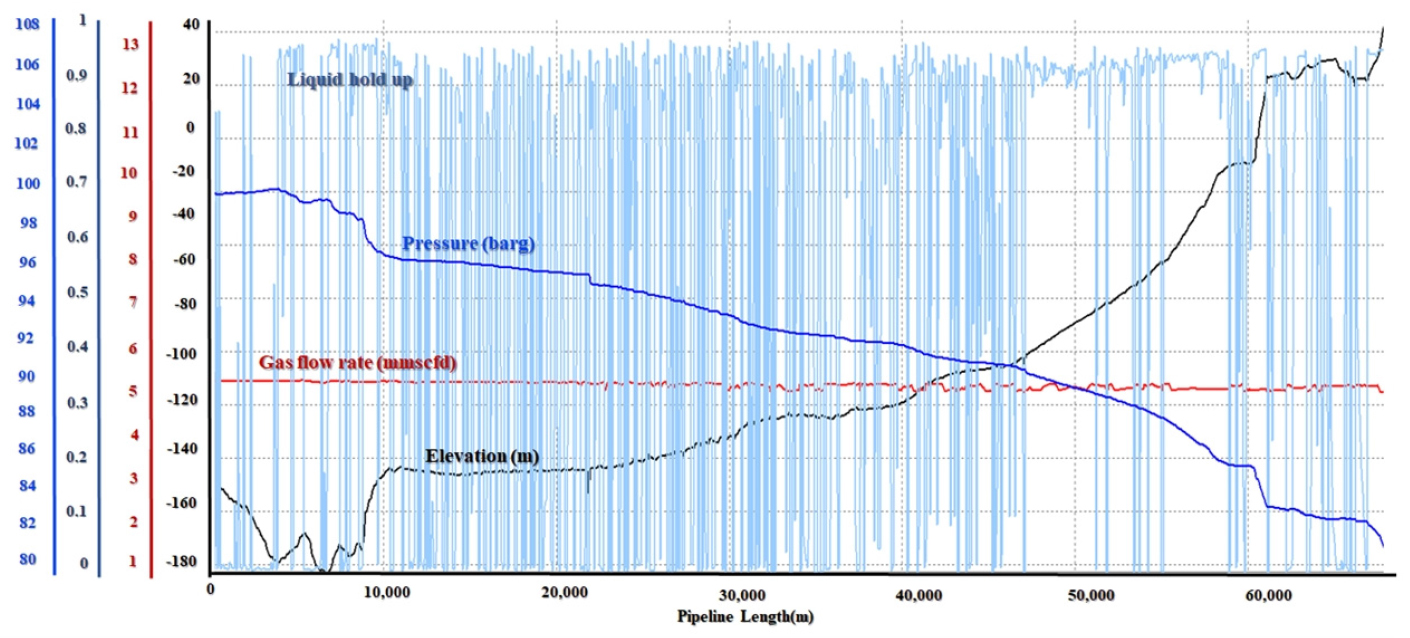
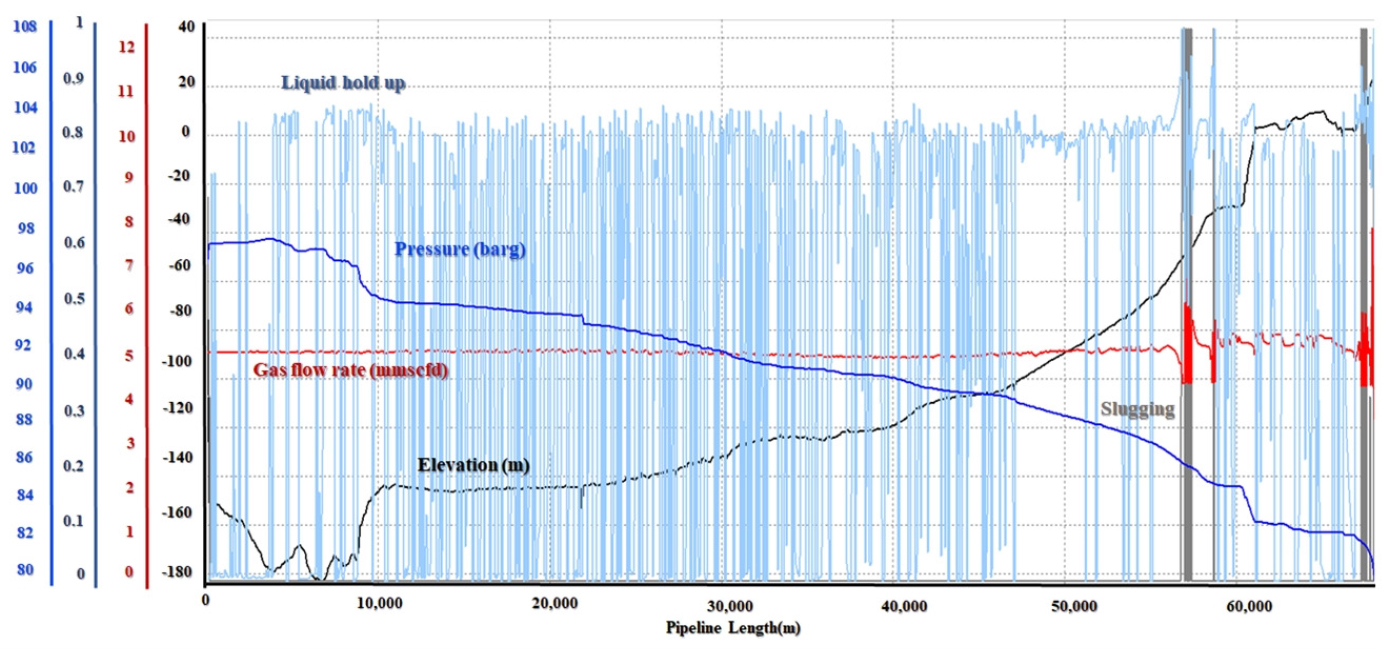
case 1과 같은 조건으로 유량 5, 4 mmscfd의 경우에 적용하였다. 이 경우, 시뮬레이션이 안정화되는 속도가 case 1에 비해서 다소 느리게 나타남을 확인하였고, 이는 시뮬레이션 시간을 각각 30일, 50일을 적용한 Fig. 11, Fig. 12에 설명한다. 아래 Fig. 10은 30일 동안 구현한 관내 유동분포 결과를 나타낸다. 육안으로는 슬러깅 현상이 크게 두드러지지 않음을 알 수 있다. Fig. 11의 액체점유율의 경우, 전 구간에서 0.9 근처로 비교적 일정하게 유지되고 있고 가스 유동량도 변동이 거의 없다. 반면, Fig. 12의 50일 경우에서는 해저배관 전반적인 액체점유율이 0.8로 상대적인 가스비율이 높아졌지만, 60 km, 67 km 지점에서 가스 유동량이 불안정한 양상을 보이고 있다.
이러한 현상의 원인은, 시뮬레이션 시스템 상에서 적은 유량이 초기 충전된 컨덴세이트를 치환은 하지만, 추가적으로 유입되는 컨덴세이트의 양이 더해져서 시간이 지날수록 컨덴세이트 치환이 안됨을 의미한다. 실제 광구 운영을 고려한다면, 송출되는 가스/컨덴세이트가 지속적으로 해저배관의 액체축적을 야기하고, 즉, 주입가스는 수반하는 컨덴세이트 양도 운반할 수 없게 됨을 의미한다.
Case 3(3, 2, 1 mmscfd)
Fig. 13, Fig. 14는 case 3에 대한 시뮬레이션 시간 50일 결과를 보여준다. Fig. 13에서 슬러깅 현상이 나타나지는 않지만, Fig. 14에서 전반적으로 liquid hold-up이 0.9 이상이고 가스가 초기에 집적해있던 액체를 밀어내지 못하고 육상공정에 도달하지 못하는 현상을 보인다. 특히 case 1에서 슬러깅이 발생한 해저배관 67 km지점에서 축적된 액체를 전혀 밀어내지 못하고 있다. 이는 해저배관이 설령 가스로 가득차 있다고 하더라도, 시간이 지남에 따라 주입하는 컨덴세이트가 지속적으로 축적이 되고, 해당 유량으로는 가스가 축적된 컨덴세이트를 전혀 운반하지 못함을 의미한다.
결과 및 분석
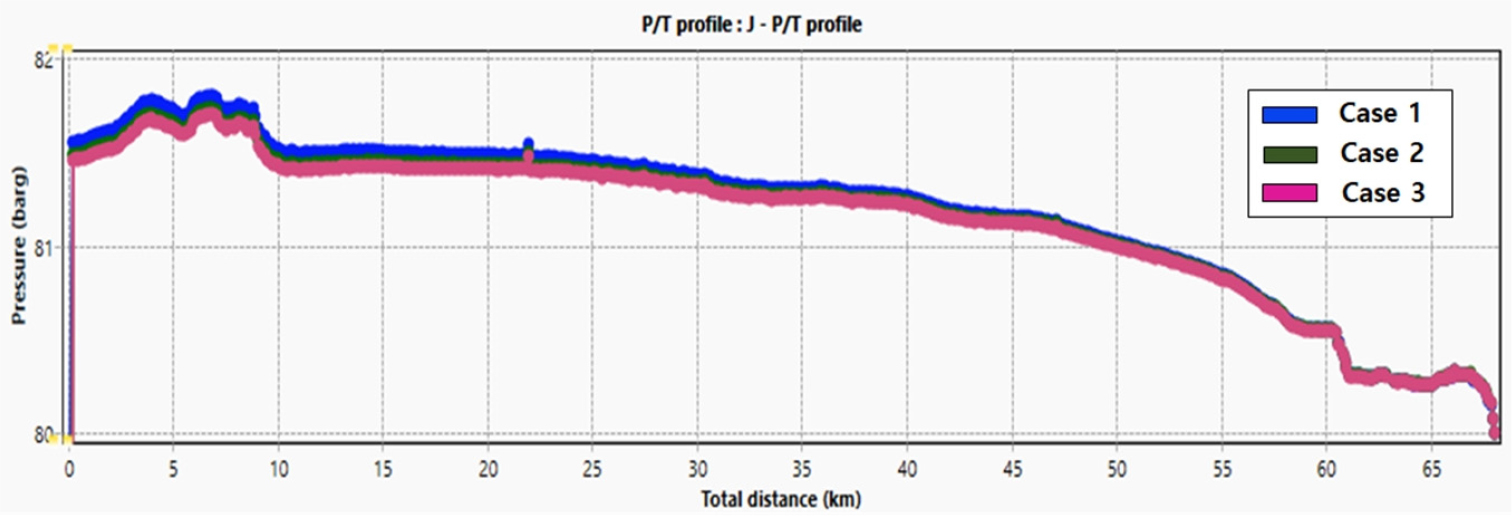
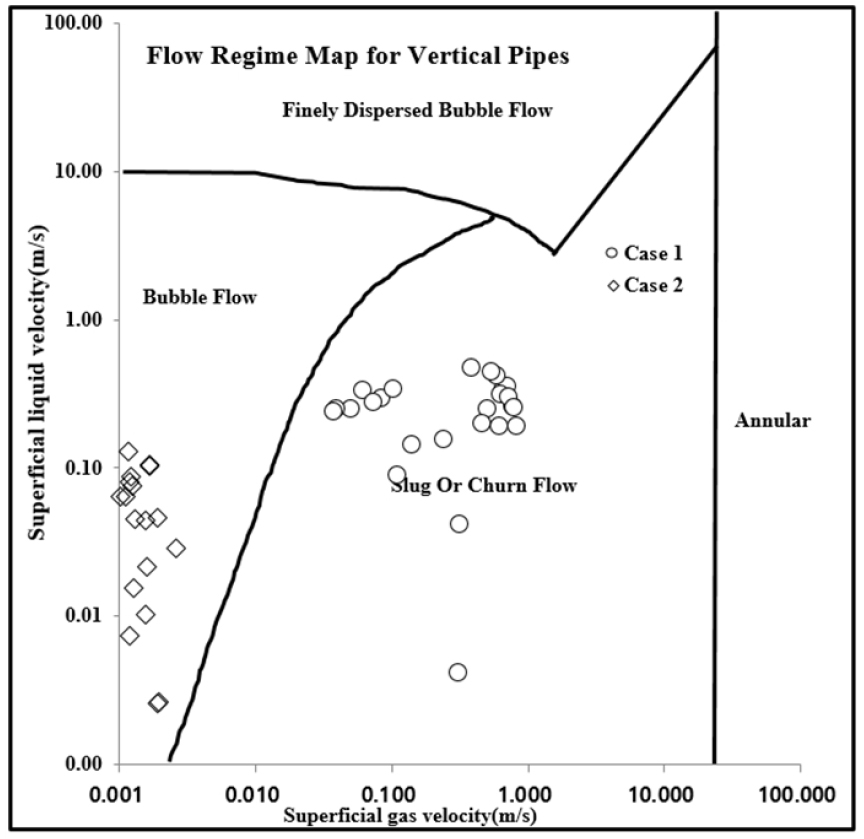
이상의 수행한 조건들의 압력 프로파일은 Fig. 15와 같다. 앞서 수행한 시뮬레이션으로부터, 해저배관 내 허락될 수 있는 최소유동가스량은 case 1 조검임을 추정할 수 있다. 하지만, 압력의 전체적인 경향은 유사하게 나타나며, 특히, 해저배관의 지형이 급하게 변하는 지점에서도 압력변화 경향이 동일함을 알 수 있다. 추가적인 분석을 위해, 기존연구(Taitel et al., 1980)와 본 연구에서의 선속도를 비교해보았다(Fig. 16). case 1(8, 7, 6 mmscfd)의 경우, 일부 이상치(outlier)의 경우를 제외한다면, 액체의 선속도에 비해 기체의 선속도가 넓은 범위를 가지며, 이는 slug 혹은 churn 유동에 해당한다. 이에 비해, case 2(5, 4 mmscfd)의 경우는 반대로 액체의 선속도가 더 큰 범위를 가지며 값의 크기는 고유량에 비해서 작게 나타난다. 그리고 case 3(3, 2, 1 mmscfd)의 경우에는 상대적으로 가스 속도가 매우 작음에 따라 동등한 비교를 수행할 수 없어서 그림에 표기하지 않았다. 특히, 60 km지점에서는, 각각 case 1 및 case 2의 가체 선속도는 지점에서 각각 0.3192 m/s, 0.0023 m/s이며, 액체 선속도는 각각 0.3052 m/s, 0.0157 m/s이다. 마지막으로 case 3에서의 가스 선속도는 0.0009 m/s, 액체 선속도는 0으로 나타난다.
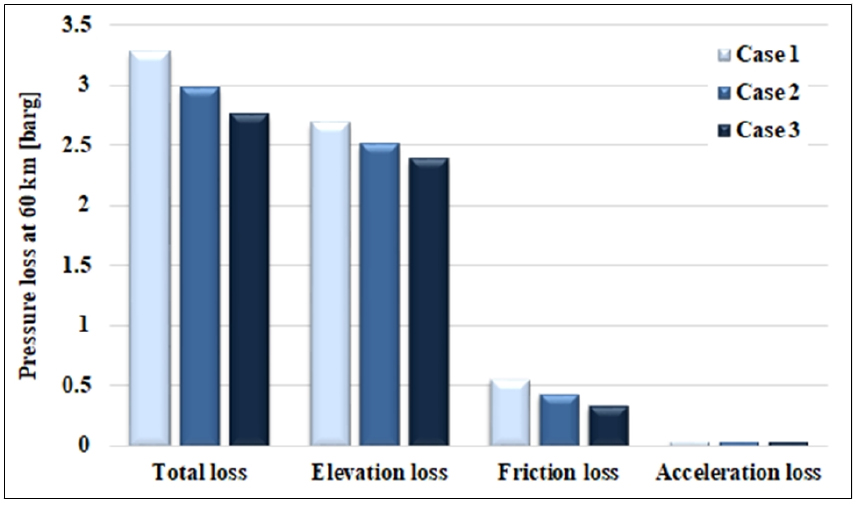
한편 Fig. 17은 60 km지점에서의 각 case 1, 2, 3 유량조건에서의 전체 압력손실과, 위치수두, 마찰, 가속 손실의 크기를 비교하고 있다. 67 km지점에서는 안정적인 유동이 형성되지 않으므로, 60 km지점에서의 압력손실을 비교하고자 하였다. Fig. 17에 의하면 전체적인 압력손실의 대부분은 수두의 차이로 기인한 현상임을 알 수 있다. 마찰손실 및 가속손실은 저유량으로 갈수록 해저배관 내 가스가 단면적에 차지하는 비율이 적어짐에 따라 압력손실도 작아짐을 알 수 있다. 이를 통해, 급격한 경사 변화를 극복하는 것이 이 해저배관 내 유동안정성의 가장 중요한 사항임을 간접적으로 알 수 있다.
결 론
이 논문에서는 해양 천연가스 생산시스템에서 공정변화 이후 해저배관의 육·해상 송출취득압력이 각각 105 barg에서 90 barg로, 취득압력은 약 90 barg에서 80 barg로 완화되어 운전할 경우, 저류층에서의 해저배관 내 유동특성을 분석하였다. 충분한 현장운영의 자료가 취득되지 않은 시점에서 수행되었고, 그로인해 구축한 모델의 타당성 검증이 완전하지 못하다는 단점이 있다. 하지만, 제한된 자료를 활용하여 다양한 조건에서의 시뮬레이션을 수행하였고, 이를 통해 다음과 같은 결론을 얻을 수 있었다.
(1) 이 연구에서는 해저배관을 컨덴세이트로 충진한 다음, 실제 현장자료를 바탕으로 가스로 액체를 치환하여 유동이 안정화되는 조건에서의 압력이 관측 압력과 유사함을 확인하였다. 이를 통해, 본 연구에서 선택한 모델 구동 방법으로 최소유동가스량 추정과 관내 유동특성을 효과적으로 모사할 수 있음을 검증하였다.
(2) 저유량을 3가지의 case로 구분하여 유동을 모사하였고, 그 결과 case 1의 경우 해저배관 60 km, 67 km 구간에서 슬러깅이 발생하여, 해저배관의 도착지점에서 슬러깅 문제가 발생할 수 있음을 예측하였다. 육상시설까지 유동은 가능하지만, 슬러깅 등에 수반되는 진동문제들에 대한 추가설비 작업의 필요성을 시사한다.
(3) case 2의 경우, 모델 초기에는 액체를 어느 정도 치환하지만, 시간이 지날수록 주입되는 액체의 영향으로 유동이 점차적으로 불안정해짐을 확인할 수 있었다. 액체점유율이 설정한 시뮬레이션 기간 내에서 점진적으로 증가하여, 모델 구현 50일에서는 액체를 치환하지 못하는 결과를 보여주었다.
(4) case 3의 경우는 주입한 가스가 해저배관 약 67 km 수직구간의 수두압으로 유동이 중단되어 더 이상 생산가스가 육상공정에 도달하지 못함을 확인하였다. 이 경우, 액체점유율이 0.9 이상으로 나타나며, 수두손실의 크기를 극복할 만한 유속이 충족되지 못함을 확인할 수 있다.
(5) 이상의 결론들을 바탕으로, 해저배관의 유동안정성을 고려할 경우, 최소유동 가스량은 case 1의 범위, 즉, 8 - 6 mmscfd의 범위에서 결정될 것으로 판단된다. 이는 저류층 관리 및 생산 플랫폼 운영, 가스가격 등 제반 운영조건들과 결합하여, 가스전 운영의 의사결정 요소로 활용가능하다.