서 론

취성은 암석에 응력이 가해질 때 극히 일부만 변형하고 파괴되는 성질을 뜻하며 다양한 암반구조물에서 발생되는 파괴현상과 밀접한 관련 있는 역학적 특성이다. 취성을 정의하고 정량화하기 위하여 다양한 취성지수(brittleness index)가 제안되고 있으며, 그 중 일축압축강도 대 인장강도의 비가 널리 사용되고 있다. 취성이 암석 자체의 특성 뿐 아니라 기하형상, 크기, 응력조건 등 형상학적, 환경적 특성 등에 영향을 받기 때문에 선행연구에서 여러 다양한 취성지수가 제안된 것으로 사료된다(Aubertin et al., 1994; Andreev, 1995; Feng et al., 2019).

암반구조물의 파괴는 현지응력의 크기, 암반강도 그리고 암반 내 존재하는 불연속면의 상태에 의해 결정된다. 일반적으로 취성파괴(brittle failure) 형태를 나타내는 경우는 높은 현지응력이 작용하여 굴착공간 주변에 생성된 유도응력에 의해 파괴되는 경우이다. 반대로 낮거나 중간 수준의 현지응력이 작용하는 경우 파괴과정이 불연속면의 분포 특성에 의해 결정된다. 따라서 현지응력의 크기와 암반강도가 취성파괴의 결정적인 변수라 할 수 있다. Fig. 1은 Hoek et al.(1995)이 제안한 응력수준과 암반등급에 따른 지하공동의 파괴 양상을 나타낸 것으로, 중간 수준의 응력에서 생성된 균열은 암반구조물 굴착면 주변에 국부적으로 형성되었으나 높은 수준의 응력에서 발생한 균열은 더 넓은 범위에 형성된 것을 볼 수 있다. Fig. 1의 사각형으로 표시된 영역이 취성파괴가 발생 가능한 영역을 의미한다.

Fig. 1.

Examples of tunnel instability and brittle failure as a function of RMR and the ratio of the maximum far-field stress to the unconfined compressive strength (after Hoek et al., 1995).

취성파괴는 지하구조물의 형상과 현지응력의 작용방향 등에 따라 암반의 강도를 초과하는 응력이 굴착면 등의 특정 영역에 집중하는 경우 발생할 수 있다. Fig. 2는 형상과 현지응력의 크기, 방향에 따른 취성파괴 발생가능 영역과 형상을 제시한 것으로, 한 변이 긴 직사각형 단면을 갖는 지하구조물이더라도 현지응력의 크기, 방향과의 관계에 따라 상대적을 안정할 수 있다.

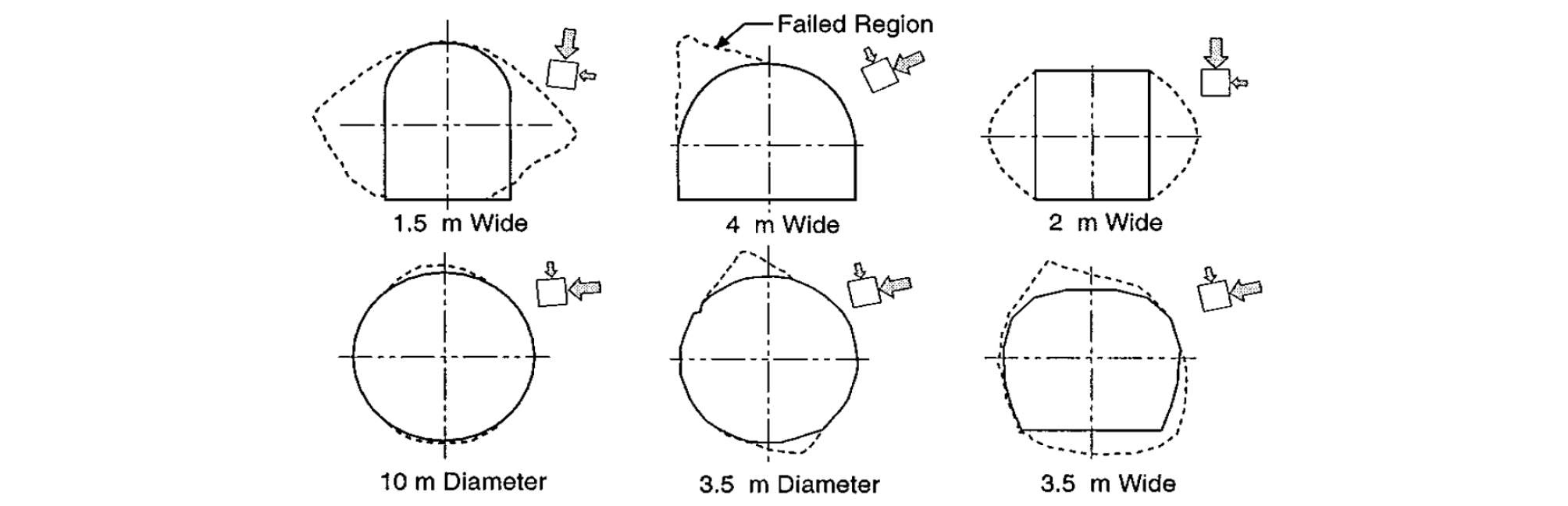
Fig. 2.

Comparison of the failed (notch) region for tunnels of different size and shape (Martin et al., 1999).

근래 다양한 분야에서 고심도에서 건설되는 지하암반구조물이 증가함에 따라 취성파괴 현상이 보고되고 있으며, 결정질암에 건설된 지하연구실험실(Underground Research Laboratory, URL)이나 수로터널 등에서도 취성파괴가 보고되고 있다. 취성파괴의 대표적인 사례로 남아프리카 금속광산, 캐나다 AECL의 URL 시험터널, 스웨덴 URL의 처분공 주변 기둥, 스위스의 Gotthard 터널 등과 국내의 도수터널, 지하유류비축기지 등이 있다(Ortlepp, 1997; Martin, 2001; Lee et al., 2004; Andersson et al., 2009). 특히 국내의 여수 지하유류비축기지에서 발생한 취성파괴의 경우 심도가 150 m인 저심도 구간에서도 현지응력 크기와 측압비 등의 영향으로 스폴링과 같은 취성파괴가 발생할 수 있음을 보여주고 있다. 따라서 암반구조물의 안정성을 확보하기 위해서 응력조건에 따라 발생 가능한 취성파괴의 파괴개시시점(failure initiation stress), 파괴범위(extent of failure) 및 파괴심도(depth of failure) 등과 같은 취성파괴의 특성이 규명되어야 한다. 본 연구에서는 지하구조물 주변에서 발생하는 취성파괴와 재하된 응력사이의 관계를 정량적으로 평가하고자 유한차분법(FLAC^3D)과 개별요소법(PFC^3D)을 이용한 수치실험을 실행하였다. 사용된 유한차분법에서는 CWFS(Cohesional Weakening Frictional Strengthening)모델을 사용하여 취성파괴 예측가능성을 분석했다.

수치해석방법

해석기법

유한차분법(FLAC^3D)

지하암반구조물에서 발생하는 취성파괴 현상을 예측하기 위하여 유한차분법 프로그램인 FLAC^3D를 이용하였다. 취성파괴는 암반의 최대강도 이후 지지력이 급격히 감소하는 거동에 따른 결과로 구조물의 안정적 설계에 있어 중요한 요인이기 때문에 최대강도 이후의 거동을 고려해야 한다는 기존 연구(Aglawe, 1999)를 참고하여, 본 연구에서 유한차분법을 이용한 수치실험은 Hajiabdolmajid et al.(2002)와 Martin(2014)이 제안한 변형률연화(strain softening)모델의 일종인 CWFS모델을 사용하였다.

CWFS 모델은 토질역학 분야에서 주로 사용되던 상호연결구조(interlocked structure)를 암석에 적용한 것으로 암석의 일반적인 강도가 입자경계의 흡착력(grain boundary adhesion) 또는 구속압과 무관한 점착력(cohesion), 구속압과 비선형적 관계인 상호연결강도(interlocking strength) 구속압과 선형적인 관계인 마찰강도(frictional strength)로 구성되어있다는 이론을 근거로 제안되었다(Cheon et al., 2007). Fig. 3은 구속압에 따른 강도 구성 요소들의 모식도를 나타내며, 재료에 따라 점착력과 상호결합강도의 형태는 서로 다른 형태를 갖는다고 보고되었다.

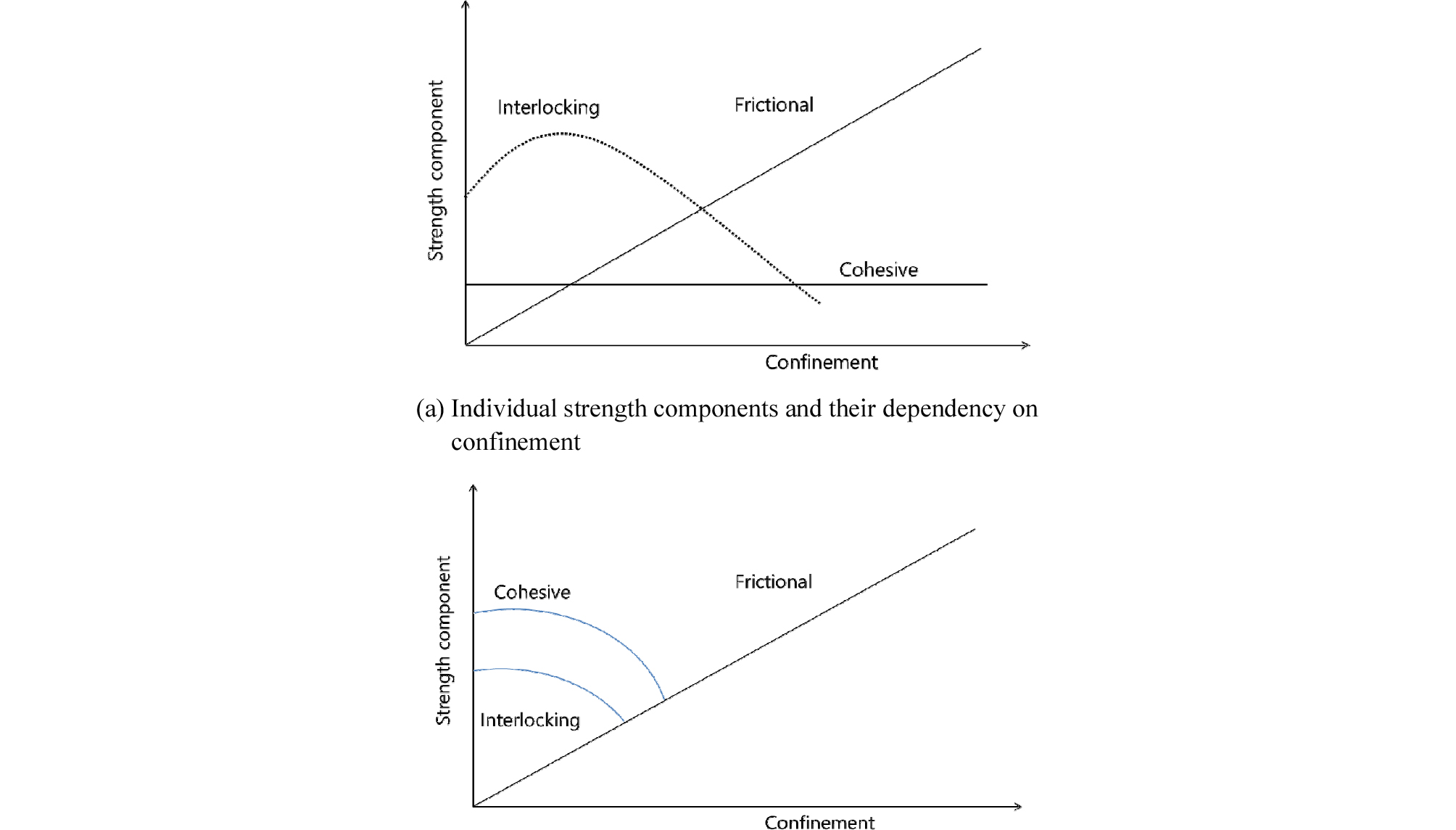
Fig. 3.

Schematic representation of the strength component in a cohesive geomaterial with interlocked structures (after Hajiabdomajid, 2001).

CWFS 모델에서는 암석이 손상을 받음에 따라 암석의 강도구성요소인 점착력이 약화되어 점차 잔류점착력으로 안정화되고, 이후에 마찰강도가 발현된다. 재료에 따라 점착력과 마찰강도가 발현되는 소성한계변형률(plastic strain limit)은 각각 다르고 경암의 경우 소성변형률의 초기단계에서 발현된 마찰강도는 무시할 정도로 작아 0으로 보아도 무방하다. 또한 기존 연구에서도 초기 파괴과정에서 마찰강도의 발현은 잔류값으로 안정화되는 소성한계변형률보다 점착력이 더 늦은 속도로 발현될 수 있다는 것이 보고된 바 있다(Hajiabdolmajid et al., 2002).

Kaiser et al.(2000)는 구속압에 따른 파괴발생양상을 압열인장파괴인 취성파괴와 전단파괴로 구분하고, 구속압에 따라 다르게 적용하는 이중선형(bi-linear) 파괴모델을 제안하였다. 이 모델에서 구속압이 낮은 경우 취성파괴 거동을, 구속압이 높은 경우 전단파괴로의 거동 변화가 발생하여 이들 사이는 취성파괴 한계선에 의해 상호 연결된다. 취성파괴 한계선은 재료에 따라 각각 다른 특성을 갖는다. Fig. 4는 Kaiser et al.(2000)가 제안한 이중선형 파괴모델을 도시한 것이다. 이 파괴모델에 있어 손상경계(damage threshold)가 취성파괴의 파괴개시시점에 해당한다고 볼 수 있다.

Fig. 4.

Bi-linear failure envelope (Kaiser et al., 2000).

본 연구에서 사용된 CWFS 모델의 입력변수는 Martin and Chandler(1994)가 제안한 손상제어시험(damage-controlled test)을 통해 소성변형률의 함수로 표현되는 점착력과 마찰력이다. 손상제어시험에 대한 자세한 내용은 Cheon et al.(2007)과 Jang et al.(2015)에 제시되어 있어 본 논문에서는 생략한다.

개별요소법(PFC^3D)

취성파괴를 모사하기 위해 유한차분법과 더불어 입자결합모델인 PFC^3D를 사용하였다. PFC^3D는 개별요소법을 통해 구상입자(spherical particle)의 운동과 상호작용을 모사하는 상용 해석프로그램으로 임의의 크기를 갖는 개별적인 구상입자들의 집합체로 역학적 거동을 모사할 수 있다. PFC^3D에서 입자들은 상호간 접촉점의 힘을 통하여 다른 입자나 벽과 상호작용을 하며, 이때 접촉모델은 임의의 접촉에서 발생하는 물리적인 거동을 지배한다. 접촉 모델은 다양한 종류가 있고 그 중 병행결합모델(parallel bond model)은 각 접촉에서 미끄러짐이 없는 상태로 회전이 발생하는 것을 방지하고자 할 경우에 적합하다. 따라서 본 연구에서는 입자의 회전보다 입자들 간의 인장에 의해 결합이 떨어지는 암석과 같은 물질에 병행결합모델이 가장 적합하다 판단하였다.

해석모델

수치실험에 의해 예측된 결과의 비교, 분석을 위하여 Cheon et al.(2006)이 수행했던 진삼축 모형실험결과를 이용하였다. Cheon et al.(2006)이 수행한 모형실험은 시멘트 모르타르를 사용한 290 mm의 정육면체 모형실험체에 60 mm 크기의 원형공동을 중간까지 형성한 후 삼축방향에서 하중을 가하여 공동주변에 발생한 취성파괴현상을 재현하였다. 이에 수치실험에서도 모형실험에 사용된 모형실험체와 동일한 크기의 해석모델을 구현하였다. 수치실험은 모형실험과의 비교를 고려하여 모형실험에서 수행된 실험순서를 따랐다. 삼축방향의 응력이 가해지기 전에 원형공동을 중간까지 굴착하고 공동 축에 평행한 수평재하응력, S_H1과 공동 축에 수직한 수평재하응력, S_H2을 미리 결정된 값으로 가한 후 공동 축에 수직한 연직재하응력, S_v(S_v > S_H1 > S_H2)을 응력제어방식에 의해 일정한 속도로 증가시켰다 PFC^3D에 의한 수치실험결과는 해석모델의 지름에 들어가는 입자의 개수로 정의되는 분해도(resolution)에 의해 영향을 받는다. 따라서 해석 목적, 정밀도 및 해석 소요시간 등을 종합적으로 고려하여 적당한 분해도의 선정이 필요하다. PFC^3D해석에서 분해도와 관련하여 Jung(2005)은 분해도가 25 이상이면 일정한 탄성계수 및 일축압축강도의 값을 보인다고 보고하였다. 따라서 본 연구에서 사용된 해석모델은 25의 분해도를 갖도록 최소 입자의 반지름은 3 mm, 최대 입자와 최소 입자의 비는 1.5로 하여 모델을 구성하였다.

입력변수 산정

유한차분법

수치실험에 사용된 입력변수는 Cheon et al.(2006)이 수행했던 진삼축 모형실험체의 재료인 시멘트 모르타르의 물성을 사용하였다. Table 1은 시멘트 모르타르의 물리적, 역학적 특성을 나타낸다. CWFS 모델의 입력변수는 손상제어시험을 통하여 구했으며, 손상제어시험의 결과는 Cheon et al.(2007)이 수행했던 연구결과를 사용하였다. 손상파라미터($\omega$)는 암반의 손상을 내타내는 지수로서 재하 - 제하의 증분에서 발생되는 영구적인 소성체적변형률로 정의되고, 최대강도(peak strength, P($\omega$))는 일정 손상파라미터에서의 최대응력을 의미한다. 균열손상응력은 체적변형률이 감소하는 지점의 응력을 의미하며, 최대강도의 약 70% ~ 80% 수준에서 발생하였다. 최대강도와 균열손상응력으로부터 소성체적변형률에 따른 점착력과 마찰각이 산정되었다.

Table 1. Physical and mechanical properties of cement mortar (After Cheon et al., 2006)

Table 2는 손상제어시험으로부터 결정된 소성변형률(plastic strain)의 변화에 따른 점착력과 마찰각의 변화를 나타낸 것이고 FLAC^3D의 변형률연화모델을 통해 CWFS 모델을 구현하는 데 사용되었다

Table 2. Cohesion and friction angle changes with plastic strain (After Cheon et al., 2007)

개별요소법

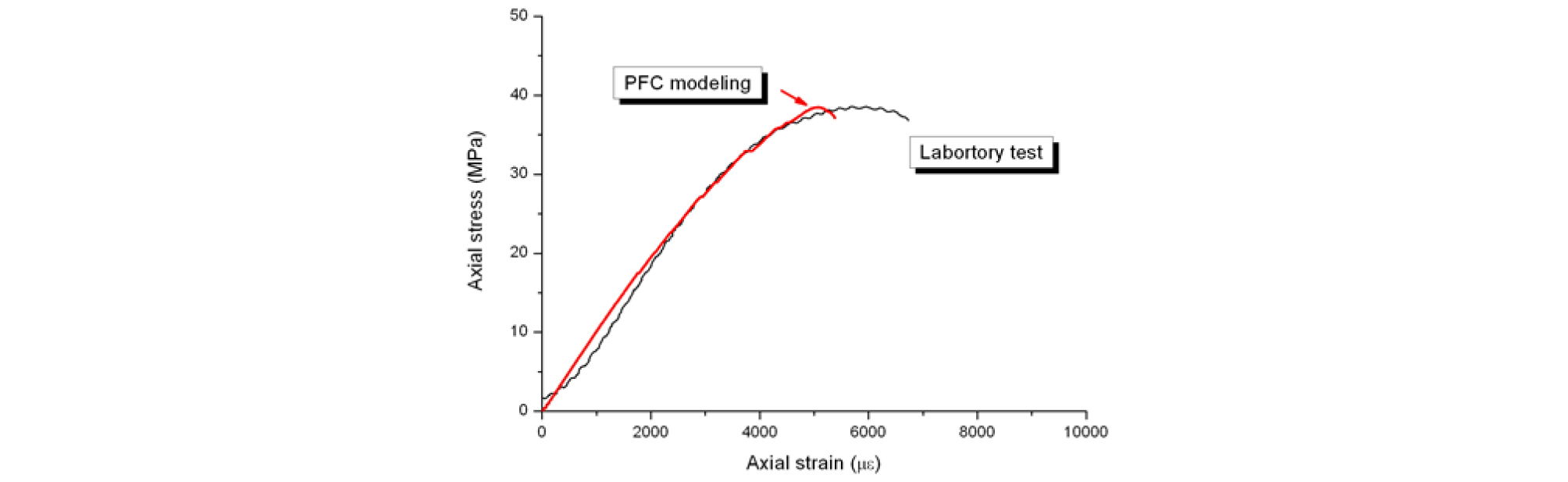
일반적으로 입력변수의 결정은 일축압축시험과 PFC^3D에 의해 수행된 일축압축모사시험을 비교하여 결정되나, 해석목적에 따라 인장강도시험이나 삼축압축시험과의 비교를 통하여 결정하기도 한다. 본 연구의 경우 구속압이 작거나 거의 없는 상황에서 발생하는 취성파괴에 대한 예측이 주된 목적이므로 일축압축시험을 모사하여 입력물성을 결정하였다. Fig. 5는 PFC^3D를 통한 모델링 결과와 실험값을 비교한 것이다. 결정된 입력변수는 Table 3에 제시하였으며 최적의 입력변수를 결정하기 위하여 10회의 반복해석을 통해 얻은 평균값으로부터 입력변수를 결정하였다.

Fig. 5.

Comparison of uniaxial compressive strength test between PFC^3D modeling and Laboratory test.

Table 3. Micro-parameters used in PFC^3D modeling

수치실험에 의한 결과분석

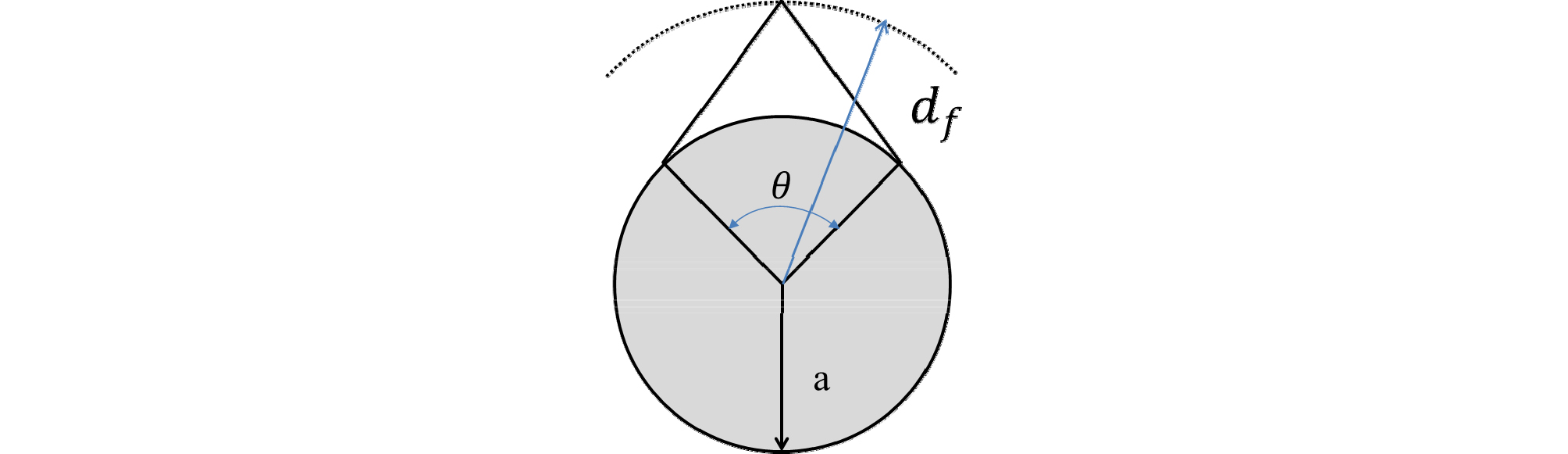
본 연구에서는 취성파괴의 특성을 파괴개시시점과 파괴범위, 파괴심도로 구분하고, FLAC^3D와 PFC^3D에 의한 수치실험을 통해 재하응력의 크기, 재하응력과 원형공동의 방향에 따른 취성파괴의 특성을 알아보았다. 특히 FLAC^3D에 의한 수치실험의 경우 구성모델에 따른 취성파괴현상의 예측가능성을 평가하였다. 파괴개시시점은 공벽에서 취성파괴가 관찰되기 시작하는 응력수준으로, 파괴범위와 파괴심도는 Fig. 6에서 각각 $\theta$와 $d_f$로 정의된다.

Fig. 6.

Determination of the extent and depth of brittle failure around a circular hole (a: radius of circular opening).

유한차분법에 의한 결과분석

응력조건에 따른 파괴특성

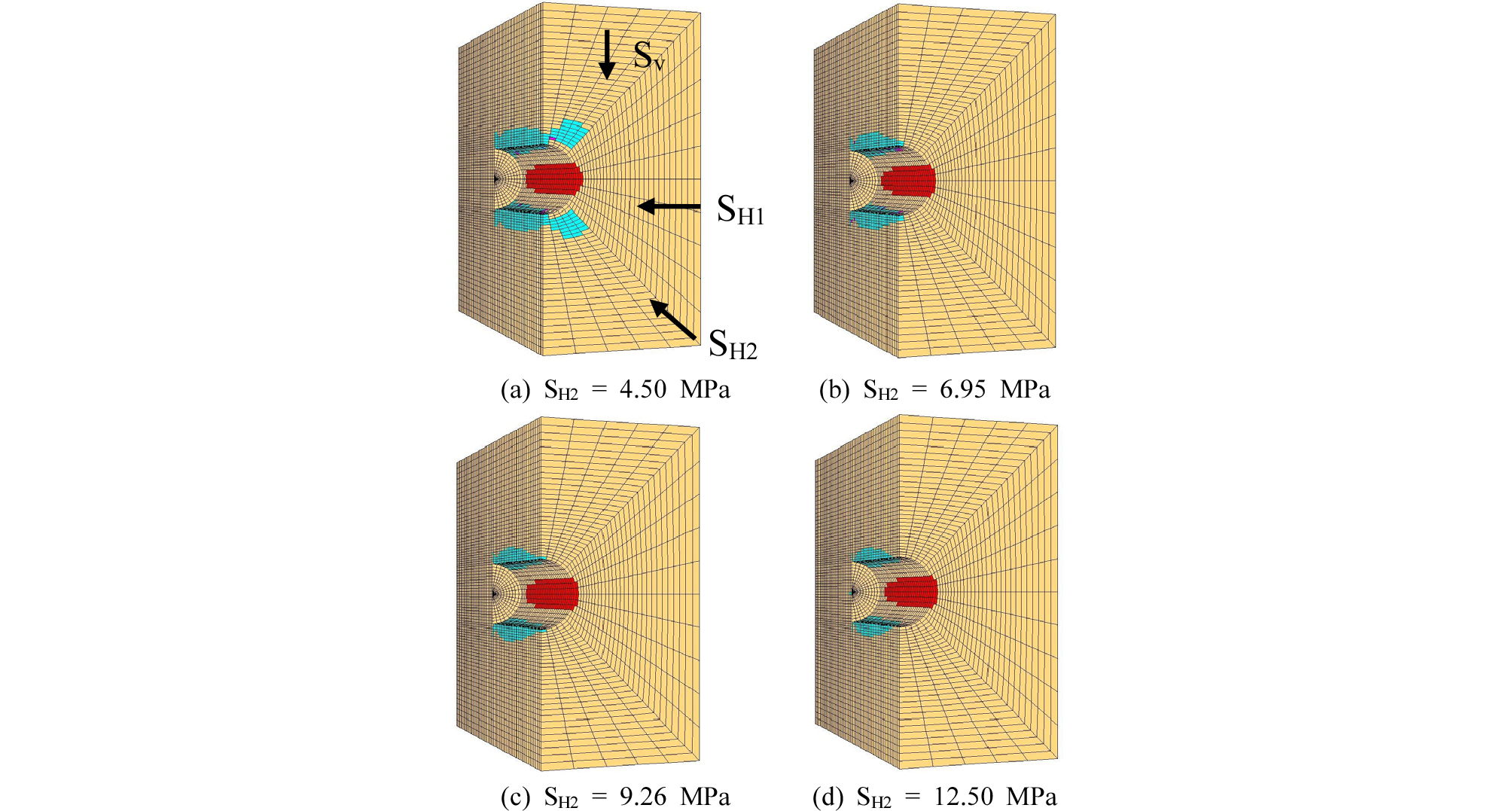
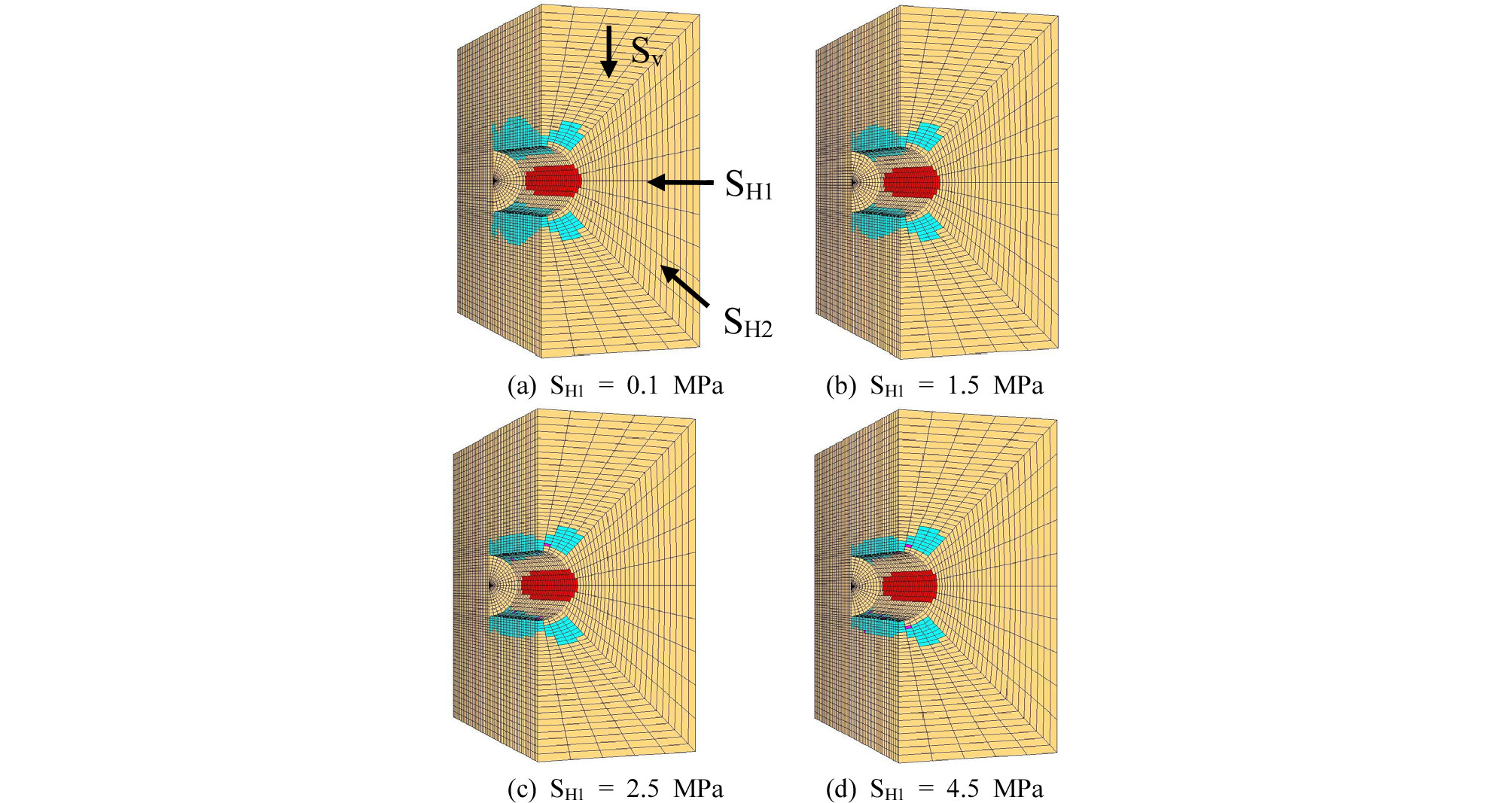
공벽에서 취성파괴가 관찰되기 시작하는 응력수준으로 정의된 파괴개시시점은 FLAC^3D의 경우 S_v에 평행한 공벽에서 전단파괴가 발생하는 시점의 S_v의 크기에 해당하며, 파괴범위와 파괴심도는 유한차분망에서 소성영역으로 나타난 요소(zone)의 높이와 깊이에 해당한다. 응력조건의 변화에 따른 파괴특성은 CWFS 모델로 수행한 수치실험에 대하여 분석한 것으로 S_v, S_H1, S_H2의 응력조건에 대하여 2가지 경우로 나눠 파괴특성을 알아보았다. S_v와 S_H1이 일정하고 S_H2의 크기가 변할 때와 S_v와 S_H2가 일정하고 S_H1의 크기가 변할 때의 파괴특성은 각각 Fig. 7과 Fig. 8에 나타냈다. 먼저 Fig. 7에서 공동 축에 수직한 수평재하응력, S_H2의 크기가 증가함에 따라 최대접선응력이 감소하고 결과적으로 공벽에서 발생되는 파괴범위와 파괴 심도가 감소하고 있음을 관찰 할 수 있다. 또한 S_H2가 클수록 공동 천단과 하부에서 발생한 인장영역이 감소하며, 공저에 의한 아치효과가 증가하여 전단파괴가 발생한 영역이 공저로부터 많이 이격되어 있음을 알 수 있다. Fig. 8에서 공동 축에 평행한 수평재하응력, S_H1이 증가함에 따라 공동입구의 경계부에서 발생한 파괴심도에 영향이 있음을 알 수 있고, 특히 S_H1은 천단부의 인장파괴와 밀접한 관련이 있어 그 크기에 따라 인장파괴의 범위와 깊이가 감소함을 관찰할 수 있다. 그러나 S_H1의 크기는 다른 재하응력에 비해 취성파괴의 특성에 상대적으로 크게 영향을 주지 않는 것으로 나타난다. 따라서 파괴범위와 파괴심도는 공동 축에 수직한 응력조건에 대해서만 조사하였다. 응력조건에 따른 파괴개시시점의 변화에 대한 수치실험결과를 Table 4에 제시하였다. 수치실험은 S_v > S_H1 > S_H2인 조건에서 수행되었다. Table 4에서 알 수 있듯이 파괴개시시점은 S_H2의 크기가 증가함에 따라 뚜렷한 증가현상을 보이나 S_H1에 대해서는 거의 영향이 없는 것으로 나타났다. 이는 CWFS 모델의 파괴기준이 취성파괴현상을 해석하기 위해 소성 변형률에 따른 재료물성의 변화를 반영하지만, Mohr-Coulomb이나 Hoek-Brown 파괴기준과 마찬가지로 중간주응력을 고려하고 있지 않기 때문으로 해석된다. 그러나 공동 축에 평행한 재하응력이 증가함에 따라 파괴개시점이 미미하게 증가하는 이유는 세 방향에서 작용하는 응력이 유한차분망의 최대주응력과 최소주응력을 증가시켜 파괴기준에 영향을 주기 때문이다. 이와 같이 CWFS 모델의 경우 아직 3차원 해석을 완벽하게 고려하지 못하기 때문에, 3차원적인 해석을 수행하는 경우 세심한 주의가 요구된다.

Fig. 7.

Comparison of failure characteristics with different S_H2.

Fig. 8.

Comparison of failure characteristics with different S_H1.

Table 4. Failure initiation stress from FLAC^3D modeling with different stress conditions (stress condition: S_H1 > S_H2)

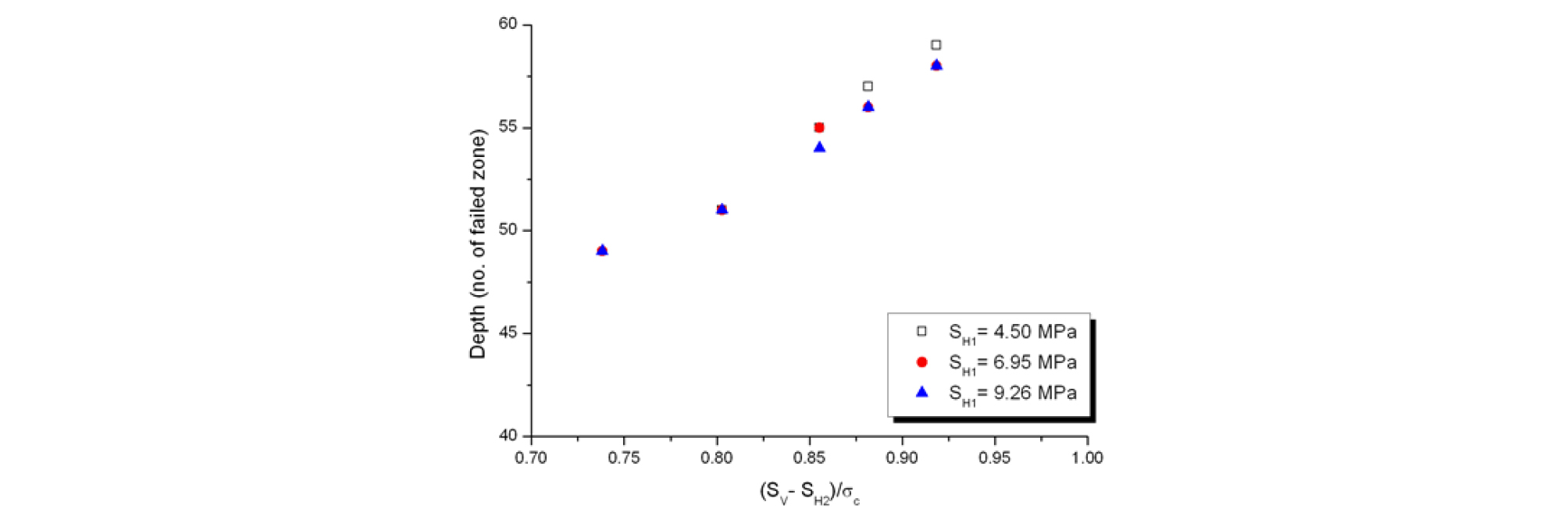
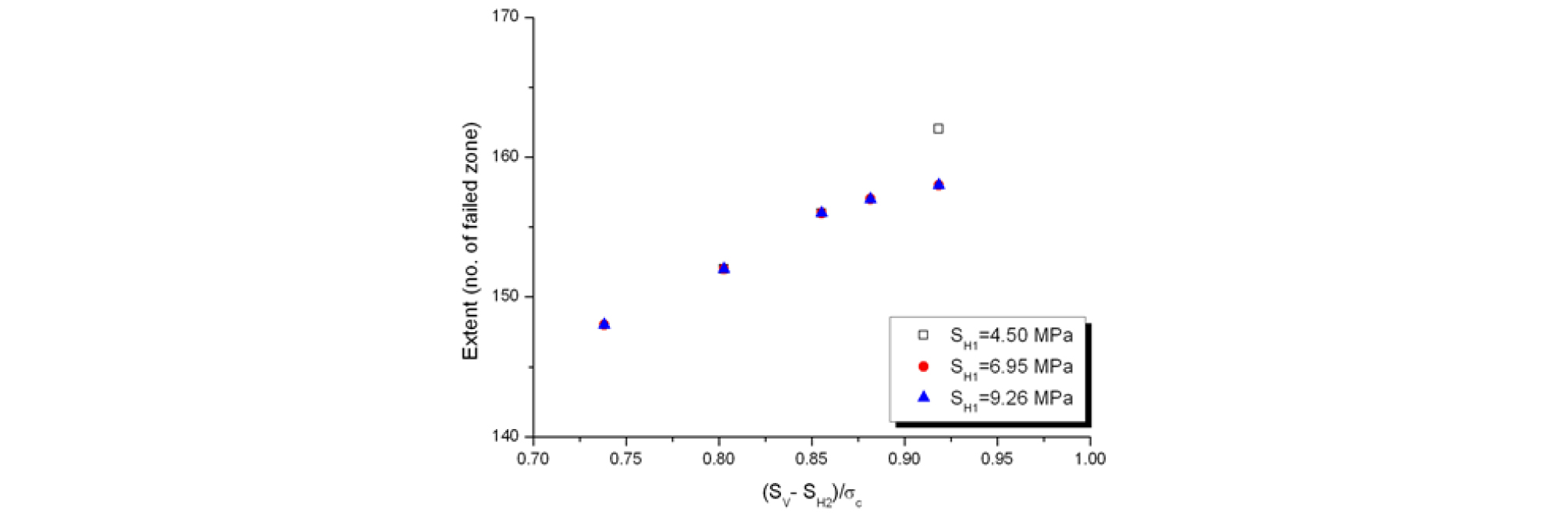
Fig. 9와 Fig. 10은 S_v가 35 MPa인 응력조건에서 산정한 파괴심도와 파괴범위를 공동 축에 수직한 축차응력(S_v - S_H2)에 대해 도시한 것이다. 축차응력이 증가함에 따라 파괴범위와 함께 파괴심도가 증가하나 S_H1의 영향은 거의 없음을 알 수 있다. 이와 같이 FLAC^3D에 의한 해석은 파괴개시시점을 예측하는 데 적합하지 않다, 하지만 손상제어시험과 현장조건에 대한 역해설 결과를 반영하는 경우, 공동 축에 수직한 응력조건에 따른 파괴범위와 파괴심도의 예측을 위한 좋은 평가방법으로 사용될 수 있을 것이라 사료된다.

Fig. 9.

Depth of failure with differential stress from FLAC^3D modeling.

Fig. 10.

Extent of failure with differential stress from FLAC^3D modeling.

원형공동의 방향에 따른 파괴특성

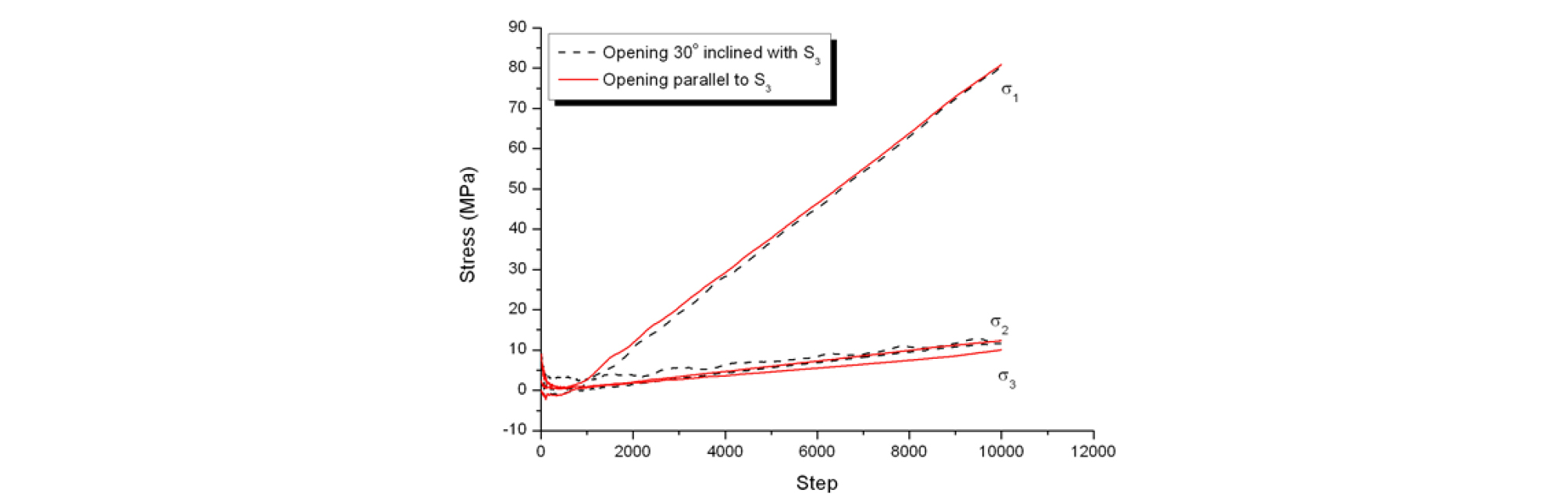
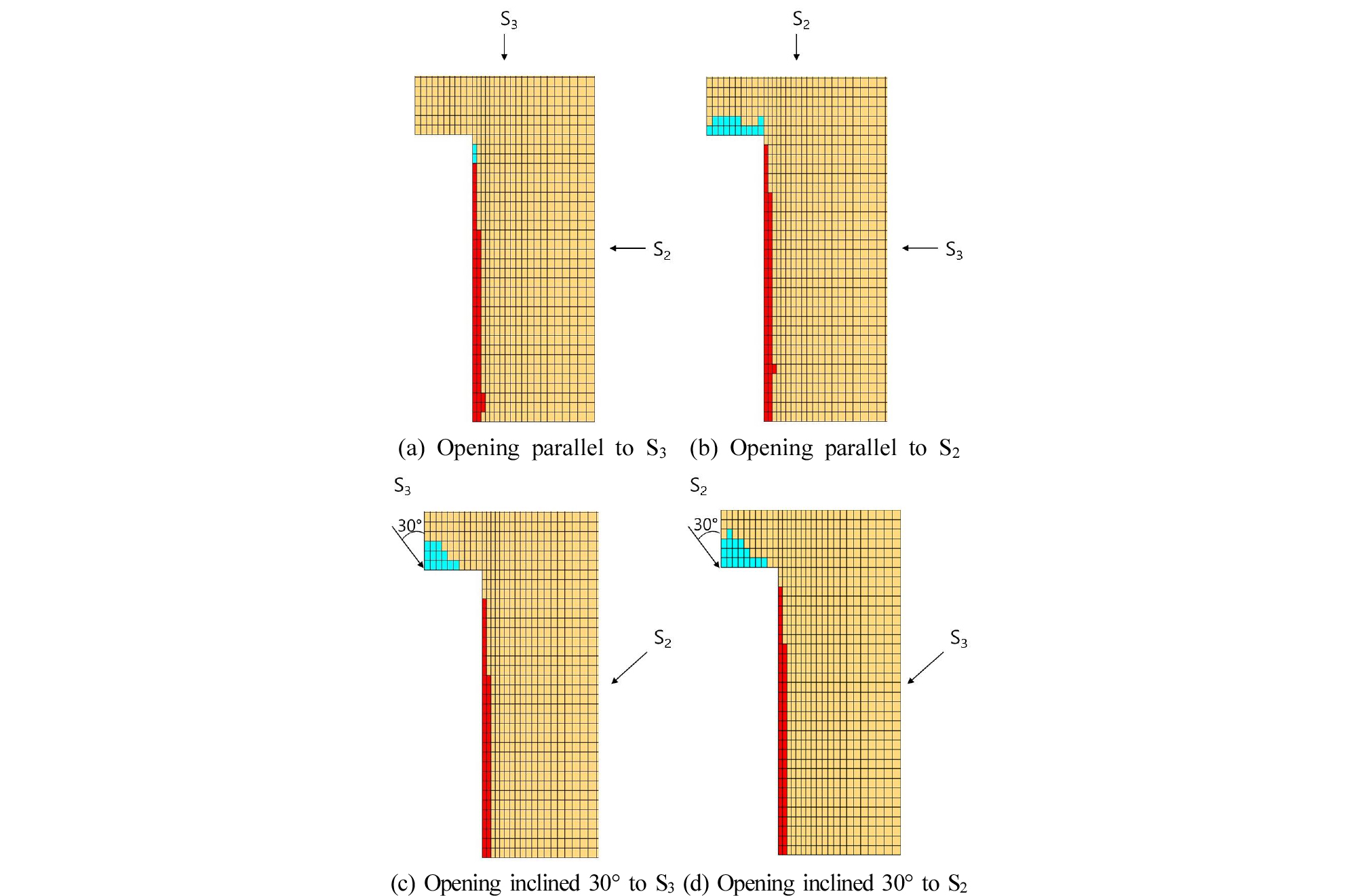
재하응력조건과 원형공동의 위치에 따른 취성파괴의 특성을 알아보기 위하여 Table 4을 고려하여 Table 5와 같이 S_H1와 S_H2가 일정한 상태에서 S_v를 증가시키면서 수치실험을 수행하였다. 이로부터 파괴개시시점은 원형공동의 방향에 영향을 받으나, 공동 축에 수직한 수평재하응력, S_H2의 크기가 파괴개시시점에 중요한 영향을 미치는 것을 알 수 있다. Fig. 11은 원형공동이 최소 재하응력, S₃와 평행한 경우와 30°경사를 이룬 원형공동 공벽의 한 지점에서의 최소, 중간, 최대주응력을 도시한 것이다. 경사를 이룬 원형공동의 최대주응력은 평행한 경우에 비해 약간 작은 값을 나타내나 중간주응력과 최소주응력은 크게 나오는 것을 알 수 있다. 이를 통해 동일한 응력조건이라도 경사를 이룬 경우 최소주응력의 증가에 따라 파괴기준이 높아지기 때문에 높은 응력수준에서 파괴가 발생하게 된다는 것을 알 수 있다(Table 5).

Table 5. Failure initiation stress from FLAC^3D modeling with different stress conditions (stress condition: S_H2 > S_H1)

Fig. 11.

Principal stress in the opening sidewall with different opening direction under same initial stress condition.

Fig. 12는 동일한 응력조건(최대 재하응력, S₁: 35 MPa, 중간 재하응력, S₂: 9.26 MPa, 최소재하응력, S₃: 2.5 MPa)에서 재하응력과 원형공동과의 관계에 따른 취성파괴현상을 보여준다. 최소 재하응력과 평행한 경우(Fig. 12(a)), 30°경사를 이룬 경우(Fig. 12(c)) 그리고 중간 재하응력과 평행한 경우(Fig. 12(b)), 30°경사를 이룬 경우(Fig. 12(d))에 대해 비교한다. 중간 재하응력과 평행한 경우가 동일한 응력조건에서 파괴영역이 가장 컸으며, 원형공동이 경사를 이룬 경우에서는 평행한 경우에 비해 전단파괴영역이 다소 감소함을 알 수 있다. 이로부터 원형공동의 방향에 따라 파괴개시시점이나 파괴영역이 다소 변화함을 알 수 있다. 그러나 Table 4에서 Table 5까지의 결과로부터 공동 축에 수직한 수평재하응력, S_H2가 파괴개시시점과 파괴영역에 더 중요한 영향을 미치는 것을 알 수 있다.

Fig. 12.

Comparisons of failure characteristics with different opening direction under same initial stress condition.

개별요소법에 의한 결과분석

응력조건에 따른 파괴특성

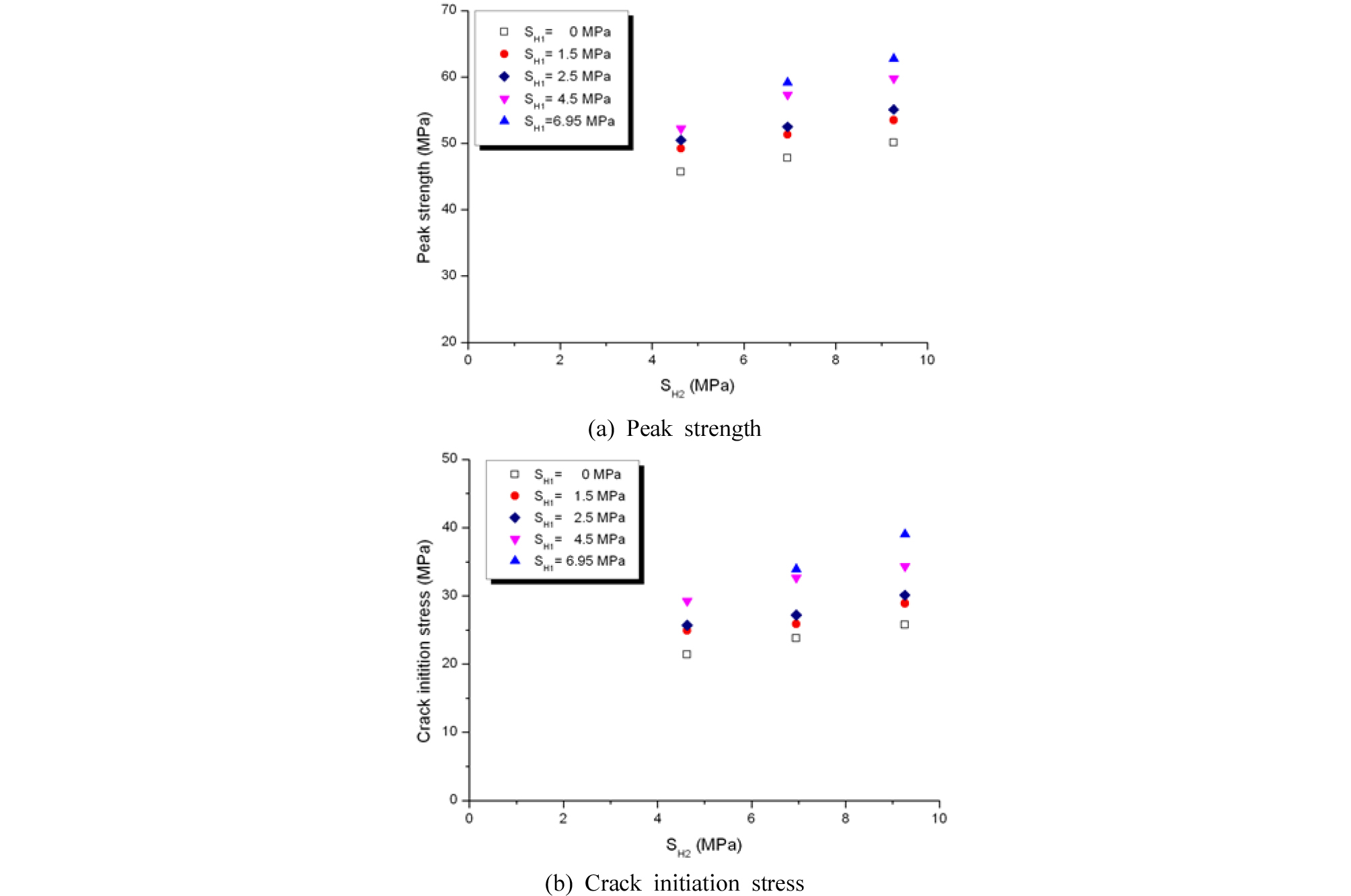
모형실험결과를 바탕으로 균열개시응력(crack initiation stress)을 파괴개시시점으로 선정하였다. 본 연구에 적용된 균열개시응력은 모델이 파괴될 때까지 발생한 균열의 10%가 발생했을 때의 응력에 해당한다. Table 6은 PFC^3D에 의해 구해진 최대강도(peak strength)와 균열개시응력을 나타낸 것이다. Table 6과 Fig. 13에서 나타난 바와 같이 S_H1, S_H2의 크기가 증가함에 따라 해석모델의 최대강도와 균열개시응력이 증가하는 것을 알 수 있었고, FLAC^3D와 달리 S_H1의 크기에도 많은 영향을 받음을 알 수 있다. 이는 S_H1의 크기가 증가함에 따라 PFC^3D에서 입자사이의 결합력이 커져 입자분리에 대한 저항력이 증가하기 때문으로 보인다.

Table 6. Peak strength and crack initiation stress measured from PFC^3D modeling with different stress condition (stress condition: S_H2 > S_H1)

Fig. 13.

Peak strength and crack initiation stress from PFC^3D modeling.

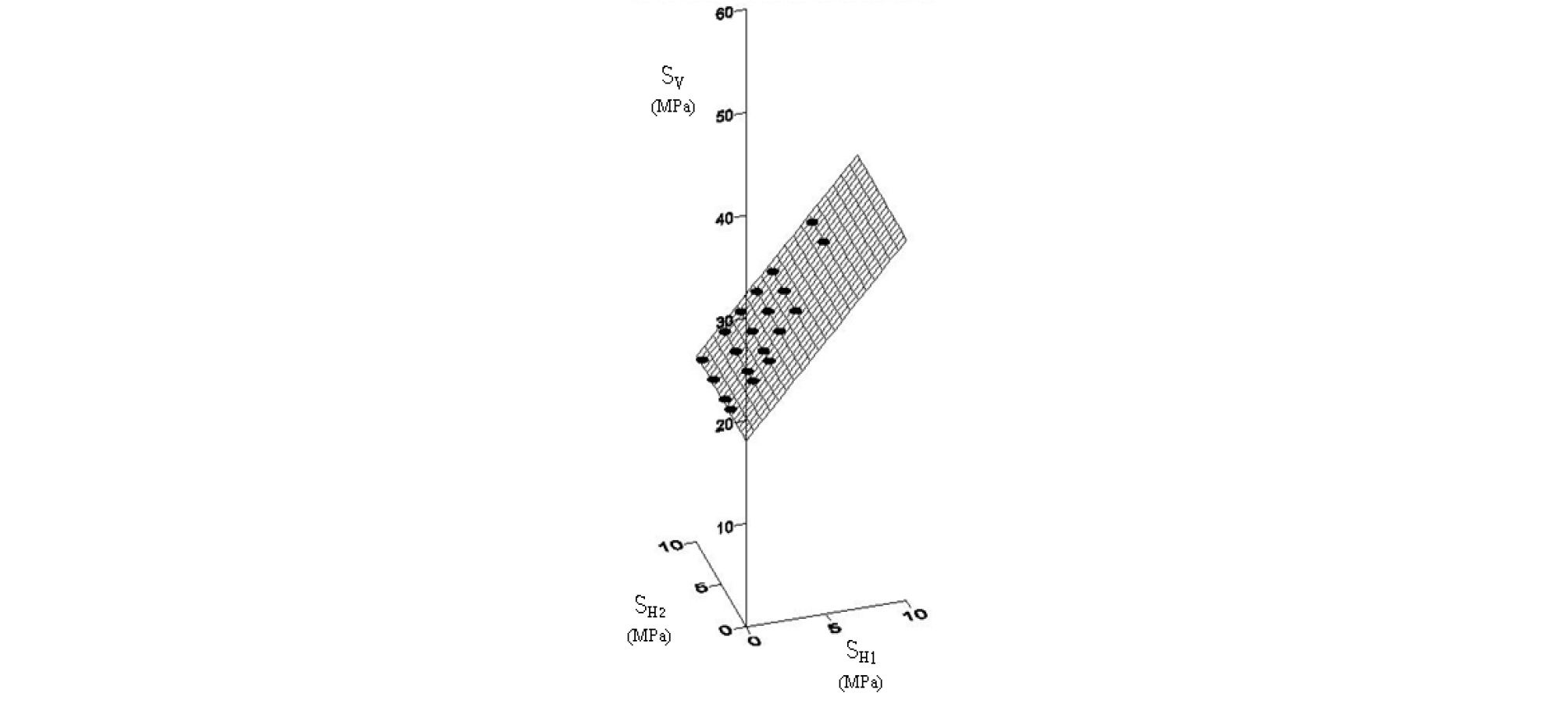
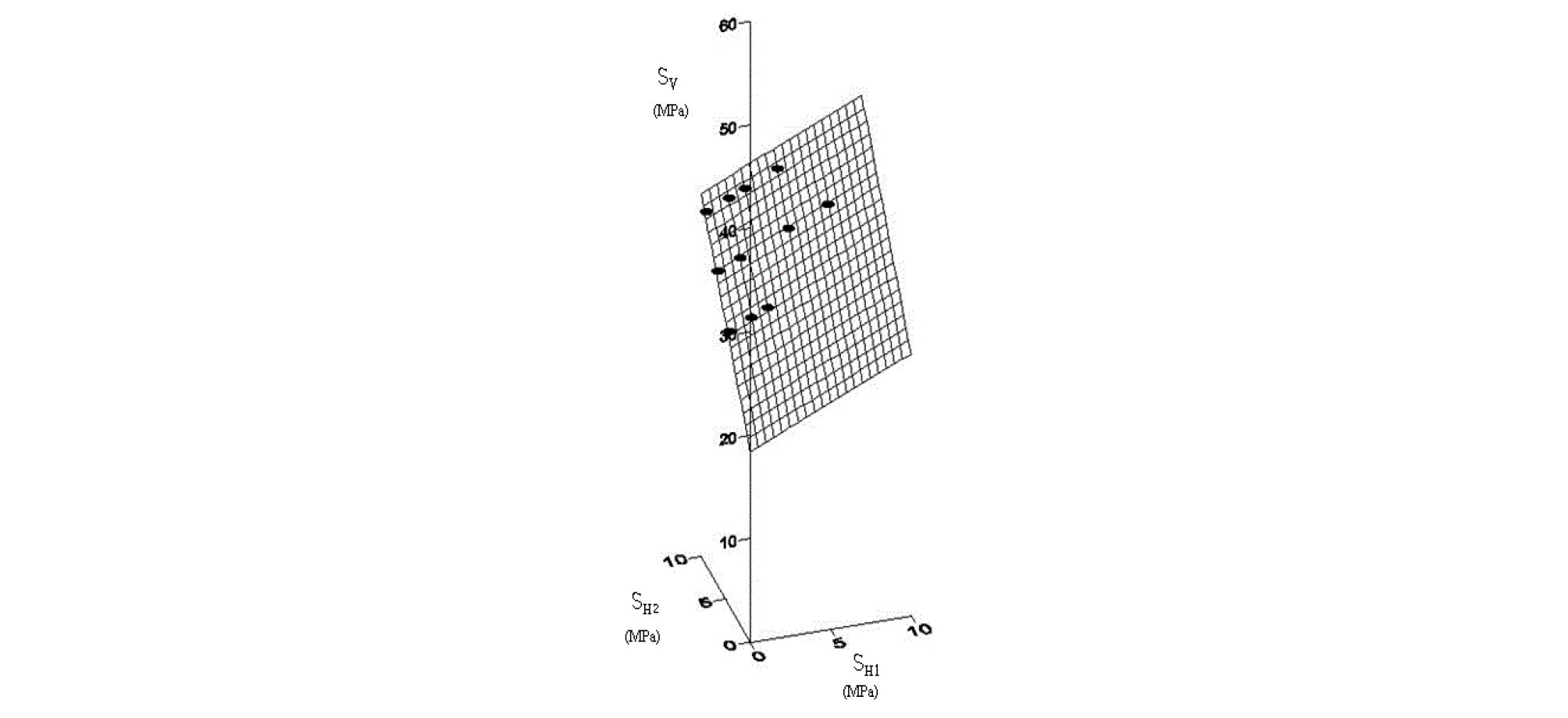
Fig. 14는 균열개시응력에 대한 응력조건의 영향을 알아보기 위해 최소자승법에 의해 구한 평면방정식을 도시 한 것이고 평면방정식은 식 (1)과 같다. 식 (1)에서 균열개시응력은 S_H2보다 S_H1(S_H2 > S_H1)에 의해 영향을 더 받음을 알 수 있다. Fig. 14의 격자망은 평면방정식을 나타내고 있으며, 검은 점은 수치실험에서 구해진 균열개시응력을 나타낸다.

Fig. 14.

Crack initiation stress from PFC^3D modeling with different stress conditions (stress condition: S_H2 > S_H1).

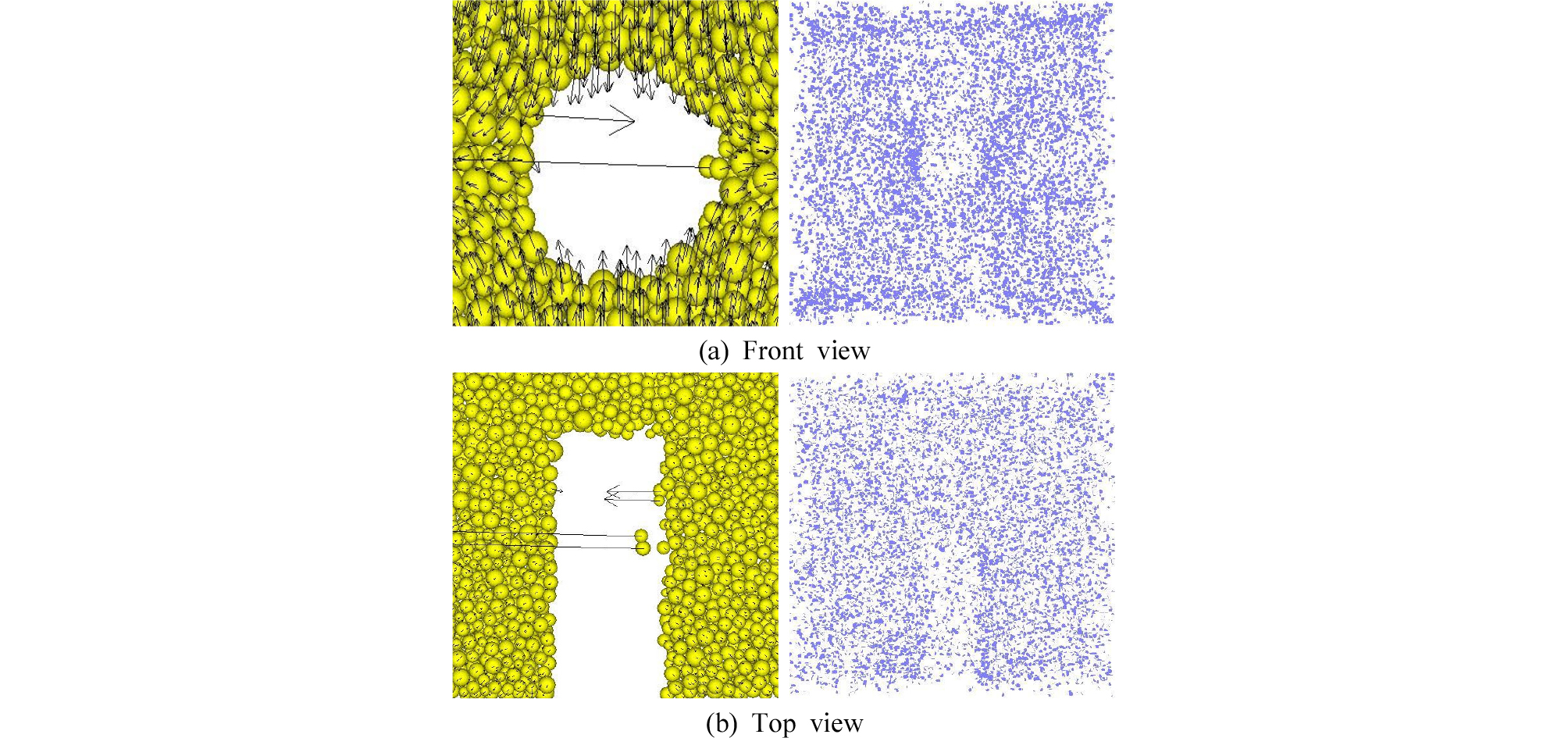
개별입자로 구성된 PFC^3D는 스폴링과 같은 분리현상을 입자탈락으로써 표현할 수 있다. 다음은 S_H1 = 1.5 MPa, S_H2 = 4.5 MPa인 응력조건에서 S_v의 변화에 따라 공동주변에서 발생한 변형 및 파괴특성에 대하여 알아본 결과이다. Fig. 15와 Fig. 16은 S_v의 크기가 증가함에 따라 발생된 균열의 양상과 입자의 변위벡터를 도시한 것이다. 균열모습은 전체 모델에서 나타나 현상을 표현한 것으로, 균열은 개개의 입자결합에서 수직성분(normal component)의 결합과 전단성분(shear component)의 결합이 깨진 상태를 나타낸다. Fig. 15는 S_v가 20 MPa에 해당될 때 발생된 현상으로 균열이 전 지역에서 고르게 발생하고 있으나 원형공동의 측벽부에서 다른 부분보다 조금 더 많은 균열이 발생하고 있음을 알 수 있다. S_v를 35MPa까지 증가시켰을 때 측벽에서 많은 균열이 집중되어 발생하였으며 공동 주변에서 관찰되는 변위벡터의 양이 전반적으로 증가하고 있다. 또한 측벽에 집중된 결합력으로 인해 일부는 공 내부로 이동하려는 양상을 보인다(Fig. 16).

Fig. 15.

Particle displacement and Crack distribution in PFC^3D at S_v = 20 MPa.

Fig. 16.

Particle displacement, Crack distribution in PFC^3D at S_v = 35 MPa.

원형공동의 방향에 따른 파괴특성

동일한 응력조건에서 원형공동의 방향에 따른 취성파괴의 특성을 알아보기 위하여 Table 6을 고려하여 Table 7과 같이 개별요소법을 이용하여 수치실험을 수행하였다. Table 6은 원형공동이 중간 재하응력에 평행한 경우에 대하여 수행한 것이며, 재하응력과 30 °의 경사를 이룬 원형공동의 경우(Table 7의 15* ~ 18**)는 재하응력에 평행한 원형공동에 비해 더 높은 균열개시응력을 나타낸다. 이는 취성파괴는 압축으로 인한 인장균열에 의해 발생하는 데, 원형 공동이 경사를 이룬 경우 압축이 작용하는 방향으로 전단력이 작용하여 인장균열의 발생을 억제하고 결과적으로 취성파괴의 개시시점을 증가시키는 것으로 볼 수 있다. 그러나 FLAC^3D에 의한 결과와 같이 원형공동의 방향보다 원형공동에 작용하는 재하응력의 크기가 균열개시응력에 더 중요한 영향을 미치는 것으로 나타났다. 식 (2)는 Table 6의 결과로부터 파괴개시시점에 해당하는 균열개시응력과 응력조건에 대해 최소자승법으로 구한 평면방정식을 나타낸다. 식 (1)과 달리 식 (2)에서 균열개시응력은 S_H1보다 S_H2에 의해 영향을 더 받는 것으로 나타났다. 이는 최소 재하응력이 공동 축에 수직하게 작용하거나, 또는 공동 축에 평행하게 작용하더라도 균열개시응력에 주된 영향을 주는 인자임을 의미한다. 따라서 취성파괴의 개시시점을 평가할 때 3차원적인 해석이 가능한 수치해석기법을 이용하여 수행되어야 할 것이다. Fig. 17에 균열개시응력과 응력조건에 대해 도시하였다. 그림에서 격자망은 식 (2)의 평면방정식을 나타내고, 검은 점은 수치실험에서 구해진 균열개시응력을 나타낸다.

Table 7. Peak strength and crack initiation stress measured from PFC^3D modeling with different stress conditions (stress condition: S_H1 > S_H2)

Fig. 17.

Crack initiation stress from PFC^3D modeling with different stress conditions (stress condition: S_H1 > S_H2).

토 의

본 연구에서는 수치실험을 통해 해석기법에 따른 취성파괴 현상의 예측가능성을 평가하고 3차원 응력조건에 따른 취성파괴 특성을 알아보았다. 유한차분법에 의한 수치실험은 FLAC^3D가 사용되었으며, 변형률연화 모델인 CWFS 모델이 이용되었다. CWFS 모델에 의한 해석결과는 Mohr- Coulomb 모델에 비하여 Cheon et al.(2006)이 수행한 모형실험에서 관찰된 v-형태의 파괴형상을 잘 모사하였다. FLAC^3D의 경우 파괴영역이 동일한 응력조건에서 모형실험과 다르게 곡률에 따른 크기효과가 존재하지 않아 파괴영역이 과장된 경향을 보였다. CWFS 모델을 이용한 수치실험으로부터 공동 축에 수직한 수평재하응력, S_H2의 크기가 클수록 파괴개시를 위한 응력수준은 증가함을 보였으며, 파괴범위와 파괴심도는 작아지는 것으로 나타냈다. 특히 파괴범위와 파괴심도는 공동 축에 수직한 축차응력과 선형적인 관계가 있음을 알 수 있었다. 그러나 CWFS 모델의 파괴기준이 중간주응력을 고려하지 않기 때문에 3차원 해석을 수행할 경우 이에 대한 주의가 요구된다.

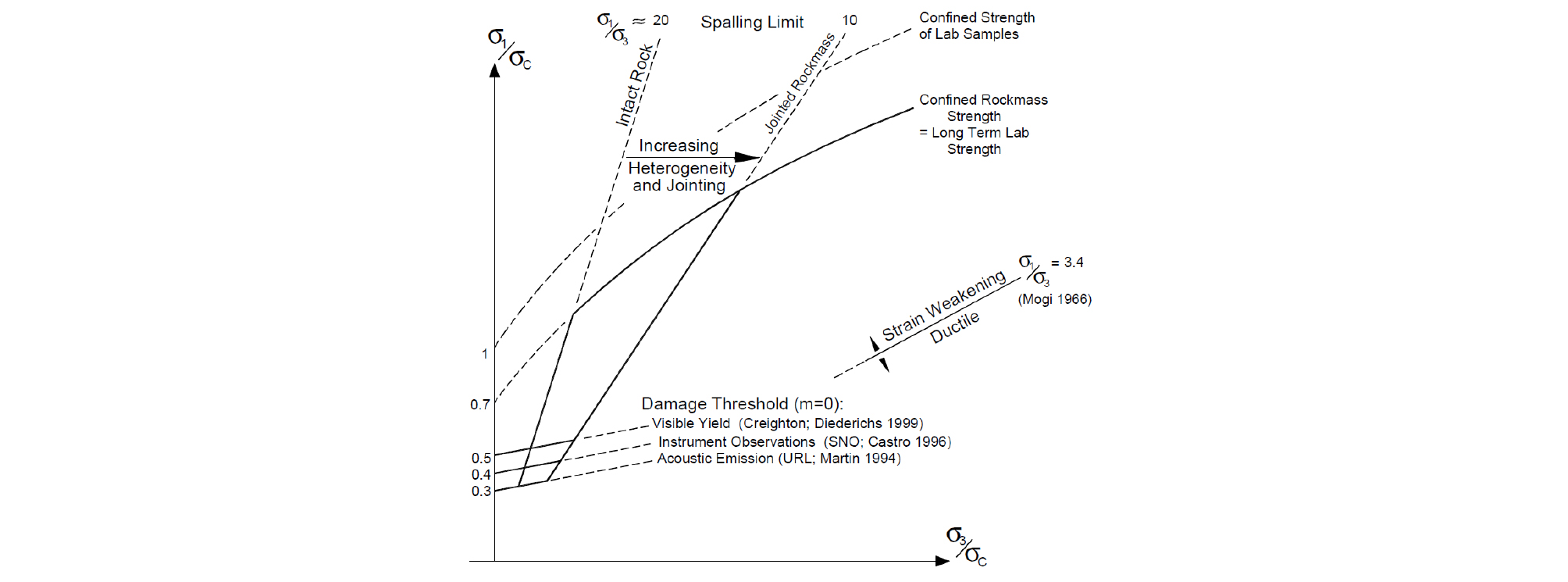
개별요소법에 의한 수치실험은 PFC^3D가 사용되었고, PFC^3D에 의한 해석결과로서 응력수준이 증가함에 따라 공벽에서 입자의 탈락현상을 관찰할 수 있었다. 또한 S_H1과 S_H2가 증가함에 따라 균열개시응력과 최대강도는 증가하였다. 균열개시응력이 취성파괴의 개시시점을 나타내는 좋은 지시자가 될 수 있음을 확인하였으며, 균열개시응력은 원형공동의 방향에 관계없이 해석모델에 작용하는 최소 재하응력에 가장 큰 영향을 받는 것으로 나타났다. Fig. 18은 PFC^3D의 수치실험에 의해 구해진 최대강도와 균열개시응력 그리고 취성파괴가 발생한 모형실험결과를 Kaiser et al.(2000)이 제안했던 이중선형 파괴포락선(bi-linear failure envelop)을 수정하여 도시한 것이다. 이중선형 파괴포락선은 실내 시험에서 얻은 결과를 Hoek-Brown의 마찰 파라미터 m, s를 사용한 기준과 취성 파라미터(m = 0)를 사용한 기준에 의해 도시한 것으로, 구속압이 낮은 응력조건에서는 취성파괴기준이 적용되며 구속압이 증가함에 따라 Hoek- Brown의 파괴기준을 적용하는 파괴모델이다. 이중선형 파괴포락선에서 취성파괴기준과 Hoek-Brown의 파괴기준과의 연결을 위해 S_v/S_H2 = 10, S_v/S_H2 = 20의 기준식이 제시되었다. 취성파라미터는 Martin(1994), Castro(1996), Diederichs(1999)에 의해 현장에서 관찰된 결과를 바탕으로 제시된 기준을 같이 도시하였다. 그리고 Fig. 18에서 작게 표현된 검은 원은 실내 시험에서 얻은 일축압축강도와 삼축압축강도를, 크게 표현된 검은 원은 모형실험에서 스폴링이 발생한 응력조건을 나타낸다. 모형실험결과에서 스폴링이 발생하기 위한 응력조건은 현장경험에 바탕을 둔 기준식에 잘 부합하고 있는 것을 알 수 있다. 또한 PFC^3D의 모사에 의한 균열개시응력이상에서 파괴가 관찰되어 균열개시응력이 취성파괴 개시시점을 평가하는 좋은 지시자가 될 수 있을 것으로 판단된다. 그러나 취성파괴가 발생하기 위한 조건으로 제시되었던 기준식(S_v/S_H2 = 10, S_v/S_H2 = 20과 두 기준식 사이의 영역)은 취성파괴의 발생영역을 과소평가할 수 있는 것으로 나타났다.

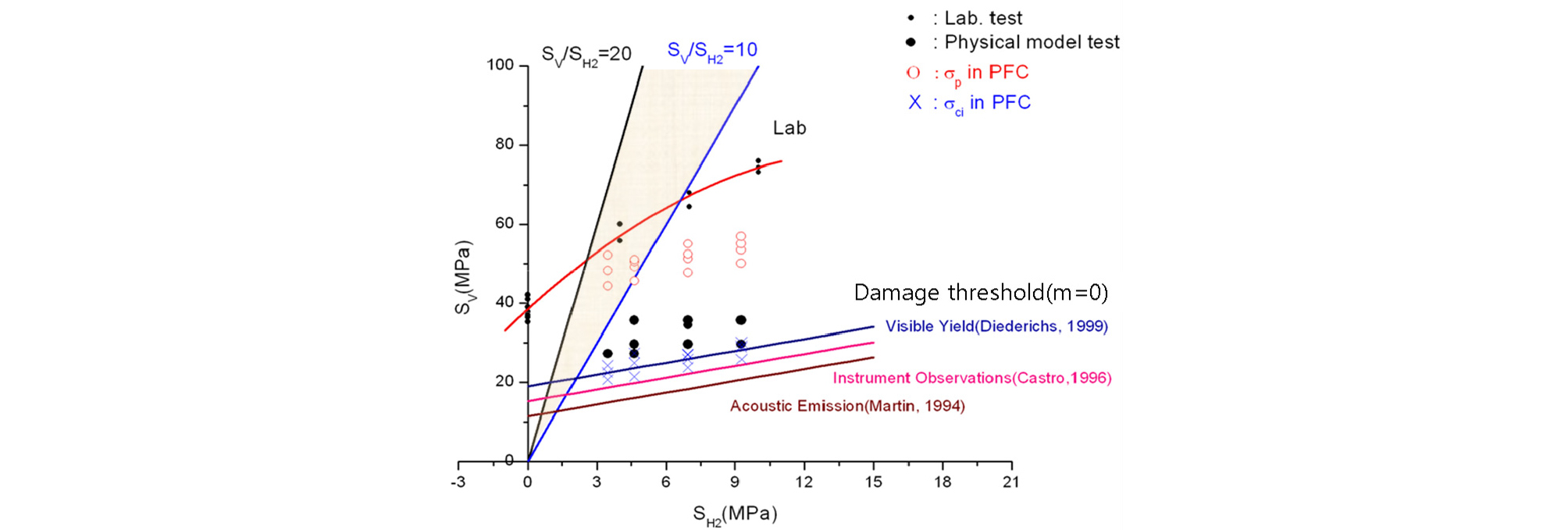
Fig. 18.

Numerical simulation results and physical model test results in bi-linear envelope (modified from Kaiser et al., 2000).

상기 결과로부터, PFC^3D는 FLAC^3D와 달리 3차원 응력조건의 영향을 반영할 수 있으나, 취성파괴의 정도를 표현하는 파괴심도와 파괴범위를 구별하는 데 어려움이 존재한다는 결론을 얻을 수 있다.

따라서 취성파괴현상을 모사하는데 있어 유한차분법인 FLAC^3D를 이용하는 경우 CWFS 모델이 적합함을 알 수 있고, 손상제어시험으로부터 구한 입력변수는 현장이나 모형실험에 의한 역해석 결과를 반영할수록 보다 정확한 해석이 될 수 있다. CWFS 모델의 파괴기준이 중간주응력을 고려하지 않기 때문에 3차원 해석보다는 2차원해석에 의한 보수적인 해석이 적합하리라 판단된다. PFC^3D는 모사시험에 의해 입력물성을 산정하여 3차원 응력조건의 영향을 반영 할 수 있다. 또한 공벽에서 입자의 탈락현상과 균열발생양상을 모사할 수 있다. 또한 PFC에서의 균열개시응력은 취성파괴의 개시시점을 나타내는 좋은 지시자가 될 수 있음을 확인하였다. 하지만 FLAC^3D에 비해 파괴 범위와 파괴심도를 평가하기가 난해하므로, 취성파괴를 예측하는 데 있어 해석목적에 맞게 유한차분법과 개별요소법의 장점을 살린 해석이 필요할 것 이다.

결 론

고심도 암반구조물에서 발생 가능한 취성파괴의 예측가능성을 알아보고자 유한차분법(FLAC^3D)과 개별요소법(PFC^3D)에 의한 수치실험을 수행하여, 기존의 진삼축 모형실험결과와 현장관찰결과를 비교하여 다음과 같은 결론을 도출하였다.

1) FLAC^3D를 이용한 수치실험을 통해 CWFS 모델에 따른 취성파괴현상의 예측가능성을 알아본 결과, CWFS 모델이 모형실험 및 현장에서 관찰된 v-형태의 파괴형상을 잘 예측하는 것으로 나타났다.

2) CWFS 모델의 입력변수는 재하-제하의 반복에 의한 손상제어시험으로부터 결정할 수 있으며, 현장결과나 모형실험결과로부터 역해석을 수행하여 입력변수를 보정하는 것이 필요하다.

3) CWFS 모델을 이용한 수치실험으로부터 공동 축에 수직한 수평재하응력(S_H2)의 크기가 증가할수록 파괴개시를 위한 응력수준은 증가하며, 파괴범위와 파괴심도는 작아지는 것으로 나타났다. 특히 파괴범위와 파괴심도는 공동 축에 수직한 축차응력(S_v - S_H2)과 선형적인 관계를 보였다. 그러나 CWFS 모델의 파괴기준은 Mohr-Coulomb이나 Hoek-Brown 파괴기준과 같이 중간주응력을 고려하지 않기 때문에 3차원 응력조건의 영향을 고려할 수는 없었다.

4) PFC^3D에 의한 해석결과 공동 축과 평행한 수평재하응력(S_H1)과 공동 축에 수직한 수평재하응력(S_H2)이 증가함에 따라 균열개시응력과 최대강도는 증가하였으며, 응력수준이 증가함에 따라 공벽에서 입자의 탈락현상을 관찰할 수 있었다. 모형실험과의 비교를 통하여 균열개시응력이 취성파괴의 개시시점을 나타내는 좋은 지시자가 될 수 있음을 확인하였다.

5) PFC^3D는 FLAC^3D와 달리 3차원 응력조건의 영향을 반영할 수 있으며, 파괴개시시점에 해당하는 균열개시응력은 원형공동의 방향보다 해석모델에 작용하는 최소 재하응력에 가장 큰 영향을 받는 것으로 나타났다. 그러나 프로그램의 특성상 파괴심도와 파괴범위를 구별하는 데 어려움이 존재하였다. 따라서 취성파괴를 예측하는 데 있어 해석목적에 맞게 유한차분법과 개별요소법의 장점을 살린 해석이 필요할 것이다.

6) PFC^3D의 수치실험에 의해 구해진 최대강도와 균열개시응력을 이중선형 파괴포락선에 도시한 결과, PFC^3D에 의한 균열개시응력이 취성파괴 개시시점을 평가하는 좋은 방법이 될 수 있음을 보였다. 그러나 취성파괴가 발생하기 위한 조건으로 제시되었던 기준식(S_v/S_H2 = 10, S_v/S_H2 = 20과 두 기준식 사이의 영역)은 취성파괴의 발생영역을 과소평가할 수 있는 것으로 나타났다.