서 론
시추공 위치측정
시추공 위치정보
위치측정기
위치계산법
시추공 위치오차와 보정
시추공 위치오차
시추스트링과 송신케이블 길이변화
위치측정기 기울어짐
자기장 모델
시추스트링 자기간섭
위치측정간격
시추공 충돌방지
시추공 거리분석
시추공 충돌방지 관리
연구 결과 및 해석
단일 시추공 위치오차와 보정
다중 시추공 위치오차와 보정
결 론
서 론
석유시추는 굴착을 통해 3차원 지하공간에 위치하는 목표지점에 도달하는 과정으로 굴진심도, 경사각 그리고 방위각을 모두 계획한 대로 유지해야 한다. 그러나 시추공 굴착은 관통되는 지층의 특성과 시추비트에 작용하는 힘의 방향에 따라 편향이 발생한다(Bourgoyne et al., 1986; Kang et al., 1990). 만약 시추공이 계획한 시추궤도에서 이탈되고 이를 수정하지 않으면 결국 목표지점에 도달하지 못한다(Choi, 2011). 따라서 계획한 시추궤도에 맞춰 시추하려면 굴착기술과 더불어 시추공 위치를 파악하기 위한 시추공 위치측정(wellbore survey)이 필수적이다.
초기 석유시추는 수직 시추로 목표지점에 도달하는 것에 그쳤으나 1920년대부터 시추공저장비(BHA; Bottom Hole Assembly)의 기하학적 배치, 전향쐐기(whipstock), 분사비트(jetting bit) 등으로 방향성 시추를 가능케 하였다. 시추공 위치는 Acid bottle이나 Totco로 경사각만을 측정하다가 기계식 위치측정기가 개발되면서 경사각과 방위각 측정이 모두 가능해졌다. 1960년대 공저이수모터(bottom hole mud motor)와 굴곡자(bent sub과 bent housing), 전자식 위치측정기가 도입되면서 방향성 시추기술은 급속도로 발전하였다. 그 후 1980년대 들어서면서 MWD(Measurement While Drilling)로 시추공 위치측정이 실시간으로 가능해졌고 1990년대 RSS(Rotary Steerable System)가 상용화되면서 복잡한 시추궤도, ERD(Extended Reach Drilling) 및 다가지 시추(multi-lateral drilling)가 더욱 활발해졌다. 또한 MWD의 원격송신(telemetry) 기술과 위치측정기를 비트에 가깝게 위치시켜 측정하는 기술(near bit measurement)의 발전, 자이로계측기와 MWD 원격송신을 결합한 GMWD (Gyro-based Measurement While Drilling)가 개발되면서 시추공 위치측정의 정확도는 더욱 향상되었다(Kim et al., 2014; Cho et al., 2015; Kim et al., 2018). 이러한 시추공 굴착기술과 위치측정기술의 발전으로 생산성 극대화를 위해 최적의 시추궤도를 찾아가는 방향제어시추(geosteering)가 가능해졌다.
방향성 시추를 하려면 시추공의 경사와 방위를 정확히 예측하고 분석해야 한다. 그러나 시추공 위치는 측정위치가 갖는 참값과 측정값 사이의 오차가 존재한다. 시추공 위치오차의 정량화 연구는 Walstrom et al.(1969)이 우연오차(random error)로 처음 소개하였으나 지구자기장의 편각, 시추스트링과 송신케이블의 길이변화 등의 계통오차(systematic error)가 적용되지 않았다. 1981년 Wolff and de Wardt 오차 모델이 도입되면서 6가지 계통오차로 분류하여 위치측정기의 종류와 품질에 따라 위치오차를 분석하였으며 오차 모델의 이론적 토대가 되었다(Wolff and de Wardt, 1981). 그 후 1995년 ISCWSA(Industry Steering Committee on Wellbore Survey Accuracy)가 설립되면서 시추공 위치오차를 표준화하고 위치측정 정확도를 높이기 위한 보정을 명문화하였다(Lake and Mitchell, 2006; ISCWSA, 2019).
이 논문에서는 방향성 시추에서 필수적인 시추공 위치측정과 오차를 알아보고, 단일 및 다중 시추공에서 오차 보정의 적용성을 분석하였다.
시추공 위치측정
시추공 위치정보
시추공 위치측정은 측정깊이, 경사각, 방위각을 기본정보로 한다. 측정된 위치정보는 목적한 목표지점의 시추 외에 안전한 시추작업을 위한 편향변화율(DLS; Dogleg Severity), 토크와 드래그 분석(torque and drag analysis), 시추공 안정성 분석(wellbore stability analysis)을 가능케 한다(Lim et al., 2009; Kwon et al., 2019). 또한, 시추공 위치측정과 더불어 물리검층(자연감마선, 전기비저항, 중성자 및 밀도 등)으로 지층평가를 수행하여 최적 시추방향을 결정한다.
시추작업은 목표지점에 도달하기 위해서 굴착과 케이싱 설치를 반복한다. 이 과정에서 다수의 시추공 위치정보가 존재하므로 기준점이 필요하다. 시추심도 기준은 작업이 이루어지는 회전테이블(rotary table)이며 경사각 기준은 시추궤도가 지표의 수직방향과 이루는 각이다. 그리고 방위각 기준은 진북(true north), 자북(magnetic north), 도북(grid north)으로 나뉘고 시추공 위치측정은 도북을 기준으로 시계방향의 수평각을 의미한다. 따라서 방위각은 위치측정기에 따라 도북 편차(grid convergence)나 자침 편차(magnetic declination)로 보정이 요구된다.
위치측정기
시추공 위치측정기는 측정깊이를 기본정보로 경사각만 측정하는 기기와 경사각과 방위각을 모두 측정하는 기기로 구분된다. 경사각만 측정하는 기기는 시추공의 수직도를 확인할 목적으로 사용하며, 경사각 및 방위각을 측정하는 기기는 방위각 측정방법에 따라 자기계측기(magnetic tool)와 자이로계측기(gyroscopic tool)로 나뉜다(Table 1).
Table 1. Typical wellbore survey tools
초기 자기계측기는 기계식으로 경사각은 경사계(inclinometer)에 내장된 추(pendulum)의 기울어짐으로 측정하고 방위각은 나침반(compass)으로 자북 방향과 시추궤도 방향의 차이로 측정하였다. 이후 전자식 자기계측기가 개발되면서 3성분 중력가속도계(accelerometer)와 자력계(magnetometer)로 시추공 위치를 측정한다. 경사각은 중력가속도계로 중력의 크기()를 측정하여 식 (1)로 예측하고, 방위각은 중력가속도계와 자력계로 측정한 중력의 크기와 자기장의 크기()로 식 (2)과 같이 계산한다(Jamieson, 2017).
| $$Inclination=cos ^{-1} \left ( \frac {A _{Z}} {\sqrt {A _{X}^{2} +A _{Y}^{2} +A _{Z}^{2}}} \right )$$ | (1) |
| $$Azimuth=tan^{-1}\left(\frac{\left(A_XB_Y-A_YB_X\right)\sqrt{A_X^2+A_Y^2+A_Z^2}}{B_Z\left(A_X^2+A_Y^2\right)-A_Z\left(A_XB_X+A_YB_Y\right)}\right)$$ | (2) |
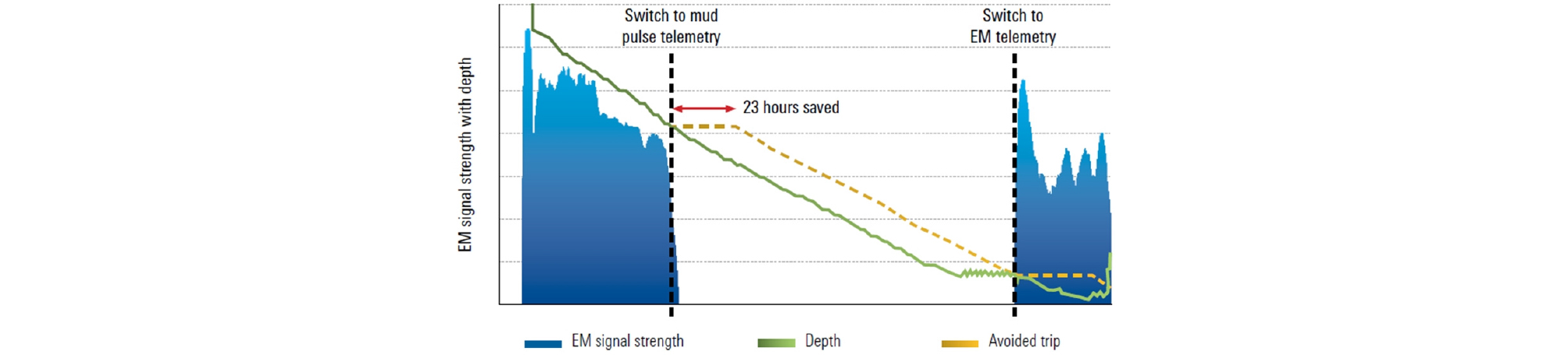
자기계측기의 자료전송 방법은 내부메모리, 송신케이블, MWD가 있다. MWD는 원격송신 방식에 따라 시추스트링 내부의 시추이수 흐름을 밸브로 제어하여 이수압력을 변화시킴으로써 지표에서 획득하는 시추이수펄스(mud pulses) 방식, 전자기파를 생성시켜 지표에서 안테나로 회수하는 전자기(EM; electromagnetic) 방식 그리고 음파(acoustic) 방식이 있다(Kim et al., 2018; Tochikawa et al., 1996). 또한 최근에는 Fig. 1과 같이 자료전송 속도가 빠른 전자기 방식과 적용성 및 안정성이 높은 시추이수펄스 방식을 결합하여 작업시간을 단축시키는 이중원격송신(dual telemetry)도 사용한다.
초기 자이로계측기는 기계식 경사계와 자유 자이로(free gyro)로 경사각과 방위각을 측정하였다. 이후 전자식 자이로계측기가 개발되면서 3성분 중력가속도계와 가속도 자이로(rate gyro)로 위치를 측정한다. 경사각은 중력가속도계로 중력의 크기()를 측정하여 식 (3)로 예측하고, 방위각은 진북을 기준으로 회전하는 지구의 자전속도를 가속도 자이로로 측정하여() 식 (4)로 계산한다(Jamieson, 2017).
| $$Inclination=tan ^{-1} \left [ \frac {\sqrt {A _{X}^{2} +A _{Y}^{2}}} {A _{Z}} \right ]$$ | (3) |
| $$Azimuth=tan^{-1}\left[\frac{\left(G_XcosTF-G_YsinTF\right)cosI}{G_XsinTF+G_YcosTF+\Omega_VsinI}\right]$$ | (4) |
| $$TF=tan ^{-1} \left [ \frac {-A _{X}} {-A _{Y}} \right ]$$ | (5) |
여기서, 는 지구 자전속도의 수직성분, 와 는 지구 자전속도의 수평성분()을 가속도 자이로로 측정한 X축과 Y축 방향의 크기, (Inclination)은 중력가속도계로 측정한 경사각 그리고 식 (5)의 (Toolface)는 중력 장비면방향의 각도이다.
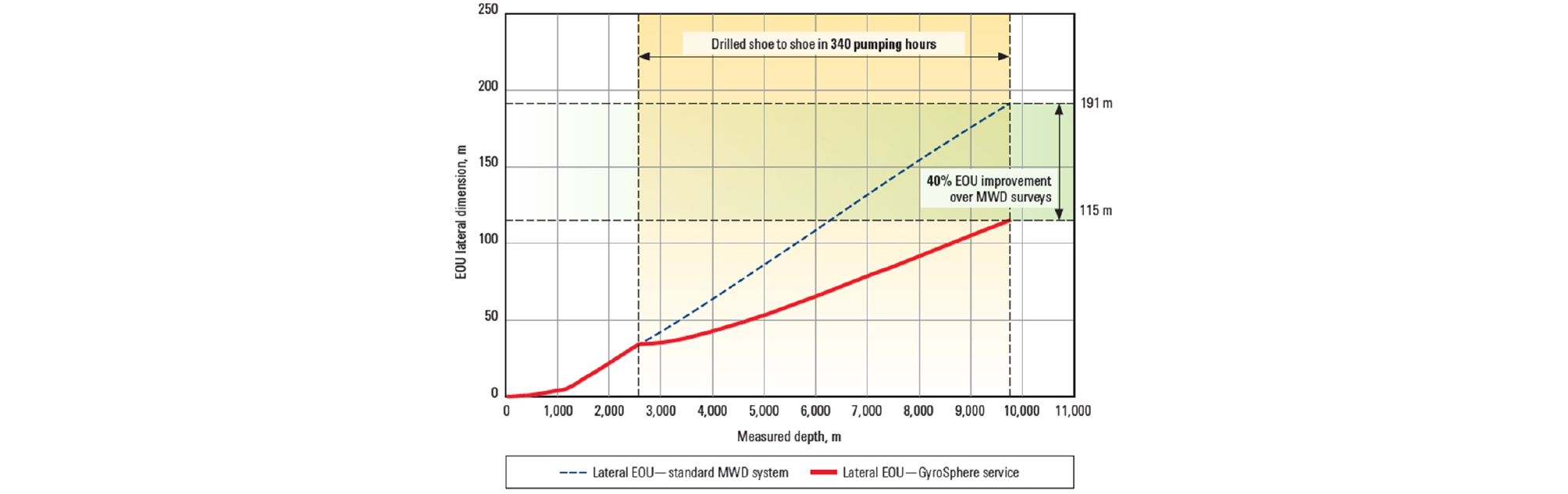
자이로계측기는 방위각을 지구자기장으로 결정하지 않아 주로 자기간섭이 높은 케이싱 내부나 사이드트랙(sidetrack), 케이싱이 설치된 인접 시추공, 플랫폼 및 시추리그 직하부에서 송신케이블로 측정하며 최근에는 Fig. 2와 같이 정확도가 높은 자이로계측기와 시추공 경사각에 따른 제약이 없는 MWD 원격송신을 결합한 GMWD도 사용된다.
위치계산법
시추공 위치는 측정된 두 지점의 측정깊이, 경사각, 방위각으로 북・남, 동・서, 수직심도를 예측한다. 위치계산법은 다양한 방법이 소개되었으며 Table 2와 같이 정확도가 높은 최소곡률법을 사용한다.
Table 2. Comparison of results of the five commonly used survey methods (Lake and Mitchell, 2006)
| Calculation methods | TVD error (ft) | Displacement error (ft) |
| Tangential | -4.76 | +14.99 |
| Balanced tangential | -0.11 | -0.03 |
| Average angle | 0.00 | -0.25 |
| Curvature radius | -0.04 | -0.31 |
| Minimum curvature | - | - |
시추공 위치오차와 보정
시추공 위치오차
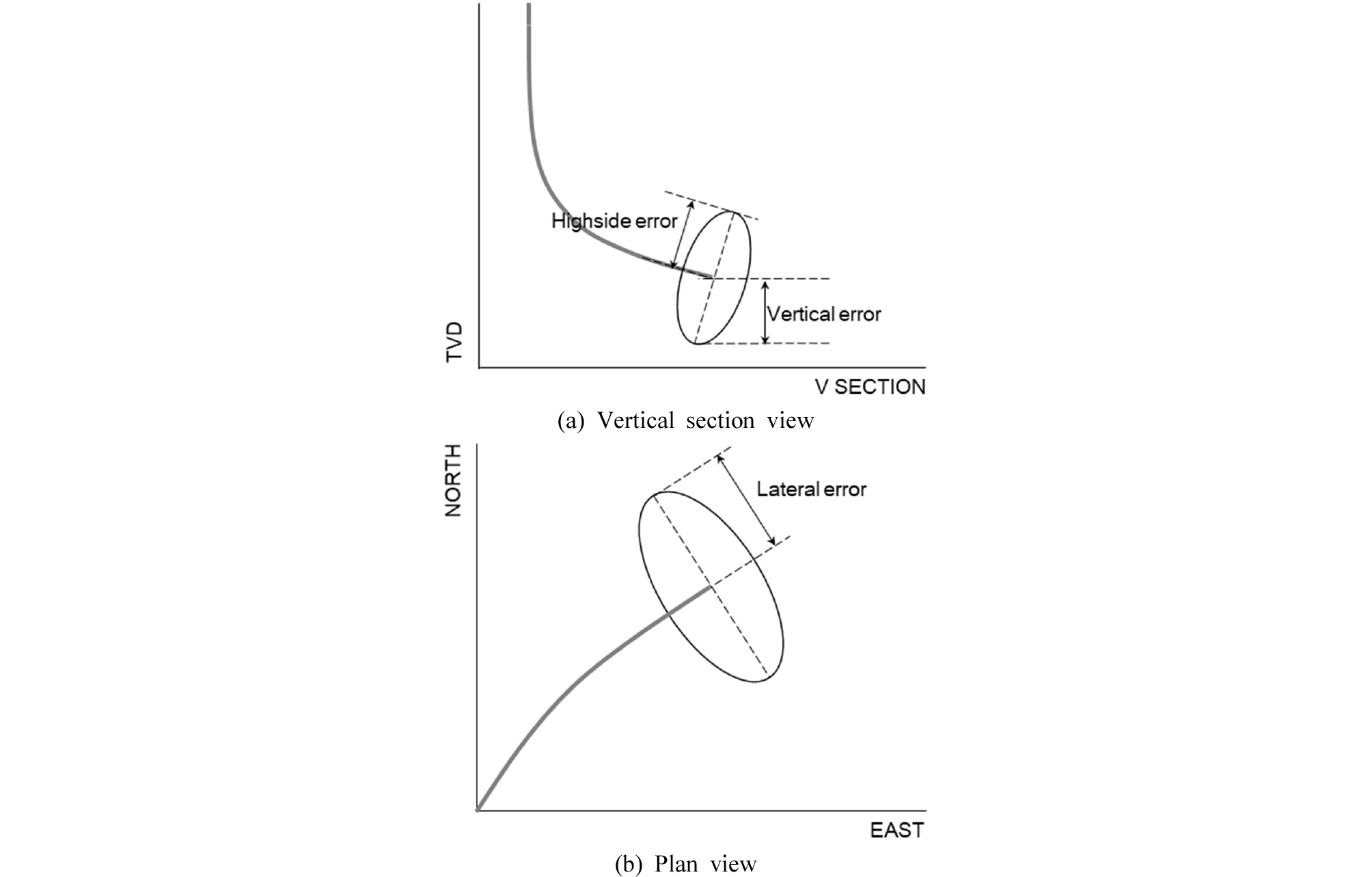
시추공 위치정보는 측정위치가 갖는 참값과 측정값 사이의 오차가 존재한다. 위치오차는 시추궤도를 기준으로 종방향 오차(highside error), 횡방향 오차(lateral error) 그리고 수직 오차(vertical error)가 나뉘며 3차원 오차타원체(EOU; Ellipsoid Of Uncertainty)를 이룬다(Fig. 3).
시추스트링과 송신케이블 길이변화
측정깊이를 결정하는 과정에서 시추스트링이나 송신케이블은 시추공 내부에 작용하는 부력, 마찰력, 온도 등의 영향으로 깊이변화가 발생한다. 측정깊이의 오차는 횡방향 오차와 수직 오차를 유발하며 대표적인 보정은 탄성 보정(elastic stretch correction)과 열팽창 보정(thermal expansion correction)이다.
위치측정기 기울어짐
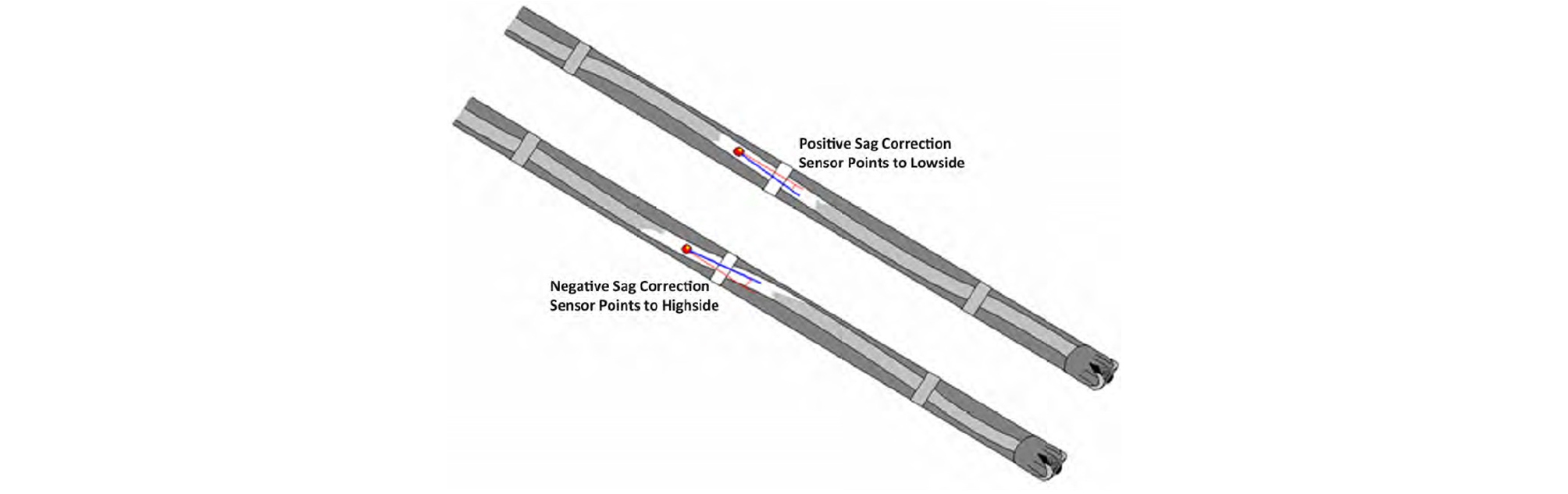
시추공저장비는 원활한 방향제어하고자 안정기(stabilizer)를 사용한다. 이 과정에서 안정기 사이에 위치한 위치측정기는 시추공저장비에 작용하는 측력에 의해 시추공 방향과 일치하지 않고 기울어진다(Fig. 4). 기울어짐의 크기는 안정기와 위치측정기의 거리와 경사각에 따라 결정되며 종방향 오차와 수직 오차를 초래한다. 따라서 정확한 수직심도를 예측하려면 기울어짐 보정(sag correction)이 요구된다.
자기장 모델
지구자기장은 시간에 따른 영년변화(secular variation), 지각내부의 자성물질에 의한 지각변화(crustal variation) 그리고 자기폭풍 등 일시적으로 발생하는 일변화(diurnal variation)로 자침 편차의 오차가 발생한다. 지구자기장의 영년변화는 5년마다 개정하는 WMM(World Magnetic Model)과 IGRF(International Geomagnetic Reference Field), 1년마다 개정하는 BGGM(British Global Geomagnetism Model)이 있는데 시추공 위치측정에는 BGGM을 주로 사용한다. 하지만 BGGM은 지각변화 및 일변화에 따른 자기장 보정이 불가함으로 지각변화가 예상되는 지역은 IFR (In-Field Referencing)을 사용하고, 일변화가 발생하는 지역은 IIFR(Interpolated In-Field Referencing)을 적용한다(British Geological Survey, 2020).
시추스트링 자기간섭
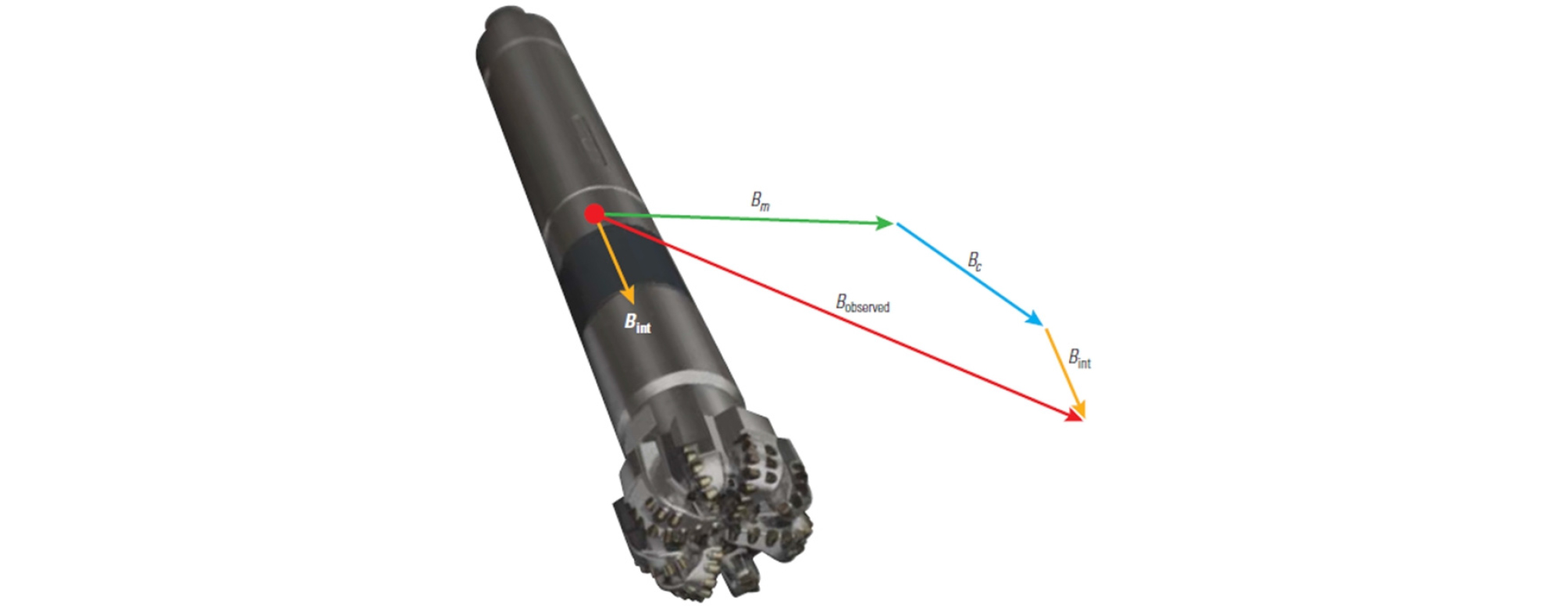
자기계측기는 방위각 측정과정에서 시추스트링, 외부케이싱, 자성물질을 함유한 지층과 시추이수 등으로 지구자기장을 국부적으로 왜곡시킨다(Fig. 5). 이러한 자기간섭은 횡방향 오차를 야기함으로 자기계측기를 비자성 시추칼라(NMDC; Non-Magnetic Drill-Collar) 내부에 위치하거나, 축 보정(axial correction)과 MSA(Multi-Station Analysis) 보정으로 최소화한다(Grindrod and Wolff, 1983; Williamson, 1999; Nyrnes et al., 2009).
위치측정간격
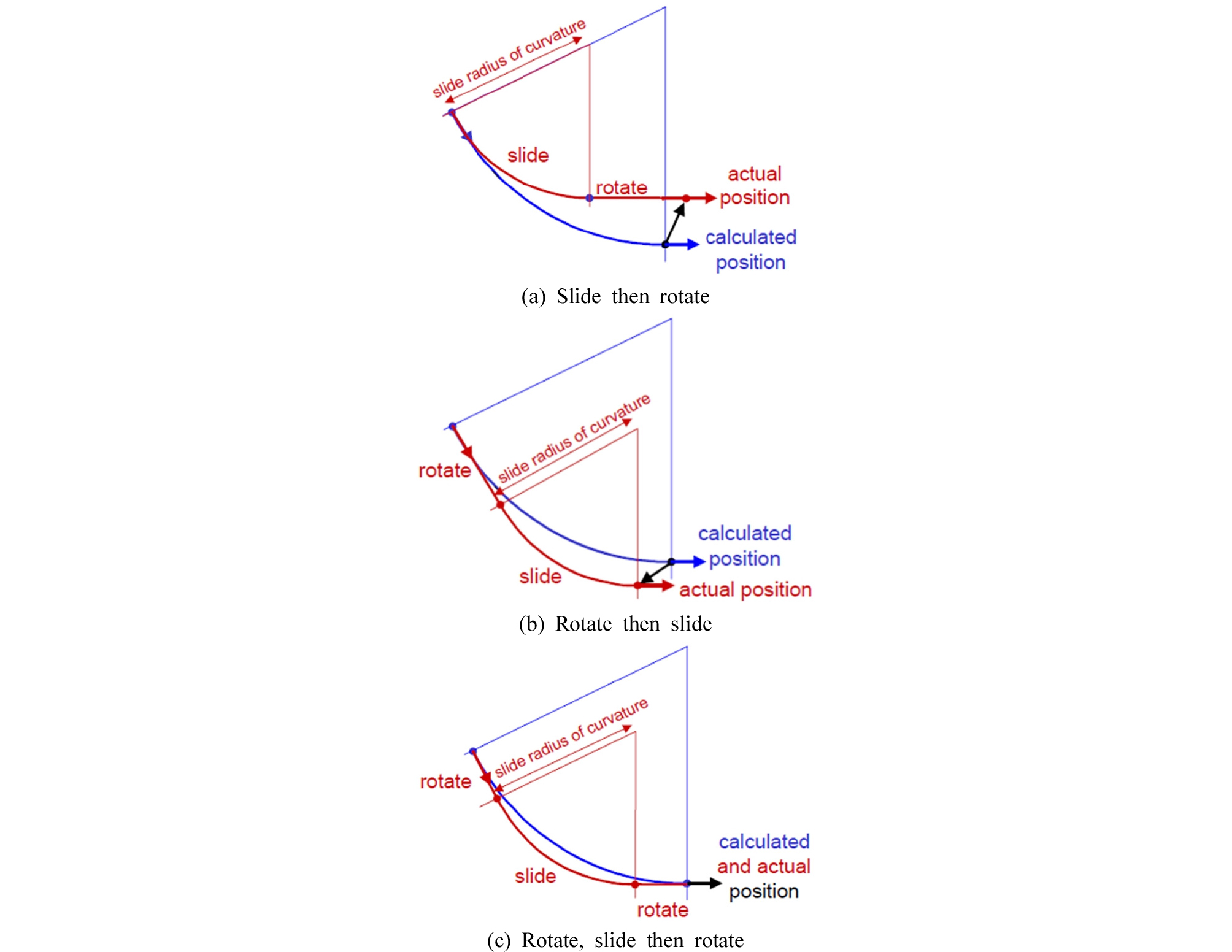
시추공 위치측정은 시추리그의 TDS(Top-Drive System) 도입으로 시추파이프를 교체하는 약 30m 간격의 고정적 위치측정(stationary survey)이며 최소곡률법으로 시추공 위치를 예측한다. 하지만 최소곡률법은 두 지점을 원호(circular arc)로 연결한다는 가정 하에 계산함으로 Fig. 6과 같이 굴착 패턴에 따라 두 지점의 측정깊이, 경사각, 방위각은 같지만 수직깊이와 수평거리의 차이가 발생한다. 이러한 측정간격에 따른 오차는 굴착 패턴을 조정하거나 연속적 위치측정(continuous survey)으로 최소화하며 최근에는 스플라인 곡선(advanced spline-curve) 위치계산법도 소개되었다(Mahmoud et al., 2016).
시추공 충돌방지
시추공 거리분석
방향성 시추기술의 발전으로 복잡한 시추궤도의 굴착이 가능해지면서 시추공 밀집도가 높은 플랫폼 시추(platform drilling), 패드 시추(pad drilling) 및 추가 시추(infill drilling) 등이 증가하고 있다. 그러나 다수의 시추공이 존재하게 되면 시추공 충돌위험이 크다. 따라서 시추공 충돌방지(anti-collision)를 위해서 계획한 시추공과 인접 시추공과의 거리를 정확히 분석해야 한다(Poedjono et al., 2009; Sawaryn, 2017).
시추공 위치오차를 고려한 두 시추공의 거리는 식 (6)과 같이 분리계수(separation factor)로 분석한다.
| $$Separation\;Factor=\frac{CCD}{R1+R2}$$ | (6) |
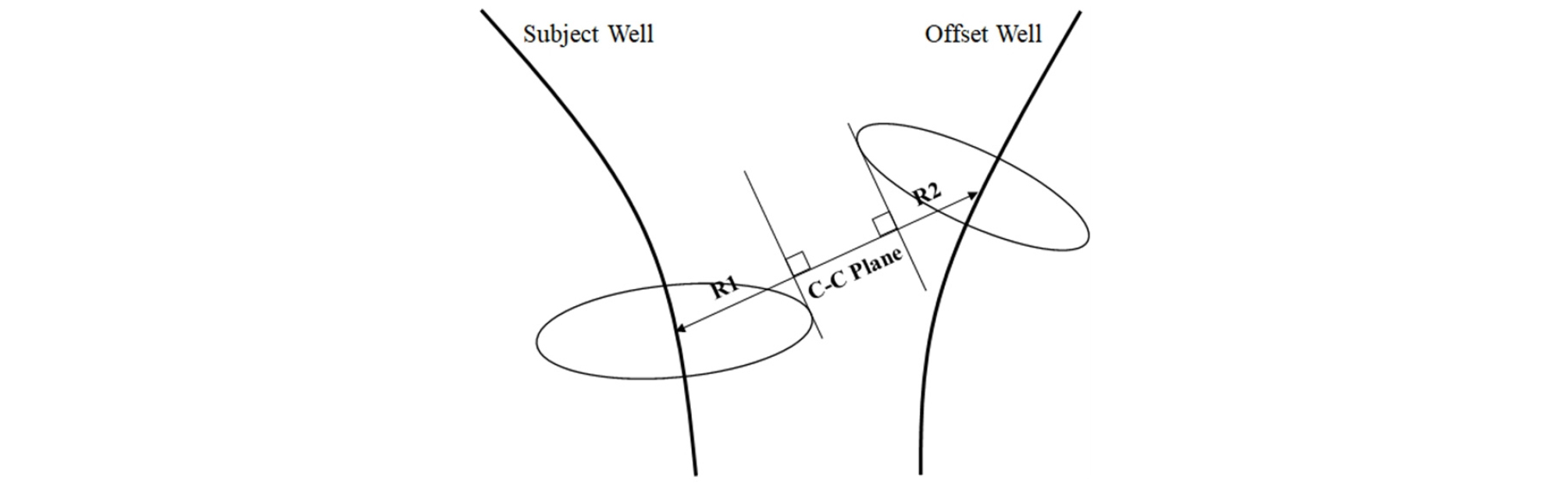
여기서, (Center to Center Distance)는 두 시추공의 중심거리로 3차원 최접근법(3D closest approach)으로 예측하고, 과 는 ISCWSA 모델로 계산된 오차크기를 Fig. 7과 같이 수족곡선법(pedal curve method)으로 계산한 거리이다(Sawaryn et al., 2017; Jamieson, 2017).
시추공 충돌방지 관리
시추공 충돌은 설계 단계와 굴착 단계로 구분하여 방지한다. 굴착 전에는 분리계수를 안전율을 고려하여 1.5 이상으로 설계하며 굴착 중에는 Table 3과 같이 분리계수에 따라 조치한다. 즉 분리계수가 1.5 이하이면 인접 시추공을 폐쇄하고, 분리계수가 1.0 이하이면 시추공 폐공 후 사이드트랙으로 시추공 충돌을 예방한다.
Table 3. Typical anti-collision monitoring criteria
연구 결과 및 해석
이 연구에 설계된 시추공은 비전통자원 개발에 주로 적용되는 수평 시추로 시추공 밀집도가 높은 다중 시추공을 모사하였다. 분석에 사용된 입력 자료는 Table 4와 같고 할리버튼사에서 개발한 상업용 소프트웨어인 COMPASS를 이용하여 시추공 위치오차를 산출하였다. 분석은 단일 시추공으로 시추공 위치오차와 보정 결과를 살펴보고 다중 시추공으로 시추공 충돌위험을 검토하였다.
Table 4. Input parameters
단일 시추공 위치오차와 보정
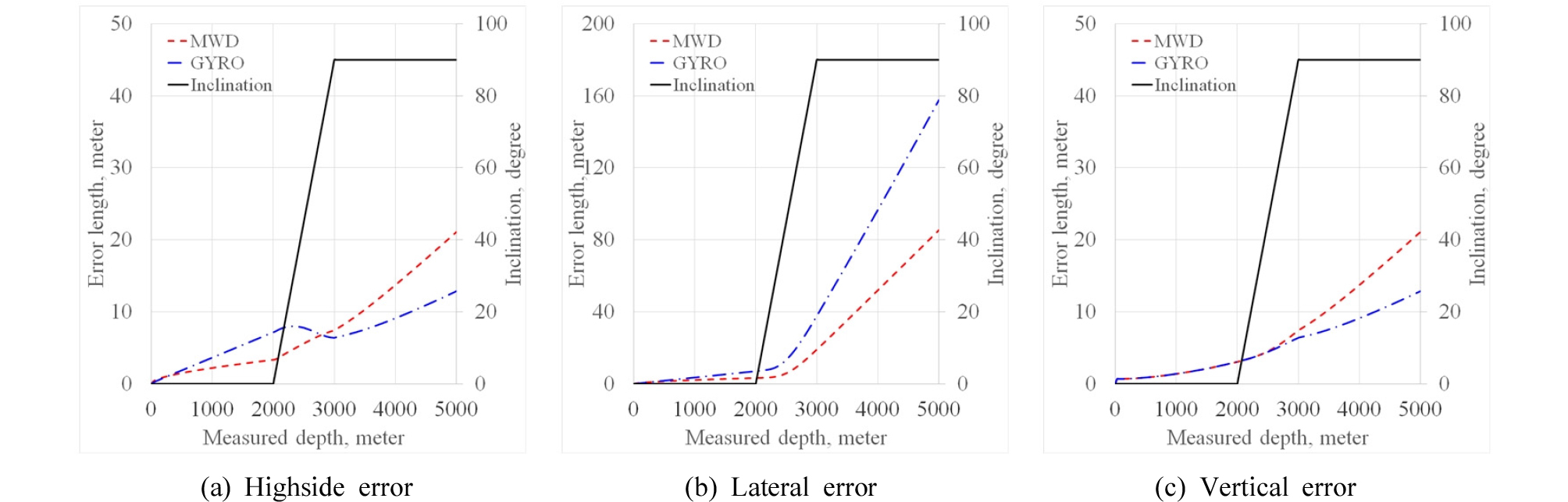
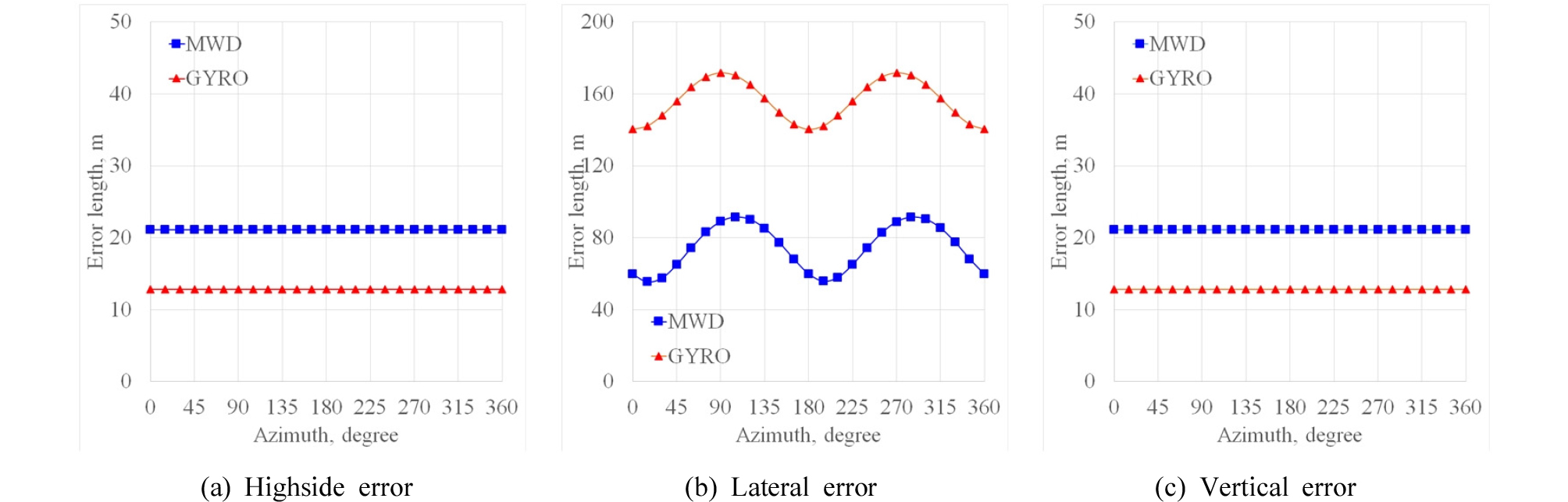
시추공 위치측정기에 따른 오차를 살펴보고자 시추현장에서 사용하는 전자식 MWD와 GYRO를 비교하였다(Fig. 8). 종방향 오차는 수직구간에서 GYRO가 MWD보다 크다가 경사구간에서 같아지며 수평구간에서 MWD가 GYRO보다 커진다. 횡방향 오차는 GYRO가 MWD보다 크며 경사구간과 수평구간에서 급격한 차이를 보인다. 수직 오차는 수직구간에서는 같으나 경사구간과 수평구간에서 MWD가 GYRO보다 커진다.
시추공 방위각에 따른 오차는 Fig. 9와 같다. 종방향 오차와 수직 오차는 최종심도에서 방위각과 무관하게 일정하며 GYRO가 MWD보다 약 39% 감소한다. 그러나 횡방향 오차는 방위각에 따라 사인곡선을 보이며 GYRO가 MWD보다 약 83-157% 증가한다.
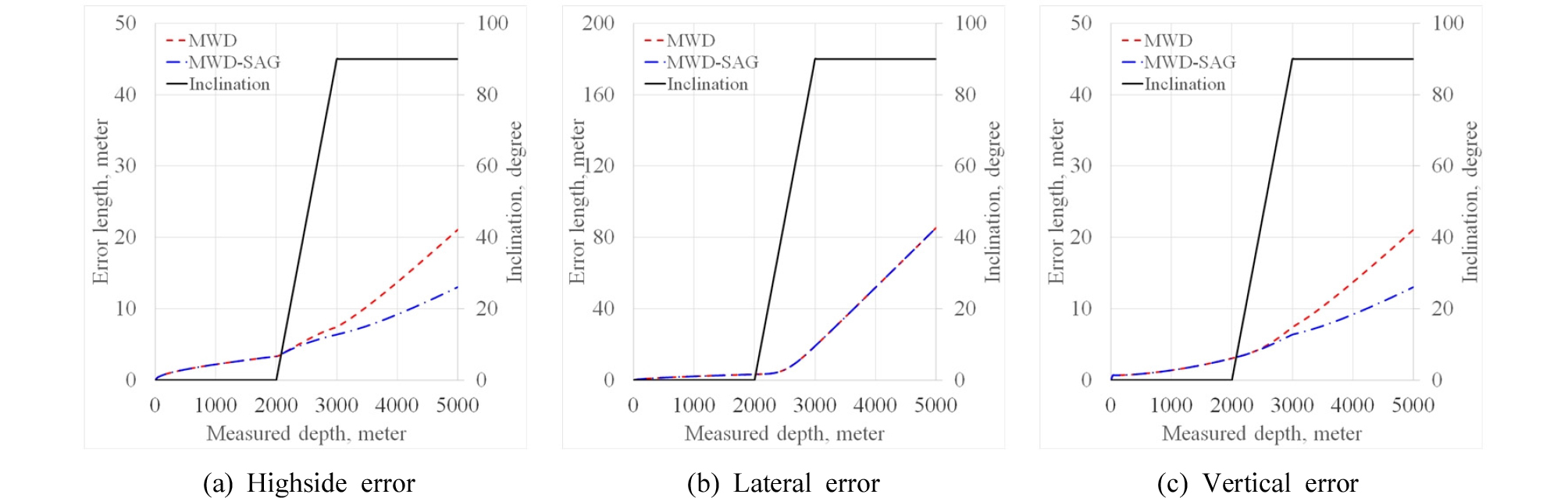
위치측정기 기울어짐에 따른 종방향 오차와 수직 오차는 경사각 10˚부터 증가하며 기울어짐 보정결과 최종심도에서 약 38% 감소한다. 그러나 횡방향 오차는 보정에 영향을 받지 않는다(Fig. 10).
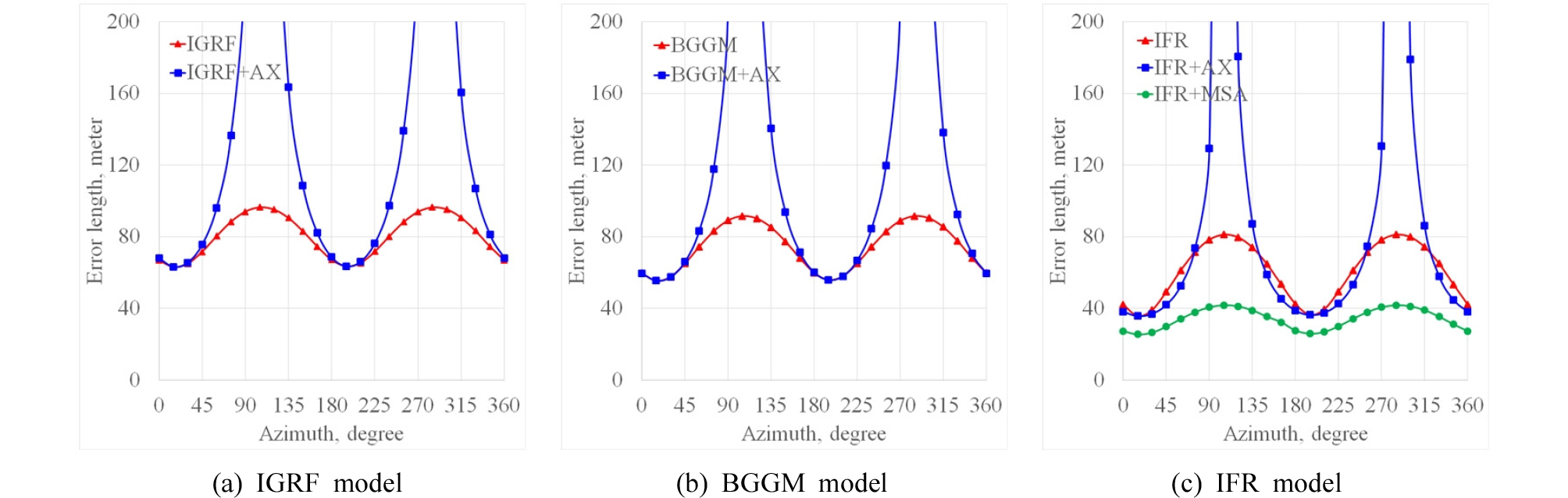
자기장 모델과 시추스트링 자기간섭의 오차와 보정은 Fig. 11와 같다. 자기장 모델에 따른 횡방향 오차는 BGGM을 기준으로 IGRF는 약 5-14% 증가하고 IFR은 약 11-36% 감소한다. 시추스트링 자기간섭에 따른 오차와 보정결과는 각 자기장 모델에 축 보정과 MSA 보정을 적용하였다. 축 보정은 모든 자기장 모델에서 동서방향 60˚-120˚, 240˚-300˚ 방위각일 때 축 보정 이전보다 횡방향 오차가 커진다. 그러나 MSA 보정은 지구자중과 지구자기장 정보를 이용하여 IFR 모델에서만 적용가능하며 횡방향 오차는 BGGM 대비 약 54% 감소한다.
다중 시추공 위치오차와 보정
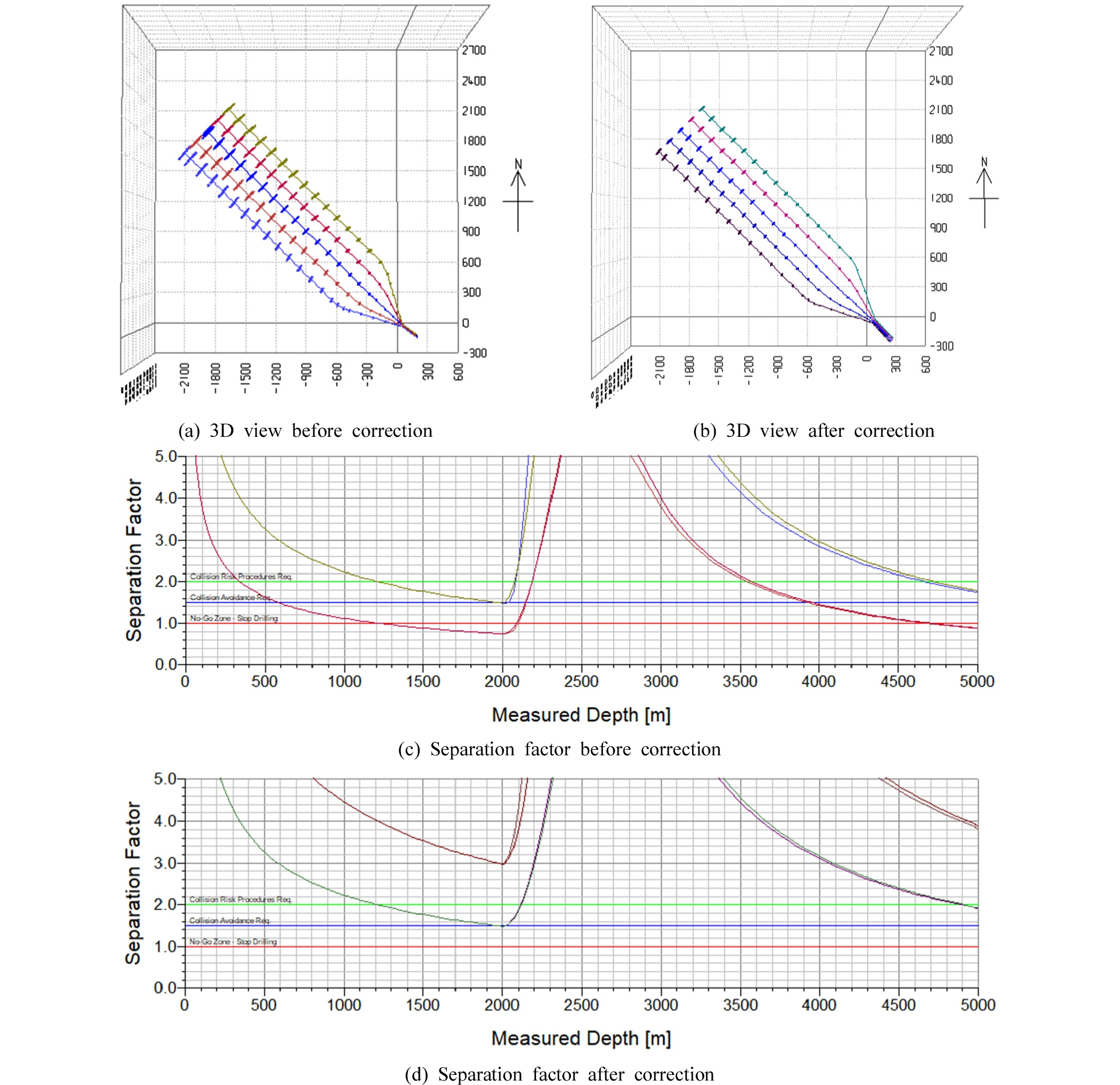
다중 시추공의 위치오차와 보정으로 시추공 충돌위험을 검토하였다. Fig. 12(a)은 보정 이전 시추공으로 BGGM 자기장 모델만을 적용하였으며, Fig 12(b)은 IFR 자기장 모델과 위치측정기 기울어짐 보정 및 MSA 보정을 적용하였다. 보정 이전 시추공은 600m에서 인접 시추공과의 분리계수가 1.5 이하로 낮아지며 1,200m에서 분리계수는 1.0 이하로 1차 시추공 충돌이 예상된다. 그리고 경사구간을 지나 측정심도 4,000mMD(수평구간 1,000m)에서 분리계수가 1.5 이하로 낮아지며 측정심도 4,700mMD에서 2차 시추공 충돌이 예상된다(Fig. 12(c)). 그러나 보정 이후 시추공은 킥오프 지점 2,000m에서만 분리계수가 1.5로 예상되고 전 구간에서 시추공 충돌위험은 없다(Fig. 12(d)).
결 론
이 논문에서는 방향성 시추에서 필수적인 시추공 위치측정, 위치오차와 보정을 단일 및 다중 시추공으로 분석하였다.
시추공 위치측정은 계획한 시추궤도에 맞춰 굴착하면서 시추공 위치를 파악하기 위해 위치자료를 취득하는 일련의 과정이다. 그러나 시추공 위치정보는 측정과정에서 오차가 존재한다. 대표적인 오차는 시추시트링과 송신케이블 길이변화, 위치측정기 기울어짐, 자기장 모델 오차, 시추스트링 자기간섭 그리고 위치측정간격이다.
단일 시추공으로 살펴본 시추공 위치오차는 위치측정기와 시추궤도에 따라 오차 성분별 차이를 보인다. 시추공 경사각이 증가함에 따라 자기계측기의 수직 오차는 자이로계측기보다 크지만 횡방향 오차는 자이로계측기가 자기계측기보다 크다. 또한 시추공 방위각에 따라 수직 오차에는 영향을 주지 않지만 횡방향 오차는 동서방향 60˚-120˚, 240˚-300˚ 방위각에서 커진다. 위치측정기 기울어짐 보정은 수직 오차를 개선하는 효과가 있으며, 자기장 모델은 지각변화를 포함한 IFR를 적용할 시 횡방향 오차가 감소한다. 시추스트링 자기간섭 최소화를 위한 축 보정은 영년변화만을 예측하는 IGRF와 BGGM에서 보정효과가 없으며 동서방향 60˚-120˚, 240˚-300˚ 방위각에서 오차가 커진다. 그러나 MSA 보정은 IFR의 중력과 지구자기장 정보를 이용함으로 보정효과가 높다.
다중 시추공으로 살펴본 시추공 위치오차는 보정 이전 시추공 충돌이 예상되었으나, IFR 자기장 모델, 위치측정기 기울어짐 보정 그리고 MSA 보정을 적용한 결과 시추공 충돌을 예방할 수 있었다.
이 논문에서 살펴본 시추공 위치오차와 보정은 향후 목적한 저류층의 굴착, 인접 시추공과의 충돌방지 및 유정폭발정의 시추공 제어를 위한 구조정 시추 시 적용될 수 있을 것으로 기대된다.