서 론
자력선별은 파분쇄, 비중선별, 정전선별 및 부유선별과 같은 광물처리의 중요한 한 분야로써 오랜 기간 동안 철광석을 비롯한 다양한 자성광물들의 선별 및 회수에 이용되어 왔다. 또한 본 선별법은 자원분야 이외에 식품, 농업, 화학분야 그리고 슬래그, 플라스틱 및 폐전기전자 등의 폐기물처리 분야에도 널리 활용되고 있다(Kelland, 1973; Oka et al., 2018; Jordans et al., 2014; Yang et al., 2018).
자력선별법은 외부에서 주어지는 자력에 대한 물질들 간의 고유한 자화율(magnetic susceptibility)의 차를 이용한 것으로써, 높은 자화율을 갖는 강자성(ferromagnetic) 물질은 자기장(magnetic field) 내에서 인력에 의해 회수되고 상자성(paramagnetic) 및 반자성(diamagnetic) 물질은 중력, 원심력, 유체의 힘에 의해 제거될 수 있다(Svoboda, 1987). 자력선별법은 수류의 유무에 따라 건식과 습식 자력선별로 대별되는데, 건식법은 미립자 처리시 엉김과 비산에 의한 효율저하의 단점이 있으나 처리가 용이하고 경제성이 높은 장점이 있으며 습식법은 건조과정 등 공정이 복잡하고 처리비용이 크다는 단점이 있으나 선별효율이 우수한 장점을 가지고 있다. 이외에 고구배 자력선별법(high gradient magnetic separation)은 처리용량이 적으나 자력이 매우 강해 점토광물 등 비자성 물질 내 미량의 자성물질 제거에 주로 이용되고 있다(Oberteuffer, 1974; Lee et al., 2018).
국외의 자력선별 연구는 초기에 자력선별 장치고안 및 광물선별효율에 관한 연구가 주를 이루었다(Gaudin and Spedden, 1943; Roe, 1958). 1960~1990년대에 걸쳐 유럽 및 북중미를 중심으로 고구배 자력선별의 이론 및 모델링 연구가 진행되었고 2000년대 이후 중국 등 아시아의 연구자 그룹을 중심으로 고구배 자력선별의 자기장모사, 입자궤적 및 매트릭스 포획구조 등에 대한 이론적 연구가 활발히 이루어지고 있다(Lubosky and Drummond, 1975; Nesset et al., 1981; Svoboda and Fujita, 2003; Luo and Nguyen, 2017; Xue et al., 2019; Zheng et al., 2019). 국내의 경우 최근 자력선별에 대한 전산모사 및 통계/설계의 기초적 연구로써, Choi et al.(2016)이 고순도실리카 정제를 위한 고구배자력선별기의 전산모사 및 변수의 영향조사를, Lee et al.(2015)이 통계적 기법을 이용한 자력선별 설계 및 자성입자 거동연구를 그리고 Lee et al.(2018)이 자력선별기의 유형/분류 및 활용분야에 대한 고찰연구를 일부 수행한 바 있으나 국가과학기술정보센터(NDSL) 검색결과, 2018년까지 자력선별에 관한 연구는 약 80건으로써 대부분 선별공정의 전처리 혹은 조건실험이 주를 이루고 있다(Choi et al., 2016; Lee et al., 2015; Lee et al., 2018; National digital science library, 2019).
이와 같이 국내의 경우, 자력선별법이 다양한 산업에 활용되고 있음에도 불구하고 타 선별법에 비해 이론적 연구는 제한적으로 이루어지고 있다. 특히 건식 자력선별의 메커니즘 및 모델링 연구는 거의 시도되지 않고 있다. 본 연구에서는 건식벨트형 자력선별기를 대상으로 한 모델링 기초연구로써 유한요소분석법을 이용하여 자기장을 모사하고 입자궤적 분석을 통해 자력선별의 주요변수를 평가하고자 하였다.
건식 자력선별 모델링
건식벨트형 자력선별 시 자성입자는 자력(Fm), 중력(Fg), 공기저항(Fd)의 크기 변화에 따라 입자의 거동 상태가 바뀌며 이 때 각 힘은 다음과 같이 구할 수 있다.
| $$\overrightarrow{F_m}=X_m\mu_0V\frac3{2+\mu_r}/\overrightarrow{(F_\nabla})$$ | (1) |
| $$\overrightarrow{F_d}=6\pi\eta rv$$ | (2) |
| $$\overrightarrow{F_g}=mg$$ | (3) |
식 (1)에서 Xm은 자화율, μ0는 진공의 투자율(1.26×10-6 H/m), V는 입자의 부피, μr은 상대 투자율, 는 자기장 세기 H0를 각 방향성분별로 미분한 것으로 H0∇H0 연산을 의미하는 연산자이다. 식 (2)에서 η는 공기의 점성계수, r은 입자의 반경, v는 입자의 이동속도를 의미하고 식 (3)에서 m은 입자의 질량 그리고 g는 중력가속도를 의미한다.
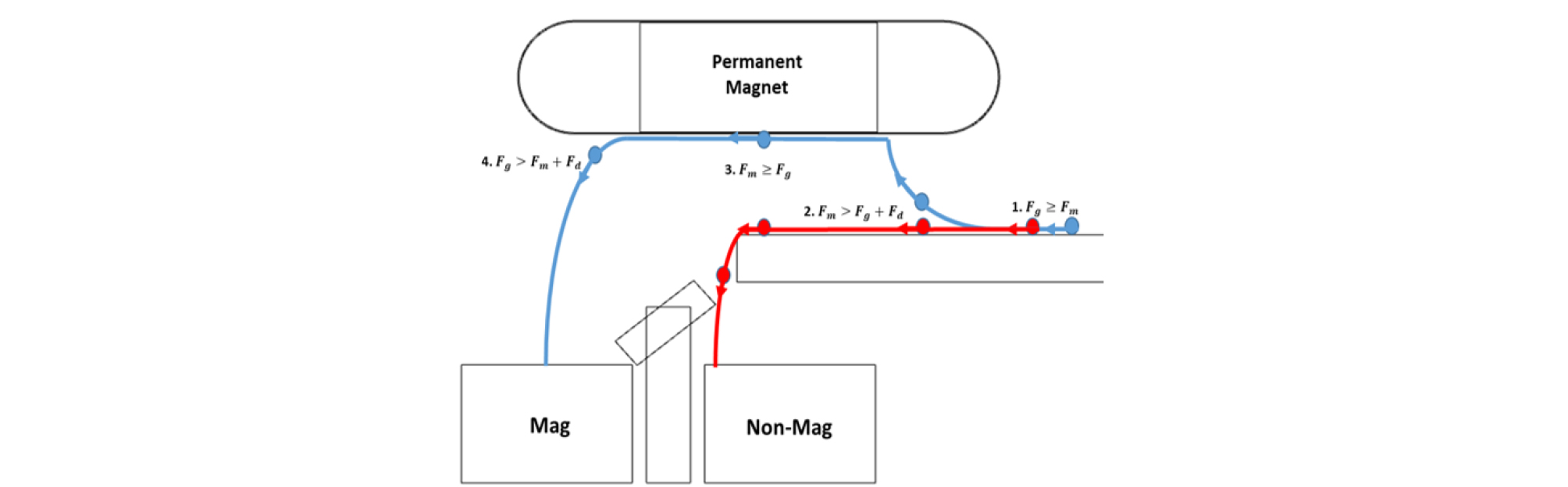
건식벨트형 자력선별시 자성입자의 운동 상태는 Fig. 1과 같이 1) 입자가 전진하고 2) 수직성분 자기력이 중력보다 커 입자가 떠오르기 시작하고 3) 자성입자가 상부자석에 부착된 후 4) 벨트에 의해 영구자석을 벗어나면서 자성입자가 받는 자력이 중력보다 약해지게 되면 상부에 부착된 입자는 낙하하게 된다.
따라서 각 입자들의 운동 상태는 방향 성분별로 다음과 같이 나타낼 수 있다.
1) 이송판으로부터 입자가 떠오르기 시작하는 시점까지 ()
| $$F_x=F_{mx}-F_{dx}$$ | (4) |
| $$F_y=F_{my}-F_g$$ | (5) |
이 때 지표면과 수평힘(Fx)은 수평자력에 대해 마찰력을 뺀 크기이고, 지표면과 수직힘(Fy)은 좌표계에서 +방향 자력에 대해 –방향 중력을 뺀 크기로써, 입자는 –방향 가속도를 받지만 이송판에 의한 수직항력에 의해서 상쇄되어 y축 방향의 이동거리는 없다.
2) 입자가 떠올라 상부 벨트에 붙는 시점까지 ()
| $$F_z=F_{mx}-F_{dx}$$ | (6) |
| $$F_y=F_{my}-F_{g}-F_{dy}$$ | (7) |
이 때 Fx는 식 (5)와 같고 Fy는 +방향 자력에 대해 –방향 중력과 공기저항을 뺀 것으로써, 상부자석의 벨트 높이인 Dmag(이송판과 상부 자석사이의 거리)까지 입자가 +방향으로 움직인다.
3) 부착된 입자가 낙하할 때까지 ()
| $$F_x=F_{mx}-F_{dx}=0(v=v_b)$$ | (8) |
| $$F_y=F_{my}-F_g$$ | (9) |
상부자석에 부착된 입자가 받는 Fx는 수평방향 자기력이 컨베이어 벨트와 입자 사이의 최대정지마찰력을 넘지 못하므로 어떠한 가속도 없다. 따라서 입자는 벨트가 움직이는 속도(vb)로 영구자석으로부터 멀어진다. Fy는 상부자석으로 인한 자력이 매우 커 자력이 중력보다 약해지는 시점까지 입자의 수직 변위는 존재하지 않는다.
4) 상부 자석에서 떨어진 후()
| $$F_x=-F_{mx}-F_{dx}$$ | (10) |
| $$F_y=F_g-F_{my}-F_{dy}$$ | (11) |
자력이 중력보다 점점 작아짐에 따라 입자는 포물선을 그리며 낙하하고 이 때 수평으로 움직이는 속도는 상부 벨트속도(vb)에서 상부자석의 수평 인력과 공기저항으로 인한 속도 감소분을 빼준 것이다. Fy는 중력에 대해 자력과 공기저항을 뺀 것으로 나타낼 수 있다.
본 연구의 궤적모사에서 입자는 완벽한 구형의 단체분리된 자철석과 티탄철석이고 입자 사이의 영향 및 자력은 무시한다는 가정 하에서 수행되었으며 입자궤적 모사에서 입자의 다음위치는 입자의 속도와 가속도의 함수로 방향성분에 따라서 식 (12)~식 (13)과 같이 구할 수 있다.
| $$x_{(i+1)}=x_i+v_x(x_i,y_i)dt+0.5a_x(x_i,y_i)dt^2$$ | (12) |
| $$y_{(i+1)}=y_i+v_y(x_i,y_i)dt+0.5a_y(x_i,y_i)dt^2$$ | (13) |
이 때 입자의 속도 v(xi,yi)는 이전 시점의 입자가 가지는 속도v(xi-1,yi-1)와 가속도a(xi-1,yi-1)를 이용하여 구할 수 있고, 입자의 가속도 a(xi,yi)는 이전 시점 입자에 가해지는 각 힘의 합력을 입자의 질량으로 나누어 구할 수 있다.
| $$v_x(x_i,y_i)=v_x(x_{i-1},y_{i-1})+a_x(x_{i-1},y_{i-1})dt$$ | (14) |
| $$v_y(x_i,y_i)=v_y(x_{i-1},y_{i-1})+a_y(x_{i-1},y_{i-1})dt$$ | (15) |
| $$a_x(x_i,y_i)=\frac{X_m\mu_0v\frac3{(2+\mu_r)}\overrightarrow{F\nabla}(x_{i-1},y_{i-1})-6\pi\eta rv_x(x_{i-1},y_{i-1})}m$$ | (16) |
| $$a_y(x_i,y_i)=\frac{X_m\mu_0v\frac3{(2+\mu_r)}\overrightarrow{F\nabla}(x_{i-1},y_{i-1})-6\pi\eta rv_x(x_{i-1},y_{i-1})}m-g$$ | (17) |
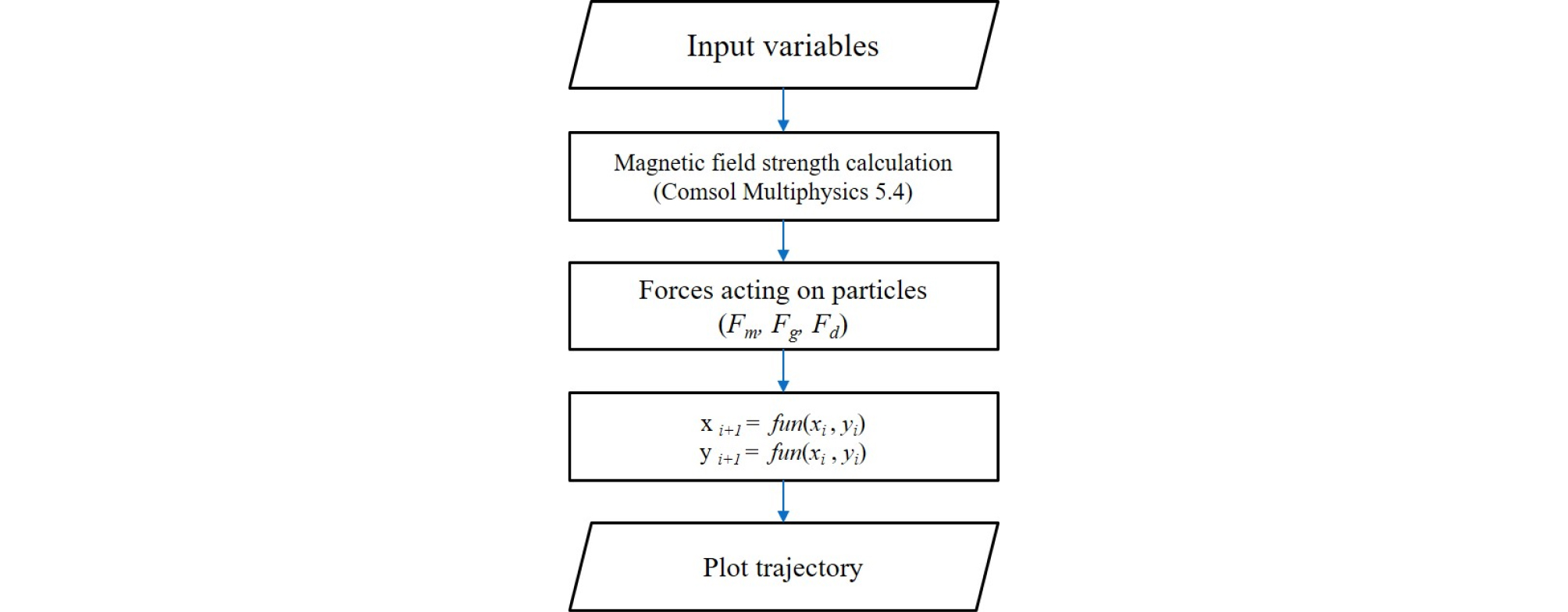
Fig. 2는 건식벨트형 자력선별에서 입자궤적분석의 방법 및 순서를 나타낸 것이다. 입자의 궤적분석 방법은 먼저 입자가 시점에 따라 받는 힘을 계산한 후, 그때의 가속도와 속도를 이용하여 입자가 이동한 궤적을 누적하여 선별 시 입자의 이동 궤적을 계산한 것으로, 앞서 식 (4)에서 식 (11)를 이용하여 입자의 이동궤적을 모사할 수 있다. 프로그램은 변수입력, 자기장계산, 각 힘들의 계산 값 및 데카르트 좌표 상에 각 입자들의 궤적모사로 진행된다.
시료 및 실험방법
시료
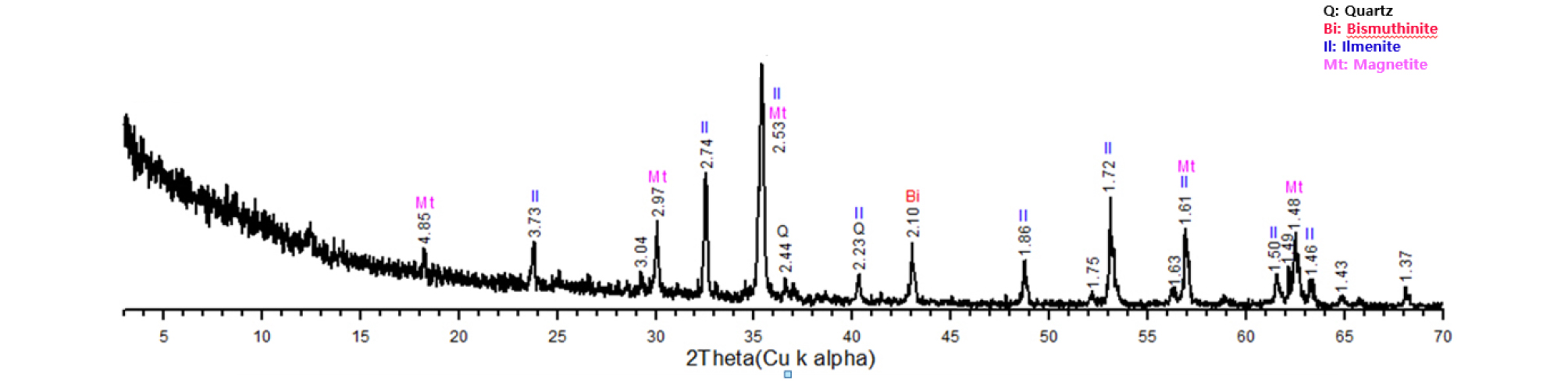
본 연구에 사용된 티탄철석은 경기도 포천시 관인면에 위치한 연천철광으로부터 수급하였다. Fig. 3은 티탄철석 원광의 XRD 분석결과를 나타낸 것으로, 주요 구성 자성광물은 티탄철석(Ilmenite, FeTiO3)과 자철석(Magnetite, Fe3O4) 으로 이루어져 있으며, 비자성광물으로는 석영(Quartz, SiO2), 백운모(Muscovite, K(OHF2)2Al3SiI3O10) 및 휘창연석(Bismuthinite, Bi2S3) 등이 존재하였다. Table 1은 주요 광물들의 물성을 나타낸 것으로써, 자철석은 비중 5.2와 자화도 약 50,000×10-9 m3/kg이며 티탄철석의 경우 비중 4.5~5.0과 자화도 약 200~1500×10-9 m3/kg인 것으로 보고되고 있다(Svoboda.J, 1987).
Table 1. Physical properties of magnetite, ilmenite, and quartz
장치 및 방법
Fig. 4는 본 연구에서 이용한 건식벨트형 자력선별 시스템을 나타낸 것으로, (A)급광기에 투입된 시료는 (B)이송판 위에서 진동기에 의해 이동되고 자성광물은 상부에 위치한 (C)영구자석에 의해 컨베이어벨트에 부착된다. 이후, 자성광물이 벨트에 의해 영구자석으로부터 멀어지면 중력에 의해 낙하하게 된다. 반면 비자성광물은 이송판 끝에서 중력에 의해 자유낙하 하게 되고 결국 자성광물과 비자성광물은 (D)분리대에서 선별이 이루어지게 된다. Table 2는 영구자석과의 이격거리에 따른 자기장세기의 측정결과를 나타낸 것으로, 이격거리가 가까울수록 자기장의 세기가 증가하는 것을 알 수 있다.
Table 2. Magnetic field strength of permanent magnet
| Distance (m) | 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | 0.12 |
| Magnetic field strength (G) | 3,220 | 2,200 | 1,550 | 900 | 600 | 320 |
자기장 모델링은 Comsol multiphysics 5.3a(Comsol Inc.)를 이용하였으며 입자의 궤적모사는 식 (12) ~ 식 (17)을 Microsoft Excel(Microsoft Inc.)에 적용하여 구현되었다. Table 3과 Table 4는 광물 구성비에 따른 입자의 자화율 및 비중 값과 궤적모사시의 조건을 나타낸 것이다. 먼저 Table 3에서와 같이 티탄철석, 자철석 및 석영의 각 구성비는 10% 단위로 변화시켜 65개의 조합을 만들었고 Table 4에서와 같이 각 조합별 입자크기는–60mesh(r : 125µm) +100 mesh(r : 75 µm)의 범위에서 반지름을 10 µm씩 변화시켜 7개의 조합을 그리고 수직 이격거리는 0.05 m에서 0.15 m까지 0.01 m씩 변화시켜 10의 조합을 만들어 총 4,550개의 궤적모사를 구현하였다. 입자 궤적모사의 해석은 입자가 상부벨트에 부착하는 구간과 탈착되는 구간을 구분하여 입자의 운동 상태에 따라 1. 이송판에서 입자가 부상하기 시작하는 위치, 2. 부상한 입자가 상부벨트에 부착되는 위치, 3. 입자가 상부벨트에서 떨어지는 위치 4. 탈착된 입자가 낙하하여 포집상자에 떨어지는 위치로 나누어 확인하였다. 본 자력선별 모델링의 방법은 앞서 언급한 “자력선별 모델링 및 입자궤적 분석”의 장에 보다 자세히 기술되어 있다.
Table 3. Composition ratio and physical properties of particle used in simulation
Table 4. Conditions of particle trajectory analysis
결과 및 토의
자기장모사
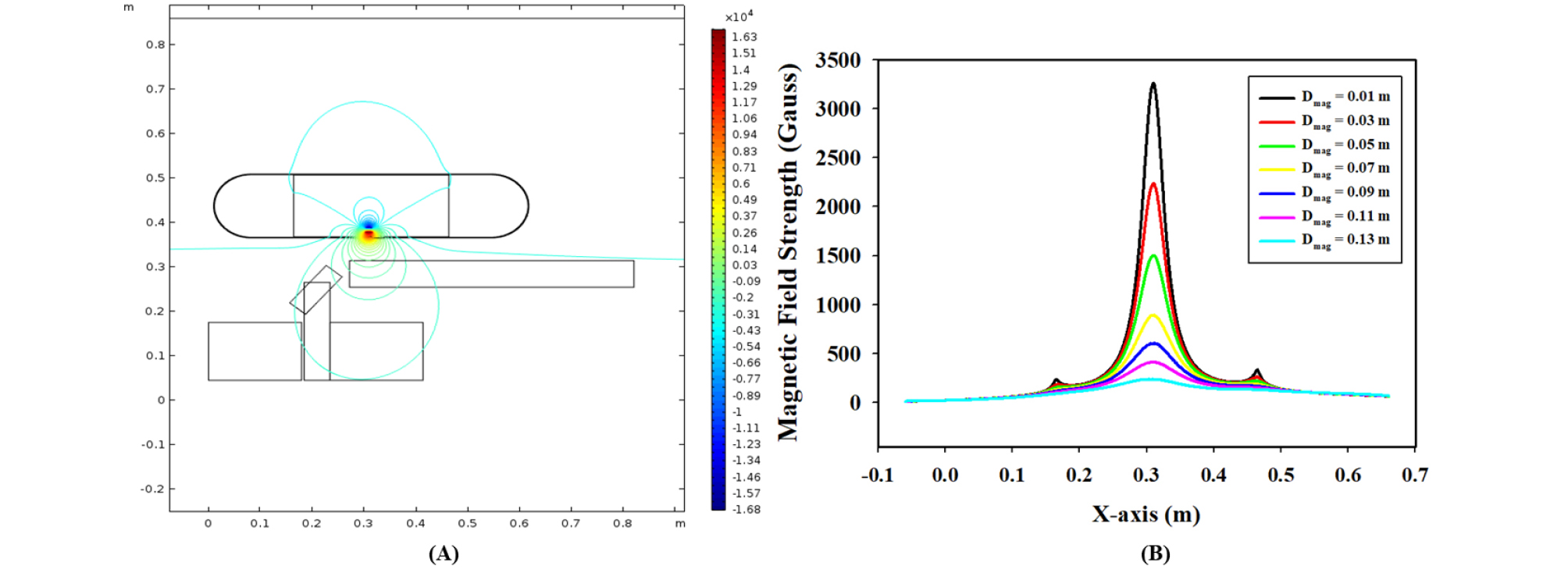
Fig. 5(a)는 Comsol multiphysics 5.3a(Comsol Inc.)와 Table 2를 이용한 건식 자력선별기의 자기장 모사 결과를 나타낸 것이다. 먼저 선별시스템의 실측크기를 재현하였으며 모사도는 자기장세기가 같은 지점을 등선으로 연결하여 도시하였다. 자력선별기 내 영구자석은 지표를 기준으로 상하방향으로 양극이 위치하고 있어 이 부분이 강한 자기장을 형성하고 있음을 알 수 있다. Fig. 5(b)는 모사된 자기장을 자석의 수직 이격거리에 대한 수평위치 변화를 자기장세기 변화와 최대 자기장세기로 표현한 것이다. 자성입자의 거동은 자성입자가 자석에 이끌리기 위해 필요한 최소 자기장과 각 이격거리별 최대 자기장과의 관계에 따라 변하므로 수직 이격거리별 최대 자기장세기는 궤적 모사에서 가장 중요한 요소이다.
자기장 모델링 결과, 이격거리별 최대 자기장 세기는 Table 2에서 측정한 자기장 크기와 같으며, 수직 이격거리에 관계없이 최대 자기장세기는 자석이 위치한 0.31 m 부근에서 형성되었다. 각 자기장 세기는 영구자석 위치(0.31 m)를 기준으로 우측 자기장이 좌측 자기장에 비해 보다 더 강하게 형성되는데 이는 건식벨트형 자력선별기의 이송판(우측) 및 분리대(좌측)의 물리적 성질 및 형상 차이에 의한 것으로 사료된다. 한편 모든 이격거리별 자기장세기 그래프에서 X축 값이 약 0.18과 0.48 m일 때 자기장 피크가 발생하는데, 이 지점은 상부벨트 안 영구자석을 감싸는 철제함의 모서리의 위치로서 그 지점에 자기력이 응집되는 것으로 판단된다.
궤적모사
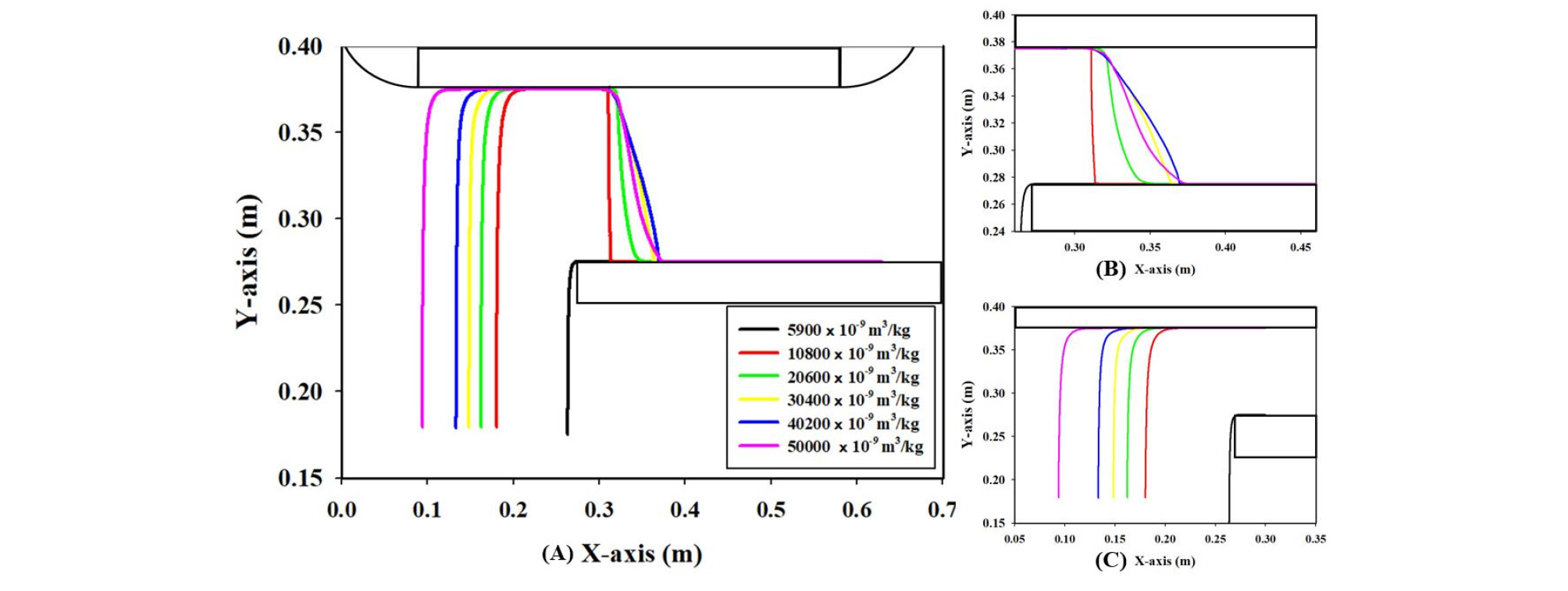
Fig. 6은 입자의 광물 구성비에 따른 입자궤적 모사결과로써, (A)는 전체궤적을 나타낸 것이며, (B)와 (C)는 각각 입자가 상부벨트로 상승 및 부착되는 영역과 탈착 및 낙하하는 영역을 확대한 것이다. 이 때 모사 조건은 입자반경: 0.000075 m, 수직 이격거리: 10 cm(max 450G), 이송판 속도: –0.2 m/s, 상부 벨트속도: –0.2 m/s이었다. 입자궤적 모사결과, 입자 부착단계의 경우 자화율이 큰 입자는 이송판의 초기 시점에서 부상하여 상부벨트에 먼저 부착되고 자화율이 작은 입자는 영구자석과 가까운 지점에서 부착되었다. 한편 자화율이 5,900 × 10-9 m3/kg보다 작은 입자는 자석에 반응하지 않고 이송판 끝에서 자유낙하 하였다. 입자의 탈착단계에서 입자의 탈착위치는 입자의 자화율이 낮을수록 회수대의 안쪽으로 낙하하였다. 광물 구성비에 따른 입자의 궤적은 자화율이 가장 큰 자철석의 비율이 높을수록 이송판 초기 지점에서 상부벨트에 부착되며 자화율이 가장 낮은 석영의 비율이 높을수록 영구자석에 반응하는 경향이 감소하였다.
궤적모사 중 비중의 영향에 있어서 비중이 큰 자철석의 구성 비율이 높을수록 중력의 영향을 많이 받고 비중이 작은 석영의 비율이 높을수록 중력의 영향을 적게 받으나, 광물들 간의 비중에 의한 영향보다 자화율의 차가 더 큰 영향을 미치므로 본 입도크기 범위 내에서 광종간의 비중 차이는 궤적 모사 결과에 큰 영향을 주지 않았다. 즉, Table 3의 No.1~45 조건에서와 같이 자철석의 비율이 20% 이상인 입자는 영구자석의 상부벨트에 부착하여 X축의 0~0.2 m 범위의 회수대로 이동하고 20% 미만에서는 자화율이 낮아 자유낙하 것으로 모사되었다.
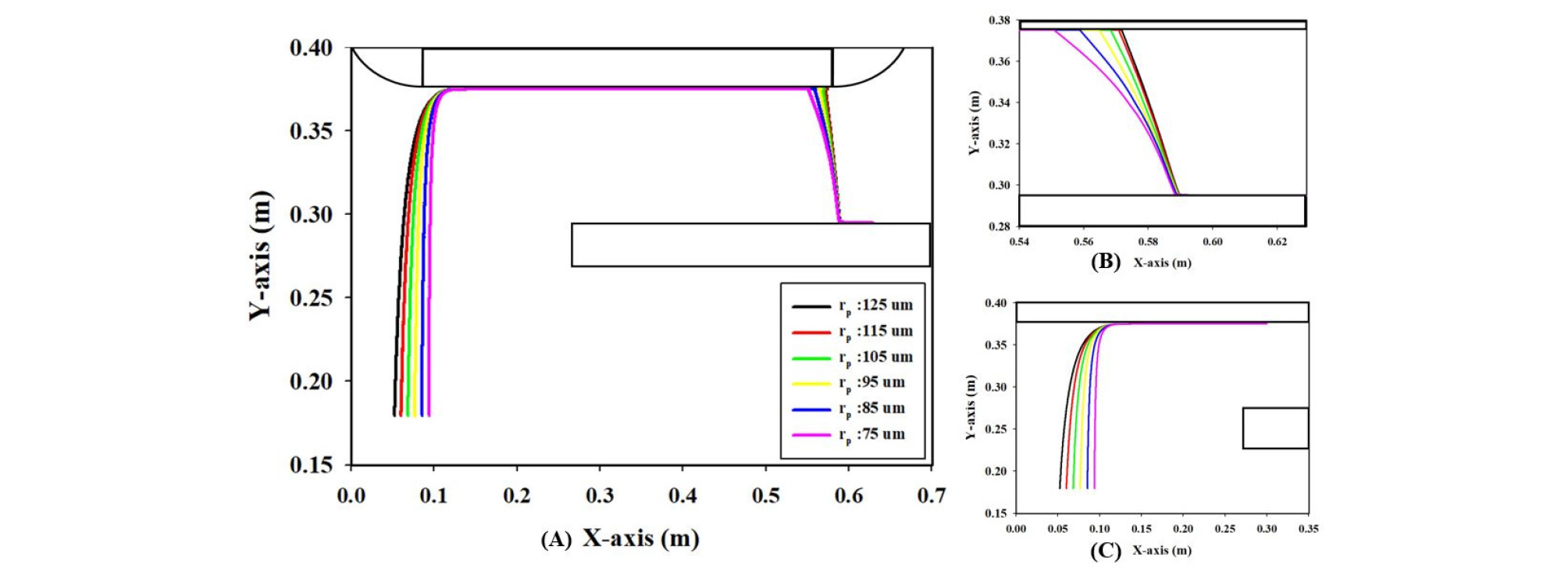
Fig. 7은 입자크기에 따른 입자궤적 모사결과로써, 입도(반경)의 범위를 0.000075~0.000125 m까지 변화시켜 모사한 것이다. Fig. 7(A)는 전체궤적, (B)와 (C)는 각각 입자가 상부벨트로 상승 및 부착되는 영역과 탈착 및 낙하하는 영역을 확대한 것이다. 이 때 모사 조건은 자화율: 50000 × 10-9 m3/kg, 입자비중: 5.2, 수직 이격거리: 8 cm, 이송판 속도: –0.2 m/s, 상부 벨트속도: –0.2 m/s이었다. 입자궤적 모사결과, 입자크기가 커질수록 이송판의 한 지점으로부터 부상하여 영구자석에 부착하는 거리는 감소하였으며 자석벨트로의 탈착지점으로부터 회수대로 낙하하는 거리는 증가하였다. 이는 식 (1)~식 (3), 식 (7)에서 보는 바와 같이 입자의 크기가 증가할수록 자기력, 중력 및 항력이 모두 증가하지만 자력의 영향이 더 커지지 때문으로, 식 (7)을 식 (1)~식 (3)으로 다시 정리하면 다음과 같이 나타낼 수 있다.
| $$F_y=X_m\mu_0V\frac3{2+\mu_r}/\overrightarrow{(F_\nabla})-\rho Vg-6\pi\eta v\frac V{r^2}$$ | (18) |
| $$F_y=\left\{X_m\mu_0V\frac3{2+\mu_r}/\overrightarrow{(F_\nabla})-\rho g-6\pi\eta v\frac V{r^2}\right\}V$$ | (19) |
여기서 자화율 및 투자율 등은 입자 운동 시 변하지 않는 변수이므로, 이들을 미지상수 A, B, C로 간략화하면 다음과 같이 나타낼 수 있다.
| $$F_y=\left\{A/(H_0\nabla H_0)-B-C\times\frac1{r^2}v\right\}V$$ | (20) |
이는 같은 입자에 작용하는 수직힘의 경우, 입자 위치에 따라 바뀌는 자기장과 입자가 받는 힘에 따라 변하는 입자 속도 외에 다른 요소는 변하지 않으므로 자기장의 변화가 가장 큰 영향을 미치게 된다. 떠오른 상태의 입자가 받는 수직힘은 상기 식에 의해 입자가 커질수록 증가하므로 더 빨리 부상하게 되고 이에 따라 자기장 세기 또한 빠르게 증가하므로 큰 입자일수록 더 작은 궤적으로 부상하게 된다. 단 본 연구의 입도범위 0.000075~0.000125 m에서는 입자의 부상위치가 유사하였으나 보다 더 넓은 입도범위에서는 입자의 부상위치의 차이가 생기므로 입자 크기에 따른 궤적의 결과도 달리질 것으로 판단된다.
회귀식도출
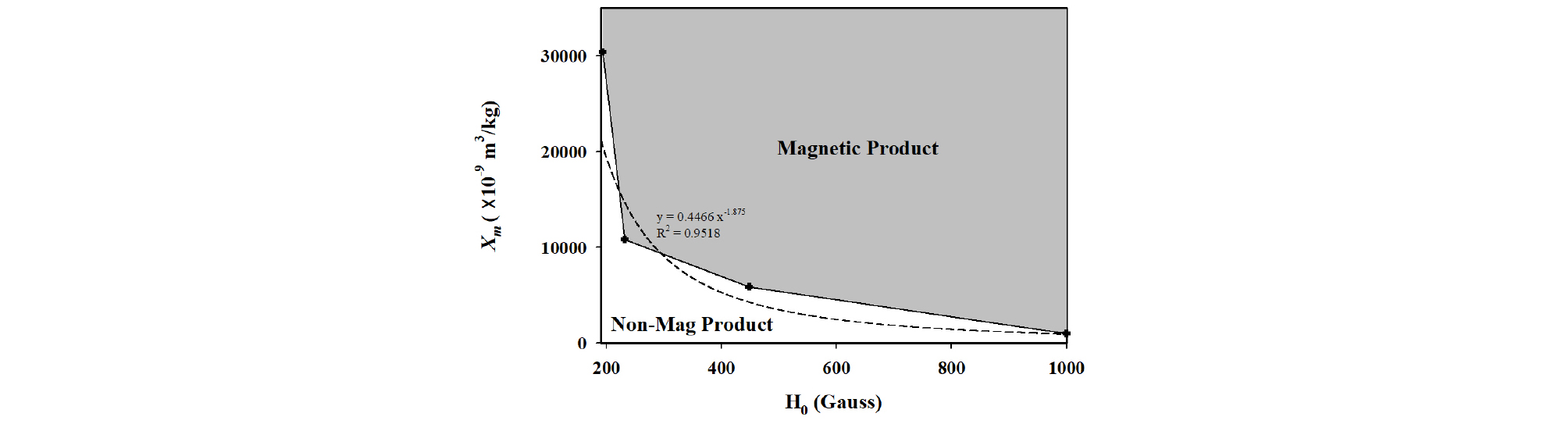
Fig. 8은 건식자력선별기의 자기장 세기와 입자들의 자화율과의 관계에 따른 자력선별 모델링 결과를 나타낸 것으로써 Table 3과 4의 조건하에서 모사된 전체결과를 자성산물과 비자성산물로 구분하여 나타내었다. 각 점은 각기 다른 자화율을 가진 입자가 궤적 모사 시 자석에 부착될 수 있는 자기장 세기를 나타낸 것으로, 그래프의 위쪽은 자성산물을 그리고 아래쪽은 비자성산물로 선별될 수 있음을 나타내고 있다.
건식벨트형 자력선별에서 입자의 자화율과 자기장 세기의 관계를 다음과 같은 회귀식으로 도출할 수 있다.
| $$X_m=0.4466\;H_0^{-1.875}$$ | (21) |
이를 다시 정리하면, 건식벨트형 자력선별기내에서 자화율 Xm를 갖는 입자가 자성산물로 회수되기 위한 최소 자기장 세기(H0)는 다음과 같이 구할 수 있다.
| $$H_0=^{-1.875}\sqrt{\frac{X_m}{0.4466}}$$ | (22) |
따라서 상기의 (21)식을 이용하여 본 연구에서 사용한 건식벨트형 자력선별기내에서 자성산물을 회수하기 위한 영구자석과 이송판사이의 수직 이격거리에 따른 자기장세기와 입자의 자화율의 관계는 Table 5와 같이 나타낼 수 있다.
Table 5. Magnetic susceptibility vs. magnetic field strength by vertical distance
| Distance (m) | 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | 0.12 |
| Magnetic field strength (G) | 3220 | 2200 | 1550 | 900 | 600 | 320 |
| Magnetic Susceptibility (×10-9 m3/kg) | 118.2 | 241.5 | 465.6 | 1290.4 | 2759.8 | 8969.4 |
궤적분석
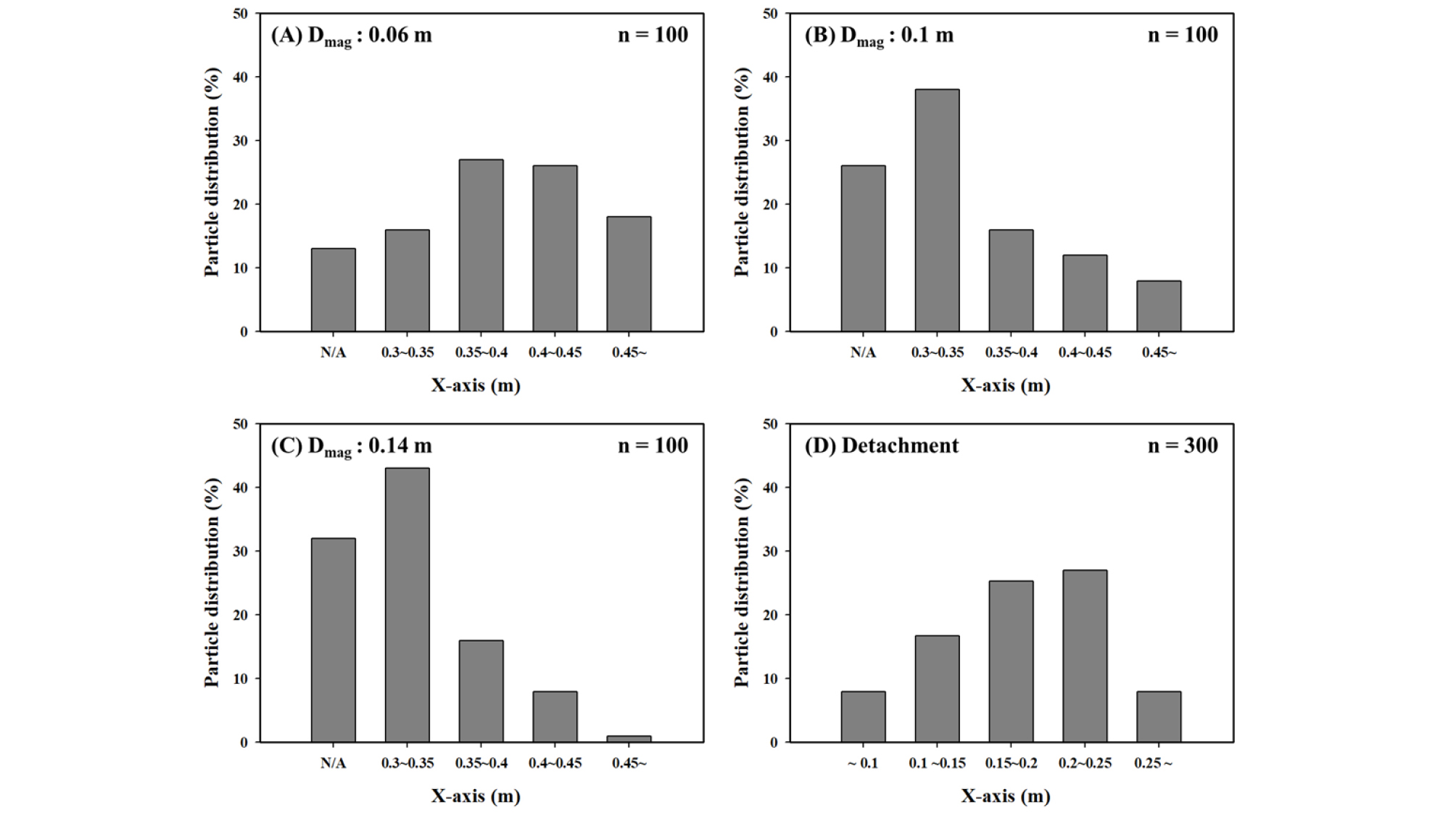
Fig. 9는 앞서 Fig 8에서와 같이 자화율 변화에 따라 선별구간이 바뀌는 것으로 확인된 세 지점 Dmag = 0.06 m(Max 1000G), Dmag = 0.1 m(Max 445G)과 Dmag = 0.14 m(Max 270G)에서 단일입자에 대한 자력선별 관찰결과를 나타낸 것이다. 이 때 n은 구간별 관찰 횟수로 각 조건별로 입자거동을 100회 관찰하였으며 부상하는 구간과 낙하하는 구간으로 구분한 후, 각 개별 입자의 부상위치와 낙하위치의 분포로 표현하였다. X축의 N/A는 입자가 부상하지 못하고 이송판 끝에서 낙하한 입자분포이며 나머지 구간은 앞선 Fig. 6과 7에서와 같은 좌표를 나타낸다.
관찰 결과, 부상구간은 이격거리가 멀어질수록 즉 자기장이 약해질수록 부착되지 못한 입자들이 늘어나고, 많은 입자가 자석의 중심과 가까워지는 0.31 m 부근에서 상부 벨트에 부착되는 것을 확인 할 수 있었다. 낙하구간의 경우, 이송판이 끝나는 지점인 0.275 m와 0.25 m 사이에 낙하한 입자들은 대부분 자석에 부착되지 못한 비자성 입자들을 나타내며 0.25 m 지점보다 더 멀리(바깥쪽으로) 떨어진 입자들은 자성 입자로서, 일단 자석에 부착되면 수직 이격거리에 상관없이 입자의 물성에 따라 낙하위치가 결정되었다. 또한 동일한 단일입자의 수직 이격거리변화에 따른 관찰결과, 수직 이격거리가 가까울수록 자석으로부터 더 먼 곳에서 부착되었고 이격거리와 관계없이 상부벨트에서 탈착 및 낙하하는 궤적과 모사궤적이 유사한 결과를 나타내었다.
결 론
본 연구에서는 건식벨트형 자력선별기의 자기장 및 입자궤적을 모사하고 자력선별의 주요 인자를 평가하였다. 건식벨트형 자력선별기의 자기장은 Comsol multiphysics 5.3a에 의해 계산 및 모사되었다. 수직 이격거리는 자기장세기에 영향을 미치는 중요한 인자이었으며 최대 자기장세기는 자석이 위치한 0.31 m 부근에서 형성되었다. 본 자력선별시스템에서 입자궤적모사는 자기장세기, 입자크기 그리고 입자의 비중과 자화율에 영향을 미치는 단체분리도에 따라 수행되었다. 먼저 광물 구성비에 따른 입자의 궤적은 자화율이 가장 큰 자철석의 비율이 높을수록 이송판 초기 지점에서 상부벨트에 부착되며 자화율이 가장 작은 석영의 비율이 높을수록 영구자석에 반응하는 경향이 감소하였다. 또한 궤적모사에서 광물간의 비중차 보다 자화율의 차가 더 큰 영향을 미치므로 본 입도크기 범위 내에서 광종간의 비중 차이는 궤적 모사 결과에 큰 영향을 주지 않았다. 입자 크기의 경우, 본 연구에서 적용한 미립 입도에서는 큰 입자가 작은 입자에 비해 더 짧은 궤적을 이동하여 상부 벨트에 부착되는 경향을 보였으나 대부분의 조건에서 입자크기와 상관없이 선별결과는 일정하였다. 주요인자는 자화율과 자기장의 세기이었고 입자크기와 비중의 영향은 크지 않았다. 따라서 자철석과 티탄철석과 같은 자성입자가 자성산물로 선별되기 위한 최소 자기장의 세기는 자화율과 자기장의 사이의 회귀식(22)에 의해 구할 수 있었다.