Development of an Integrated Simulator for Coupled Flow,  Geomechanics,  and Geophysics Based on Sequential Approaches

Sangcheol Yoon; Evan Schankee Um; Jihoon Kim

doi:10.32390/ksmer.2020.57.3.309

Preview

General Remarks

Journal of the Korean Society of Mineral and Energy Resources Engineers. 30 June 2020. 309-317
https://doi.org/10.32390/ksmer.2020.57.3.309

Development of an Integrated Simulator for Coupled Flow, Geomechanics, and Geophysics Based on Sequential Approaches

순차적 수치 해석법에 기반한 유체유동, 지반역학, 지구물리학의 통합 전산모델 개발

Sangcheol Yoon¹

Evan Schankee Um²

Jihoon Kim¹^*

윤 상철¹

엄 찬기²

김 지훈¹^*

¹Harold Vance Department of Petroleum Engineering, Texas A&M University

²Earth and Environmental Sciences, Lawrence Berkeley National Laboratory

¹텍사스 A&M 대학교 석유공학과

²로렌스 버클리 국립연구소 지구물리학과

^{* Corresponding Author}

License (open-access):

Ⓒ Journal of the Korean Society of Mineral and Energy Resources Engineers. This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/ licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

We have identified complex coupled physical processes exist in CO₂ sequestration or development of unconventional resources including shale gas plays and gas hydrate deposits. These coupled physical processes include multiphase flow, geomechanics, and geophysics, which requires a simulator that integrates those individual simulators to understand the complex physics in reservoir engineering. In this study, we first introduce how to integrate the individual existing simulators stably and effectively. Specifically, we focus on a sequential method that can provide numerical stability and accuracy. Then, we introduce an example of electromagnetic application to CO₂ sequestration.

Keywords

Coupled flow and geomechanics

Integrated reservoir simulation

Sequential approach

Numerical stability

이산화탄소 지중저장, 셰일가스 및 가스 하이드레이트의 비전통석유자원 개발과정에서 복잡한 물리현상의 해석이 필수적이다. 보다 현장지향적인 분석을 위해서는 다상 유체거동, 지반공학, 지구물리 이론을 통합한 전산모델 개발이 요구된다. 이 논문에서는 개별 공학이론을 안정적이고 효과적으로 통합할 수 있는 순차적 전산모델 개발과정을 서술하였다. 이산화탄소 지중저장 전산모사를 통해 개발한 순차적 통합전산모델의 적용성을 검증하였다.

키워드

유동과 지반역학의 연계성

통합 저류층 전산모사

순차 해석법

수치적 안정성

MAIN

서 론
수치해석의 수학적 모델링
지구 물리 모니터링 기술의 통합
전산모사 결과 및 토의
결 론

서 론

비전통석유자원의 개발은 안정적인 에너지자원의 수급을 위하여 북미를 중심으로 활발히 이루어지고 있다(Cipolla et al., 2010; Kargbo et al., 2010; Zoback and Kohli, 2019). 최근 셰일혁명으로 평가되고 있는 셰일가스의 생산은 과거에 비해 깊은 심도에 시추된 수평정과 수압파쇄의 혁신적 기술혁신이 뒷받침되었다(King, 2012; Fisher and Warpinski, 2012). 수압파쇄는 유체 투과도가 극히 낮은 셰일가스 층에 높은 유체압력을 가하여, 저류층에 인공균열을 연속적으로 생성시켜 저류층의 유효 유체 투과도와 유효 공극률을 증대하는 방법이다(Dean and Schmidt, 2008; Fjaer et al., 2008; Ji et al., 2009; Kim and Moridis, 2015; Nordren, 1972; Perkins and Kern, 1961). 수압파쇄로 인한 저류층 물성 변화는 석유자원의 생산성을 상업수준으로 향상시키는 반면, 저류암 파괴과정에서 미소 지진파를 야기하거나 예기치 않은 저류층 가스의 대수층으로의 유입과 같은 환경 문제를 야기할 수도 있다(Osborn et al., 2011; Page and Miskimins, 2009; Rutqvist et al., 2013; Zoback et al., 2010; Zoback and Kohli, 2019). 비전통석유자원의 수치모델링을 위해서는 석유공학, 지반공학, 지구물리학에 대한 종합적이고 정밀한 분석기술이 요구되고 있다. 기존의 다상유체 거동해석에만 한정된 전산모델링으로는 수압파쇄 후 셰일가스의 현장 생산특성을 제대로 반영하지 못하는 한계가 있다.

셰일가스전 개발 외에도 이산화탄소 지중저장은 주입성(injectivity)과 저장성 향상과 더불어 지반 및 저류층 안정성분석이 필요하다(Rutqvist et al., 2007). 저류층 덮개암의 파괴 또는 인근 단층의 활성화는 주입된 이산화탄소의 누출은 물론 환경적인 피해도 막대할 수 있으므로, 유체유동 및 지반공학의 복합적인 동시해석(integrated and real- time analysis)은 상당히 중요한 요소로 평가되고 있다(Lee et al., 2017; Rutqvist, 2012; Zoback and Gorelick, 2012).

가스 하이드레이트 개발도 생산정의 안정성이 보장되어야 한다. 울릉 분지의 경우, 감압법에 의한 가스 생산으로 지반이 침하될 수 있다는 전산모델링 결과가 보고된 사례가 있다(Kim and Lee, 2019; Moridis et al., 2014). 지반침하는 생산시스템의 상부 구조물과 케이싱의 안정성에 영향을 끼치기 때문에, 감압에 의한 지반 및 케이싱의 응력상태와 변위를 정확히 예측하여야 한다(Zoback, 2007).

저류공학에서의 지반 안정성을 평가하기 위해서는 정확한 수치 전산모사와 함께 기술적〮비용적 측면에서 효과적인 모니터링 기술이 확보되어야 한다(Rutqvist et al., 2010). 유정에서의 압력 및 생산량〮주입량 측정, 지표면의 변화 및 미소 진동을 관측하고 전자기 지구물리를 이용한 유체 유동 모니터링 등 다양한 모니터링법이 존재하며, 측정(관측)자료는 다양한 시공간 척도와 정확도를 가진다(Borglin et al., 2000; Johnson and Shrallow, 2011; Oldenburg et al., 2000; Um et al., 2013; Um et al., 2019; Vasco et al., 2010; Warpinski et al., 2005). 예를 들면, 유정 근처에서 측정된 압력/생산 자료는 높은 정확도를 보이지만 국지적으로만 유의미하며 저류층 전체 상태를 설명하지는 못한다. 반면, 지표면 변화 관측은 저류층 전 지역을 관측할 수 있지만 자료의 정확도는 유정 자료에 비하여 낮다. 따라서, 통합 전산 모델을 통해 관측자료를 종합적으로 분석함으로써 신뢰할 수 있는 저류층 특성화(characterization) 및 미래거동 예측이 이루어질 수 있다(Kim et al., 2018). 이 연구에서는 유동(flow), 지반역학(geomechanics), 지구물리학(geophysics) 특성을 통합하여 전산모델로 구현하는 방법론을 서술하고자 한다. 특히 지반역학과 유체유동의 복합문제에 관련해 논의하고 이산화탄소 지중저장 문제를 통해 특성화하는 과정을 살펴보고자 한다.

수치해석의 수학적 모델링

지반역학과 유체유동의 복합문제를 이해하기 위해서는 단상 유동-탄성 역학이 연계된 지배 방정식이 필요하다. 질량보존법칙에 의하여 단상 유동방정식(식 (1))과 역학 평형법칙(식 (2))은 다음과 같다(Coussy, 2004).

$$\frac{\partial m_f}{\partial t}+\mathbf{Div}\cdot{\boldsymbol w}_f=0$$

(1)

$$\mathbf{Div}\boldsymbol{\mathit･}\boldsymbol\sigma+\rho_b\boldsymbol g\boldsymbol=\mathbf0\boldsymbol{\mathit.}$$

(2)

여기서, $m_{f}$ 는 유체질량, $w_{f}$ 는 유체질량유동, Di는 다이버전스 연산자이다. $σ$ , $ρ_{b}$ , $g$ 는 각각 전체 응력 텐서, 체적 밀도, 중력 벡터를 의미한다. 유체 유동과 역학의 상호 연계는 식 (3)과 같은 구성 관계식에서 결정된다.

$$\delta\boldsymbol\sigma={\boldsymbol C}_d\delta\boldsymbol\epsilon-b\delta p\boldsymbol1\mathit,\boldsymbol{\mathit\;}(\delta\sigma_v=K_d\delta\epsilon_v-b\delta p),\;\frac{\delta m_f}{\rho f}=\frac1{M_f}\delta p+b\delta\epsilon_v,\;\frac1{M_f}=\Phi_0c_f+\frac{b-\Phi_0}{K_s},\;b=1-\frac{K_d}{K_s}$$

(3)

식 (3)에서, $C_{d}$ , $ε$ , b, p, 1, $σ_{v}$ , $K_{d}$ , $ε_{v}$ , $ρ_{f}$ , $M_{f}$ , $c_{f}$ , $K_{s}$ , $Φ_{0}$ 는 각각 탄성 계수 텐서, 변형률 텐서, Biot 상수, 유체 압력, 단위 2차 텐서, 전체 평균(체적) 응력, 체적 강성계수, 체적 변형률, 유체 밀도, Biot 강성계수, 유체 압축계수, 암석입자 고유 체적 강성계수, 초기 공극률을 의미한다. $δ$ 는 매질의 운동변화에 대한 상대적 물리 변화량을 나타낸다. 액상인 오일과 같이 약 압축성 유체를 가정하고, 달시의 법칙(Darcy’s equation)을 적용하면, 식 (1)과 (2)는 다음과 같이 유체 압력과 변형률에 관한 식으로 표현할 수 있다.

$$\frac1{M_f}\frac{\partial p}{\partial t}+b\frac{\partial\epsilon_v}{\partial t}-\mathbf{Div}･\frac{k_p}\mu(\mathbf{Grad}p-\rho_f\boldsymbol g)=0$$

(4)

$$\mathbf{Div}･({\boldsymbol C}_d\boldsymbol\epsilon-b(p-p_0)\mathbf1+{\boldsymbol\sigma}_0)+\rho_b\boldsymbol g=\mathbf0$$

(5)

여기서, $p_{0}$ 와 $σ_{0}$ 는 초기 유체압력 및 초기응력이며, 초기 변형률은 0이다. 식 (3)에 있는 응력변화에 대해서 초기 응력과 현재 응력의 관계를 선형화 하였다(즉, {bold{sigma }} - {bold{sigma }} _{0} = rm {bold{C}} _{it d rm} ` {bold{epsilon }} ``- $b (p - p_{0}) 1$ ). $k_{p}$ 는 유체투과도, $μ$ 는 유체점성도, Grad는 그레디언트 연산자이다. 식 (4)와 (5)에서와 같이 유체 유동과 역학 문제가 유체 압력과 저류층의 변형으로 연계되어 있으며, 연계성은 식 (6)과 같이 연계강도(coupling strength; $τ$ )를 정의함으로써 정량화 할 수 있다(Kim et al., 2011a).

$$\tau=\frac{b^2M_f}{K_d}$$

(6)

즉, 유체가 압축성이 작고, 저류층 강성계수가 낮을 수록 두 물리 문제의 연계성은 높아 진다. 이 두 문제를 풀기 위해서는 완전 음역법(fully implicit method) 또는 순차 음역법(sequential implicit method)을 사용한다(Kim et al., 2011a). 완전 음역법은 시간 및 공간에 대한 편미분 방정식 (식 (4) 및 식 (5)) 을 뉴턴-랩슨(Newton-Raphson)방식으로 동시에 이산화(discretization) 한다. 그 결과로 식 (7)과 같은 선형 행렬식을 얻는다.

$$\underbrace{\begin{bmatrix}\mathbf K&\boldsymbol-\mathbf L^{\mathbf T}\\\mathbf L&\mathbf F\end{bmatrix}}_{\boldsymbol J}\;\underbrace{\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}\;}_{\boldsymbol\delta\boldsymbol x}\;{}^{n+1,k}=-\underbrace{\;\begin{bmatrix}\mathbf R^{\mathbf m}\\\mathbf R^{\mathbf f}\end{bmatrix}\;}_{\boldsymbol R}\;{}^{n+1,k}\;,\;\boldsymbol F=\boldsymbol Q+\triangle\mathrm t\;\boldsymbol T$$

(7)

식 (7)에서, K, L,F, u, p, Q, T, Δt, R^m, R^f을 역학문제에서의 강성행렬, 연계 행렬, 유동 문제에서의 이산 행렬, 미지수 변위 벡터, 미지수 유체 압력 벡터, 유체 압축행렬, 유체 전달율(transmissibility)행렬, 단위 시간량, 역학문제에 대한 나머지 식, 유체 유동에 대한 나머지식을 의미한다. 윗첨자 n은 이산화된 시간 단계, k는 반복 수행 단계를 나타내며, $δ x^{k} = x^{k + 1} - x^{k}$ 이다. n+1은 현재 시간단계, k+1는 현재 반복수행 단계를 의미하므로 미지수에 해당된다. 식 (7) 에서 처음 부분 행렬 식은 역학 문제(식 (5) 참조)를 이산화하여 구한 것이며, 두 번째 부분행렬식을 유동문제인 식 (4)를 이산화하여 구한다. 여기서, 행렬식 $J δ x = - R$ 를 풀어야 하지만 많은 전산량을 요구하고, 연계 강도가 높을수록 행렬 J는 불량상태(ill-conditioned)가 되어 수학적으로 알맞은 전처리 방법(preconditioning)을 찾아야 한다. 또한 새로운 전산 코드를 재구성하는 과정에서도 많은 시간과 노력이 들어가기 때문에 순차 음역법을 대부분의 연구에서 선호한다(Felippa and Park, 1980). 또한 순차 음역법에서 착안한 완전 음역법의 적절한 전처리 방법을 제공하기도 한다(White et al., 2016).

순차 음역법은 각각의 문제들을 음역적으로 풀이한다. 좀 더 구체적으로 설명하면, 식 (4)에서 변형률에 관련된 식은 이전 단계의 값으로 넣고, 현재 압력값만을 미지수로 설정 한 후 음역법으로 압력값을 구한다. 식 (7)에서 행렬 J는가 식 (8)과 같이 수정될 수 있다.

$$\begin{bmatrix}\mathit K&\mathit-\mathit L^{\mathit T}\\\mathit L&\mathit F\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k}\rightarrow\begin{bmatrix}\mathit K&\mathit-\mathit L^{\mathit T}\\\mathit0&\mathit F\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k}+\begin{bmatrix}\mathbf0&\mathbf0\\\mathbf L&\mathbf0\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k-1}$$

(8)

여기서, 마지막 부분은 이전 반복 수행단계에서 구한 값들로 구성된다. 이 경우 훨씬 작은 크기의 행렬 F 만을 풀이하면 되기 때문에 많은 전산량이 필요하지 않을 뿐만 아니라, 기존의 유동 전산 모사 코드도 쉽게 활용할 수 있다. 이렇게 계산한 압력값을 식 (5) (또는 식 (7)의 첫번째 부분행렬) 에 대입하여 역학문제를 풀때, 현재 변위값을 미지수로 놓고 음역법으로 변위값과 변형율을 구한다. Fig. 1은 순차적 음역법을 간단하게 도식화한 것이다.

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F1.jpg

Fig. 1.

A schematic diagram of a sequential approach for integrated simulation of coupled flow, geomechanics, and geophysics. MEQ and EM stand for Microearthquake and Electromagnetics, respectively.

그러나, 순차 음역법은 여러 장점에도 불구하고 수치해의 수렴성을 보장하지 못한다. 다양한 순차 해석법이 존재하지만 이 가운데 일부만이 수치 안정성과 정확도를 제공한다. 앞서 언급한 순차적 방식은 직관적으로 제안할 수 있는 방법이지만, 연계강도가 높은 경우에는 수치적 불안정성을 야기하고, 이 불안정성은 단위 시간을 줄이더라도 해결하기 어렵다. 최근식 (9)와 같은 고정응력(Fixed-stress)법이 개발되어 무조건적인 수치안정성과 높은 정확도를 제공하는 연구가 수행되고 있다(Kim et al., 2011b; Mikelic and Wheeler, 2013).

$$\begin{bmatrix}\mathit K&\mathit-\mathit L^{\mathit T}\\\mathit L&\mathit F\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k}\rightarrow\begin{bmatrix}\mathit K&\mathit-\mathit L^{\mathit T}\\\mathit0&\mathit F\mathit+\mathit L\mathit K^{\mathit-\mathit1}\mathit L^{\mathit T}\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k}+\begin{bmatrix}\mathbf0&\mathbf0\\\mathbf L&\boldsymbol-\mathbf L\mathbf K^{\boldsymbol-\mathbf1}\mathbf L^{\mathbf T}\end{bmatrix}\;\begin{bmatrix}\delta\boldsymbol u\\\delta\boldsymbol p\end{bmatrix}^{n+1,k-1}$$

(9)

여기서, $L K^{- 1} L^{T}$ 은 실제적으로 역행렬을 구할 필요가 없으며 국지적으로 계산할 수 있다. 특히, 수학적 등가적으로 일반적인 저류층 전산모델에서는 다음과 같이 공극률 함수를 수정함으로써 간단히 복합문제를 풀 수가 있다.

$$\mathrm\Phi^{n+1,k+1}-\mathrm\Phi^n=\left(\frac1{M_f}+\frac{b^2}{K_d}\right)\left(p^{n+1,k+1}-p^n\right)-\frac{b^2}{K_d}\left(p^{n+1,k}-p^n\right)+b\left(\epsilon_v^{n+1,k}-\epsilon_v^n\right)$$

(10)

$Φ$ 는 초기 체적 부피에 대한 현재 공극 부피의 비율로 라그랑지(Lagrange) 공극률 또는 저류층 공극률으로 정의된다. 이 공극률은 저류층 전산모사에 쓰이는 공극률과 동일하며 참 공극률(true porosity)과 대비된다. 참 공극률은 현재 체적부피에 대한 현재 공극부피로 정의 한다. 식 (10) 우변의 마지막 2개항은 이전 단계에서 구해진 값이고, $p^{n + 1, k + 1}$ 이 미지값이다. 좀 더 어려운 다상 유동 및 탄소성의 비선형 복합문제의 경우도 식 (11)과 같이 식 (10)을 확장함으로써 쉽게 풀수 있다(Kim et al., 2012; Kim et al., 2013).

$$\mathrm\Phi^{n+1,k+1}-\mathrm\Phi^n=\left(\frac1{M_f}+\frac{b^2}{K_d}\right){\textstyle\sum_J}S_J\left(p_J^{n+1,k+1}-p_J^n\right)-\frac{b^2}{K_d}{\textstyle\sum_J}{\textstyle{\scriptstyle S}_J}\left(p_J^{n+1,k}-p_J^n\right)+b\left(\epsilon_v^{n+1,k}-\epsilon_v^n\right)$$

(11)

여기서, $K_{e p}$ 는 탄소성 체적계수 이다. 아래 첨자 J는 유체 상을 의미하고, $S_{J}$ 와 $p_{J}$ 는 각 유체 상의 유체 포화도와 압력을 의미한다. 잘 설계된 각각의 저류층 전산 모사 코드와 역학 전산모델이 존재한다면 식 (10)과 식 (11)을 이용하여 전산 코드를 수정하여 유체 유동 문제를 풀이한다. 그렇게 구한 유체 유동 압력을 식 (5) 에 대입하여 역학 전산모사를 진행하면, 유체유동-지반 역학의 복합문제를 풀 수 있다.

지구 물리 모니터링 기술의 통합

지반역학의 수치해는 지표면을 포함한 지질층의 변형상태를 알려준다. 지표면의 변위 변화는 인공위성 실측자료와 비교 할 수 있고, 지질층의 파괴는 단층 활성화 및 미소 지진 자료와 비교 된다. 예를 들면, 수치해석에서 구한 단층의 파괴 상태 및 면적과 변위값을 이용하면, 탄성파 모멘트(seismic moment; $M_{0}$ ) 및 모멘트 규모(moment magnitude; $M_{w}$ )을 식 (12)를 통해 구할 수 있고, 실측 자료와의 비교를 통해 저류층 특성화 및 미래의 단층 활성화 가능성을 예측할 수 있다(Aki and Richards, 2002).

$$M_0=\mu_sAd,\;\;M_w=\frac{(\log_{10}M_0-16.1)}{1.5}+4.667.$$

(12)

여기서, $μ_{s}$ 는 전단강성계수, A는 단층 파열면적, d는 단층 이동변위이다.

이와 더불어, 다상유동 수치해석에서 구한 유체 포화도는 저류층 전기 전도도( $C_{t}$ )의 분포에 대한 정보를 제공한다. 식 (13)과 같이 아치법칙(Archie’s law)을 이용하면, 수치해를 통해 시간에 따른 전기 전도도의 변화를 나타낼 수 있다. 이러한 수치적 자료는 전자기 탐사를 통한 실측 자료와의 비료를 통해 저류층 특성화에 활용될 수 있다.

$$C_t=\frac1{\mathrm a}C_w\mathrm\Phi^mS_w^n$$

(13)

식 (13)에서 S_w는 수포화도, C_w는 공극수의 전기 전도도, $a$ 는 비틀림 인자(tortuosity factor)이다. 지수인 m과 n은 매질과 관련된 특성인자이며 시료을 이용한 실험 또는 경험적으로 결정된다. 주목할 점은 식 (12) 는 탄성파 지구물리와 결합될 수 있는 반면, 식 (13)은 전자기 지구물리와 결합된다는 사실이다. 이산화탄소 저류층에 대한 지구물리 전산 모사를 위하여3차원 병렬계산 유한차분(Commer and Newman, 2008) 과 유한 요소법(Um et al., 2013)이 개발되었다. 두 개의 지구 물리 관측 방법은 서로 독립적이며, 다른 시공간 스케일을 가진 자료로써 고유한 저류층 특성화정보를 제공한다. 따라서 이렇게 다양하고 방대한 자료를 정량적으로 통합하여 ‘어떻게 적절하고 정확하게 저류층 특성화 및 거동 예측을 할 수 있는가?’에 대한 연구 문제를 낳고, 이 문제를 풀기 위하여 복합역산(joint inversion) 및 신경망을 이용한 딥러닝 기술이 최근 활발히 연구 되고 있다(Colombo et al., 2020; Oh et al., 2018; Oh et al., 2019).

전산모사 결과 및 토의

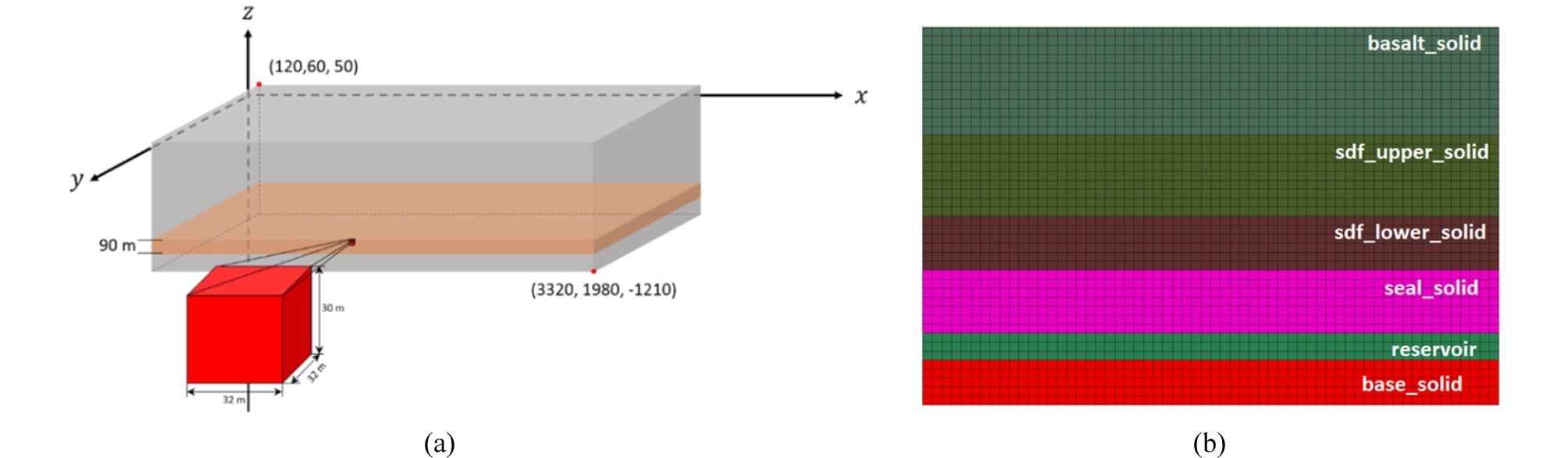
이산화탄소 지중저장은 지하유체 유동 및 지반공학 복합문제의 대표적인 예라고 할 수 있다. 본 연구에서는 실제 지층특성과 유사한합성 지층 모델을 도입하여 지하유체-지반역학 복합 수치해석을 수행하고, 구한 수치해를 전자기물리 탐사 전산 모사에 적용하였다. 다상 유체 유동은 자체 개발한 전산 모델을 이용하였고, 지반 역학은 상용 소프트웨어인 FLAC3D를 사용하였다. 그리고, 지반역학 모델 영역은 저류층을 포함하여 지표까지 확장하였고, 저류층은 약 1 km심도의 지하에 있다고 가정하였다. 자세한 모델 정보는 Table 1과 Fig. 2에 정리하였다. Table 2는 저류층 암석 및 유체 특성자료는 요약하였고(Lee et al., 2020), Table 3은 저류층 응력분포 및 역학적 특성자료를 정리하였다. 수직정을 가정하였고, 이산화탄소 주입량은 300 ton/day이다. 초기 저류층 중심부 압력은 약 11.26 MPa 이며, 초기 함수율(물 포화도)는 100%이다.

Table 1.

Summary of the numerical model

Variable	Unit	Geological model	Reservoir model
Dimension	m	3200×1920×1260	3200×1920×90
Gird size	m	32 × 32 × 30	32 × 32 × 30
NX		100	100
NY		60	60
NZ		42	3
Total		252,000	18,000

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F2.jpg

Fig. 2.

The (a) domain (Unit: m) and (b) geological layers for simulation of geological CO₂ storage. The size of gridblocks is uniformly 32 m×32 m×30 m in the x, y, z directions, respecitvely, as shown in the red gridblock.

Table 2.

Summary of petrophysical properties assumed in this study

Variable	Units	Value
Matrix porosity	fraction	0.126
Permeability	mD	16.9
Depth	m	1030
Reservoir temperature	°C	45
Relative permeability	Corey's equation (2-phase)
Capillary pressure	Van Genuchten's equation

Table 3.

Summary of geomechanical properties

Variable	Units	Value
In-situ stress (X-direction)	Pa/m	27,214
In-situ stress (Y-direction)	Pa/m	19,792
In-situ stress (Z-direction)	Pa/m	24,740
Young's modulus	GPa	2.89
Poison's ratio	fraction	0.21

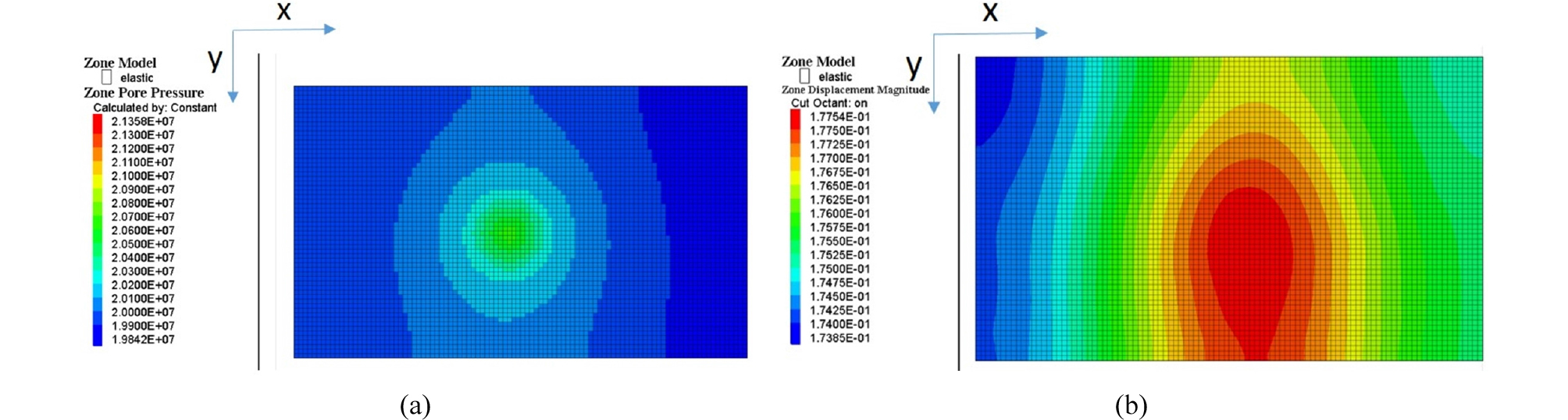
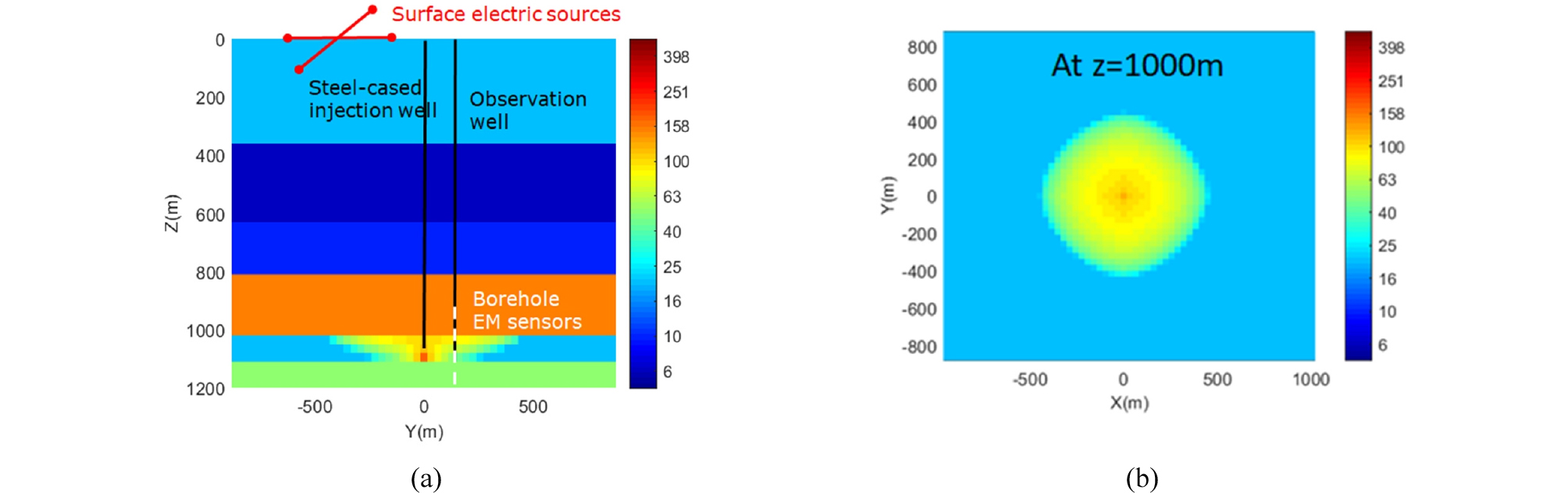
Fig. 3은 이산화탄소의 주입 5년후의 저류층의 압력 분포와 지표면 변화를 보여준다. 이산화탄소의 주입은 공극 압력을 증가 시키고, 지층 변형을 야기한다. 지표면의 상승은 추후에 실측된 자료가 존재할 경우, 저류층 특성화에 사용가능하다. Fig. 4는 이산화탄소의 주입 5년후와 15년후의 저류층 내 이산화탄소 포화도 분포를 보여준다. 주입이 진행됨에 따라, 주입정을 중심으로 이산화탄소가 차지하는 영역이 넓어진다. 주입된 전기비저항이 높은 이산화탄소가 저류암 내 낮은 전기비저항을 가지는 공극수를 대체하게됨에 따라, 저류층에서의 전기 전도도 분포에 점진적인 변화가 관찰된다(Fig. 5). 따라서 다양한 전자기지구물리기법이 비저항의 변화를 모니터링하는데 이용될수 있다.

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F3.jpg

Fig. 3.

Distributions of (a) reservoir pressure and (b) surface deformation after 5 years. Unit: Pa, m.

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F4.jpg

Fig. 4.

Distributions of gas saturation after (a) 5 years and (b) 15 years, respectively.

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F5.jpg

Fig. 5.

(a) A schematic diagram of surface-to-borehole EM Monitoring and (b) the converted electrical conductivity field after 15 years. Unit: Ohm-m.

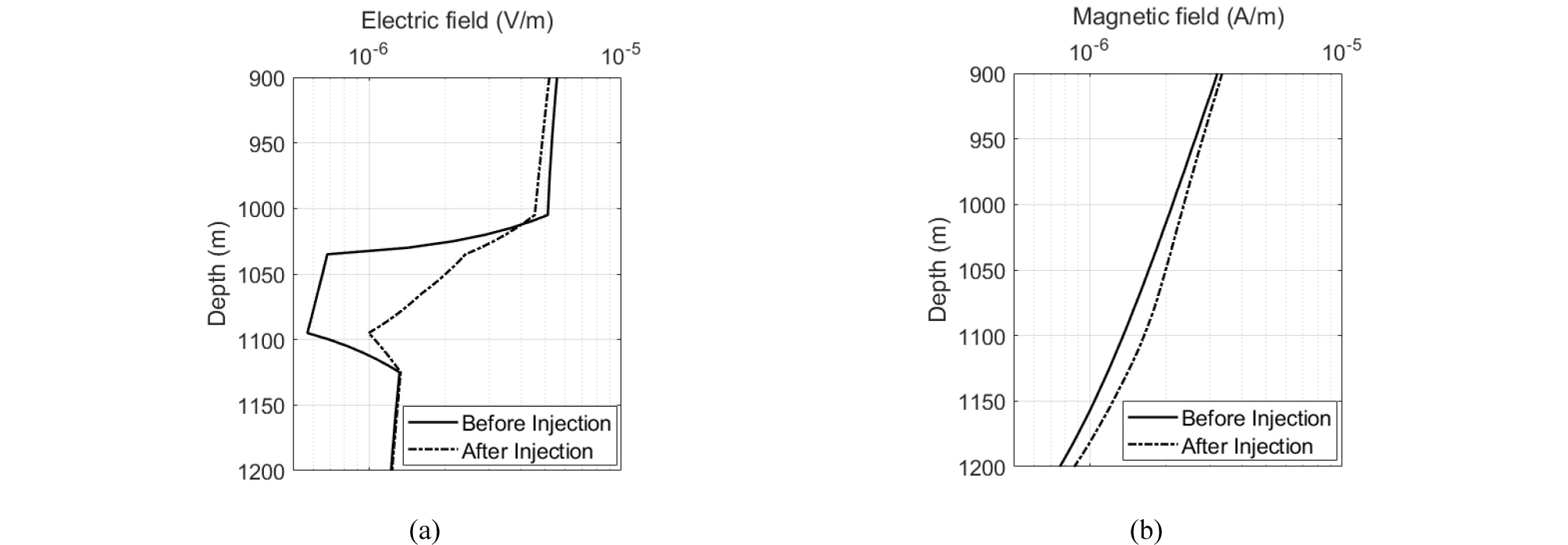
이 연구의 전자기 지구물리 전산모사는 지표-시추공(surface-to-borehole, STB) 지구물리탐사를 고려한다(Um et al., 2020). Fig. 5(a)에서 보여지듯이, 지표 쌍극자 송신기는 금속 케이싱에 근접함으로써 많은 양의 전자기 에너지를 지하심부까지 전달할수 있도록 설치되며, 수신기는 관측정에 설치된다. 저류암주변의 관측정은 천공을 가지고 있다고 가정함으로서, 자기장뿐 아니라 전기장의 반응도 고려한다. 교차 시추공 전자기(crosswell electromagnetic) 모니터링과 달리, 지표-시추공 전자기모니터링은 단일 유정만을 이용하여 이산화탄소를 모니터링함으로써 물리탐사의 비용과 시간이 절감되는 장점이 있다. 또한 소형 시추공 송신기와 달리, 큰 출력의 지표 송신기를 사용함으로써 신호대비잡음을 크게 향상시킬수 있다. 이러한 장점으로 인해 지표-시추공 전자기모니터링은 현재 해외의 다양한 이산화탄소 지중저장 실증 실험장에서 검증이 이루어지고 있다(Um et al., 2020). 전산모사의 결과 Fig. 6에서 알 수 있듯이, 초기 이산화탄소 포화도가 0%인 것을 감안할 때, 이산화탄소 주입 전과 후의 확연한 차이가 관측된다. 시추공내에서 전기장의 측정은 저류암이 존재하는 깊이에서 높은 민감도를 보여주는 반면, 자기장 측정치는 이산화탄소 저류층 이전 혹은 이후 깊이에서도 민감도를 보여주지만 민감도는 완만하다. 이러한 민감도는 역산을 통한 이산화탄소 거동의 영상화 및 관측이 가능함을 제시한다.

http://static.apub.kr/journalsite/sites/ksmer/2020-057-03/N0330570307/images/ksmer_57_03_07_F6.jpg

Fig. 6.

Electric and magnetic fields before and after CO₂ injection.

결 론

지금까지 석유공학에서는 다상 유체 유동과 저류층 특성화를, 암석 역학 및 지반 공학에서는 지반역학 해석을, 지구 물리학에서는 탐사 물리 전산 모사를 각각 중점적으로 연구하여 왔다. 그러나, 앞으로는 이산화탄소 지중저장, 가스 하이드레이트 개발, 비전통석유자원의 개발 등을 위해서 각 연구분야의 기술들이 효과적이면서도 체계적으로 통합이 되어야 한다. 이를 위해 유체 유동-지반역학 복합 전산모사에 대한 기본적인 개념 및 순차 음역법에 근거한 해법을 설명하였다. 복합 전산 모사와 탄성파/전자기/InSAR(Interferometric Synthetic Aperture Radar) 지구 물리 탐사 기법의 결합 방법론을 기술하였다. 전산 모사의 예로 현장 지층특성을 반영한 이산화탄소 지중저장의 수치모델링을 수행하고 저류층 특성화 및 역산에 대한 용이하면서도 신뢰도 높은 전방향 전산 모델의 개발가능성을 서술하였다.

Acknowledgements

이 연구는 텍사스 A&M대학교 Larry A. Cress '76 Faculty Fellowship의 지원을 받았습니다(This work was supported by Larry A. Cress '76 Faculty Fellowship from Texas A&M University).

References

Aki, K. and Richards, P.G., 2002. Quantitative Seismology (2nd Ed.) Chapter 3, University Science Books, Sausalito, CA, USA.

Borglin, S.E., Moridis, G.J., and Oldenburg, C.M., 2000. Experimental studies of the flow of ferrofluids in porous media, Transport Porous Med., 41, p.61-80.

10.1023/A:1006676931721

Cipolla, C.L., Lolon, E.P., Erdle, J.C., and Rubin. B., 2010. Reservoir modeling in shale-gas reservoirs. SPE Reserv. Eval. Eng., 13(4), p.638-653.

10.2118/125530-PA

Colombo, D., Li, W., Sandoval-Curiel, E., and McNeice, G.W., 2020. Deep-learning electromagnetic monitoring coupled to fluid flow simulators, Geophysics, 85(4), WA1- WA12.

10.1190/geo2019-0428.1

Commer, M. and Newman, G., 2008. New advances in controlled-source electromagnetic inversion, Geophys. J. Int., 172(2), p.513-535.

10.1111/j.1365-246X.2007.03663.x

Coussy, O., 2004. Poromechanics, John Wiley and Sons, Chichester, UK.

10.1002/0470092718

Dean, R.H. and Schmidt, J.H., 2008. Hydraulic fracture predictions with a fully coupled geomechanical reservoir simulation, SPE J., 14(4), p.707-714.

10.2118/116470-PA

Felippa, C.A. and Park, K.C., 1980. Staggered transient analysis procedures for coupled mechanical systems: formulation, Comput. Methods Appl. Mech. Eng. 24(1), p.61-111.

10.1016/0045-7825(80)90040-7

Fisher, K. and Warpinski, N., 2012. Hydraulic fracture-height growth: Real data. SPEProd. Oper. 27(1), p.8-19.

10.2118/145949-PA

Fjaer, E., Holt, R.M., Horsrud, P., Raaen, A.M., and Risnes, R., 2008. Petroleum Related Rock Mechanics (2nd Ed), Elsevier, Amsterdam, The Netherlands.

Ji, L., Settari, A., and Sullivan, R.B., 2009. A novel hydraulic fracturing model fully coupled with geomechanics and reservoir simulation. SPE J., 14(3), p.423-430.

10.2118/110845-PA

Johnson, R. and Shrallow, J., 2011. Ambiguity in microseismic monitoring, 2011 SEG Annual Meeting, 18-23 September, San Antonio, TX. (SEG-2011-1514).

10.1190/1.3627490

Kargbo, D.M., Wilhelm, R.G., and Campbell, D.J., 2010. Natural gas plays in the Marcellus shale: Challenges and potential opportunities. Environ. Sci. Technol.,44(15), p.5679-5684.

10.1021/es903811p20518558

Kim, J., Um, E.S., Moridis, G.J., 2018. Integrated simulation of vertical fracture propagation induced by water injection and its borehole electromagentic responses in shale gas systems, J. Pet. Sci. Eng., 165, p.13-27.

10.1016/j.petrol.2018.01.024

Kim, J. and Lee, J.Y., 2019. Wellbore stability and possible geomechanical failure in the vicinity of the well during pressurization at the gas hydrate deposit in the Ulleung Basin, The 53rd US Rock Mechanics/Geomechanics Symposium, 24-29 June, New York, NJ, USA. (ARMA- 2019-2011).

Kim, J. and Moridis, G.J., 2015. Numerical analysis of fracture propagation during hydraulic fracturing operations in shale gas systems, Int. J. Rock. Mech. Min., 76, p.127-137.

10.1016/j.ijrmms.2015.02.013

Kim, J., Moridis, G.J., Yang, D., and Rutqvist, J., 2012. Numerical studies on two-way coupled flow and geomechanics in hydrate deposits, SPE J., 17(2), p.485-501.

10.2118/141304-PA

Kim, J., Tchelepi, H.A., and Juanes, R., 2011a. Stability, accuracy, and efficiency of sequential methods for coupled flow and geomechanics, SPE J., 16(2), p.249-262.

10.2118/119084-PA

Kim, J., Tchelepi, H.A., and Juanes, R., 2011b. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits, Comput. Methods Appl. Mech. Eng., 200(13-16), p.1591-1606.

10.1016/j.cma.2010.12.022

Kim, J., Tchelepi, H.A., and Juanes, R., 2013. Rigorous coupling of geomechanics and multiphase flow with strong capillarity, SPE J., 18(6), p.1591-1606.

10.2118/141268-PA

King, G.E., 2012. Hydraulic fracturing 101: What every representative, environmentalist, regulator, reporter, investor, university researcher, neighbor and engineer should know about estimating frac risk and improving frac performance in unconventional gas and oil wells. SPE Hydraulic Fracturing Technology Conference, 6-8 Feburary, The woodland, TX.

10.2118/152596-MS

Lee, H., Shinn, Y.J., Ong, S.H., Woo, S.W., Park, K.G., Lee, T.J., and Moon, S.W., 2017. Fault reactivation potential of an offshore CO₂ storage site, Pohang Basin, South Korea, J. Pet. Sci. Eng., 52, p.427-442.

10.1016/j.petrol.2017.03.014

Lee, H., Yoon, S., Kim, T., Kim, J., Shinn, Y., and Ong, S.H., 2020. Fault reactivation analysis and estimation of maximum sustainable pressure during geological CO₂ sequestration at a pilot-scale storage site in SE Korea, J. Pet. Sci. Eng. (under review)

Mikelic, A. and Wheeler, M., 2013. Convergence of iterative coupling for coupled flow and geomechanics, Comput. Geosci., 17, p.455-461.

10.1007/s10596-012-9318-y

Moridis, G.J., Kim, J., Reagan, M.T., and Kim, S., 2014. Feasibility of gas production from a gas hydrate accumulation at the UBGH2-6 site of the Ulleung basin in the Korean East Sea, J. Pet. Sci. Eng., 108, p.180-210.

10.1016/j.petrol.2013.03.002

Nordren, R.P., 1972. Propagation of a vertical hydraulic fracture, SPE J., 12(4), p.306-314.

10.2118/3009-PA

Oh, S., Noh, K., Seol, S.J., and Byun, J., 2019. Cooperative deep learning inversion of CSEM data for salt delineation, Geophysics, 85(4), p.E121-E137.

10.1190/geo2019-0532.1

Oh, S., Noh, K., Yoon, S.J., Seol, S.J., and Byun, J., 2018. Salt delineation from electromagnetic data using convolutional neural networks, IEEE Geosci. Remote S., 16(4), p.519-523.

10.1109/LGRS.2018.2877155

Oldenburg, C., Borglin, S.E., and Moridis, G.J., 2000. Numerical simulation of ferrofluid flow for subsurface environmental applications, Transport Porous Med., 38, p.319-344.

10.1023/A:1006611702281

Osborn, S.G., Vengosh, A., Warner, N.R., and Jackson, R.B., 2011. Methane contamination of drinking water accompanying gas-well drilling and hydraulic fracturing, PNAS, 108(20), p.8172-8176.

10.1073/pnas.110068210821555547PMC3100993

Page, J.C. and Miskimins, J.L., 2009. A comparison of hydraulic and propellant fracture propagation in a shale gas reservoir, J. Can. Petrol. Technol., 48(5), p.26-30.

10.2118/09-05-26

Perkins, T.K. and Kern, L.R., 1961, Widths of hydraulic fractures, J. Petrol. Tech., 13(9), p.937-949.

10.2118/89-PA

Rutqvist, J., Vasco, D.W., and Myer, L., 2010. Coupled reservoir-geomechanical analysis of CO₂ injection and ground deformation at In Salah, Int. J. Greenh. Gas Con., 2(2), p.225-230.

10.1016/j.ijggc.2009.10.017

Rutqvist, J., 2012. The geomechanics of CO₂ storage in deep sedimentary formations, Geotech. Geol. Eng. 30, p.525-551.

10.1007/s10706-011-9491-0

Rutqvist, J., Birkholzer, J., Cappa, F., and Tsang, C-F., 2007. Estimating maximum sustainable injection pressure during geological sequestration of CO₂ using coupled fluid flow and geomechanical fault-slip analysis, Energy Convers. Manag., 48(6), p.1798-1807.

10.1016/j.enconman.2007.01.021

Rutqvist, J., Rinaldi, A.P., Cappa, F., and Moridis, G.J., 2013. Modeling of fault reactivation and induced seismicity during hydraulic fracturing of shale-gas reservoirs, J. Pet. Sci. Eng., 107, p.31-44.

10.1016/j.petrol.2013.04.023

Um, E.S, Kim, J., Wilt, M., Commer, M., and Kim, S-S., 2019. Finite element analysis of top-casing electric source method for imaging hydraulically active fracture zones, Geophysics, 84(1), p.E23-E35.

10.1190/geo2018-0451.1

Um, E.S., Commer, M., and Newman, G., 2013. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the earth: Finite-element frequency- domain approach, Geophys. J. Int., 193(3), p.1460-1473.

10.1093/gji/ggt071

Um, E.S., Kim, J., and Wilt, M., 2020. 3D borehole-to-surface and surface electromagnetic modeling and inversion in the presence of steel infrastructure, Geophysics, 85(5), p.1-54.

10.1190/geo2019-0034.1

Vasco, D.W., Rucci, A., Ferretti, A., Novali, F., Bissell, R.C., Ringrose, P.S., Mathieson, A.S., and Wright, I.W., 2010. Satellite-based measurements of surface deformation reveal fluid flow associated with the geological storage of carbon dioxide, Geophys. Res. Lett. 37, L03303.

10.1029/2009GL041544

Warpinski, N.R., Kramm, R.C., Heinze, J.R., and Waltman, C.K., 2005. Comparison of single- and dual-array microseismic mapping techniques in the Barnett shale, SPE Annual Technical Conference and Exhibition, 9-12 October, Dallas, TX.

10.2118/95568-MS15872164

White, J.A., Castelletto, N., and Tchelepi, H.A., 2016. Block- partitioned solvers for coupled poromechanics: a unified framework, Comput. Methods Appl. Mech. Eng., 303, p.55-74.

10.1016/j.cma.2016.01.008

Zoback, M.D. and Gorelick, S.M., 2012. Earthquake triggering and large-scale geologic storage of carbon dioxide, PNAS, 109(26), p.10164-10168.

10.1073/pnas.120247310922711814PMC3387039

Zoback, M.D. and Kohli, A.H., 2019. Unconventional Reservoir Geomechanics: Shale Gas, Tight Oil, and Induced Seismicity, Cambridge University Press, Cambridge, UK.

10.1017/9781316091869

Zoback, M.D., 2007. Reservoir Geomechanics, Cambridge University Press, Cambridge, UK.

10.1017/CBO978051158647718163876

Zoback, M.D., Kitasei, S., and Copithorne, B., 2010. Addressing the Environmental Risks from Shale Gas Development, Worldwatch Institute Briefing Paper 1, Worldwatch Institute, Washington DC, USA.

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지