Comparison of Convolutional Neural Networks for Dividing Seismic Sequences

Hye-Jin Moon; Hyeong-Tae Jou; Sang Hoon Lee; Han-Joon Kim; Hyunggu Jun

doi:10.32390/ksmer.2020.57.6.541

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 31 December 2020. 541-553
https://doi.org/10.32390/ksmer.2020.57.6.541

Comparison of Convolutional Neural Networks for Dividing Seismic Sequences

탄성파 층서 구분을 위한 합성곱 신경망 기법 비교 연구

Hye-Jin Moon¹

Hyeong-Tae Jou²

Sang Hoon Lee²

Han-Joon Kim²

Hyunggu Jun³^{^*}

문 혜진¹

주 형태²

이 상훈²

김 한준²

전 형구³^{^*}

¹Engineer, Marine Active Fault Research Unit, Korea Institute of Ocean Science and Technology

²Principal Researcher, Marine Active Fault Research Unit, Korea Institute of Ocean Science and Technology

³Senior Researcher, Marine Active Fault Research Unit, Korea Institute of Ocean Science and Technology

¹한국해양과학기술원 해저활성단층연구단 기술원

²한국해양과학기술원 해저활성단층연구단 책임연구원

³한국해양과학기술원 해저활성단층연구단 선임연구원

^*hgjun1026@kiost.ac.kr

ABSTRACT

Application of the machine learning technique is expanding to the field of seismic exploration. For the purpose of feasibility assessment, we applied the machine learning technique to seismic sequence identification, which is important in seismic interpretation. From among the convolutional neural network techniques used in image analysis, we applied four models to seismic data obtained in the F3 block, offshore Netherlands, which have yielded remarkable results. One of the four models was ResNet34. The others were encoder–decoder models: U-Net, Residual U-Net, and FD U-Net. We first performed a qualitative analysis of the predicted images and then conducted quantitative analysis using pixel accuracy, mean class accuracy, mean intersection over union, and frequency weighted IU equations. The numerical results showed that ResNet34 had the lowest accuracy and that the encoder–decoder type models had higher accuracy. Considering the number of parameters required for calculation and the learning time, we confirmed that U-Net is the most efficient model.

Keywords

Machine learning

Convolutional neural network

Seismic sequence identification

Encoder–decoder model

Netherlands F3 block

머신 러닝 기술은 탄성파탐사 분야로 그 적용 범위를 확장하고 있다. 탄성파 해석에서 중요한 탄성파 층서 구분에 머신 러닝의 적용 가능성을 알아보았다. 이미지 분야에 탁월한 결과를 보여온 합성곱 신경망 기법 중 4가지 모델을 네덜란드 F3 block에 적용시켰다. 4가지 모델은 ResNet34 모델, 인코더-디코더 형태를 가지는 U-Net, Residual U-Net, FD U-Net이다. 예측된 이미지의 정성적 분석 수행 후 정량적 분석을 위해 pixel accuracy, mean class accuracy, mean intersection over union, frequency weighted IU의 수식을 활용하였다. 본 연구의 분석 결과 ResNet34의 정확도 결과가 가장 낮았고, 인코더-디코더 형태를 가지는 모델들이 높은 정확도를 보여주었다. 그리고 계산에 필요한 파라미터수와 학습시간을 고려 할 때 U-Net이 가장 효율적임을 확인할 수 있었다.

키워드

머신 러닝

합성곱신경망

탄성파층서구분

인코더-디코더 모델

네덜란드 F3 block

MAIN

서 론
CNN 기계학습 모델과 방법
ResNet34
U-Net
Residual U-Net
FD U-Net
실험 및 평가
실험 데이터
학습자료 및 시험자료
학습 수행
정확도 평가
결과 분석
결 론

서 론

상 분석(facies analysis), 속성분석(attribute analysis), 구조분석(structure analysis)과 같은 탄성파 단면을 활용한 연구는 자원을 탐사하고 개발하는 분야에서 중요한 역할을 수행하고 있으며 이러한 연구를 위해서는 우선 탄성파 층서면 해석이 이루어져야 한다. 탄성파 층서를 구분하기 위해서는 지질학적으로 중요한 반사 지점을 발췌(picking) 또는 추적(tracking)하여 층서를 구분한다(Onajite, 2013). 2-D 뿐만 아니라 3-D 탐사에서 획득되는 탄성파 자료는 일반적으로 그 양이 방대하며, 해석자는 반복되는 해석 작업을 수행해야 한다. 실질적으로 제한된 인력, 비용, 시간의 물리적인 한계로 인해 많은 경우 방대한 탄성파 자료 중 일부만을 해석한 후 반사면을 자동 발췌 하는 방법을 수행하는데, 해석결과는 전체 정보를 반영하지 못하고 핵심내용들을 요약한 경우가 많다. 이러한 전통적인 자동 발췌 방법은 복잡한 지질구조에서 많이 확인할 수 있는 약한 반사면과 불연속면에서 발췌가 어렵다는 단점을 가지고 있으며, 2-D 탄성파 단면과 시추공 자료를 통합시키는 경우 부정확한 자동 발췌 부분이 포함될 경우 자료간 교차지점에서의 불일치를 발생시키게 된다. 최근에는 국부지역의 경사각과 방위각 정보를 활용하여 목표지점의 반사면을 자동 발췌하는 딥-드라이븐(dip-driven) 방법, 탄성파 속성값을 가지는 작은 패치들을 비교하여 전체를 구현해내는 층서 패치(horizon patch) 방법, 탄성파 자료를 시뮬레이션하는 전역 최적화(global optimization) 방법이 활용되고 있다(Cho et al., 2020).

최근 머신 러닝 알고리즘과 계산 자원의 발전 덕분에 많은 분야에서 머신 러닝이 활발히 연구되고 있으며 탄성파 분야에도 머신 러닝을 적용하는 연구가 증가하는 추세이다(Choi et al., 2020). 탄성파 탐사 분야에서는 현재까지 탄성파 상 분석(Wrona et al., 2018; Keynejad et al., 2019), 저류층 특성화(Chaki, 2015; Tian and Daigle, 2018; Smith et al., 2019), 단층해석(Zhang et al., 2014; Xiong et al., 2018; Kumar and Sain, 2018), 암염구조 해석(Guillen et al., 2015; Shi, et al., 2019; Sen et al., 2019), 탄성파 속성분석(Zhao, 2018b; Griffith et al., 2019) 등 다양한 분야에서 머신 러닝이 적용되었다.

합성곱 신경망은 학습 자료의 특징을 추출할 때 공간적인 정보도 고려할 수 있다는 장점을 가지고 다양한 분야에서 활용되고 있다. Zhang et al.(2018)은 도로 이미지 자료를 활용하여 도로를 추출하기 위해 Residual U-Net을 제안하였고, U-Net과의 비교에서 더 높은 정확도로 도로 이미지를 추출하는 것을 확인하였다. Zhang et al.(2019)은 홍채이미지 자료를 활용하여 FD U-Net을 적용하는 연구를 수행하였고, 해당 연구에서 FD U-Net이 U-Net 보다 더 정확하게 홍채이미지를 분류해 내는 것을 확인하였다.

탄성파 층서 구분을 위해서는 합성곱 신경망(Convolutional Neural Networks, CNN)을 활용한 세그멘테이션 분류 연구가 다수 수행되었다. Chevitarese et al.(2018)은 AlexNet (Krizhevsky et al., 2012)과 VGGNet(Simonyan and Zisserman, 2014)을 공개 탄성파 자료인 네덜란드 F3 block 및 Penobscot 자료에 적용하여 높은 정확도로 주요 층 및 암염돔 층을 분류하였다. Dramsch and Lüthje(2018)은 F3 block의 탄성파 자료에 Waldeland CNN(Waldeland and Solberg, 2016), VGG16, ResNet50(He et al., 2016a) 기법을 적용하여 Waldeland CNN 기법과 VGG16 기법이 암상분류에 효과적이고 ResNet50 기법은 과적합 문제를 가지는 것으로 확인하였다. Qian et al.(2018)은 오토인코더(Auto-encoder) 네트워크와 비지도학습전략(unsupervised training strategy)의 두가지 방법을 활용하여 중합전 탄성파 자료의 상(facies)을 분류하는 연구를 수행하였다. Zhao(2018a)는 ResNet34 모델과 U-Net (Ronnenberger et al, 2015) 모델을 비교하여 U-Net모델이 더 좋은 결과를 낸다는 것을 확인하였다. Alaudah et al.(2019a)은 학습 자료를 패치(patch) 또는 섹션(section)으로 구성하고 데이터 증강 기법을 활용하여 DeconvNet(Noh et al., 2015)을 이용한 머신 러닝 비교 연구를 수행하였다.

본 연구는 현재까지 소개되고 있는 다양한 인공지능 모델을 동일한 탄성파 자료에 적용하고 그 결과를 비교·분석하여 탄성파 층서를 구분하는데 적합한 모델을 제안하고자 한다. 사용된 합성곱 신경망 기법은 ResNet34, U-Net, Residual U-Net(Zhang et al., 2018), Fully Dilated convolution combining U-Net(FD U-Net)(Zhang et al., 2019)의 4가지모델이다. 정확도 평가를 위해서 Pixel Accuracy(PA), Mean Class Accuracy(MCA), Mean Intersection Over Union(MIU), Frequency Weighted IU(FWIU)의 4가지 정량적 수치를 계산하였다.

CNN 기계학습 모델과 방법

합성곱 신경망은 학습 자료의 특징을 추출할 때 공간적인 정보를 고려할 수 있다는 장점을 가지고 있다. 이미지 분류 수행 시 합성곱 신경망 기법은 각 픽셀들의 강도 값 정보만 활용하는 것이 아니라 픽셀들 간의 패턴이 가지는 특징도 함께 활용하여 피처 맵을 추출한다. 탄성파 자료도 일종의 물성 분포를 영상화한 3D 토모그래피(tomography) 이미지로 간주할 수 있기 때문에 합성곱 신경망을 탄성파 자료에 적용시킬 수 있다(Zhao, 2018a). 합성곱 신경망은 특징 추출과 토폴로지(topology)가 연산에 반영될 수 있도록 하는 합성곱층(convolutional layer)과 특징을 강화시키고 이미지의 크기를 조절하는 풀링층(pooling layer) 등이 사용된다(Yi, 2019).

ResNet34

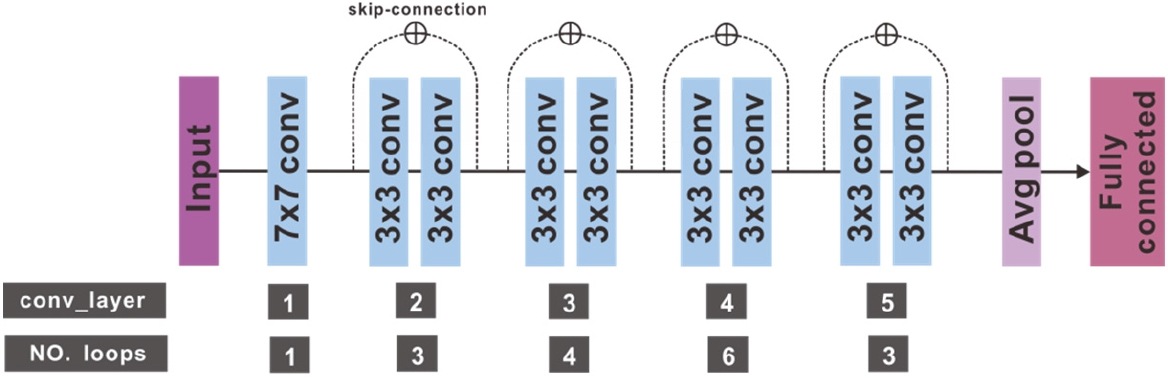
일반적으로 네트워크 망의 깊이가 깊을수록 학습 결과는 좋아지지만(Szegedy et al., 2015) 동시에 층이 깊어질수록 경사 값이 너무 작아져 학습의 효과가 줄어드는 문제도 발생한다(Bengio et al, 1994; Glorot and Bengio, 2010). 이에 He et al.(2016a)은 망을 깊게 하여도 학습효과를 유지할 수 있는 Residual learning 방법을 고안하여 ResNet을 제안하였다. Residual learning은 2개의 합성곱 층 마다 skip- connection을 연결하는데, 이 연결을 통해 입력 값을 출력에 바로 더해주는 작업을 수행한다. ResNet은 네트워크의 복잡성을 증가시키지 않기 위해 맥스 풀링, 드롭 아웃 등을 사용하지 않으며 추출된 특징을 최종적으로 분류하기 위해 완전연결층(fully-connected layer)을 사용한다. ResNet의 합성곱 층은 3×3 필터를 사용하며, 각 층 내에서 동일한 피처 맵 개수를 유지하기 위해 같은 층 안의 합성곱 연산에서 같은 수의 필터를 사용한다. 또한, 학습 중 피처 맵의 크기가 절반으로 줄어든다면 필터의 수를 두 배로 늘려 층 당 시간 복잡도(the time complexity per layer)를 유지시켜준다.

Zhao(2018a)는 34개의 층 수를 가지는 ResNet34 모델을 활용하여 탄성파 상 해석을 수행하여 좋은 결과를 확인한 바 있으며, 본 연구에서도 해당 모델을 활용하여 탄성파 층서구분을 수행하였다. 연구에 사용된 모델의 구조는 Fig. 1과 같으며, 각 층마다 피처 맵의 개수는 증가하나 크기를 감소시켜 계산 량을 크게 늘리지 않으면서 자료의 다양한 특징을 추출할 수 있도록 설계 되었다. Fig. 1의 “n × n conv”는 n × n 의 커널 크기로 합성곱 연산을 수행하는 합성곱 블럭을 의미한다. Resnet34의 합성곱 블럭은 배치 정규화, Rectified Linear Unit(ReLU) 활성화함수, 합성곱 순서의 full pre-activation(He et al., 2016b) 구조를 가진다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F1.jpg

Fig. 1

Network architecture of ResNet34.

U-Net

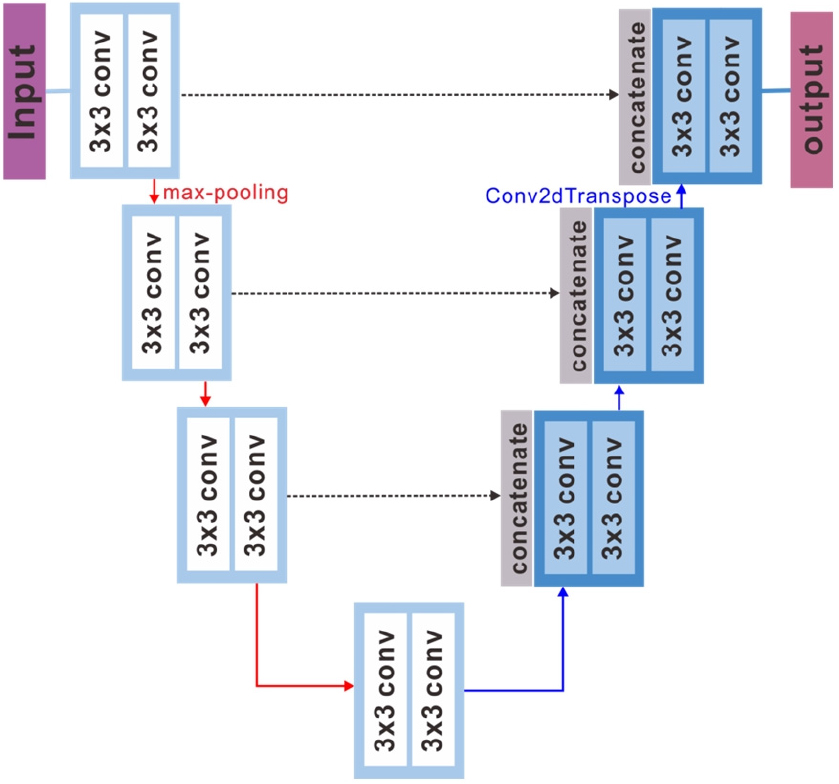
Ronneberger et al.(2015)은 머신 러닝의 학습 속도를 개선하고, 이미지의 특정 영역을 레이블(Label)로 표현하고자 U-Net 모델을 고안하였다. U자 형태를 가지는 이 모델은 이미지의 크기를 줄여나가는 인코더 부분과 반대로 이미지의 크기를 키워나가는 디코더 부분으로 구성되어있다. 그리고 인코더와 디코더 영역이 수평적인 관계에 있을 때, 인코더 부분의 출력물을 디코더의 입력 값에 결합(Concatenate) 하여 사용한다. Fig. 2는 본 연구에 사용된 U-Net 모델 구조이며 기존의 U-Net 구조에서 피처 맵의 개수와 층의 개수를 감소시켰다. U-Net은 3×3 합성곱을 사용하고, 제로 패딩(zero-padding)을 통해 같은 층의 피처 맵 크기를 동일하게 유지시킨다는 특징을 가지고 있다. 또한 다운 샘플링 단계에서 맥스 풀링을 통해 피처 맵의 가로와 세로의 크기를 각각 절반으로 감소시키고, 업 샘플링 단계에서 전치 합성곱(transpose convolution)을 통해 피처 맵의 가로와 세로의 크기를 각각 2배로 증가시킨다. 기존 U-Net은 배치 정규화를 사용하지 않지만 Zhou and Yang(2019)의 연구 등 최근 U-Net을 활용한 연구에서는 배치 정규화를 사용하는 것이 일반적이다. 그리고 본 연구에 사용된 다른 모델들인 Residual U-Net과 FD U-Net은 배치 정규화를 사용하므로 본 연구에서는 동등한 비교를 위해 U-Net에도 배치 정규화를 추가하였다. 따라서 본 연구에 사용된 U-Net의 합성곱 블록은 합성곱, 배치 정규화, ReLU 활성화 함수의 순서로 구성되어있다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F2.jpg

Fig. 2

Network architecture of U-Net. In this study, unlike in the original U-Net model, the number of layers and feature maps was reduced.

Residual U-Net

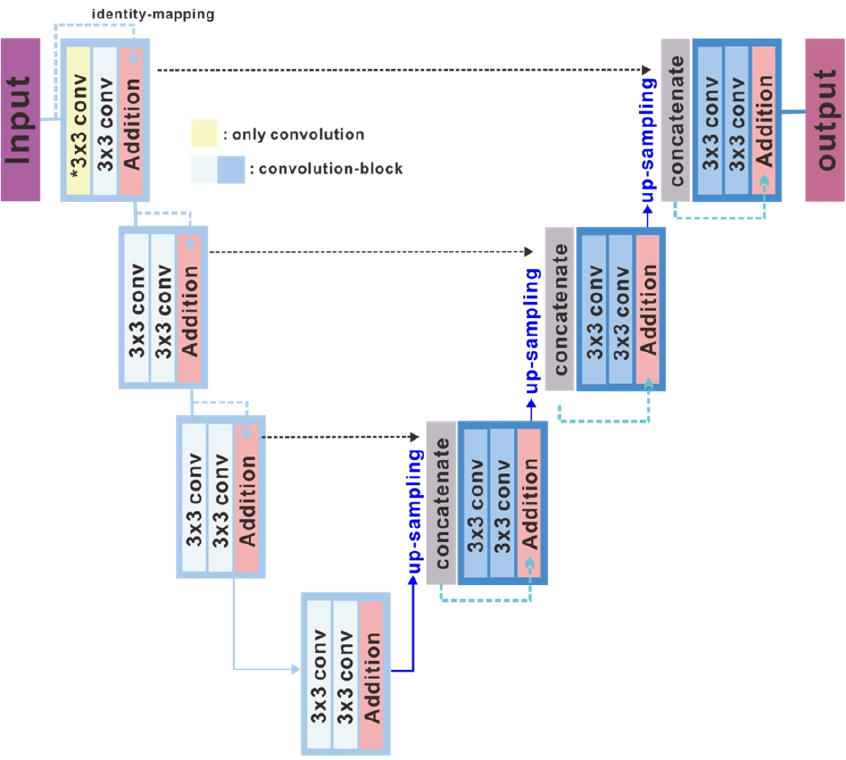
U-Net의 틀을 유지하면서 층이 깊어짐에 따라 학습 효율 감소 문제를 해결하기 위해서 Zhang et al.(2018)은 U-Net에 residual learning을 적용한 Residual U-Net을 제안하였다. Residual U-Net 네터워크는 인코더, 브릿지, 디코더의 세 부분으로 구성되며(Fig. 3) 각 부분은 모두 2개의 3×3 합성곱과 identity mapping을 기본 residual unit으로 가진다. 합성곱 블럭은 배치 정규화, ReLU 활성화 함수, 합성곱의 순서로 구성되어있다. Identity mapping은 배치 정규화, ReLU 활성화 함수, 1-D 합성곱으로 구성되어 해당 층의 입력과 출력을 연결시킨다(He et al., 2016a; He et al. 2016b).

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F3.jpg

Fig. 3

Network architecture of Residual U-Net.

FD U-Net

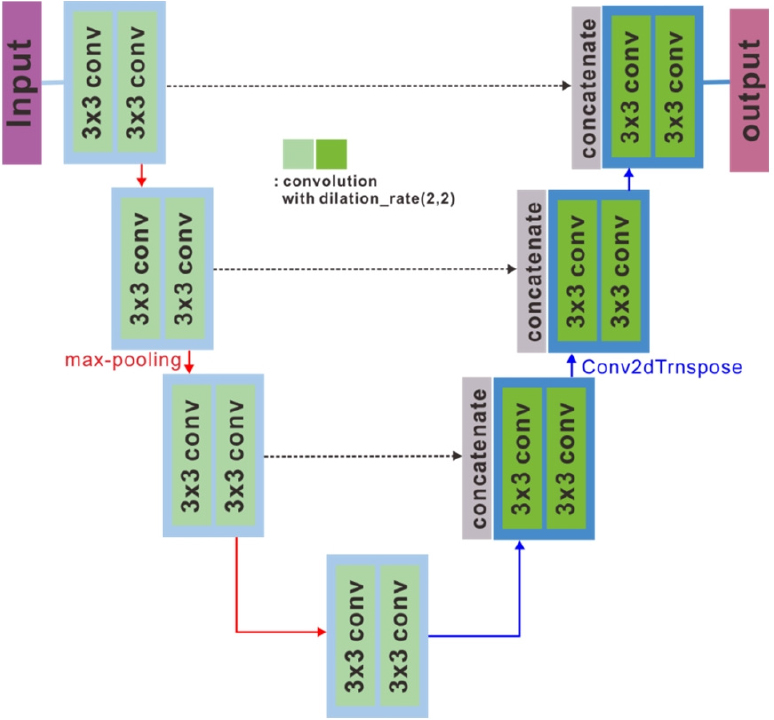
기존 U-Net의 합성곱 대신 확장 합성곱(dilated convolution)을 사용하여 파라미터의 수를 늘리지 않고 이미지의 공간적인 특징을 더욱 활용할 수 있는 방법이 Zhang et al.(2019)에 의해 제안되었다. FD U-Net의 구조는 Fig. 4에 나타나 있다. 합성곱 블록은 합성곱, 배치 정규화, ReLU 활성화 함수로 구성되어있다. 네트워크 모델의 모든 풀링과 업 샘플링은 기존 U-Net과 동일하고, 네트워크 안 마지막 층의 1×1 합성곱을 제외한 모든 3×3 합성곱들을 확장 비율(dilation rate) 2의 확장 합성곱으로 대체하였다. 확장 합성곱은 Yu and Koltun(2015)에 의해 고안된 방법으로, 필터 내부에 제로 패딩을 추가하여 필터를 적용시키는 공간 영역을 늘리는 방법이다. 이 방법은 제로 패딩의 부분이 0 값을 가지기 때문에 계산 파라미터를 늘리지 않아 기존 합성곱과 동일한 연산량을 가지지만 더 넓은 수용 영역(receptive field)을 가진다는 장점이 있다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F4.jpg

Fig. 4

Network architecture of FD U-Net.

실험 및 평가

실험 데이터

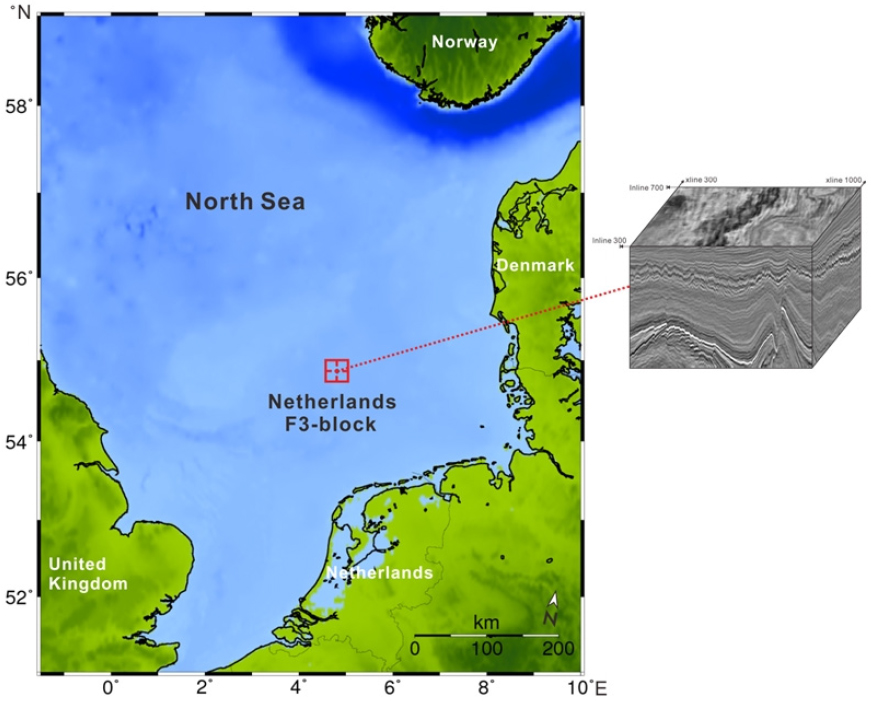
본 연구는 탄성파 층서 구분를 위한 머신 러닝 모델 학습 및 검증에 네덜란드 F3 block 자료를 활용하였다. Fig. 5에서 네덜란드 F3 block의 위치를 확인할 수 있다. 원시 데이터 셋은 1987년 네덜란드 해안에서 약 180 km 떨어진 the central graben basin 지역에서 취득된 3-D 해양 탄성파 자료이며, 384 m²의 탄성파 시간 영역 구조보정 3-D 자료로 총 651개의 인라인(inline)과 951개의 크로스라인(crossline)을 가진다. 탄성파 자료는 1848 ms까지 기록되었고, 샘플간격은 4 ms, 격자(bin) 크기는 25 m×25 m이다. 그리고 탄성파 자료와 함께 4개의 시추(검층) 자료, 8개 해석 층서 자료를 포함한다. 해당 자료는 다운랩, 탑랩, 온랩, 잘림구조를 포함하는 대규모 시그모이드형태의 층서를 특징적으로 가지고, 명점을 명확히 확인할 수 있다(Silva et al., 2019). 본 논문에 사용된 3-D 탄성파 영상을 Fig. 5에서 확인할 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F5.jpg

Fig. 5

Location of the Netherlands F3 block in the North Sea and 3-D seismic cube used in this paper.

학습자료 및 시험자료

4가지의 합성곱 신경망 모델들은 네덜란드 F3 해역에서 취득된 자료의 일부분을 활용해 학습되었다. 학습 자료의 레이블은 10개의 층의 종류에 따라서 0~9 까지의 값으로 이루어진 이미지다. Alaudah et al.(2019a)은 인공지능을 활용한 탄성파상분석 연구에서 F3 block의 인라인 100에서 700 범위와 크로스라인 300에서 1200 범위의 자료를 활용하여 인공지능 학습과 검증 자료를 구성하였다. 본 연구에서는 Alaudah et al.(2019b)가 활용한 F3 block 자료 중 인라인 300에서 700 범위와 크로스라인 300에서 1000 범위의 자료를 활용하였다. 총 401개의 인라인 중 3개 간격으로 134개의 인라인을 제외하고 남은 267개 인라인을 학습 자료로 활용하였다. 검증자료는 학습 자료를 제외한 인라인 134개와 크로스라인 701개 중 각각 13개씩 무작위로 선택하여 총 26개 라인을 활용하였다. 그리고 시험자료는 학습 자료와 검증자료를 제외한 나머지 인라인과 크로스라인 자료 중 무작위로 각각 100개의 자료를 선택하여 총 200개 라인을 활용하였다. 본 연구에 사용된 자료는 Fig. 10(a)와 Fig. 11(a)와 같은 단순한 수평적인 층서 형태와 Fig. 9(a)와 Fig. 12(a)와 같이 수평층서 및 하층부에 복잡한 구조를 포함하는 지질학적 구조로 구성되어있다. 인라인 시험자료의 경우 지층의 형태 및 탄성파 진폭값으로 나타나는 층의 성질이 학습 자료와 유사하지만 크로스라인 시험자료의 경우 학습 자료와 비교적 다른 지층의 형태를 가진다.

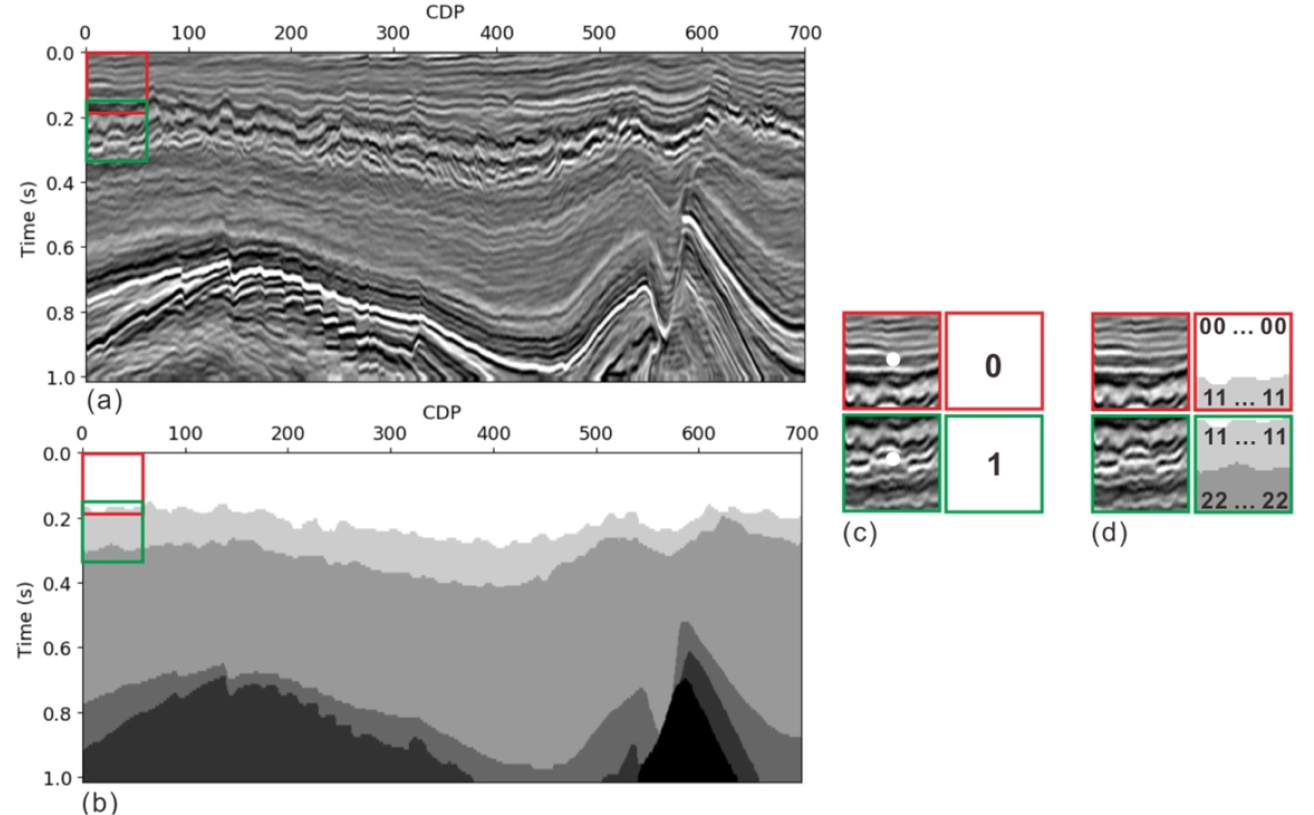
총 9개의 해석 층서 중 왕복주시 1.02s 까지의 6개 층 자료를 이용하여 실험을 진행하였다. 제한된 학습 자료의 양을 늘려주기 위해 각 인라인 단면을 20개 픽셀 간격으로 이동하며 64×64 픽셀 크기의 작은 패치(Patch)들로 나누어 총 85440개의 패치들을 학습 자료로 활용하였다(Fig. 6(a), (b), (c), (d)). 검증자료 또한 64×64 픽셀 크기의 작은 패치로 나누었으며, 총 6370개의 패치를 생성하여 검증에 활용하였다. 4가지 모델 모두 동일한 입력 자료 패치들을 이용하여 학습을 수행하였으며, 레이블 자료는 신경망 구조에 따라 2가지로 나누어 구성하였다. 우선 ResNet34 학습을 위해서 64×64 픽셀 크기 패치의 가운데 지점에 해당하는 층서를 레이블 자료로 사용하였다(Fig. 6(c)). 반면 나머지 인코더-디코더 모델들을 위해서는 64×64 픽셀 크기의 탄성파 패치와 동일한 영역에 해당하는 탄성파 층서 값을 레이블 자료로 사용하였다(Fig. 6(d)). Fig. 6(d)의 그림에서 확인 할 수 있듯이 64×64 크기의 각 픽셀에 해당하는 층서값이 레이블값으로 활용된다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F6.jpg

Fig. 6

(a) A seismic section used in training and (b) its labeled section with six different sequences. Patches used for (c) ResNet34 and (d) encoder–decoder model training. (c) and (d) are patches of size 64 × 64. The red and green square boxes are cropped from images (a) and (b), respectively.

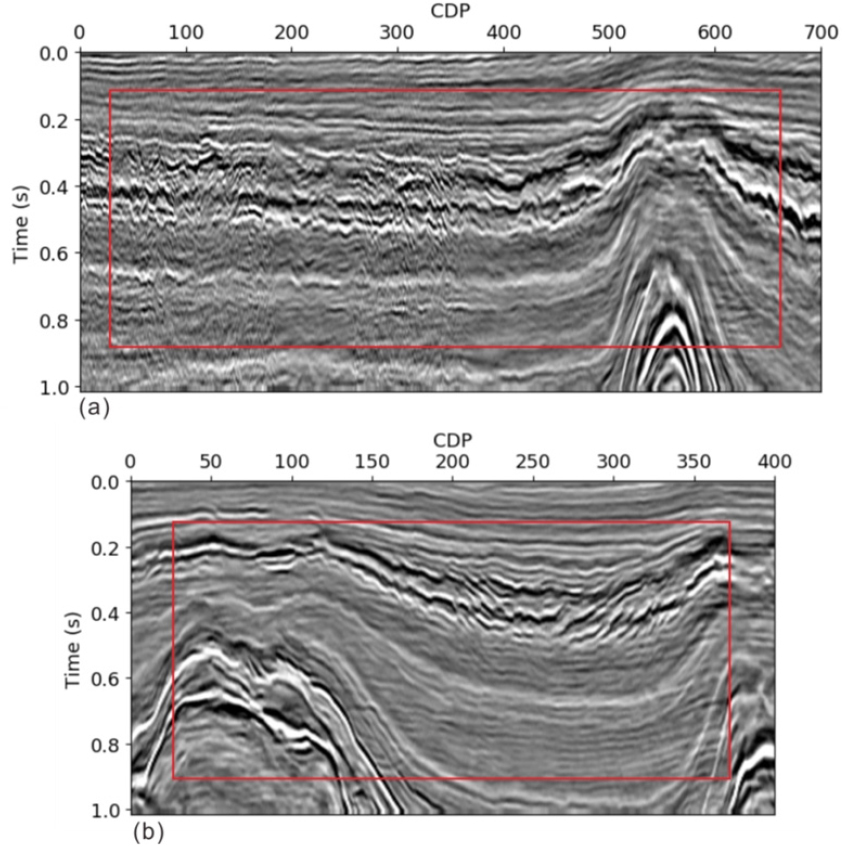
학습의 결과를 확인하기 위해 학습 자료와 비슷한 성질을 가지는 인라인 자료와 학습 자료와 성질이 다른 크로스라인을 사용하여 두 번의 시험을 수행하였다. Fig. 7(a)와 (b)는 각각 701×255과 401×255 픽셀 크기를 가지는 인라인과 크로스라인 탄성파 자료의 예시이다. 해당 자료에서 빨간 사각형 범위의 자료를 시험에 활용하였다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F7.jpg

Fig. 7

Seismic sections with a size of (a) 701 × 255 and (b) 401 × 255. The red squares represent sizes of 633 × 185 and 336 × 184, respectively, and were used to test the four different CNN models.

학습 수행

학습 수행을 위해 GeForce GTX 1080 Ti GPU 카드 1개를 가진 리눅스 서버를 사용하였다. 학습은 4가지 모델 모두에 대해 동일하게 200 에포크(epoch)를 수행하였다. 배치 크기는 ResNet34의 경우 100을 사용 하였고 U-Net, Residual U-Net, FD U-Net은 128을 사용하였다.

정확도 평가

결과의 정확도를 평가하기 위해 Alaudah et al.(2019a)의 탄성파 상분석 논문에서 사용된 4가지의 수식을 활용하였다. 이 수식들은 컴퓨터비전에 주로 이용되는 평가 수식이다. 아래의 식 (1) 에서 식 (6)의 $G_{i}$ 는 예측 결과에서 i 번째 층서로 예측된 픽셀을 나타내고, $F_{i}$ 는 정답 레이블의 i 번째 층서의 픽셀을 표시한다. $F_{i} \cap G_{i}$ 는 정확하게 분류된 픽셀을 나타낸다. $| \cdot |$ 은 해당 세트의 개수를 말한다. 식 (1)은 Pixel Accuracy(PA)로 전체 층서에 대해 제대로 분류된 픽셀을 나타낸다. 식 (2)는 Class Accuracy(CA)로 개별 층서 내에서 올바르게 분류된 픽셀을 말한다. 식 (3)은 Mean Class Accuracy(MCA)로 CA의 평균값을 나타낸다. 여기서 $N_{c}$ 는 층서의 개수이다. 식 (4)와 (5)는 각각 Intersection Over Union(IU)과 그것의 평균값인 MeanIU를 나타낸다. IU는 $F_{i}$ 와 $G_{i}$ 의 합집합인 데이터 세트에 대해 교집합이 되는 데이터 세트의 비율을 말하며, 이 수식은 두 데이터 셋이 얼마나 겹치는 가를 측정한다. 식 (6)은 Frequency Weighted IU(FWIU)로 층서의 크기에 따라 가중치를 두어 IU를 구하는 방법이다.

(1)

PA = \frac{\sum_{i} | F_{i} \cap G_{i} |}{\sum_{i} G_{i}}

(2)

C A_{i} = \frac{| F_{i} \cap G_{i} |}{G_{i}}

(3)

MC A_{i} = \frac{1}{N_{c}} \sum_{i} C A_{i} = \frac{1}{N_{c}} \sum_{i} \frac{| F_{i} \cap G_{i} |}{| G_{i} |}

(4)

I U_{i} = \frac{| F_{i} \cap G_{i} |}{| F_{i} \cup G_{i} |}

(5)

MeanIU = \frac{1}{N_{c}} \sum_{i} I U_{i} = \frac{1}{N_{c}} \sum_{i} \frac{| F_{i} \cap G_{i} |}{| F_{i} \cup G_{i} |}

(6)

FWIU = \frac{1}{\sum_{i} |g_{i}|} \underset{i}{\cdot \sum |g_{i}|} \frac{| F_{i} \cap G_{i} |}{| F_{i} \cup G_{i} |}

결과 분석

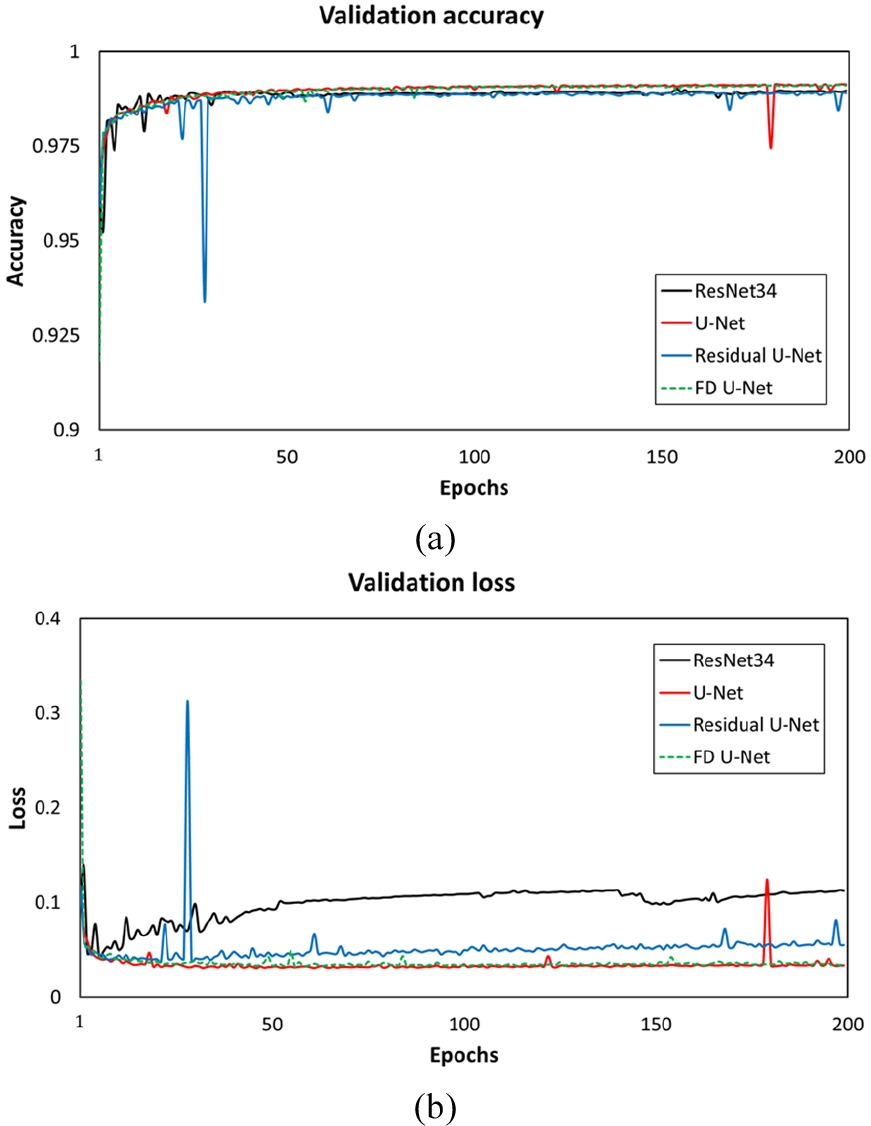
앞서 설명한 4가지 합성곱 신경망들을 학습시키고 학습된 모델들을 시험자료에 적용하였다. Fig. 8(a)와 (b)는 각각 검증 정확도(validation accuracy)와 검증 손실(validation loss)을 보여주는 그래프로, 가로축은 학습이 진행되는 에포크를 나타내고 세로축은 정확도와 손실 값을 나타낸다. ResNet34, U-Net, Residual U-Net, FD U-Net 4가지의 학습 모델 모두 총 에포크 200번이 진행되는 동안 검증 정확도의 값은 개선되고 있으며 손실값이 발산하지 않고 잘 수렴하고 있는 것을 확인 할 수 있다. Fig. 8(b)에서 ResNet34의 경우 과적합이 발생하는 것으로 보이는데, 이는 ResNet 모델이 네트워크의 복잡성을 증가시키지 않기 위해 맥스 풀링, 드롭 아웃 등을 사용하지 않기 때문으로 판단된다. Fig. 8(a)와 (b)의 정확도값과 손실값은 모델에 따라 계산되는 방법이 다르기 때문에 직접적인 비교는 크게 의미가 없을 것으로 판단된다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F8.jpg

Fig. 8

(a) Validation accuracy curve and (b) validation loss curve of four models: ResNet34, U-Net, Residual U-Net, and FD U-Net.

ResNet34, U-Net, Residual U-Net, FD U-Net의 학습 결과 중 최적의 모델을 선정하기 위해 총 200번의 동일한 학습 횟수를 적용하고, 그 중 검증 정확도가 가장 높은 모델을 선정하였다. 최종 시험자료에 적용 된 최적의 모델은 ResNet34, U-Net, Residual U-Net, FD U-Net의 순서대로 각각 101번째, 199번째, 177번째, 197번째 모델이 사용되었다.

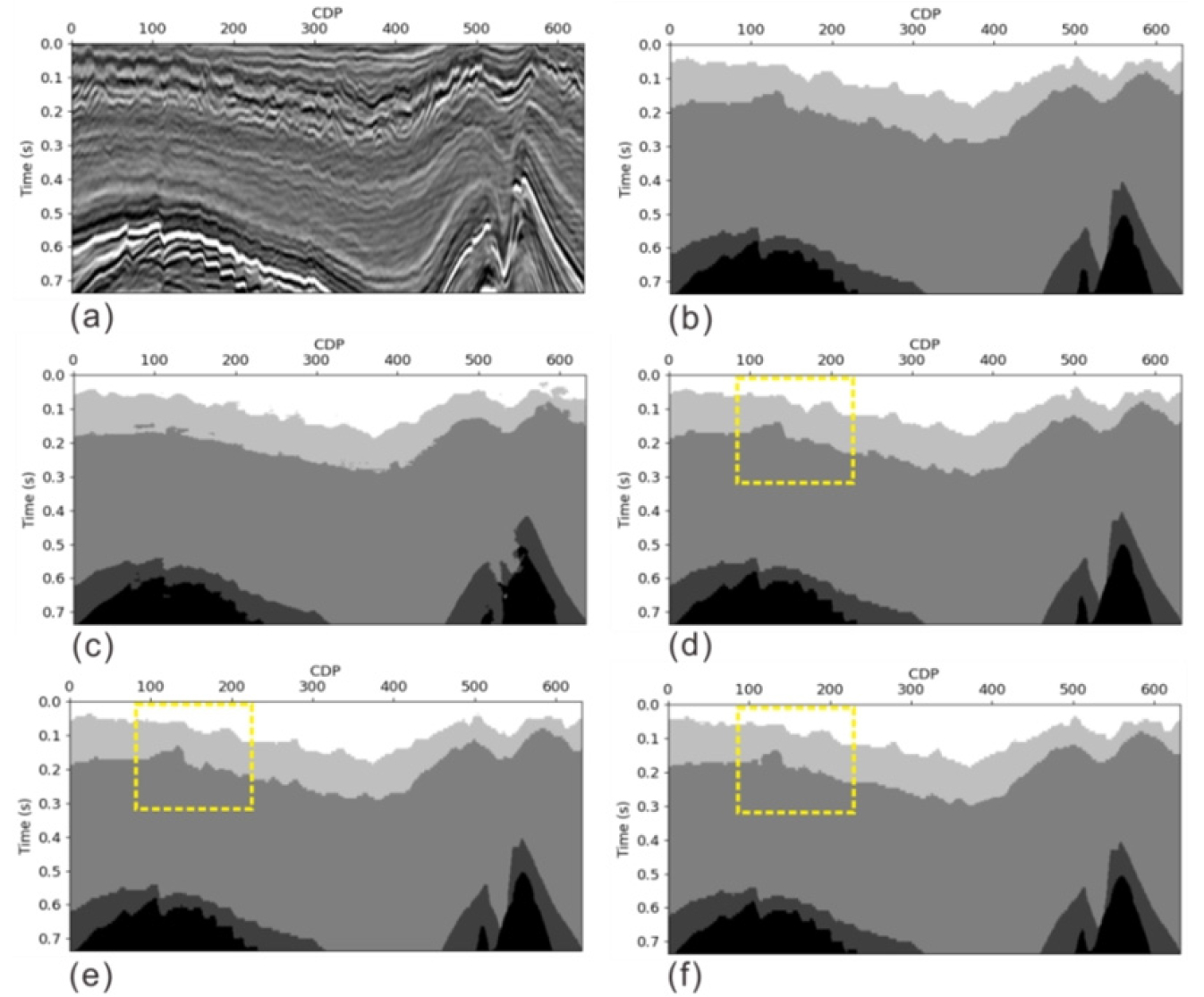
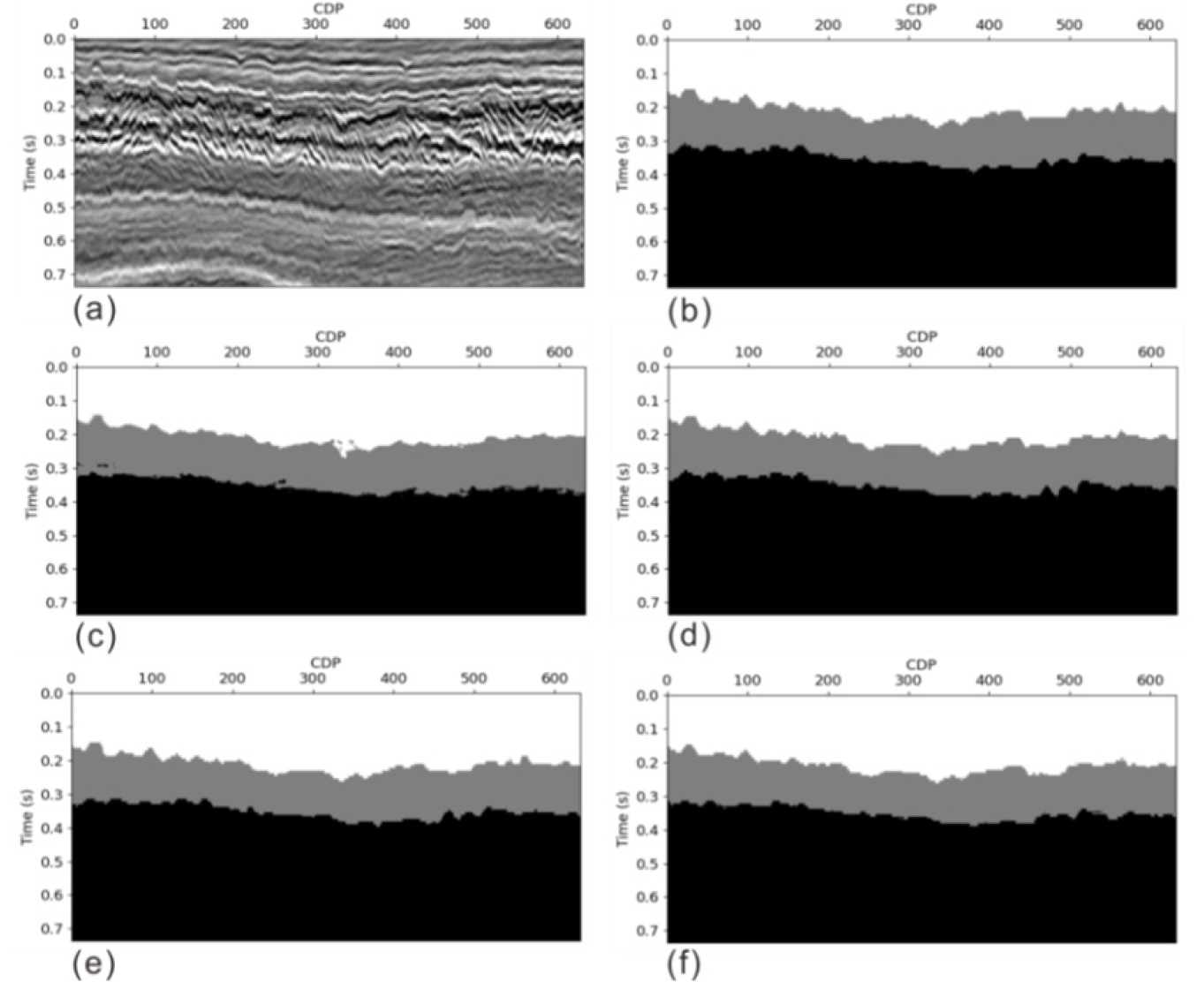
Fig. 9와 Fig. 10은 인라인을 활용한 학습 시험의 결과이다. 전체 시험에 사용된 인라인 자료의 개수는 총 100개이나 본 연구의 결과분석을 위해 무작위로 2개의 인라인 예측 결과 이미지를 사용하여 머신러닝 적용 결과를 살펴보았다. Fig. 9와 Fig. 10의 결과 이미지 내의 (a)~(f)는 각각 시험에 사용된 탄성파 이미지, 해당 탄성파의 정답 레이블, ResNet34 모델의 예측 결과, U-Net 모델의 예측 결과, Residual U-Net 모델의 예측 결과, FD U-Net 모델의 예측 결과를 나타낸다. Fig. 9와 Fig. 10의 (c) ResNet34 예측 이미지의 경우, 다른 모델의 예측 결과 이미지에 비해 상대적으로 현저하게 부정확한 층서 구분이 수행된 것을 확인할 수 있다. Fig. 9의 노란 점선 박스 부분에서 U-Net, Residual U-Net, FD U-Net의 순서대로 결과가 좋은 것을 확인할 수 있다. Fig. 10은 ResNet34를 제외한 나머지 세 모델의 결과가 비슷하게 층서를 잘 예측한 것으로 확인된다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F9.jpg

Fig. 9

In-line 13 with size of 633 × 185. (a) Its seismic section and (b) labeled data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net. Yellow dotted boxes indicate good results in the order of U-Net, Residual U-Net, and FD U-Net.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F10.jpg

Fig. 10

In-line 304 with size of 633 × 185. (a) Its seismic section and (b) labeled data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net.

2개의 인라인에 대해 정확도 평가를 수행하고 시험 결과들을 정량적으로 비교 해 보았다. Table 1은 인라인 시험자료 전체에 대한 4개 모델의 정량적인 수치를 나타낸다. 4개의 모델에 대해 PA, MCS, MIU, FWIU의 정확도를 (%)단위로 확인할 수 있다. ResNet34의 결과가 인코더-디코더 형태를 가지는 나머지 3가지 모델과 비교하여 모든 정확도 평가에서 가장 낮은 평균 정확도를 가진다. 반대로 U-Net의 경우 네 가지 평가에서 모두 가장 높은 정확도를 가진다. Residual U-Net과 FD U-Net은 각각 두번째와 세번째로 높은 정확도를 보인다. ResNet34를 제외한 나머지 U-Net, Residual U-Net, FD U-Net 모델의 정확도 평균은 순서대로 98.58%, 98.39%, 98.16%이다.

Table 1.

In-line test results of four model architectures tested on the Netherlands F3 dataset

Models	PA (%)	MCA (%)	MIU (%)	FWIU (%)	Avg.
ResNet34	97.69	94.17	90.26	95.58	94.43
U-Net	99.34	98.95	97.35	98.70	98.58
Residual U-Net	99.24	98.58	97.21	98.51	98.39
FD U-Net	99.09	98.57	96.76	98.21	98.16

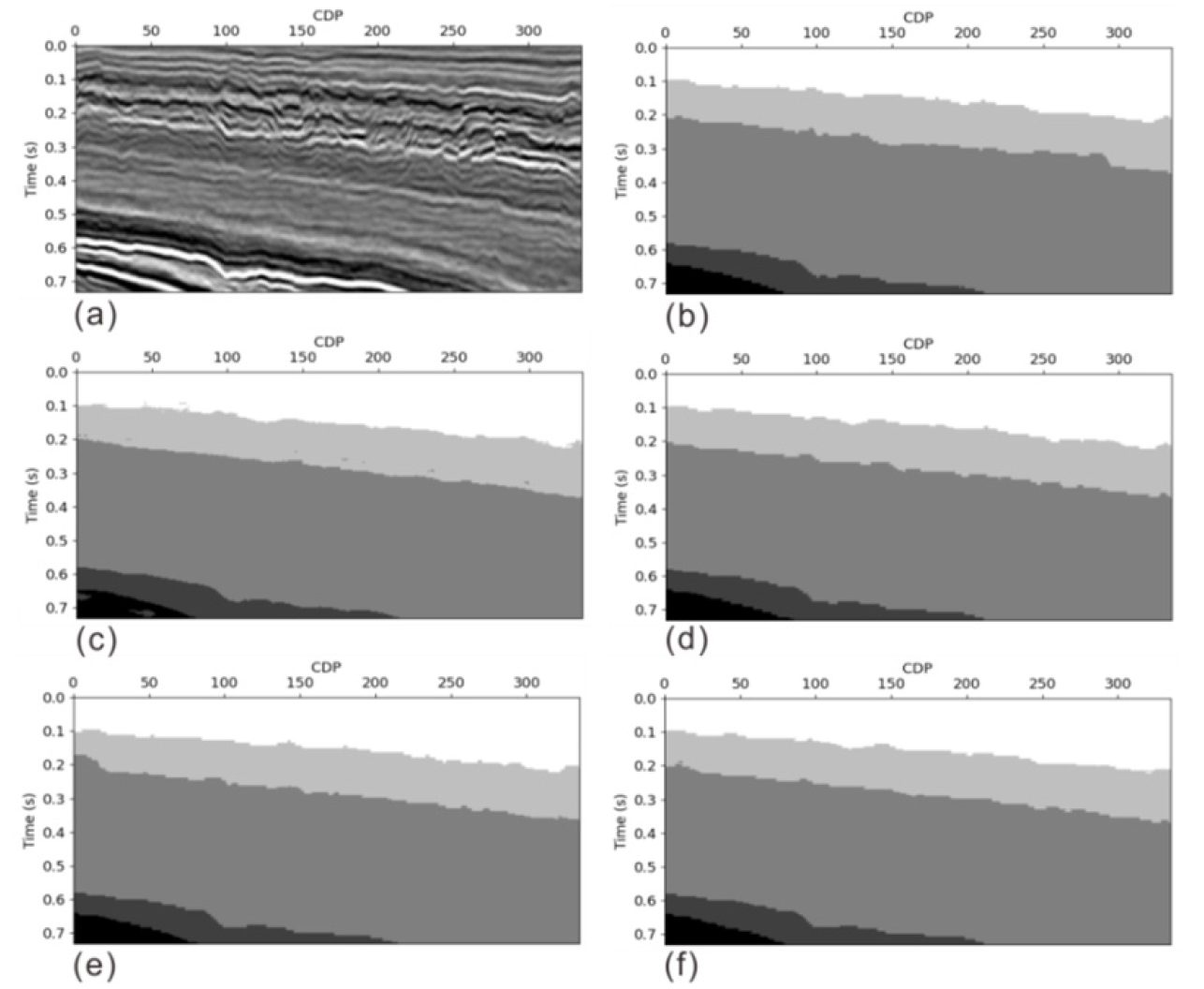
Fig. 11과 Fig. 12는 학습에 사용되지 않은 층서의 특징을 가지는 크로스라인 자료를 활용한 학습 시험의 결과이다. 전체 시험에 사용된 크로스라인 자료의 개수는 총 100개이나 본 연구의 결과분석을 위해 무작위로 2개의 크로스라인 예측 결과 이미지를 사용하여 정성적인 분석을 하였다. Fig. 11과 Fig. 12 내의 (a)~(f) 이미지 구성은 인라인과 동일하다. 간단한 층서 형태를 나타내는 Fig. 11의 예제의 경우, 예측결과 이미지에서 4가지 모델 모두 층서 예측을 잘 하는 것으로 확인된다. 반면 Fig. 12의 경우처럼 다소 복잡한 층들은 예측 정확도가 떨어진다. 이러한 결과는 Fig.12(a)의 하부에 존재하는 복잡한 지층 형태가 학습시 자료에 포함되지 않았기 때문으로 생각된다. Fig. 12는 앞서 인라인의 시험 결과와 같이 (c) ResNet34 예측 이미지의 경우, 다른 모델의 예측 결과 이미지에 비해 상대적으로 현저하게 부정확한 층서 예측이 수행된 것을 확인할 수 있다. Fig. 12의 노란 점선 박스로 표시된 부분에서 U-Net의 결과가 다른 모델들의 결과보다 좋고, FD U-Net의 결과가 그 다음으로 좋은 것으로 확인된다.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F11.jpg

Fig. 11

Cross-line 192 with size of 336 × 184. (a) Its seismic section and (b) masking data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net.

https://static.apub.kr/journalsite/sites/ksmer/2020-057-06/N0330570602/images/ksmer_57_06_02_F12.jpg

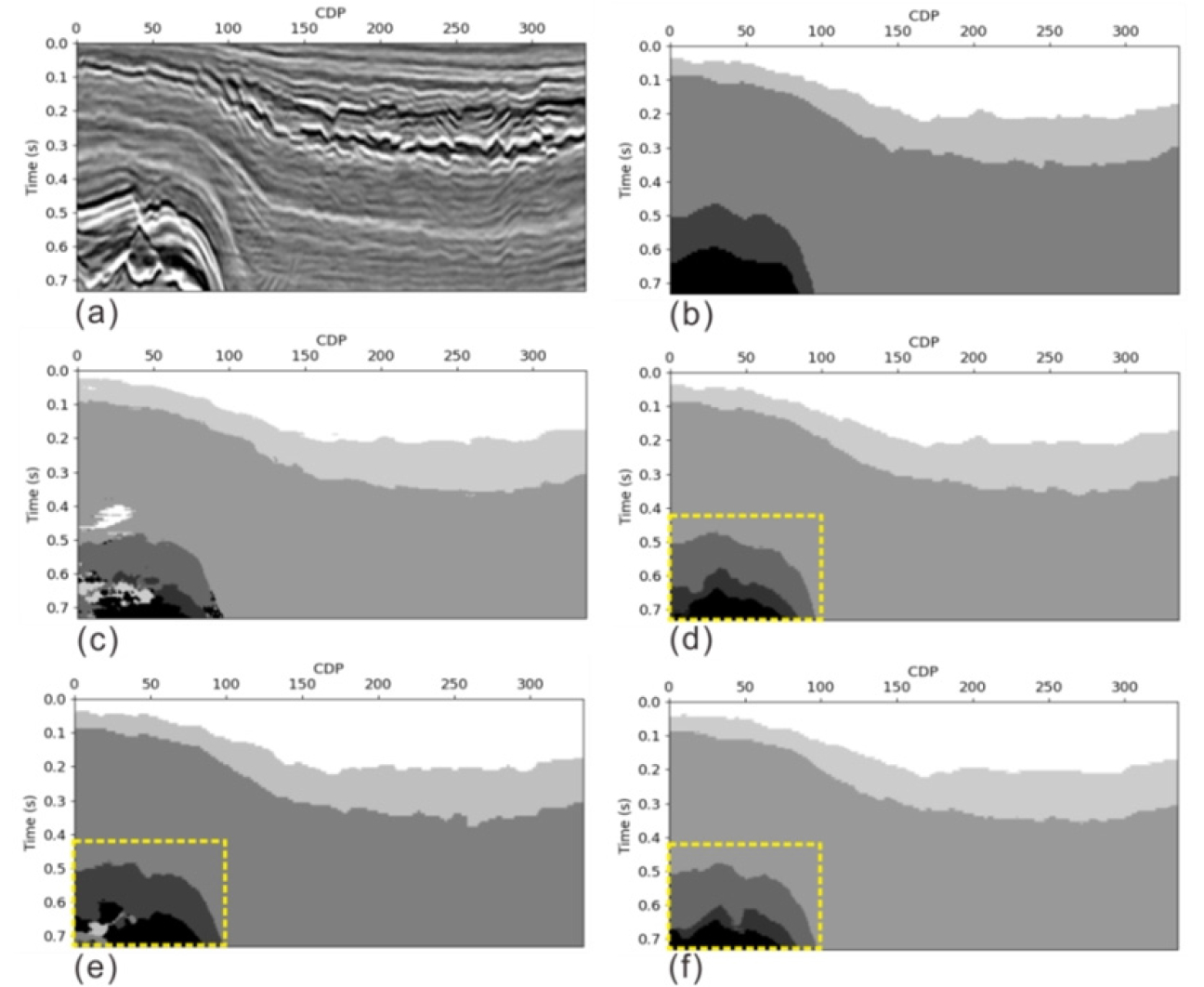
Fig. 12

Cross-line 614 with size of 334 × 184. (a) Its seismic section and (b) masking data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net. Yellow dotted boxes indicate that the result of U-Net is better than those of the other models and that the result of FD U-Net is second best.

인라인을 이용한 시험과 마찬가지로 크로스라인 시험 결과에도 정확도 평가를 수행하였다. Table 2는 크로스라인 시험자료 전체에 대한 4개 모델의 정량적인 수치를 나타낸다. ResNet34와 U-Net의 결과가 인라인 시험 결과와 동일하게 각각 가장 낮고 높은 정확도값을 가진다. 반면에 Residual U-Net과 FD U-Net은 크로스라인 시험 결과에서 각각 세번째와 두번째의 정확도 값을 가지는데, 이는 인라인의 정확도 결과와 상이한 것으로 확인된다. 그러나 이 두 모델의 정확도 값의 차이가 근소하므로 순위 비교의 의미가 크지 않은 것으로 판단된다. ResNet34를 제외한 나머지 U-Net, Residual U-Net, FD U-Net 모델의 정확도 평균은 순서대로 95.83%, 95.38%, 95.57%이다. 크로스라인의 평균 정확도는 인라인과 비교하여 다소 낮은 수치로 나타나지만 95% 이상의 정확도를 나타내고 있다. 이는 인라인으로만 구성된 학습 자료로 학습된 인공지능 모델이 상대적으로 다른 특성을 가지는 크로스라인 시험 자료에 대해서도 층서 분류를 비교적 정확하게 수행할 수 있음을 나타낸다.

Table 2.

Cross-line test results of four model architectures tested on the Netherlands F3 dataset

Models	PA (%)	MCA (%)	MIU (%)	FWIU (%)	Avg.
ResNet34	97.49	93.29	88.31	95.31	93.60
U-Net	98.33	95.91	92.28	96.82	95.83
Residual U-Net	98.18	95.15	91.65	96.55	95.38
FD U-Net	98.20	95.59	91.91	96.59	95.57

Table 3은 모델별로 학습에 사용되는 파라미터수와 총 200회 에포크가 진행되는데 걸리는 시간을 확인할 수 있다. 모델별 학습에 사용된 파라미터의 수는 ResNet34, U-Net, Residual U-Net, FD U-Net의 순서대로 각각 21,292,360개, 537,766개, 560,280개, 537,766개가 사용되었고 총 200번의 에포크가 진행되는데 사용된 시간은 순서대로 178분, 143분, 184분, 207분이 소요되었다. U-Net의 경우 학습시간이 가장 짧으며, 파라미터 수와 시간을 고려할 때 가장 효율적으로 학습을 수행 할 수 있는 것으로 판단된다.

Table 3.

Total number of parameters used in training and the time of 200 epochs

Models	Train params	Time (min)
ResNet34	21,292,360	178
U-Net	537,766	143
Residual U-Net	560,280	184
FD U-Net	537,766	207

본 연구에서는 네덜란드 F3 block의 탄성파 이미지를 활용하여 머신 러닝 기법을 적용하였으며, U-Net이 나머지 모델들에 비해 근소하게 더 좋은 정확도를 가진다고 판단된다. Zhang et al.(2018), Zhang et al.(2019), 본 연구의 3가지 실험 결과를 비교해보면 세 경우 모두 U-Net 기반의 세그멘테이션 기법에 해당하지만 데이터의 특성에 따라 적용되는 머신 러닝 모델의 결과가 근소하게 뒤바뀔 수 있는 것으로 판단되어, 어떠한 모델이 가장 확실하게 우월하다고 확정 지을 수 없다. 다만, 본 연구에서는 Table 3의 결과에서도 확인 하였듯이 U-Net의 학습 파라미터수가 가장 작았고 학습 시간이 가장 짧았기 때문에 U-Net이 가장 효율적인 모델이라고 할 수 있다.

결 론

탄성파 층서를 구분하는 것은 단층, 암염돔, 명점 등의 특정 구조를 정의하기 이전에 기본적으로 수행되는 중요한 해석과정이다. 본 연구에서는 최근 머신 러닝 연구에 많이 활용되고 있는 네덜란드 F3 block 공개자료를 활용하여 탄성파 층서 분류를 위한 몇 가지의 합성곱 신경망 모델에 대한 연구를 수행하였다. ResNet34, U-Net, Residual U-Net, FD U-Net의 4가지 모델 중 층서 구분 연구를 위해서는 ResNet34 모델 보다 U자 형태를 가지는 U-Net, Residual U-net, FD U-Net의 인코더-디코더 모델이 더 적합한 것으로 확인 되었다. 이는 결합을 통해 인코더 과정에서 추출된 정보가 디코더 모델에 추가되는 인코더-디코더 모델의 특징적인 과정이 탄성파 층서 구분에 효과적으로 작용하는 것으로 생각된다. 특히, 인코더-디코더 모델 중 U-Net 모델이 가장 높은 정확도 결과를 보여주는 것으로 확인하였다. 또한, 학습 자료와 동일한 성질을 가지는 인라인과 다른 성질을 가지는 크로스 라인 두 자료 모두에 대해 인코더-디코더 모델이 비교적 정확히 층서 구분을 수행할 수 있음을 확인하였다. 학습 시간 및 학습 파라미터를 고려할 때 학습 효율도 U-Net이 좋은 것으로 확인되었다.

하지만, 앞서 결과 분석의 마지막에 언급하였듯이 다양한 연구 사례에서 모델별 정확도 차이가 근소하며, 적용되는 데이터의 특성에 따라 변할 수 있는 것을 확인하였다. 본 연구의 결과 탄성파 층서 구분에서 머신 러닝 기법의 적용은 기존 해석 방법의 시간과 인력의 한계를 개선할 수 있는 방법으로 판단된다.

Acknowledgements

이 연구는 한국해양과학기술원의 주요사업인 ‘해양방위 및 안전기술 개발’ 사업(PE99841)의 지원을 받아 수행되었습니다.

References

Alaudah, 2019b, Facies_classification_benchmark, 2019.11.28, https://github.com/yalaudah/fa cies_classification_benchmark.

Alaudah, Y., Michałowicz, P., Alfarraj, M., and AlRegib, G., 2019a. A machine-learning benchmark for facies classification. Interpretation, 7(3), p.SE175-SE187. 10.1190/INT-2018-0249.1

Bengio, Y., Simard, P., and P. Frasconi., 1994. Learning long-term dependencies with gradient descent is difficult, IEEE Transactions on Neural Networks, 5(2), p.157-166. 10.1109/72.27918118267787

Chaki, S., 2015. Reservoir characterization: A machine learning approach, MS Thesis, Indian Institute of Technology, India, 98p.

Chevitarese, D., Szwarcman, D., Silva, R. M. D., and Brazil, E. V., 2018. Seismic facies segmentation using deep learning. AAPG Annual Convention and Exhibition. Salt Lake City, Utah.

Cho, Y., Jeong, D., and Jun, H., 2020. Semi‐auto horizon tracking guided by strata histograms generated with transdimensional Markov‐chain Monte Carlo. Geophysical Prospecting, 68(5), p.1456-1475. 10.1111/1365-2478.12933

Choi, W.C., Lee, G.H., Cho, S.I., Choi, B.H., and Pyun, S.J., 2020. Fault Detection for Seismic Data Interpretation Based on Machine Learning: Research Trends and Technological Introduction. Geophysics and Geophysical Exploration, 23(2), p.97-114.

dGB Earth Sciences, Seismic interpretation software & services, 2018.

Dramsch, J.S. and Lüthje, M., 2018. Deep-learning seismic facies on state-of-the-art CNN architectures. SEG Technical Program Expanded Abstracts 2018, Society of Exploration Geophysicists. p.2036-2040. 10.1190/segam2018-2996783.1

Glorot, X. and Bengio, Y., 2010. Understanding the difficulty of training deep feedforward neural networks. Proceedings of the thirteenth international conference on artificial intelligence and statistics, AISTATS, 2010, p.249-256.

Griffith, D.P., Zamanian, S.A., Vila, J., Vial-Aussavy, A., Solum, J., Potter, R.D., and Menapace, F., 2019. Deep learning applied to seismic attribute computation. Interpretation, 7(3), p.SE141-SE150. 10.1190/INT-2018-0227.1

Guillen, P., Larrazabal, G., González, G., Boumber, D., and Vilalta, R., 2015. Supervised learning to detect salt body. SEG Technical Program Expanded Abstracts 2015, Society of Exploration Geophysicists, p.1826-1829. 10.1190/segam2015-5931401.1

He, K., Zhang, X., Ren, S., and Sun, J., 2016a. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, p.770-778. 10.1109/CVPR.2016.9026180094

He, K., Zhang, X., Ren, S., and Sun, J., 2016b. Identity mappings in deep residual networks. In European conference on computer vision. Springer, Cham., p.630-645. 10.1007/978-3-319-46493-0_38

Keynejad, S., Sbar, M.L., and Jhonson, R.A., 2019. Assessment of machine-learning techniques in predicting lithofluid facies logs in hydrocarbon wells. Interpretation, 7(3), p.SF1-SF13. 10.1190/INT-2018-0115.1

Krizhevsky, A., Sutskever, I., and Hinton, G.E., 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems, p.1097- 1105.

Kumar, P.C. and Sain, K., 2018. Attribute amalgamation-aiding interpretation of faults from seismic data: An example from Waitara 3D prospect in Taranaki basin off New Zealand. Journal of Applied Geophysics, 159, p.52-68. 10.1016/j.jappgeo.2018.07.023

Noh, H., Hong, S., and Han, B., 2015. Learning deconvolution network for semantic segmentation. Proceedings of the IEEE international conference on computer vision (ICCV), p.1520-1528. 10.1109/ICCV.2015.178

Onajite, E., 2013. Seismic data analysis techniques in hydrocarbon exploration. Elsevier. 256p.

Qian, F., Yin, M., Liu, X.Y., Wang, Y.J., Lu, C., and Hu, G.M., 2018. Unsupervised seismic facies analysis via deep convolutional autoencoders. Geophysics, 83(3), p.A39-A43. 10.1190/geo2017-0524.1

Ronneberger, O., Fischer, P., and Brox, T., 2015. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, p.234-241. 10.1007/978-3-319-24574-4_28

Sen, S., Kainkaryam, S., Ong, C., and Sharma, A., 2019, Regularization strategies for deep-learning-based salt model building. Interpretation, 7(4), p.T911-T922. 10.1190/INT-2018-0229.1

Shi, Y., Wu, X., and Fomel, S., 2019, SaltSeg: Automatic 3D salt segmentation using a deep convolutional neural network. Interpretation, 7(3), p.SE113-SE122. 10.1190/INT-2018-0235.1

Silva, R.M., Baroni, L., Ferreira, R.S., Civitarese, D., Szwarcman, D., and Brazil, E.V., 2019. Netherlands dataset: A new public dataset for machine learning in seismic interpretation. arXiv preprint arXiv:1904.00770.

Simonyan, K. and Zisserman, A., 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.

Smith, R., Mukerji, T., and Lupo, T., 2019. Correlating geologic and seismic data with unconventional resource production curves using machine learning. Geophysics, 84(2), p.O39-O47. 10.1190/geo2018-0202.1

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., and Rabinovich, A., 2015. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition, p.1-9. 10.1109/CVPR.2015.7298594

Tian, X. and Daigle, H., 2018. Machine-learning-based object detection in images for reservoir characterization: A case study of fracture detection in shales. The Leading Edge, 37(6), p.435-442. 10.1190/tle37060435.1

Waldeland, A. and A. Solberg, 2016. 3D Attributes and Classification of Salt Bodies on Unlabelled Datasets. 78th EAGE Conference and Exhibition 2016, EAGE Publications BV. 10.3997/2214-4609.201600880

Wrona, T., Pan, I., Gawthorpe, R.L., and Fossen, H., 2018. Seismic facies analysis using machine learning. Geophysics, 83(5), p.O83-O95. 10.1190/geo2017-0595.1

Xiong, W., Ji, X., Ma, Y., Wang, Y., ALBinHassan, N.M., Ali, M.N., and Luo, Y., 2018. Seismic fault detection with convolutional neural network. Geophysics, 83(5), p.O97-O103. 10.1190/geo2017-0666.1

Yi, H.U., 2019, Case Analysis of Applications for Deep Learning Technology in the Mining Industry. Journal of the Korean Society of Mineral and Energy Resources Engineers, 56(5), p.435-446. 10.32390/ksmer.2019.56.5.435

Yu, F. and Koltun, V., 2015. Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122.

Zhang, C., Frogner, C., Araya-Polo, M., and Hohl, D., 2014. Machine-learning based automated fault detection in seismic traces. 76th EAGE Conference and Exhibition 2014, European Association of Geoscientists & Engineers, 2014(1), p.1-5. 10.3997/2214-4609.20141500

Zhang, W., Lu, X., Gu, Y., Liu, Y., Meng, X., and Li, J., 2019. A Robust Iris Segmentation Scheme Based on Improved U-Net. IEEE Access, 7, p.85082-85089. 10.1109/ACCESS.2019.2924464

Zhang, Z., Liu, Q., abd Wang, Y., 2018. Road extraction by deep residual u-net. IEEE Geoscience and Remote Sensing Letters, 15(5), p.749-753. 10.1109/LGRS.2018.2802944

Zhao, T., 2018a. Seismic facies classification using different deep convolutional neural networks. SEG Technical Program Expanded Abstracts 2018, Society of Exploration Geophysicists, p.2046-2050. 10.1190/segam2018-2997085.1

Zhao, T., Li, F., and Marfurt, K.J., 2018b. Seismic attribute selection for unsupervised seismic facies analysis using user-guided data-adaptive weights. Geophysics, 83(2), p.O31-O44. 10.1190/geo2017-0192.1

Zhou, X. Y. and Yang, G. Z., 2019. Normalization in training U-Net for 2-D biomedical semantic segmentation. IEEE Robotics and Automation Letters, 4(2), p.1792-1799. 10.1109/LRA.2019.2896518

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Comparison of Convolutional Neural Networks for Dividing Seismic Sequences

ABSTRACT

MAIN

Fig. 1

Network architecture of ResNet34.

Fig. 2

Network architecture of U-Net. In this study, unlike in the original U-Net model, the number of layers and feature maps was reduced.

Fig. 3

Network architecture of Residual U-Net.

Fig. 4

Network architecture of FD U-Net.

Fig. 5

Location of the Netherlands F3 block in the North Sea and 3-D seismic cube used in this paper.

Fig. 6

(a) A seismic section used in training and (b) its labeled section with six different sequences. Patches used for (c) ResNet34 and (d) encoder–decoder model training. (c) and (d) are patches of size 64 × 64. The red and green square boxes are cropped from images (a) and (b), respectively.

Fig. 7

Seismic sections with a size of (a) 701 × 255 and (b) 401 × 255. The red squares represent sizes of 633 × 185 and 336 × 184, respectively, and were used to test the four different CNN models.

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 8

(a) Validation accuracy curve and (b) validation loss curve of four models: ResNet34, U-Net, Residual U-Net, and FD U-Net.

Fig. 9

In-line 13 with size of 633 × 185. (a) Its seismic section and (b) labeled data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net. Yellow dotted boxes indicate good results in the order of U-Net, Residual U-Net, and FD U-Net.

Fig. 10

In-line 304 with size of 633 × 185. (a) Its seismic section and (b) labeled data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net.

Table 1.

In-line test results of four model architectures tested on the Netherlands F3 dataset

Fig. 11

Cross-line 192 with size of 336 × 184. (a) Its seismic section and (b) masking data. The predicted results on (c) ResNet34, (d) U-Net, (e) Residual U-Net, and (f) FD U-Net.

Fig. 12

Table 2.

Cross-line test results of four model architectures tested on the Netherlands F3 dataset

Table 3.

Total number of parameters used in training and the time of 200 epochs

Acknowledgements

References