서 론
본 론
순환신경망(RNN)
장단기기억(LSTM)
대상광구 개요 및 분석대상 설정
자료 전처리 및 일관성 검토
LSTM-RNN 설계
Period B 구간의 THP 예측
입력 시퀀스 길이에 따른 예측성능 분석
결 론
서 론
유가스정의 생산량 및 압력에 대한 정보는 회수율 극대화를 위한 계획수립 및 저류층 관리에 있어 반드시 획득되어야 하는 정보에 속한다. 일일 생산량은 각 생산정에 다상유량계(multiphase flowmeter)를 설치하여 계측하거나, 다수의 생산정이 연결된 분리기에서 총 유량을 측정하고 이를 생산량 분배(production back-allocation)기법으로 개별 생산정에 할당한다. 생산량 분배기법은 생산정의 생산능력을 시험 분리기를 통해 파악하고 이를 바탕으로 총량에서 개별 생산정으로 생산량을 할당하는 방식이다.
일반적으로 압력은 생산거동 분석을 위한 저류층 시뮬레이션(reservoir simulation), 생산천이거동분석(rate transient analysis) 등에 생산량과 함께 직접 입력자료로 사용될 뿐 아니라, 압력변화 자체가 생산거동 변화를 모니터링하는 중요한 지표로 사용된다. 생산에 따라 변하는 정두압(Well Head Pressure, WHP or Tubing Head Pressure, THP) 및 정저압(Bottom Hole Pressure, BHP)은 압력게이지를 설치하여 실시간으로 측정하거나, 압력게이지를 회수한 후 일괄적으로 획득한다. 그러나 장기간 운영에 따른 게이지의 오작동이 발생할 경우 자료의 일부구간이 누락 또는 소실되거나 피크값이 포함되고, 정상범위를 벗어난 비상식적인 오차나 잡음이 포함되기도 한다(Carvajal et al., 2018). 또한, 생산장비 교체 등 생산정 유지보수나 현장 생산테스트 과정에서 비정상치(abnormal data)가 발생하기도 한다. 이러한 자료들은 의사결정에 활용하기 전 데이터 정리(cleaning), 조건화(conditioning), 필터링(filtering) 등 다양한 사전 처리를 거쳐야 한다. 일부 압력자료가 소실된 경우 저류층 시뮬레이션 또는 생산관 유동 모델링을 통해 이를 복원할 수 있다. 하지만, 이 경우 충분한 전문지식 및 분석자료가 구비되어야만 신뢰할 수 있는 결과를 도출할 수 있다.
누락되거나 오염된 압력자료를 예측하기 위해 데이터기반 머신러닝(machine learning) 기법이 활용되기도 한다. 머신러닝은 대상이 되는 시스템의 작동원리를 이론적 또는 수치해석적으로 분석하는 대신 시스템에 입력되거나 출력되는 자료들 사이의 상호관계를 파악하여 분석하는 방법이다. 최근들어 E&P 분야에서도 딥러닝(Deep Neural Network, DNN)을 포함한 머신러닝 기법이 활발히 적용되고 있다. 셰일저류층의 생산량 감쇄경향 및 궁극가채량 분석(Kotezhekovt et al., 2017; Vyas et al., 2017; Bowie, 2018; Sagheer and Kotb, 2019), 공저압력 분석(Osman et al., 2005; Ashena and Moghadasi, 2011; Jahanandish et al., 2011; Ebrahimi and Khamehchi, 2015; Spesivtsev et al., 2018; Tian and Horne, 2019), 시추시 발생하는 이벤트의 자동 감지(Jacos, 2015; Unrau et al., 2017), 시추위치 최적화(Guyaguler et al., 2002; Min et al., 2011; Sayyafzadeh, 2017; Jang et al., 2017), 생산이력 기반 저류층 역산모델 생성(Ahn et al., 2018; Lee et al., 2018) 등의 연구에 다양한 머신러닝이 적용되고 있다.
Osman et al.(2005)는 수직정에서 압력감소를 예측하기 위해 ANN(Artificial Neural Network) 모델을 사용하였다. 모델 학습을 위해 실제 현장자료를 사용하였으며 기존의 경험식을 사용하여 모델의 예측성능을 비교분석하였다. 또한 ANN 모델의 구조를 변경시키거나 최적화 알고리즘을 다양하게 하여 압력 예측력을 높이려는 시도도 이루어졌다(Jahanandish et al., 2011; Ebrahimi and Khamehchi, 2015). Ashena and Moghadasi(2011)는 ANN을 사용하여 생산정의 환체(annulus)의 압력을 예측하는 연구를 진행하였다. Spesivtsev et al.(2018)은 생산정의 다상유동에 대해 DNN을 사용하여 BHP를 예측하는 모델을 제시하였다. 이때, DNN의 은닉층은 2개로 구성되었으며, 입력자료로서 THP, 유량, 생산정 형태를 사용하여 다양한 유동 상태에 대한 예측력을 높였다.
순환신경망(Recurrent Neural Network, RNN)은 시계열 자료 분석에 특화된 딥러닝의 한 종류이다. RNN은 특정 길이의 시계열 자료에 대한 패턴을 분석하여 다음 시점의 값을 예측하는 딥러닝 모델로서 주식가격, 시점별 수요예측, 자동변역 등에 활용되고 있다. 이와 같이 RNN은 과거의 과거의 시계열 정보를 반영하여 미래 예측에 적합하도록 구성되었지만, 은닉층이 많아지거나 시계열 자료가 길어질 경우 학습이 잘 이루어지지 않는 경향이 나타난다. 이를 보완하기 위해 LSTM(Long Short-Term Memory)이 제시되었다(Hochreiter and Schmidhuber, 1997). Sagheer and Kotb(2019)는 LSTM-RNN을 사용하여 셰일저류층의 생산량 자료를 학습시켜 미래 생산을 예측하였고, Tian and Horne(2017)은 공저 게이지의 온도와 압력자료를 RNN으로 학습시켜 저류층의 생산능력을 예측하였다.
이 연구에서는 LSTM-RNN을 활용하여 해양 가스 생산정에서 센서오류로 인해 누락된 구간의 THP를 추정하였다. 1년 7개월간의 가스생산량, THP 및 BHP를 사용하여 신경망을 학습시켰으며, 이후 2년간의 가스생산량과 BHP를 바탕으로 누락된 THP를 예측하였다. 또한 생산관 유체 모델을 통해 예측한 압력과 비교하여 LSTM-RNN 모델 적용의 타당성을 분석하였다.
본 론
순환신경망(RNN)
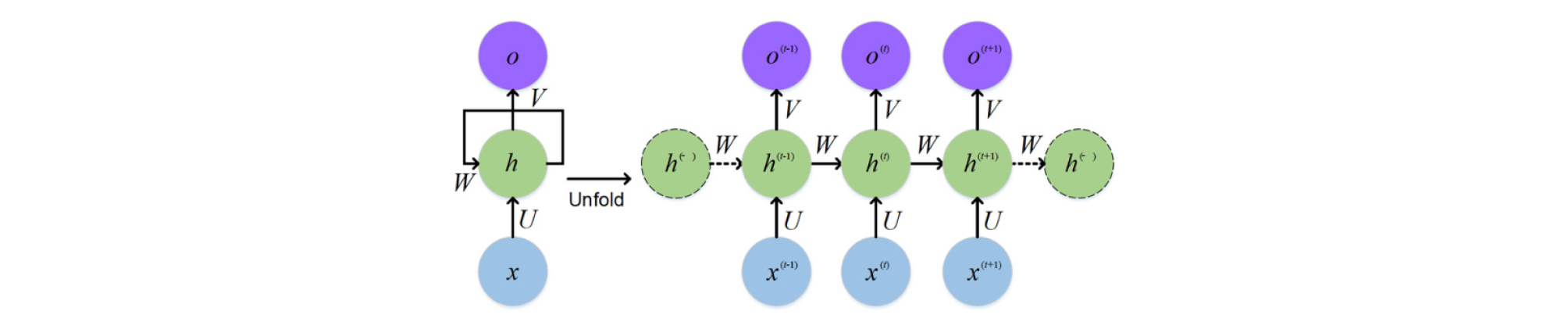
RNN은 주식가격, 음성인식, 자동번역 등 시계열 데이터 분석에 주로 사용된다. 일반적인 신경망은 입력에서 출력으로 한 방향으로만 값이 전달되는 반면, RNN에서는 입력에서 출력으로 값이 전달될 뿐만 아니라 출력이 다시 입력으로 전달되어 순환한다는 점에서 일반 신경망과 차이점이 있다. RNN의 기본구조는 Fig. 1과 같다. Fig. 1에서 x는 입력층, h는 은닉층, o는 출력층을 나타내며, U는 입력-은닉층 사이, V는 은닉-출력층 사이의 연결 가중치를 의미한다. W는 시계열이 입력됨에 따라 은닉층 상태가 순환할 때의 가중치를 나타낸다. Fig. 1의 오른쪽 그림은 순환구조를 시간별로 펼쳐놓은 것으로서 작동원리는 다음과 같다. (t-1) 시점의 입력값(xt-1)이 입력될 때 이전 시점의 은닉층 상태(ht-2)와 결합하여 (t-1) 시점의 은닉층 상태(ht-1)를 결정한다. 이 은닉층 값은 출력층으로 전달됨과 동시에 다음 시점의 입력인 xt와 함께 (t) 시점의 은닉층 상태를 결정하는데 사용된다. 이와 같이 RNN에서는 이전 시점의 입력값이 은닉층을 통해 다음시점으로 전달됨으로써 시계열의 과거자료가 미래에 영향을 주도록 설계된다. 이러한 과정은 식(1) 및 식 (2)와 같이 수식화시킬 수 있다.
| $$h_t-f(Ux_t+Wh_{t-1}+b)$$ | (1) |
| $$o_t=g(Vh_t+c)$$ | (2) |
여기서 xt, ht, 그리고 ot는 각각 (t) 시점의 입력, 은닉, 그리고 출력층의 값을 의미한다. U, W, 그리고 V는 연결된 층사이의 가중치를 의미하며, f와 g는 각각 은닉층과 출력층의 활성화함수(activation function)를 나타낸다. b와 c는 편향(bias)으로서 상수값을 가진다.
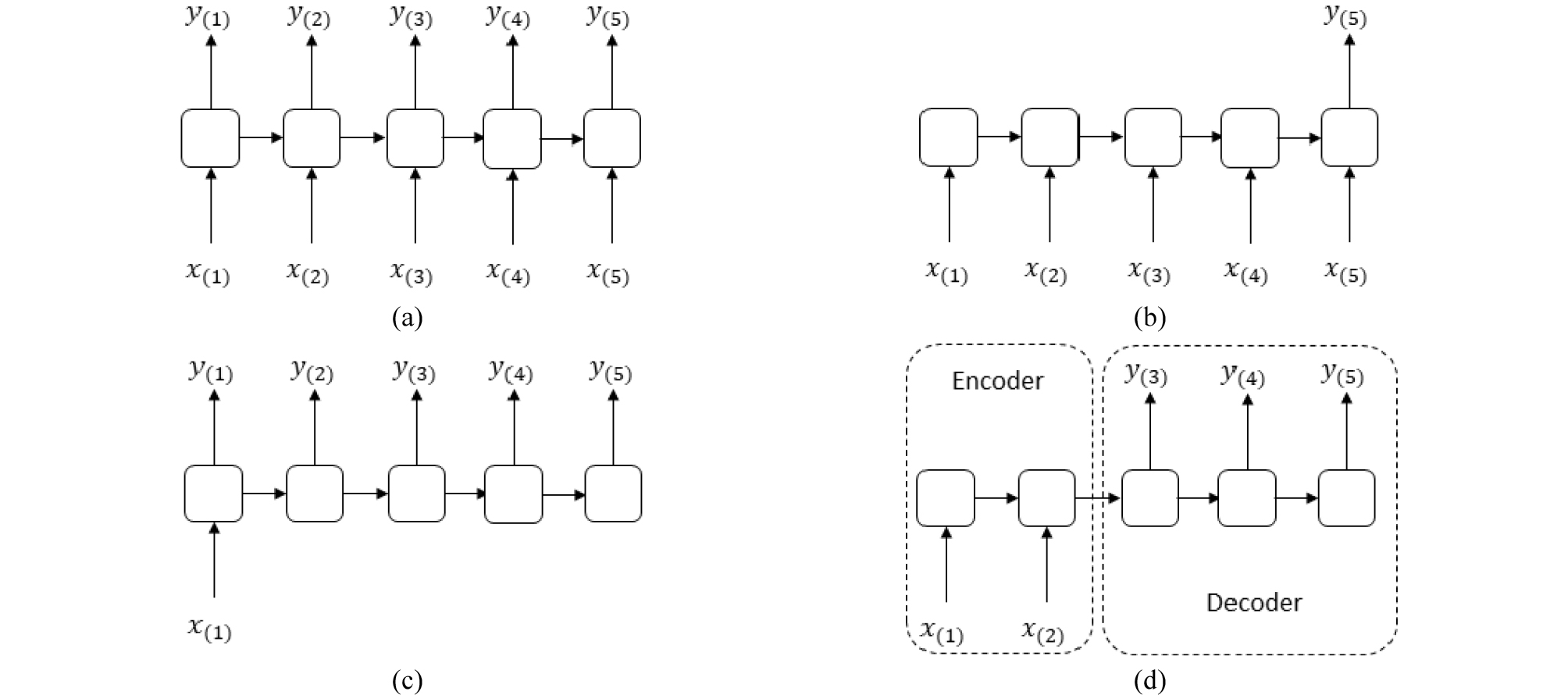
RNN은 목적에 따라 입출력을 다양한 형태로 구성할 수 있다. Fig. 2는 다양한 형태의 순환신경망 구조를 나타낸 것이다. Fig. 2(a)의 sequence-to-sequence는 시계열에서 각 시점에 대응하는 출력을 1대 1로 대응시켜 예측에 사용하는 구조로서 주식예측 모델에 적용가능하다. 일련의 시계열을 받아들여 하나의 출력을 예측하는 모델은 Fig. 2(b)의 sequence-to-vector에 해당한다. 특히 이 모델은 유가스정 생산량 예측 문제에 적용되는 대표적인 모델이다. Vector- to-sequence는 하나의 입력만으로 일련의 시계열을 예측하는 것으로 이는 이미지 캡셔닝에 적용가능하다(Fig. 2(c)). 마지막으로 Fig. 2(d)의 delayed-sequence-to-sequence는 자동번역과 같이 모든 입력을 받은 후 분석이 가능한 문제에 적용될 수 있다.
장단기기억(LSTM)
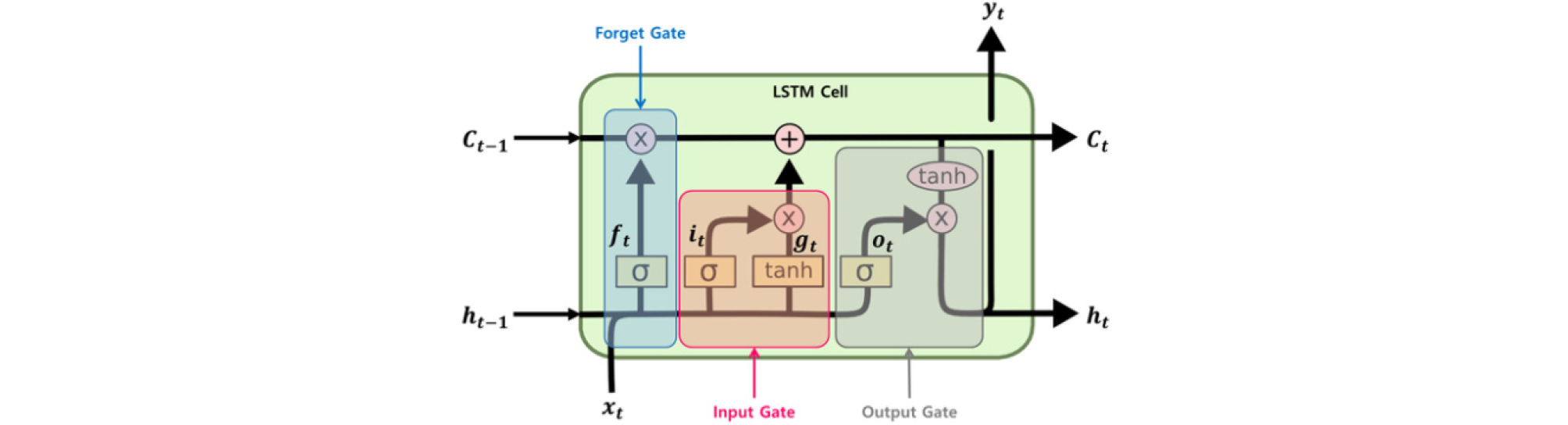
순환신경망은 과거의 시계열 정보를 반영하여 미래예측에 적합하도록 구성되어 있지만 입력하는 시계열이 길어지면 심층신경망에서 나타나는 기울기 소실문제(gradient vanishing problem)와 더불어 초기 입력정보가 후기 입력정보에 제대로 반영되지 않는 문제가 발생하게 된다. 즉, 장기기억 의존성(long-term dependencies)이 사라지는 문제가 발생하게 되며, 이를 극복할 수 있는 방법으로 LSTM이 제안되었다(Hochreiter and Schmidhuber, 1997). Fig. 3은 LSTM 셀 구조를 나타낸 것으로서 Fig. 1의 순환신경망에서 은닉층 뉴런을 대체하여 구성된다. LSTM 셀은 단기상태(short-term state)인 ht와 장기상태(long-term state)인 Ct가 다음 시점으로 전달된다. 이때 Ct에 의해 장기기억이 보존되어 장기기억 의존성 문제를 해결할 수 있다.
LSTM의 내부구조에는 3가지 게이트가 존재한다. 장기기억에서 필요없는 정보를 삭제하는 망각게이트(forget gate), 장기기억에 저장할 정보를 입력하는 입력게이트(input gate), 그리고 다음 시점으로 전달할 단기상태를 결정하는 출력게이트(output gate)가 있다. 이와 같은 과정은 식 (3)에서 식 (8)로 나타낼 수 있다.
| $$f_t=\sigma(U_fx_t+W_fh_{t-1}+b_f)$$ | (3) |
| $$i_t=\sigma(U_ix_t+W_ih_{t-1}+b_i)$$ | (4) |
| $$o_t=\sigma(U_ox_t+W_oh_{t-1}+b_o)$$ | (5) |
| $$g_t=\sigma(U_gx_t+W_gh_{t-1}+b_g)$$ | (6) |
| $$C_t=F_t\otimes C_{t-1}+i_t\otimes g_t$$ | (7) |
| $$h_t=o_t\otimes\tanh(C_t)$$ | (8) |
여기서, ft, fi, 그리고 fo는 각각 망각게이트, 입력게이트, 그리고 출력게이트의 값을 의미하며, gt는 현재의 정보를 분석하여 장기상태에 전달하는 역할을 한다. Uf, Ui, Uo, 그리고 Ug는 입력값인 xt에 연결된 가중치를 나타내고, Wf, Wi, Wo, 그리고 Wg는 입력 이전시점의 단기상태인 ht-1에 연결된 가중치를 의미하며, bf, bi, bo, 그리고 bg는 편향을 의미하는 상수값이다. σ는 시그모이드 함수이며, ⊗는 원소곱을 나타내는 기호이다.
대상광구 개요 및 분석대상 설정
이 연구의 대상인 해상 생산정은 약한 경사를 가진 경사정으로서 2009년 11월 7일부터 가스와 컨덴세이트를 생산하고 있다. 탐사시추 시 MDT(Modular formation Dynamics Tester)를 통해 수직깊이에 따른 압력경사(pressure gradient)를 측정하였고, 이를 통해 대수층의 존재를 확인하였다. 생산 초기에는 지층수 생산이슈가 없었으나 생산후기인 최근에는 지층수 생산이슈로 인해 생산량을 줄이면서 생산하고 있다. 이 과정에서 가스 생산량이 줄게 되면 생산관내 액체축적현상(liquid loading)이 발생할 가능성이 커지므로 생산거동을 면밀히 모니터링하고 있다. 특히 정기 유지보수를 하면서 생산을 중지할 경우 축적된 물의 저류층 역유입이 발생할 수 있으며, 생산 재개 시 가스 생산이 이루어지지 않을 경우 메탄올을 주입하는 등의 유정보수가 요구된다. 따라서, 생산정 및 저류층 거동의 면밀한 예측을 위해, 다양한 공학적 기법들을 적용하고 상호검증을 통해 예측의 불확실성을 감소시키는 작업이 필수적이다.
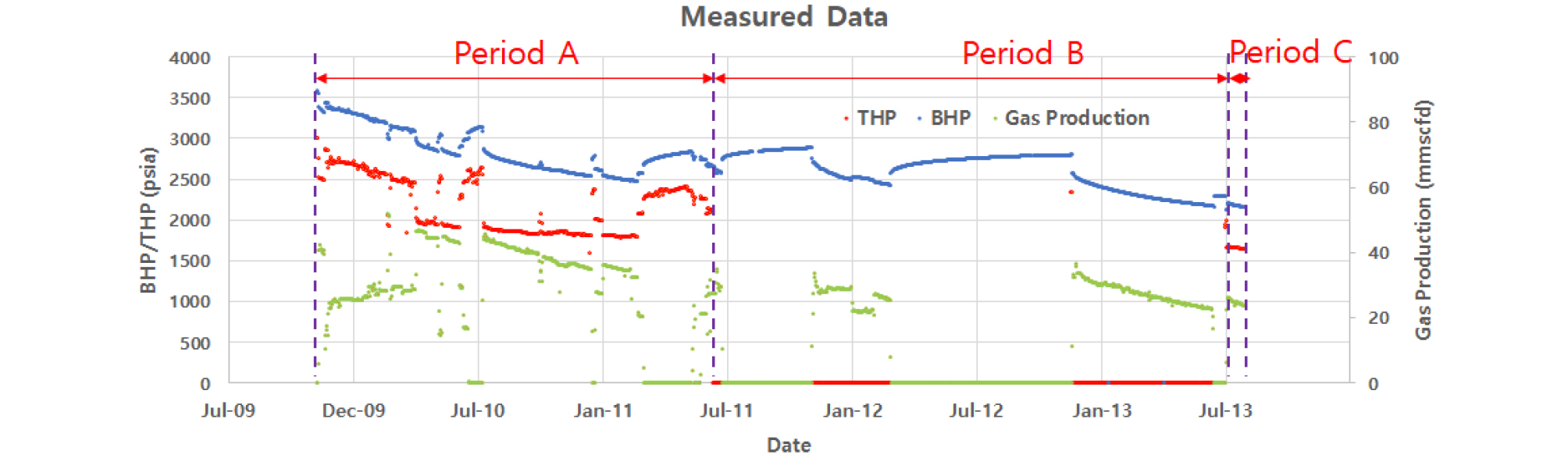
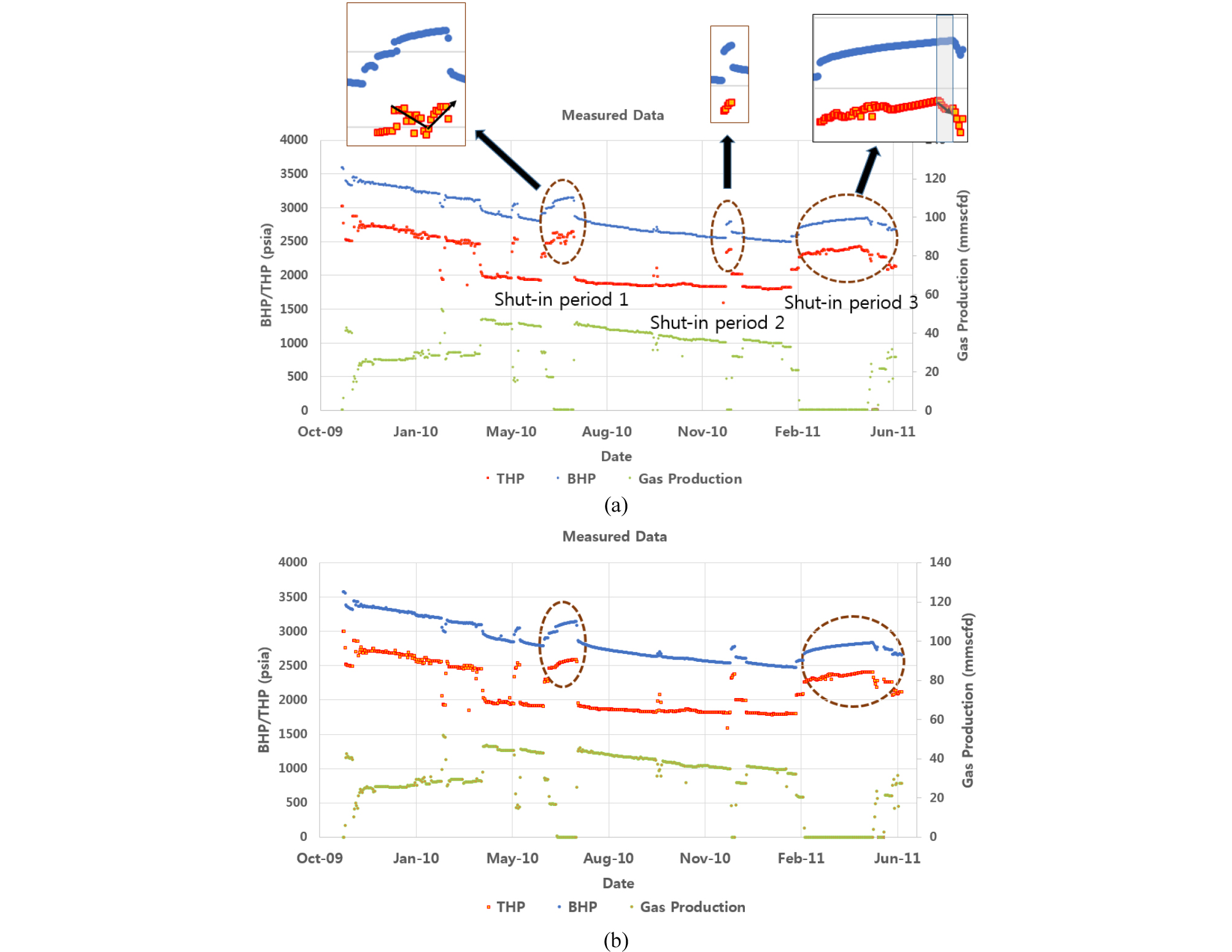
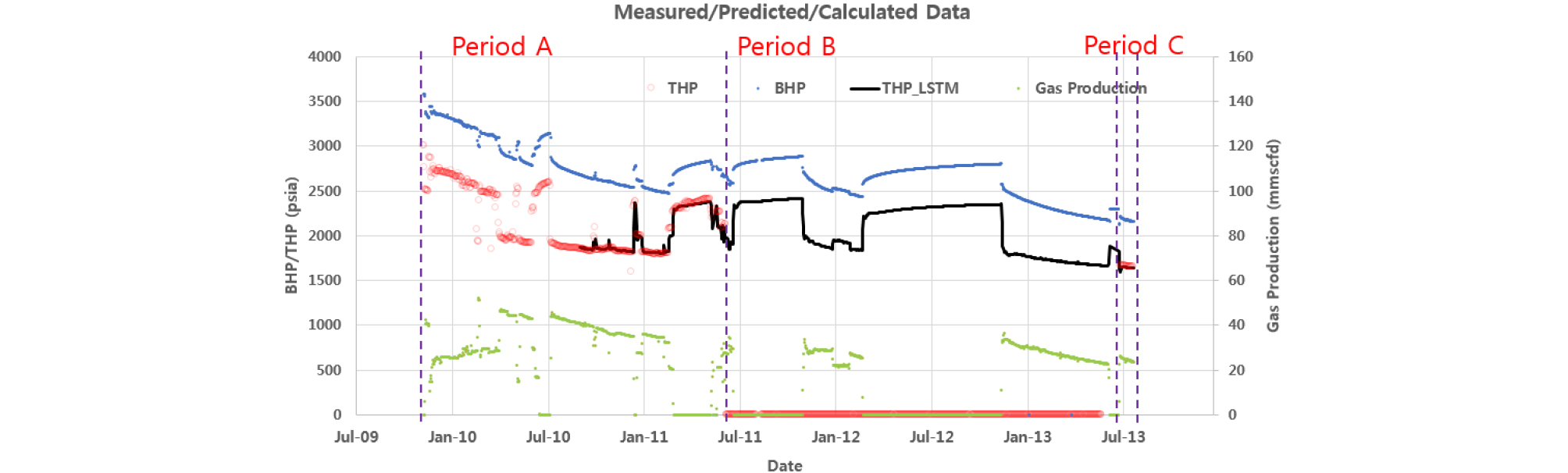
Fig. 4는 대상 생산정의 주요 동적자료 즉, 가스 생산량, BHP, 그리고 THP의 일별 취득결과이다. 여기서, 가스 생산량은 분리기에서 측정한 결과를 생산량 할당기법으로 할당한 양이다. 유동압력들은 해당일자의 특정시각 측정값을 기록한 것이다. 해당 생산정은 전체 대상광구 생산정 중의 하나로, 필드 규모의 운영 이슈 및 저류층 관리계획에 따라, 초크 사이즈 조절을 통해 생산량을 제어해 왔다.
Fig. 4의 Period A, B, C의 데이터 개수와 종류를 Table 1에 정리하였다. Period A는 2009년 11월부터 약 17개월의 자료로서 가스 및 컨덴세이트 생산량, BHP, THP 구성되어 있다. 이 기간 동안에는 THP를 비교적 일정하게 유지하려 하였으며 그 결과 BHP 및 생산량 변동이 다소 크게 나타났다. 이와 같이 압력의 급격한 변화는 원시부존량이 크지 않음에 기인하는 것으로 분석되었으며, CGR은 24 stb/mmscf의 비교적 작은 값으로 유지되었다.
Table 1. Summary of data acquisition
| Period | Days | Data Acquisition |
| A | 575 | Qg, Qcon, BHP, THP |
| B | 751 | Qg, Qcon, BHP |
| C | 31 | Qg, Qcon, BHP, THP |
Period B는 Period A 이후 약 2년 동안 가스 및 컨덴세이트 생산량, THP가 측정된 것이다. 생산 및 정지과정을 반복하여 운영하였으며, BHP 측정값들이 매우 양호한 것으로 보인다. 다만, 생산정지 시 BHP가 장기간에 걸쳐 지속적으로 상승하는 점은 약대수층(weak-aquifer)이 존재할 가능성이 높음을 암시한다. 이 기간 동안의 THP가 누락되었기 때문에 이에 대해 예측하는 것을 이 연구의 주요 대상으로 설정하였다.
Period C에서는 게이지가 복구되어 1개월간 가스 및 컨덴세이트 생산량, THP, BHP 모두 측정되었다. 이 구간은 Period B의 THP 예측의 신뢰도를 평가하는데 활용되었다. 저류층 유체상태는 습가스(wet gas)에 해당되어 CGR의 급격한 변화가 없다. 즉, 컨덴세이트 생산량은 가스 생산량과 동일한 경향을 가지므로 자료의 중복성을 피하고 연산효율을 높이기 위해 순환신경망 입력자료 선정 시 제외하였다. 또한, 모든 해당 기간 동안 물은 아직 생산되지 않았다.
자료 전처리 및 일관성 검토
Fig. 5는 모든 자료가 취득된 Period A기간을 표시한 것이다. 이 기간 동안 총 3번의 생산정지 기간이 있었으며, Fig. 5(a)에 점선의 타원으로 표시하였다. 일반적으로 생산정지 기간에는 BHP와 THP 모두 지속적으로 상승하는 형태가 나타나야 한다. 생산정지 1번(shut-in period 1) 구간의 BHP와 THP를 살펴보면, BHP는 매끄러운 곡선으로 압력이 상승하는 반면, THP는 V자 형태의 거동을 보여 중반분의 압력이 비정상적인 것으로 판단된다. 생산정지 2번 구간은 짧은 기간이지만 두 압력 모두 지속 상승하는 일관성있는 형태를 보였다. 생산정지 3번 구간에서는 중반까지 THP의 변동성이 다소 있으며, 후반부의 회색으로 표시한 영역에서는 BHP가 정상적으로 증가하는 반면 THP는 감소하는 압력거동을 보여 비정상적인 형태로 판단된다. 이와 같은 THP만 비정상적인 거동을 보이는 이유를 추론할 만한 합리적인 근거를 찾기는 어려우며 현재로서는 게이지의 오작동으로 판단된다.
이런 비정상적인 압력형태를 수정하기 위해 생산정지 1번 구간에서는 BHP 및 THP 차이의 평균값을 사용하여 THP를 보정하였으며, 생산정지 3번 구간에는 회색영역 이전의 압력 차이에 대한 평균값을 사용하여 THP를 수정하였다. 그 결과, Fig. 5(b)와 같이 생산정지 1과 3번 구간에서 정두압력이 어느 정도 개선된 것을 볼 수 있다.
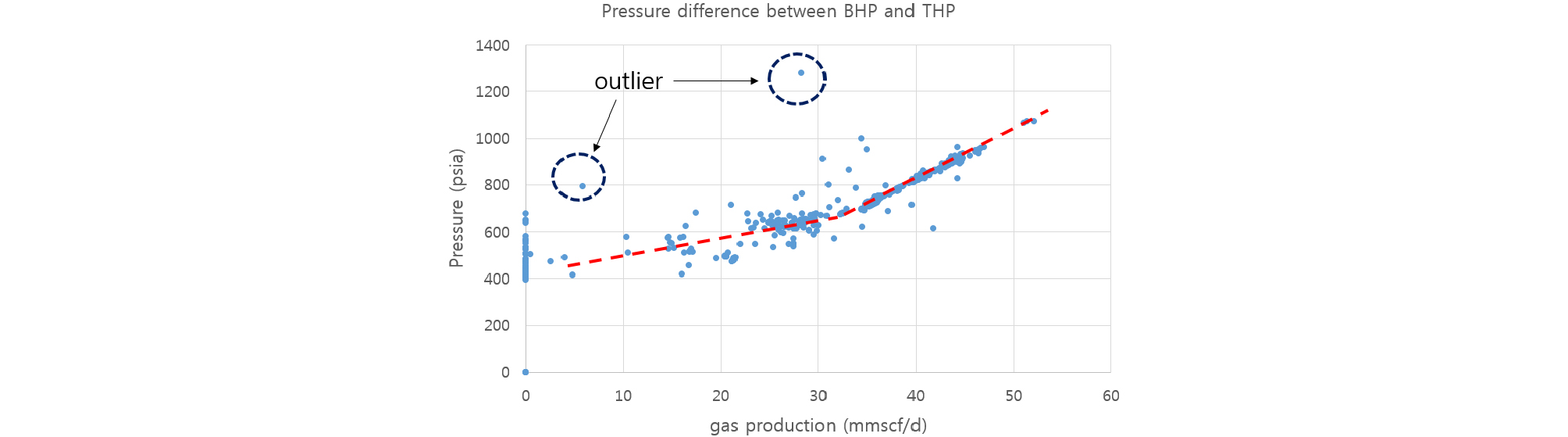
다음으로 가스 생산이 발생하는 구간에 대한 자료 검토를 수행하였다. 이를 위해 BHP/THP 차이를 가스유량에 대해 그래프로 표시하였다(Fig. 6). 그래프에서 32 mmscfd 이상의 유량일 때 강한 상관관계가 나타났으며, 그 이하의 유량에서는 분산이 다소 큰 형태를 보였다. 2개의 점선으로 표시한 것과 같이 취득된 압력은 대부분 합리적인 것으로 판단된다. 또한 이 그래프를 통해 재검토가 필요한 데이터도 확인할 수 있다. 그래프에서 이상치(outlier)로 표시된 데이터는 일반적인 생산량과 압력범위를 과도하게 벗어나 있기 때문에 삭제 또는 주변의 평균값으로 대체하는 것이 필요하다. 이 연구에서는 주변의 평균값으로 대체하는 방법을 적용하였다.
LSTM-RNN 설계
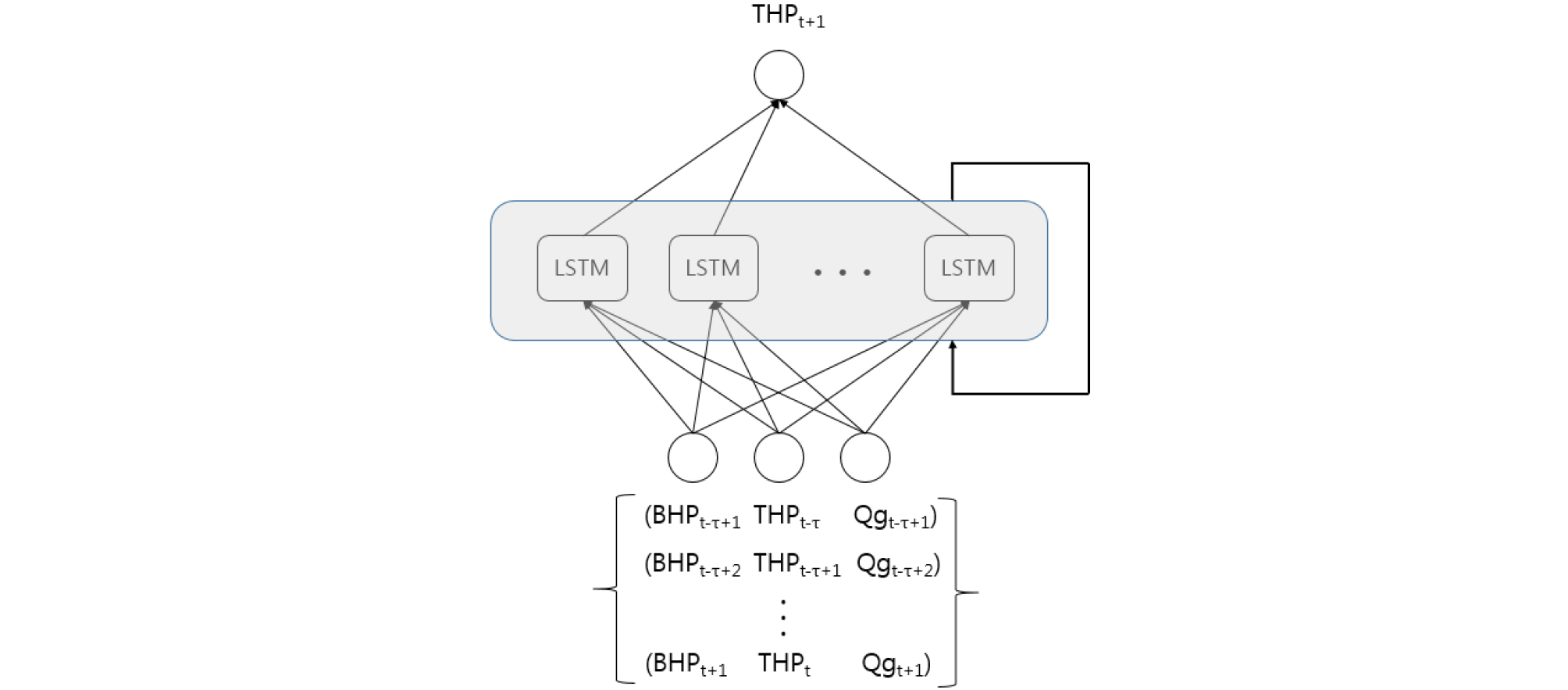
LSTM-RNN을 구축하고 Period A의 자료를 사용하여 학습(training)-검증(validation)-시험(test)을 거친 후 Period B의 THP를 예측해 보았다. Fig. 7은 이 연구에서 구성한 순환신경망의 구조를 나타낸 것으로 (t) 시점으로부터 τ개의 이전 시퀀스를 입력하여 (t+1) 시점의 THP를 예측하는 시스템이다. 입력자료는 THP, BHP, 그리고 가스유량(Qg)을 사용하였다. (t+1) 시점의 THP는 (t+1) 시점의 BHP와 Qg에 직접적인 영향을 받으므로, 입력자료를 구성할 때 BHP와 Qg는 THP 대비 한 시점을 평행 이동시켜 (t+1) 시점의 값도 입력자료로 사용할 수 있게 하였다.
순환신경망의 내부변수는 Table 2에 정리하였다. 앞에서 서술한 바와 같이 Period B는 생산 및 중지 과정을 반복적으로 적용하여 운영한 상황이므로 순환신경망의 학습을 위한 입력자료를 구성할 때 생산과 중지과정이 모두 포함되도록 충분히 긴 시퀀스의 자료로 구성하는 것이 바람직하다. 따라서 입력자료의 시퀀스의 길이 즉, τ = 300으로 정하였다. 즉, 특정 시점의 THP를 예측하는데 이전 300개의 연속된 시퀀스를 입력자료로 사용하는 것이다. Period A의 생산자료가 575개로 구성되어 있으므로 총 275개의 데이터 세트를 구성할 수 있다. 이중 125개(46%)는 학습자료, 100개(36%)는 검증자료, 나머지 50개(18%)는 시험자료로 구성하였다. 입력자료는 모두 식 (9)를 사용하여 0과 1 사이의 값을 가지도록 데이터 표준화를 수행하였다.
| $$x_{norm}=\frac{x_{max}-x}{x_{max}-x_{min}}$$ | (9) |
여기서, x는 임의의 입력자료이고, xnorm은 표준화된 입력값이며, xmax와xmin은 해당 입력자료의 최대 및 최소값을 의미한다.
Table 2. Hyper-parameters of LSTM-RNN for THP prediction
LSTM 셀은 100개로 구성하였으며, 오차 역전파(back- propagation)시 학습율을 조정하고 학습 방향의 모멘텀을 고려할 수 있는 Adam으로 최적화알고리즘을 설정하였다. 그리고 최적화 척도로는 평균절대오차(MAE)를 사용하였다.
| $$MAE=\frac1n\sum_{i=1}^n\left|O_i^{true}-O_i^{pred}\right|$$ | (10) |
여기서, 는 i번째 데이터의 목표값이며, 는 신경망의 출력값을 의미하고, n은 데이터의 갯수를 나타낸다. 사용언어는 파이썬이며, LSTM-RNN 구현은 tensorflow- keras를 사용하였다(Tensorflow, 2019). 데이터 세트를 총 300회 반복하여 학습시켰으며, 검증자료의 MAE가 가장 작게 예측된 모델을 사용하여 Period B 구간의 THP 예측에 적용하였다.
Period B 구간의 THP 예측
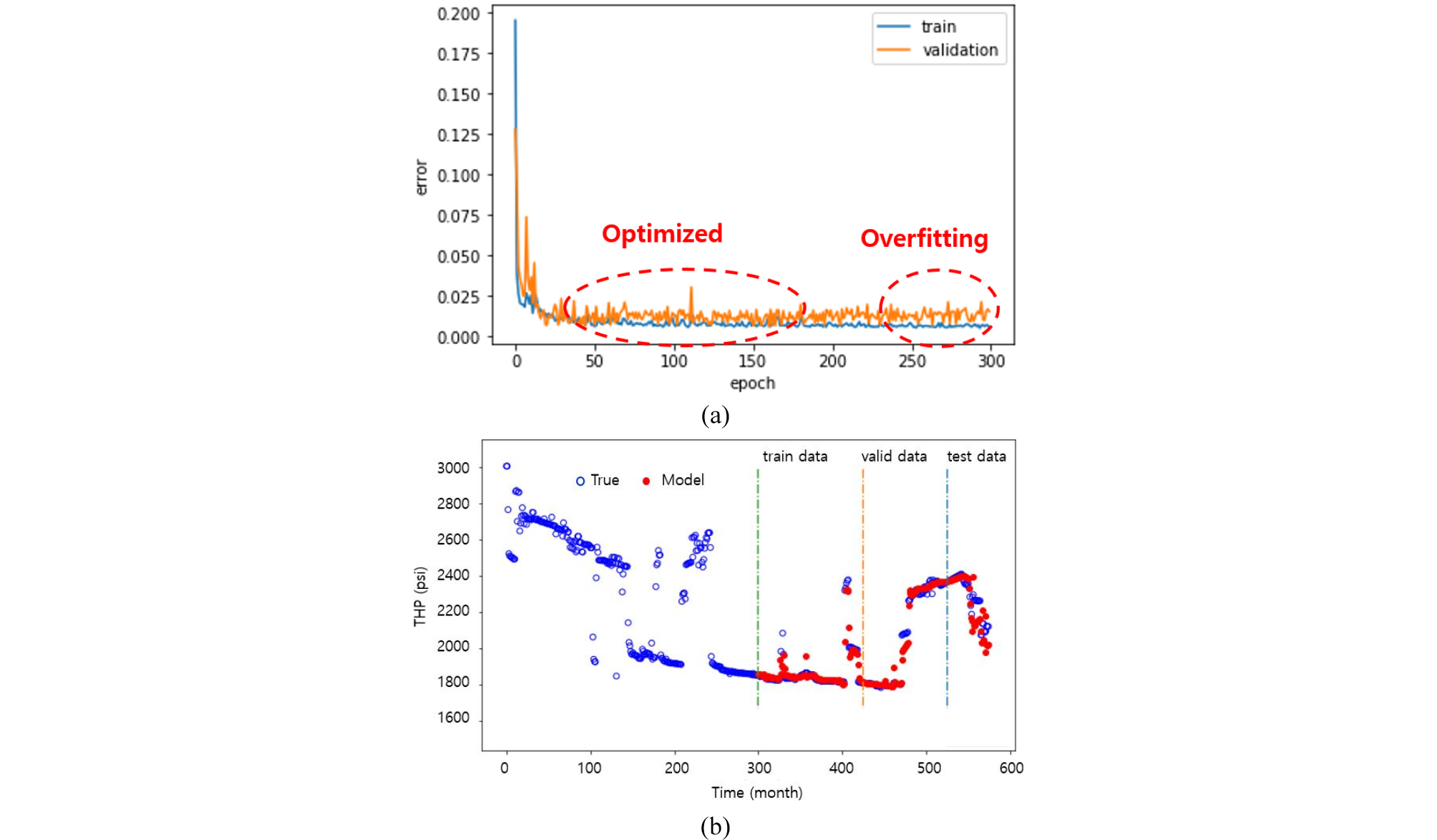
Period A 구간에서의 데이터를 사용하여 LSTM 순환신경망을 학습한 결과가 Fig. 8에 표시되어 있다. Fig. 8(a)는 학습이 진행되는 동안 학습자료와 검증자료의 MAE를 각각 나타낸 것이다. 학습의 후반부를 분석하면 학습자료에 대한 오차는 줄어드는 반면 검증자료에 대한 오차는 개선되지 않아 모델의 과적합이 나타나고 있음을 알 수 있다. 최적해 탐색의 151번째 반복(epoch)에서 검증자료의 MAE가 최소가 되어 최종 순환신경망 모델로 채택되었다. Table 3은 최종 학습모델에서 최종 MAE를 요약한 것이다. Fig. 8과 Table 3으로부터 LSTM-RNN을 통한 학습이 우수하게 진행된 것으로 판단된다. Fig. 8(b)는 학습구간, 검증구간, 시험구간의 예측결과를 실제값과 비교한 것이다. 전반적으로 실제값의 변화 트렌드를 잘 따르고 있다. 시험구간의 자료는 대부분 실제 운영을 안정적으로 하지 않은 기간에 해당하며, 이 구간을 제외한 학습자료 및 검증자료 구간의 예측값은 실제 THP와 매우 유사함을 확인할 수 있다.
Table 3. Mean absolute errors of the LSTM-RNN training
| Training | Validation | Test | |
| MAE | 0.00787 | 0.00590 | 0.01586 |
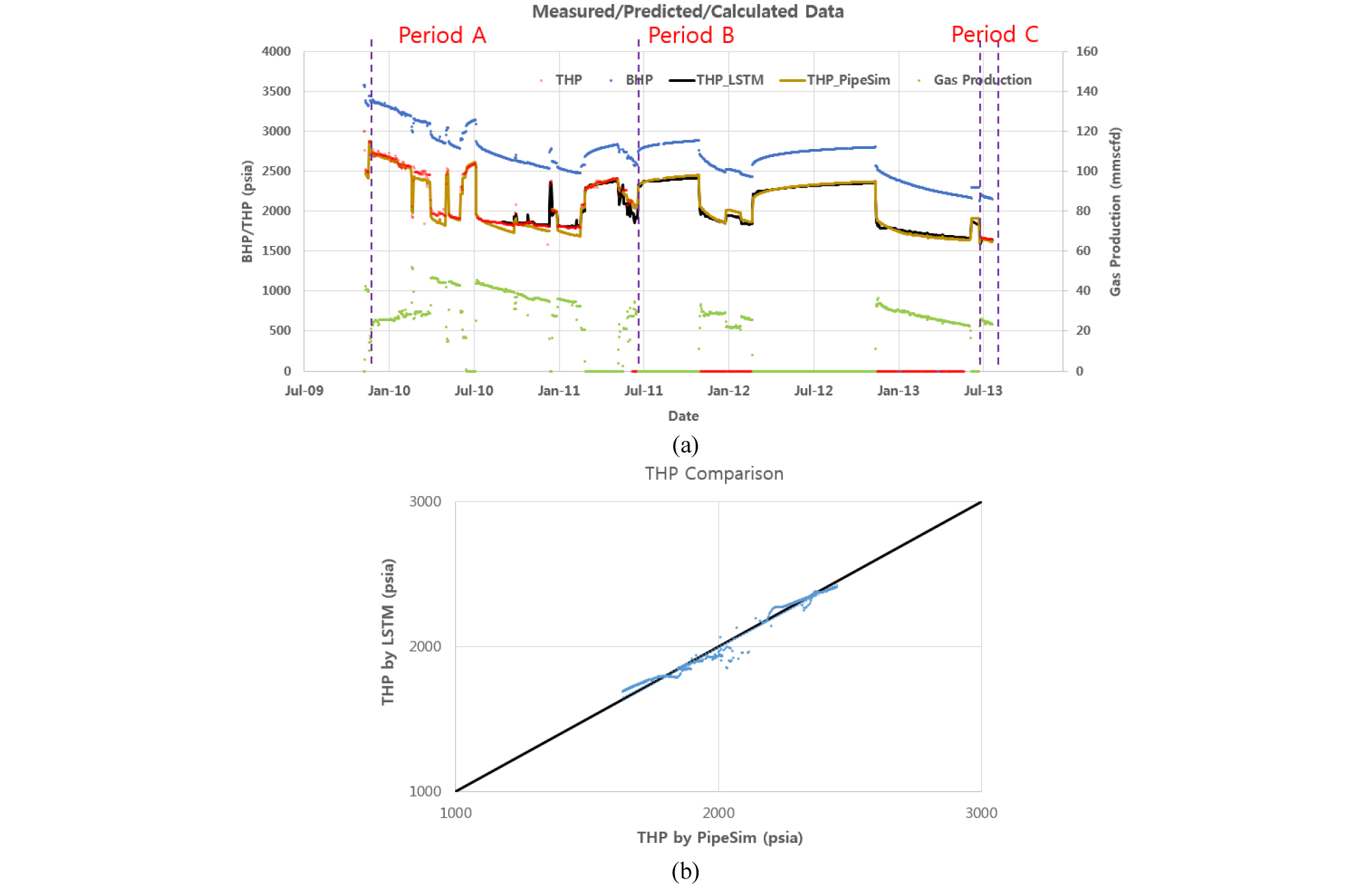
Fig. 9는 이상의 과정을 통해 도출된 LSTM-RNN 모델을 이용하여 Period B와 C의 모든 자료에 대해 THP를 예측한 결과이다. Period B 구간의 THP에 대한 예측 신뢰도는 Period C의 THP 예측을 분석하여 간접적으로 평가할 수 있다. 실제 THP는 붉은색 점으로, 모델을 통한 예측결과는 검은색 실선으로 표시하였다. Period C는 모델 학습에 사용되지 않은 자료이며 LSTM-RNN은 실제 값보다 평균 16.8 psi 작게 예측하였다. 이는 상대오차 1.02%에 해당하는 것으로 예측성능이 매우 우수함을 의미한다.
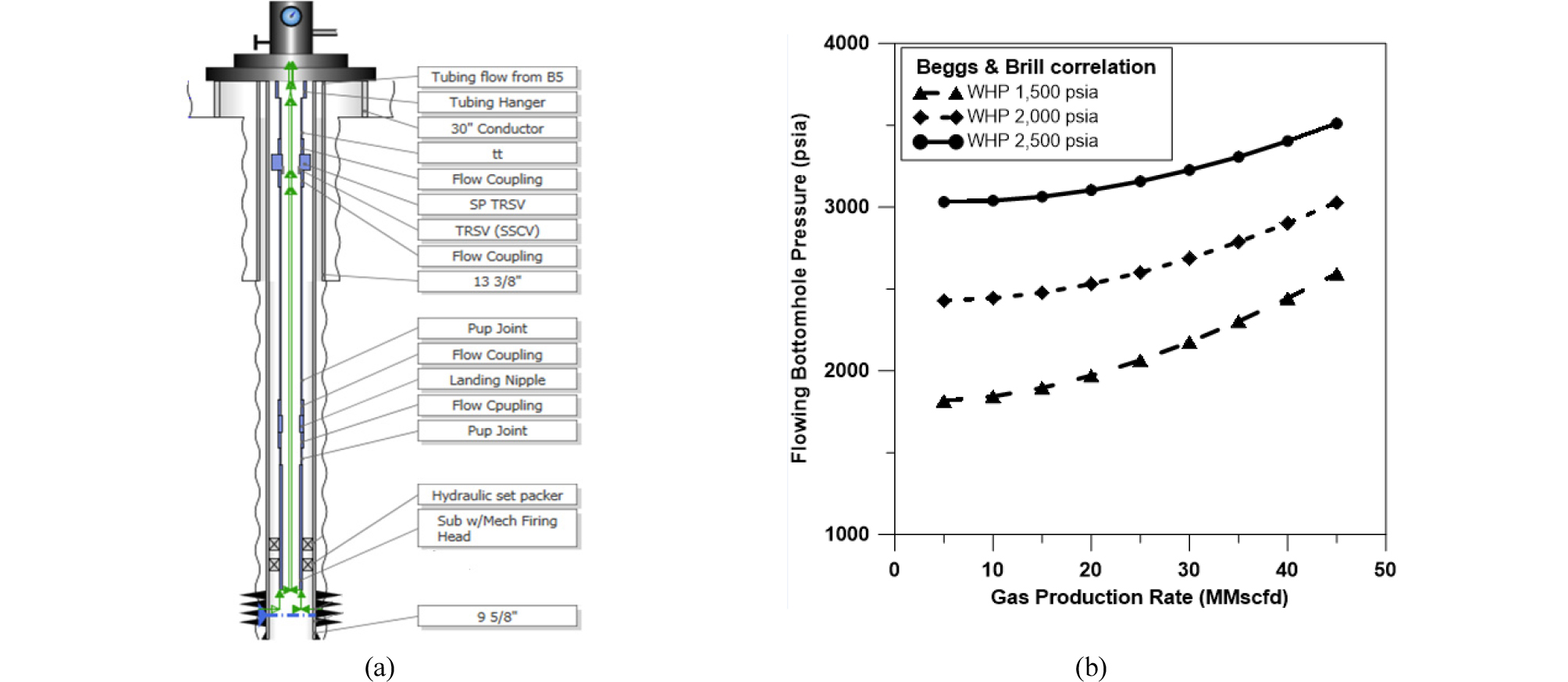
Period B에 대한 예측결과의 신뢰도를 평가하는 또 다른 방법으로 생산정 유동 모델링을 수행하고 결과를 비교하였다. 즉, PipeSim을 통해 생산관을 모델링하고 생산 운영에 따른 압력변화를 계산하였다. Fig. 10은 구축한 모델의 개념도와 생산관 유동능력 그래프를 나타낸 것이다. 생산정에서의 압력감소 상관관계(correlation)는 Beggs & Brill 모델(Beggs, 1991)을 적용하였다.
Fig. 11에 LSTM-RNN의 THP 예측값과 PipeSim의 계산값을 함께 도시하였다. Period A에서 실제값과 PipeSim 계산값을 비교하면 생산구간에서 차이가 조금씩 발생하나 모델링이 전반적으로 적절한 것으로 확인된다(Fig. 11(a)). Period B와 C 구간에서는 LSTM-RNN과 PipeSim 결과가 극히 일부를 제외한 대부분의 구간에서 매우 유사한 것을 알 수 있다. Fig. 11(b)는 LSTM-RNN과 PipeSim 모델사이의 THP를 그래프로 나타낸 것이다. 이때 LSTM-RNN 예측의 평균 상대오차는 1.24% 내로 나타나 LSTM-RNN의 예측능력이 매우 우수함을 알 수 있다. 이와 같이 PipeSim을 사용할 경우 생산정의 형태 및 크기, 유체의 특성과 같은 추가정보가 필요한 반면, LSTM-RNN은 생산량과 압력자료만으로도 동일한 예측이 가능한 장점이 있다.
입력 시퀀스 길이에 따른 예측성능 분석
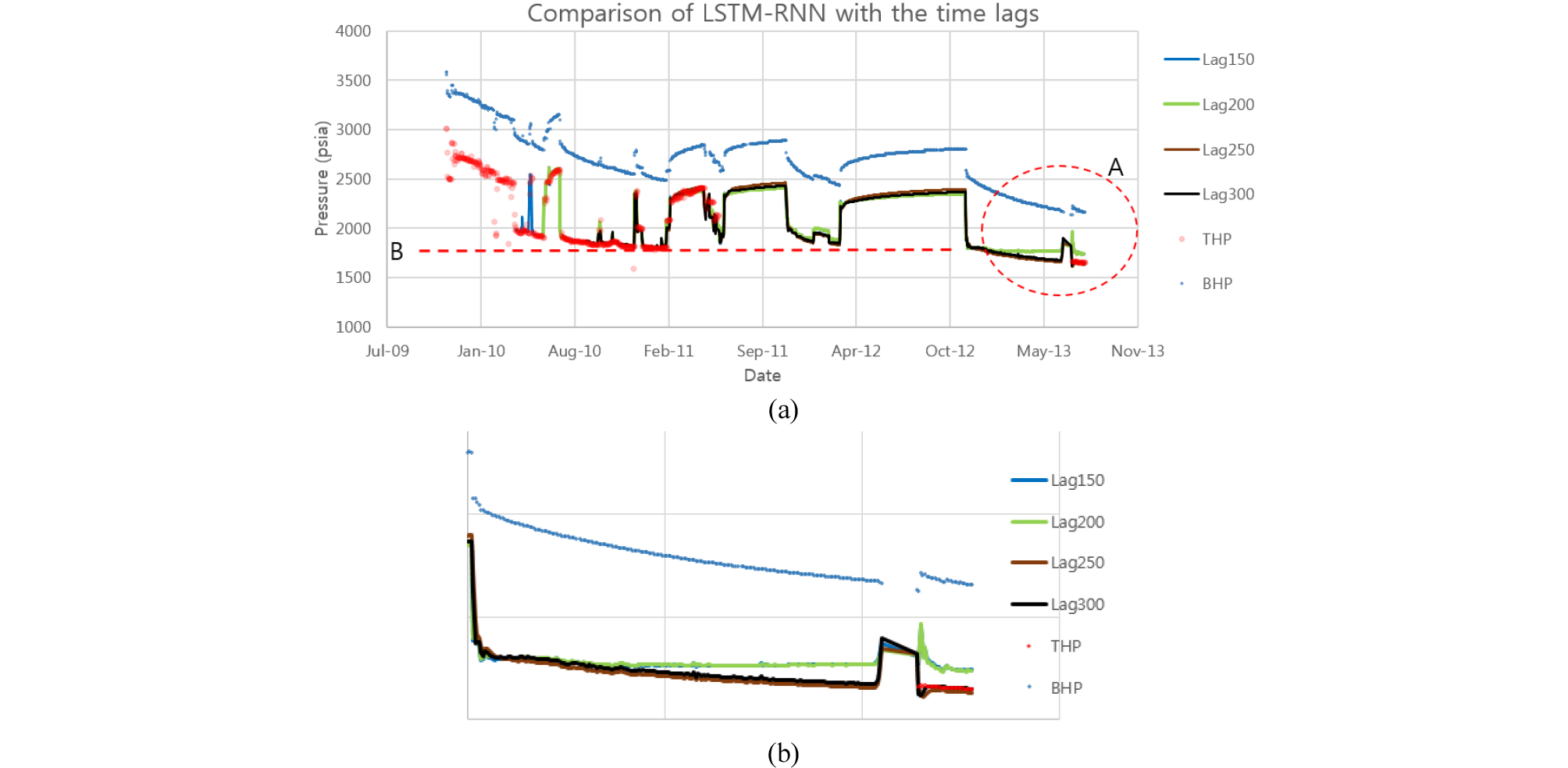
입력시퀀스 길이, 즉 앞에 제시한 Table 2의 τ를 변화시킬 때 LSTM-RNN의 성능을 비교분석하였다. 입력시퀀스 τ를 150에서 300까지 변화시켜 학습시킨 결과를 Fig. 12에 제시하였다. 모든 경우에 대해 A 구간(Fig. 12에서 점선 타원형 영역)으로 표시된 영역을 제외하면 큰 오차 없이 비슷한 경향을 보인다. 그러나 A 구간에서는 τ에 따라 차이를 보이며 이를 정량적으로 분석하여 Table 4에 정리하였다. 즉, τ = 300을 기준으로 시퀀스 길이가 150에서 250까지의 예측압력의 평균오차와 분산을 계산하였다. 입력 시퀀스의 길이가 250일 경우 기준인 300인 경우와 유사하며, 250보다 작을 때 오차가 다소 큰 결과를 보였다. 따라서, 입력 시퀀스의 길이를 최소 250 이상으로 설정하여 생산-정지의 다양한 운영환경을 반영한 입력 시퀀스로 구성하는 것이 신경망 학습에 중요한 사항임을 알 수 있다. 그리고 A 구간에서 오차가 크게 나타나는 이유를 분석하면 다음과 같은 유추가 가능하다. LSTM-RNN의 학습자료로 사용된 압력은 모두 Fig. 12의 점선 B를 기준으로 위쪽에 위치한 값들이다. 즉, 학습에 사용된 압력 범위 내에 위치한 압력을 예측하면 신뢰성이 높은 결과를 보이는 반면, 해당 범위를 벗어나는 영역에 대한 예측은 경우에 따라 오차를 발생시킨다는 것을 유추할 수 있다.
Table 4. Comparison of the relative pressure difference for several time-lag cases
| Time lag | 150 | 200 | 250 |
| mean of pressure difference (%)* | 2.99 | 3.01 | 1.11 |
| variance | 6.23 | 6.13 | 0.19 |
결 론
본 연구에서는 실제 운영광구의 생산량 및 압력자료를 바탕으로 미측정된 구간의 압력자료를 예측하는 방법에 대해 분석하였다. LSTM-RNN 모델을 효과적으로 적용하여 미취득 구간의 압력자료를 예측하였고, 이 과정에서 다음과 같은 결론을 도출할 수 있었다.
첫째, 현장에서 취득한 자료의 전처리를 통해 자료의 일관성을 확보하였다. 관측자료 수정, 아웃라이어 제거 등의 전처리 작업을 거친 이후, 학습-검증-시험 자료로 활용하였으며, 이를 통해 모델의 예측성능을 높일 수 있었다. 이 과정에서 저류층 압력이 감소함에 따른 BHP, THP 및 가스 생산량 변수의 거동특성을 효과적으로 분석할 수 있었다.
둘째, 예측하고자 하는 구간의 운영특성 즉, 생산 및 중지를 반복하는 운영계획을 반영할 수 있도록 학습자료 및 신경망 내부변수를 설정함으로써, 미취득 THP를 높은 신뢰도로 예측할 수 있었다. 또한, 대상 운영 기간에서 생산량의 급격한 변동없이 점진적으로 변화시키는 등 단순한 운영형태를 유지한 것도 우수한 예측성능에 도움이 된 것으로 판단된다.
셋째, 본 연구의 결과, 즉 1년 7개월의 주어진 자료를 바탕으로 2년 간 누락된 THP 자료를 예측한 것은, 이후 생산기간에 대한 확대적용 가능성을 암시한다. 현재 본 대상 생산정은 연구에 사용된 기간 이후에서 물 생산이 이루어지고 있으며, BHP 자료의 누락이 발생하였다. 이에 이번 연구결과는 생산량 할당의 일관성 확인, 미취득 BHP 자료 예측, 지층수 생산 및 유정보수 작업으로 인한 생산성 변화 가능성에 대해 분석할 수 있는 툴로서 활용될 수 있다. 향후 이 연구에서 구축한 LSTM-RNN 모델의 확대적용을 통해, 실제 현장의 데이터 기반 자료예측 기법의 활용성에 대한 추가 검증을 수행할 예정이다.