서 론

최근 분포형 음향 센싱(Distributed Acoustic Sensing, DAS) 기술의 발전으로 인해, 교통 모니터링 시스템에서 DAS가 혁신적인 대안으로 주목받고 있다. 효율적인 교통망 운영을 위해서는 실시간 도로 상태 감시가 필수적이며, 이를 위해 광범위한 센서 네트워크가 필요하다. 현재 교통 모니터링은 카메라(Tang et al., 2018; Fernandez-Sanjurjo et al., 2019), 유도 루프 검출기(Sheik Mohammed Ali et al., 2012), 동적 축중 측정 시스템(Weigh-in-Motion, WIM) (Gajda et al., 2015)과 같은 점 센서(point sensor) 기반으로 이루어지는 경우가 많다. 그러나 이러한 방식은 설치와 유지보수에 상당한 비용과 시간이 소요될 뿐만 아니라, 여러 종류의 센서를 조합할 경우 시스템의 복잡성이 증가하는 한계가 있다. 이에 반해, DAS 기술은 기존의 광섬유 네트워크를 활용하여 광범위한 영역에 대해서 점이 아닌 연속적으로 모니터링을 수행할 수 있는 혁신적인 접근법을 제공한다. DAS를 활용하면 온도, 변형률(strain), 파동장(wave field) 등의 다양한 물리량을 측정할 수 있으며, 기존 교통 모니터링 시스템 대비 운영비용 측면에서 효율성이 뛰어나 부담이 적다는 장점이 있다. 최근 연구에서는 DAS가 과속 및 과적 차량 탐지와 같은 교통 모니터링 영역에서 높은 신뢰도를 보이는 것으로 확인되었으며(Liu et al., 2024), 도로 안전 및 인프라 보호 측면에서도 유용한 기술로 평가되고 있다(Wang et al., 2023).

즉, DAS는 차세대 지능형 교통 시스템(Intelligent Transportation Systems, ITS) 구축을 위한 핵심 기술로 자리 잡을 가능성이 높으며, 기존의 점 센서 방식이 가진 한계를 극복할 수 있는 강력한 대안이 될 수 있다. 그러나 DAS 기반 차량 모니터링 기술의 실질적인 적용을 위해서는, 단순한 신호 수집을 넘어, 차량이라는 움직이는 송신원이 만들어내는 지반 반응의 특성, 그리고 이에 대한 DAS의 민감도 및 반응 양상을 종합적으로 이해해야 한다. 특히 DAS 신호는 송신원(차량)의 속도, 거리, 지반 특성, 게이지 길이 등의 변수에 민감하게 반응하기 때문에, 이러한 다양한 조건을 체계적으로 조절·해석할 수 있는 수치 모델링(synthetic modeling)이 필수적이다. 따라서 본 연구에서는 현실적인 가정에 기반한 수치 모델을 통해 차량 주행에 따른 DAS 신호의 특성을 분석하고, 차량 모니터링에 가장 적합한 매개변수들을 규명할 수 있는 레퍼런스를 구축하고자 한다. 이러한 접근은 향후 DAS 기반 교통 모니터링 기술이 더욱 정밀하고 신뢰성 있는 방향으로 발전하기 위한 기초 자료로서의 구실을 할 수 있을 것이다.

최근 연구에 따르면, 차량이 DAS 신호에 미치는 영향은 크게 두 가지 요소로 구분할 수 있다(Jousset et al., 2018). 첫 번째는 준정적(quasi-static) 성분으로, 차량의 중량에 의해 지면이 변형되면서 발생하는 약 1 Hz 수준의 저주파 신호이다. 준정적이라 일컫는 이유는 이 영역이 순수한 정적(static) 하중에 의해 발생하는 변형을 모사하여 일시적(transient) 송신원에 의해 전파되는 파동과는 다르기 때문이다. 즉, 차량의 하중이 지면을 누르면서 발생하는 도로의 변형이 주된 원인이지만, 그 하중이 시간에 따라 이동하기 때문에 온전한 정적 상태로 볼 수 없으며, 이를 고려하여 ‘준정적’이라는 표현을 사용한다. 두 번째는 동적(dynamic) 상호작용 성분으로, 도로 표면의 요철을 지날 때 차량이 도로에 가하는 힘에 의해 발생하는 표면파(surface wave)가 주요 원인이며, 주파수 범위는 3~20 Hz에 이른다(Liu et al., 2023).

차량에 의해 유발되는 준정적 성분을 정밀하게 모사하기 위해서는 일반적인 파동 방정식 기반의 수치 시뮬레이션과는 다른 접근법이 요구된다. 이는 차량이 생성하는 표면파가 차량의 이동 속도보다 훨씬 빠르게 전파되기 때문이다. 수치해석 모델링에서 흔히 적용되는 CFL(Courant-Friedrichs-Lewy) 안정 조건에 따르면, 매질의 전파 속도에 따라 시간 간격(time step)과 격자 간격(grid spacing) 사이의 최대 비율이 제한된다. 그러나 이러한 제한조건은 실제 차량의 움직임을 모사하기에 충분한 공간 해상도를 제공하지 못하며, 그 결과 차량의 위치가 수백 개의 시간 스텝이 지나도 같은 격자 상에 머무르는 비현실적인 상황이 발생할 수 있다. 이러한 한계를 극복하기 위해, Flamant-Boussinesq 근사법을 활용하여 차량에 의해 유발되는 준정적 신호를 모사하는 방법이 사용되고 있다.

본 연구에서는 두 영역으로 나뉘는 차량 신호 특성을 반영하여 차량 신호 모니터링을 수행하기 위한 준정적 영역의 도로 변형 및 DAS 신호 모델링을 수행한다. 모니터링에 적합한 매개변수 값을 얻어내기 위해 다양한 게이지 길이(gauge length), 채널 간격, 차량 속도, 차량 유형에 따른 광섬유의 응답 특성을 분석하고 이를 현장 자료와 비교하여 평가한다. ‘광섬유 신호 모델링’ 부분에서는 광섬유 위치에서의 변형률을 통해 DAS 신호를 모사하는 과정을 설명한다. ‘차량 유발 신호의 준정적 영역 모델링’ 부분에서는 차량의 하중에 의한 도로 변형률을 근사하는 방식을 설명한다. 이후에는 간단한 합성 모델에서 신호의 특성을 살펴본 후에 현장 자료와 비교하여 평가한다. 이러한 연구는 도로 안전 향상, 교통 관리 개선, 과적 차량으로 인한 인프라 손상 방지 등의 목표를 달성하는 데 기여할 것으로 기대된다.

광섬유 신호 모델링

DAS는 광섬유 내부 광펄스 신호의 레일리 후방 산란(Rayleigh backscattering)을 통하여 광섬유의 변형을 간접적으로 측정한다(Li et al., 2022). 샘플링된 산란 신호는 광신호 계측 장비(Interrogator unit)의 광학계 연산을 거쳐 특정 구간에서의 산란 신호의 시간에 따른 위상 차이를 연산한다. 이때, 특정 구간의 길이를 게이지 길이(Gauge length, GL)라고 일컫고, 이는 DAS 반응 신호 특성을 결정짓는 중요한 요소이다. 따라서, 게이지 길이에 따른 평균 변형률, 또는 평균 변형률 속도를 측정하는 DAS는 기존 점 센싱에서 벗어나 광범위한 영역의 물질 변형을 측정하는 데 사용될 수 있다. 한 지점에서의 DAS 반응성을 모사하기 위해서는 해당 지점을 포함하여 광섬유 전후로 게이지 길이의 절반에 해당하는 영역만큼의 변형률 또는 변형률 속도를 평균하는데, 이때 이 3차원 텐서 중 DAS가 고려하는 성분은 광섬유의 접선방향에 해당하는 부분으로 한정된다. 만약, 광섬유가 직선으로 깔려있다고 가정한다면, 모든 광섬유 구간에 대해 접선 벡터가 동일하므로 연산이 쉽지만, 실제 지형을 반영한다면 광섬유의 곡률을 무시하는 가정은 쉽게 적용할 수 없다. 따라서 해당 논문에서는 임의의 광섬유 배치에서 DAS 반응성을 모사하기 위해 광섬유 각 로컬한 영역에서의 접선 성분을 TNB 좌표계를 통해 나타내었다. TNB 좌표계란 광섬유가 배치되어있는 곡선을 위치벡터 r(s)=(x(s),y(s),z(s))로 표시할 시, 각 국소 지점에서의 접선(t(s)=dr/ds), 법선(n(s)=dt/ds), 그리고 그 두 벡터의 외적 성분인 쌍법선 벡터(binormal vector)까지 서로 직교하는 벡터들을 이용해 표현한 좌표계이다(Eaid et al., 2020). 여기서 s는 곡선을 따라 진행되는 호의 길이(arclength)를 뜻한다. 이 연구에서는 자동차가 움직이는 상황을 2차원으로 제한하고 있기 때문에, 직교 좌표계(Cartesian coordinate)에서는 y성분을 제외하고 TNB 좌표계에서는 쌍법선 벡터 성분을 제외하고 DAS 반응을 다룬다.

일반적인 2차원 직교 좌표계에서 접선방향과 대응하는 법선벡터로 이루어진 로컬 TNB 좌표계로 이동시키기 위해 다음과 같은 텐서 변환 행렬을 사용한다:

vi는 i성분의 속도를 뜻하며, εij˙는 i방향에 대한 j방향으로의 변형률 속도를 나타낸다. 위의 식을 이용하면, 특정 지점의 접선방향 변형률 속도(εtt˙) 및 특정 지점에서의 DAS 반응(ε˙DAS)은 다음과 같은 식으로 표현될 수 있다:

여기서 GL은 위에서 언급한 게이지 길이이며, C는 배치된 광섬유 중 게이지 길이만큼의 길이에 해당하는 곡선을 의미한다. 주목해야 할 점은 εtt˙를 계산할 때 각 지점에서 곡선의 접선 벡터만을 요구한다는 점이다. 따라서, DAS 신호를 모델링하기 위해서는 직교 좌표계 상에서의 변형률 또는 변형률 속도를 측정한 후에 광섬유 내 샘플링 지점마다 접선방향 벡터를 고려하여 설정해 준 게이지 길이만큼 적분해 주어야 한다.

모델링 작업을 수행하는 단계에서는 각 샘플링 지점에서의 접선 벡터를 알아야 하지만, 실제 현장에서 광계측 장비의 샘플링 해상도로 각 광섬유의 정확한 위치 및 접선 벡터 성분을 알기 어렵다. 그러므로 본 연구에서는 광섬유 포설 시 급격하게 광섬유가 휘는 구간이나, 특정 간격마다 광섬유의 정확한 위경도 정보를 기록한다. 해당 정보는 곡선을 부드럽게 이어주는 스플라인 보간법(Spline interpolation)을 수행할 때 사용되며 이를 통해 임의 샘플링 지점에서의 접선방향 성분을 간접적으로 구할 수 있다.

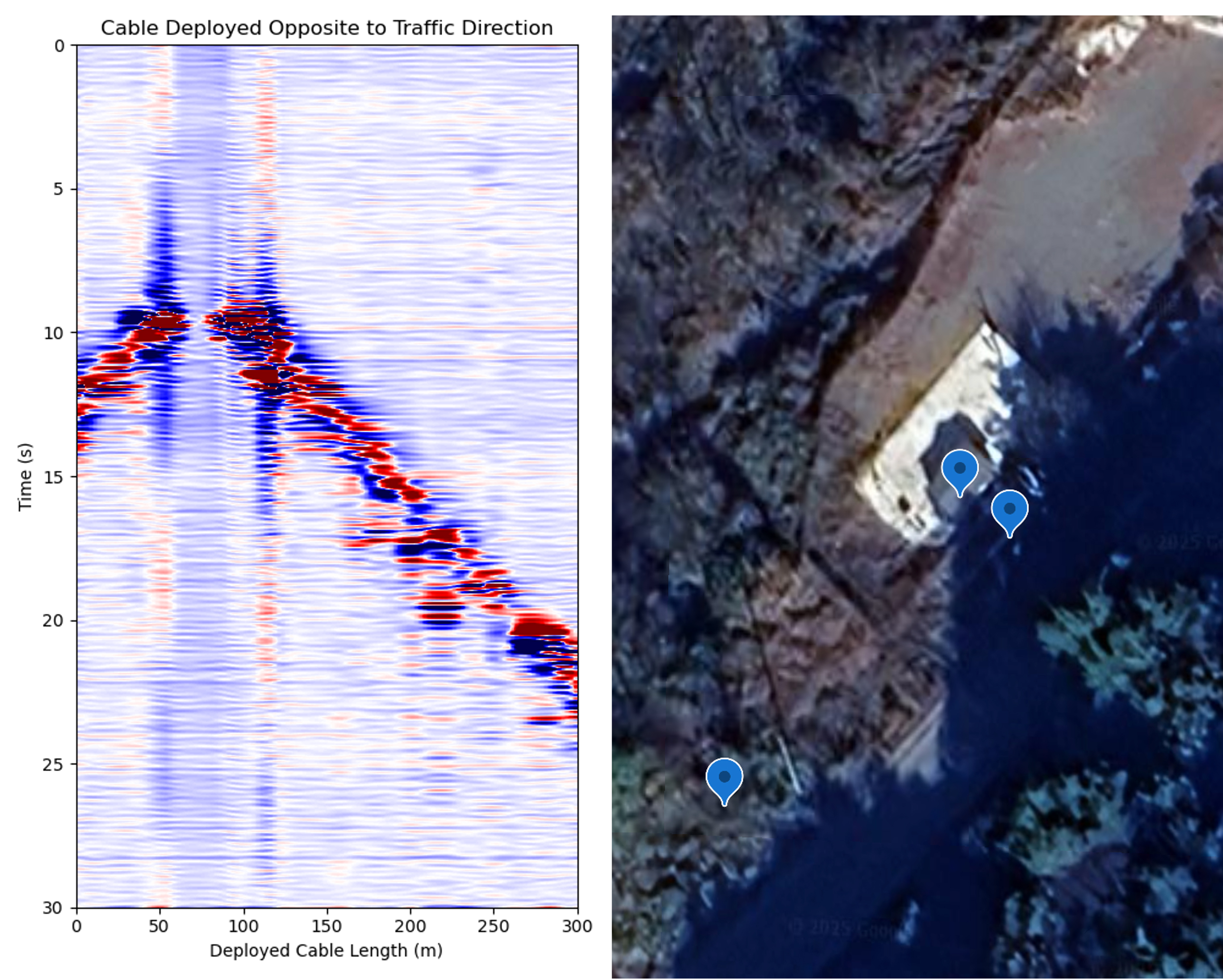
이번 현장에서는 포설된 광섬유의 위치를 정확히 파악할 수 있었지만, 일반적으로 실험자가 이미 포설된 광섬유의 경로를 명확히 알지 못하는 상황이 발생할 수 있다. 이러한 경우에는 신호 해석 이전에 몇 가지 전처리 과정이 필요하다. 예를 들어, fiber spooling과 같이 수십에서 수백 미터에 달하는 광섬유가 말려 지하에 보관된 구간이 포함된 경우, 해당 구간에서는 차량 신호가 비정상적으로 단절된 후 일정 채널 이후부터 신호가 다시 나타난다. 이러한 패턴을 통해 이상대 구간을 유추할 수 있으며, 해당 채널 구간을 제거한 후 앞뒤 채널을 연결하여 데이터 연속성을 회복할 수 있다. 또한, 광섬유의 대략적인 경로는 알고 있지만 급격한 굴곡이나 미확인된 방향 전환이 포함된 경우, 차량에 의해 발생하는 선형 신호의 기울기가 불규칙하게 변하거나 신호가 예상 방향과 반대로 나타날 수 있다. 이와 같은 구간은 모니터링에서 제외하거나 별도로 처리하는 것이 바람직하다. Fig. 1은 광섬유 위치 정보가 제한된 상황에서 준정적 신호 분석이 어떻게 유용하게 활용될 수 있는지를 보여준다. 오른쪽 패널에 표시된 파란색 점은 매설된 광섬유의 위치를 기록한 지점들이다. 왼쪽 패널에서는 차량이 유발한 신호가 상하로 굽은 궤적임을 확인할 수 있다. 이는 케이블이 도로 진행 방향과 반대 방향으로 포설되었다가 다시 정방향으로 회귀한 구조임을 시사하며, 준정적 신호 영역의 해석을 통해 광섬유 위치의 불확실성을 보완하고, 유효한 신호 채널을 선별할 수 있는 실마리를 제공한다.

Fig. 1.

Time-space plot of DAS response near the base camp (left). Plane view using Google Earth near the base camp (right). Blue points match sampled fiber locations.

차량 유발 신호의 준정적 영역 모델링

차량이 이동하면서 만들어내는 복합적인 신호는 주파수 영역대를 기준 삼아 크게 두 영역으로 나눌 수 있다. 약 1 Hz 근방에서 나타나는 준정적 성분은 차량의 무게에 의해 발생하는 변형에서 비롯된다. 해당 변형은 순간적인 하중이 아닌 정적인 하중에 의해 유발되는 물체의 탄성 변형을 뜻한다. 또한, 비교적 고주파수 영역대에 나타나는 동적 성분은 차량이 이동하면서 도로의 요철에 의해 순간적으로 차량의 하중이 강하게 지면에 작용하는 일시적인 하중이 그 원인이며 지표로부터 약 2~3 m가량 묻혀있는 광섬유 배치 특성상 레일리 파와 같은 표면파 성분이 그 에너지 대부분을 차지한다. 에너지적인 측면에서는 준정적 성분보다 동적 성분이 차지하는 비율이 월등히 높지만, 도로의 요철을 일일이 분석한 후 이를 고려하여 파동장을 예측하기는 쉽지 않기 때문에, 준정적 영역을 활용하여 교통 모니터링 혹은 지하 물성 분석에 사용한 연구가 다수 진행되어 왔다(Yuan et al., 2020; Thomas et al., 2024).

점 하중에 의해 발생하는 준정적인 변형은 일반적으로 Flamant-Boussinesq 근사법을 사용해 표현할 수 있다(Fung, 1965; Landau et al., 1986). 해당 모델은 균질한 무한 반공간(Homogeneous infinite half-space) 위에 놓인 수직 하중이 만드는 정적 변위를 기술한다. 이때, 원통 좌표계에서의 수평 및 수직 변위(ur,uz)는 다음과 같이 주어진다:

여기서 F는 점 하중의 크기를 뜻하고, R은 하중이 가해진 점으로부터 떨어진 거리이며, 𝜈는 매질의 포아송 비, 𝜇는 전단탄성계수, 마지막으로 z,r은 각각 지면(z=0)으로부터 떨어진 수직 방향 거리와 수평 방향 거리를 뜻한다. 원통 좌표계에서 변위를 나타낸 값이기 때문에 대칭성을 고려해 보았을 때 uθ가 0임은 자명하다. 본 연구는 2차원 상황을 가정하고 있기 때문에, 수평 방향 거리 r를 x로 두고 해석하며 자연스럽게 R=x2+z2를 만족한다. 주목할만한 점은, 시간에 따른 변위의 변화를 나타내는 파동과 달리 정적변화를 나타내는 Flamant-Boussinesq 근사법은 시간에 대한 항이 하중이 움직이는 것 이외에는 존재하지 않는다.

기존 연구에서는 간단한 직선 형태의 광섬유 배치를 가정하여 Flamant-Boussinesq 근사법을 사용하거나, 전통적인 파동방정식의 해를 통해 계산한 변위량만으로 DAS 신호를 구할 수 있었다. DAS는 정해진 구간 내에서 계산된 변형률을 공간에 대해 적분한 형태로 구할 수 있는데, 변형률은 변위의 공간에 대한 미분 값이기 때문에 식으로 정리하면 광섬유 배치가 단순할 시 다음과 같이 간단하게 DAS 반응 신호를 구해낼 수 있다:

그러나, 이는 εtt=εxx인 특수한 경우이기 때문에 가능한 경우이며 광섬유가 각 지점에서 다른 접선방향 벡터를 가지는 경우라면 그 접선 벡터를 항상 적분 계산 시에 고려해주어야 한다. 따라서, 근사법으로 구한 정적 변위를 DAS 반응 신호로 연결 짓기 위해서는 정적 변위 값을 응력으로 변환한 후 다시 변형률로 변환하여 적분해야 한다.

동일한 가정하에 직교 좌표계에서의 σxx,σzz,τzx값은 다음과 같이 구할 수 있다:

위 식에서 유도한 응력을 바탕으로 Hooke’s law를 사용해 이를 변형률 값으로 변환해 주면 식은 다음과 같다:

위와 같이 얻어낸 샘플링 지점에서의 변형률 값은 주어진 게이지 길이 적분 구간 내에서 샘플링 지점에서의 접선방향 벡터성분만을 고려하며 적분하여 εDAS(s)를 구한다. 변형률 속도는 시간에 따라 변화하는 하중에 의한 변형을 고려하여 1차 후방차분을 통해 다음과 같이 구한다.

여기서 Δt는 이산 시간 간격을 뜻하며 n은 정수로서 t=nΔt 위치에서의 값은 n번째 시간 스텝에서의 값을 의미한다. 서술한 Flamant-Boussinesq 근사법을 이용한 준정적 신호 모델링을 수행하기 위해서는 몇 가지 가정들이 필요하다.

첫 번째는 광섬유 전체가 지형으로부터 일정한 수직 거리만큼 떨어져서 존재한다는 가정이다. 광섬유를 포설할 때의 정확한 위치정보는 얻어낼 수 있지만, 포설할 당시 광섬유가 어느 정도 깊이만큼 매설되었는지는 정확하게 알아내기 어렵다. 따라서 해당 지형의 물성 및 평균적인 깊이만을 고려하여 광섬유들이 지형으로부터 일정한 수직거리만큼 이격되어있다고 가정한다. 해당 연구에서는 광섬유가 지표면으로부터 2 m 아래에 묻혀있다고 설정해 두었다. 이 가정을 통해 도출해 낼 수 있는 또 다른 특징은 광섬유의 접선 성분이 동일한 수직거리만큼 떨어져 있는 도로의 접선 성분과 같다는 점이다.

두 번째 가정은, 지형 정보를 고려하더라도 하중이 가해진 지점을 기준으로 균질한 반무한 매질을 상정한다는 것이다. 즉, 근사식에 사용된 물성은 모든 지점에서 동일하게 적용된다. 이러한 가정은 지형과 접선 방향으로 평행한 반무한 매질을 전제로 하므로, 특정 광섬유 구간이 가상의 반무한 매질 영역을 벗어나는 경우도 발생할 수 있는데 이러한 경우에는 해당 변위값을 0으로 설정한다. 물론, 이 근사 방식은 지형이 매우 불규칙한 경우에는 정확도가 떨어질 수 있다. 그러나 지형의 굴곡이 심한 지형이 아니라면, 하중으로부터 일정 거리 이내의 영역에서는 신뢰할 만한 근사 결과를 제공할 수 있다. 또한, 준정적 신호의 특성상 점하중이 영향을 미치는 도로의 영역은 상대적으로 좁으므로, 이러한 위험을 감수하더라도 반무한 매질 가정을 기반으로 한 Flamant-Boussinesq 근사를 선택하였다.

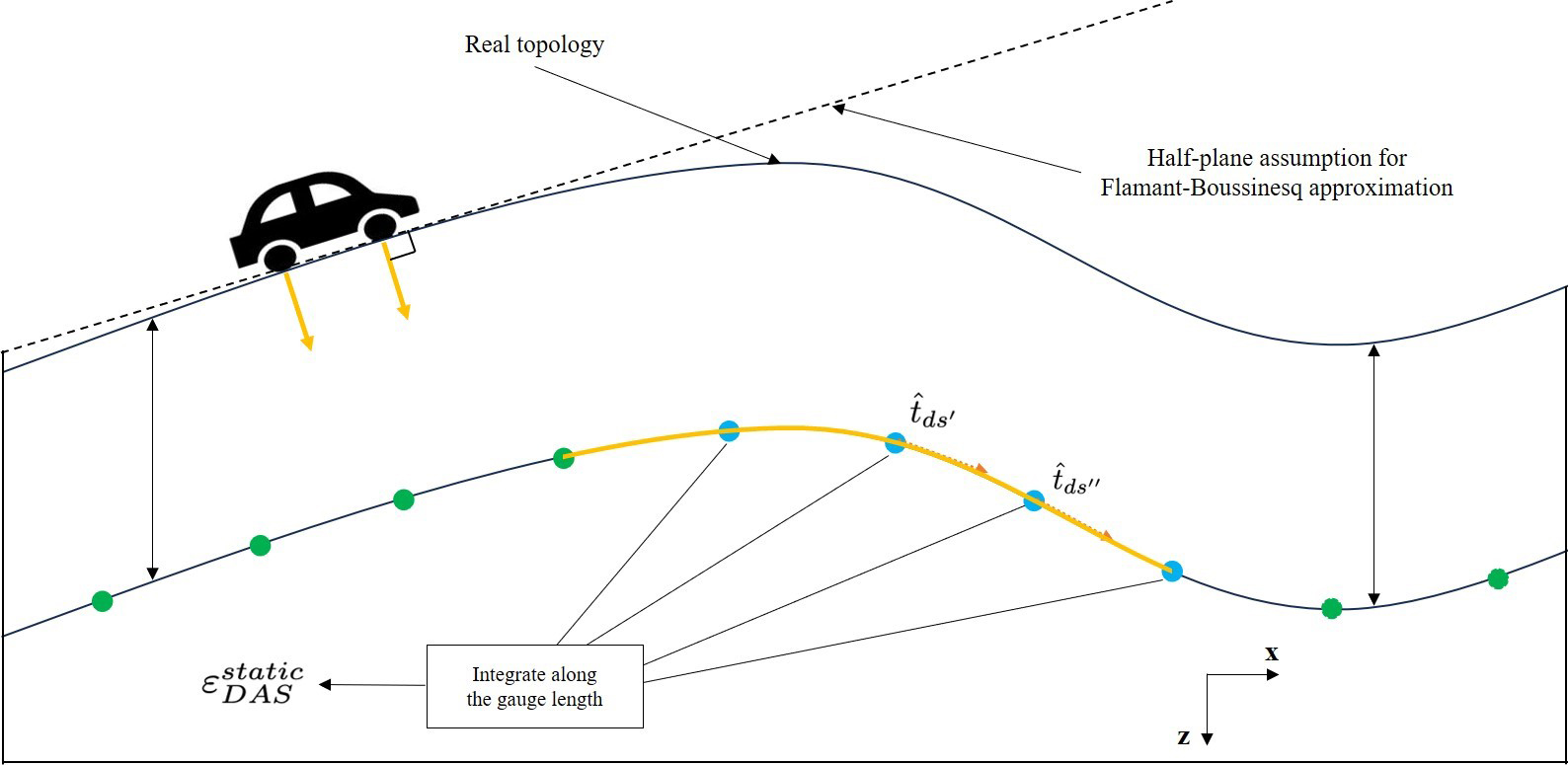
마지막 가정은 차량이 도로에 가하는 하중이 오직 도로에 수직인 방향으로만 작용한다는 것이다. 완벽한 등속운동이 아닌 이상 차량이 도로의 전후 방향으로 수평 방향의 힘을 가하지 않을 수 없지만, 모델이 너무 복잡해질 것을 우려해 차량은 항시 같은 속도로 움직인다고 가정한다. Fig. 2에서는 차량의 준정적 신호 모델링과 이를 위해 세웠던 가정들, 그리고 DAS 신호를 적분으로 구하는 과정을 모사하였다.

Fig. 2.

Assumptions for applying the Flamant-Boussinesq in this study: 1) the road is evenly spaced from the fiber, forming a pseudo half-plane tangential along the road; 2) the force exerted by the vehicle is regarded as a vertical point load.

차량 이동 시나리오에 따른 Flamant-Boussinesq근사 DAS 준정적 신호 모델링 결과

해당 섹션에서는 차량 이동 시나리오에 따른 DAS 준정적 신호를 위에서 언급한 Flamant-Boussinesq 근사법을 사용해 모사하였다. 해당 모델링을 위해 사용된 지하 물성은 Table 1에 명시하였다. 후술할 현장의 대부분이 산간지형이며, 광섬유가 매설된 지점이 콘크리트 하단의 노상(subgrade)아 아닌 풍화토(weathered soil)임을 고려하여, 해당 지반 조건에 적합한 물성을 적용하였다.

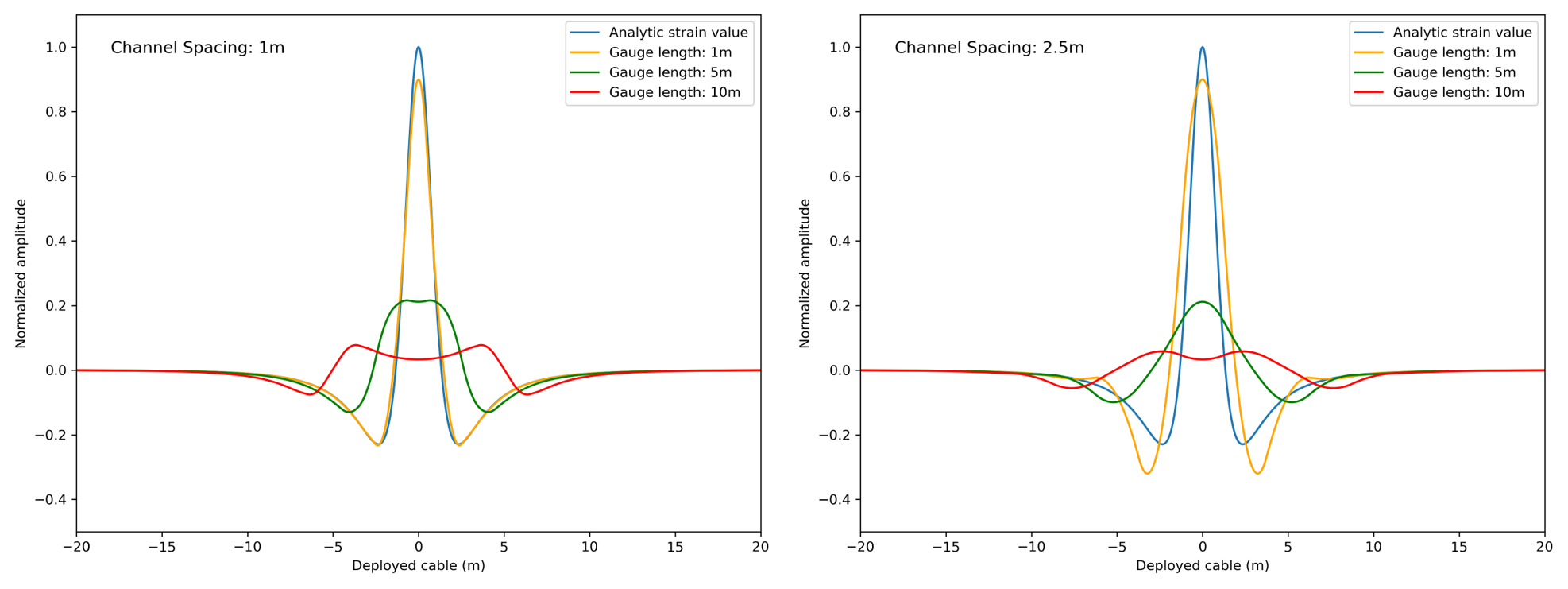
Fig. 3에서는 다른 게이지 길이와 채널 간격에 의한 DAS 신호의 경향성을 비교한 그림이다. 파란색으로 그려진 ‘Analytic strain value’는 점 센싱으로 측정한 차량 유발 변형률인데, 이를 보면 점 하중이 가해진 굉장히 좁은 영역에 대해서만 날카롭다는 것을 알 수 있다. 게이지 길이 구간 내에서 평균 변형률을 측정하는 DAS 신호는 그 길이가 길수록, 그리고 채널 간격이 넓을수록 본래 차량에 의한 변형 특성은 점점 무뎌지고 넓은 영역에 걸쳐 신호가 나타나는 것을 알 수 있다. 채널 간격이 넓어진다는 것은 연속적인 변형률 함수를 샘플링하는 간격이 커진다는 의미이기 때문에, 신호의 세부 특성을 잘 담지 못하고 점점 더 부드럽게 나타난다. 또한, 게이지 길이는 적분 구간에 해당하므로 그 길이가 길어질수록 신호는 평균화 필터링 효과를 더 강하게 받게 된다. 비록 긴 게이지 길이는 배경 잡음에 강인하다는 장점이 있지만 좁은 영역에서의 날카로운 변형 특성을 측정해야 하는 교통 모니터링은 게이지 길이가 우선 짧아야 분석할 수 있다는 점을 알 수 있다.

Fig. 3.

Effect of gauge length and channel spacing on strain.

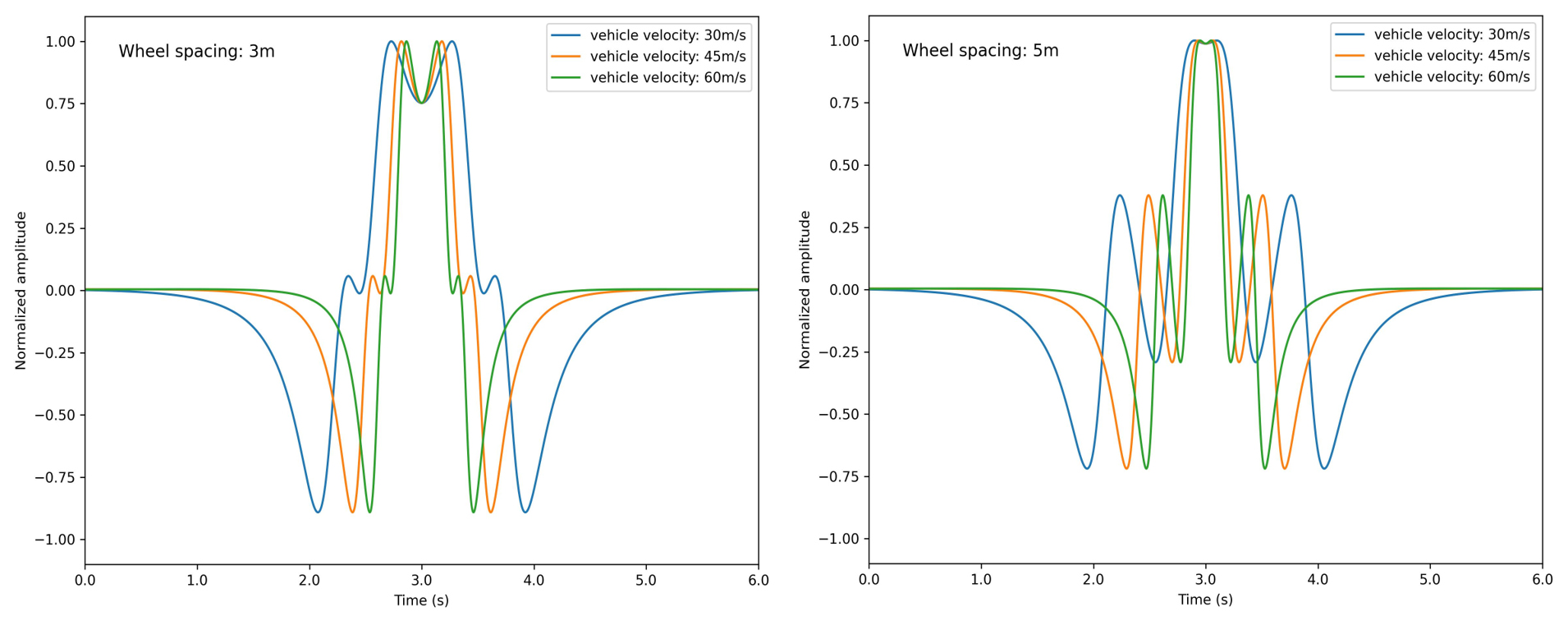
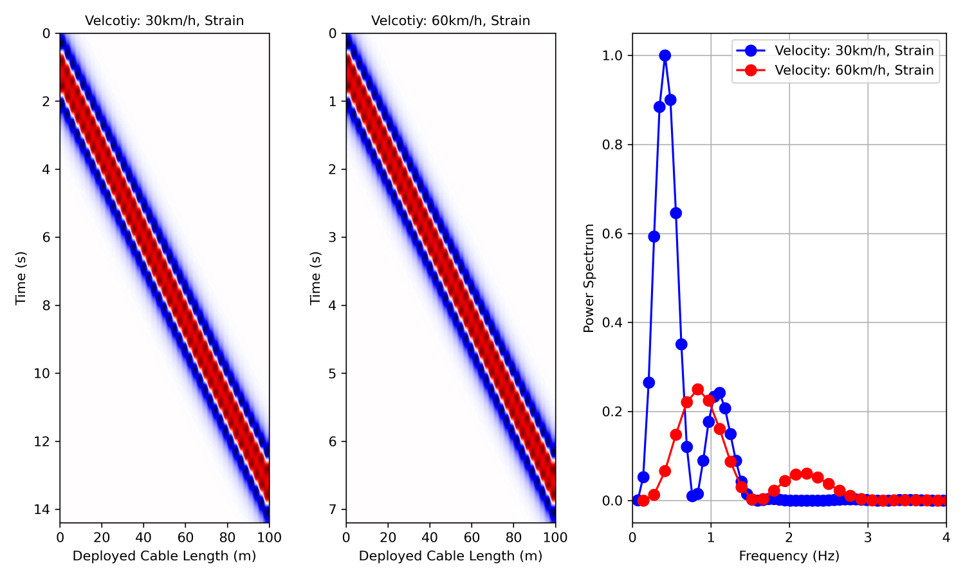
Fig. 4에는 차량 속도 및 차량 축 간격에 따른 DAS 신호를 도시하였다. 왼쪽은 축 간격이 3 m, 오른쪽은 축 간격이 5 m일 때의 차량 속도에 따른 DAS 신호이다. 이때 채널 간격과 게이지 길이는 각각 2.5 m와 10 m로 같다. 차량의 속도가 빠르면 빠를수록 신호가 날카로워지는 특성이 있으며 DAS에 기록되는 신호의 특성이 축 간격에 따라서 달라짐을 알 수 있다. 이는 추후 모델링을 이용한 차량 유발 표면파 성분을 분석할 때, 차량의 축 간격 및 축의 개수, 속도 등이 송신원 파형과 주파수 영역에 큰 영향을 미칠 수 있음을 암시한다.

Fig. 4.

Effect of vehicle velocity and wheel spacing on strain. The gauge length and channel spacing were set as 10 m and 2.5 m, respectively.

모델링 결과와 현장 자료와의 비교

모델링 결과의 유효성을 검증하기 위해 경주 박달리 A-2 현장의 모니터링 데이터를 사용하였다. 경주 A-2 현장에서는 2개의 광신호 계측 장비가 사용되었다. iDAS 2.4.1유닛은 영국의 Silixa 사의 제품으로 10 m 게이지 길이에 1 m 채널 간격으로 자료를 수집하였다. 독일 AP Sensing 사의 N5225B도 마찬가지로 10 m 게이지 길이로 모니터링을 수행하였으며 채널 간격은 더 넓은 2.5 m 간격이 사용되었다. iDAS는 변형률 속도를 측정하는 반면 AP Sensing은 변형률을 측정한다는 점 이외에는 기술적 차이점이 없으므로, 모델링 결과와의 비교 분석에서는 AP Sensing의 변형률 자료를 사용하였다.

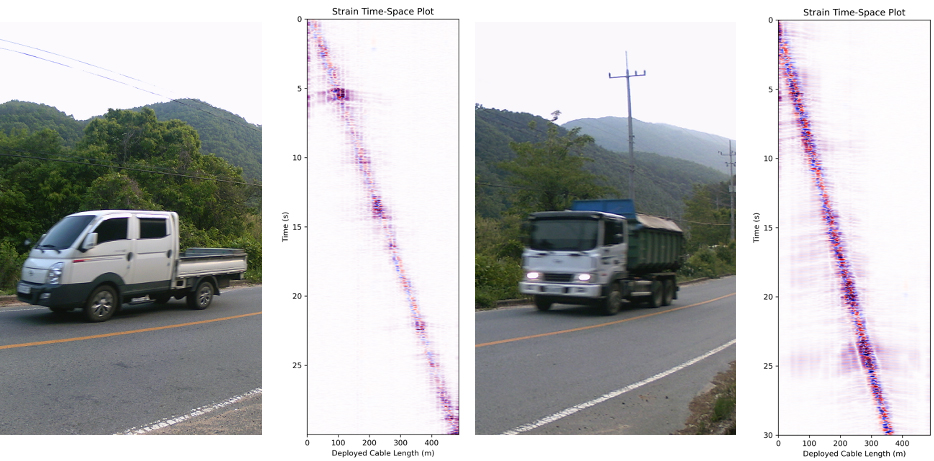
Fig. 5는 현장에서 얻은 DAS 모니터링 데이터 중 일부 차량이 만들어낸 신호를 도시하였다. 그림의 첫 번째와 세 번째 패널은 움직이는 차량을 CCTV로 촬영한 사진이다. 두 번째와 네 번째 패널에는 각각 N5225B 유닛으로 측정한 DAS 자료의 시간-채널 영역 데이터의 일부이다. 케이블의 접선방향 평균 변형률을 계산하는 DAS 특성상, 광섬유를 매설하는 작업(coupling)이 중요한데, 해당 현장은 특별한 수평 방향(common-mode noise), 혹은 수직 방향(fading) 잡음 없이 좋은 품질을 가지는 것을 직관적으로 확인할 수 있다. 시간-채널영역에 도시한 DAS 신호의 왼쪽 끝에서부터 오른쪽 끝까지 직선 형태로 내려오는 신호는 차량이 직접 도로에 변형을 가해 생기는 준정적 영역의 흔적이며, 해당 선형 신호를 중심으로 양옆으로 완만한 직선 형태로 퍼져 나오는 신호가 차량에 의해 생성된 동적 영역, 표면파 성분들이다. 선형 신호의 기울기가 더 가파른 두 번째 차량은 차량의 이동속도가 느리다는 것을 알 수 있고, 같은 컬러 스케일을 사용했다는 것을 고려했을 때 전체적인 신호의 진폭이 크게 나타나는 두 번째 차량의 하중이 더 큰 것을 유추할 수 있다.

Fig. 5.

Two types of vehicles captured during field monitoring (first and third), and their corresponding strain time-space plots (second and fourth), obtained using DAS.

Fig. 6에서는 Fig. 5에서 보여준 신호의 채널별 PSD(Power spectrum density)의 평균값을 도시하였다. 또한, 뚜렷한 선형 신호가 준정적 영역 신호임을 보이기 위해 1 Hz 주변 영역의 신호만을 강조하는 저주파 통과 Ormsby 필터를 적용한 후 마찬가지로 시간-채널영역을 그려놓았다. 사용한 필터의 저역 통과 주파수는 0.1 Hz, 고역 통과 주파수는 5 Hz, 고역 차단 주파수는 6 Hz이다. 해당 그림으로부터 알 수 있는 점은, 차량이 만들어내는 신호는 현장 데이터로도 잘 설명될 수 있듯이 1 Hz 주변의 저주파 부분 신호와 5 Hz 이상에서 나타나는 상대적인 고주파 영역의 신호들로 확연히 구분되며, 저주파 부분 신호만을 시간-채널 영역에서 도시할 시 양옆으로 진행하는 완만한 직선형태의 표면파 성분을 제외하고 차량 자체 무게에 의한 정적 변화만을 나타내는 신호가 추출된다는 것이다.

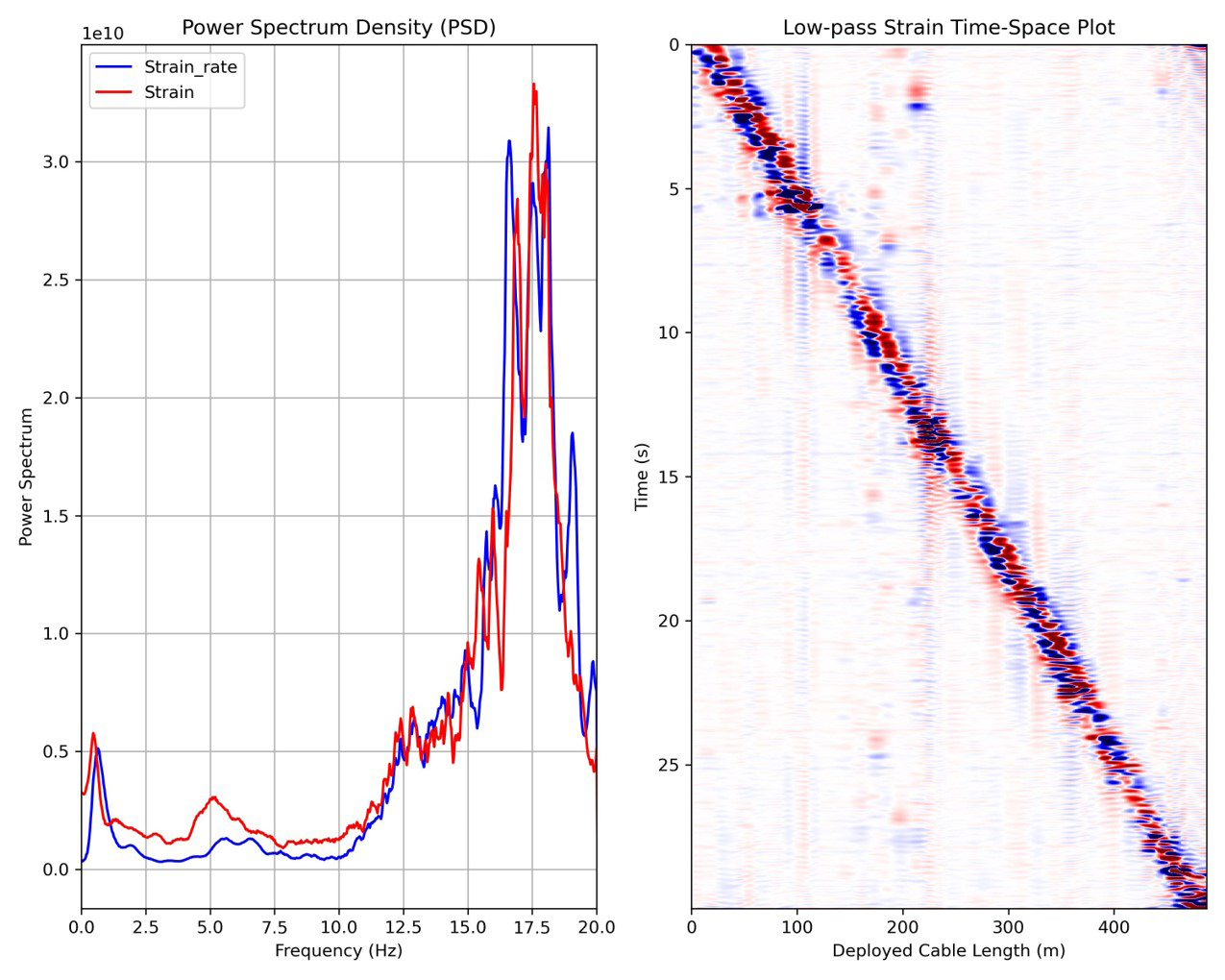
Fig. 6.

Mean power spectrum density of the time-space data represented in Fig. 5 (left); low-pass Ormsby filtered strain (right). Low-cut: 0 Hz; low-pass: 0.1 Hz; high-pass: 5 Hz; high-cut: 6 Hz.

Fig. 7은 Fig. 5의 첫 번째 차량이 만들어낸 DAS 신호의 준정적 영역을 모사한 시간-채널 영역 그림 및 평균 PSD이다. 사용된 물성은 앞에서 사용된 Table 1의 값과 같다. Fig. 4에서도 언급되었듯 차량이 만들어내는 준정적 신호의 특징은 차량의 속도에 크게 의존한다. 차량의 축 간격은 CCTV로 촬영한 사진을 토대로 대략적인 축 간격 3 m를 임의로 설정하였다. 차량의 속도는 준정적 선형 신호의 기울기를 통해 구할 수 있었는데, 특정 임계값 이상의 값을 기준으로 임의의 좌표들에 대해 가장 잘 들어맞는 직선을 구하는 Hough transform을 통해 대략적인 속도를 구한 후, 이를 바탕으로 차량의 속도를 설정하였고 차량의 속도는 약 60 km/h 수준이었다.

Fig. 7.

Synthetic time-space plot of DAS strain response at different velocities (left, middle); power spectrum density comparison (right).

결과에서 확인할 수 있듯이, 차량에 의한 모델링 DAS 신호의 PSD는 Fig. 6에 도시된 현장 DAS 데이터의 준정적 영역에서 관측된 것과 유사하게 약 1 Hz 부근에 뚜렷한 피크 주파수를 가진다. 또한, 이 피크 주파수 이후인 약 1~2 Hz 구간에서는 진폭이 점진적으로 감소하거나 미세한 notch 패턴이 형성되는 경향을 보인다. 이러한 경향은 Fig. 7의 수치 모델링 결과와 비교했을 때, 피크 주파수의 위치는 유사하지만, 현장 데이터에서 나타나는 명확한 notch 패턴이 모델링 결과에서는 관찰되지 않는다는 차이점이 존재한다. 이는 수치 모델에서 잡음 요소가 배제되었기 때문으로, 실제 현장 DAS 데이터는 저주파수 대역에서 지속적인 배경 잡음(광섬유 시스템 자체의 진동, 환경 진동, 기기 잡음 등)이 존재하며, 이에 따라 특정 주파수 구간의 notch가 완화되거나 흐려지는 양상을 보이는 것으로 해석된다. 한편, 고주파수 성분은 차량이 유발하는 표면파와 관련되므로, Fig. 7에서는 Flamant-Boussinesq 근사법으로 묘사한 저주파수 영역에 한정된 해석만 제시하였다. 또한, 차량 속도의 변화에 따라 피크 주파수 위치와 상대 진폭이 달라지는 양상을 통해, 차량의 속도가 준정적 신호 기반 하중 추정 과정에서 중요한 변수로 작용할 수 있음을 확인하였다.

광섬유 매설 상태가 좋은 상황에서 실험이 진행되었음에도 본 연구의 명확한 한계점으로는 바로 2차원으로 차원이 한정되었던 탓에 광섬유가 도로 바로 밑에 있었다고 가정할 수밖에 없었다는 점이었다. Fig. 8은 실제 광섬유의 GPS 좌표와 그 옆에 있는 도로를 Google Earth를 통해 도시한 것이다. 실제 도로의 위치는 광섬유의 실제 위치보다 수평 방향으로 약 4 m 정도 이격되어 있는데, 이는 준정적 신호를 모사하는 Flamant-Boussinesq 근사법에서 상당히 큰 영향을 줄 수 있는 요소로 작용한다. 해당 근사법을 2차원에 한정하여 응력을 해석하는 것은 3차원에서 하중이 선 하중 형태로 적용되는 것과 동일하지만, 실제 3차원에서는 점 하중이 작용한다. 차량이 만들어내는 신호를 정확하게 모사하기 위해서는 위 근사법을 3차원으로 확장하여 광섬유와 도로 간의 상대적인 위치를 3차원 지오메트리 상에 반영해야 한다.

Fig. 8.

Plane view using Google Earth; it shows the substantial shift distance between the road and the exact location of the fiber.

결 론

본 연구에서는 차량 이동 때문에 발생하는 신호를 분석하고, 분포형 광섬유 센싱(DAS)의 반응성을 모델링하기 위해 Flamant-Boussinesq 근사법을 적용하였다. 다양한 차량 이동 시나리오를 통해 DAS 신호에 영향을 미치는 주요 변수(차량 속도, 게이지 길이, 채널 간격, 축 간격 등)를 분석하였으며, 그 결과 DAS가 차량 유도 신호를 감지하는 데 효과적으로 활용될 수 있음을 확인하였다. 모델링 결과에 따르면, 차량 속도가 증가할수록 DAS 신호의 특성이 더욱 뚜렷해지며, 차량의 축 간격 또한 신호 패턴에 영향을 미치는 중요한 요소임을 확인하였다. 또한, 게이지 길이와 채널 간격이 증가할수록 신호가 평탄화되는 경향이 있으며, 이는 신호의 해상도를 결정짓는 중요한 요소임을 시사한다. 현장 데이터와 모델링 결과를 비교한 결과, Flamant-Boussinesq 근사법을 활용한 준정적 신호 모델링이 실제 측정된 DAS 신호와 매우 유사한 주파수 영역대에서 나타나는 것으로 보아 해당 근사법이 준정적 신호를 잘 모사함을 알 수 있었다. 그러나 본 연구에서는 2차원 모델을 적용하였기 때문에, 향후 연구에서는 더욱 정밀한 3차원 모델링을 적용하여 도로와 광섬유 간의 수직 및 수평 이격 거리를 더 정확히 반영할 필요가 있다. 또한, 다차선 도로와 같은 다양한 도로 환경 및 차량 유형을 고려한 추가적인 실험 및 데이터 분석이 필요하다.

결론적으로, 본 연구는 DAS 기반 차량 모니터링 시스템의 가능성을 확인하고, DAS 신호를 활용한 교통 모니터링 및 지능형 교통 시스템(ITS)의 발전에 기여할 수 있는 기초 데이터를 제공하였다. 특히 수치 모델링을 통해 도출된 차량 신호 특성은 다양한 도로 조건 및 센서 매설 환경에서의 신호 응답을 사전에 예측하고, 이에 따른 센서 설계 기준(게이지 길이, 채널 간격 등)을 수립하는 데 활용될 수 있다. 또한, 본 연구에서 제시한 모델링 결과는 차량의 하중, 위치, 속도 등의 정보를 신호로부터 추정하는 알고리즘 개발의 기반 자료로도 활용될 수 있으며, 실제 도로 환경에서의 DAS 신호 해석 정밀도를 높이는 데 기여할 수 있다. 향후 연구를 통해 보다 정밀한 분석이 이루어진다면, DAS를 활용한 교통 모니터링 시스템이 기존 점 센서 기반 모니터링 시스템을 대체할 수 있는 강력한 기술로 자리 잡을 것으로 기대된다.