서 론

일반화된 Hoek-Brown 파괴조건식(Generalized Hoek-Brown failure criterion, GHB)식은 오늘날 암반공학 분야에 특화된 표준 암반파괴기준식의 하나로 인정받고 있다. 이 식은 무결암의 취성파괴 조건식으로 개발된 비선형 경험식인 Hoek-Brown(H-B, Hoek and Brown, 1980) 식에 기원을 두고 있으며 이후 적용범위를 절리성 암반으로 확장시키기 위해 수차례 개정과정을 거쳐 2002년 GHB 파괴함수(Hoek et al., 2002)가 제안되었다. GHB식의 개발 역사는 Hoek and Marinos(2007)에 요약되어 있다. GHB식의 가장 주목할 만한 특징은 현장 암반의 양호 정도를 정량화하는 GSI (Geological Strength Index, Hoek et al., 1995; Hoek, 1999; Hoek and Marinos, 2000) 지수의 도입에 있다. GHB 파괴함수를 구성하는 강도정수 값들은 GSI를 변수로 하는 경험식들에 의해 결정된다. 암종과 절리상태에 따라 GSI 지수는 0과 100 사이의 값을 가지며 GSI = 100은 무결암을 의미한다. 따라서 GSI = 100일 때 GHB식은 본래의 H-B식과 일치한다. 그러므로 GHB식은 현장조건을 고려하여 무결암의 강도를 절리암반의 강도로 낮추어 주는 합리적인 체계를 제공하고 있다.

그러나 GHB식은 최대주응력과 최소주응력의 관계식으로 표시되며 이 식에 대응되는 Mohr 파괴포락선 즉, 파괴면의 전단강도와 수직응력의 관계가 명시적인(explicit) 해석적 수식으로 표시되지 않는다는 큰 단점을 가지고 있으므로 수치해석적 활용 측면에서 많은 제약을 받고 있다. 한계평형해석(limit equilibrium analysis, Wylli and Mah, 2004; Kumar et al., 2021), 한계해석(limit analysis, Chen, 2008), 임계평면법(critical plane approach, Pietruszczak and Mroz, 2001) 등 암반구조물 안정성 해석과정에서 자주 활용되는 수치해석법은 명시적인 Mohr 파괴포락선식을 기반으로 한다. 다만 GSI = 100일 경우에는 GHB식의 Mohr 포락선을 정확한 해석적 수식으로 표현하는 것이 가능하다 (Hoek, 1983; Ucar, 1986; Londe, 1988; Lee and Pietruszczak, 2017, 2021; Lee, 2018).

GSI≠100이면 GHB식에 대응되는 Mohr 파괴포락선식을 정확하게 유도하는 것이 어렵다는 문제점을 극복하기 위한 대안을 찾기 위해 지금까지 근사 Mohr 포락선을 활용하는 연구들이 시도되고 있다. 그 중 가장 간단한 접근법은 특정 최소주응력 구간에서 GHB식을 최적 근사하는 직선식 즉, 등가 Mohr-Coulomb(M-C)식을 구하는 것이며 Hoek et al.(2002), Sofianos and Nomikos(2006), Lee(2019)의 연구가 이에 해당한다. 그러나 이러한 선형근사법은 GHB식의 중요한 특징 중 하나인 비선형 강도예측 성능을 충분히 활용하지 못하는 단점이 있다. 최근 Lee(2018), Lee and Pietruszczak(2017, 2021)는 비선형 함수를 다항함수 공간으로 직교 투영시키는 선형대수학적 원리를 기반으로 실제 Mohr 포락선에 매우 근사하는 비선형 근사 Mohr 포락선을 수식화하는 방법을 개발하여 GHB 파괴함수의 적용 영역을 대폭 확장시킬 수 있는 계기를 마련하였다.

이 연구에서는 Lee(2018)가 제안한 GHB 기준식의 비선형 근사 Mohr 포락선식을 바탕으로 전단강도 계산 성능이 더욱 향상된 근사 Mohr 파괴포락선식을 제안하였다. 새로 제안된 Mohr 포락선식의 활용 가능성과 정확성을 확인하기 위해 이 식을 적용하여 암반사면의 평면파괴 안전율을 계산하였고, 그 결과를 Hoek et al.(2002)이 제안한 선형근사 M-C식을 적용한 결과와 비교 분석하였다. 암반사면의 안전율은 Bishop의 간편법(Das, 1998)을 적용하여 계산하였다. 해석대상 암반사면은 상부면에 수직 인장균열이 존재하는 것으로 가정하였고, 인장균열의 하부와 사면의 하단을 연결하는 면을 잠재적 파괴면으로 가정하였다. 안전율 해석결과에 근거하여 선형근사 포락선을 활용한 안전율 계산의 문제점이 지적되었다.

GHB 파괴기준식

최대주응력-최소주응력 관계식

GHB 파괴기준식에서는 암반이 파괴되는 시점의 최대주응력(σ1)이 최소주응력(σ3)의 비선형 함수로 다음 식과 같이 표시된다(Hoek et al., 2002).

여기서 σci는 무결암의 일축압축강도이며 mb, s, a는 강도정수로서 GSI 지수를 활용하는 다음 경험식들을 이용하여 계산된다.

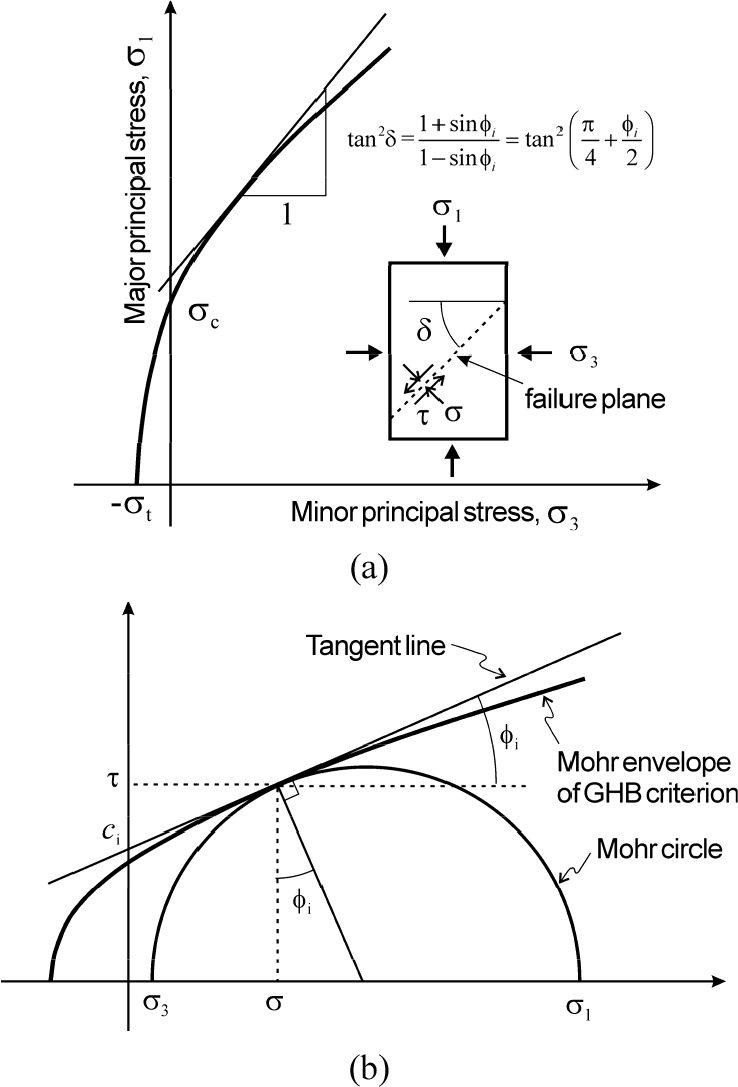
식 (2)에서 mi는 무결암의 강도정수이다. D는 암반 교란지수(disturbance factor)로서 0과 1사이의 값을 가지며 발파손상이나 응력이완에 따른 암반의 교란정도를 반영한다. TBM으로 굴착된 터널의 주변암반과 같이 굴착과정에서 손상이 미미한 경우 0D=이며, 노천채굴광산의 생산발파 과정에서 형성된 사면처럼 발파손상을 심하게 받은 암반의 경우 1D=이다. Fig. 1(a)은 식 (1)을 도시한 것으로 GHB식이 예측하는 일축압축강도(σc)와 일축인장강도(σt)는 각각 σcisa, σcis/mb이다.

Fig. 1.

The GHB failure criterion in (a) σ3-σ1 space and (b) σ-τ space.

GHB 함수와 M-C 강도정수

GHB 파괴함수가 비선형 함수이므로 수치해석적 활용 측면에서 선형함수에 비해 불편하다는 약점을 극복하기 위해 GHB식을 M-C식의 틀 안에서 수치해석적으로 실행시키려는 연구들이 시도되었다(Li, et al., 2008; Shen et al., 2012). Fig. 1(b)에 도시한 것과 같이 GHB 파괴포락선의 한 점에서 접선을 그으면 이 직선의 기울기각과 연직축 절편값은 각각 순간마찰각(instantaneous friction angle, ϕi)과 순간점착력(instantaneous cohesion, ci)이 된다. 그러므로 GHB식을 마찰각과 점착력이 연속적으로 변하는 M-C 파괴기준식으로 간주하여 수치해석적으로 실행시킬 수 있다(Dawson et al., 2000). Yang and Yin(2006), Lee(2014), Lee and Pietruszczak(2017)은 ci와 ϕi 사이에 다음의 관계식이 성립함을 보였다.

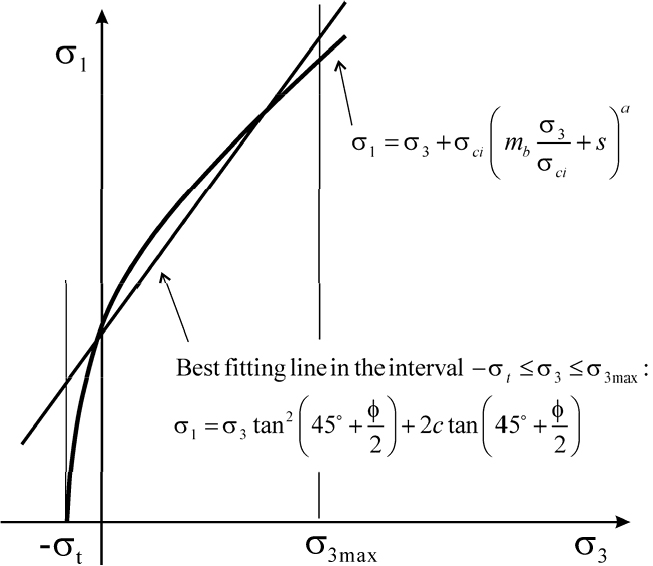
한편, 특정 최소주응력 구간에서 GHB식을 선형 M-C식으로 근사시키는 방법도 시도되었다(Sofianos and Nomikos, 2006; Lee, 2019). Hoek et al.(2002)은 Fig. 2와 같이 구간 -σt≤σ3≤σ3max에서 식 (1)을 최적 근사시키는 M-C식의 마찰각과 점착력을 암반의 등가강도정수로 제안하였고 그 결과는 식 (6), 식 (7)과 같다. Lee(2019) 또한 이와 동일한 결과 식을 유도하였다.

여기서 σ3n=σ3max/σci이고, σ3max는 사면해석의 경우 다음 식으로 계산하는 것이 제안되었다.

Fig. 2.

Linear approximation of the GHB criterion (modified from Hoek et al., 2002).

식 (8)에서 γ는 암반의 단위중량이고 H는 사면의 높이다. 또한 σcm은 암반의 일축압축강도로서 다음 식을 이용하여 추정할 수 있다(Hoek et al., 2002).

GHB함수의 근사 Mohr 파괴포락선식

Mohr 파괴포락선의 근사식

전술한 바와 같이 GSI≠100 일 때 GHB식의 전단강도(τf)와 수직응력(σ)의 관계, 즉 Mohr 파괴포락선을 명시적 수식으로 정확히 표현하는 방법이 아직까지 개발되지 못하고 있다. 최근 Lee(2018)와 Lee and Pietruszczak(2021)은 비선형 함수를 3차 다항식으로 최적 근사시키는 수학적 방법에 기초하여 근사 Mohr 파괴포락선을 매우 정확한 해석적 수식으로 표현하는 방법을 개발하였다. 이 중 Lee(2018)가 유도한 근사 Mohr 파괴포락선은 다음과 같은 일련의 수식으로 구성된다.

여기서

수직응력 σ에 대응되는 전단강도 τf는 식 (10), (11), (12), (13), (14), (15), (16), (17), (18), (19)을 역순으로 차례로 적용하면 계산할 수 있다. 순간마찰각과 순간점착력의 근사 값은 다음 수식을 이용하여 계산할 수 있다.

한편, Mohr 포락선의 접선 방정식은 τf=σtanϕi+ci의 형태로 표현되므로 GHB식에 내포된 순간마찰각과 순간점착력의 관계가 식 (5)과 같다는 사실을 이용하면 Mohr 파괴포락선의 근사식을 다음과 같이 표현하는 것이 가능하다.

Mohr 파괴포락선 근사식의 정확성 검증

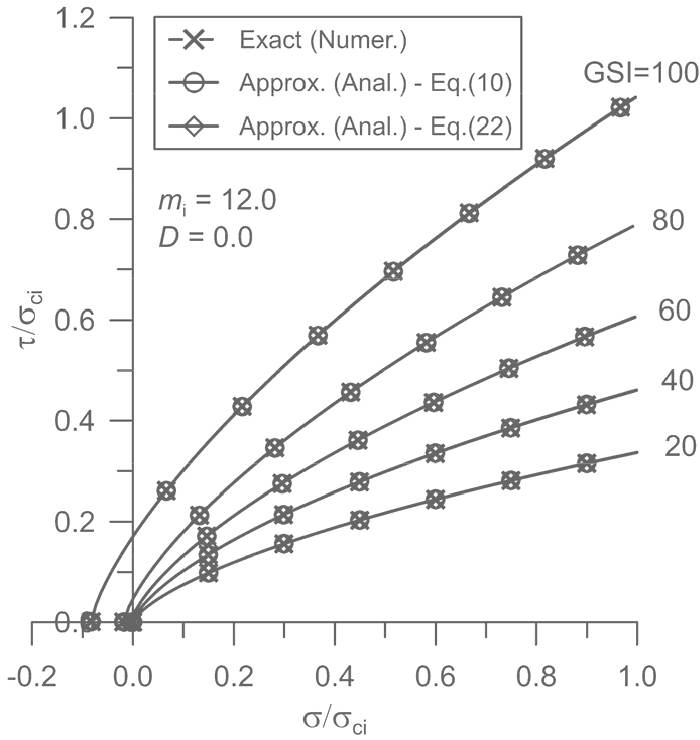
mi12.0, 0.0D=을 가정한 후 다섯 가지 GSI 값 즉, GSI = 20, 40, 60, 80, 100인 경우에 대해 식 (10)과 식 (22)을 이용하여 계산한 근사 Mohr 파괴포락선을 수치해석적으로 구한 정해와 비교하여 Fig. 3에 도시하였다. 두 근사포락선은 정해와 거의 일치하는 정확성을 보여주고 있다. 두 근사포락선의 상대적 정확성을 더 자세히 분석하기 위해 GSI = 60이고 σ/σci= 0.0, 0.2, 0.4, 0.6, 0.8, 1.0인 경우의 전단강도 계산 결과를 Table 1에 제시하였다. 식 (10)으로 계산한 전단강도의 백분율 오차의 차수가 10^-1~10^-2의 범위에 있다는 사실이 이 식의 뛰어난 정확성을 확인해준다. 식 (22)의 정확성은 식 (10)에 비해 훨씬 더 우수한 것으로 나타났다. 식 (22)으로 계산한 전단강도의 백분율 오차 차수가 10^-5~10^-7의 범위에 있으므로 식 (22)으로 계산한 전단강도는 훨씬 더 정해에 근사한다는 사실을 확인할 수 있다.

Fig. 3.

Approximate Mohr envelopes compared with the exact envelopes calculated numerically for five different GSI values.

암반의 Mohr 포락선식은 파괴면의 방향을 계산하는 목적으로도 유용하게 활용될 수 있다. 근사 Mohr 포락선의 정확성을 검증하는 또 다른 시도로서 식 (22)을 임계평면법(Pietruszczak and Mroz, 2001)에 적용하여 암반의 파괴면 방향을 계산한 후 그 결과를 이론적으로 정확하게 계산한 파괴면의 방향과 비교하였다. 임계평면법은 주어진 응력조건에서 전단파괴 안전율이 최소가 되는 면의 방향을 찾는 수치해석적 기법이다. 전단파괴 안전율이 최소가 되는 임계면에 작용하는 수직응력(σ)과 전단응력(τ)이 Mohr 파괴포락선식을 만족하면 이 면은 파괴면으로 간주할 수 있다.

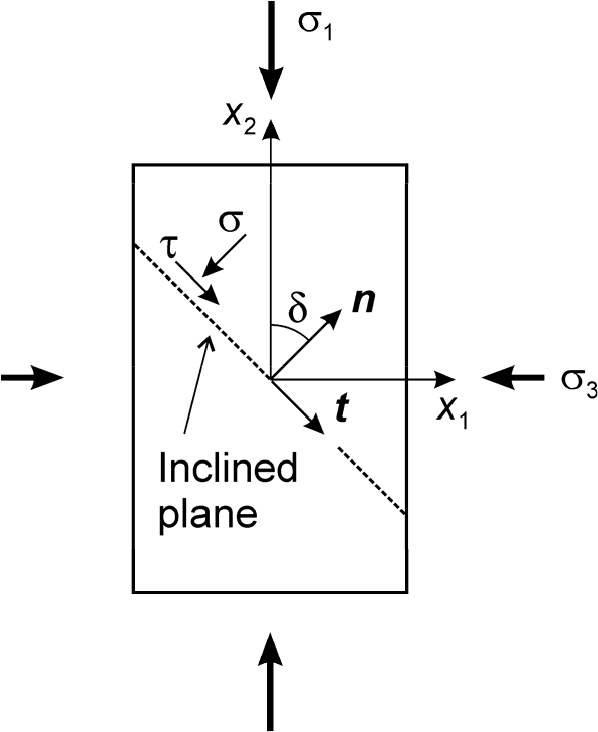
Fig. 4는 임계평면 해석을 위한 2차원 모델로서 경사각이 δ인 경사면을 고려할 때 경사면에 수직한 단위벡터와 평행한 단위벡터는 다음과 같이 표시할 수 있다.

Fig. 4의 모델에 작용하는 2차원 응력텐서는 다음과 같이 표시할 수 있다.

그러므로 경사면에 작용하는 수직응력과 전단응력은 각각 σ=nσnT, τ=tσnT으로 계산할 수 있다. 이 결과와 식 (22)을 이용하면 임계평면법의 목적함수를 다음과 같이 정의할 수 있다.

Fig. 4.

Model for the demonstration of the potential application of the approximate Mohr envelope of the GHB criterion to the critical plane approach.

이제 주어진 응력조건에서 목적함수 F를 최대화시키는 δ값을 찾으면 이 값이 임계면의 경사각이 되고 F=0을 만족하는 임계면의 경사각은 파괴면의 경사각이 된다. 한편 Fig. 1을 참조하면 식 (1)을 이용하여 파괴면의 정확한 경사각은 다음 식과 같이 계산할 수 있다.

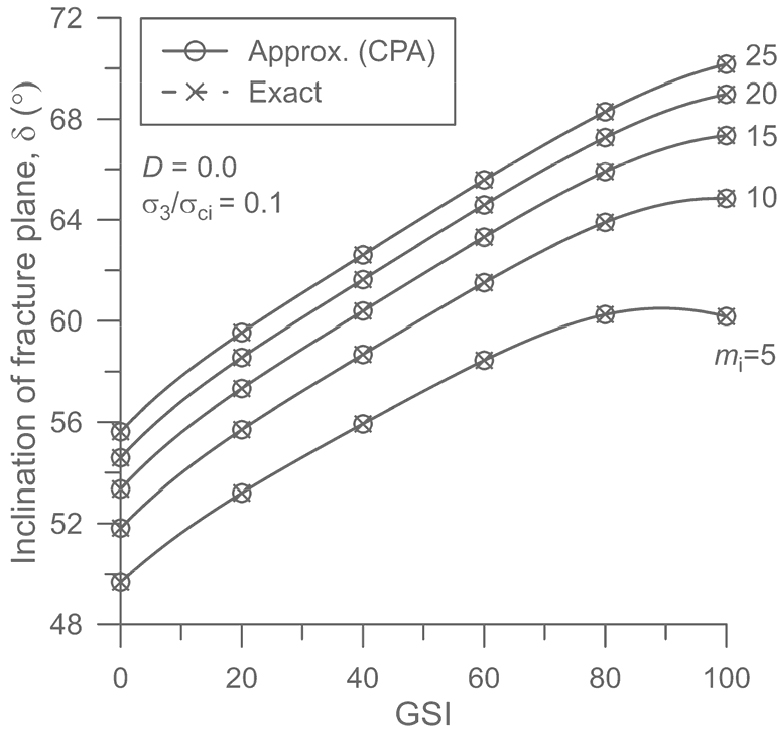
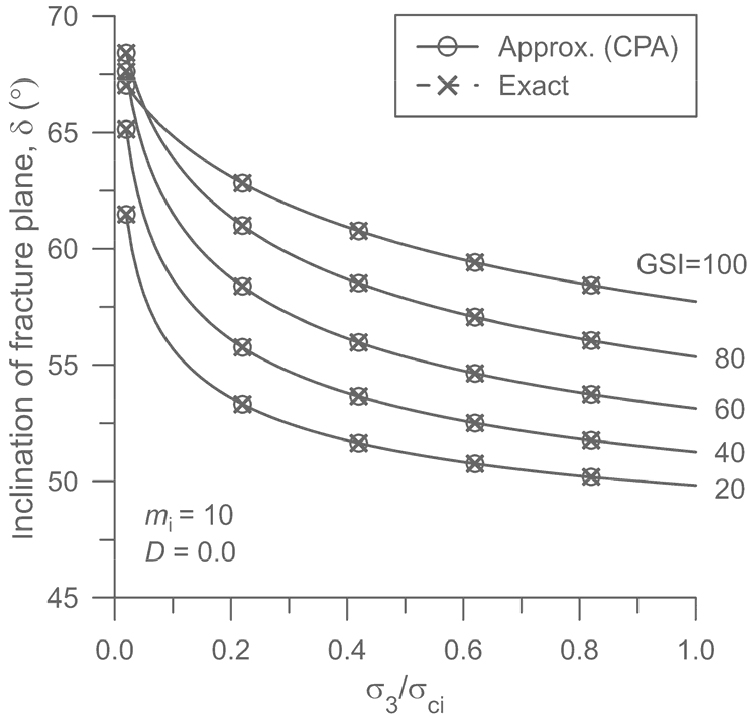
Fig. 5는 σ3/σci=0.1,D=0.0을 가정하고 mi=5,10,15,20,25 일 때 GSI값의 변화에 따른 파괴면의 경사각 변화를 임계평면법으로 계산하고 그 결과를 정확한 값과 비교 도시한 것이다. 임계평면법에서는 근사 Mohr 파괴포락선식 (22)이 이용되었고 정해는 식 (26)으로 계산하였다. GSI와 mi의 증가 즉, 암반의 양호도와 강도가 증가함에 따라 파괴면의 경사가 증가하는 경향을 잘 보여주고 있으며 2가지 방법으로 계산한 결과는 거의 일치하는 결과를 보여준다. mi=5일 때 GSI = 100 부근에서 파괴면의 경사각이 소폭 감소하는 경향을 보이는 것은 mi가 매우 작은 값일 때 GHB 파괴함수가 나타내는 고유한 특성으로 판단된다. Fig. 6은 mi=10,D=0.0을 가정한 후 다섯 가지 GSI 값 즉, GSI = 20, 40, 60, 80, 100의 경우에 대해 구속압(σ3/σci)의 변화에 따른 파괴면 경사각 변화를 임계평면법과 식 (26)으로 각각 계산한 결과를 보여준다. GSI값의 감소와 구속압의 증가에 따라 파괴면 경사가 감소하는 경향을 잘 보여주고 있으며 여기에서도 두 계산 결과는 거의 차이를 보이지 않는다. Fig. 5와 Fig. 6은 이 연구에서 제시한 근사 Mohr 파괴포락선식인 식 (22)이 임계평면법에 잘 활용될 수 있음을 보여줌과 동시에 이 근사 Mohr 포락선식의 정확성을 재차 확인하여 준다.

Fig. 5.

Evolution of the dip angle of the fracture plane with GSI for five different mi values. The approximate dip was calculated by the critical plane approach with Eq. (22), while the exact dip was calculated with Eq. (26).

Fig. 6.

Evolution of the dip angle of the fracture plane with the confining pressure for five different GSI values. The approximate dip was calculated by the critical plane approach with Eq. (22), while the exact dip was calculated with Eq. (26).

근사 Mohr 파괴포락선식을 이용한 사면의 평면파괴 안전율 계산

Bishop의 간편법을 이용한 파괴 안전율 계산 개요

GHB 파괴기준식이 Mohr 파괴포락선식으로 변환되면 GHB 기준식을 손쉽게 한계평형해석법에 적용할 수 있다. 이 연구에서는 새로 제안한 근사 파괴포락선식인 식 (22)의 활용 가능성을 제시하기 위하여 Bishop의 간편법을 이용한 암반사면의 평면파괴 안전율을 계산하였다. 한계평형해석법의 일종인 Bishop의 간편법을 흙사면 해석에 적용하는 경우 일반적으로 원호파괴면을 가정하지만 암반사면의 파괴는 평면파괴가 더 우세하므로 이 연구에서는 평면파괴를 가정하였다. 원호파괴면의 반경을 무한대로 가정할 경우 Bishop의 간편법은 평면파괴 안전율 계산에 적용가능하다.

Fig. 7은 안전율 계산을 위해 설정한 암반사면 해석모델을 보여준다. 사면상부 선단에서 xc 만큼 떨어진 위치에 존재하는 깊이 d의 연직 인장균열 바닥과 사면의 하단을 연결하는 평면을 잠재적 평면파괴면으로 가정하였다. 그림에서 βf,βp는 각각 사면각과 파괴면의 경사각이다. b는 절편의 폭이고, Ei와 Vi은 각각 i번째 절편(slice)의 좌우측 경계면에 작용하는 수직력과 전단력이다. Ni와 (Ti)m은 각각 절편의 바닥면에 수직한 방향과 평행한 방향으로 발생하는 반력성분이고, σi와 τf,i/FS는 대응되는 수직응력과 전단응력이다. Bishop의 간편법에서 흔히 가정하는 것처럼 절편의 경계면에 작용하는 전단력의 변화를 무시하면 i번째 절편의 연직방향 평형조건식은 다음식과 같이 표시된다.

또는

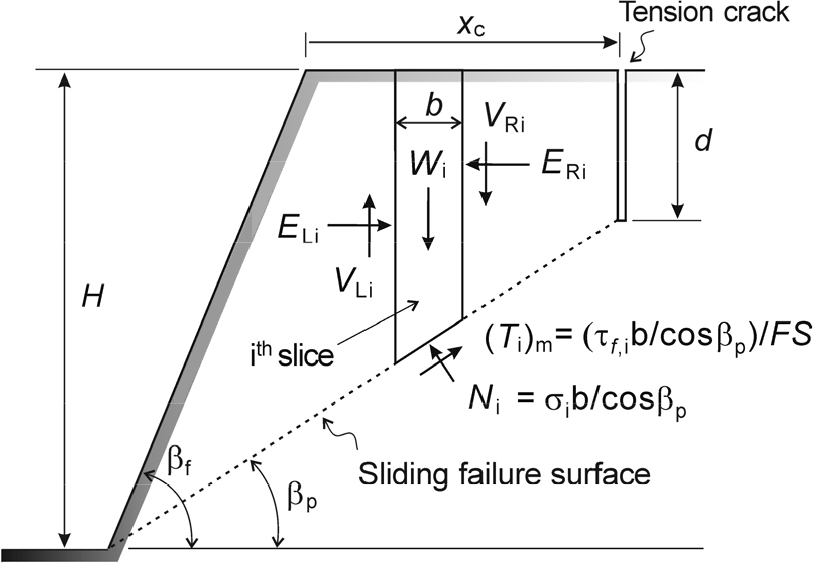
Fig. 7.

Rock slope model for the calculation of the factor of safety for the plane failure based on the simplified method (modified from Lee and Pietruszczak, 2021).

한편 암반블록 전체의 미끄러짐에 대한 모멘트 평형조건은 다음 식으로 표시할 수 있다.

사면의 평면파괴 안전율 계산은 식 (28)과 식 (29)의 FS가 충분히 가까워지도록 시행착오적으로 FS를 결정하는 문제로 귀착된다.

근사 Mohr 파괴포락선과 등가 Mohr 강도정수를 이용한 사면 안전율 계산 결과 비교

앞 절에서 설명한 Bishop의 간편법을 이용하여 Fig. 7의 사면모델에 대해 평면파괴 안전율을 계산하였다. 식 (22)로 주어지는 비선형 근사 Mohr 포락선식과 식 (6)과 (7)로 정의되는 선형근사 Mohr 포락선식을 각각 암반의 전단강도 함수 τf(σi)로 적용하여 계산한 안전율 결과를 비교하였다. 암반의 역학적 상수 값으로 mi=12,σci=20MPa,D=0.0,γ=0.026MPa/m을 가정하였다. 사면의 높이(H)는 30 m, 사면각(βf)은 70°, 평면파괴면의 경사각(βp)는 50°로 가정하였고 사면 상부 면에 존재하는 연직 인장균열은 깊이(d)가 각각 5 m, 10 m인 2가지 경우를 해석하였다. βp=50°을 가정하였으므로 사면 상단에서 두 연직균열까지의 수평거리(xc)는 각각 10.06 m, 5.86 m이 된다.

Fig. 8은 GSI값의 변화에 따른 사면 평면파괴 안전율의 변화를 도시한 것이다. 예상과 같이 GSI값이 커지면 안전율이 커지는 경향을 잘 보여준다. 특히 GSI > 60 일 때 안전율의 증가율이 급격히 커짐을 보여준다. 균열 깊이를 달리하여 해석한 2가지 경우 모두 구간 0 < GSI < 80에서는 Hoek et al.(2002)의 선형근사 Mohr 포락선을 적용할 때 더 큰 안전율이 계산되었고, 구간 80 < GSI < 100에서는 비선형 근사 Mohr 파괴포락선 즉, 식 (22)을 이용할 때 더 큰 안전율이 계산되었다. 균열깊이 변화에 따른 안전율의 변화는 예상보다 크지 않음을 보여준다. 이는 βp가 50°로 일정한 상황에서 균열깊이가 깊어지면 xc가 작아져서 미끄러지는 암반블록 전체의 부피가 감소 즉, 암반블록의 중량이 감소한다는 사실과 관련성이 있는 것으로 추측된다. Fig. 8에서 관찰되는 차이를 보다 정량적으로 분석하기 위해 두 파괴포락선으로 계산한 안전율의 차이를 식 (22)이 적용된 안전율 기준 백분율로 계산하고 그 결과를 Fig. 9에 도시하였다. 인장균열 깊이가 다른 두 가지 경우 모두 GSI≈32일 때 안전율의 차이가 가장 크게 나타나며 그 크기는 d=5 m, d=5 m일 때 각각 29%, 27% 정도이다. 구간 80 < GSI < 100에서 안전율의 차이는 4%이내로서 8% 이상 차이를 보이는 구간 0 < GSI <70의 경우보다 상대적으로 크지 않는 것으로 나타났다. 결론적으로 Heok et al.(2002)이 제안한 선형근사 Mohr 파괴포락선을 이용하여 사면의 평면파괴 안전율을 계산하면 구간 0 < GSI < 80에서는 원 GHB파괴함수를 활용하는 경우보다 안전율이 과대평가될 가능성이 있는 것으로 분석되었다.

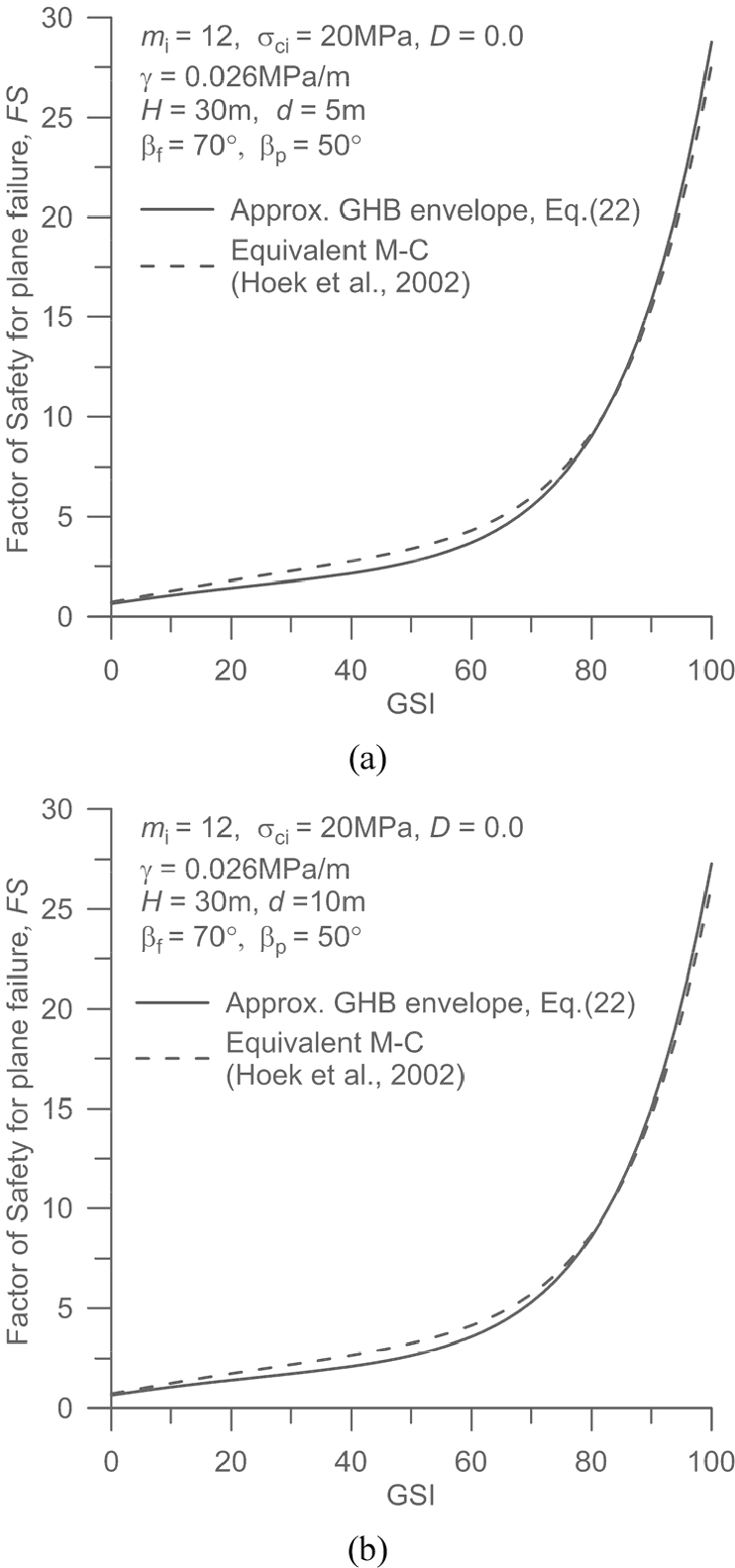
Fig. 8.

Variation of the factor of safety (FS) with GSI for rock slope embedding a vertical tension crack of depth (a) d=5 m and (b) d=10 m. The geometry and rock mass properties of the slope are directly indicated in the figure. The factors of safety based on Eq. (22) are compared with those from the linear approximation of the GHB criterion by Hoek et al. (2002).

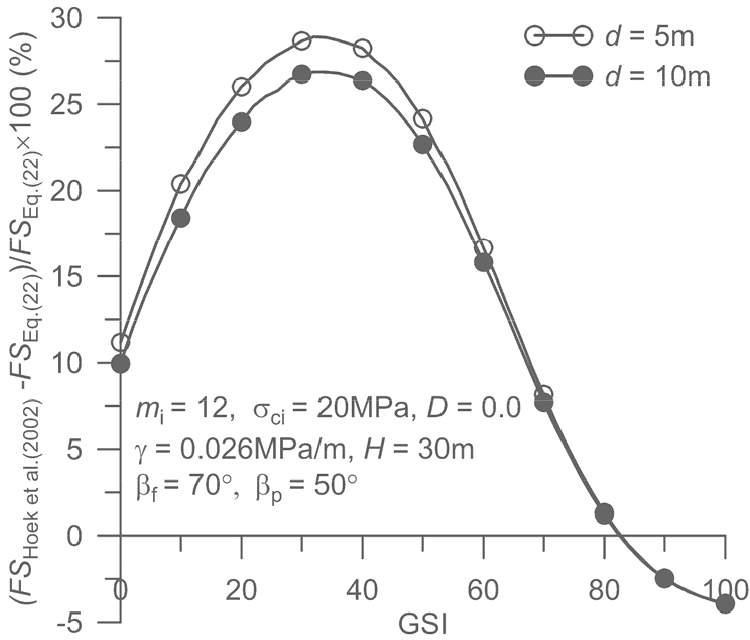
Fig. 9.

Variation of the difference in FS calculated by two different approaches: Eq. (22) and Hoek et al. (2002), with GSI.

Fig. 10은 GSI = 20, 40, 60, 80, 100인 다섯 가지 경우에 대해 사면각 βf의 변화에 따른 안전율의 변화를 보여준다. βf를 제외한 해석조건은 Fig. 8의 경우와 동일하다. 사면각이 커질수록 안전율이 감소하는 경향을 잘 보여준다. 또한 사면각이 낮아짐에 따라 Hoek et al.(2002)의 선형근사식을 이용한 결과와 비선형 GHB 식을 이용한 결과의 차이가 커지는 경향이 있음을 확인할 수 있다. Fig. 11은 GSI = 40인 경우에 대해 두 방법으로 계산한 안전율의 차이를 식 (22)이 적용된 안전율 대비 백분율로 나타낸 것으로서 사면각이 낮아질수록 안전율의 차이가 지수 함수적으로 커지고 있음을 보여준다. 사면의 상단이 인장균열 상부와 만나게 되는 사면각 56°의 경우 선형근사 Mohr 포락선을 이용하여 계산한 안전율은 비선형 GHB 포락선을 이용한 경우보다 약 93% 큰 안전율이 계산되었다.

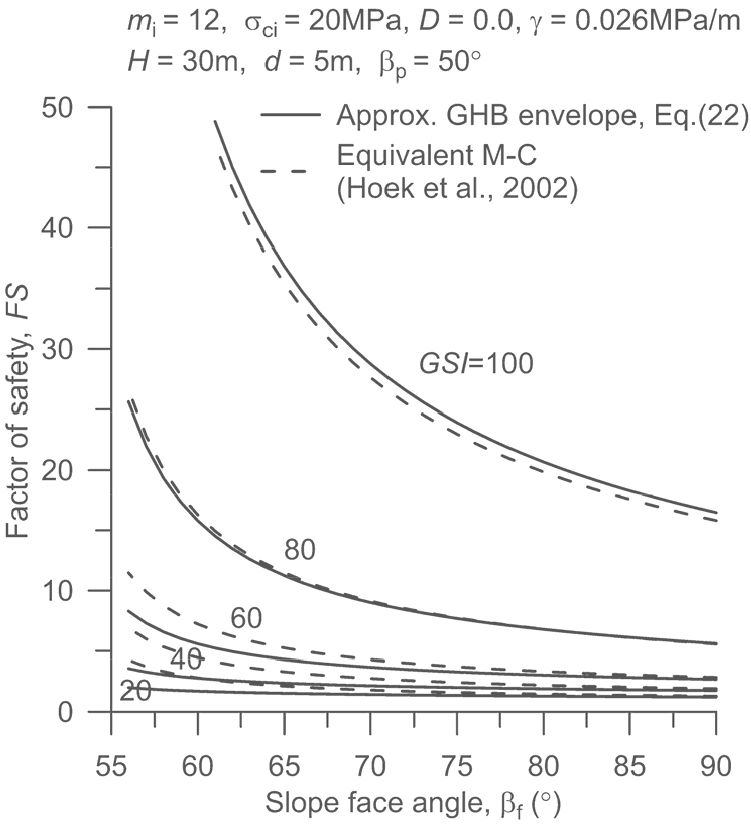
Fig. 10.

Variation of the factor of safety (FS) with the slope face angle βf when the vertical tension crack of depth d is 5 m. The factors of safety based on Eq. (22) are compared with those calculated by adopting the equivalent M-C criterion by Hoek et al. (2002).

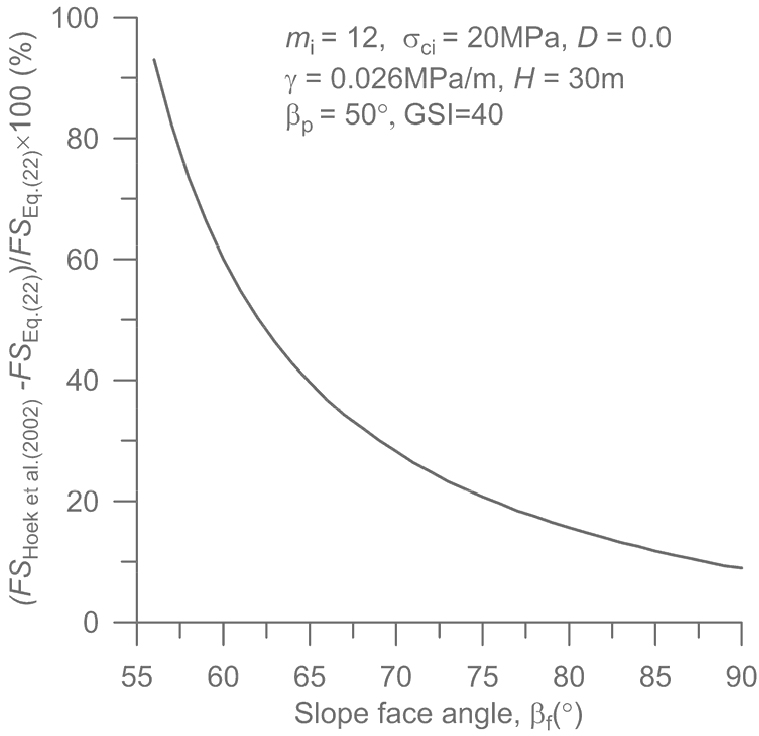
Fig. 11.

Variation of the difference in FS calculated by two different slope sliding conditions: Eq. (22) and Hoek et al. (2002), with the face angle βf.

결 론

최근 활용빈도가 높아지고 있는 GHB 파괴기준식에서는 현장 암반의 양호성을 고려하여 파괴기준식을 구성하는 강도정수를 체계적으로 결정하는 경험식을 제공함과 동시에 암반강도의 비선형성을 고려하고 있으므로 GHB식은 현장 적용성과 강도 예측성능이 매우 우수한 것으로 평가받고 있다. 그러나 이 식은 전단강도와 수직응력의 명시적 관계식 즉, Mohr 파괴포락선식으로 표현하는 것이 곤란하다는 점이 단점으로 지적되어 왔다. Mohr 파괴포락선식을 활용할 수 있으면 암반구조물 안정성 해석에 자주 이용되는 한계평형해석, 상계정리에 기초한 한계해석, 임계평면법 등의 수치해석기법들을 수치해석 코드로 구현하는 작업이 훨씬 수월해진다.

이 연구에서는 Lee(2018)의 연구결과를 바탕으로 정해에 매우 근사하는 GHB 파괴기준식의 Mohr 파괴포락선식을 제안하고 정확성을 검증하였다. 또한 제안된 Mohr 포락선식의 활용사례를 제시하기 위해 이 식을 Bishop의 간편법에 적용하여 암반사면의 평면파괴 안전율을 계산하였고 그 결과를 Hoek et al.(2002)의 선형근사 M-C식을 적용한 경우와 비교 분석하였다. 이 연구를 통해 얻은 주요 결론은 다음과 같다.

(1) GHB함수의 근사 Mohr 파괴락선식으로 계산한 파괴포락선은 수치해석적으로 계산한 정해 파괴포락선과 거의 일치하는 정확성을 보여주었다. 정해에 대한 근사식의 오차 백분율 차수가 10^-5~10^-7 범위라는 점이 제안된 근사 Mohr 포락선식의 정확성을 객관적으로 증명해 준다.

(2) 제안된 근사 Mohr 파괴포락선식이 임계평면법에 활용될 수 있음을 보이기 위해 삼축압축시험을 수치적으로 모사하였다. 수치 삼축압축시험에서는 이 연구에서 제안한 근사 Mohr 파괴포락선식을 파괴면의 활동조건으로 적용하였다. GSI값 및 구속압을 변화시키면서 임계평면법으로 계산한 파괴면의 경사각은 이론적으로 계산한 값과 거의 정확히 일치하는 것으로 나타났다.

(3) 이 연구에서 제안한 근사 Mohr 파괴포락선식과 Hoek et al.(2002)이 제안한 선형근사 M-C을 이용하여 암반사면의 평면파괴 안전율을 계산한 결과 0 < GSI < 80 범위에서 선형근사 Mohr 포락선식이 안전율을 과대평가하는 것으로 나타났다. 특히 GSI = 32 부근에서 가장 큰 안전율 차이를 나타내었다.

(4) 0 < GSI < 80 범위에서 선형근사 Mohr 포락선이 비선형 GHB 포락선에 비해 과대평가하는 평면파괴 안전율 차이는 사면 경사각이 낮을수록 더욱 커지는 것으로 나타났다.

(5) 이 연구는 GHB식이 암반사면의 안전율 계산에 활용되는 것을 전제로 진행되었다. 그러나 지표 근처의 매우 낮은 지압조건과 불량한 암반조건에서 암반사면의 안전율 계산 시 GHB식의 적용성에 대한 의문이 있을 수도 있다. 그러므로 이 연구 결과가 암반사면의 안전율 계산 시 GHB식의 절대적 우수성을 의미하지는 않는다는 점에 주의할 필요가 있다.