서 론
디고스팅 이론
디시그니쳐 이론
합성자료에의 디고스팅 및 디시그니쳐 기법 적용
디고스팅 기법 적용
디시그니쳐 기법 적용
현장자료에 대한 디고스팅 및 디시그니쳐 기법 적용
디고스팅 기법 적용
디시그니쳐 기법 적용
결 론
서 론
고해상 탄성파 탐사는 높은 주파수 대역의 음원을 활용하여 높은 해상도의 지질구조를 나타낼 수 있기 때문에 해양 구조물 설치를 위한 안정성 평가, 지하 매설물 탐지 등 해양 엔지니어링 분야에서 활용하고 있다. 과거에 고해상 탄성파 탐사는 단일채널 아날로그 자료를 획득하여 지하매질에 관한 대략적인 구조를 확인했다. 최근에는, 기술의 발전으로 단일채널 아날로그 탐사뿐만 아니라, 다중채널 디지털 탐사가 가능하게 되어 기존 석유개발 목적의 탐사자료 처리에 사용되는 기법을 적용할 수 있게 되었다(Lee et al., 2004; Lee et al., 2019). 그러나 석유탐사 목적의 탄성파 탐사자료의 처리기법은 상당히 고도화된 반면, 엔지니어링 목적의 고해상 탄성파 탐사의 자료처리는 주로 빈닝(binning), 공통 중심점 모음(Common-Mid-Point gather), NMO보정(Normal-Moveout correction), 중합(stacking) 등의 기본적인 자료처리 기법만이 적용되고 있는 상황이다. 안정성 평가나 지하 매설물 탐지와 같은 목적을 수행하기 위해서는 높은 해상도의 지하 지질구조 영상화가 필수적이어서 탐사자료의 해상도를 향상시킬 수 있는 자료처리 기법 적용이 요구된다.
탄성파 탐사자료의 해상도를 저하시키는 여러 요인 중 고스트(Ghost)는 해수면으로부터 반사되어 기록되는 매우 짧은 주기를 갖는 신호를 의미한다(Lindsey, 1960). 해수층과 공기층의 급격한 임피던스 차이로 인해 해수면의 반사계수는 -1에 가까운 값을 갖게 되어 해수면에서 반사되어 기록되는 고스트는 일차 반사파에 대해 역전된 위상을 갖는다. 또한 추가적인 전파경로로 인해 시간 지연이 발생하게 되는데, 이 시간 지연에 의해 고스트는 일차반사파에 뒤따라 기록되어 탐사자료의 해석을 어렵게 한다. 탐사자료에 기록된 고스트는 고스트 지연시간의 역수에 해당하는 주파수에서 상쇄간섭을 일으켜 유의미한 주파수 대역의 주파수 성분을 상쇄시키기 때문에 탐사자료의 해상도를 저하시키는 요인이 된다. 석유개발 목적의 탐사자료에 대해서는 크게 자료취득과정에서 고스트 신호를 억제하는 기법(Posthumus, 1993; Carlson et al., 2007; Soubaras and Dowle, 2010)과 취득된 자료에 대해 고스트를 제거하는 기법 등이 활발히 연구되고 있다(Grion et al., 2015; Hardwick et al., 2015; Zarkhidze et al., 2016; Sun and Verschuur, 2018). 석유탐사자료와 마찬가지로, 엔지니어링 분야의 고해상 탐사자료 처리에서도 마찬가지로 해상도를 향상시키기 위해서는 고스트를 제거하는 디고스팅 기법이 필요하다.
또한, 탐사 시스템에서 사용하는 음원 송신파형의 영향도 탐사자료 해상도 및 해석에 영향을 미칠 수 있다. 에어건 발파 시 발생하는 버블 효과(bubble effect) 등이 발생할 수 있으며, 이를 완화시키기 위해 송신파형의 영향을 제거하고 원하는 파형요소로 변환하는 과정인 디시그니쳐를 적용할 수 있다(Poole et al., 2013). 디시그니쳐를 수행하기 위해서는 근거리 파형요소(near-field signature)로부터 직접 계산하거나 또는 정교한 모델링 소프트웨어(PGS사의 Nucleus, Oakwood Computing Associates Ltd의 Gundalf 등)를 통해 원거리 파형요소(far-field signature)를 모사해야 한다(Ziolkowski et al., 1982). 많은 연구들이 파형요소들을 모사하여 디시그니쳐를 수행하고 있으며 대부분 석유탐사 자료에 대해 적용되고 있다(Haavik and Landrø, 2016; Davison and Poole, 2015). 그러나 소형선박을 활용하여 고해상 탄성파 탐사를 수행하는 경우, 근거리 파형요소를 기록하기에는 어려움이 있어 원거리 파형요소를 계산하기 어렵다. 따라서 효율적으로 송신파형을 추정할 수 있는 기법을 토대로 송신파형의 영향을 제거하는 디시그니쳐 기법이 고해상 탄성파 탐사자료에도 적용되어야 할 필요가 있다.
본 연구에서는 고해상 탄성파 탐사자료에의 디고스팅과 디시그니쳐의 적용가능성을 확인해보고자 하였다. 디고스팅의 경우에는 음원 고스트를 제거하는 것을, 디시그니쳐는 음원 파형요소의 영향을 제거하고 트레이스를 영위상으로 만드는 과정인 제로 페이징에 목적을 두었다. 본 논문은 먼저, 디고스팅과 디시그니쳐에 대한 이론을 간략히 소개한 후, 합성자료를 이용하여 수치실험을 진행하였다. 디고스팅 수치 예제로는 변동이 포함된 고스트 지연시간을 기반으로 생성된 고스트를 목적함수 기반과 음원심도를 가정했을 경우의 결과를 비교하였으며, 디시그니쳐의 경우에는 그린함수를 이용한 음원추정과 영위상을 갖는 새로운 송신파형을 활용하여 알고리듬의 적용가능 여부를 판단하였다. 수치실험 결과를 기반으로 한국지질자원연구원 포항지질자원실증연구센터에서 취득한 고해상 탄성파 탐사자료에 디고스팅과 디시그니쳐를 적용함으로써 현장자료에 대한 적용성을 확인하고자 한다.
디고스팅 이론
고스트가 포함된 탄성파 트레이스는 일차반사파와 고스트 연산자의 콘볼루션으로 나타낼 수 있으며, 탄성파 트레이스와 고스트 연산자를 주파수 영역에서 표현하면 각각 식 (1, 2)와 같이 나타낼 수 있다.
여기서, 는 각주파수(angular frequency), 는 탄성파 트레이스의 주파수 성분, 는 일차반사파의 주파수 성분, 는 고스트 연산자의 주파수 성분, 은 해수면의 반사계수, 는 허수(), 그리고 는 고스트의 지연시간을 의미한다. 디고스팅 즉, 고스트 제거는 식 (3)과 같이 탄성파 트레이스에서 고스트 연산자를 디콘볼루션하는 결정론적 디고스팅 기법(deterministic deghosting method)을 통해 수행할 수 있다.
여기서, 는 켤레 복소수, 그리고 은 0으로 나눠지는 것을 방지하기 위한 안정화 요소이다. 고스트 제거를 성공적으로 수행하기 위해서는 정확한 고스트 지연시간의 추정이 필수적이다(Zhang et al., 2016). 정확한 고스트 지연시간을 추정하기 위해 본 연구에서는 L1-norm 기반의 목적함수를 사용하여 고스트 지연시간을 추정하고자 하였다(Kim et al., 2016). L1-norm 기반의 목적함수는 식 (4)와 같이 표현할 수 있다.
여기서 는 디고스팅이 적용된 트레이스, 는 해당 트레이스의 샘플을 의미한다. 고스트는 일차반사파와 거의 유사한 진폭을 갖는 반대위상의 신호이기 때문에 고스트가 존재하는 경우 트레이스는 추가 신호를 포함하고 있다. 즉 해당 목적함수를 계산하게 되면 큰 값을 갖는다. 그러나 성공적으로 고스트가 제거되면 일차반사파만이 존재하기 때문에 목적함수의 값이 최소가 되며, 이러한 특성을 이용하여 목적함수를 기반으로 고스트 지연시간을 추정하고자 하였다.
디시그니쳐 이론
디시그니쳐를 수행하기 위한 과정에서, 송신파형 추정을 위해 근거리 파형요소 또는 원거리 파형요소가 필요하다. 그러나 일반적으로 이러한 송신파형을 기록하는 것은 어렵기 때문에 본 연구에서는 기존 완전파형역산, 역시간 구조보정 등에서 사용되고 있는 송신파형추정 기법을 사용하여 디시그니쳐를 수행하고자 하였다. 송신파형 추정은 탄성파 자료에서 직접파에 대해 수행할 수 있으며, 이는 식 (5)와 같이 표현할 수 있다.
여기서, 는 직접파의 주파수 성분, 는 그린함수, 는 실제 송신파형의 주파수 성분을 의미한다. 직접파는 그린함수와 송신파형의 콘볼루션으로 나타낼 수 있으므로 직접파에 그린함수를 디콘볼루션하여 송신파형을 추정할 수 있다. 완전파형역산이나 역시간 구조보정에서의 위 방법을 활용한 송신파형 추정은 디락 델타 함수(Dirac delta function)를 활용한 수치모델링을 통해 그린함수를 계산하여 송신파형을 추정한다(Kim et al., 2013). 그러나 수치모델링 자체의 계산량이 상당히 크기 때문에 디시그니쳐를 위한 송신파형 추정에서는 해당 방법을 적용하기 어렵다고 판단하였다. 본 연구에서는 Koo et al.(2011)이 제안한 방법과 유사하게 균질매질에서의 3차원 그린함수를 활용하여 송신파형을 추정하고자 하였다. 3차원 그린함수를 식 (6)과 같이 표현할 수 있다.
여기서, 은 임의의 위치, 은 송신원의 위치, 그리고 는 배경매질의 속도를 의미한다. 실제로 탄성파 탐사를 수행할 때 이용되는 송신원은 점 송신원이므로, 3차원 그린함수를 이용하였다. 수치모델링을 통해 그린함수를 계산하는 기법에 비해, 3차원 그린함수를 이용할 경우 매우 적은 계산량으로 송신파형을 추정할 수 있다.
디시그니쳐는 추정된 송신파형을 이용하여 탐사자료에 대해 디콘볼루션을 수행한 후, 영위상을 갖는 임의의 송신파형을 콘볼루션하는 과정으로 진행된다. 이는 식 (7)과 같이 나타낼 수 있다.
여기서, 는 디시그니쳐가 적용된 트레이스의 주파수 성분, 는 추정된 송신파형의 주파수 성분, 그리고 는 영위상을 갖는 새로운 송신파형이다.
합성자료에의 디고스팅 및 디시그니쳐 기법 적용
디고스팅 기법 적용
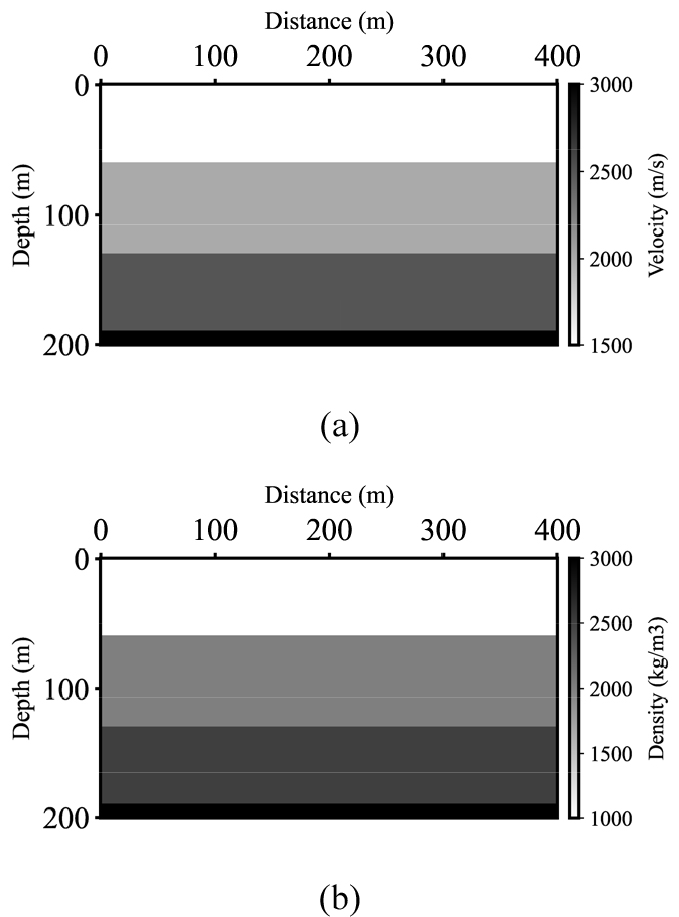
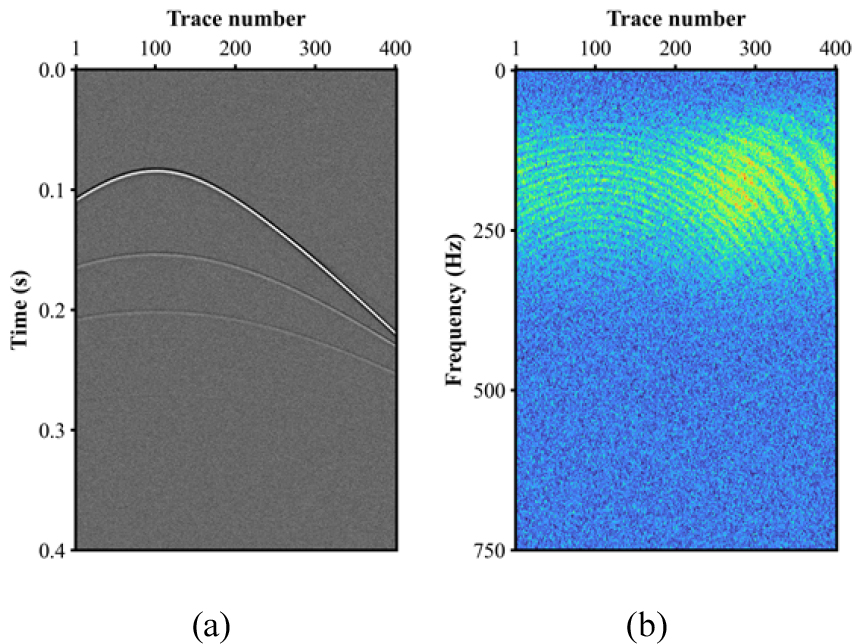
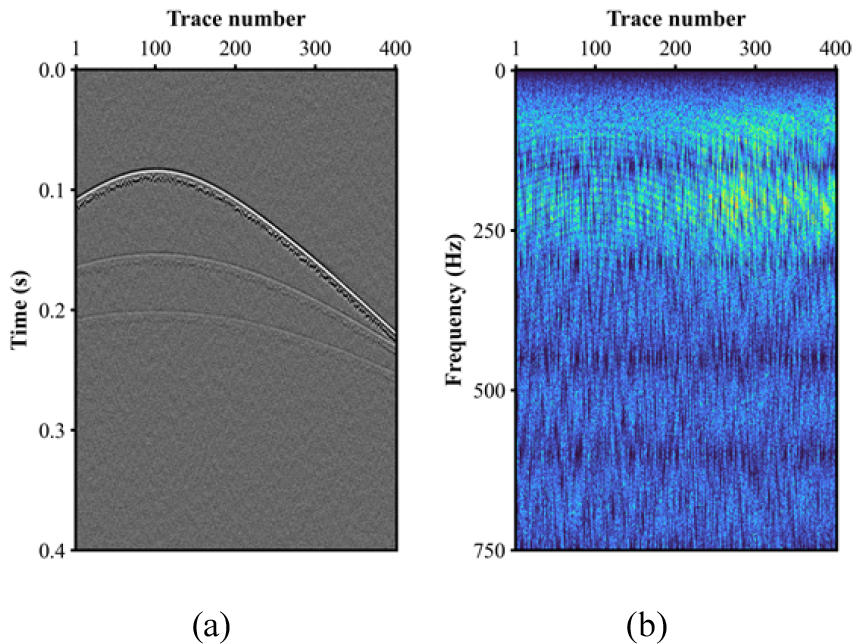
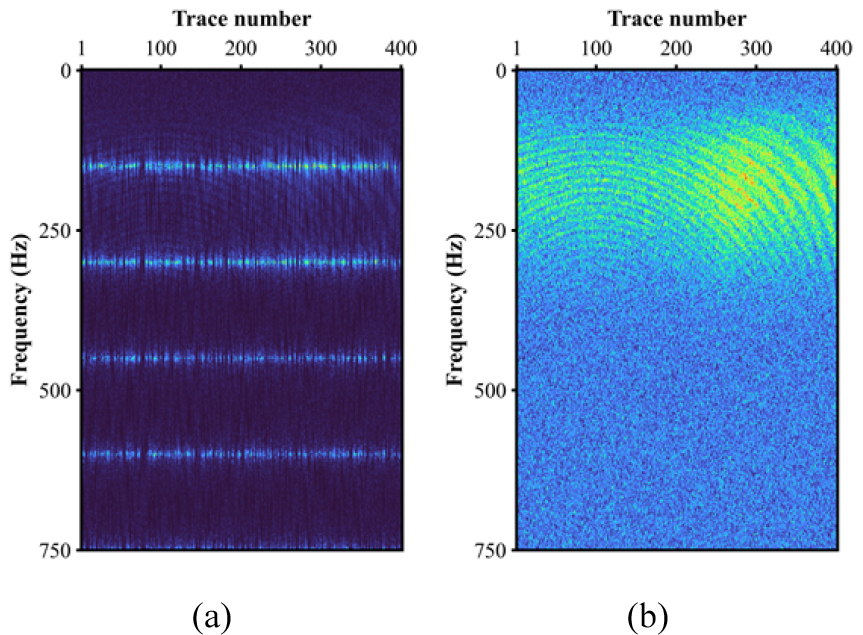
고해상 탄성파 탐사자료에 디고스팅 기법을 적용하기 위해 2차원 유한차분 파동방정식을 기반으로 하는 수치모델링을 활용하여 탄성파 자료를 생성하였다. 자료 생성에 사용된 음원으로는 중심 주파수 200 Hz를 갖는 리커 파형요소를 사용하였으며, 속도 및 밀도 모델은 수층을 포함한 총 4층구조의 모델을 이용하였고(Fig. 1), 채널은 401개, 시간 간격은 0.0001초, 격자 간격은 1 m, 그리고 총 기록시간은 0.4초이다. 합성자료 내 직접파는 수층속도로 구성된 균질 속도 및 밀도매질을 이용하여 모델링한 합성자료를 통해 제거하였다. 생성된 탄성파 합성자료에 신호대 잡음비 5에 해당하는 백색잡음을 추가하였다. 합성자료 및 진폭 스펙트럼은 Fig. 2와 같다. 소규모 고해상 탐사를 수행할 때, 수신기는 심도조절장치가 부착되지 않아 해수면에 매우 근접한 상태이므로 본 연구에서는 음원 고스트 제거만을 고려하였다. 해상에서 발생할 수 있는 고스트 신호를 모사하기 위해 식 (2)와 같이 표현된 고스트 연산자를 이용하였다. 고스트 신호 생성에 사용된 고스트 지연시간은 음원 깊이 5 m를 기준으로 하였으며, 다양한 환경적 변수로 인한 고스트 지연시간의 변동을 고려하기 위해 0.0003 ~ 0.005 ms 사이의 시간지연을 추가적으로 가감하였다. 해수면의 반사계수는 -0.9로 가정하였다. 백색잡음과 고스트 신호가 추가된 탄성파 합성자료와 진폭 스펙트럼은 Fig. 3과 같다. 일차반사파에 뒤이어 역전된 위상을 갖는 고스트 신호가 모사된 것을 확인할 수 있으며(Fig. 3(a)), 고스트 지연시간의 역수에 해당하는 주파수 대역에서 고스트 노치가 발생하여 주파수 성분을 상쇄시키는 것 또한 확인할 수 있다(Fig. 3(b)).
L1-norm 목적함수를 이용한 디고스팅은 고스트 지연시간 추정을 위한 음원 심도의 범위를 3 m ~ 7 m(0.04 m 간격, 101개 구간)로 설정하여 해당 심도에 따른 고스트 지연시간을 계산하였으며, 매 고스트 지연시간에 따른 디고스팅이 적용된 트레이스의 L1-norm 값을 계산하여 최소가 되는 지점의 고스트 지연시간을 최적값으로 간주하였다. L1-norm 목적함수를 이용한 디고스팅 결과와 비교하기 위해 음원 심도가 5 m로 가정된 상황에서의 고스트 지연시간을 이용하여 고스트 제거를 추가적으로 수행하였다.
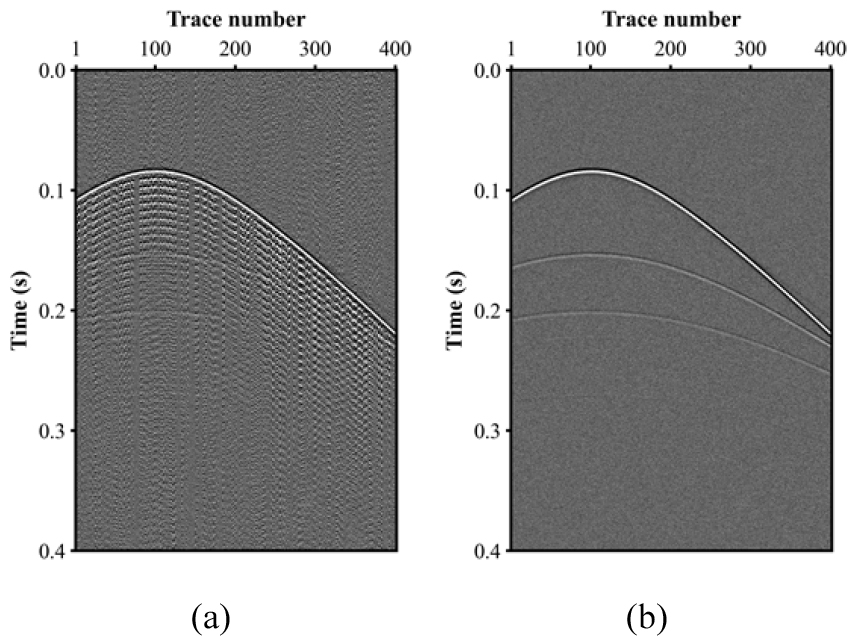
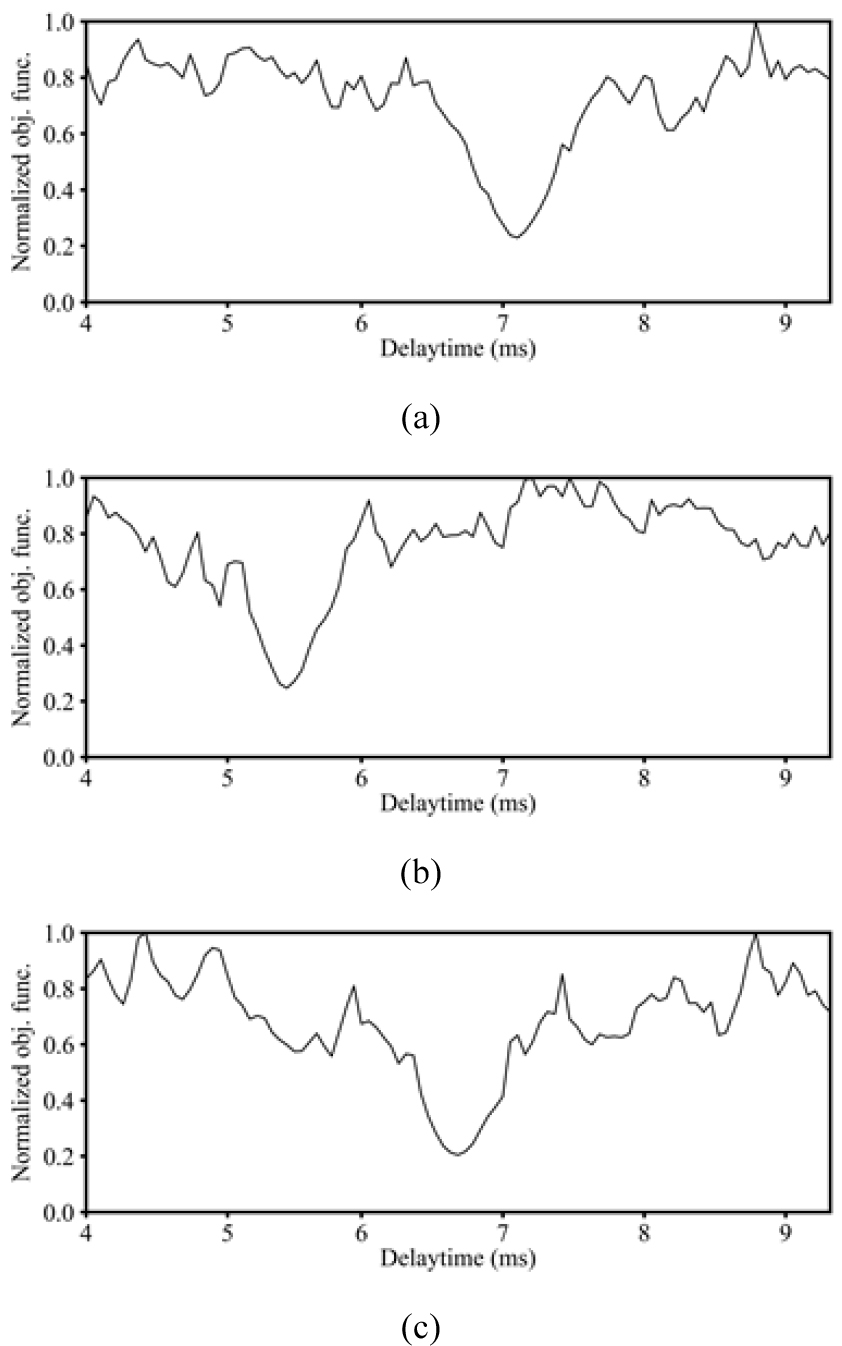
Fig. 4는 음원 심도를 5 m로 가정하여 디고스팅을 수행한 경우와 L1-norm을 통해 고스트 지연시간을 추정하여 디고스팅을 수행한 경우의 결과를 나타낸다. Fig. 4(a)의 경우 정확하지 않은 고스트 지연시간으로 인해 일차반사파에 뒤이어 상당한 떨림 효과(ringing effect)가 발생한 것을 확인할 수 있다. 반면, L1-norm을 기반으로 고스트 지연시간을 추정하여 디고스팅을 수행할 경우 상당히 높은 정확도로 고스트가 제거된 것을 확인할 수 있다(Fig. 4(b)). 보다 더 정확한 비교를 위해 각 결과의 진폭 스펙트럼을 Fig. 5와 같이 도시하였다. Fig. 5(a)의 경우 실제 고스트가 발생시킨 노치와 고스트 제거 연산자가 보상하는 노치의 주파수가 일치하지 않기 때문에 특정 주파수 성분들이 증폭된 것을 확인할 수 있다. 즉, 고스트 지연시간이 정확하게 추정되지 않을 경우 특정 주파수 성분들의 증폭으로 인해 탐사자료 전반에 걸쳐 떨림 현상이 발생하게 된다. 한편, Fig. 5(b)의 경우, 보다 더 정확한 고스트 지연시간으로 인해 노치 주파수에 해당하는 주파수 성분이 정확히 복원된 것을 확인할 수 있으며, 기존 고스트가 존재하지 않는 자료의 진폭 스펙트럼(Fig. 2(b))과 매우 흡사한 것을 통해 고스트가 제거된 것을 확인할 수 있다. 추가적으로 50번째, 150번째 그리고 250번째 트레이스에서의 디고스팅 수행에 사용된 L1-norm 값을 도시하였다(Fig. 6). Fig. 6과 같이 목적함수 값이 최소가 되는 지점의 고스트 지연시간을 활용하였다. 해당 트레이스에서의 실제 고스트 지연시간은 각각 7.09, 5.43, 6.67 ms이며, L1-norm 목적함수를 통해 추정된 고스트 지연시간은 각각 7.09, 5.44, 6.67 ms로 상당한 정확도로 추정한 것을 확인할 수 있다.
디시그니쳐 기법 적용
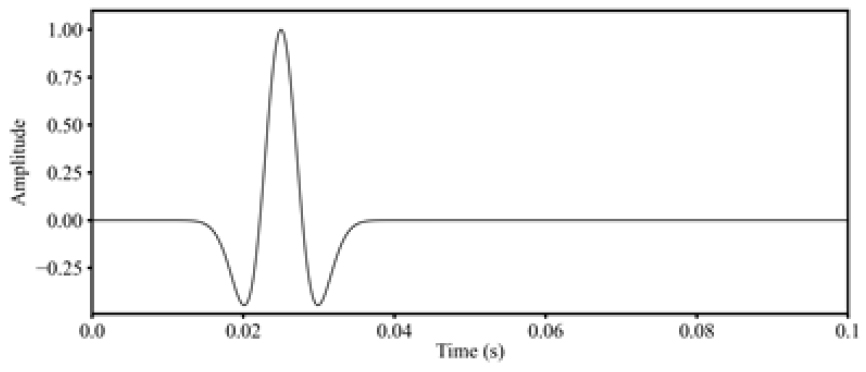
현장자료에 디시그니쳐 기법을 적용하기 앞서, 3차원 유한차분 파동방정식에 기반한 수치모델링을 활용하여 합성자료를 생성하였다. 합성자료 생성에 사용된 송신파형은 240 Hz의 최대 주파수를 갖는 1차 미분 가우스 신호이다. 자료는 총 100채널, 근거리 오프셋은 80 m, 채널간격은 1 m, 시간간격 0.1 ms, 그리고 총 기록시간은 0.2 s이다.
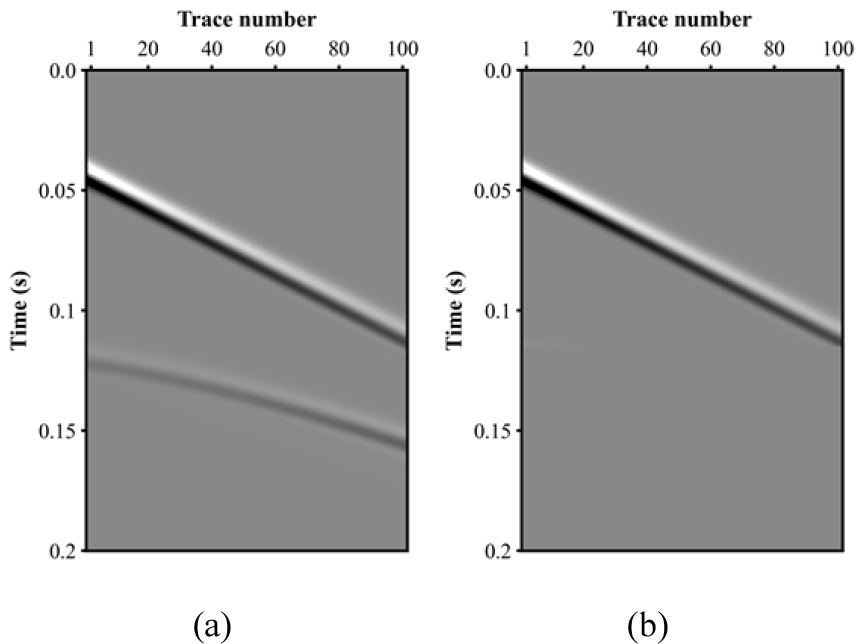
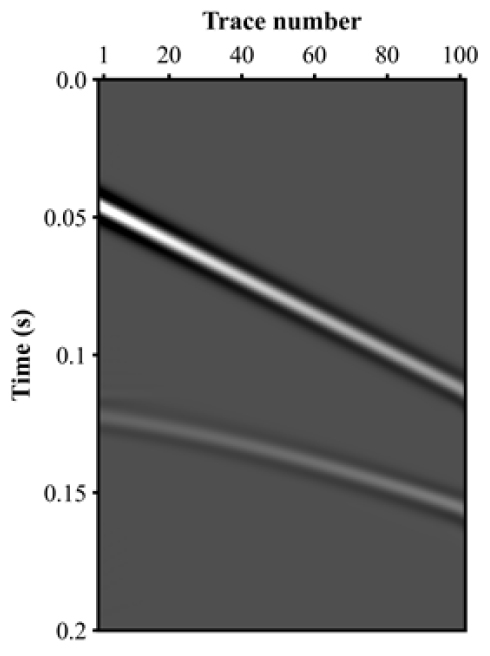
합성자료 생성에 사용한 모델은 2층구조 속도모델 이용하였다(0 ~ 80 m : 1,500 m/s, 80 ~ 200 m : 2,500 m/s). 생성된 자료와 디시그니쳐 기법을 적용하기 위해 일차반사파를 뮤팅한 자료는 Fig. 7과 같다.
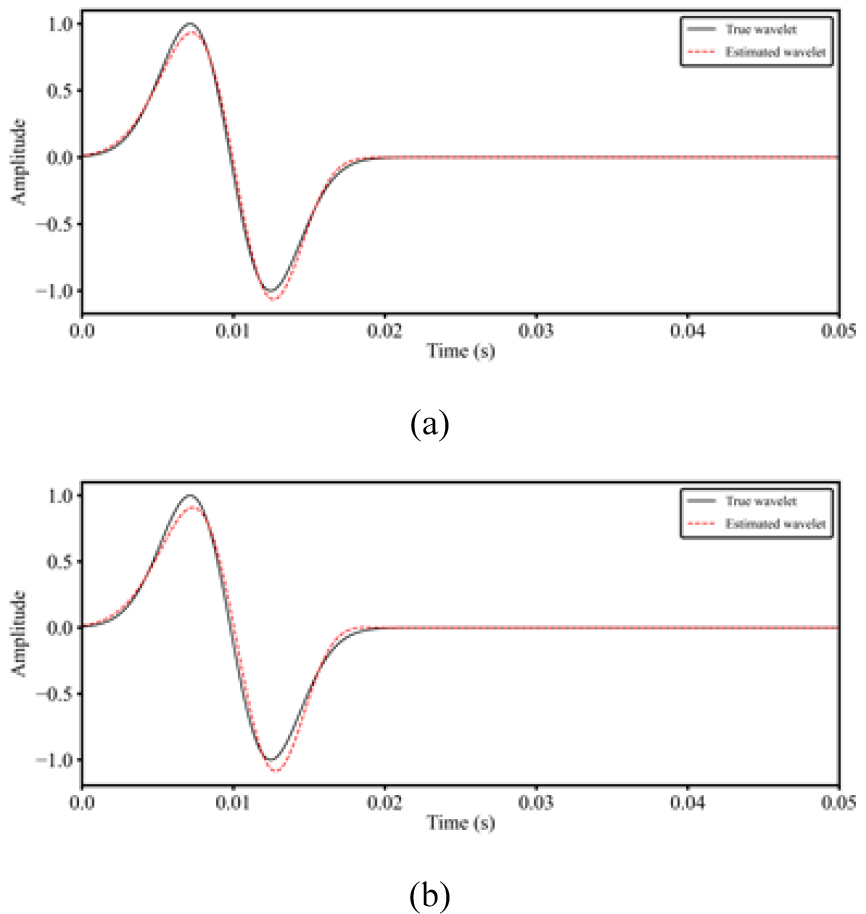
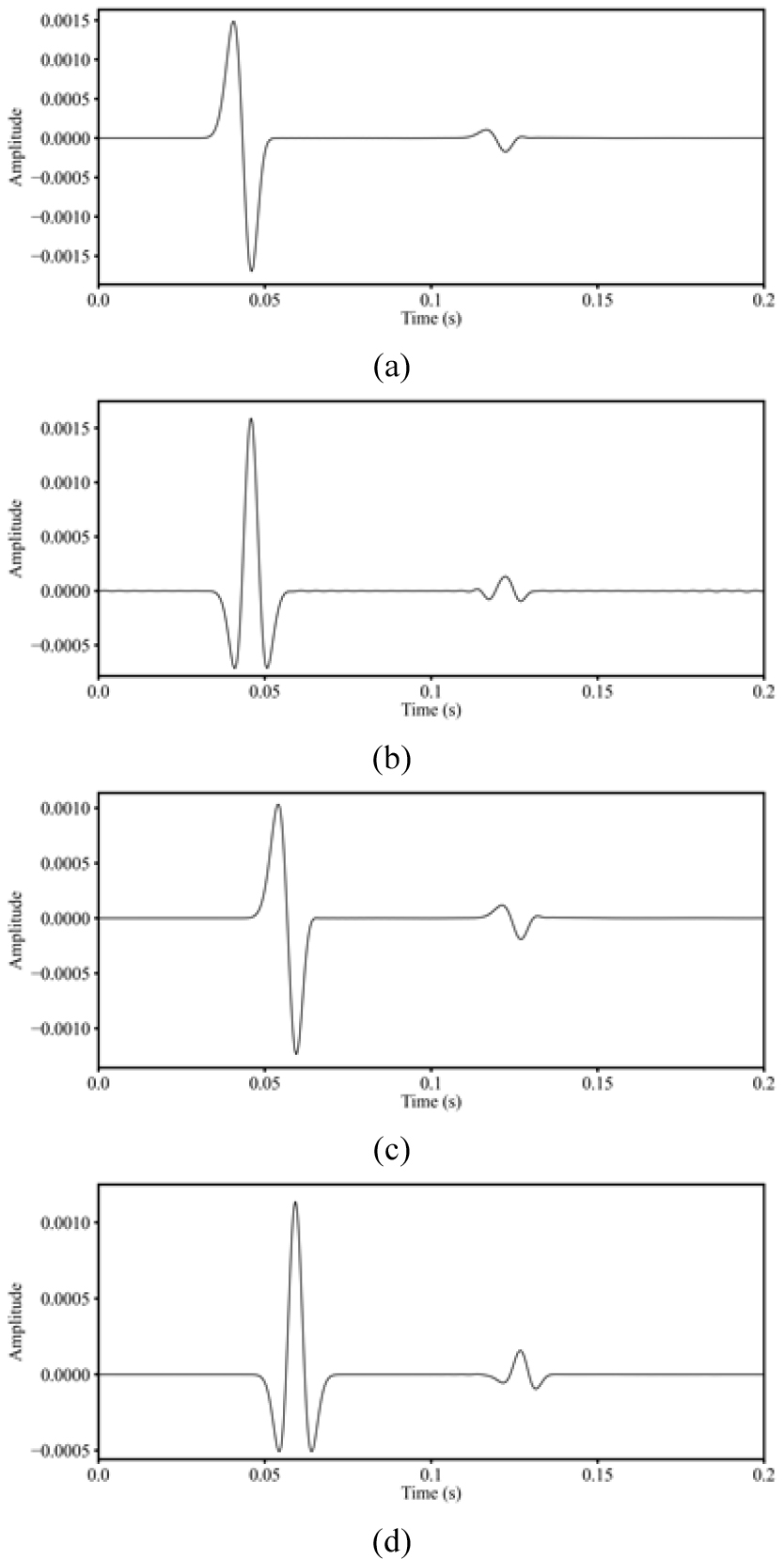
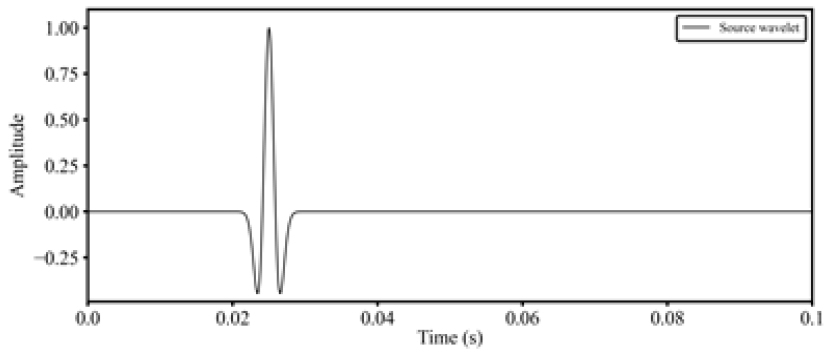
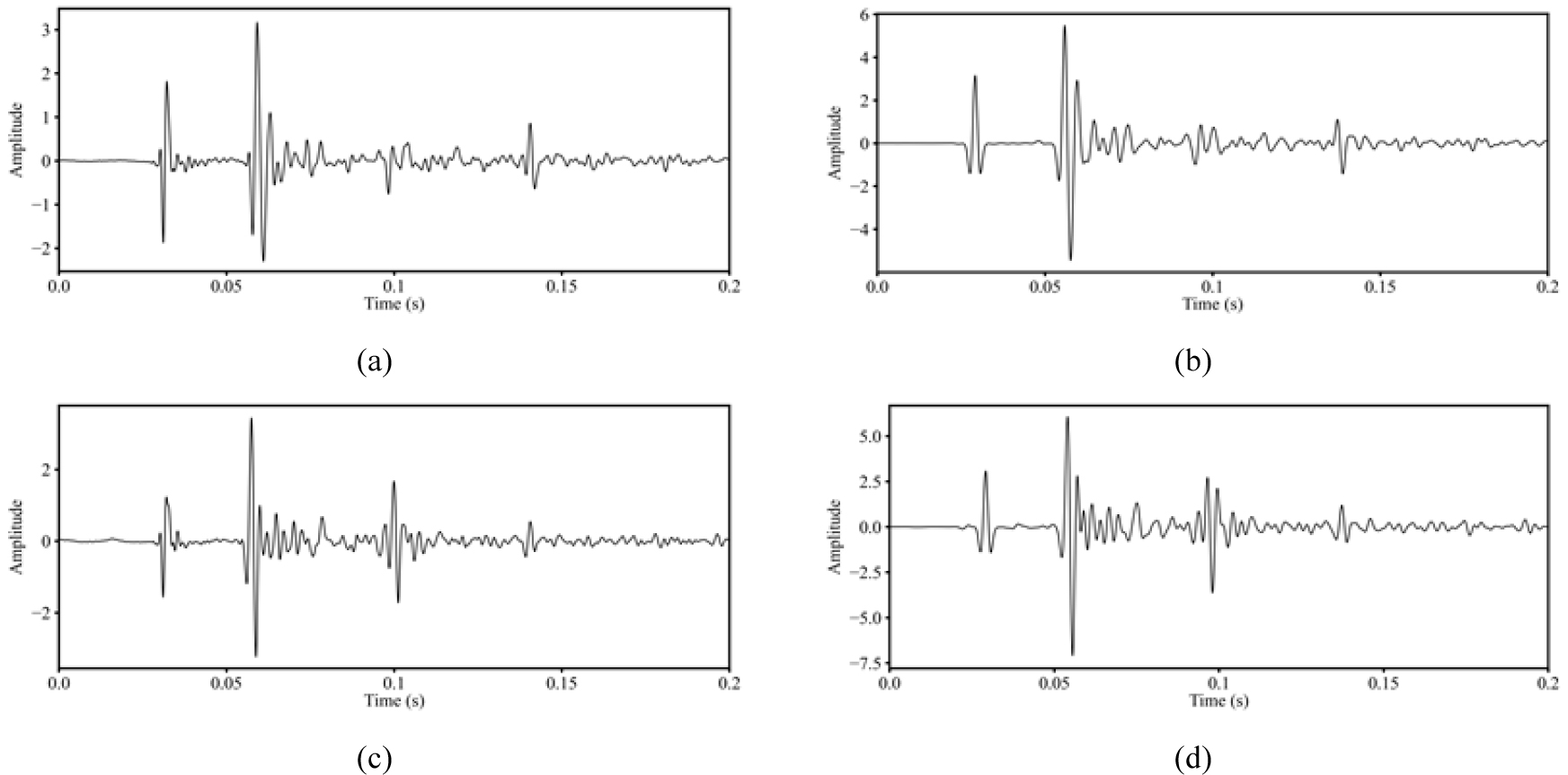
3차원 그린함수와 직접파 신호를 활용하여 디시그니쳐를 수행하기 위한 음원 추정을 수행하였다. 실제 사용된 송신파형과 송신파형 추정을 통해 도출된 송신파형은 Fig. 8에 도시한 바와 같다. 기존 송신파형과 거의 유사하게 송신파형이 추정된 것을 확인할 수 있다. 추정된 송신파형을 이용하여 탐사자료를 디콘볼루션하고, 영위상을 갖는 새로운 송신파형을 콘볼루션하여 디시그니쳐를 수행하였다. 해당 예제에서는 영위상을 갖는 송신파형으로서, 80 Hz의 지배 주파수를 갖는 리커 파형요소를 이용하였다(Fig. 9). 디시그니쳐 기법이 적용된 탐사자료는 Fig. 10과 같다. 전체적으로 신호의 위상이 영위상 형태로 변환된 것을 확인할 수 있다. 보다 더 자세한 비교를 위해, 원자료와 디시그니쳐 기법이 적용된 자료에서 1번 및 21번 채널의 트레이스를 추출하여 도시하였다(Fig. 11). 원자료와 비교하였을 때, 탐사자료의 직접파 및 일차반사파 신호의 위상이 영위상에 가까워진 것을 확인할 수 있다.
현장자료에 대한 디고스팅 및 디시그니쳐 기법 적용
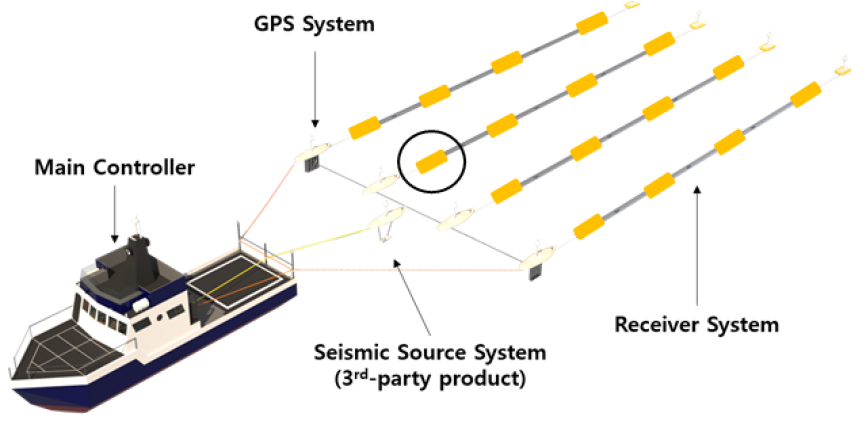
본 연구에서 사용한 현장 탐사자료는 한국지질자원연구원 포항지질자원실증연구센터에서 개발된 EOS-Streamer 시스템을 활용하여 취득되었다. EOS-Streamer는 10톤급 소형 선박을 활용하여 3차원 탄성파 자료취득을 수행할 수 있도록 소형화 및 경량화가 이루어진 4채널 스트리머 4조로 구성된 초고해상 탄성파탐사 시스템이다(Fig. 12) 이는 주 컨트롤러(Main Controller), 탄성파 음원(Source System), 수진 시스템(Receiver System), GPS 측위 시스템 등으로 이루어지게 된다.
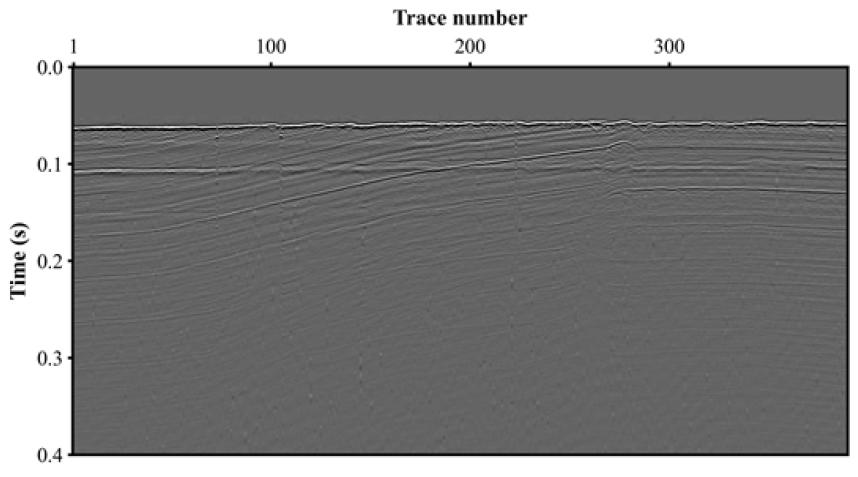
자료취득은 2019년 포항 인근 해역에서 이루어졌다. 4조의 4채널 스트리머를 통해 취득하였으며 시간 샘플링 간격은 0.1 ms, 총 시간 샘플링 개수는 6000개이다. 본 연구에서는 전체 탐사자료 중 3번째 스트리머의 1번 채널을 기준으로 분류된 공통 수신기 모음에 대해 기록시간 0.4초까지의 데이터를 추출하여 사용하였다. 추출된 자료에 디고스팅과 디시그니쳐 기법을 적용하기 전, 너울에 의한 잡음 등을 제거하기 위한 목적으로 대역통과필터(20-50-750-1000 Hz)를 적용하였다.
디고스팅 기법 적용
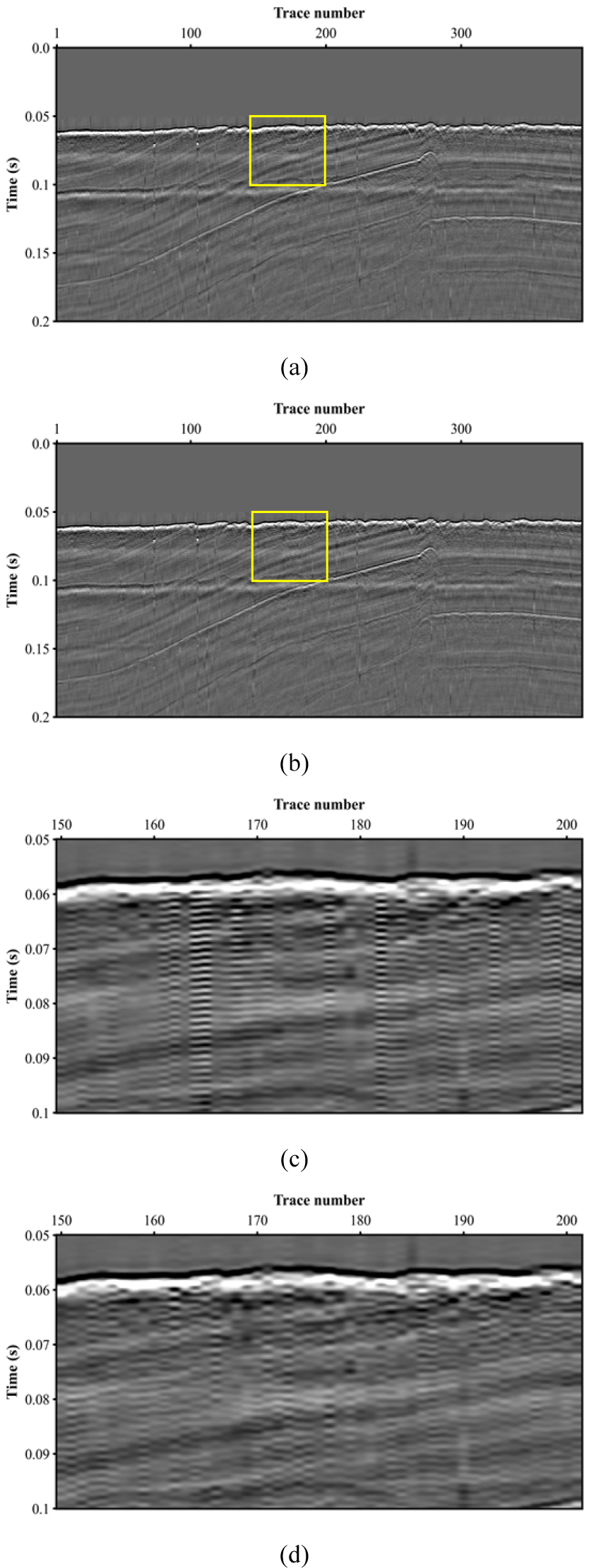
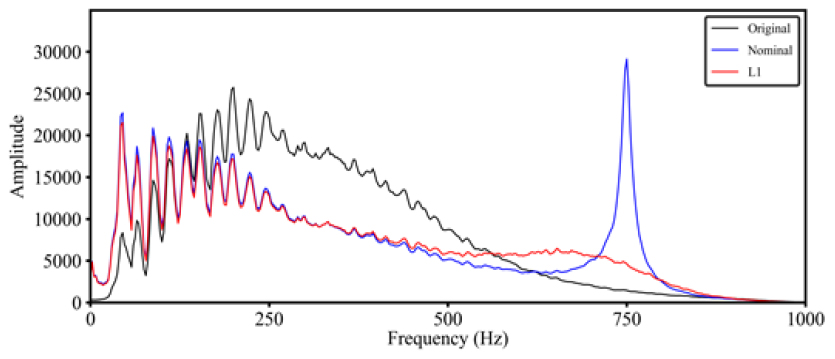
현장자료에 디고스팅을 적용하기 전, 직접파 신호를 뮤팅하였다(Fig. 13). 디고스팅을 수행하기 위한 변수설정으로는, 우선 해수면의 반사계수는 -0.95로 가정하였다. 그리고 고스트 지연시간의 추정을 위한 음원 심도 범위는 0.5 ~ 1.5 m 내 0.01 m 간격으로 선정하였다. 앞선 합성자료 예제와 마찬가지로 목적함수 기반의 디고스팅 결과를 비교하기 위해 음원 심도를 1 m로 가정하여 디고스팅을 추가로 수행하였다. 각각 디고스팅을 통해 도출된 결과는 Fig. 14와 같다. 전체적으로 일차반사파에 바로 뒤이어 기록되던 고스트 신호가 제거된 것을 확인할 수 있으나, 음원 심도를 고정하여 디고스팅을 수행한 결과에서 보다 더 떨림현상이 발생하는 것을 확인할 수 있다. 보다 더 정확한 비교를 위해 원자료와 각 결과의 진폭 스펙트럼을 도시하였다(Fig. 15).
L1-norm 목적함수를 통해 고스트 지연시간을 추정하여 디고스팅을 수행한 결과는 주파수 대역이 보다 더 넓어짐과 동시에 적절하게 균형을 이루는 것을 확인할 수 있다. 그러나 음원 심도를 고정하여 디고스팅을 수행한 결과는 특정 주파수 성분이 비정상적으로 증폭된 것을 확인할 수 있다. 증폭된 주파수 성분으로 인해 탐사자료 상에서 떨림 현상이 심하게 나타나게 되며, 이는 곧 탐사자료의 품질 저하를 야기하게 된다.
디시그니쳐 기법 적용
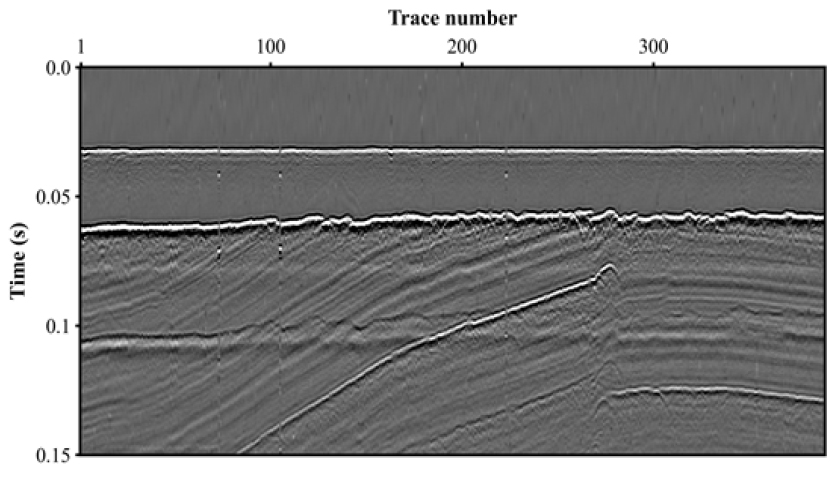
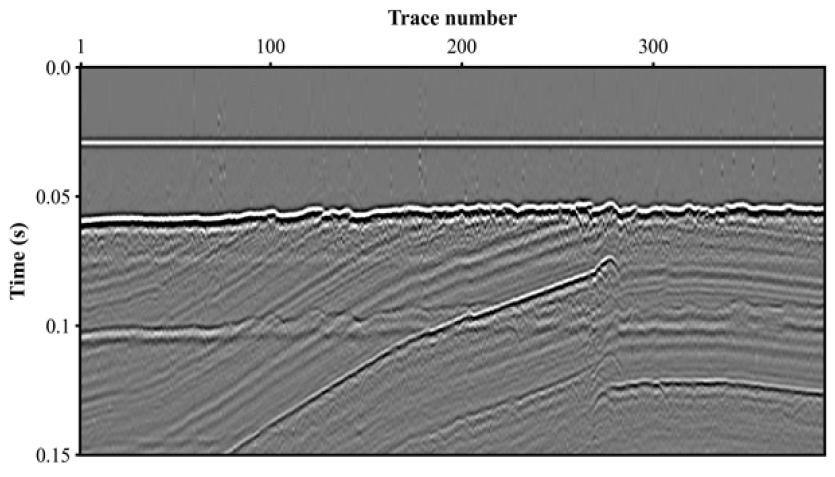
디시그니쳐 적용에 사용될 현장자료는 Fig. 16과 같으며, 탐사자료에 디시그니쳐를 적용하기 위해 먼저 일차반사파를 뮤팅한 후, 직접파를 이용하여 송신파형을 추정하였다. 추정된 송신파형을 이용하여 탐사자료를 디콘볼루션한 후, 지배 주파수 250 Hz의 영위상을 갖는 파형요소(Fig. 17)를 새로 정의하였다. 이 파형요소를 기존 송신파형이 디콘볼루션된 트레이스에 콘볼루션하여 디시그니쳐를 수행하였다. 디시그니쳐를 수행한 결과(Fig. 18)를 확인해보면, 전체적으로 모든 트레이스별 직접파의 위상이 균일하게 형성된 것을 확인할 수 있다. 보다 더 자세한 비교를 위해, 원자료와 디시그니쳐 기법이 적용된 자료에서 100번째 및 200번째 트레이스를 추출하였다(Fig. 19). 원자료의 트레이스와는 달리 디시그니쳐를 적용한 트레이스는 영위상을 갖는 신호를 포함하는 것을 확인할 수 있다.
결 론
본 연구에서는 고해상 탄성파 탐사 자료에 대해 디고스팅과 디시그니쳐 기법의 적용 가능성을 확인하고자 하였다. 먼저 디고스팅은 고스트로 인해 상쇄된 주파수 성분을 복원함으로써 자료의 해상도를 향상시키는 목적으로 수행되었다. 성공적인 디고스팅을 위해서는 정확한 고스트 지연시간을 추정하는 것이 중요하다. 이를 위해 타 목적함수에 비해 강인한 L1-norm 기반의 목적함수를 활용하여 고스트의 지연시간을 추정하였다. 백색잡음과 고스트를 모사한 합성자료에 대해 목적함수를 이용하여 디고스팅을 수행한 결과 상당한 정확도로 고스트 지연시간을 추정하는 것을 확인하였다. 특정 고스트 지연시간을 가정하고 수행한 디고스팅 결과와 비교했을 때, 목적함수 기반의 디고스팅 결과에서는 고스트로 인해 상쇄된 주파수 성분이 복원되었으며 탄성파 자료상에서 고스트가 제거된 것을 확인할 수 있었다. 합성자료의 결과를 기반으로 한국지질자원연구원 포항지질자원실증센터에서 취득한 현장자료에 디고스팅을 적용하였다. 음원 심도를 고정하여 수행한 디고스팅 결과에서는 특정 주파수 성분이 증폭되어 탐사자료 전반에 걸쳐 떨림현상이 발생하였다. 반면 L1-norm 목적함수를 기반으로 한 디고스팅 결과에서는 일차반사파에 뒤이어 기록된 고스트 신호가 약화되었으며, 더 넓은 진폭 스펙트럼을 형성함을 확인하였다. 따라서 L1-norm 목적함수 기반으로 한 디고스팅을 통해 고스트를 효과적으로 약화시킬 수 있음을 확인할 수 있었다.
디시그니쳐는 탐사자료에서 송신파형의 영향을 제거하고 자료처리 수행자가 원하는 파형요소 형태(일반적으로 영위상)로 변환하는 목적으로 수행되었다. 우선 3차원 유한차분 모델링으로부터 제작된 합성자료에서 직접파에 대해 균질 매질에서의 3차원 그린함수를 활용하여 음원 추정을 수행하였다. 실제 사용한 송신파형과 유사하게 추정된 송신파형을 이용하여 트레이스를 디콘볼루션하고, 새롭게 정의된 영위상 파형요소를 콘볼루션하여 디시그니쳐를 수행하였다. 디시그니쳐가 적용된 트레이스는 영위상의 신호를 나타내는 것을 확인할 수 있었다. 합성자료와 마찬가지로, 현장자료에도 디시그니쳐를 적용하여 송신파형의 영향이 제거된 영위상의 신호를 도출할 수 있었다.