Underground EM 1D Modeling and Inversion

In-ky Cho; Kyoung-chan Ahn

doi:10.32390/ksmer.2021.58.5.464

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 31 October 2021. 464-474
https://doi.org/10.32390/ksmer.2021.58.5.464

Underground EM 1D Modeling and Inversion

지중 전자탐사 1차원 모델링 및 역산

In-ky Cho¹^*

Kyoung-chan Ahn²

조 인기¹^*

안 경찬²

¹Professor, Division of Geology & Geophysics, Kangwon National University, Chuncheon, Korea

²Master’s course student, Department of Geophysics, Kangwon National University, Chuncheon, Korea

¹강원대학교 지질·지구물리학부 교수

²강원대학교 지구물리학과 석사과정

^{*Corresponding Author}

ABSTRACT

Electromagnetic (EM) methods have been widely used to detect conductive anomalous bodies. Research and field surveys have focused mainly on surface or airborne EM survey, but few research and field applications for underground EM surveys have been conducted. An underground EM survey, in which the transmitter and receiver are located in a narrow underground space, relies on a one-dimensional (1D) survey because, unlike with a surface EM survey, performing conventional two- or three-dimensional survey is difficult. Accordingly, to interpret underground EM data accurately, proper 1D modeling and inversion that consider the induced-currents generated in both the upper and lower layers of the transmitter are necessary. In this study, 1D underground EM modeling and inversion programs were developed. Then, through 1D inversion experiments on the synthetic data, it was confirmed that frequency and time-domain underground EM surveys could effectively recover underground resistivity stratification.

Keywords

Underground EM

1D Modeling

1D Inversion

전자탐사는 전도성 이상체 탐지에 효과적인 물리탐사법으로 자원탐사, 지반조사 등 다양한 분야에 널리 사용되어 왔다. 전자탐사는 지표 및 항공탐사 위주로 연구 및 현장조사가 수행되었으나, 터널이나 지하 공간 조사 등에 필요한 지중 전자탐사는 연구 및 적용 사례가 많지 않다. 지하에 송수신기가 위치하는 지중 전자탐사는 공간적 제약으로 통상적인 2차원 혹은 3차원 탐사가 어렵기 때문에 1차원 탐사에 의존해야 한다는 제약이 있다. 또한 지중 전자탐사 자료의 정확한 해석을 위해서는 송신기 상부 및 하부 지층에서 발생하는 유도전류를 모두 고려하는 모델링 및 역산법이 필요하다. 이 연구에서는 지중 전자탐사 자료의 해석을 위한 1차원 모델링 및 역산 프로그램을 개발하였다. 또한 수치자료에 대한 역산실험을 통하여 주파수 영역 및 시간 영역 지중 전자탐사는 지하의 전기비저항 층서 구조에 대한 정량적 해석이 가능함을 확인하였다.

키워드

지중 전자탐사

1차원 모델링

1차원 역산

MAIN

서 론
1차원 모델링
1차원 역산
역산 실험
주파수 영역
시간 영역
결론 및 토의

서 론

송수신기가 지하에 위치하는 지중 전자탐사(underground EM, UEM)는 지표 전자탐사(surface EM, SEM)에 비하여 널리 사용되지 못하고 있다. 이는 지하의 경우 접근성이 제한되며, 송수신 시스템의 설치를 위한 공간 확보에 어려움이 있기 때문이다. 그러나 갱도나 터널 내에서 수행되는 물리탐사에서 분해능을 높이기 위해서는 대상체에 근접하여 자료를 획득해야 하며, 이 경우 송수신기는 지하에 위치해야 한다. 또한 자기 송신원(magnetic source)을 사용하는 지중 전자탐사는 비접촉식이라는 강점으로 인하여 단단한 암반으로 이루어진 지하 공간에서도 적용이 가능하다는 장점이 있으며, 터널 시공 중 막장 전방 이상대 탐지 등에 효과적으로 사용될 수 있다(Li et al., 2017).

전자탐사는 대개 지표면에 송수신기가 위치하며, 이때 상부 공기층에서는 유도전류는 물론 반사되어 돌아오는 전자기장은 무시할 수 있다. 그러나 지하에 송신기가 위치하는 전자탐사에서는 송신기 상부와 하부 영역 모두에서 유도전류가 발생하며, 이들은 수신점에서 측정되는 자기장에 영향을 미치게 된다. 따라서 지표 전자탐사 자료해석 프로그램을 사용하여 지중 전자탐사 자료를 해석하게 되면 오차가 수반된다. 물론 송신기 상부층이 전기적으로 거의 부도체에 가까울 경우에는 공기층으로 가정해도 큰 문제가 없으나, 전도성 지층이 발달한 경우에는 심각한 해석상의 오류를 피하기 어렵다(Krivochieva and Chouteau, 2002).

해양 전자탐사가 중요한 물리탐사 문제로 부각되면서 전기 송신원(electric source)이 수중에 위치하는 전자탐사에 관한 연구는 비교적 활발하게 진행되어 왔다(Chave and Cox, 1982; Xiong, 1989; Edwards, 2005; Constable and Weiss, 2006; Um and Alumbaugh, 2007; Key, 2009). 그러나 자기 송신원을 사용하는 지중 전자탐사 모델링 및 역산에 관한 연구는 상대적으로 적은 편에 속한다. 루프 송신원이 지하에 존재할 경우에 대한 시간 및 주파수 영역 자기장 계산식(Das, 1995), 시추공내에서 수행되는 전자탐사 2차원 및 3차원 모델링(Cho and Choi, 1999; Lee et al., 1999), 다양한 송신원에 의한 1차장의 계산(Kim et al., 2009), 시간 영역 전자기장의 계산(Jang and Kim, 2013), 갱내 시간 영역 전자탐사 1차원 모델링에 관한 연구(Krivochieva and Chouteau, 2002) 등이 있으나, 주로 모델링 문제에 편중되어 있다. 한편 소형 루프를 사용하는 전자탐사 1차원 역산에 관한 연구는 수없이 많지만(Huang and Fraser, 2003; Cho and Lim, 2003a, 2003b), 대개 지표 탐사에 국한된다. 반면 지중 전자탐사 자료의 역산에 관한 연구, 특히 갱도나 터널과 같이 좁은 공간에 송수신원이 위치하는 전자탐사 자료의 1차원 역산에 관한 연구는 미미하다. 그러나 최근 터널이나 지하 공간의 개발이 활발해지면서 터널이나 지하 공간 주변의 이상대 탐사를 위한 지중 전자탐사의 적용이 요구되고 있으며, 이들 자료의 해석에 관한 연구가 필요한 실정이다(Li et al., 2017).

이 연구에서는 터널과 같은 좁은 지하 공간에서 수행되는 지중 전자탐사 자료의 해석을 위하여 지중 전자탐사 1차원 모델링 및 역산 프로그램을 개발하였다. 개발된 모델링 프로그램을 사용하여, 지중 전자탐사 자료의 거동 특성을 분석하였다. 또한 순차 모델링을 통하여 얻어진 수치자료에 대한 역산실험을 통하여 지중 전자탐사 자료의 1차원 해석기술을 제시하고자 하였다.

1차원 모델링

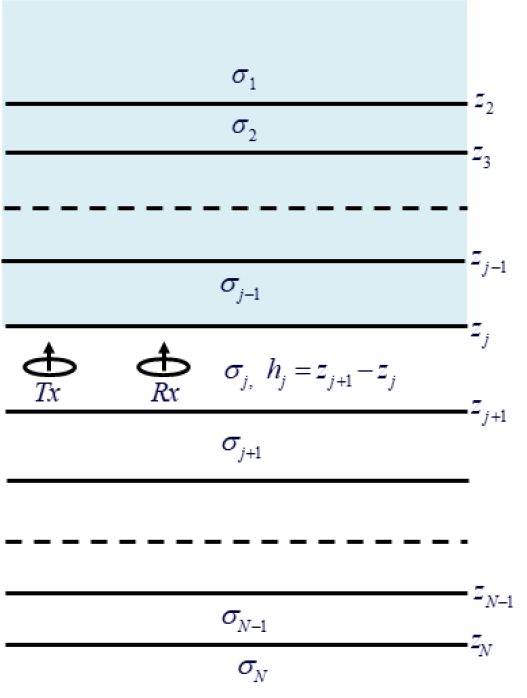
Fig.1에서와 같이 $i$ 번째 층의 전기전도도 $σ_{i}$ , 유전율 $ε_{i}$ , 투자율 $μ_{i}$ 인 수평 다층 구조를 가정하자. 이 경우 수평 다층 구조 내의 $j$ 번째 층에 쌍극자 모멘트 $m$ 인 수평 루프 송신원이 $(0, 0, z_{s})$ 에 위치할 경우, $i$ 번째 층의 일점 $(z, ρ)$ 에서의 TE(transverse electric) 포텐셜은 다음과 같이 Hankel 변환으로 주어진다(Ward and Hohmann, 1988).

(1)

F_{z} (ρ, z) = \frac{{\hat{z}}_{i} m}{2 π} \int_{` 0}^{\infty} {\hat{F}}_{z} (λ) λ J_{0} (λ, ρ) d λ (z_{i} \leq z \leq z_{i + 1}), w h e r e {\hat{F}}_{z} (λ) = a_{i} e^{u_{i} (z - z_{i + 1})} + b_{i} e^{- u_{i} (z - z_{i})} + δ_{i j} \frac{e^{- u_{j} | z - z_{s} |}}{2 u_{j}} .

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F1.jpg

Fig. 1

N-layered 1D model. Each layer $j$ has conductivity $σ_{j}$ and layer top depth $z_{j}$ .

식 (1)에서 $J_{0}$ 는 0차 Bessel 함수, $ρ^{2} = x^{2} + y^{2}, \hat{z_{i}} = i ω μ_{i}, \hat{y_{i}} = σ_{i} + i ω ϵ_{i}, k_{i}^{2} = - \hat{z_{i}} \hat{y_{i}}, u_{i}^{2} = λ^{2} - k_{i}^{2}, a_{i}$ 및 $b_{i}$ 는 감쇠계수, $δ_{i j}$ 는 Kronecker 델타 함수이다. 이 경우 수신점에서의 전기장은

(2)

E = - \nabla \times F = - \nabla \times (F_{z} u_{z}) = \frac{\partial F_{z}}{\partial ρ} u_{ϕ},

자기장은

(3)

H = - {\hat{y}}_{i} F + \frac{1}{{\hat{z}}_{i}} \nabla (\nabla \cdot F) = - {\hat{y}}_{i} F_{z} u_{z} + \frac{1}{{\hat{z}}_{i}} (u_{ρ} \frac{\partial^{2} F_{z}}{\partial ρ \partial z} + u_{z} \frac{\partial^{2} F_{z}}{\partial z^{2}})

로 주어진다(Ward and Hohmann, 1988). 식 (1)을 식 (2)에 대입하면 전기장은

(4)

E_{ϕ} (ρ, z) = \frac{\partial F_{z}}{\partial ρ} = \frac{{\hat{z}}_{i} m}{2 π} \int_{0}^{\infty} (a_{i} e^{u_{i} (z - z_{i + 1})} + b_{i} e^{- u_{i} (z - z_{i})} + δ_{i j} \frac{1}{2 u_{j}} e^{- u_{j} | z - z_{s} |}) λ^{2} J_{1} (λ ρ) d λ

로 주어지며, 식 (1)을 식 (3)에 대입하면 자기장의 수평성분(radial component)은

(5)

H_{ρ} (z, ρ) = \frac{m}{2 π} \int_{0}^{\infty} (a_{i} u_{i} e^{u_{i} (z - z_{i + 1})} - b_{i} u_{i} e^{- u_{i} (z - z_{i})} + δ_{i j} \frac{l}{2} e^{- u_{j} | z - z_{s} |}) λ^{2} J_{1} (λ ρ) d λ

로 주어지며, $l = s i g n (z_{s} - z)$ 이다. 자기장의 수직성분(vertical component)은

(6)

H_{z} (z, ρ) = \frac{m}{2 π} \int_{0}^{\infty} (a_{i} e^{u_{i} (z - z_{i + 1})} - b_{i} e^{- u_{i} (z - z_{i})} + δ_{i j} \frac{1}{2 u_{j}} e^{- u_{j} | z - z_{s} |}) λ^{3} J_{0} (λ ρ) d λ

로 주어진다. 이 연구에서 식 (4), (5), (6)에 주어진 Hankel 변환은 Anderson(1975)의 ZHANKS를 이용하여 계산하였다.

이제 송수신가 모두 $j$ 번째 층에 위치할 경우, 지층 경계면에서 전기장과 자기장의 수평성분은 연속이므로 상향 및 하향 감쇠계수 $a_{j}$ 및 $b_{j}$ 는 다음과 같이 계산된다(Key, 2009).

(7)

a_{j} = (e^{- u_{j} | z_{j + 1} - z_{s} |} + R_{j}^{-} e^{- u_{j} | z_{j} - z_{s} |}) \frac{R_{j}^{+} e^{u_{j} h_{j}}}{1 - R_{j}^{+} R_{j}^{-}} \frac{1}{2 u_{j}},

(8)

b_{j} = (R_{j}^{+} e^{- u_{j} | z_{j + 1} - z_{s} |} + e^{- u_{j} | z_{j} - z_{s} |}) \frac{R_{j}^{-} e^{u_{j} h_{j}}}{1 - R_{j}^{+} R_{j}^{-}} \frac{1}{2 u_{j}} .

식 (7)과 식 (8)에서 $h_{j} = z_{j + 1} - z_{j}$ 로 지층의 두께, $R_{i}^{\pm}$ 는 감쇠계수 비, 즉 TE(transverse electric) 모드 반사계수로 송신원 상부 지층 $(i < j)$ 에서 $R_{i}^{-} = b_{i} / a_{i}$ , 하부 지층 $(i > j)$ 에서는 $R_{i}^{+} = a_{i} / b_{i}$ 로 정의되며, 경계조건을 사용하면 다음과 같은 점화식으로 표현된다.

(9)

R_{i}^{\pm} = \frac{(r_{i}^{+ -} + R_{i \pm 1}^{\pm} e^{- u_{i} h_{i}}) e^{- u_{i} h_{i}}}{1 + r_{i}^{+ -} R_{i \pm 1}^{\pm} e^{- u_{i} h_{i}}}, r_{i}^{\pm} = \frac{u_{i} - u_{i + - 1}}{u_{i} + u_{i + - 1}} and R_{1}^{-} = R_{N}^{+} = 0 .

송신원이 위치한 지층에서의 감쇠계수 비 $R_{i}^{-}$ 는 $R_{1}^{-} = 0, R_{i}^{+}$ 는 $R_{N}^{+} = 0$ 으로부터 식 (9)를 사용하여 순차적으로 계산할 수 있으며, 수신점이 송신기와 다른 지층에 위치할 경우에도 감쇠계수 $a_{i}$ 및 $b_{i}$ 의 유도가 가능하다.

한편 송신원이 반경 $a$ 인 원형 루프일 경우에는 TE 포텐셜은 루프 면에 대한 자기쌍극자 모멘트 $m$ 의 면적분

(10)

F_{z} (ρ, z) = \frac{{\hat{z}}_{i} I}{4 π} \int_{` 0}^{\infty} λ {\hat{F}}_{z} (λ, z) \int_{0}^{a} \int_{0}^{2 π} J_{0} (λ | ρ - ρ^{'} |) ρ' d ϕ d ρ^{'} d λ

로 주어지며, 식 (10)의 면적분은 Bessel 함수의 addition theorem을 적용하면

(11)

F_{z} (ρ, z) = {\hat{z}}_{i} I a \int_{0}^{\infty} {\hat{F}}_{z} (λ) J_{1} (λ a) J_{0} (λ ρ) d λ

로 계산된다(Ward and Hohmann, 1988). 식 (11)은 $a$ 가 매우 작을 경우 $J_{1} (λ a) \approx λ a / 2$ 이므로, 식 (1)의 자기쌍극자 송신원의 TE 포텐셜과 같게 된다. 또한 중앙 루프법(central loop)의 경우 $ρ = 0, J_{0} (0) = 1$ 이므로 식 (11)을 사용하여 TE 포텐셜을 계산할 수 있다.

한편 시간 영역 전자탐사의 경우에는 주파수 영역 반응을 Fourier 변환하여 계단반응(step response)과 충격반응(impulse response)을 계산할 수 있다(Kaufman, 1994). 즉 계단반응은

(12)

h_{z} (t) = \frac{2}{π} \int_{0}^{\infty} \frac{Im H_{z} (ω)}{ω} \cos ω t d ω,

로 주어지며, 충격반응은 계단반응을 미분하여 구할 수 있다.

(13)

\frac{d h (t)}{d t} = - \frac{2}{π} \int_{0}^{\infty} Im H_{z} (ω) \sin ω t d ω .

이 연구에서는 식 (12), (13)에 주어진 Fourier 변환은 Anderson(1975)의 RLAGF0 및 RLAGF1 사용하여 계산하였다.

Fig. 2는 개발된 지중 송신원 전자탐사 1차원 모델링을 검증하기 위하여 2층 구조에 대한 지표 전자탐사 모델링 결과와 개발된 지중 송신원 전자탐사의 1차원 모델링 결과를 비교한 것이다. 제1층은 두께 50 m, 전기비저항 100 Ω․m이며, 2층의 전기비저항은 1000 Ω․m이다. 송수신원은 모두 지표에 위치하며, 송수신 간격 100 m인 HCP(horizontal coplanar) 배열을 사용하였다. 지중 송신원 전자탐사의 경우에는 지표면 상부에 전기전도도가 0인 공기층이 존재하는 것으로 가정하였다. 주파수 영역과 시간 영역(계단반응) 모두 지표 전자탐사와 지중 송신원 전자탐사 결과가 일치하고 있으며, 이는 적어도 지중 송신원 전자탐사 모델링이 지표에 송수신원이 위치해도 모델링이 가능함을 의미한다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F2.jpg

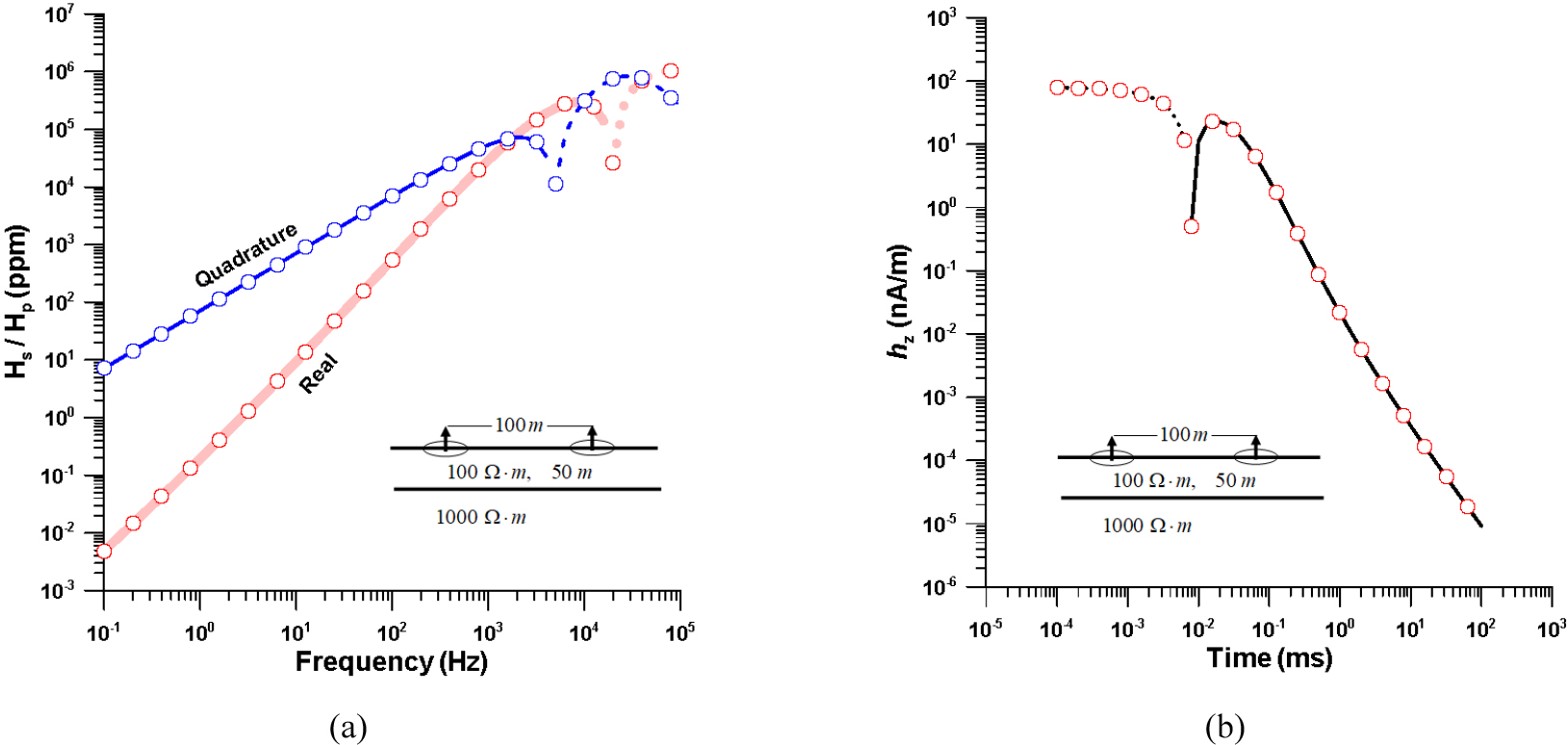
Fig. 2

Vertical magnetic field 100 m from a vertical magnetic dipole with moment 1 A-m² when the source and receiver are at surface of two-layered earth. Solid lines and open circles denote the surface and underground EM responses, respectively. The dashed line indicates the negative response: (a) frequency-domain response and (b) time-domain response (step response).

1차원 역산

물리탐사 자료의 역산은 측정값과 이론값의 오차를 최소화시키는 모델변수를 찾아가는 문제로 물리탐사 자료의 해석에 널리 사용되고 있다. 그러나 역산은 근본적으로 비선형 문제로 자료 개수의 한계, 부정확성이 더해지면서 비유일해의 문제점을 갖고 있다. 이러한 역산의 문제점을 해결하기 위하여 사전정보를 사용하여 모델에 제한을 가하는 감쇠최소제곱법(damped least-squares method)에 기반을 둔 반복적 비선형 역산법이 도입되었다.

감쇠최소제곱법을 사용하는 물리탐사 자료의 역산은 다음의 목적함수 $S$ 를 최소화하는 모델변수를 추정하는 방법이다.

(14)

S = {||W_{d} (e - J ∆ p||}^{2} + {||W_{m} ∆ p||}^{2} .

식 (14)에서 $∆ p$ 는 모델 증분벡터, $e$ 는 측정자료와 이론자료 사이의 오차벡터(data misfit), $J$ 는 감도행렬(sensitivity, Jacobian matrix), $W_{d}$ 와 $W_{m}$ 은 각각 자료벡터와 모델변수에 가해지는 가중행렬(weighting matrix)이다. 식 (14)를 $∆ p$ 에 대하여 미분하여 0으로 놓으면, $S$ 를 최소화하는 증분벡터 $∆ p$ 는 다음과 같이 주어진다.

(15)

∆ p = {(J^{T} W_{d}^{T} W_{d} J + W_{m}^{T} W_{m})}^{- 1} J^{T} W_{d}^{T} W_{d} e .

식 (14)에 주어진 모델제한자 $W_{m} = \sqrt{Λ} C$ 로 주어지며, 여기서 $Λ$ 는 라그랑지 곱수, $C$ 는 거칠기 행렬이다. 물리탐사 자료의 최소제곱역산에서 모델제한을 가하지 않으면 역산은 매우 불안정해진다. 따라서 이 모델제한은 역산의 안정성과 수렴 정도, 분해능 등을 고려하여 최적화된 라그랑지 곱수를 선정하는 문제로 귀착된다. 이 연구에서는 상수 라그랑지 곱수를 사용하고 모델이 공간적으로 부드럽게 변화하도록 평활화 제한을 가하는 Occam법(Constable et al., 1987)과 역산의 분해능 향상과 안정화를 위하여 변수 분해 행렬(model resolution matrix)과 분산 함수(spread function)에 따라 정량적으로 라그랑지 곱수를 결정하는 ACB 법(Yi et al., 2003)이 가능하도록 프로그램을 작성하였다. 또한 모델변수인 각 층의 전기전도도에 자연대수를 취하여 모델변수가 음의 값을 보이는 것을 방지하였으며, 오차벡터는 현장자료와 이론자료의 차이를 현장자료로 정규화하여 로그를 취한 것과 유사한 특성을 갖도록 하였다.

역산에서 가장 중요한 과정 중의 하나가 감도행렬 $J$ 의 계산이다. 감도는 모델변수의 변화에 따른 자료의 변화량을 나타내며, 수평 다층 구조의 경우 모델변수는 각 지층의 전기전도도이다. 주파수 영역과 시간 영역 전자탐사 자료의 1차원 역산에서 감도행렬의 유도가 복잡하기 때문에 차분법을 이용하는 경우가 있으나, 이 경우 모델 변화량의 크기에 따라 편미분의 오차가 발생할 가능성이 크다. 따라서 이 연구에서는 다소 복잡하기는 하지만 해석적으로 감도를 계산하였다. 송수신기가 모두 $j$ 번째 층에 위치하는 HCP 배열의 경우, 식 (6)을 모델변수인 각 층의 전기전도도로 편미분하여 감도를 해석적으로 계산할 수 있다(Key, 2009).

(16)

J_{i j} = \frac{\partial H_{z j}}{\partial σ_{i}} = \frac{m}{2 π} \int_{0}^{\infty} [\begin{matrix} \frac{\partial a_{j}}{\partial σ_{i}} e^{u_{j} (z - z_{j + 1})} + a_{j} \frac{\partial}{\partial σ_{i}} (e^{u_{j} (z - z_{j + 1})}) + \frac{\partial b_{j}}{\partial σ_{i}} e^{- u_{j} (z - z_{j})} \\ + b_{j} \frac{\partial}{\partial σ_{i}} (e^{- u_{j} (z - z_{j})}) + \frac{\partial}{\partial σ_{i}} (\frac{1}{2 u_{j}} e^{- u_{j} |z - z_{s}|}) \end{matrix}] λ^{3} J_{0} (λ, ρ) d λ

편의상

(17)

q = R_{j}^{-}, s = R_{j}^{+}, p = e^{- u_{j} | z_{j + 1} - z_{s} |}, r = e^{- u_{j} | z_{j} - z_{s} |}, t = e^{u_{j} h_{j}}, u = 1 / 2 u_{j}

라 하면, 식 (7)과 식 (8)에 주어진 감쇠계수는

(18)

a_{j} = (p + q r) \frac{s t u}{1 - q s}, b_{j} = (r + s p) \frac{q t u}{1 - q s}

로 간단하게 표현된다. 따라서 식 (16)에 주어진 감쇠계수의 편미분은

(19)

\frac{\partial a_{j}}{\partial σ_{i}} = (p' + q' r + q r') \frac{s t u}{1 - q s} + \frac{p + q r}{1 - q s} (s' t u + s t' u + s t u') + \frac{(p + q r) s t u}{(1 - q s)^{2}} (q' s + q s'),

(20)

\frac{\partial b_{j}}{\partial σ_{i}} = (s' p + s p' + r') \frac{q t u}{1 - q s} + \frac{s p + r}{1 - q s} (q' t u + q t' u + q t u') + \frac{(s p + r) q t u}{(1 - q s)^{2}} (q' s + q s')

로 주어진다. 이때 $'$ 는 $σ_{i}$ 에 대한 편미분을 의미하며, $p', r', t', u'$ 는 $i = j$ 일 경우에만 0이 아닌 값을 갖는다. $q' = \partial R_{j}^{-} / \partial σ_{i}, s' = \partial R_{j}^{+} / \partial σ_{i}$ 이므로, chain rule을 이용하여 빠르게 계산할 수 있다.

(21)

q' = \frac{\partial R_{j}^{-}}{\partial u_{i}} \frac{\partial u_{i}}{\partial σ_{i}} = \frac{\partial R_{j}^{-}}{\partial R_{j - 1}^{-}} \frac{\partial R_{j - 1}^{-}}{\partial R_{j - 2}^{-}} \dots \frac{\partial R_{i + 2}^{-}}{\partial R_{i + 1}^{-}} \frac{\partial R_{i + 1}^{-}}{\partial u_{i}} \frac{\partial u_{i}}{\partial σ_{i}},

(22)

s' = \frac{\partial R_{j}^{+}}{\partial u_{i}} \frac{\partial u_{i}}{\partial σ_{i}} = \frac{\partial R_{j}^{+}}{\partial R_{j + 1}^{+}} \frac{\partial R_{j + 1}^{+}}{\partial R_{j + 2}^{+}} \dots \frac{\partial R_{i - 2}^{+}}{\partial R_{i - 1}^{+}} \frac{\partial R_{i - 1}^{+}}{\partial u_{i}} \frac{\partial u_{i}}{\partial σ_{i}},

편의상 $x_{j \pm 1}^{\pm} = R_{j \pm 1}^{\pm} e^{- u_{i \pm 1} h_{i \pm 1}}$ 라 하면, 식 (21)과 식 (22)의 계산에 필요한 편미분은 다음과 같이 주어진다.

(23)

\frac{\partial R_{j}^{\pm}}{\partial R_{j \pm 1}^{\pm}} = \frac{(1 + r_{j}^{\pm}) (1 - r_{j}^{\pm}) e^{- u_{j} ` h_{j}} e^{- u_{j \pm 1} h_{j \pm 1}}}{(1 + r_{j}^{\pm} x_{j \pm 1}^{\pm})^{2}},

(24)

\frac{\partial R_{i \pm 1}^{\mp}}{\partial u_{i}} = \frac{e^{- u_{i \pm 1} h_{i \pm 1}}}{(1 + r_{i \pm 1}^{\mp} x_{i}^{\mp})^{2}} [(1 - x_{i}^{\mp}) (1 + x_{i}^{\mp}) \frac{\partial r_{i \pm 1}^{\mp}}{\partial u_{i}} + (1 - r_{i \pm 1}^{\mp}) (1 + r_{i \pm 1}^{\mp}) \frac{\partial x_{i}^{\mp}}{\partial u_{i}}],

(25)

\frac{\partial x_{i}^{\pm}}{\partial u_{i}} = \frac{e^{- 2 u_{i} h_{i}}}{(1 - r_{i}^{\pm} x_{i \pm 1}^{\pm})^{2}} [(1 - x_{i \pm 1}^{\pm}) (1 + x_{i \pm 1}^{\pm}) \frac{\partial r_{i}^{\pm}}{\partial u_{i}} - 2 h_{i} (r_{i}^{\pm} + x_{i \pm 1}^{\pm}) (1 + r_{i}^{\pm} x_{i \pm 1}^{\pm})] .

물론 수신점이 송신기와 다른 지층에 위치할 경우에는 점화식을 이용하여 감도행렬을 계산할 수 있으나(Key, 2009), 여기서는 생략한다.

역산 실험

개발된 역산 프로그램을 사용하여 수치자료에 대한 역산실험을 수행하였다. 지중 송신원을 사용하는 전자탐사의 경우 송수신기 상부층의 정보는 이미 확보된 것으로 가정하였다. 예를 들어 송신기가 지하에 위치한다면 터널이나 갱도 등이 이미 개설된 상태이므로 터널 굴진 자료 등으로부터 송수신원 후방에 위치한 층의 전기전도도 및 두께에 관한 정보를 직간접적으로 얻어낼 수 있다. 해양 전자탐사의 경우에는 이미 알려진 전기비저항을 갖는 해수 중에 송신기가 위치한다. 지중 송신원 전자탐사의 주된 탐사 대상은 송수신원 하부에 위치한 지층의 정보 추출이다. 따라서 지중 전자탐사 자료의 역산실험에서는 송신원 상부층의 정보는 사전정보로 제공하였으며, 역산에서는 송수신원 하부에 위치한 지층의 전기전도도를 모델변수로 설정하였다. 송수신원 하부 모델은 송신기 직하부 지층의 두께를 1 m로 설정하고, 송신원으로부터 심도가 증가함에 따라 지수 함수적으로 각 층까지의 심도를 증가시켰다. 또한 전자탐사의 가탐심도를 고려하여 송신원에서 가장 먼 지층까지의 거리가 가탐심도 보다 작도록 설정하였다.

한편 송신원 상부의 지층구조에 대한 정보가 없을 경우에는 지하 송신원 전자탐사의 자료해석은 어려울 것으로 생각된다. 이 경우 모델변수가 제한된 자료의 수에 비하여 지나치게 많아지는 문제는 물론이거니와, 수직성분만을 측정할 경우에는 상부 지층과 하부 지층의 물성이 자료에 미치는 영향이 동일하기 때문에 식별이 거의 불가능할 것으로 보인다. 따라서 상부층에 관한 사전정보가 없을 경우에는 다중 성분 측정이나 다른 탐사자료와의 복합 해석을 통해서만 해석이 가능할 것으로 판단된다.

주파수 영역

주파수 영역 전자탐사에서 가장 널리 사용되는 HCP 배열을 적용한 이론자료에 대하여 역산실험을 수행하였다. 지하에 수행되는 전자탐사의 경우 공간적 제약이 있으므로 송수신 간격은 10 m로 좁게 설정하였다. 신호원의 주파수 대역은 현재 상용화된 탐사장비를 고려하여 10 Hz에서 100 kHz로 설정하였으며, 대수적으로 등간격인 21개의 자료를 사용하여 역산을 수행하였다. 측정자료는 1차장에 대한 2차장의 동상성분과 이상성분을 1차장으로 정규화한 값을 사용하였으며, 잡음을 고려하여 3% 무작위 잡음을 추가하였다.

송신원이 1000 Ω․m인 균질 공간에 위치하고 송신원 하부 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층이 발달한 모델에 대하여 1차원 모델링을 통하여 이론자료를 계산하고, 이론자료에 대하여 역산을 수행한 결과이다(Fig. 3). 이 역산실험에서 송신원 상부층의 전기비저항은 실제 참값인 1000 Ω․m로 설정하였으며, 역산방법은 공간에 따라 변하는 평활화 제한을 가하는 ACB법을 적용하였다. 모든 역산 실험에서 라그랑지 곱수는 0.02~1.0의 범위로 설정하였으며, 반복계산횟수는 20회로 고정하였다. 최종 역산 오차는 모든 경우에 3% 이하로 수렴하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F3.jpg

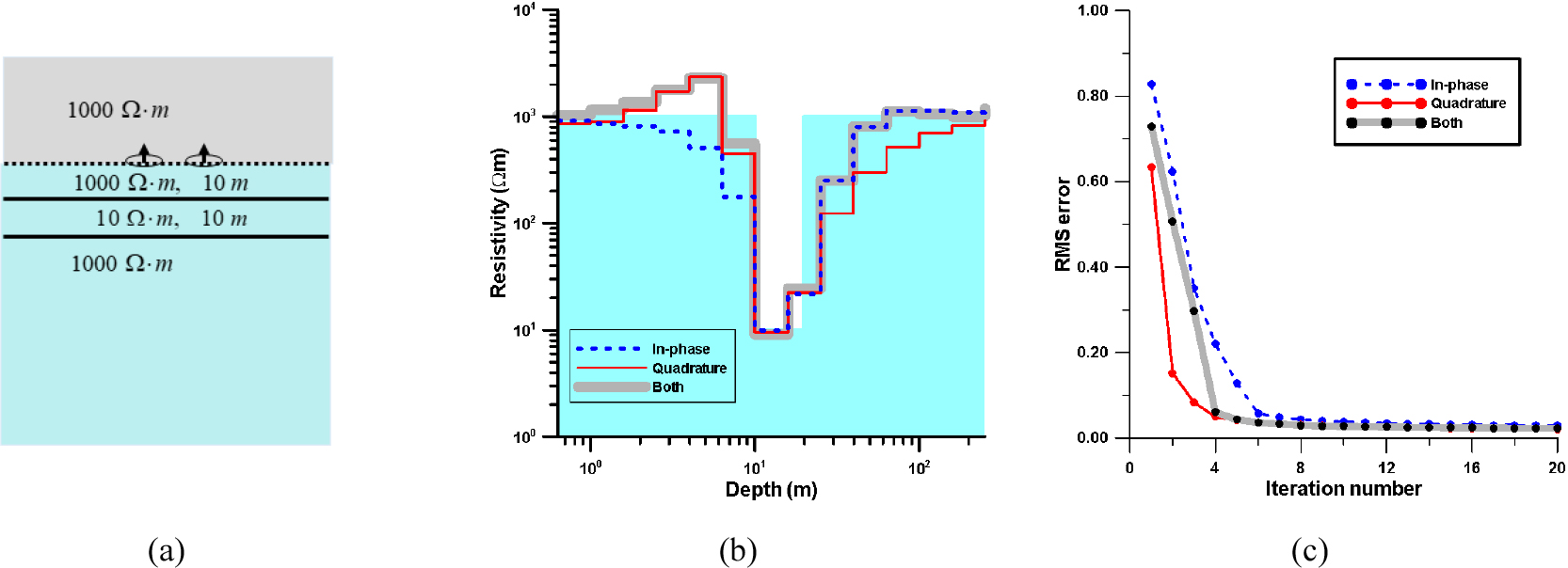
Fig. 3

(a) True layer model, (b) recovered model from the 1D inversion of synthetic frequency-domain underground EM data, and (c) rms errors with iteration numbers when the in-phase data (dotted line), quadrature data (solid line) and both types of data (thick gray line) are used in the inversion. The shaded region in (b) indicates the true resistivity model.

일반적으로 송수신 간격이 작은 경우 주파수 수직탐사는 어려운 것으로 알려져 있다. 그러나 10 kHz 이상의 고주파수 대역에서는 유도상수(induction number)가 비교적 크고, 송신원으로부터 전도성 지층까지의 거리가 가깝기 때문에 주파수 수직탐사가 가능한 것으로 해석된다. 물론 현장탐사의 경우에는 신호의 크기가 너무 작아 측정기기의 측정한계로 인하여 안정적 자료획득이 어려울 수 있으나, 여기서는 작은 신호도 정밀 측정이 가능하다는 가정 아래 역산에 의한 주파수 수직 전자탐사 자료의 해석 가능성을 살펴보고자 한다.

전자파의 표피심도(skin depth)는 주파수에 따라 달라지므로, 송신원에서 가까운 천부 모델은 주로 고주파수 대역의 자료에 의해 결정되며, 심부는 저주파수 대역 자료에 의해 결정된다. 고주파수 대역의 경우 유도상수가 비교적 커서 근접장 영역에 속하며, 이 경우 주파수 수직탐사가 가능하다. 따라서 고주파수 대역은 동상 및 이상성분 모두 의미있는 분해능을 가지며, 전도성 지층이 송신원에서 가까운 거리에 존재할 경우에는 효과적 해석이 가능한 것으로 판단된다. 그러나 HCP 배열을 사용한 주파수 영역 전자탐사에서 저주파 대역은 저유도상수 대역에 근접하며, 이상성분은 심부에 대한 분해능이 낮다는 문제점이 있다. 반면 동상성분은 이상성분에 비하여 심부에 대한 분해능이 높기 때문에 보다 참 모델에 근접한 역산 모델을 추정하게 된다. 물론 현장탐사의 경우에는 저주파수 대역에서 동상성분의 크기는 이상성분에 비해 매우 작기 때문에 안정적 자료획득이 어렵다는 문제가 있다.

Fig. 3은 동상성분, 이상성분, 그리고 두 자료를 모두 사용하여 역산을 수행 결과와 rms 오차를 나타낸 것이다. 모든 역산 결과에서 송신원 하부 10 m 지점에 위치한 전도성 지층을 잘 추정하고 있으나, 사용된 자료에 따라 역산 결과는 약간의 차이를 보인다. Fig. 3(b)는 반복계산횟수에 따른 오차 곡선으로 동상성분, 이상성분과 이들 모두를 사용한 역산이 안정적으로 수렴함을 보여주고 있으며, 반복계산횟수를 20회로 크게 설정하였으나 실제 반복계산횟수 10회 정도에서 rms 오차는 이미 3% 이하로 수렴하고 있다.

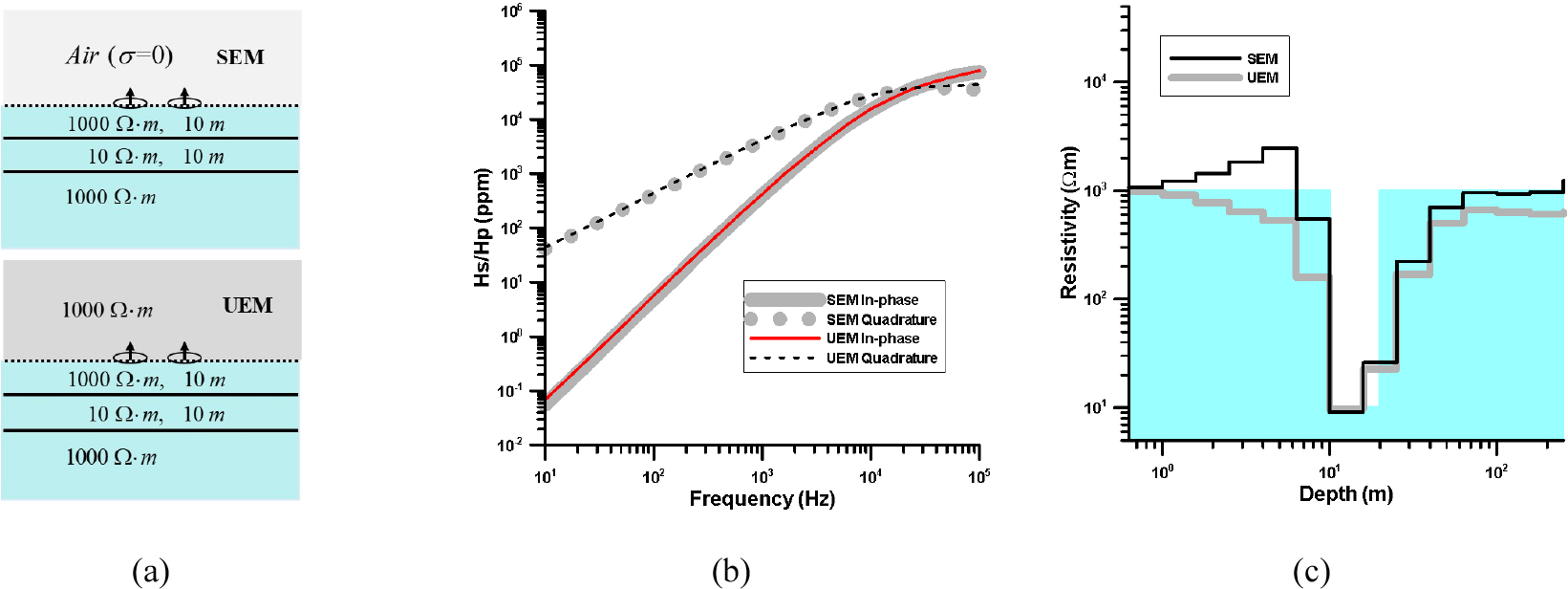
전자탐사에서 송수신원이 지하에 존재할 경우, 지표에 송수신원이 위치한 것으로 가정하고 해석하면 문제점이 발생한다. 이는 지중 전자탐사의 경우 송수신원 상부층에 유도된 유도전류에 의한 2차장이 측정결과에 영향을 미치기 때문이다. Fig. 4는 송수신원이 지표면에 있을 경우와 지하에 존재할 경우, 송수신 간격 10 m인 HCP 배열을 사용하여 얻어진 자료와 그 역산결과를 나타낸 것이다. 지표 전자탐사 자료는 심도 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층이 존재하는 모델에 대한 수치자료이며, 지중 전자탐사 자료는 송수신기 상부층의 전기비저항은 1000 Ω․m, 송수신기 하부 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층이 발달한 모델에 대한 수치자료이다. Fig. 4(a)에서 지표와 지중 전자탐사 자료는 그래프 상에서는 뚜렷한 차이를 보이지 않지만, 실제로는 지중 전자탐사 반응값이 지표 전자탐사 반응값에 비하여 약간 크게 나타난다. 이 수치실험의 경우, 지중 전자탐사 반응은 송수신기 상부의 전기비저항이 1000 Ω․m로 상당히 높기 때문에 상부층에 발생하는 유도전류가 작아 지표 전자탐사 반응에 비하여 큰 차이를 보이지 않는다. 지표에 송수신기가 위치하는 것으로 가정하고 동상 및 이상성분을 모두 사용하여 지표 및 지중 전자탐사 자료에 대한 역산을 수행한 결과인 Fig. 4(b)에서는, 두 경우 모두 하부의 전도성 지층을 잘 추정하고 있다. 그러나 지표 전자탐사를 가정하고 역산을 수행하였기 때문에, 지중 전자탐사에 비하여 지표 전자탐사가 참 모델에 조금 더 근접한 역산 결과를 보인다. 따라서 송수신기 상부층의 전기비저항이 매우 높고 균질할 경우에는 지중 전자탐사 자료의 해석은 지표 전자탐사를 가정하고 역산을 수행해도 큰 문제가 없는 것으로 해석된다. 그러나 송수신기 상부에 전기전도도 이상대가 존재하거나, 매질의 전기전도도가 높은 경우에는 상부층의 영향이 커지기 때문에 지표 전자탐사를 가정한 해석은 무리가 있을 것으로 판단된다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F4.jpg

Fig. 4

(a) Surface EM (SEM) and Underground EM (UEM) models, (b) frequency-domain responses when the transmitter and receiver are located at the surface (thick gray line) and underground (solid line), and (c) recovered models from the SEM 1D inversion.

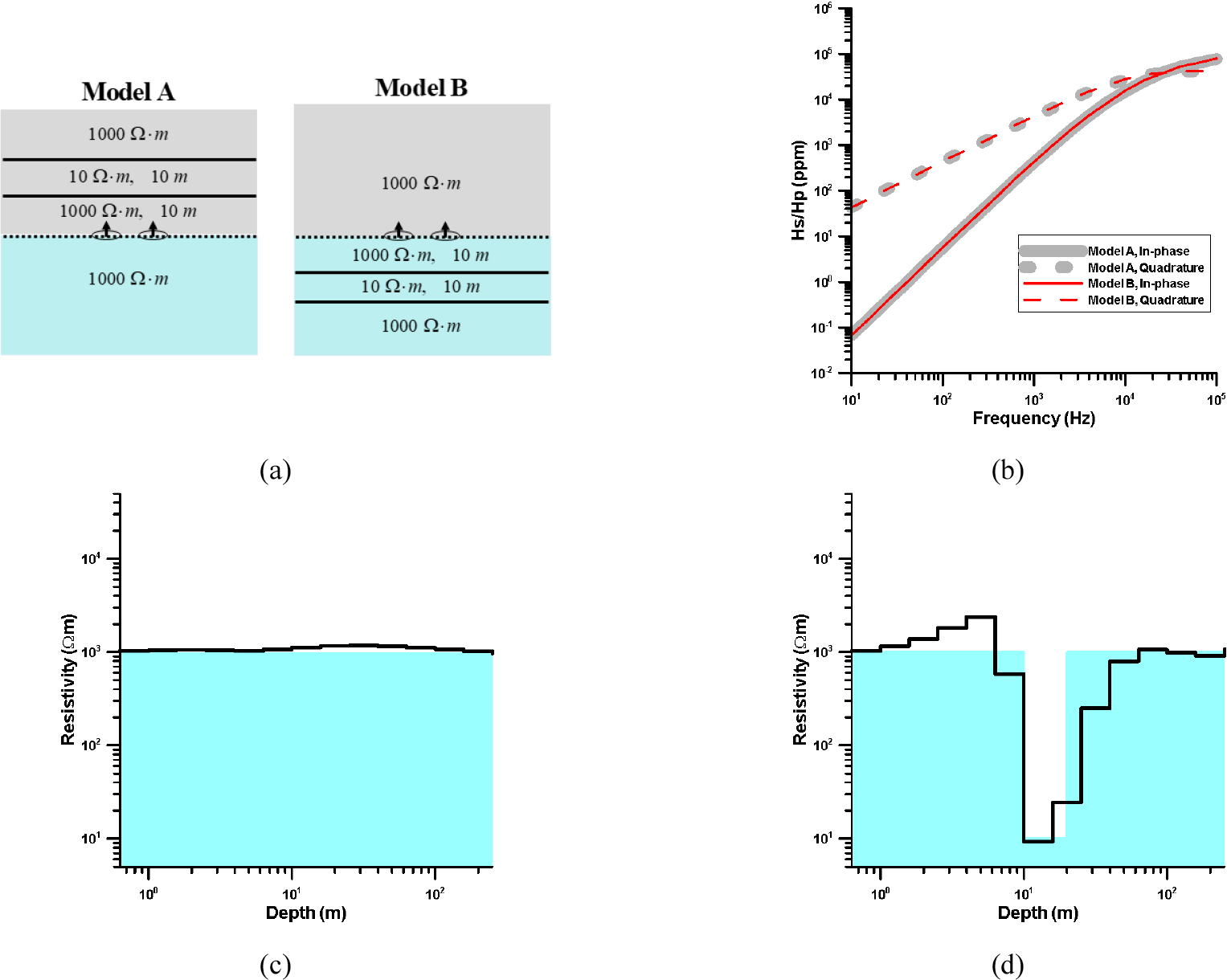
HCP 배열을 사용하는 지중 전자탐사에서 송수신기 상부에 존재하는 이상체와 하부에 존재하는 이상체는 대칭성으로 인하여 동일한 반응을 생성한다. 따라서 지중 전자탐사에서 상부의 이상대에 대한 사전정보가 없으면 해석이 매우 복잡해진다. 이 문제는 자기장의 수평성분을 측정하는 방식 등으로 해결할 수 있으나, 이 경우 그 측정값이 매우 작기 때문에 실제 현장 적용에는 한계가 있다. 따라서 가장 실질적인 해석방법은 상부층에 대한 사전정보를 사용하여 역산을 수행하는 것으로 보인다. Fig. 5(a)에 주어진 송수신기 상부 및 하부 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층이 존재하는 HCP 배열 전자탐사 모델에 대한 반응 양상인 Fig. 5(b)를 살펴보면, 예상한 바와 같이 상부 및 하부의 이상대는 대칭성으로 인하여 동일한 반응 양상을 나타낸다. 따라서 만약 송수신기 상하부 지층을 모두 모델변수로 설정하면, 역산에서 이를 식별할 수 없다. Fig. 5(c)에 나타낸 바와 같이 송신기 상부의 전도성 지층에 대한 정보를 알고 있다는 가정 아래 하부층의 전기비저항만을 모델변수로 설정하고 역산을 수행한 결과로, 송수신기 하부가 균질한 반무한 공간임을 잘 추정하고 있다. 또한 송신기 상부는 1000 Ω․m의 균질 매질이고 하부에 전도성 지층이 존재할 경우에 대한 수치자료에 대한 역산 결과인 Fig. 5(d)는 하부 10 m지점에 발달한 두께 10 m의 전도성 지층을 잘 추정하고 있다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F5.jpg

Fig. 5

Inversion experiment when a conductive layer is developed above (model A) or below (model B) the source layer in a 1000 Ω․m whole-space : (a) true models A and B, (b) frequency-domain responses, (c) inverted model A, and (d) inverted model B.

시간 영역

시간 영역 전자탐사는 주파수 영역 전자탐사에 비하여 잡음에 취약하다는 단점이 있으나, 수 $μ \sec$ 이하의 초기시간에서 자료획득이 가능하다면 천부의 정보 획득이 가능하다는 장점이 있다. 대부분의 상용 시간 영역 전자탐사 시스템은 수 $μ \sec$ 보다 이른 초기시간에서의 측정이 어렵지만, 일부 시스템, 예를 들어 GTEM(Geonics), nanoTEM(Zonge) 등은 천부조사를 목적으로 초기 시간대의 측정이 가능하도록 특별히 개발되었으며, 여기서는 이 측정시스템을 사용하여 얻어진 시간 영역 전자탐사 자료의 1차원 역산에 대하여 기술한다.

해양탐사의 경우는 제외하면 터널과 같은 지중에서 수행되는 전자탐사에서 가장 문제가 되는 점은 공간적 제약으로 인하여 송수신기의 크기는 물론 송수신 간격도 작아야 한다는 점이다. 따라서 이 연구에서는 송수신 간격 10 m인 HCP 배열을 적용하였다. 지연시간의 범위는 1 $μ \sec$ ~10 msec로 설정하였으며, 대수적으로 등간격인 21개의 지연시간에서의 반응값을 사용하여 역산을 수행하였다. 개발된 지중 전자탐사 1차원 모델링 프로그램을 사용하여 시간 영역 전자탐사 계단반응 자료를 계산하고, 실제 현장자료를 모사하기 위하여 3%의 무작위 잡음을 추가하였다. 이 역산실험에서도 앞의 주파수 영역과 마찬가지로 역산방법은 ACB법을 사용하였으며, 라그랑지 곱수의 범위는 0.02~1.0, 반복계산횟수는 20회로 설정하였다.

시간 영역 전자탐사 역산시험을 위하여, 송수신기가 1000 Ω․m인 균질 매질에 존재하고, 하부 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층이 발달된 1차원 모델을 가정하였다(Fig. 5의 모델 B). 역산에서 송수신기 상부의 전기비저항은 1000 Ω․m로 설정하였으며, 송신기 하부의 전기비저항은 역산을 통하여 추정하였다. Fig. 6(a)에 주어진 역산결과를 보면, 송수신기 하부의 전도성 지층을 잘 추정하고 있으며, 현장자료와 이론자료도 Fig. 6(b)에 나타낸 바와 같이 잘 일치하고 있다. 또한 rms 오차도 반복계산횟수 10 이하에서 3%이하의 값에 안정적으로 수렴하고 있다(Fig. 6(c)).

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F6.jpg

Fig. 6

Inversion experiment for synthetic underground TEM data : (a) recovered model, (b) measured and calculated TEM step responses and (c) rms errors.

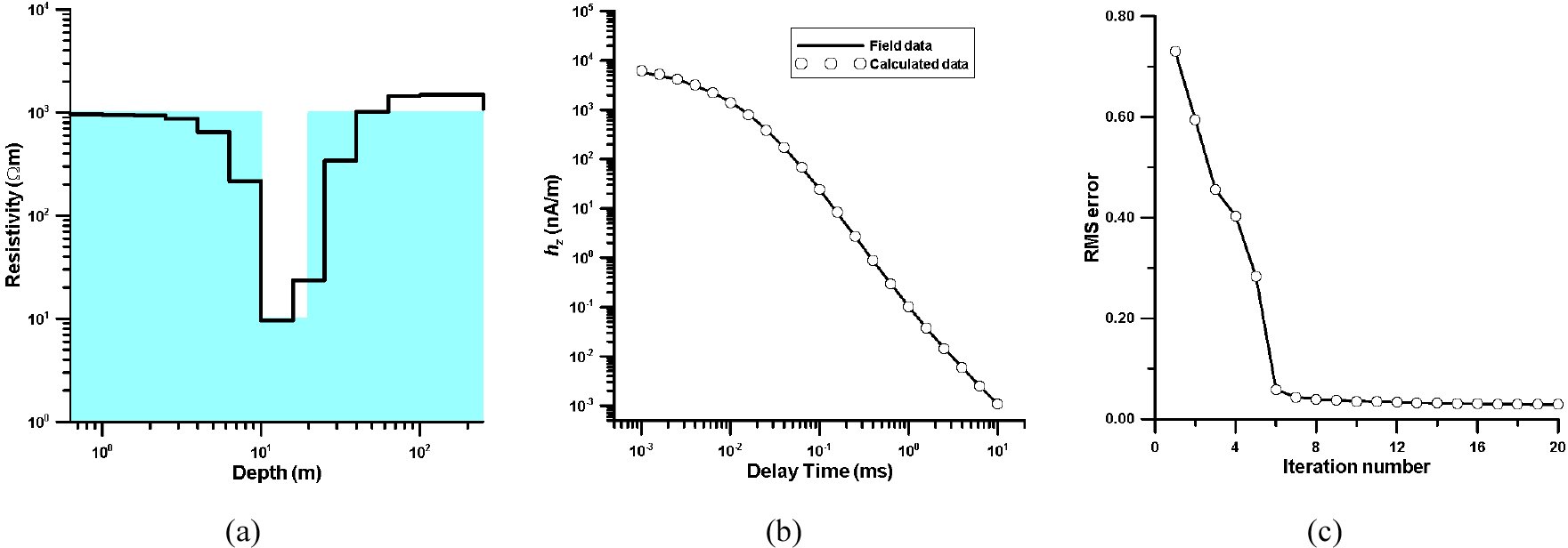
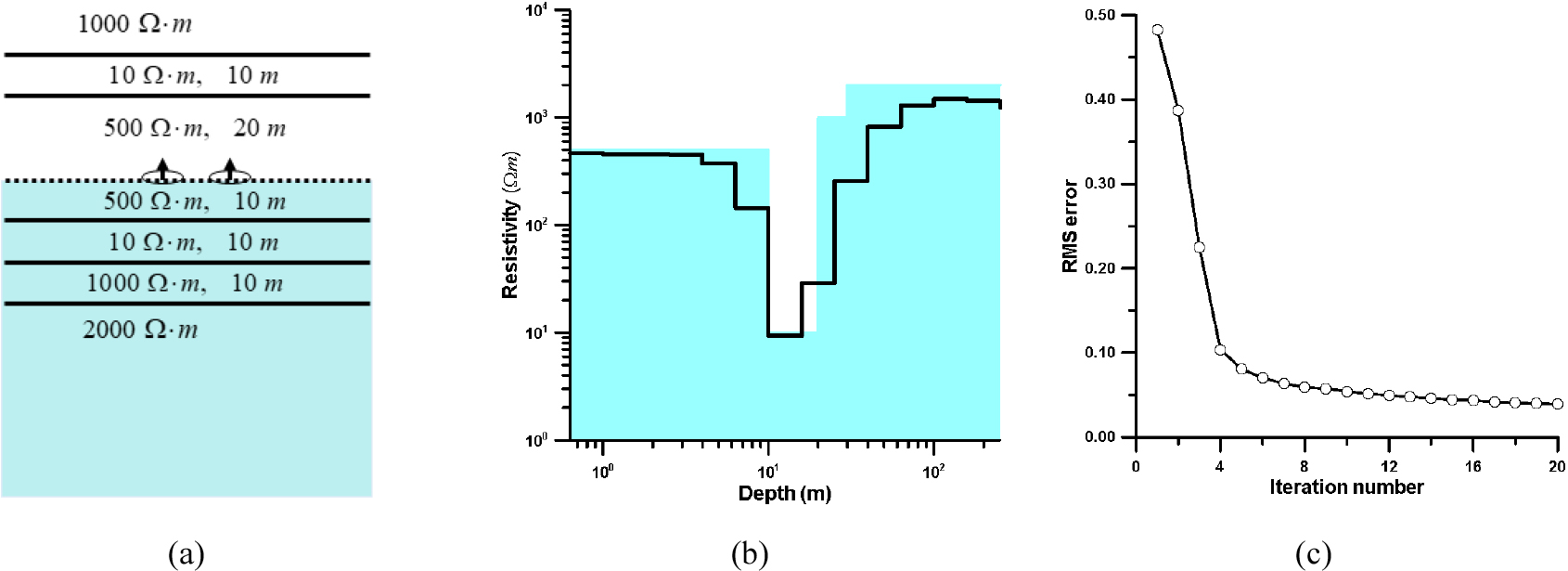
지중 전자탐사 자료의 역산에서 송수신기 상부층의 두께 및 전기전도도는 사전정보로 제공되어야 한다. Fig. 6의 역산실험에서는 상부층이 균질하고, 전기전도도가 낮으므로 상부층의 영향이 크게 나타나지 않는다. 따라서 측정 자료에 큰 영향을 주는 전도성 지층이 송수신기 상부에 존재할 경우에 대한 역산실험을 수행하였다. Fig. 7(a)에 나타낸 바와 같이 송수신기는 전기비저항은 500 Ω․m인 지층 내에 위치하며, 송수신기 상부 20 m 지점에 두께 10 m, 전기비저항 10 Ω․m인 전도성 지층, 전도성 지층 상부에 1000 Ω․m 고비저항대 발달하고 있다. 또한 송수신기 하부 10 m 지점에 두께 10 m, 전기비저항 10 Ω․m의 전도성 지층이 발달하고 있으며, 심도가 증가함에 따라 전기비저항이 1000 Ω․m에서 2000 Ω․m로 증가한다. Fig. 7(a)에 주어진 모델에 대하여 이론자료를 계산한 다음, 3% 잡음을 추가한 이론자료에 대한 역산을 통하여 추정된 역산 모델(Fig. 7(b))은 송수신기 하부의 전기비저항 구조를 잘 반영하고 있다. 송수신기가 위치한 지층의 전기비저항(500 Ω․m), 송수신기 10 m 하부 전도성 지층의 전기비저항(10 Ω․m), 심부의 고비저항 층(1000~2000 Ω․m)을 비교적 잘 추정하고 있다. 반복계산횟수에 따른 rms 오차(Fig. 7(c))도 역산이 안정적으로 수렴하는 것을 잘 보여주고 있다. 이러한 역산 결과는 송수신기 상부층의 정보가 정확히 제공된다면, 지중 전자탐사를 통하여 송수신기 하부의 층서 정보를 얻어낼 수 있음을 의미한다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F7.jpg

Fig. 7

Inversion experiment for synthetic underground TEM data : (a) true model, (b) recovered model, and (c) rms errors.

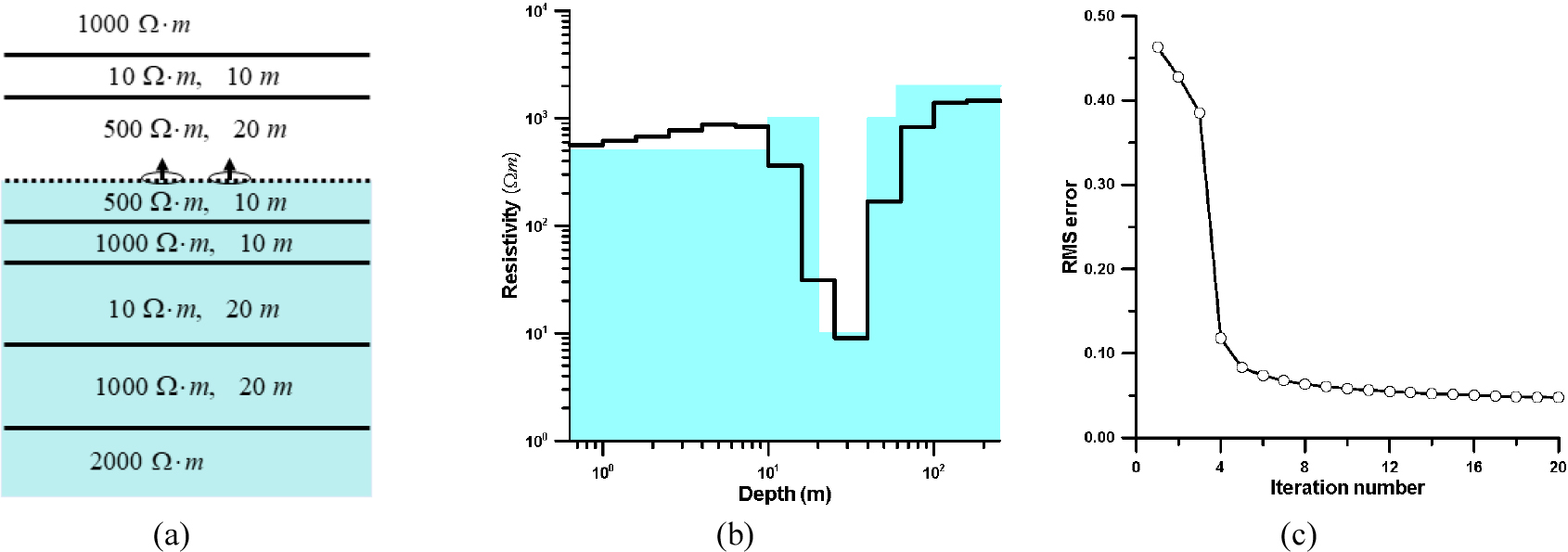
앞의 경우와 비교하여 더 복잡한 층서 모델에 대한 시간 영역 전자탐사 자료의 역산실험을 수행하였다. Fig. 8(a)에 나타낸 바와 같이 송수신기 상부의 전기비저항 구조는 Fig. 7의 경우와 동일하며, 송신기 하부에는 전기비저항 10 Ω․m, 두께 20 m인 전도성 지층이 송신기로부터 거리 20 m 지점에 위치하며, 그 상부에 전기비저항 1000 Ω․m, 두께 10 m인 고비저항 층이 위치한다. 역산시 초기모델, 즉 송수신기 하부 층은 송수신기가 위치한 층의 전기비저항인 500 Ω․m의 균질매질로 설정하였다. 역산을 통하여 얻어진 추정 모델인 Fig. 8(b)는 송수신기 바로 아래에 발달한 500 Ω․m 층과 그 하부의 1000 Ω․m 층, 20 m 하부의 전도성 지층, 심부에 발달한 고비저항 층도 비교적 정확하게 추정하고 있다. rms 오차 곡선(Fig. 8(c))도 역산이 안정적으로 수렴하고 있음을 보여주고 있다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580508/images/ksmer_58_05_08_F8.jpg

Fig. 8

Inversion experiment for synthetic underground TEM data : (a) true model, (b) recovered model, and (c) rms errors.

결론 및 토의

지하에 송수신기가 위치하는 지중 전자탐사 1차원 모델링과 역산 프로그램을 개발하고, 수치자료에 대한 역산실험을 통하여 지중 전자탐사 자료의 해석기술을 제시하고자 하였다. 지중 전자탐사 1차원 모델링 및 역산은 주파수 영역과 시간 영역 모두 가능하며, 송수신 배열법중 HCP 배열과 중앙루프법 모두 가능하도록 개발되었다. 그러나 지중 전자탐사에서는 송수신기가 지하에 위치하므로 공간적 제약을 고려하여 HCP 배열에 대한 모델링 및 역산실험을 수행하였다.

지중 전자탐사 1차원 모델링은 송수신기가 지하에 위치하므로 송수신기 상부 및 하부 지층의 영향을 모두 고려해야 한다. 이 연구에서는 상부 및 하부 지층 경계면에서의 반사계수를 유도하였으므로 송신 및 수신기의 위치에 관계없이 자기장의 계산이 가능하다. 개발된 모델링 프로그램은 반무한 공간 모델, 층서구조 모델에 대한 해석해와 비교하여 그 정확성을 검증하였다. 역산은 감쇠최소제곱법을 적용하였으며, 역산에서 가장 중요한 감도행렬을 해석적으로 계산하여 역산의 정확성을 확보하였다. 무작위 잡음을 추가한 수치자료에 대한 역산실험 결과, 송수신 하부의 전기비저항 층서 구조를 비교적 정확하게 추정하였다.

한편 HCP 배열을 사용하는 지중 전자탐사의 경우 상부 이상대와 하부 이상대가 같은 반응을 보이므로, 구분이 불가능하다. 따라서 역산을 통하여 지중 전자탐사를 해석하기 위해서는 송수신기 상부의 전기비저항 층서 구조에 대한 정보가 확보되어야 한다. 상부의 전기비저항 층서 구조는 시추자료, 검층 등과 다른 탐사 방법을 통하여 확보되어야 하며, 이에 관한 정보가 정확할수록 지중 전자탐사 자료의 역산 결과도 정확해 진다. 또한 이 연구에서는 송수신원에서 가까운 곳에 위치한 이상대의 탐지에 중점을 두었으므로 주파수 영역의 경우에는 고주파수 대역, 시간 영역의 경우에는 초기 시간대의 안정적 자료획득이 우선되어야만 역산에 의한 정밀해석이 가능할 것으로 판단된다.

References

Anderson, W.L., 1975. Improved digital filters for evaluating Fourier and Hankel transform integrals. USGS-GD-75-012.

Chave, A.D. and Cox, C.S., 1982. Controlled electromagnetic sources for measuring electrical conductivity beneath the oceans: 1. Forward problem and model study, Journal of Geophysical Research: Solid Earth, 87, NB7, p.5327-5338. 10.1029/JB087iB07p05327

Cho, I.K. and Choi, K.H., 1999. 3-D crosshole EM modeling by the extended Born approximation, Geophysics and Geophysical Exploration, 2(3), p.142-148.

Cho, I.K. and Lim, J.T., 2003a. Frequency sounding in small- loop EM surveys, Geophysics and Geophysical Exploration, 6(3), p.119-125.

Cho, I.K. and Lim, J.T., 2003b. One-dimensional inversion of electromagnetic frequency sounding data, Geophysics and Geophysical Exploration, 6(4), p.180-186.

Constable, S. and Weiss, C.J., 2006. Mapping thin resistors and hydrocarbons with marine EM methods: Insights from 1D modeling, Geophysics, 71(2), p.G43-G51. 10.1190/1.2187748

Constable, S.C., Parker, R.L., and Constable, C.G., 1987. Occam's inversion: a practical algorithm for generating smooth models from electromagnetic sounding data, Geophysics, 52(3), p.289-300. 10.1190/1.1442303

Das, U., 1995. A reformalism for computing frequency- and time-domain EM responses of a buried, finite-loop. Annual Meeting Abstracts. SEG, Houston, TX, p.811-814. 10.1190/1.1887562

Edwards, N., 2005. Marine controlled-source electromagnetics: Principles, methodologies, future commercial applications, Surveys in Geophysics, 26(6), p.675-700. 10.1007/s10712-005-1830-3

Huang, H. and Fraser, D.C., 2003. Inversion of helicopter electromagnetic data to a magnetic conductive layered earth, Geophysics, 68(4), p.1211-1223. 10.1190/1.1598113

Jang, H. and Kim, H.J., 2013. A scheme for computing time-domain electromagnetic fields of a horizontally layered earth, Geophysics and Geophysical Exploration, 16(3), p. 139-144. 10.7582/GGE.2013.16.3.139

Kaufman, A.A., 1994. Geophysical Field Theory and Method: Part B. Academic Press. Inc.

Key, K., 2009. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers, Geophysics, 74(2), p.F9-F20. 10.1190/1.3058434

Kim, H.J., Choi, J.H., Han, N.R., Song, Y.H., and Lee, K.H., 2009. Primary solution evaluations for interpreting electromagnetic data, Geophysics and Geophysical Exploration, 12(4), p.361-366.

Krivochieva, S. and Chouteau, M., 2002. Whole-space modeling of layered earth in time-domain electromagnetic measurements, Journal of Applied Geophysics, 50(4), p.375-391. 10.1016/S0926-9851(02)00164-7

Lee, S.K., Kim, H.J., and Suh, J.H., 1999. Three-dimensional cross-hole EM modeling using the extended Born approximation, Geophysics and Geophysical Exploration, 2(2), p.86-95.

Li, S., Liu, B., Xu, X., Nie, L., Liu, Z., Song, J., Sun, H., Chen, L., and Fan, K., 2017. An overview of ahead geological prospecting in tunneling, Tunnelling and Underground Space Technology, 63, p.69-94. 10.1016/j.tust.2016.12.011

Um, E.S. and Alumbaugh, D.L., 2007. On the physics of the marine controlled-source electromagnetic method, Geophysics, 72(2), p.WA13-WA26. 10.1190/1.2432482

Ward, S.H. and Hohmann, G.W., 1988. Electromagnetic theory for geophysical applications, in M. N. Nabighian, ed., Electromagnetic methods in applied geophysics, 1, Theory: SEG, p.1-132.

Xiong, Z., 1989. Electromagnetic fields of electric dipoles embedded in a stratified anisotropic earth, Geophysics, 54(12), p.1643-1646. 10.1190/1.1442633

Yi, M.J., Kim, J.H., and Chung, S.H., 2003. Enhancing the resolving power of least-squares inversion with active constraint balancing, Geophysics, 68(3), p.931-941. 10.1190/1.1581045

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Underground EM 1D Modeling and Inversion

ABSTRACT

MAIN

(1)

Fig. 1

N-layered 1D model. Each layer j has conductivity σj and layer top depth zj.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 2

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

Fig. 3

Fig. 4

(a) Surface EM (SEM) and Underground EM (UEM) models, (b) frequency-domain responses when the transmitter and receiver are located at the surface (thick gray line) and underground (solid line), and (c) recovered models from the SEM 1D inversion.

Fig. 5

Inversion experiment when a conductive layer is developed above (model A) or below (model B) the source layer in a 1000 Ω․m whole-space : (a) true models A and B, (b) frequency-domain responses, (c) inverted model A, and (d) inverted model B.

Fig. 6

Inversion experiment for synthetic underground TEM data : (a) recovered model, (b) measured and calculated TEM step responses and (c) rms errors.

Fig. 7

Inversion experiment for synthetic underground TEM data : (a) true model, (b) recovered model, and (c) rms errors.

Fig. 8

Inversion experiment for synthetic underground TEM data : (a) true model, (b) recovered model, and (c) rms errors.

References

N-layered 1D model. Each layer $j$ has conductivity $σ_{j}$ and layer top depth $z_{j}$ .