Prediction of Water Saturation from Well Log Data using Deep Learning Algorithms

Minsoo Ji; Seoyoon Kwon; Gayoung Park; Baehyun Min; Xuan Huy Nguyen

doi:10.32390/ksmer.2021.58.3.215

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 30 June 2021. 215-226
https://doi.org/10.32390/ksmer.2021.58.3.215

Prediction of Water Saturation from Well Log Data using Deep Learning Algorithms

물리검층자료를 활용한 딥러닝 기반 수포화도 예측

Minsoo Ji¹

Seoyoon Kwon²

Gayoung Park¹

Baehyun Min³^*

Xuan Huy Nguyen⁴

지 민수¹

권 서윤²

박 가영¹

민 배현³^*

Nguyen Xuan Huy⁴

¹Master's Degree, Department of Climate and Energy Systems Engineering, Ewha Womans University, Seoul, Korea

²PhD Student, Department of Climate and Energy Systems Engineering, Ewha Womans University, Seoul, Korea

³Associate Professor, Department of Climate and Energy Systems Engineering, Ewha Womans University, Seoul, Korea

⁴Assistant Professor, Faculty of Geology and Petroleum Engineering, Ho Chi Minh City University of Technology, Vietnam

¹이화여자대학교 기후‧에너지시스템공학과 석사과정

²이화여자대학교 기후‧에너지시스템공학과 박사과정

³이화여자대학교 기후‧에너지시스템공학과 부교수

⁴호치민시기술대학교 지질석유공학과 조교수

^{*Corresponding Author}

ABSTRACT

This study develops a surrogate model to predict water saturation from well log data using neural-network-based deep learning algorithms. The model performance is evaluated by comparing the water saturation estimates obtained using deep learning algorithms and Archie’s law. The surrogate model evaluates the water saturation of a target reservoir using four well-log data types (density, porosity, resistivity, and gamma ray). Long Short-Term Memory (LSTM) is employed as the deep neural network algorithm, and its performance is compared with that of a multi-layer artificial neural network. Prediction via the LSTM based model showed outstanding results with the coefficient of determination above 0.7. Sensitivity analysis is conducted through sequence tuning, switching of well type, and k-fold cross-validation. The applicability of the model has been validated for the Volve oilfield in the North Sea and an offshore oilfield in Vietnam.

Keywords

Well log data

Water saturation

Long Short-Term Memory

Sensitivity analysis

이 연구는 다양한 물리검층자료를 학습한 딥러닝 알고리듬을 이용하여 저류층의 수포화도를 예측하는 대리 모델을 구축한다. 딥러닝 알고리듬으로 계산한 수포화도 추정치를 Archie 방정식 결과와 비교함으로써 개발 모델의 성능 평가를 수행하였다. 이 연구는 4가지 물리검층자료(밀도, 공극률, 비저항, 감마선)를 심층신경망의 입력인자로 활용하여 수포화도를 평가하였다, 심층신경망 기법으로는 장단기메모리학습법을 사용하였으며 전형적인 다층 인공신경망과의 비교를 통해 성능을 확인하였다. 장단기메모리학습법을 기반으로 수포화도를 예측한 결과, 결정계수의 값이 0.7 이상으로 우수한 성능을 보이는 것으로 확인하였다. 모델의 민감도 분석으로는 시퀀스 조정, 유정 역할 전환, k-폴드 교차검증을 시행하였다. 모델의 적용 가능성은 북해 Volve 유전과 베트남 해상 유전에 적용하여 성능을 검증하였다.

키워드

물리검층자료

수포화도

장단기메모리학습법

민감도 분석

MAIN

서 론
연구 방법
Archie 방정식
인공신경망
장단기메모리학습법
연구 결과
신경망 구조 설계
사례 연구
사례 연구 1 - Volve 유전
사례 연구 2 - 베트남 A 유전
결 론

서 론

석유탐사단계에서 물리탐사는 물리검층, 탄성파 자료 등 다양한 유형의 저류층 자료를 제공한다. 물리탐사는 ‘비파괴 탐사’라고도 불리며 지반을 파괴하지 않고 물리적 성질인 밀도(density), 공극률(porosity), 유체투과율(permeability), 비저항(resistivity) 등의 정보를 얻는다. 이 과정에서 획득한 저류층 물성을 통해 저류층을 평가한다. 수포화도(water saturation)는 탄화수소 생산을 위한 저류층 평가에 핵심 인자로 활용되며 수포화도를 추정하기 위해 다양한 경험식이 활용된다(Miah et al., 2020). 사암층에서는 주로 Archie 방정식(Archie, 1952), 셰일층에서는 Simandoux 모델(Simandoux, 1963) 등이 활용된다. 하지만, 경험식을 활용하여 수포화도를 추정할 경우, 지층의 이방성과 비균질성을 고려한 보정인자(비틀림 계수, 고결 지수 등) 선정에 어려움이 존재한다. 따라서, 보정인자를 특정하지 않고 비선형 관계를 분석하기 위해 기계학습을 활용한 연구가 증가하고 있다(Al-Bulushi et al., 2009; Park et al., 2021).

최근 석유 산업에서는 물리검층 경험식의 한계를 극복하기 위해 기계학습(machine learning)을 활용한 연구가 진행되고 있다. 서포트 벡터 머신(support vector machine), 퍼지 로직(fuzzy logic), 인공신경망(Artificial Neural Network, ANN) 등 다양한 기계학습법을 활용하여 공극률, 유체투과율 등 저류층의 물성을 추정하고 있다. Akinnikawe et al. (2018)은 다양한 종류의 기계학습 선형회귀(linear regression), 의사결정나무(decision tree), 기울기 부스팅(gradient boosting), 랜덤 포레스트(random forest), ANN의 성능을 비교하여 가장 우수한 기법의 결과를 채택하는 앙상블 학습법을 활용하여 합성 물리검층자료(synthetic well log)를 생성하였다. Onalo et al.(2018)은 셰일층에서 음파 검층(sonic log)을 추정하기 위해 밀도, 셰일의 부피, 감마선을 입력인자로 사용했다. Dalvand and Falahat(2020)은 P파 속도, 공극률, 밀도, 감마선을 입력인자로 사용하여 S파 속도를 도출하였다. 하지만, ANN 모델은 전형적인 점대점(point-to-point) 방식으로 구성되므로 이를 통해 도출한 값은 동일 심도에서의 입력인자와만 관계를 갖게 되어 물리검층자료의 깊이에 따른 유기적 성질을 보존하기 어렵다(Zhang et al., 2018). 상기 연구들에서 사용하여 온 ANN의 한계점을 극복하기 위해 Sherstinsky(2020)는 신경망을 구성하는 노드(node) 또는 뉴런(neuron)들의 내부순환 구조를 통해 이전단계의 정보를 기억하는 순환신경망(Recurrent Neural Network, RNN)을 활용하였다.

RNN은 한 노드에서 연결이 양방향이며 순환 구조를 띄는 인공신경망의 한 종류이다. 시계열 정보의 양방향 흐름을 통해 도출한 결과는 입력인자와의 내부 경향을 고려하여 생성되기 때문에 심도에 따른 지층 물성의 순차적인 변화를 보존해야 하는 지질학적 관점에서도 합리적인 접근법으로 볼 수 있다. 최근 RNN의 일종인 장단기메모리(Long Short-Term Memory, LSTM) 알고리듬이 다양한 순차 자료(sequential data) 해석연구에 적용되고 있다. Sun et al. (2018)과 Lee et al.(2019)는 전통적인 생산감퇴곡선분석(Decline Curve Analysis, DCA)과 LSTM을 사용하여 각각 생산량을 예측한 결과, LSTM의 생산량 예측치가 DCA의 예측치에 비하여 생산량 관측치와의 부합성이 높음을 확인하였다. Zhang et al.(2018)은 LSTM을 활용하여 감마선, 공극률, P파 속도로부터 비저항과 S파 속도를 예측하였다. Temizel et al.(2020)은 DCA와 LSTM 기법을 사용하여 탄화수소 종류(휘발성 오일, 경질유, 콘덴세이트, 건성가스)별 생산비율을 예측하였다. Ki et al.(2019)은 동적자료(가스생산량, 정저압)를 입력자료로 하여 LSTM을 통한 미측정 구간의 정두압 예측을 시행하였다. Pham et al. (2020)은 감마선, 밀도, 공극률을 LSTM의 입력자료로 활용하여 P파 속도를 추정한 후, Gardner 방정식(Gardner et al., 1974)과 비교하여 LSTM의 우수한 성능을 확인하였다.

이 연구는 보정인자를 특정하지 않고 비선형 관계를 분석하기 위해 물리검층자료를 활용하는 딥러닝 기반 수포화도 예측 신경망 모델을 다음과 같이 설계하고 실행한다. 첫째, 딥러닝 알고리듬의 입력인자는 수포화도를 도출하는 방정식인 Archie 방정식을 바탕으로 밀도, 공극률, 셰일 부피를 추정할 수 있는 4가지 인자(밀도 검층, 비저항 검층, 중성자 공극률 검층, 감마선 검층)를 선정한다. 둘째, 선정된 인자들에 대응하는 물리검층자료를 바탕으로 ANN과 LSTM 모델을 구축하여 학습한 후 각 모델의 성능을 비교평가한다. 본 연구에서 제안한 알고리듬들은 ANN, LSTM으로 지칭한다. 셋째, 신경망 모델의 하이퍼파라미터 조정, 유정 역할 전환(학습, 시험), k-fold 교차검증(k-fold cross validation)을 시행하여 모델의 일관성을 검증한다. 개발한 LSTM 신경망 기반 모델은 노르웨이 Volve 해상 유전과 베트남 해상 유전의 현장 자료를 활용하여 그 신뢰도를 평가한다.

연구 방법

Archie 방정식

수포화도( $S_{w}$ )를 도출하는 가장 전통적인 방법은 Archie 방정식을 사용하는 것이다(Archie, 1952). Archie 방정식은 암석의 공극률, 비저항, 수포화도 사이의 양적 관계를 보이는 수식으로 식 (1)과 같이 표현한다(Agbasi, 2013).

(1)

S_{w} = \frac{a R_{w}}{R_{t} ϕ^{m / n}}

이때, $α$ 는 비틀림 계수(tortuosity factor), $m$ 은 교결 지수(cementation exponent), $n$ 은 포화 지수(saturation exponent), $ϕ$ 는 공극률, $R_{t}$ 는 유체 포화 암석 비저항, $R_{w}$ 는 물의 비저항을 의미한다.

공극률(ϕ)은 암석의 총 부피(V_b) 대비 암석 내 공극 부피(V_p)의 비로 정의되며 식 (2)와 같이 계산한다. 공극률을 추정할 수 있는 중성자 공극률(Neutron Porosity, NPHI) 검층 값을 수포화도 예측에 사용한다. 중성자 검층은 공극률을 반영할 수 있는 셰일 또는 점토암에 따른 중성자 검층 값이다.

(2)

ϕ = \frac{V_{p}}{V_{b}}

암석 내 셰일 함량은 공극률, 유체투과율, 수포화도 등 저류층 물성에 영향을 끼친다(Moradi et al., 2016). 저류층 내 셰일의 부피 비율( $V_{s h}$ )은 식 (3)과 같이 감마선(Natural Gamma ray, GR)을 통해 도출할 수 있다(Szabó, 2011).

(3)

V_{s h} = \frac{G R - G R_{\min}}{G R_{\max} - G R_{\min}}

이때, $G R_{\min}$ 과 $G R_{\max}$ 는 각각 감마선의 최솟값과 최댓값을 의미한다.

인공신경망

ANN은 인간의 뉴런이 정보를 처리하는 과정을 바탕으로 만들어졌으며 인자들 간의 관계를 명확하게 알지 못하거나 복잡한 비선형적인 관계가 있을 때 많이 활용되는 알고리듬이다. ANN은 McCulloch와 Pitts가 1943년에 최초로 개발하였다(McCulloch and Pitts, 1943). 자료 간의 관계나 패턴을 인식하여 정보를 수집하고, 수집된 정보로 입력인자와 출력인자 간의 복잡하고 비선형적인 관계를 수치적으로 풀어나간다는 특징을 갖는다(Agatonovic-Kustrin and Beresford, 2000).

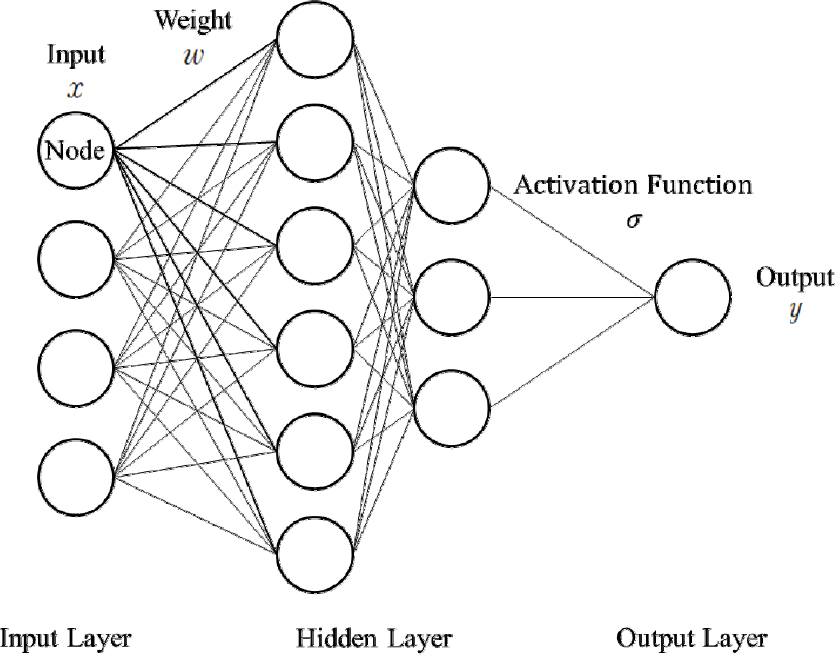
ANN은 정보를 받아들이는 입력층(input layer), 입력값이 변환되는 은닉층(hidden layer), 결과를 출력하는 출력층(output layer)으로 구성되며 각 층은 다수의 노드로 구성된다(Fig. 1). 은닉층은 1개 이상으로 구성할 수 있다. 은닉층의 개수가 2개 이상일 경우 심층신경망(Deep Neural Network, DNN)으로 지칭하지만 ANN과 DNN은 혼용되어 사용되기 때문에 ANN과 DNN의 용어 중 편의상 ANN으로 지칭한다. 각 노드는 인접한 층과 가중치(weight, $w$ )로 연결되며 최적의 가중치 배열을 찾기 위해 모델을 학습시킨다. 각 노드는 식 (4)와 같이 이전 층으로부터 전달받은 입력값 $x$ 에 가중치 $w$ 를 곱하고 편향값 $b$ 를 더한 후, 활성화함수(activation function, $σ$ )가 적용된 출력값 $y$ 를 할당받는다. 다음 층에서도 동일한 과정을 반복하여 최종적으로 출력층에서의 출력값을 도출한다.

(4)

y = σ (w x + b)

활성화함수의 종류에는 선형 전달 함수, 시그모이드 함수, 쌍곡 탄젠트 함수(hyperbolic tangent, tanh), ReLU (Rectified Linear Unit) 등이 있으며, 최근 심층신경망에서는 ReLU가 널리 활용되고 있다(Lin and Shen, 2018). 신경망 알고리듬은 자료 간 알려지지 않은 관계를 분석할 수 있는 장점이 있으나 만족스러운 결과를 얻기 위해 신뢰할 수 있는 자료를 사용해야 한다. 이를 위해 자료의 품질을 높일 수 있는 전처리 과정이 필수적이다(Chitsazan et al., 2015).

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F1.jpg

Fig. 1.

Schema of the ANN architecture.

장단기메모리학습법

LSTM은 RNN의 한 종류로 전통적인 RNN의 단점을 보완한 학습법이다. 전통적인 RNN은 순환적인 네트워크 흐름을 통해 이전 단계를 반영하여 다음 단계의 값을 선정한다는 특징을 갖는다. 길이가 긴 시계열 자료를 활용할 시 멀리 떨어진 자료의 영향력이 미약하게 작용하여 학습 능력이 저하되는 점을 보완하기 위해 LSTM 학습법이 등장하였다(Hochreiter and Schmidhuber, 1997). LSTM은 RNN과 유사하게 시계열 자료에서 정보를 추출할 뿐만 아니라, 더 나아가 이전 단계의 영향을 장기적으로 보존할 수 있다는 장점이 있다. 이로 인해 시계열 자료와 유사하게 연속성, 연결성을 갖는 물리검층자료에 적합하며, 합성 물리검층 자료를 생성하기에 유용한 도구로 활용할 수 있다(Zhang et al., 2018).

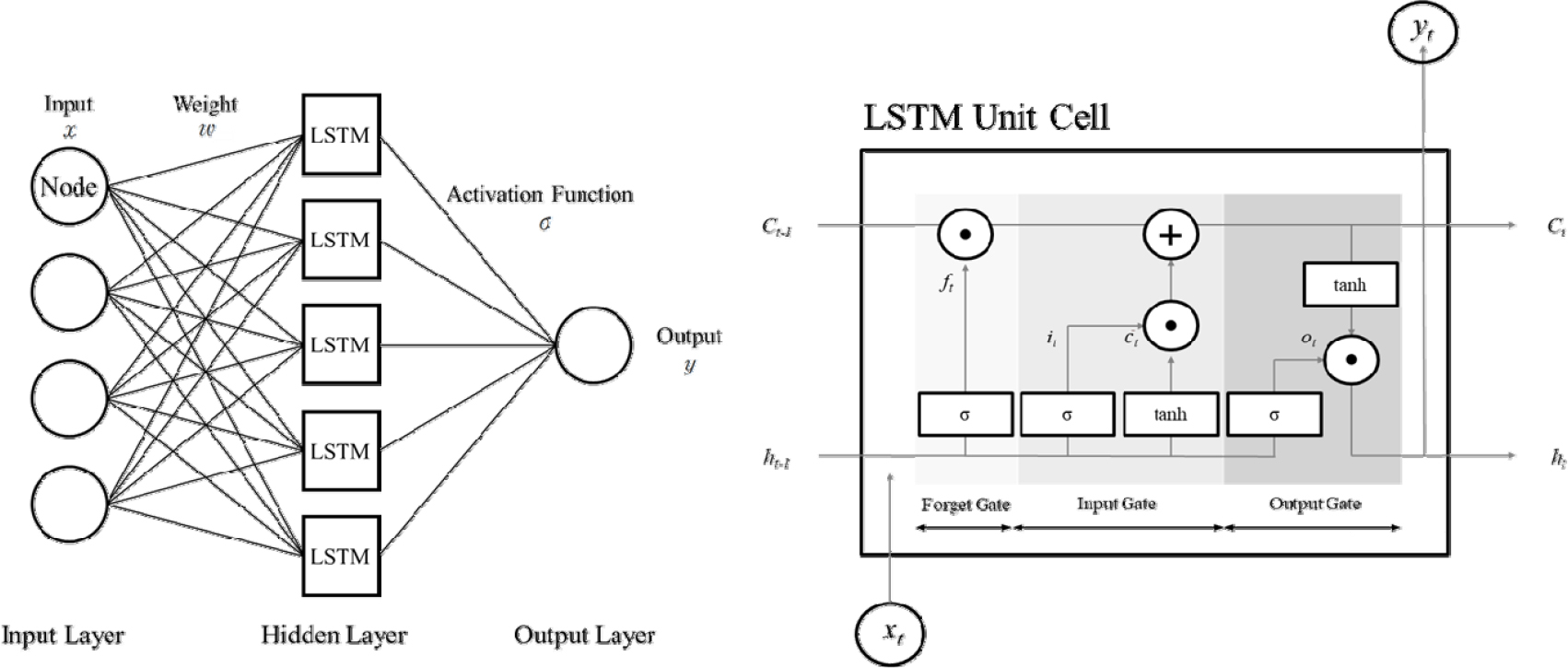
Fig. 2는 LSTM의 기본 구조를 나타내고 있다. LSTM은 RNN과 다르게 4가지 층(입력 게이트 층, 망각 게이트 층, 출력 게이트 층, tanh 층)과 셀 상태(cell state, $C_{t}$ )가 추가된 구조를 갖는다. 각 게이트 층은 은닉층에서의 상태에 따라 셀 상태에 정보를 추가하거나 제거하기 위해 사용된다. 망각 게이트는 잊어버릴 정보를 결정하는 층이며 입력 게이트는 입력된 정보 중 얼마나 셀 상태에 저장할지 결정한다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F2.jpg

Fig. 2.

Schema of the LSTM unit cell architecture.

망각 게이트 층의 결과값 $f_{t}$ 는 이전단계 은닉층으로부터 받은 $h_{t - 1}$ 과 현재 시점의 입력자료인 $x_{t}$ 에 가중치 $w_{f}$ 를 곱한 후 편향값 $b_{f}$ 를 합한 값에 활성화함수 $σ$ 를 적용하여 구한다(식 (5)). 입력게이트의 결과값 $i_{t}$ 는 이전단계 은닉층으로부터 받은 $h_{t - 1}$ 과 현재 시점의 입력자료인 $x_{t}$ 에 가중치 $w_{i}$ 를 곱한 후 편향값 $b_{i}$ 를 합한 값에 활성화함수 $σ$ 를 적용한 값이다(식 (6)). 출력게이트의 결과값 $o_{t}$ 는 이전단계 은닉층으로부터 받은 $h_{t - 1}$ 과 현재 시점의 입력자료인 $x_{t}$ 에 가중치 $w_{o}$ 가 곱해진 후 편향값 $b_{o}$ 를 더해 전체에 활성화함수 $σ$ 를 적용한 값이다(식 (7)). 이때, $h_{t}$ 는 출력층에서의 결과 $o_{t}$ 와 셀 상태에 tanh가 적용된 값 $\tanh (C_{t})$ 의 아다마르곱(Hadamard product, ∘)으로 나타낸다(식 (8)). tanh 층은 셀 상태에 더해질 후보 값 ${\bar{C}}_{t}$ 를 생성하여 입력 게이트와 함께 다음 셀 상태에 반영할 정보를 결정한다. ${\bar{C}}_{t}$ 는 이전 단계 은닉층으로부터 받은 $h_{t - 1}$ 과 현재 시점의 입력자료인 $x_{t}$ 에 가중치 $w_{c}$ 를 곱한 후 편향값 $b_{c}$ 를 합한 값에 활성화함수 tanh를 적용한 값이다(식 (9)). 출력 게이트 층은 얼마나 자료가 출력될지 결정하는 층으로 셀 상태에 저장된 현 시점의 자료와 함께 계산되어 결과가 도출된다. 앞의 과정을 바탕으로 셀 상태 $C_{t}$ 는 망각 게이트에서 계산된 $f_{t}$ 와 이전 상태의 셀 상태 $C_{t - 1}$ 이 아다마르곱으로 계산된 값과 입력 게이트에서 계산된 $i_{t}$ 와 후보 값 ${\bar{C}}_{t}$ 가 아다마르곱으로 계산된 값의 합으로 계산된다(식 (10)). 위와 같은 과정이 진행됨에 따라 셀 상태가 변화하며 마지막으로 변경된 셀 상태와 은닉 상태는 다음 단계로 전송될 출력자료를 결정한다(Osarogingbon et al., 2020).

(5)

f_{t} = σ (w_{f} ∙ [h_{t - 1}, x_{t}] + b_{f})

(6)

i_{t} = σ (w_{i} ∙ [h_{t - 1}, x_{t}] + b_{i})

(7)

o_{t} = σ (w_{o} ∙ [h_{t - 1}, x_{t}] + b_{o})

(8)

h_{t} = o_{t} \circ \tanh (C_{t})

(9)

\bar{C_{t}} = \tanh (w_{c} ∙ [h_{t - 1}, x_{t}] + b_{c})

(10)

C_{t} = f_{t} \circ C_{t - 1} + i_{t} \circ \bar{C_{t}}

연구 결과

신경망 구조 설계

신경망의 입력인자는 Archie 방정식 식 (1)을 참고하여 밀도, 공극률, 비저항, 감마선의 물리검층 값으로 선정하였으며 선정된 인자를 바탕으로 수포화도를 예측하는 ANN과 LSTM의 구조를 설계하였다. 이 연구에서 ANN은 1개의 입력층, 2개의 은닉층, 1개의 출력층으로 총 4개의 층을 가지며, LSTM은 1개의 입력층, 1개의 은닉층, 1개의 출력층으로 총 3개의 층을 갖는다. ANN과 LSTM의 학습과정에서 학습인자의 수를 최대한 동등한 조건으로 설정하기 위해 입력층 노드 수는 입력인자의 수에 따라 4가지 인자(밀도 검층, 비저항 검층, 중성자 공극률 검층, 감마선 검층), 출력층 노드 수는 수포화도 예측을 위한 1개, ANN의 은닉층 노드 수는 265개와 64개, LSTM의 은닉층 노드 수는 64개로 설정하였다. ANN의 훈련 파라미터(trainable parameter)는 17,793개, LSTM은 17,985개로 유사한 구조임을 확인하였다. ANN의 활성화함수는 ReLU이며 LSTM은 시그모이드 함수를 사용하였다. 일관적이지 않은 품질의 자료로 모델을 구축하는 경우 성능이 감소할 수 있으므로, 모델 성능 향상을 위해 결측값이 존재하는 부분은 제외하고 사용하였다. 물리검층의 자료 유형마다 보이는 범위가 다른 점을 보완하기 위해 각 입력자료의 범위를 0부터 1까지 표준화한 후 신경망에 입력하였다. LSTM의 경우 입력시퀀스의 길이는 5로 설정하였다. 입력시퀀스는 다음 깊이(t+1)의 자료를 예측하기 위해 사용되는 이전 깊이(t)의 연속된 자료의 개수를 의미한다. 본 연구에서 사용되는 LSTM 기반 모델의 입력시퀀스가 t일때 입력자료로 활용되는 데이터의 개수는 4t이다. 본 연구는 다수의 입력인자로 하나의 출력인자를 도출하는 모델을 사용하므로 출력시퀀스의 크기는 다음 깊이의 출력값인 1이 된다. 저류층 심도를 기준으로 물리검층 자료 중 상부 60%는 각 신경망의 학습에 사용하였고 하부 40% 중 20%는 신경망의 검증, 나머지 20%는 신경망의 시험에 사용하였다.

사례 연구

본 연구는 설계한 신경망의 적용성을 평가하기 위하여 두 가지 현장 사례에 적용하였다. 사례 연구 1(Case 1)은 노르웨이 Volve 해상 유전의 3개 유정을 대상으로 신경망을 설계한 경우, 사례 연구 2(Case 2)는 베트남 A 해상 유전의 2개 유정을 대상으로 신경망을 설계한 경우이다.

사례 연구 1 - Volve 유전

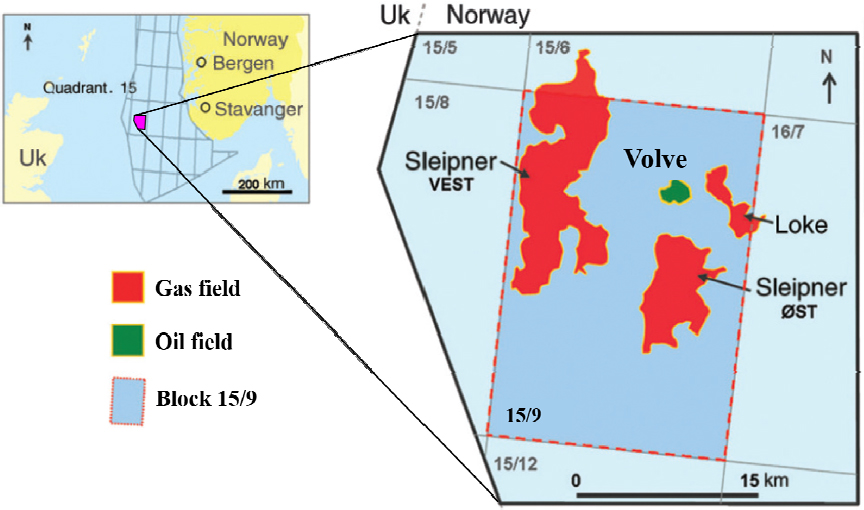
개발 기법의 성능은 북해(North Sea) 대륙붕에 위치한 노르웨이 Volve 유전 현장자료를 사용하여 검증하였다. Fig. 3은 Volve 유전의 위치를 나타낸다. Volve 유전의 면적은 약 6 km², 석유 부존 심도는 2,750~3,120 m, 저류층 평균 두께는 약 20 m이다(Equinor, 2019). Volve 유전의 석유 부존은 1993년에 확인되었으며 생산은 2008년 시작하여 2016년 종료되어 약 8년간 지속되었다(Sen and Ganguli, 2019). Volve 유전의 저류층은 사암, 이암, 셰일, 석회암 등 다양한 암상으로 구성된다(Samo, 2020). 본 연구에서 Volve 유전의 가스 포화도는 0으로 설정하여 저류층 유체유동을 오일-물 이상유동(two phase flow)으로 간주하였다. Volve 유전에는 3개의 주입정과 7개의 생산정으로 총 10개의 유정이 존재한다. Table 1은 본 연구에서 사용한 생산정 3개(P-F-11B, P-F-5, P-F-1C)의 운영 기간, 입력자료로 활용한 심도, 신경망 내에서 활용되는 유정의 역할을 나타낸다. 입력자료로 활용된 3개 유정의 심도에서의 지층은 대부분 Hugin formation으로 구성되어 있으며, P-F-11B 유정에는 미세하게 Heather formation 구간이 존재한다. 유정의 역할은 모델 구축(neural network design)과 시험(test)으로 구분되며 P-F-11B는 신경망 구축, P-F-1C와 P-F-5는 모델을 시험하기 위해 활용된다. 모델 구축은 신경망 설계에 활용한 자료들을 학습(training), 검증(validation), 시험(test) 자료로 세분화하여 진행하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F3.jpg

Fig. 3.

Location of the Volve Oilfield (Ravasi et al., 2015).

Table 1.

Well data used for designing a neural network model

Well Name	Purpose	Operation			True Vertical Depth (TVD) (m)	Data Point
Well Name	Purpose	Start Date	End Date	Months (Days)	True Vertical Depth (TVD) (m)	Data Point
P-F-11B	Neural Network Design	2014.04.19.	2016.04.28.	24.6 (740)	3,001.4 – 3,097.1	3,870
P-F-1C	Test	2016.04.18.	2016.04.28.	0.3 (10)	3,047.4 – 3,093.1	1,531
P-F-5	Test	2013.08.12.	2016.09.20.	37.8 (1,135)	2,831.2 – 2,972.3	316

신경망 모델의 성능은 평균제곱오차(Mean Squared Error, MSE)와 결정계수(coefficient of determination) R²을 계산하여 평가하였다. Volve 유전에서 제공하는 공공데이터에는 코어자료가 없어, 이 연구에서는 Volve 유전에서 제공하는 $S_{w}$ 를 참조값(reference data)으로 활용하였다. 제공된 $S_{w}$ 는 Archie 방정식 식 (1)으로 계산되었다. 손실함수 $J$ 는 MSE와 L2 정규화 항이 더해진 값으로 설정하였으며 $w$ 는 가중치를 의미한다(식 (11)). 신경망 모델의 예측값과 참조값의 비교를 위한 지표는 R²으로 설정하였다(식 (12)).

(11)

J = MSE + L (w) = \frac{1}{n} \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2} + \frac{α}{2} ∥ w ∥^{2}

(12)

R^{2} = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - \hat{y_{i}})^{2}}{\sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}}

이때, $n$ 은 자료의 개수, $y_{i}$ 는 참조값, ${\hat{y}}_{i}$ 는 예측값, $\bar{y}$ 는 평균을 의미한다.

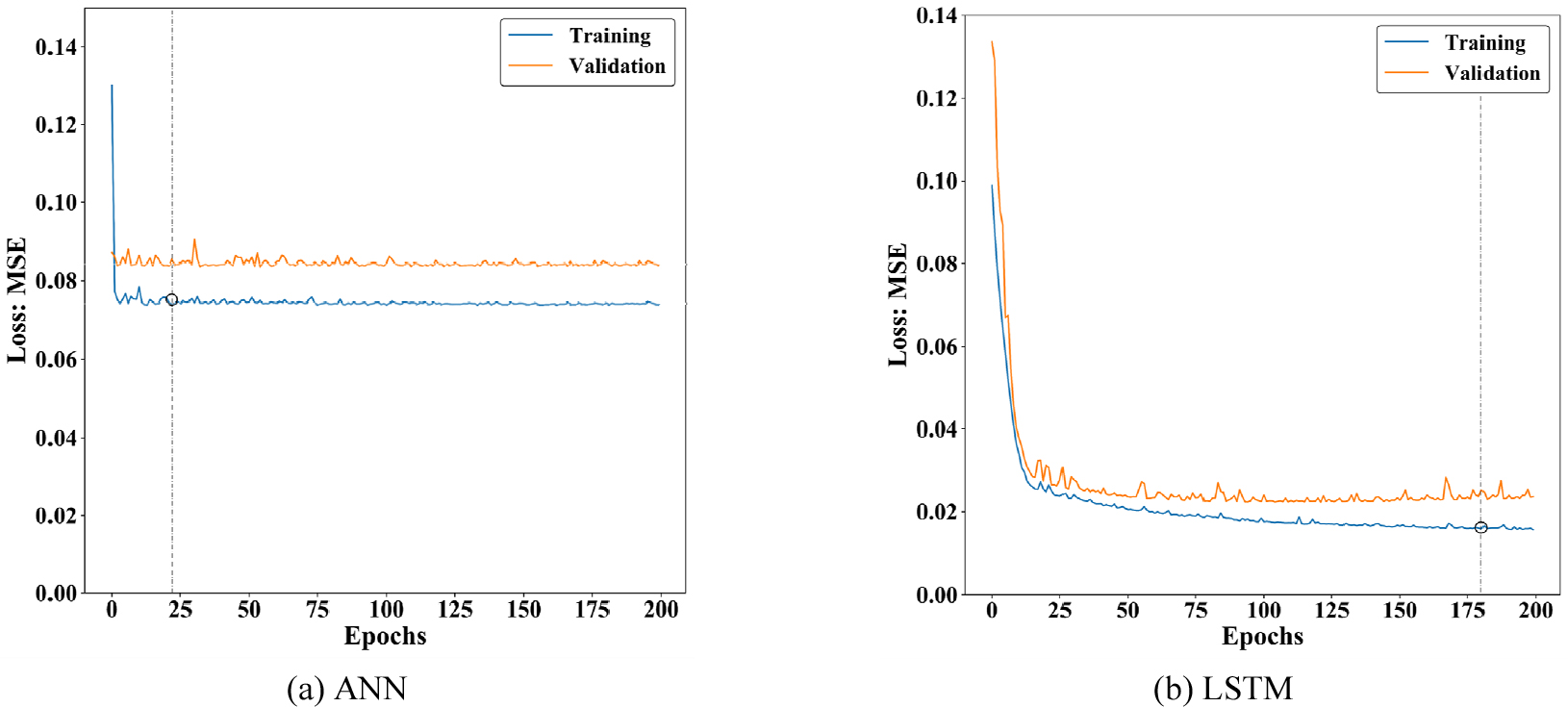
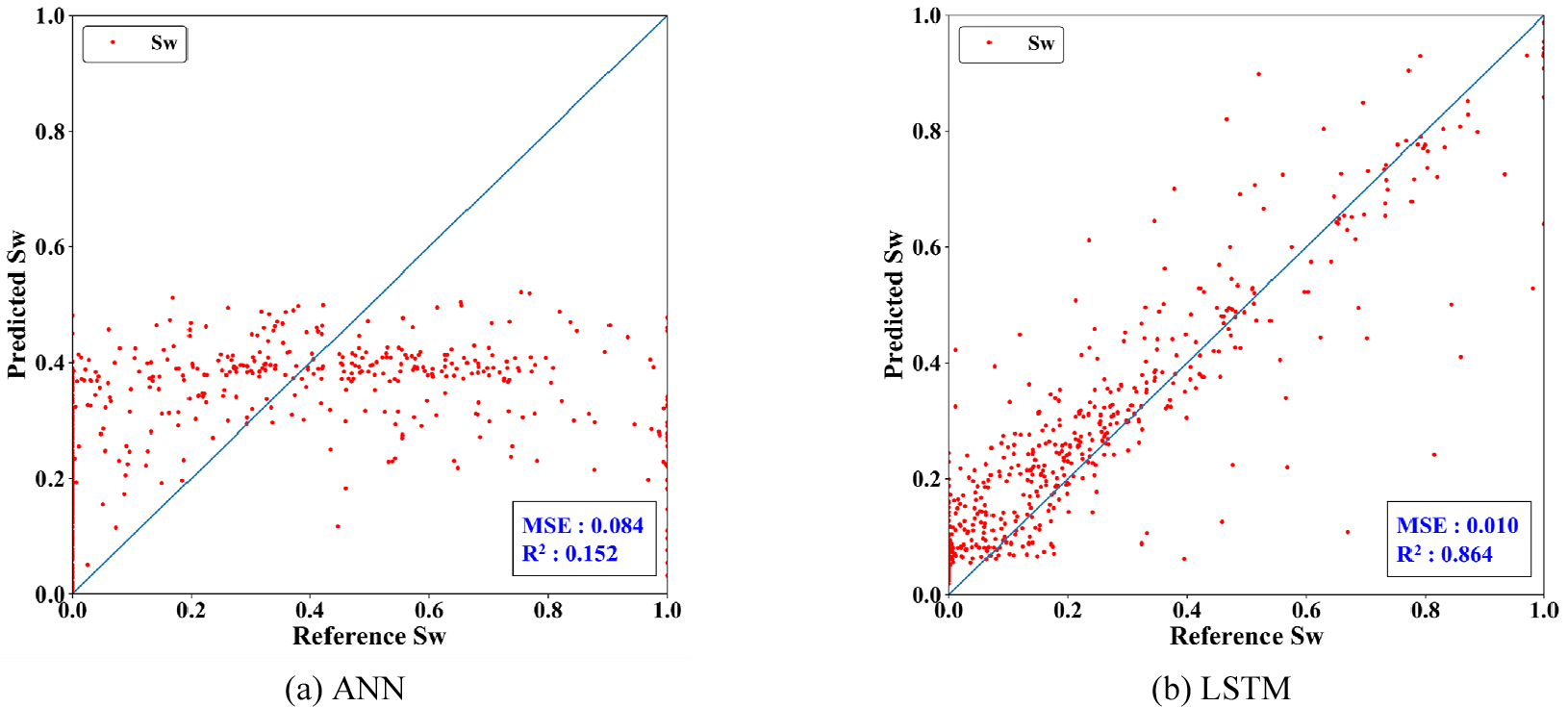
Fig. 4는 각각 ANN과 LSTM 모델의 학습, 검증, 시험 결과를 비교한다. 점선은 과적합 방지를 위해 학습의 조기 종료(early stopping)된 시점을 나타낸다. 조기 종료는 검증 오차를 기준으로 20회 이상 J가 개선되지 않을 시에 적용된다. 두 신경망 모델 모두 학습이 진행됨에 따라 손실함수가 안정적으로 감소하였다. Fig. 5는 P-F-11B 시험 자료로 ANN과 LSTM을 통한 수포화도의 예측값과 참조값을 비교한 산포도를 보여준다. Fig. 4와 Fig. 5의 결과를 바탕으로 ANN과 LSTM의 평가 성능을 비교한 결과, LSTM을 사용했을 때 R²은 0.152에서 0.864로 0.70 이상 향상되었으며 MSE는 0.07 이상 감소하였다. 이를 통해 LSTM이 ANN보다 물리검층자료를 활용한 수포화도 예측에 적합함을 확인하였다. 이는 시계열 자료와 마찬가지로 순차 자료에 해당하는 심도별 물리검층자료의 해석의 경우, LSTM이 전통적인 신경망에 비해 구조적 장점이 있음을 의미한다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F4.jpg

Fig. 4.

Trend of loss function values for the training and validation data of ANN and LSTM.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F5.jpg

Fig. 5.

Scatter plot to compare the reference and prediction results of water saturation on the P-F-11B test data.

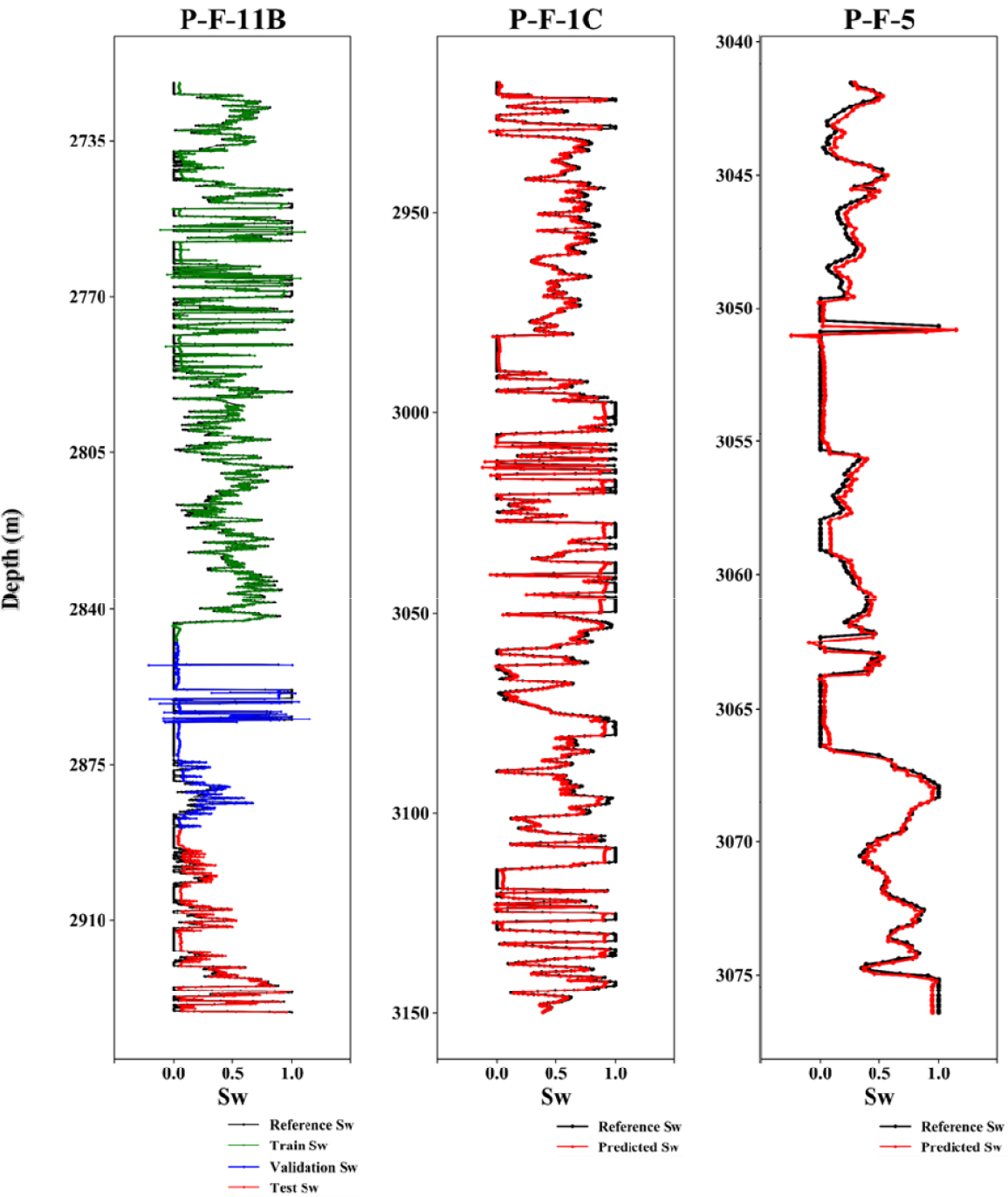
Table 2는 세 개의 유정 자료로 LSTM을 학습, 검증 및 시험했을 때의 결과를 나타낸다. P-F-11B의 물리검층 자료는 모델을 구축하는 데 사용되었으며 학습, 검증, 시험의 R² 모두 0.70 이상의 값을 갖고, MSE 또한 0.025 이하의 값을 갖는다. LSTM이 ANN에 비해 우월한 평가 성능을 보임에 따라 P-F-11B의 자료를 바탕으로 LSTM을 사용하여 학습 및 검증에 포함하지 않은 나머지 두 개의 유정(P-F-1C, P-F-5)에 대해서 시험을 진행하였다. 모델을 적용한 결과, 두 유정 모두 0.80 이상의 R²을 보여 우수한 평가 성능을 제시하였다. 이를 통해 참조값과 예측값이 비교적 일치한다고 판단하였으며 설계된 모델은 일반화가 잘 이루어졌음을 확인하였다(Fig. 6).

Table 2.

Results of LSTM for the Volve Oilfield

Well Name	Purpose	R²		MSE
P-F-11B	Neural Network Design	Train	0.839	0.015
		Validation	0.729	0.022
		Test	0.864	0.010
P-F-1C	Test	0.952		0.007
P-F-5	Test	0.897		0.011

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F6.jpg

Fig. 6.

Comparison of the reference and predicted water saturation profiles for the three production wells of the Volve Oilfield.

구축된 신경망의 일반화 성능을 평가하기 위해 k-폴드 교차검증을 시행하였다. k-폴드 교차검증은 신경망의 일반화 검증을 위한 방법으로 전체 자료를 사용하여 학습, 검증 및 시험을 진행한다. 전제 데이터를 k 개의 집합으로 나누어 (k-1)개의 학습 자료와 1개의 시험 자료로 선정한 후 총 k번의 검증을 실행한다(Kwon et al., 2020). 신경망의 궁극적인 목표는 모든 자료에 대해 높은 정확도로 균일한 성능을 보이는 것이다. 하지만 고정된 학습자료로 신경망을 구축할 경우, 특정 자료에 대해 편중되는 현상이 나타날 가능성이 존재한다. 따라서 k-폴드 교차검증은 모든 자료를 활용하여 자료에 대한 편중과 과적합을 방지하기 위한 과정이다.

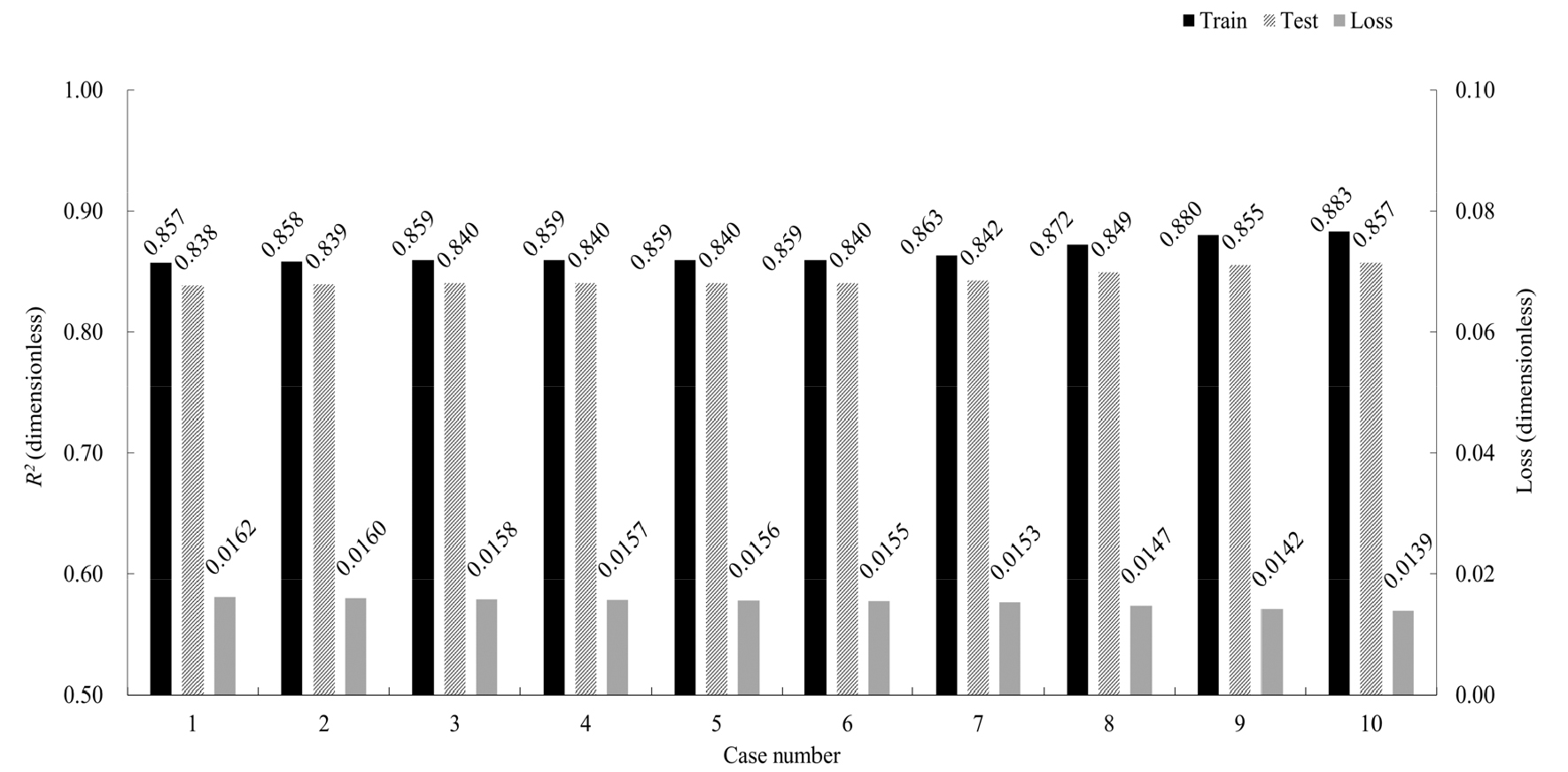
Fig. 7은 사례 연구 1을 바탕으로 구축된 신경망에 k-폴드 교차검증을 시행한 결과를 나타낸다. k = 10으로 설정하였으며 총 10개의 폴드로 구성된다. 각 폴드의 학습, 시험 R²과 손실함수의 값은 평균적으로 0.844±0.007, 0.865±0.009, 0.015±0.0007으로 비교적 높은 상관계수와 적은 편차를 보인다. 따라서 구축된 신경망의 일반화 가능성을 확인하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F7.jpg

Fig. 7.

Performance of ten-fold cross validation for Case 1.

Table 3은 기존에 구축되었던 신경망과 동일한 조건으로 P-F-11B 대신 P-F-1C를 통해 학습, 검증 및 시험한 후 유정 P-F-11B와 P-F-5에 적용한 결과를 나타낸다. 모든 경우의 R²이 0.75 이상, MSE는 0.030 이하의 값을 갖는 것을 통해 사례 연구 1이 전반적으로 우수한 성능을 보임을 확인하였다. 일반적으로 학습 구간의 결정계수가 시험 구간보다 높게 나타나지만, P-F-1C는 특히 시험 구간의 결과가 좋은 특징을 보인다. 이는 본 연구에서 설계된 모델이 수포화도 범위의 경곗값에 대한 예측 성능이 떨어지는 현상으로 인해 경곗값인 0과 1이 상대적으로 적게 분포하는 시험 구간의 성능이 높은 것으로 판단된다. P-F-11B로 설계한 결과와 P-F-1C로 설계한 결과를 비교하였을 때, 지정학적 위치가 다름에도 불구하고 일정한 성능을 보여줌을 통해 신경망이 특정 자료에 편중되지 않았음을 확인하였다.

Table 3.

Results of a LSTM model designed with P-F-1C for the Volve Oilfield

Well Name	Purpose	R²		MSE
P-F-1C	Neural Network Design	Train	0.820	0.021
		Validation	0.840	0.026
		Test	0.957	0.010
P-F-11B	Test	0.850		0.020
P-F-5	Test	0.752		0.029

Table 4는 구축된 신경망의 입력시퀀스를 변화시킬때 P-F-11B 유정으로 신경망을 학습, 검증 시험한 민감도 분석의 결과를 나타낸다. 입력시퀀스를 5에서 150까지 변화시킨 결과 시퀀스 길이가 5 이상인 경우 모두 R²이 0.70 이상의 우수한 성능을 보이며, 50 이상으로 설정할 경우 5로 선정한 결과와 비슷한 성능을 보이지만 학습에 걸리는 시간은 124초로 두 배 이상 소요된다. 따라서 시퀀스 길이를 5로 선정하는 것이 신경망에 가장 적합함을 판단하였다. 모든 계산과정은 다음의 컴퓨터 하드웨어 사양 하에 진행되었다: AMD Ryzen 7 3700X 8-Core Processor CPU @ 3.6 GHz, 32.0 GB RAM, NVIDIA GeForce RTX 2080 SUPER.

Table 4.

Comparison of the performances with sequence variation

P-F-11B	Train (R²) / Data Points	Validation (R²) / Data Points	Test (R²) / Data Points	Computational Time (Sec.)
Lag 5	0.839 / 2,320	0.728 / 772	0.859 / 772	24.9
Lag 50	0.832 / 2,923	0.728 / 763	0.859 / 763	124
Lag 100	0.839 / 2,263	0.727 / 753	0.863 / 753	260
Lag 150	0.839 / 2,233	0.727 / 743	0.863 / 743	377

사례 연구 2 - 베트남 A 유전

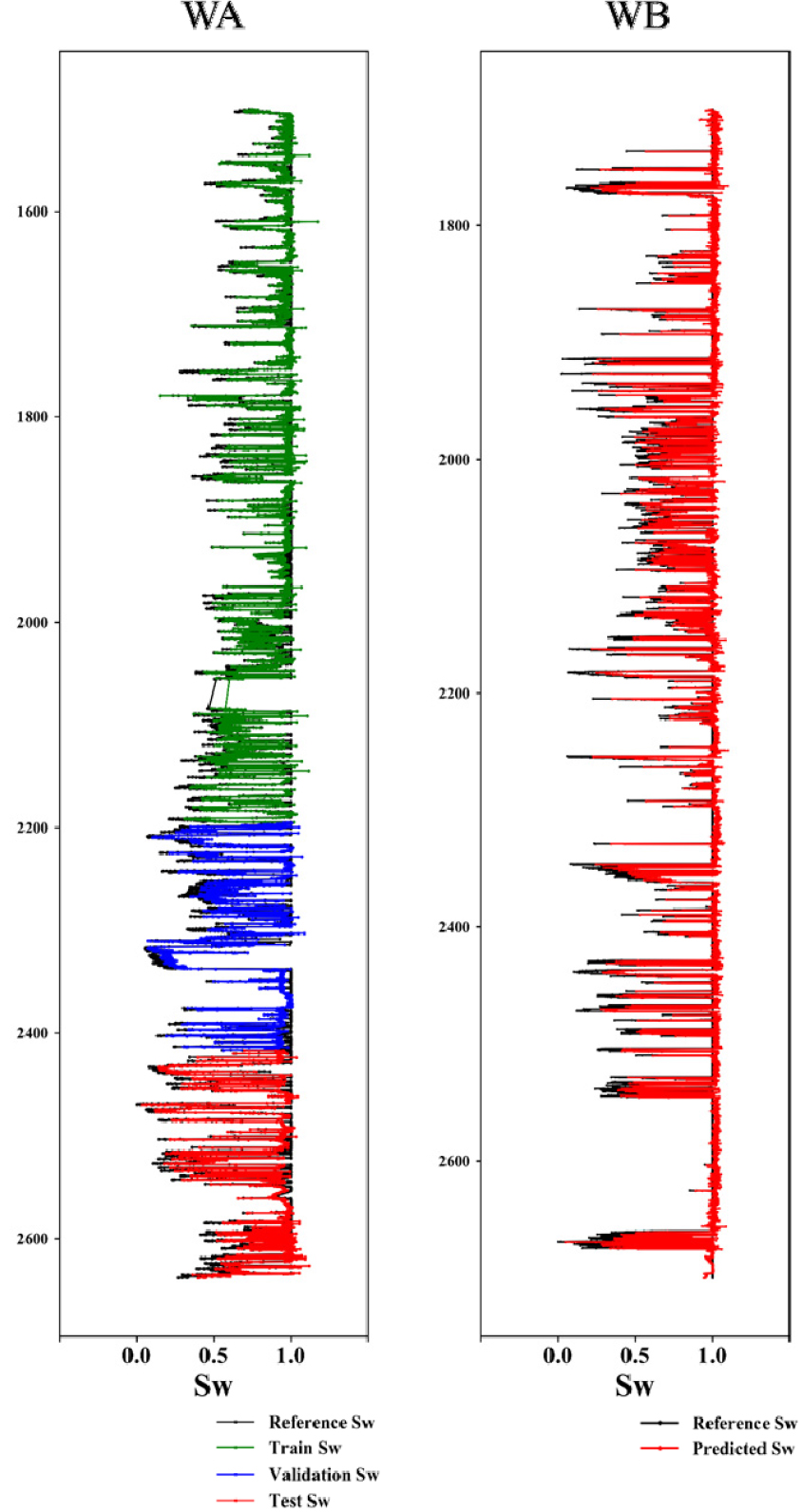
사례 연구 2는 베트남 A 해상 유전에 위치한 2개의 유정에 사례연구 1과 동일한 조건의 LSTM 모델을 적용한 결과를 나타낸다. Table 4의 결과에 따라 사례 연구 2는 입력시퀀스를 5로 고정하여 적용하였다. 사용된 유정 WA와 WB는 각 8,880개와 7,813개의 자료를 포함한다. 사례 연구 2는 Archie 방정식을 바탕으로 총 4가지 입력인자(밀도, 유효 공극률, 비저항, 감마선)를 선정하였으며 Fig. 8은 선정된 입력인자를 바탕으로 유정 WA를 통해 학습한 후 유정 WB에 적용한 결과이다. WA의 학습, 검증, 시험 모두 R²이 0.78 이상, MSE는 0.016 이하의 값을 갖는 것을 통해 사례 1에서 구축된 신경망의 구조는 Volve 유전에 국한되지 않으며 다른 유전에 대한 적용 가능성을 확인하였다(Table 5).

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F8.jpg

Fig. 8.

Comparison of the reference and predicted water saturation profiles for the two wells in the A field, Vietnam.

Table 5.

Results of LSTM for A Oilfield in Vietnam

Well Name	Purpose	R²		MSE
WA	Neural Network Design	Train	0.778	0.008
		Validation	0.842	0.017
		Test	0.780	0.020
WB	Test	0.486		0.023

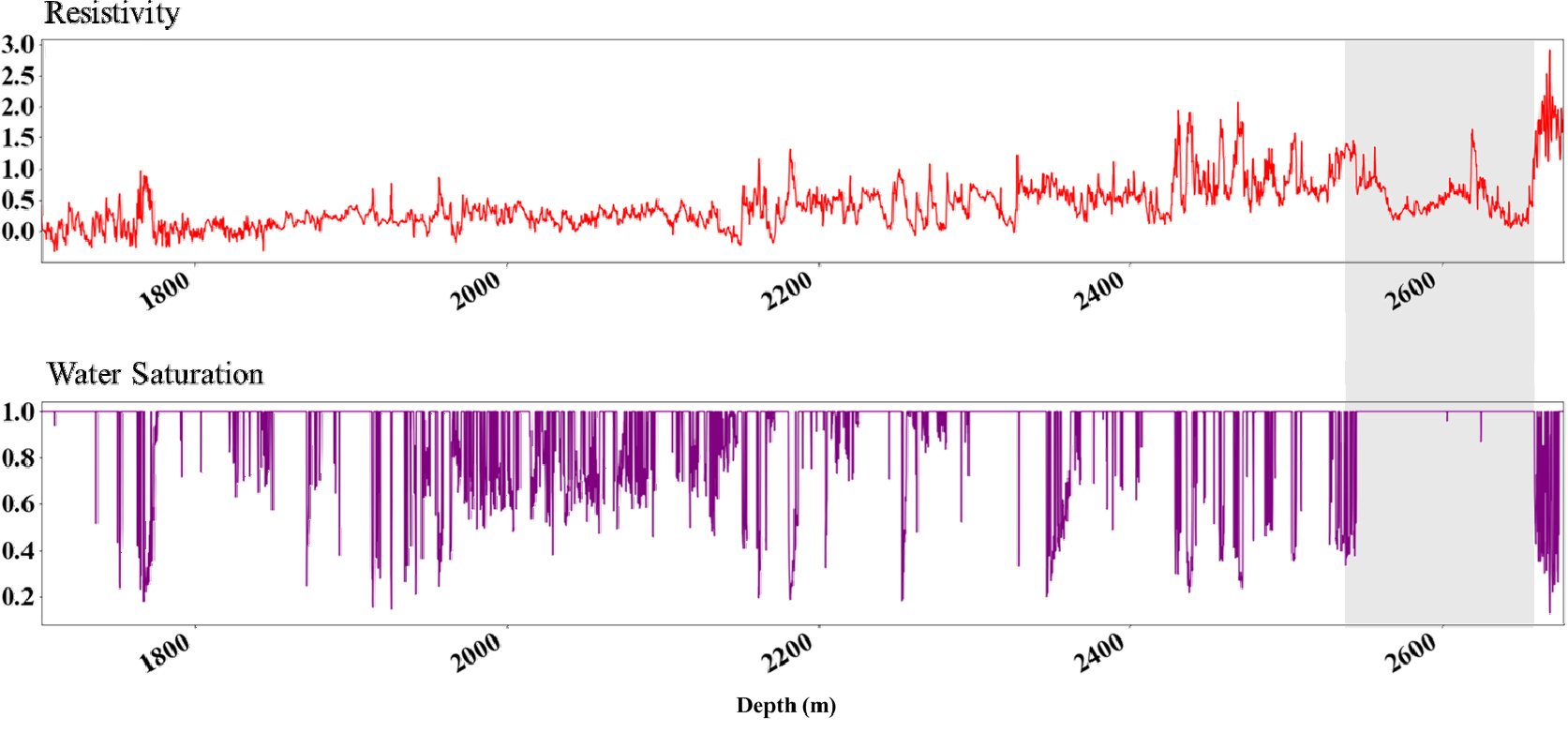
반면, WB에 적용한 결과와 다른 결과들을 비교하였을때 상대적으로 낮은 $R^{2}$ 을 보인다. 일반적으로 수포화도가 높은 경우 비저항 값은 낮은 양상을 보인다. WB의 비저항값과 수포화도를 비교하였을 때 서로 반대되는 경향을 보이지만, 2,600 m 부근에서의 비저항값이 변동이 있음에도 불구하고 수포화도는 대부분 1의 값을 나타낸다(Fig. 9). 이로 인해 WB는 기존에 학습되었던 패턴과 다른 데이터 양상을 갖기 때문에 다른 유정에 비해 상대적으로 낮은 $R^{2}$ 를 보이는 것으로 판단하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-03/N0330580302/images/ksmer_58_03_02_F9.jpg

Fig. 9.

Trend of resistivity and water saturation for the WB well in A oilfield.

본 연구에서 Volve 유전 자료에 신경망 모델을 적용하였을 때 모두 0.7 이상의 높은 R²의 값을 갖는 우수한 성능을 보였으며 Volve 자료에 편중되지 않았음을 확인하기 위해 베트남 유전의 자료에 적용하였다. 활용된 Volve 유전의 자료는 대부분 Hugin formation을 통과하며 P-F-11B에 미세하게 Heather formation이 존재하였다. 이에 사례 연구 1은 지질학적으로 유사한 지층에서의 자료로 학습하였기에 모델의 좋은 성능에 기여한 것으로 판단된다. 사례 연구 2는 활용된 유전에 대한 지질학적 정보를 미확보하였기에 상대적으로 다른 양상을 보이는 자료로 인해 다소 낮은 R²의 결과를 얻었다. 본 연구는 지층정보가 반영되지 않은 한계점이 존재한다. 따라서, 향후 코어에서 채취한 수포화도 참값 비교 또는 코어 자료 및 지층정보를 신경망 학습에 활용할 수 있다면 제안한 신경망 알고리듬의 성능을 보다 개선시킬 수 있을 것이다. 본 연구를 기반으로 코어자료와 검층자료 간 해상도 매칭을 위해 S_w의 고해상도 검층 곡선 생성 후, 코어자료를 활용하여 S_w를 보정한 검층 곡선을 생성하는 연구로 확장할 수 있을 것으로 기대한다.

결 론

이 연구는 물리검층자료로 설계한 장단기메모리학습법을 사용하여 북해 Volve 유전과 베트남 유전의 유정에서 심도별 수포화도를 추정한 후, 모델의 일관성을 평가하였다. 연구결과를 바탕으로 다음의 결론을 도출하였다.

(1) 수포화도를 추정하기 위해 Archie 방정식을 바탕으로 4가지 물리검층 인자(암석의 밀도, 공극률, 비저항, 감마선)를 선정하였다. 선정한 입력인자들을 기반으로 수포화도를 예측하는 ANN과 LSTM 모델을 설계하였고, 두 모델의 비교를 통해 순차적 자료에 해당하는 물리검층 해석에서 LSTM의 우수한 성능을 확인하였다. 이를 바탕으로 설계한 LSTM 모델을 학습에서 배제한 유정에 적용하여 일반화 여부를 확인하였으며, 이를 바탕으로 각 유정의 수포화도 평균값을 도출하였다.

(2) 구축된 신경망을 Volve 유전에 적용한 결과, 모든 경우에 대해 결정계수가 0.7 이상의 우수한 성능을 보였다. 모델의 일관성을 확인하기 위해 k-폴드 교차검증을 시행하였으며 LSTM의 하이퍼파라미터 중 가장 중요한 역할을 하는 입력시퀀스를 변화시켰을 때 모든 경우에 대해 0.7 이상의 우수한 성능을 보였다. k-폴드 교차검증을 적용한 경우, 모든 폴드에서의 학습 결과가 균일하였으며 0.8 이상의 성능을 보였다. 학습에 적용한 유정과 성능 평가에 활용된 유정들의 역할을 전환했을 때 또한 일관적인 성능을 보였다. 모델의 적용 가능성을 확인하기 위해 베트남의 유전에 신경망을 적용하였으며 이를 통해 구축된 모델이 특정 자료에 편중되지 않고 타 유전에 대한 적용성을 확인하였다.

(3) 이 연구는 설계한 LSTM을 기반으로 수포화도를 예측할 때 지층정보가 반영되지 않은 한계점이 존재한다. 채취한 수포화도 참값 비교 또는 코어 자료 및 지층정보를 신경망 학습에 활용할 수 있다면 제안한 신경망 알고리듬의 성능을 보다 개선시킬 수 있을 것이며, 향후 국내외 석유·가스전의 물리검층 자료로 확장해나갈 뿐만 아니라 코어 자료 및 지층정보를 함께 활용한다면 본 연구에서 제시한 모델의 효용성을 향상시킬 수 있을 것이다. 또한, 개발기술은 국내 강점 산업인 IT와의 연계를 통해 디지털 오일필드 등 다양한 국내외 사업으로 확장할 수 있을 것으로 기대한다.

Acknowledgements

이 연구는 한국지질자원연구원 가스하이드레이트 기계학습기반 분석 연구(No. GP2021-010), 한국연구재단 한-베트남 국가간 협력기반조성사업(No. 2017K1A3A1A05069660), 박사과정생연구장려금지원(No. 2021R1A6A3A13046159)의 지원을 받았습니다. 또한 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행하였습니다(No. 20214710100060). Dr. N.X. Huy was funded by the Ministry of Science and Technology of Vietnam (grant No. NĐT.48.KR/18). 이에 감사드립니다.

References

Agatonovic-Kustrin, S. and Beresford, R., 2000. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research, Journal of Pharmaceutical and Biomedical Analysis, 22(5), p.717-727. 10.1016/S0731-7085(99)00272-1

Agbasi, O.E., 2013. Estimation of water saturation using a modeled equation and Archie's equation from wire-line logs, Niger Delta Nigeria, IOSR Journal of Applied Physics, 3, p.66-71. 10.9790/4861-0346671

Akinnikawe, O., Lyne, S., and Roberts, J., 2018. Synthetic well log generation using machine learning techniques. Unconventional Resources Technology Conference, Houston, Texas, USA, July 23-25. 10.15530/urtec-2018-2877021

Al-Bulushi, N., King, P.R., Blunt, M.J., and Kraaijveld, M., 2009. Development of artificial neural network models for predicting water saturation and fluid distribution, Journal of Petroleum Science and Engineering, 68(3-4), p.197-208. 10.1016/j.petrol.2009.06.017

Archie, G.E., 1952. Classification of carbonate reservoir rocks and petrophysical considerations, AAPG Bulletin, 36(2), p.278-298. 10.1306/3D9343F7-16B1-11D7-8645000102C1865D

Chitsazan, N., Nadiri, A.A., and Tsai, F.T.C., 2015. Prediction and structural uncertainty analyses of artificial neural networks using hierarchical Bayesian model averaging, Journal of Hydrology, 528, p.52-62. 10.1016/j.jhydrol.2015.06.007

Dalvand, M. and Falahat, R., 2020. A new rock physics model to estimate shear velocity log, Journal of Petroleum Science and Engineering, 196, 107697. 10.1016/j.petrol.2020.107697

Equinor, 2019.02.19, https://data-equinor-com.azurewebsites.net/dataset/volve

Gardner, G.H.F., Gardner, L.W., and Gregory, A.R., 1974. Formation velocity and density-The diagnostic basics for stratigraphic traps, Geophysics, 39(6), p.770-780. 10.1190/1.1440465

Hochreiter, S. and Schmidhuber, J., 1997. Long short-term memory, Neural Computation, 9(8), p.1735-1780. 10.1162/neco.1997.9.8.17359377276

Ki, S., Seo, J., Kwon, O., and Jang, I., 2019. Prediction of missing tubing head pressure using recurrent neural network, Journal of The Korean Society of Mineral and Energy Resources Engineers, 56(5), p.416-426. 10.32390/ksmer.2019.56.5.416

Kwon, S., Park, G., Min, B., Kim, K., Lee, T., and Han, J., 2020. Evaluation of CO2-EOR efficiency in carbonate reservoirs using multiple nonlinear regression analysis, Journal of The Korean Society of Mineral and Energy Resources Engineers, 57(2), p.185-194. 10.32390/ksmer.2020.57.2.185

Lee, K., Lim, J., Yoon, D., and Jung, H., 2019. Prediction of Shale-Gas Production at Duvernay Formation Using Deep- Learning Algorithm, SPE Journal, 24(6), p.2423-2437. 10.2118/195698-PA

Lin, G. and Shen, W., 2018. Research on convolutional neural network based on improved Relu piecewise activation function, Procedia Computer Science, 131, p.977-984. 10.1016/j.procs.2018.04.239

McCulloch, W.S. and Pitts, W., 1943. A logical calculus of the ideas immanent in nervous activity, Bulletin of Mathematical Biology, 5(4), p.115-133. 10.1007/BF02478259

Miah, M.I., Zendehboudi, S., and Ahmed, S., 2020. Log data-driven model and feature ranking for water saturation prediction using machine learning approach, Journal of Petroleum Science and Engineering, 194, 107291. 10.1016/j.petrol.2020.107291

Moradi, S., Moeini, M., Al-Askari, M.K.G., and Mahvelati, E.H., 2016. Determination of shale volume and distribution patterns and effective porosity from well log data based on cross-plot approach for a shaly carbonate gas reservoir. IOP Conf. Series: Earth and Environmental Science, 44(042002), p.1755-1315. 10.1088/1755-1315/44/4/042002

Onalo, D., Adedigba, S., Khan, F., James, L.A., and Butt, S., 2018. Data driven Model for Sonic Well Log Prediction, Journal of Petroleum Science and Engineering, 170, p.1022- 1037. 10.1016/j.petrol.2018.06.072

Osarogiagbon, A., Oloruntobi, O., Khan, F., Venkatesan, R., and Butt, S., 2020. Gamma ray log generation from drilling parameters using deep learning, Journal of Petroleum Science and Engineering, 195, 107906. 10.1016/j.petrol.2020.107906

Park, G., Kwon, S., Ji, M., Min, B., Huy, N.X., Kim, K., Kim, S., Lee, K.B., 2021. A review on deep learning applications in logging data to model gas-hydrate-bearing sediments, Journal of The Korean Society of Mineral and Energy Resources Engineers, 58(2), p.161-178. 10.32390/ksmer.2021.58.2.161

Pham, N., Wu, X., and Zabihi Naeini, E., 2020. Missing well log prediction using convolutional long short-term memory network, Geophysics, 85(4), p.WA159-WA171. 10.1190/geo2019-0282.1

Ravasi, M., Vasconcelos, I., Curtis, A., and Kristi, A., 2015. Vector-acoustic reverse time migration of Volve ocean-bottom cable data set without up/down decomposed wavefields, Geophysics, 80(4), p.S137-S150. 10.1190/geo2014-0554.1

Samo, A.O., 2020. Reservoir Characterization of the Volve Field North Sea, using rock-physics modeling, MS Thesis, Texas A&M University-Kingsville, USA.

Sen, S. and Ganguli, S. S., 2019. Estimation of Pore Pressure and Fracture Gradient in Volve Field, Norwegian North Sea. SPE Oil and Gas India Conference and Exhibition, Mumbai, India, April 9-11. 10.2118/194578-MS

Sherstinsky, A., 2020. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network, Physica D: Nonlinear Phenomena, 404, 132306. 10.1016/j.physd.2019.132306

Simandoux, P., 1963. Dielectric measurements on porous media, application to the measurements of water saturation: study of behavior of argillaceous formations, Revue de l'Institut Francais du Petrol, 18(suppl), p.93-215.

Sun, J., Ma, X., and Kazi, M., 2018. Comparison of decline curve analysis DCA with recursive neural networks RNN for production forecast of multiple wells. SPE Western Regional Meeting, California, USA, April 22-26. 10.2118/190104-MS

Szabó, N.P., 2011. Shale volume estimation based on the factor analysis of well-logging data, Acta Geophysica, 59(5), 935. 10.2478/s11600-011-0034-0

Temizel, C., Canbaz, C.H., Saracoglu, O., Putra, D., Baser, A., Erfando, T., Krishna S., and Saputelli, L., 2020. Production forecasting in shale reservoirs through conventional DCA and machine/deep learning methods. Unconventional Resources Technology Conference, Virtual, July 20-22. 10.15530/urtec-2020-2878PMC7869042

Zhang, D., Chen, Y., and Meng, J., 2018. Synthetic well logs generation via recurrent neural networks, Petroleum Exploration and Development, 45(4), p.629-639. 10.1016/S1876-3804(18)30068-5

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Prediction of Water Saturation from Well Log Data using Deep Learning Algorithms

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

Fig. 1.

Schema of the ANN architecture.

Fig. 2.

Schema of the LSTM unit cell architecture.

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 3.

Location of the Volve Oilfield (Ravasi et al., 2015).

Table 1.

Well data used for designing a neural network model

(11)

(12)

Fig. 4.

Trend of loss function values for the training and validation data of ANN and LSTM.

Fig. 5.

Scatter plot to compare the reference and prediction results of water saturation on the P-F-11B test data.

Table 2.

Results of LSTM for the Volve Oilfield

Fig. 6.

Comparison of the reference and predicted water saturation profiles for the three production wells of the Volve Oilfield.

Fig. 7.

Performance of ten-fold cross validation for Case 1.

Table 3.

Results of a LSTM model designed with P-F-1C for the Volve Oilfield

Table 4.

Comparison of the performances with sequence variation

Fig. 8.

Comparison of the reference and predicted water saturation profiles for the two wells in the A field, Vietnam.

Table 5.

Results of LSTM for A Oilfield in Vietnam

Fig. 9.

Trend of resistivity and water saturation for the WB well in A oilfield.

Acknowledgements

References