서 론
학습자료 구축과 인공 신경망 구조
동해 탄성파 자료취득
인공 신경망 구조
학습자료 구축
수치 예제
학습 수행
학습 모델 적용: 인공 합성 자료
학습 모델 적용: 현장 자료
토의 및 결론
서 론
탄성파 탐사는 지하 지층 구조 및 매질의 물성정보를 얻기 위해서 사용되는 지구물리학적 방법 중 하나로 석유 및 가스 탐사, 단층분포 파악, 지각구조 연구, 지반조사 등에 널리 활용된다. 탄성파 탐사를 통해 지하의 정보를 취득하기 위한 과정은 크게 자료취득, 자료처리, 자료해석의 단계로 나눌 수 있다(Yilmaz, 2001). 자료취득 단계는 탄성파 송신원과 수신기를 이용하여 반사파, 굴절파 등 지층에서 발생하는 다양한 종류의 탄성파를 취득하는 단계로 탐사설계와 탐사수행으로 이루어진다. 높은 품질의 탄성파 자료를 취득하기 위해서는 탐사목적에 맞는 탐사설계가 필수적이며 이때 탐사 장비 및 탐사 환경도 반드시 고려되어야 한다. 탐사수행 단계에서는 적절한 지층 탄성파 자료가 취득될 수 있도록 장비를 운용해야 하며 특히 탄성파 자료의 신호 대 잡음비를 높이기 위해 탐사 과정 중 발생할 수 있는 다양한 잡음 요인들을 고려하여야 한다. 자료처리 단계는 취득된 탄성파 자료로부터 지층 탄성파단면 또는 물성 값을 도출하는 과정이며 전통적인 자료처리는 주로 시간영역에서 중합 후 구조보정 단면을 도출하는 것을 가리킨다. 자료처리는 취득한 자료를 사전 가공하는 전처리 단계, 다양한 무작위 잡음 또는 일관성 잡음을 제거하는 잡음 억제 단계, 지하 매질의 속도정보를 도출하는 속도분석 단계, 속도정보를 바탕으로 반사면 보정을 수행하고 중합단면을 도출하는 중합 단계, 중합 단면에서 반사면의 위치를 보정해주는 구조보정 단계 등으로 나눌 수 있다(Dondurur, 2018). 자료해석 단계는 도출된 탄성파 단면뿐만 아니라 다른 지구물리학적 및 지질학적 자료를 함께 활용하여 지층의 구조, 발달과정, 암상 등의 정보를 얻는 과정이다.
위 과정들 중 잡음 억제는 탄성파 자료의 품질에 큰 영향을 주는 요인 중 하나이므로 주의 깊게 설계되고 수행되어야 한다. 탄성파 자료에 기록되는 잡음은 선박 소음, 해류의 흐름이나 파도, 장비 운용 등으로 인해 발생한 무작위 잡음과 다중 반사파(multiple), 공기파(air wave), 표면파(surface wave) 등과 같은 일관성 잡음이 있다(Ebadi, 2017; Hlebnikov et al., 2021). 탄성파 탐사를 수행하는 과정에서 잡음이 발생하는 요인을 완전히 억제하는 것은 매우 어렵고 탐사환경에 따라 상이하기 때문에 탄성파 자료마다 서로 다른 잡음특성을 가지고 있다(Kragh and Christie 2002; Nasser et al., 2016; Waage et al., 2019). 따라서 탄성파 자료에서 잡음을 적절히 억제하기 위해서는 자료 특성에 맞는 잡음 억제 절차를 설계해야 한다. 탄성파 자료의 잡음 억제는 일반적으로 잡음의 종류 및 특성에 따라 여러 절차를 통해 수행되며 널리 사용되는 방법으로는 대역 필터, f-k 필터, f-x 디콘볼루션, 라돈 변환, 예측 디콘볼루션 등이 있다. 각각 절차의 세부 설정 변수들은 경험적으로 또는 자료특성에 따라 많은 시행착오를 통해 결정되기 때문에 탄성파 자료의 잡음 억제는 많은 노력과 시간이 필요한 과정이다.
최근 기계학습 알고리즘의 발달과 계산자원의 발전으로 인해 탄성파 탐사 분야에 기계학습을 적용하고자 하는 다양한 연구가 이루어지고 있으며, 그 중 탄성파 자료처리의 각 과정들을 기계학습으로 대체하고자 하는 연구가 활발히 수행되고 있다. 특히 탄성파 자료에 기록된 여러 형태의 잡음을 효과적으로 제거하기 위해 기계학습을 적용하는 연구가 다수 수행되었다. 탄성파 자료에서 다중 반사파(Nam et al., 2020), 표면파(Li et al., 2018; Si, 2020), 선형 잡음(Zheng et al., 2020)과 같은 일관성 잡음 억제에 기계학습이 활용되었으며 기존의 잡음 제거 방법들에 비해 효과적으로 잡음을 억제하였다. 무작위 잡음 억제를 위해서도 다양한 기계학습 모델들이 적용되었으며 중합 전(Si and Yuan, 2018; Kim et al., 2019; Zheng et al., 2020), 중합 후(Liu et al., 2018; Jun et al., 2020) 탄성파 자료 등에 존재하는 무작위 잡음을 성공적으로 억제하였다. 학습자료의 구축은 기계학습에서 가장 중요한 부분 중 하나이며 특히 학습자료의 양 뿐만 아니라 품질도 고려되어야 한다. 지도학습을 이용한 탄성파 자료 잡음 억제를 위해서는 학습자료에 포함된 탄성파 잡음의 특성과 잡음을 제거하고자 하는 탄성파 자료의 잡음 특성이 유사해야 한다. 만약 학습자료의 특성이 대상 자료의 특성과 유사하다면 학습자료를 통해 학습된 기계학습 모델이 대상 자료에 잘 적용될 수 있을 것이다. 하지만 학습자료의 특성이 대상 자료의 특성과 크게 다르다면 학습된 모델이 대상 자료에 적용되었을 때 올바른 결과를 도출하기 어렵다. 따라서 적절한 학습자료의 구축은 기계학습에서 가장 중요한 요소 중 하나이다. 잡음 제거를 위한 지도학습의 경우 학습자료 구축을 위해 기 취득 탄성파 자료의 처리 결과로부터 잡음을 얻거나(Li et al., 2018; Zhao et al., 2019; Liu et al., 2018; Jun et al., 2020) 인공적으로 생성한 잡음(Kim et al., 2019; Zheng et al., 2019) 을 활용하는 경우가 대부분이다. 하지만 기 취득 탄성파 자료의 탐사환경이 대상 자료의 탐사환경과 다르다면 잡음의 특성 또한 서로 다를 수 있다. 또한 인공적으로 생성한 잡음을 통해 학습된 모델의 경우 현장 탄성파 자료에 대한 적용성에 한계가 있을 수 있다. 따라서 대상 탄성파 자료에 포함된 잡음의 특성과 유사한 잡음 자료를 이용하여 학습자료를 구축하는 것이 필수적이다. 본 연구에서는 대상 탄성파 자료의 잡음과 유사한 특성의 잡음 자료를 얻기 위해 현장 탄성파 자료취득을 위한 탐사측선 진입 전 송신원 발파 없이 수신기에 수신되는 배경 잡음만을 기록하여 학습자료로 활용하였다.
본 논문에서는 우선 현장 탄성파 자료 및 잡음 자료의 취득 과정을 간단히 언급하고 본 연구에 사용한 기계학습 모델에 대해 설명한다. 그리고 취득된 현장 잡음 자료를 이용한 학습자료 구축 방법과 모델 학습에 대해 설명한다. 학습된 기계학습 모델을 인공 합성 자료 및 현장 탄성파 탐사 자료에 적용한 수치 예제를 통해 제안된 방법의 타당성을 검증한다. 마지막으로 토의 및 결론에서 제안된 방법의 특성에 대해 논의한다.
학습자료 구축과 인공 신경망 구조
동해 탄성파 자료취득
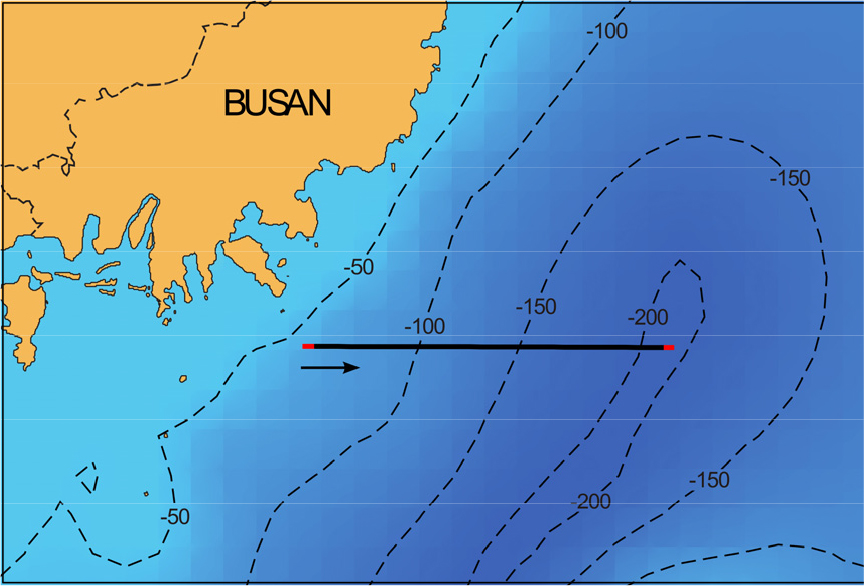
본 연구는 동해에서 취득한 스파커(sparker) 송신원 탄성파 탐사 자료의 잡음 제거를 목적으로 한다. 해당 자료는 SIG Pulse L5 장비를 활용하여 취득되었으며 5,000 J의 송신원 에너지, 5초의 발파 간격이 사용되어 총 2,274개의 공통 송신원 모음(common shot gather) 을 취득하였다. 수신기의 개수는 24개, 수신기 간격은 6.25 m, 기록 시간은 1초, 샘플링 간격은 0.25 ms이다. 선박의 이동 속도는 약 5 kn 였다. 탐사 지역과 측선은 Fig. 1에 도시되어 있다.
본 연구의 목표는 탄성파 탐사 자료취득 시 탐사환경에 의해 발생하는 무작위 잡음을 제거하는 것이다. 만약 목표지역 탄성파 자료에 포함된 무작위 잡음과 유사한 특성을 가진 잡음 자료를 취득할 수 있다면, 기계학습을 통해 목표지역 탄성파 자료의 무작위 잡음을 성공적으로 제거할 수 있을 것이다. 따라서 우리는 탄성파 탐사 측선 1 km 전과 후에 송신원 발파 없이 수신기에 수신되는 신호를 기록하여 잡음만 포함된 탄성파 자료(noise gather)를 총 638개 취득하였다. 잡음만 존재하는 자료와 목표지역에서 취득한 탄성파 자료는 동일한 탐사 환경에서 취득한 자료이므로 서로 유사한 잡음 특성을 가지고 있다고 간주할 수 있다.
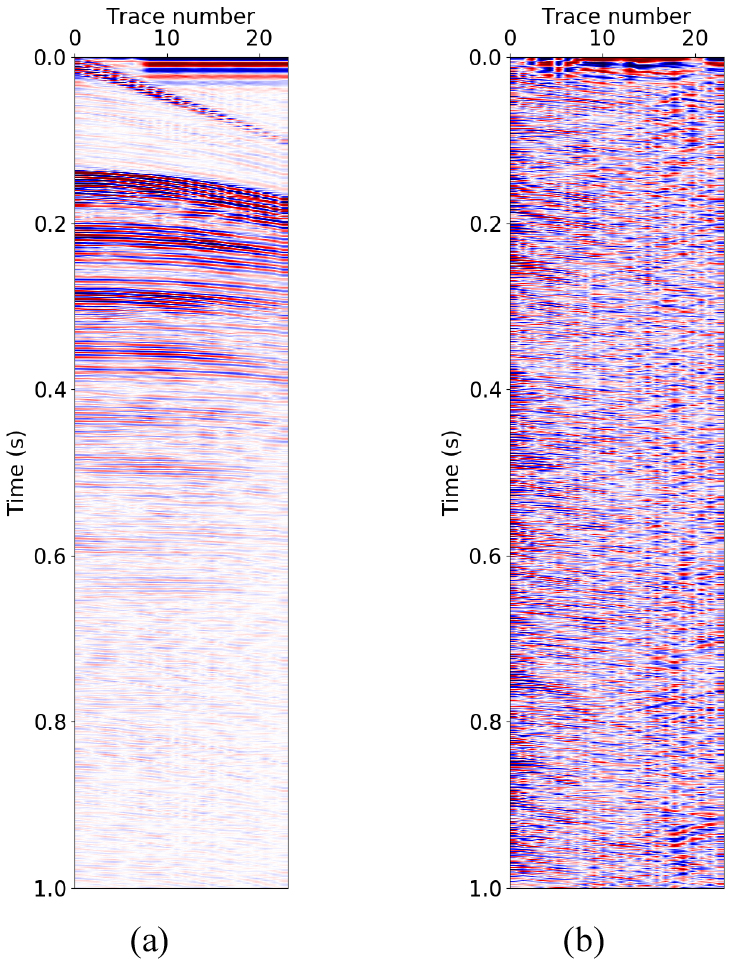
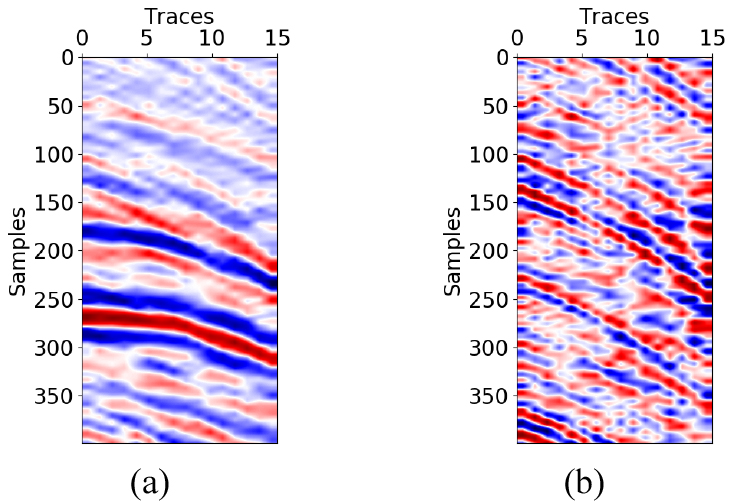
Fig. 1에 검은색 실선은 탐사 대상지역의 측선을 나타내고 빨간색 실선은 잡음 자료를 취득한 위치를 나타낸다. Fig. 2는 취득한 탄성파 자료와 잡음 자료에서 50-80-400- 500 Hz의 통과 대역(passband) 을 가지는 사다리꼴 형태의 대역 필터를 통해 저주파수 및 고주파수 잡음을 제거한 결과이다. 탄성파 탐사 측선에서 취득한 자료(Fig. 2(a))는 지층 반사파와 잡음이 모두 포함되어 있으며 약 0.28초에 나타나는 다중 반사파와 같은 일관성 잡음뿐만 아니라 자료 전체적으로 포함되어 있는 무작위 잡음도 관찰할 수 있다. 또한 0.0 ~ 0.02초에는 스파커 송신원 발파와 관련된 일관성 있는 전기잡음이 기록되어 있다. 하지만 이 잡음은 송신원 발파와 동시에 기록되며 반사파가 기록되기 전에 나타나는 일관성 잡음이므로 이번 연구에서 제거하고자 하는 대상이 아니다. 잡음 자료(Fig. 2(b))의 경우 무작위 잡음이 기록되어 있으나 송신원 발파와 관련 있는 일관성 잡음은 포함되어 있지 않은 것을 확인할 수 있다.
인공 신경망 구조
기계학습에서는 인공 신경망을 구성하고 원하는 결과를 도출하기 위해서 인공 신경망의 가중치들을 학습시킨다. 탄성파 자료의 다양한 잡음 제거를 위해서 사용된 인공 신경망 모델은 오토인코더 기반 모델(Saad and Chen, 2020), 잔차 신경망 기반 모델(Kim et al., 2019; Jun et al., 2020), 적대적 생성 신경망 기반 모델(Alwon, 2018; Kaur et al., 2019; Si, 2020) 등이 대표적이다. 본 연구에서는 잡음만 존재하는 자료를 취득하였기 때문에 잡음을 포함한 탄성파 자료에서 자료의 변화를 최소화 하면서 잡음을 예측하는 모델인 잔차 신경망(He et al., 2016) 기반 denoising convolutional neural network(DnCNN) 모델(Zhang et al., 2017)을 활용하였다.
잡음이 포함된 탄성파 자료 (c)는 잡음이 없는 탄성파 자료 (s)와 잡음 자료 (n)의 합으로 구성되어 있으며 식 (1)과 같이 표현할 수 있다.
DnCNN은 잡음이 포함된 탄성파 자료로부터 잡음을 예측하는 모델이므로 손실함수 (L)는 식 (2)와 같이 나타낼 수 있다.
N은 학습자료의 수, M(c;e)은 탄성파 자료 (c)로부터 잡음 (e)을 예측하는 DnCNN 모델, 는 오차 제곱 합 (sum of squared error) 이다. 즉, 모델 M을 통해 잡음이 포함된 탄성파 자료 c에서 잡음 e를 예측하고, 잡음이 포함된 탄성파 자료 c와 잡음이 없는 탄성파 자료 s간의 차이를 통해 실제 잡음 n을 구한 후, 예측된 잡음 e와 실제 잡음 n과의 차이를 줄이는 방향으로 모델 M을 학습한다.
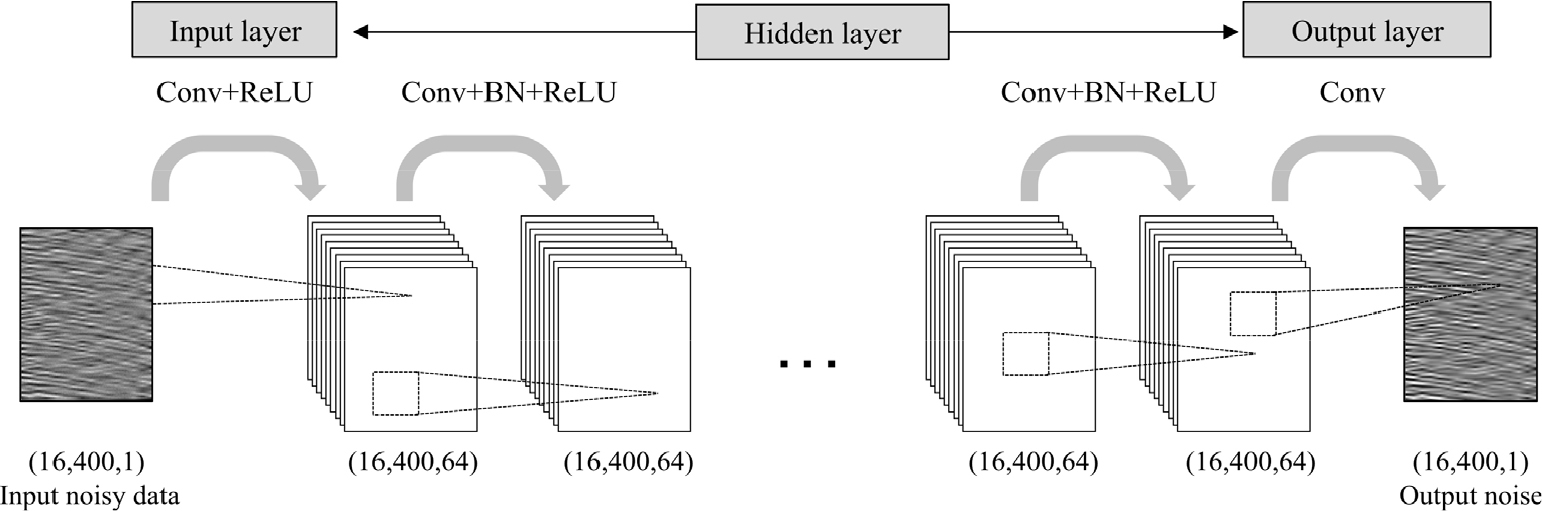
DnCNN 모델의 구조는 Jun et al.(2020)과 유사하게 구성되었으며 세부 사항들은 다음과 같다. DnCNN은 일반적인 인코더-디코더 구조의 합성곱 신경망과는 다르게 자료의 압축과 팽창 과정이 없기 때문에 모든 층(layer)에서 입력 자료의 크기와 출력 자료의 크기가 변하지 않는다. 입력 층(input layer)과 출력 층(output layer)의 크기는 학습자료 패치 크기에 따라 결정된다. 본 연구에서 입력 층과 출력 층의 크기는 (16,400,1)이며 모든 은닉 층(hidden layer)의 크기는 (16,400,64)로 동일하다. 학습자료 구축에 대해서는 다음 절에서 다룰 예정이다. 합성곱 연산의 크기는 3 × 3 이며 각 층 입력 자료 모든 변에 0값을 추가해주어(zero padding) 합성곱 입력 자료와 출력 자료의 크기를 동일하게 유지시켰다. 합성곱 연산 결과 값의 분포는 배치 정규화(batch normalization) (Ioffe and Szegedy, 2015)를 이용하여 조절되었으며 ReLU(Rectified Linear Units) (Krizhevsky et al., 2012) 활성함수를 통해 비선형성을 추가하였다. Fig. 3은 본 연구에 사용한 DnCNN 구조의 모식도이다.
학습자료 구축
지도학습을 통해 모델을 학습하고 잡음을 제거하고자 한다면 잡음 제거 대상 탄성파 자료에 포함된 잡음과 유사한 성질을 가지는 잡음을 이용하여 학습자료를 구축하는 것이 필수적이다. 본 연구에서는 대상 탄성파 자료의 잡음과 유사한 특성의 잡음 자료를 얻기 위해 탐사측선 진입 전 및 종료 후 잡음 자료를 취득하였다.
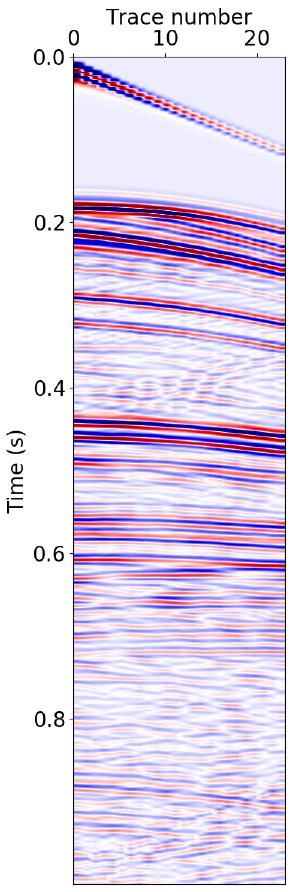
본 연구에 사용한 인공 신경망인 DnCNN은 잡음이 포함된 자료에서 잡음을 추출하는 기계학습 방법이다. 따라서 취득한 잡음을 잡음이 없는 자료에 더함으로써 학습자료를 구축할 수 있다. Jun et al.(2020)의 연구에서 잡음이 없는 인공 합성 탄성파 자료에 현장 자료의 잡음을 더하여 학습을 수행한 경우 잡음이 성공적으로 억제되었다. 따라서 본 연구에서도 잡음이 없는 자료로 시간 영역 파동 전파 모델링을 통해 생성한 인공 합성 탄성파 공통 송신원 모음을 사용하였으며, 이때 지하 매질 속도는 Marmousi-2 속도 구조를 사용하였다. Fig. 4는 파동 전파 모델링을 통해 생성한 인공 합성 공통 송신원 모음이다. 동해 탄성파 탐사 자료와 유사한 수신기 배열을 가지도록 24개의 수신기를 6.25 m 간격으로 배열하고 총 1초 동안 0.25 ms 간격으로 모델링하여 총 315개의 공통 송신원 모음을 생성하였다. 생성된 공통 송신원 모음을 6:2:2의 비율로 나누어 189개는 학습자료, 63개는 검증자료, 63개는 실험자료를 구축하여 활용하였다. 또한 현장 탄성파 탐사를 통해 얻은 638개의 잡음 자료 중 126개를 무작위로 선택하여 63개는 검증자료, 나머지 63개는 실험자료 구축에 활용하였고 남은 512개의 잡음자료 중 189개를 매 이포크(epoch)마다 무작위로 선택하여 학습자료 구축에 활용하였다. 생성한 인공 합성 자료와 취득한 잡음 자료에서 강한 진폭을 가지는 값들이 학습에 큰 영향을 미치는 현상을 줄이기 위해 상위 및 하위 1 퍼센트에 해당하는 진폭 값을 최대 및 최솟값으로 가지도록 보정해주었고 각 공통 송신원 모음을 각각의 최댓값으로 정규화시켰다. 진폭이 보정된 공통 송신원 모음 각각의 크기는 (nx,nt) = (24,4000) 이며, 학습자료 패치 생성을 위해 각 공통 송신원 모음을 (16,400) 크기로 분할하였다. 이때 x 방향으로는 4개, t 방향으로는 20개 샘플씩 이동하며 패치를 생성하였다. 현장 탄성파 탐사를 통해 취득한 잡음 자료도 동일한 과정을 통해 (16,400) 크기의 패치로 나누었으며 인공 합성 자료 패치와 잡음 자료 패치들을 특정 범위의 진폭 비율로 더하여 학습자료를 구축하였다. 본 연구에서는 keras의 fit_generator 함수 (Keras, 2021)를 사용하여 매 이포크마다 102,528개의 학습자료 패치를 새롭게 생성하였으며 검증자료는 미리 생성해놓은 34,209개의 패치를 활용하였다. fit_generator 함수는 매 이포크마다 필요한 만큼 학습자료를 생성하여 학습하기 때문에 대용량의 데이터를 효율적으로 학습할 수 있다는 장점이 있다. 또한 학습자료를 생성 시 무작위성을 추가할 수 있어 매 이포크 마다 다른 특성을 포함하는 학습자료를 사용할 수 있다는 것 또한 장점이다.
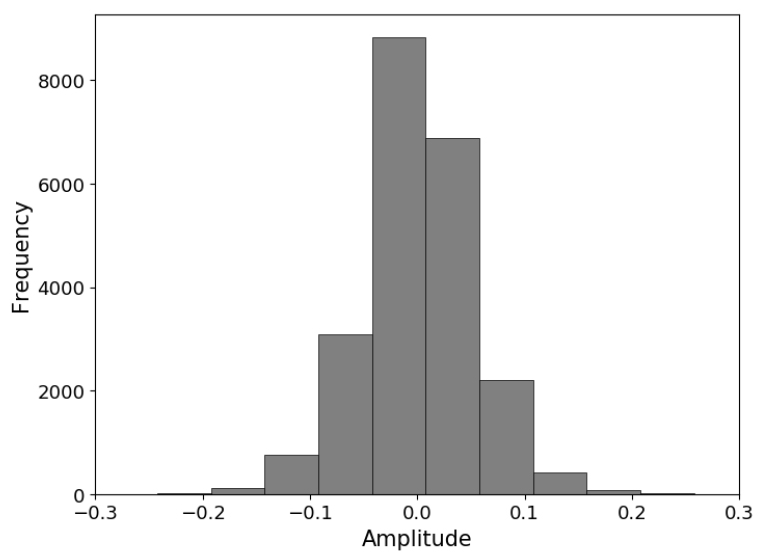
학습자료 구축 시 적용한 인공 합성 자료와 잡음 자료의 진폭 비율에 따라 학습자료의 신호 대 잡음비(signal to noise ratio)가 달라진다. 따라서 대상 자료의 특성을 통해 대략적인 진폭 비율의 범위를 설정하는 것이 필요하다. 현장 탄성파 탐사를 통해 취득한 공통 송신원 모음(Fig. 2(a))에서 수층에 해당하는 부분은 의미있는 탄성파 신호가 기록되지 않기 때문에 잡음만 존재하는 것을 확인할 수 있다. 그리고 무작위 잡음의 특성은 공통 송신원 모음에서 시간에 따라 크게 변하지 않고 전체에 걸쳐 비교적 일관되게 나타난다고 가정할 수 있다. 따라서 우리는 잡음의 진폭 값 분포를 파악하기 위해 현장 탄성파 공통 송신원 모음 중 20개를 무작위로 선택하고 각각의 최댓값으로 정규화한 후 수층 잡음의 진폭 분포를 계산하여 Fig. 5에 히스토그램으로 나타내었다. 매우 작은 빈도수를 가지는 특이 값들을 제외하면 잡음의 진폭은 –0.2 ~ 0.2의 분포를 가진다. 따라서 각 학습자료 패치를 생성하기 위한 인공 합성 자료 패치와 잡음 자료 패치의 진폭 비율은 0.99:0.01 ~ 0.8:0.2 사이 균일분포에서 무작위로 선택되었다. Fig. 6는 구축된 학습자료 예시이다.
수치 예제
학습 수행
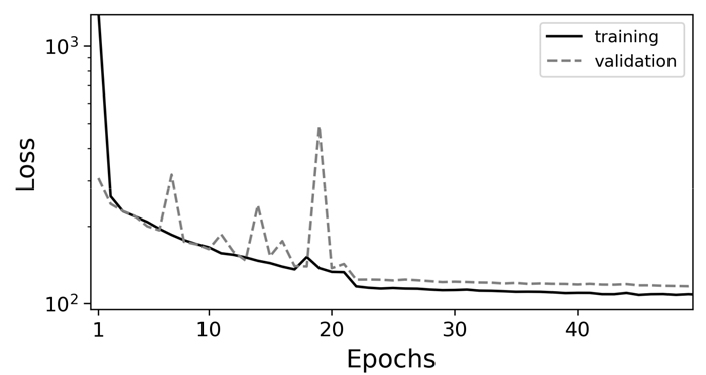
본 연구에서는 GPU 기반의 Keras 패키지로 학습을 수행하였고 백엔드로 Tensorflow를 사용하였다. 매 이포크마다 102,528개의 학습자료 패치를 새롭게 생성하여 학습을 수행하였고, 미리 생성해놓은 34,209개의 검증자료 패치를 이용하여 검증 오차를 계산하였다. 학습의 배치 크기는 128 이고 학습오차가 충분히 작아져서 수렴했다고 판단될 때까지 학습을 진행하였으며, 그 중 가장 낮은 검증 오차를 가진 모델을 최종 모델로 선정하였다. 학습은 NVIDIA GTX 1080 Ti GPU 1개를 사용하였으며 학습자료 생성 시간을 포함하여 1 번의 이포크에 평균 480초가 소요되었다. Fig. 7은 학습 및 검증 오차를 도시한 그래프이다. 가장 낮은 검증 오차를 보이는 모델이 49 번째 모델이므로 49 번째 모델을 최종 모델로 선정하였다.
학습 모델 적용: 인공 합성 자료
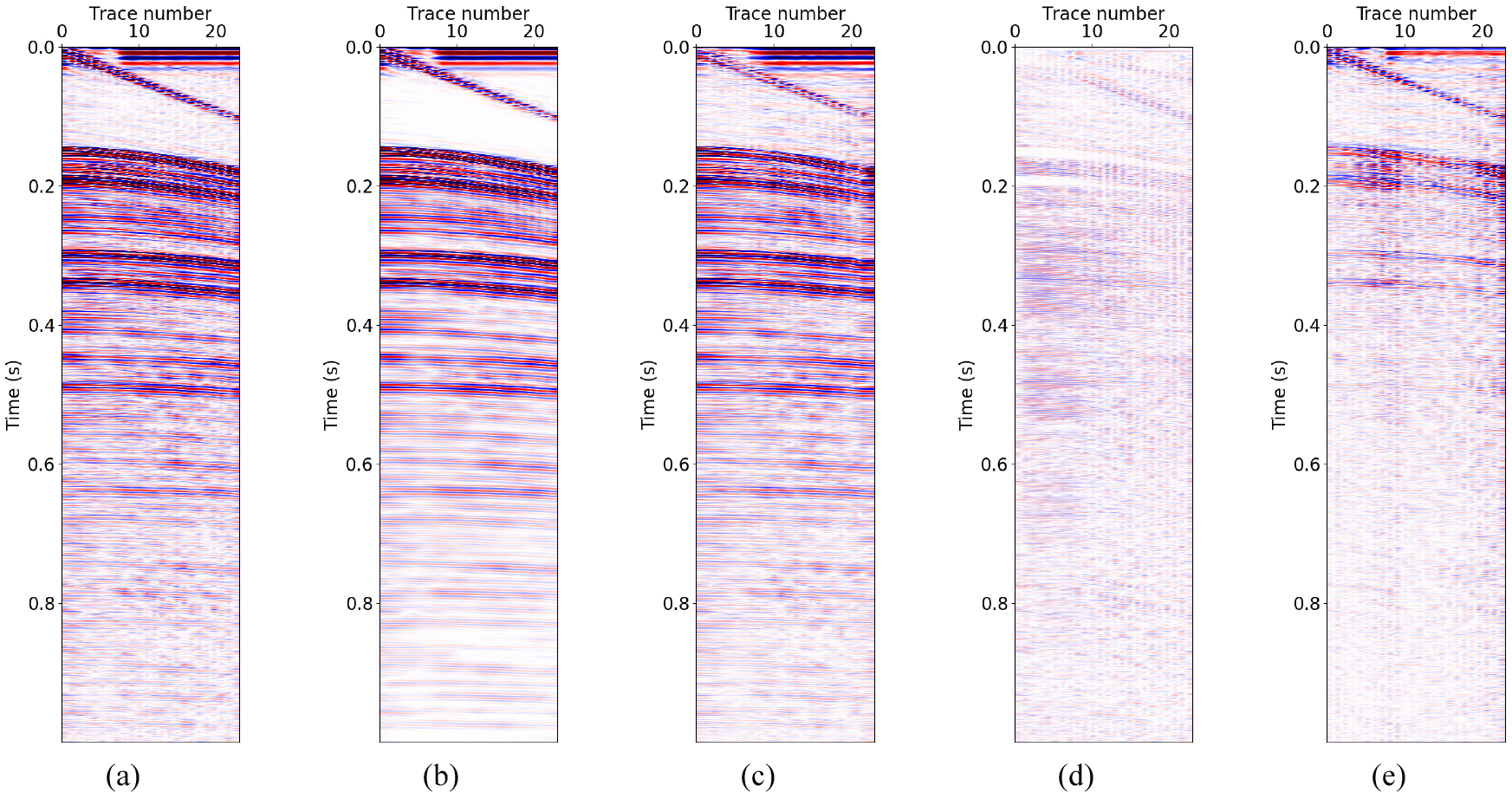
학습된 모델의 유효성을 확인하기 위해 학습 및 검증에 사용되지 않은 63개의 인공 합성 공통 송신원 모음에 현장 자료에서 취득한 잡음자료 중 학습 및 검증에 사용하지 않은 63개를 각각 더하여 실험 자료를 생성하고 학습된 모델을 적용하였다. 학습 모델 적용 과정에서는 각각의 공통 송신원 모음 전체에 대해 잡음 제거를 수행하였으며 적용 결과를 Fig. 8에 도시하였다. Fig. 8(a)는 실험에 사용한 인공 합성 자료의 공통 송신원 모음 예시이다. 무작위 잡음으로 인해 반사파 신호가 오염된 것을 확인할 수 있다. Fig. 8(b)는 잡음이 전혀 포함되어 있지 않은 원본 인공 합성 공통 송신원 모음이고 Fig. 8(c)는 DnCNN 모델 적용을 통해 잡음이 제거된 공통 송신원 모음이다. 잡음이 성공적으로 억제되어 잡음을 더하기 전 공통 송신원 모음(Fig. 8(b)) 과 DnCNN을 이용하여 잡음을 억제한 공통 송신원 모음(Fig. 8(c)) 이 서로 매우 유사한 것을 확인할 수 있다. Fig. 8(d)에 도시되어 있는 잡음은 현장 탄성파 탐사에서 취득한 잡음 자료로 기계학습을 통해 예측해야 하는 참 값(ground truth) 이며 Fig. 8(e)는 DnCNN 모델을 통해 예측한 잡음이다. 학습된 DnCNN 모델이 예측한 잡음과 실제 잡음이 일부분을 제외하고는 서로 잘 일치함을 볼 수 있다. 또한 실제 잡음과 예측한 잡음의 차이를 계산하여 Fig. 8(f)에 도시하였다. 두 잡음 간 차이가 전혀 없는 것은 아니지만 실제 잡음에서 나타나는 강한 잡음들은 대부분 잘 예측되었기 때문에 Fig. 8(f)에는 약한 진폭을 가지는 잡음들만 일부 남아있는 것을 확인할 수 있다.
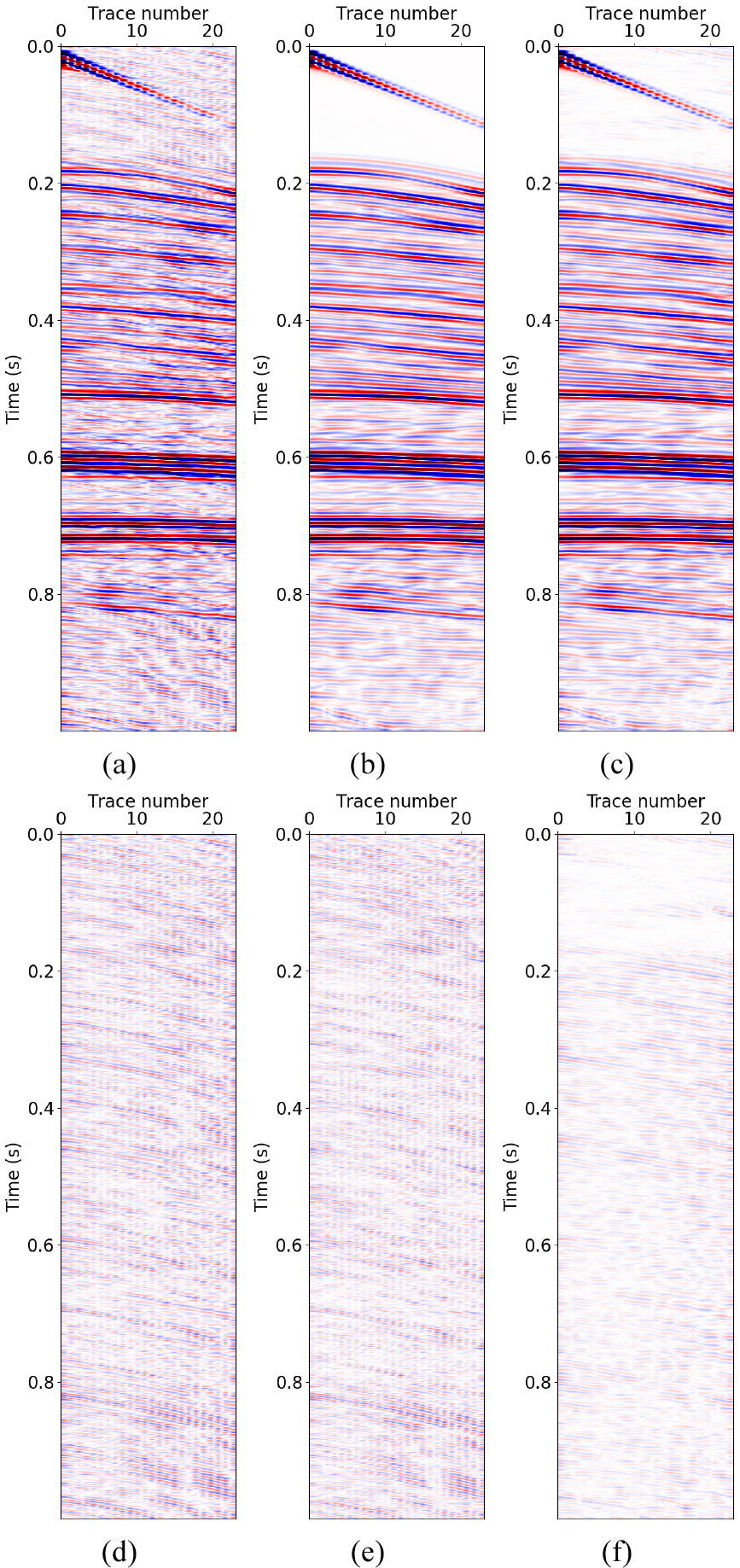
Fig. 8
Result of synthetic data test. (a) noise-added test data, (b) noise-free synthetic data (reference), (c) noise-attenuated data after the application of the trained DnCNN model, (d) true noise, which is the ground truth, and (e) estimated noise using DnCNN, (f) difference between true noise (d) and estimated noise (e).
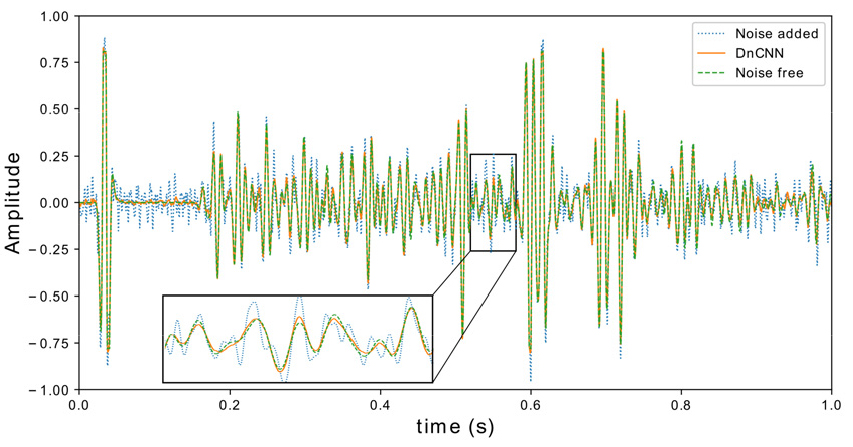
잡음 제거의 전후를 더 정확히 비교해보기 위해 잡음 제거 전후의 공통 송신원 모음(Fig. 8(a), (c)) 중 5번째 수신기의 시간 기록을 추출하고 비교해보았다. Fig. 9는 트레이스 비교 결과이며 잡음이 추가되기 전의 원본 인공 합성 자료의 트레이스(Fig. 8(b)) 또한 추출하여 함께 도시하였다. 잡음 제거 전의 트레이스는 잡음의 영향으로 원본 자료의 트레이스와 차이가 있음을 확인할 수 있으나, 기계학습을 통해 잡음을 제거한 트레이스의 경우 원본 자료의 트레이스와 유사함을 확인할 수 있다.
결과를 수치적으로 검증하기 위해 이미지처리 분야에서 널리 사용되는 최대 신호 대 잡음비(Peak Signal to Noise Ratio; PSNR)와 구조 유사도(Structural Similarity Index Measurement; SSIM)를 (Hore and Ziou, 2010) 계산하여 Table 1에 나타내었다. 높은 PSNR 값은 신호 대 잡음비가 좋음을 의미하고 높은 SSIM 값은 원본 자료와 구조적으로 유사함을 의미한다. 잡음 제거 전 PSNR은 36.57 dB, SSIM은 0.84 인데 잡음 제거 후 PSNR은 42.89 dB로 증가, SSIM은 0.95로 증가하였다. 위 검증 결과를 통해 우리는 제안된 학습자료 구축 방법을 통해 학습된 DnCNN 모델이 탄성파 자료의 잡음을 효과적으로 제거할 수 있음을 확인하였다.
Table 1.
Average PSNR and SSIM of the test data before and after applying DnCNN.
| Before | After | |
| PSNR | 36.57 | 42.89 |
| SSIM | 0.84 | 0.95 |
학습 모델 적용: 현장 자료
현장 자료 적용성을 확인하기 위해 인공 합성 공통 송신원 모음과 현장 잡음 자료를 이용하여 학습된 DnCNN 모델을 동해 스파커 탄성파 자료에 적용하여 무작위 잡음을 억제하였다(Fig. 10). 또한 결과 비교를 위해 무작위 잡음 억제에 널리 사용되는 f-x 디콘볼루션으로 잡음을 억제하여 Fig. 10에 함께 도시하였다. Fig. 10(a)는 잡음 억제 전의 현장 탄성파 공통 송신원 모음이고, Fig. 10(b)와 (d)는 각각 학습된 DnCNN 모델을 이용하여 잡음을 억제한 공통 송신원 모음과 예측된 잡음이다. Fig. 10(c)와 (e)는 각각 f-x 디콘볼루션을 적용하여 잡음을 억제한 공통 송신원 모음과 제거된 잡음이다. f-x 디콘볼루션에 사용한 변수는 50 ~ 500 Hz의 주파수 범위, 윈도우 크기 10개 트레이스, 필터 크기 4개 트레이스이다. Fig. 10(b)는 무작위 잡음이 성공적으로 억제되어 반사파가 명확히 드러난 것을 확인할 수 있으나 Fig. 10(c)의 경우 일부 잡음이 억제되었지만 여전히 잡음이 상당부분 제거되지 않고 남은 것을 볼 수 있다. 또한 DnCNN을 통해 예측된 잡음인 Fig. 10(d)는 반사파 성분은 거의 존재하지 않으며 무작위 잡음만 성공적으로 예측된 반면, Fig. 10(e)는 무작위 잡음과 함께 강한 반사파 신호도 함께 존재하므로 f-x 디콘볼루션이 잡음과 반사파를 성공적으로 분리하지 못했음을 확인할 수 있다.
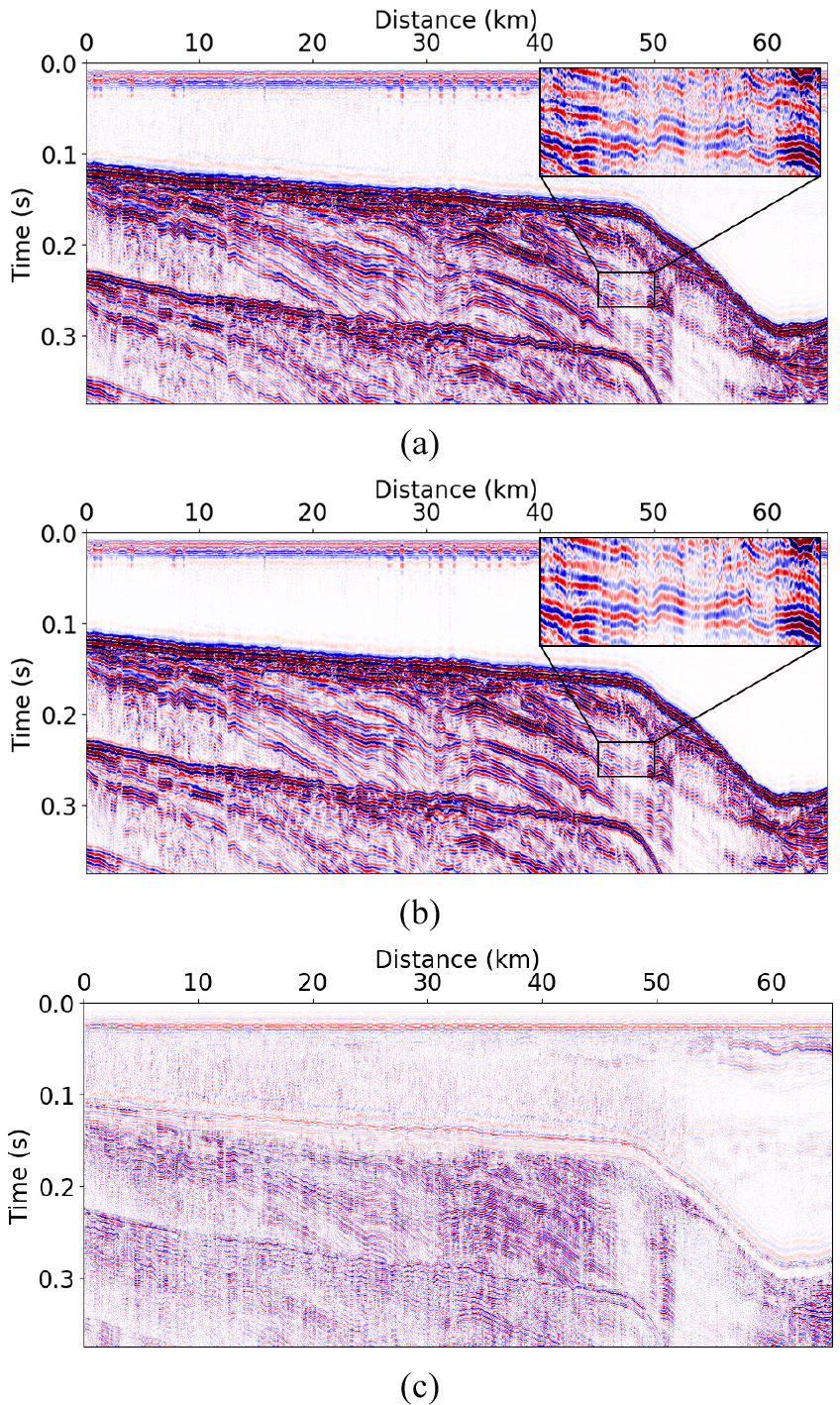
잡음 억제 효과를 확인하기 위해 잡음 억제 전과 후의 자료에 대해 기본적인 자료처리를 수행하고 중합 단면을 생성하여 비교하였다(Fig. 11). 중합 단면은 0.375초까지 도시되었으며 잡음 억제 전 중합 단면에 존재하던 무작위 잡음이 상당부분 억제되어서 반사면들이 상대적으로 명확해졌다. 잡음 억제 전후의 차이(Fig. 11(c))를 보면 해저면과 주요 지층 반사면에서 변형이 발생하지 않고 무작위 잡음이 성공적으로 억제되었음을 확인할 수 있다. Fig. 11(a)와 (b) 오른쪽 상단 사각형은 확대된 단면이며, 잡음 억제 전에는 반사면들이 잡음에 의해 오염되어 있지만 잡음 억제 후에는 반사면들의 연속성이 더 향상되었음을 볼 수 있다. 하지만 스파커 자료의 특성상 400 Hz 이상의 고주파수 성분도 탄성파 자료에 기록되는데 일부 반사면의 고주파수 성분 또한 잡음 억제 과정에서 함께 제거되었다. Fig. 11(c)의 거리 약 30 ~ 45 km 시간 약 0.15 ~ 0.25 s 사이에 일부 반사면의 고주파 성분이 포함되어있다. 중합 단면에서의 잡음 제거 효과는 중합 전 공통 송신원 모음에서의 잡음 제거 효과만큼 두드러지지는 않는다. 공통 중간점 모음을 중합하는 과정에서 중합수에 따라 신호 대 잡음비가 향상되는데, 본 자료의 경우 중합수가 약 6이므로 중합을 통해 의 신호 대 잡음비 향상 효과가 있다. 따라서 중합 단면에서의 잡음 제거 효과가 공통 송신원 모음에서의 잡음 제거 효과에 비해 상대적으로 적게 나타난다.
토의 및 결론
본 연구에서는 탄성파 무작위 잡음 억제를 위해 기계학습을 적용하였으며 학습자료 구축을 위해 현장 탄성파 탐사 도중 송신원 발파 없이 수신기 기록만 수행하여 잡음 자료를 취득하였다. 취득된 잡음 자료와 잡음이 없는 인공 합성 자료를 조합하여 학습자료를 구축하였으며, 기계학습 모델로는 잔차 학습을 통해 잡음을 추출하는 DnCNN 방법을 이용하였다. 구축된 학습자료로 DnCNN 모델 학습을 수행하였고 학습결과를 인공 합성 자료 및 현장 자료에 적용하여 무작위 잡음을 억제하였다.
제안된 방법의 장점은 크게 두 가지로 요약할 수 있다. 첫 번째는 학습자료 구축을 위해 추가적인 자료처리를 통해 잡음을 추출하거나 인위적인 잡음을 생성하는 과정이 필요 없다는 점이다. 탄성파 자료취득 과정에서 측선을 추가하여 송신원 발파 없이 잡음을 취득하면 되기 때문에 간단히 잡음 자료를 취득할 수 있다. 일반적으로 2차원 또는 3차원 탐사에서는 수십 ~ 수백 km의 측선을 탐사하기 때문에 1 km 내외의 측선을 추가한다면 5.5 knots의 선속으로 약 6 분의 시간이 필요하므로 가시적인 탐사 시간 또는 비용의 상승을 야기하지 않는다. 본 연구에서는 약 1 km 길이의 측선을 탄성파 자료취득 측선 양쪽에 추가하여 잡음을 취득하였다. 또한 하나의 측선을 종료하고 인근에 위치한 다음 측선으로 이동하는 과정에서는 장비회수를 하지 않는 것이 일반적이므로 이동 중 잡음을 기록한다면 추가적인 비용 상승이 전혀 없다. 두 번째는 잡음 억제 대상 현장 탄성파 자료에 포함된 잡음과 유사한 특성을 가지는 잡음 자료를 이용하여 학습자료를 구축할 수 있다는 점이다. 잡음 자료는 측선 시작 직전 또는 종료 직후에 취득된다. 따라서 탄성파 탐사 자료를 취득할 때와 유사한 해류, 파고, 바람, 선박 운항 조건, 수신기 상태 등에서 무작위 잡음을 취득할 수 있으므로 잡음 억제 대상 탄성파 탐사 자료에 포함된 무작위 잡음과 취득된 잡음 자료의 특성은 거의 동일하다.
하지만 해당 방법에도 몇 가지 한계가 존재한다. 우선 탄성파 자료취득 도중 발생하는 돌발적인 변수나 갑작스러운 주변 환경의 변화로 인해 발생하는 잡음을 대상으로는 해당 방법을 적용하기 어려울 수 있다. 예를 들어 탐사 도중 수신기에 근접하여 이동하는 선박이 있을 경우 강한 프로펠러 잡음이 시간에 따라 변하면서 기록되지만 잡음 취득 과정에서 해당 사건이 동일하게 발생하지 않는다면 해당 사건으로 인해 발생한 잡음은 억제하기 어려울 것이다. 두 번째로는 송신원 발파와 관련된 일관성 잡음에 대해서는 적용이 불가능하다는 점이다. 예를 들어 다중 반사파나 송신원 버블로 인한 일관성 잡음은 취득한 잡음 자료에 포함되지 않기 때문에 제안된 방법으로 억제가 불가능하다.
탄성파 탐사 자료처리에서 다양한 종류의 잡음을 효과적으로 억제하는 것은 매우 중요한 부분이다. 제안된 방법은 현장 탄성파 탐사를 수행하는 과정에서 매우 적은 시간과 비용을 통해 양질의 학습자료를 구축하고 현장 자료의 무작위 잡음 제거할 수 있다는 특징을 가지고 있다. 따라서 제안된 방법을 현장 탄성파 탐사에 활용한다면 무작위 잡음을 효과적으로 제거할 수 있으므로 탄성파 탐사 자료처리 과정의 효율성 제고 및 처리 결과 향상에 기여할 수 있을 것으로 기대한다.