Estimation of the Put Option Value for Solar Power Plant Operators Participating in the Renewable Portfolio Standard (RPS) Spot Market

Sangmin Cho

doi:10.32390/ksmer.2024.61.5.363

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 31 October 2024. 363-372
https://doi.org/10.32390/ksmer.2024.61.5.363

Estimation of the Put Option Value for Solar Power Plant Operators Participating in the Renewable Portfolio Standard (RPS) Spot Market

신재생에너지 공급의무화제도 현물 시장 참여 태양광 발전의 풋옵션 가치 추정

Sangmin Cho¹^*

조 상민¹^*

¹Korea Energy Economics Institute, Ulsan, Korea

¹에너지경제연구원

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this study, we employ a binomial lattice tree model to estimate the value of American put options granted to solar power plant operators under renewable portfolio standard schemes with different sub-markets. The analysis revealed that the value of these options is equivalent to approximately 7% of the total revenue, translating to an REC multiplier of approximately 0.15. PV operators do not pay a premium for the option to convert to fixed-price contracts in the spot market. This could mitigate the dual uncertainties of SMP and REC prices faced by spot market participants. However, this arrangement may disrupt optimal portfolio composition across sub-markets, with the cost of the option premium ultimately being passed on to electricity consumers. To address this issue, we propose charging market participants an appropriate premium for the option and eventually phasing out the spot market in favor of fixed-price contracts.

Keywords

RPS

solar power plant operator

spot market

fixed-price contract

american put option

본 논문은 신재생에너지 공급의무화제도(RPS) 하에서 태양광 발전사업자에게 부여된 아메리칸 풋옵션의 가치를 이항격자모형을 활용하여 추정하였다. 분석 결과 해당 옵션의 가치가 전체 수익의 7%에 달하는 것으로 나타났고 이는 신재생에너지인증서(REC) 가중치 기준 0.15에 해당하는 수준이다. 태양광 발전사업자는 현물 시장에서 고정가격계약으로 전환할 수 있는 해당 옵션에 대한 프리미엄을 지불하지 않는데 이는 현물 시장 참여자가 노출되는 계통한계가격(SMP)와 REC의 이중 불확실성 대응에 기여할 수 있다. 그러나 이는 세부 시장간 최적 포트폴리오 구성을 저해하고 옵션 프리미엄이 전기소비자에게 전가되는 문제가 있다. 문제해결을 위해 현물 시장 참여자로 하여금 풋옵션의 가치에 상응하는 프리미엄을 지불하게 하고 장기적으로 현물 시장을 일몰하고 고정가격계약으로 시장을 통합하는 방안을 제안한다.

키워드

신재생에너지 공급의무화제도

태양광 발전

현물 시장

고정가격계약

아메리칸 풋옵션

MAIN

서 론
본 론
선행연구
방법론
분석결과
결 론

서 론

한국은 2012년부터 수량 기반의 재생에너지 정책수단인 신재생에너지 공급의무화제도(이하 RPS 제도)를 운영하고 있다. 한국 정부는 공급의무사의 원활한 의무이행을 위해 다양한 세부 시장을 개설하고 여러형태의 조달방식을 허용하고 있다. 공급의무자가 태양광 발전사업자와 계약을 체결할 수 있는 시장은 현물 시장, 고정가격계약 시장, 자체계약 시장 등이 있다. 이 중 현물 시장의 경우 다른 시장, 혹은 조달방식을 통해 의무를 이행한 이후 부족한 부분을 메울 수 있는, 일종의 밸런싱 시장으로서의 기능을 기대하고 정부에 의해 개설되었다. 그러나 현재 현물 시장은 태양광 발전사업자들이 가장 선호하는 시장 중 하나로 부상하였고 비중 또한 RPS 이행 초기에 비해 높은 수준을 유지하고 있다. Table 1은 RPS 세부 시장별 거래 실적 추이를 보여준다(Cho, 2024).

Table 1.

Proportion of Transaction by RPS Sub-markets

	Self Construction	Spot Market	Bilateral Contract	Government REC	Sum.
2012	41.6%	4.4%	8.3%	45.7%	100.0%
2013	40.0%	7.0%	16.5%	36.5%	100.0%
2014	54.4%	7.6%	27.1%	10.9%	100.0%
2015	49.4%	16.0%	30.4%	4.3%	100.0%
2016	46.0%	15.3%	34.7%	4.0%	100.0%
2017	39.9%	15.5%	44.5%	0.2%	100.0%
2018	37.6%	25.0%	37.5%	-	100.0%
2019	33.1%	27.2%	39.7%	-	100.0%
2020	27.4%	23.4%	49.2%	-	100.0%
2021	25.2%	21.6%	53.2%	-	100.0%
2022	15.1%	17.9%	66.6%	-	100.0%

특히 최근들어 이러한 현물 시장에 대한 선호가 더욱 크게 증가하고 있다. 그 이유는 우선, 현물 시장에서의 기대 수익 즉, 전력시장 계통한계가격(이하 SMP)과 신재생에너지 인증서(이하 REC)의 합산가격이 고정가격계약 상한가에 비해 높기 때문이다. 그런데 우리가 주목해야할 또 다른 이유는 바로 현물 시장에 진입하는 태양광 발전사업자가 현물 시장의 단점이라고 할 수 있는 수익의 불확실성에 대응할 수 있는 수단, 즉 옵션을 보유하고 있기 때문이다.

좀 더 자세히 살펴보면 우선, 최근들어 RE100에 참여하는 기업들이 증가하면서 RPS 수요와 RE100 수요 경합으로 인해 재생에너지 수급의 불안정성이 증가하고 있다(Cho, 2024). 게다가 지자체의 이격거리 규제의 지속적인 강화(Chang and Cho, 2023)와 전력계통 수용성 하락 등의 제약요인의 부각으로 인한 공급 감소 등으로 수급 여건이 악화되면서(Kim et al., 2019) 현물 시장의 $S M P + R E C$ 합산가격이 크게 상승하였다. 이로 인해 SMP와 REC 가격 상승이 단기에 반영되는 현물 시장에 대한 선호가 증가하고 가격 상승 요인의 반영이 느리고 사실상의 상한 제약이 존재하는 고정가격계약 시장에 대한 선호는 반대로 감소하였다. Table 2에 고정가격계약 입찰 시행결과를 정리하였다(Korea New and Renewable Energy Center, 2024).

Table 2.

Results of Fixed-price Contract Bidding Implementation

Round	Announced Quantity (MW)	Bid Quantity (MW)	Awarded Quantity (MW)	Fixed-price Contract Ceiling (KRW/kWh)	Spot Market $S M P + R E C$ (KRW/kWh)
H2 2023	1,000	65.8	59.7	153.5	240
H1 2023	1,000	298.2	272.1	153.5	240
H1 2022	2,000	1,380.7	1,354.9	160.6	254
H2 2021	2,200	3,487.4	2,203.1	160.6	129
H1 2021	2,205	5,098.3	2,053.3	161.6	129
H2 2020	1,410	4,650.2	1,415.1	172.5	112
H2 2020	1,200	5,887.0	1,296.6	172.5	112

한편, 태양광 발전사업자는 RPS 시장에 진입한 이후 현물 시장의 $S M P + R E C$ 합산가격이 고정가격계약 시장의 상한가 보다 높을 경우 현물 시장에 잔류하고 반대의 상황에서는 고정가격계약으로의 전환하는 선택이 가능하다. 그러나 고정가격계약 체결 시에는 다시 현물 시장으로의 재전환은 허용되지 않기 때문에 현물 시장의 수익성이 높은 상황에서는 고정가격계약 체결 유인이 거의 없다. 따라서 태양광 발전사업자가 현물 시장에 진입할 경우 일정가격 이하, 즉 고정가격계약 낙찰가에서 행사할 수 있는 풋옵션이 부여되는 것으로 간주할 수 있다. 그리고 매년 1~2회 고정가격계약 시장이 개설되고 있으므로 해당 풋옵션은 만기일 이전에도 가능한 아메리칸(American) 풋옵션의 형태임을 알 수 있다.

일반적으로 수익의 불확실성은 리스크 프리미엄을 요구하고 해당 리스크를 헷지하기 위한 옵션을 보유하기 위해서는 옵션의 가치에 상응하는 옵션 프리미엄을 지불해야 한다. 그러나 현물 시장에 참여하는 태양광 발전사업자는 옵션 프리미엄을 별도로 지불하지 않는다. 이는 태양광 발전사업자의 시장 진입을 촉진한다는 장점은 있으나, 태양광 발전사업자가 누리는 옵션의 가치를 전기소비자가 부담해야한다는 점은 단점으로 지적될 수 있다.

본 논문은 RPS 현물 시장의 참여자가 보유하는 이러한 아메리칸 풋옵션의 가치를 추정하여 현행 RPS 제도가 발전사업자에게 다양한 시장 진입 경로를 제공함으로써 부여하는 편익의 형태와 크기를 분석하는 것을 목적으로 한다. 그리고 이러한 상황이 가지는 정책적 시사점과 정책방향에 대해 논의하고자 한다. 본 논문은 크게 두 가지 점에서 학술적, 정책적 차별성이 있다. 우선, 아메리칸 옵션을 실증 적용한 연구 사례를 찾아보기 어렵다. 특히 수량이나 형태가 고정적이지 않고 현금흐름을 발생시키는 자산과, 매년 가격 수준이 하락하는 행사가격을 대상으로 하는 실물옵션 연구 사례는 찾아보기 어렵다. 다음으로, RPS 현물 시장에서 태양광 발전사업자가 누리는 풋옵션의 존재를 최초로 제기하고 이를 실증분석을 수행한 후 정책적 시사점을 도출한 최초의 연구라는 점에서 차별적이다.

본 논문은 다음과 같이 구성된다. 우선 재생에너지 분야에 적용된 실물옵션 선행연구를 분석한 후 시사점을 도출하, 본 논문에 적용한 이항격자모형 방법론에 대해 설명한다. 다음으로 해당 모형을 통해 RPS 현물 시장 참여자가 보유하게 되는 아메리칸 풋옵션의 가치를 추정하고, 마지막으로 결론 및 시사점을 제시한다.

본 론

선행연구

실물옵션 방법론은 불확실성이 존재하는 투자에 대해, 의사결정의 유연성이 갖는 선택권(option)의 가치를 평가하는 방법론이다(Lee et al., 2012). 이러한 선택권에는 투자의 확장, 포기, 연기, 전환 등이 있다. 실물옵션 방법론을 재생에너지 분야에 적용한 연구 사례들은 최근 크게 증가하였다(Kozlova, 2017). Kim(2021)은 새만금 지역 수상 태양광 발전 사업의 투자 수익성을 평가하기 위해 실물옵션 기법을 적용하였다. 이 연구는 기존의 순현재가치(NPV) 분석이 불확실성을 충분히 반영하지 못하는 한계를 지적하고 이항격자모형을 활용하여 불확실성이 큰 태양광 발전사업에서 투자 유연성이 가지는 가치를 실증적으로 평가하였다. Park et al.(2020)은 $S M P + R E C$ 합산가격 변동성이 태양광 발전의 투자 가치에 미치는 영향을 분석하였다. 일반적인 옵션가격결정 모형 연구들이 자산의 변동성을 기하학적 브라운(geometric Brownian motion) 확률과정을 가정하는데 반해 해당 연구에서는 평균회귀성향의 Ornstein-Uhlenbeck 확률과정에 대한 가정을 추가했다는 점에서 차별적이다. Kim and Jeon(2022)은 전력 가격과 연료 가격의 이중 가격 불확실성을 고려하였다는 점에서 기존의 다른 연구들과 차별적이다. 해당 논문이 불확실성으로 인한 리스크 프리미엄을 연료전지 발전사업자의 비용으로 가정하고 연료전지 발전소의 경제성 분석에 반영함으로써 불확실성이 경제성에 미치는 영향을 정량적으로 평가하였다는 점에서는 앞서 제시한 논문들과 유사하다. Choi and Kim(2003)은 대규모 장기 에너지 프로젝트의 단계별 투자 결정을 실물옵션 방법론으로 분석하였고, Kim and Li(2021)는 실물옵션 기법을 적용하여 해상풍력 발전 사업의 최적 행사 시점을 결정하는 연구를 수행하였다.

이처럼 대부분의 재생에너지 관련 실물옵션 방법론 선행연구는 불확실성이 경제성에 미치는 영향 즉, 투자옵션을 분석하거나 불확실성을 고려하여 진입 시점이나 사업 지속 여부를 고려하는 연기옵션이나 포기옵션을 주요 분석 대상으로 한다. 또한 방법론적으로는 블랙-숄즈(Black-Scholes Model) 모형을 선택하고, 방법론적 한계와 연구의 목적 상 옵션의 유형은 만기에만 행사 가능한 유러피언(European) 옵션을 가정한 것이 주를 이룬다. 반면, 만기 이전 행사 가능한 아메리칸 옵션을 분석 대상으로 하는 연구는 제한적이다.

방법론

실물옵션 분석에 일반적으로 활용되는 옵션가격 결정모형으로는 블랙-숄즈 모형(Black and Scholes, 1973), 몬테카를로 시뮬레이션(Monte Carlo Simulation), 그리고 Cox et al.(1979)이 제시한 이항격자모형(Binomial Lattice Tree Model) 등이 있다. 본 연구에서는 이들 모형 중 이항격자모형을 채택하였는데, 그 이유는 크게 두 가지이다.

첫 번째 이유는 본 논문에서 분석 대상으로 하고 있는 옵션은 일반적인 실물옵션 모형 분석 대상인, 만기일에만 행사가 가능한 유러피언 옵션이 아니라, 만기일 이전에도 행사가 가능한 아메리칸 옵션이기 때문이다. 서론에서 밝힌 바와 같이 REC 현물 시장에 진입하는 시장 참여자는 만기일이라고 할 수 있는 설비수명 20년 이전에 매년 1~2회 개최되는 고정가격계약 입찰에 참여하여 고정가격계약으로의 전환을 선택할 수 있다. 이는 만기일 이전에 옵션 행사가 가능한 전형적인 아메리칸 옵션의 형태이다. 그런데, 블랙-숄즈 모형과 몬테카를로 시뮬레이션은 아메리칸 옵션의 분석에 적합하지 않다. 두 번째로, 본 논문에서 채택하는 기초자산은 일반적으로 분석의 대상이 되는, 가격은 변화하나 수량은 변화하지 않는 형태의 자산이 아니기 때문이다. 본 논문의 기초자산은 발전소에서 매년 생산되는 전력에 기반한 수익의 현금흐름을 현가화한 것으로, 매기의 자산가격이 해당 기의 $S M P + R E C$ 합산가격과 발전소의 잔여 수명기간에 따라 변화하는 구조를 가진다. 이러한 구조를 고려할 때 분석의 용이성으로 인해 널리 활용되는 블랙-숄즈 모형과 몬테카를로 시뮬레이션을 본 논문에 적용하기 어렵다고 판단된다. 이에 본 논문에서는 분석 모형으로 이항격자모형을 채택하였다.

$n$ 기의 아메리칸 풋옵션의 가치는 (1)과 같이 결정되며 이는 유러피언 풋옵션의 가치 (2)와 차별적이다. 그 이유는 유러피언 풋옵션과 달리 아메리칸 풋옵션은 매 기 옵션 행사를 결정할 수 있기 때문에 역귀납법(backward induction)으로 계산되는 옵션의 가치( $e^{- r f ∆ n} [p P_{u} + (1 - p) P_{d}]$ )와 해당 기에 옵션을 행사할 경우의 옵션의 가치( $K_{n} - S_{n}$ )를 비교하여 큰 값을 택하기 때문이다.

(1)

P_{n} = max {K_{n} - S_{n}, e^{- r f Δ n} [p P_{u} + (1 - p) P_{d}]}

여기서, $P_{u}$ 는 차기( $n$ +1 기) 가격 상승 시의 옵션 가치,

$P_{d}$ 는 차기 가격 하락 시의 옵션 가치,

$K_{n}$ 는 $n$ 기의 행사가격,

$S_{n}$ 은 $n$ 기의 자산가격,

$r f$ 는 무위험 수익률,

$p$ 는 위험중립 확률

(2)

P_{n} = e^{- r f Δ n} [p P_{u} + (1 - p) P_{α}]

한편, $P_{n}$ 산정 식에 대입되는 주요 계수들은 다음과 같은 방식으로 산정된다.

(3)

p = \frac{(e^{r f Δ n} - d)}{(u - d)}

(4)

u = e^{σ \sqrt{∆ n}}

(5)

d = \frac{1}{u}

(6)

σ = \log (\frac{S_{n - 1}}{S_{n}})

여기서 𝜎는 자산가격의 변동성을 의미하는 것으로 일반적으로 기간 평균 로그수익률로 정의된다. 본 논문에서는 기초자산의 기반이 되는 전력 한 단위를 전력 시장과 현물 시장에 합산가격으로 판매하는 것으로 가정했기 때문에 $S M P + R E C$ 의 평균 로그수익률을 자산 $S_{n}$ 의 𝜎로 가정하였다. RPS 제도가 시행된 2012년부터 2023년까지의 $S M P + R E C$ 평균 로그수익률은 29.1%로 추정되었고, 본 연구에서는 이 값을 𝜎로 채택하였다. 이렇게 추정한 𝜎를 통해 도출한 상승폭 $u$ 와 하락폭 $d$ 는 각각 1.338, 0.747이며 해당 수치를 기반으로 산정한 위험중립확률 $p$ 는 0.505이다.

본 논문에서 $n$ 기의 자산은 단순히 해당 기의 전력 1단위와 REC 1단위를 결합한, $S M P + R E C$ 로 표시되는 자산이 아니라 매년 생산되어서 판매되는 전력 1단위와 REC 1단위로부터 예상되는 수익의 현금흐름을 현재화한 값이다. 그런데 이러한 수익은 (7)과 같이 다음 기에 위험중립확률 $p$ 에 따라 $u$ 로 전개될 수도 있고 1- $p$ 에 따라 $d$ 로 전개될 수 있다.

(7)

\begin{aligned} (M + R)_{n + 1} = (1 - c) u (M + R)_{n}; p 의 확률 \\ (M + R)_{n + 1} = (1 - c) d (M + R)_{n}; 1 - p 의 확률 \end{aligned}

여기서, $(M + R)_{n}$ 은 $n$ 기의 현물 시장 $S M P + R E C$ 합산가격

$c$ 는 모듈의 성능저하율

따라서 $n$ 기의 자산가격 $S_{n}$ 은 (8)과 같이 구할 수 있고 이를 정리하면 (9)와 같다. 자산의 전체 현금 흐름은 여기에 초기 투자비와 운영 유지비와 같은 비용의 현금흐름도 포함되나, 해당 비용 항목들은 자산가격 $S_{n}$ 과 추후 정의할 행사가격 $K_{n}$ 에서 동일한 형태를 가지기 때문에 분석의 편의성을 위해 제외하고 수익의 현금흐름만을 분석에 포함하였다. 이는 이후 옵션의 가치를 REC 가중치의 크기와 비교함에 있어서도 수익의 현금흐름을 바탕으로 옵션 가치를 산정하는 방식이 적정하기 때문이기도 하다.

(8)

\begin{aligned} S_{n} = & (M + R)_{n} \times \{1 + [\frac{(1 - c) p u + (1 - c) (1 - p) d}{(1 + r f)}] + {[\frac{(1 - c) p u + (1 - c) (1 - p) d}{(1 + r f)}]}^{2]} + \dots\} \end{aligned}

(9)

S_{n} = (M + R)_{n} \times \{\frac{{[\frac{(1 - c) (p u + (1 - p) d)}{(1 + r f)}]}^{T - n} - 1}{\frac{(1 - c) (p u + (1 - p) d)}{(1 + r f)} - 1}\}

한편 본 논문에서는 행사가격이 고정되어있는 기존의 연구들과 달리 행사가격 $K_{n}$ 또한 매기 변화한다고 가정하였다. 그 이유는 정부에서 재생에너지 발전단가 하락과 소비자 부담 완화를 위해 고정가격계약의 상한가를 매년 낮춰 나가는 것을 정책 방향으로 하기 때문이다. 이는 태양광 LCOE(균등화발전원가, Levelized Cost of Electricity)가 매년 하락하고 있고 앞으로도 하락할 것으로 전망되는 상황을 반영한 것이기도 하다. 본 논문에서는 고정가격계약의 상한가가 매년 일정한 비율로 하락한다고 가정하고 이를 바탕으로 먼저 $n$ 기의 고정가격 $F_{n}$ 을 (10)과 같이 도출하였다.

(10)

F_{n} = F_{o} \times \frac{(1 - f)^{n} - 1}{(1 - f)}

여기서, $F_{0}$ 는 초기 고정가격계약 상한가

$f$ 는 고정가격계약 상한가 연간 하락률

마찬가지로 수익의 현금흐름을 고려하여 $n$ 기의 행사가격 $K_{n}$ 은 (11)과 같이 구할 수 있다. 고정가격계약의 경우 계약이 체결되면 이후 명목가격의 하락이나 상승은 허용되지 않는다.

(11)

K_{n} = F_{n} \times \{\frac{{[\frac{1}{(1 + r f)}]}^{T - n} - 1}{\frac{1}{(1 + r f)} - 1}\}

분석결과

본 논문에서 설정한 실물옵션 모형의 분석에 활용되는 주요 변수의 값을 정리하면 Table 3과 같다. 단, 매기 변화하는 값들은 초기값만을 제시하였다는 점을 참고하기 바란다. 여기서 현물 시장 $S M P + R E C$ 합산가격과 고정가격계약의 초기값 $(M + R)_{0}$ , $F_{0}$ 은 2023년 하반기 고정가격 경쟁입찰 상한가를 기준으로 설정하였다. $(M + R)_{0}$ 를 $F_{0}$ 와 동일하게 설정한 이유는 본 논문이 특정 시점의 풋옵션 가치 추정이 아니라 변동성 자산에서 변동성이 없는 자산으로 전환할 수 있는 풋옵션이 가지는 가치를 밝히는데 초점을 맞추기 때문이다. 그리고 이를 위해서는 두 자산의 초기가격을 동일하게 설정하는 것이 합리적이라고 판단한다. 다만 $(M + R)_{0}$ 가정에 따라 풋옵션의 가치가 변화할 수 있으므로 이후 시나리오 분석 및 민감도 분석을 추가적으로 수행하여 $(M + R)_{0}$ 에 따른 풋옵션 가치 변화를 분석한다.

Table 3.

Description and Initial Values of Key Variables

Variables	Description	Values	Units	Reference
$(M + R)_{n}$	Spot Market SMP+REC	153.5	KRW/kWh	H2 2023 Fixed-price Contract Ceiling (Table 2)
$F_{n}$	Fixed-price	153.5	KRW/kWh	Same as above
$S_{n}$	Asset Price	3,112.4	KRW
$K_{n}$	Strike Price	3,112.4	KRW
$T$	Maturity	20	yr.
$∆ n$	Time Interval	1	yr.
$c$	Degradation Rate	0.45%	-	Lee and Lim(2023)
$f$	Fixed-price Decline Rate	0.9%	-	Lee and Lim(2023)
$r f$	Risk-free Interest Rate	4.5%	-	Lee and Lim(2023)
𝜎	Volatility	0.291	-
$u$	Up Factor	1.338	-
$d$	Down Factor	0.747	-
$p$	Risk Neutral Probability	0.505	-

성능저하율 $c$ 는 Lee and Lim(2023)에서 제시한 수치를 인용하였다. 고정가격계약 하락률 $f$ 는 Lee and Lim(2023)에서 제시한 2023년부터 2043년까지의 태양광 LCOE 전망결과 중 시나리오1의 연평균 하락률을 계산한 값이다. 무위험수익률 $r f$ 는 Lee and Lim(2023)에서 제시하고 있는 할인율을 인용하였다.

이상의 값들을 바탕으로 자산가격 $S_{n}$ 에 대한 이항격자모형을 구성하기 위해 우선적으로 도출한 $(M + R)_{n}$ 의 이항격자는 Table 4와 같다. 마지막 열의 prob.는 해당 격자의 사건이 발생할 확률을 의미한다.

Table 4.

Binomial Lattice Tree Expansion Results of $(M + R)_{n}$

n=0	1	2	...	20	prob.
153.5	205.4 $(u)$	275.0 $(u^{2})$	...	...	...
	114.7 $(d)$	153.5 $(u d)$	...	492.5 $(u^{12} d^{8})$	12.5%
		85.7 $(d^{2})$	...	275.0 $(u^{11} d^{9})$	16.4%
			...	153.5 $(u^{10} d^{10})$	17.6%
				85.7 $(u^{9} d^{11})$	15.7%
				47.8 $(u^{8} d^{12})$	11.5%
				...	...

이를 바탕으로, 수익의 현금흐름에 기반하여 산정한 자산가격 $S_{n}$ 에 대한 이항격자모형을 구성하면 Table 5와 같다. 여기서 $P_{n}'$ 은 $n$ 기에 평가한 옵션 가치 즉 $K_{n} - S_{n}$ 을 의미한다. 여기에 추가적으로 역귀납법을 통해 옵션 가치 $e^{- r f ∆ n} [p P_{u} + (1 - p) P_{d}]$ 를 구하고 이 둘 중 최대값을 선택하면( $\max {K_{n} - S_{n}, e^{- r f ∆ n} [p P_{u} + (1 - p) P_{d}]}$ ) $n$ 기의 옵션 가치 $P_{n}$ 이 된다. 단, 마지막 기의 옵션 가치 $P_{n}$ 은 $\max (K_{n} - S_{n}, 0)$ 으로 결정된다.

Table 5.

Binomial Lattice Tree Expansion Results of $S_{n}$ , $P_{n}$

n=0		1		2		...		20		prob.
$P_{n}'$	-	$P_{n}'$	-	$P_{n}'$	-	$P_{n}'$	...	$P_{n}'$	...	...
$P_{n}$	208.0	$P_{n}$	120.5	$P_{n}$	65.8	$P_{n}$	...	$P_{n}$	...
$S_{n}$	3,112.4	$S_{n}$	3,974.1	$S_{n}$	5,061.8	$S_{n}$	...	$S_{n}$	...
		$P_{n}'$	-	$P_{n}'$	-	$P_{n}'$	...	$P_{n}'$	-	12.5%
		$P_{n}$	316.9	$P_{n}$	187.6	$P_{n}$	...	$P_{n}$	-
		$S_{n}$	1,634.7	$S_{n}$	2,825.8	$S_{n}$	...	$S_{n}$	492.5
				$P_{n}'$	337.8	$P_{n}'$	...	$P_{n}'$	-	16.4%
				$P_{n}$	478.7	$P_{n}$	...	$P_{n}$	-
				$S_{n}$	1,577.5	$S_{n}$	...	$S_{n}$	275.0
						$P_{n}'$	...	$P_{n}'$	-	17.6%
						$P_{n}$	...	$P_{n}$	-
						$S_{n}$	...	$S_{n}$	153.5
								$P_{n}'$	41.5	15.7%
								$P_{n}$	41.5
								$S_{n}$	85.7
								$P_{n}'$	79.4	11.5%
								$P_{n}$	79.4
								$S_{n}$	47.8
								$P_{n}'$	...	...
								$P_{n}$	...
								$S_{n}$	...

앞서 밝힌 바와 같이 태양광 발전사업자가 진입하는 시점의 현물시장 가격에 따라 풋옵션의 가치는 달라질 수 있다. Table 6은 태양광 발전사업자의 현물시장 진입 여건에 따른 풋옵션의 가치 변화를 분석한 결과이다. 초기 고정가격 $F_{0}$ 는 모든 시나리오에서 동일하게 153.5 원/kWh로 고정하였다. 시나리오는 총 5개로 Base Case는 $(M + R)_{0}$ 을 $F_{0}$ 와 동일하게 가정한 것이고 Lowest Case는 RPS 제도가 시행된 2012년 이후 최저점 기준이다. Average 1 Case는 고정가격 경쟁입찰이 도입된 2017년 이후의 평균, Average 2 Case는 2012년 이후 평균이다. 마지막으로 Highest Case는 2012년 이후 최고점 기준이다. 결과에서 확인할 수 있듯이 $(M + R)_{0}$ 에 따라 풋옵션의 가치가 크게 달라진다. 최근에는 SMP 상승으로 인해 $(M + R)_{0}$ 이 높기 때문에 풋옵션 행사 가능성이 적고 가치 또한 낮다. 2024년의 $(M + R)_{0}$ 은 Average 2와 유사한 수준이다. 그러나 재생에너지, 가령 해상풍력 보급 증가로 인한 현물 수요 감소, 정부의 제도 개편 등으로 인해 2020년의 사례와 같이 $(M + R)_{0}$ 이 하락하면 풋옵션의 가치는 크게 늘어날 수도 있다.

Table 6.

Results of Put Option Valuation under SMP+REC ( $(M + R)_{0}$ ) Scenarios

Scenario	Notes	Spot Market SMP+REC ( $(M + R)_{0}$ )	Put Option Value	Ratio to Asset Price (𝜌)
Base	H2 2023 Fixed-price Contract Ceiling	153.5	208.0	6.7%
Lowest	2020	112.0	342.0	15.1%
Average 1	2017~2023 average	183.4	152.4	4.1%
Average 2	2012~2023 average	207.8	125.8	3.0%
Highest	2022	254.0	87.7	1.7%

Table 7.

Results of Put Option Valuation under Volatility (𝜎) Scenarios

Scenario	Notes	Volatility (𝜎)	Put Option Value	Ratio to Asset Price (𝜌)
Base	2012~2023	0.291	208.0	6.7%
Low	2012~2020	0.201	82.3	2.6%
High	2017~2023	0.325	261.9	8.4%

풋옵션은 자산가격의 변동성에 큰 영향을 받는다. 여기서는 자산가격 변동성(𝜎) 가정에 따른 풋옵션 가치의 변화를 분석하기 위해 총 3개의 시나리오를 도입하였다. 첫 번째 시나리오 Base Case는 RPS 제도가 시행된 2012년 이후의 $S M P + R E C$ 평균 로그수익률, 두 번째 시나리오(Low Case)는 $S M P$ 급등 이전인 2012년부터 2020년까지의 $S M P + R E C$ 평균 로그수익률, 그리고 세번째 시나리오(High Case)는 고정가격 경쟁입찰이 도입된 2017년 이후의 평균 로그수익률을 자산가격 변동성으로 가정한 것이다. 결과에서 확인할 수 있듯 변동성이 커질수록 풋옵션의 가치는 증가하는 것으로 나타났다(Table 7). 2021년 이후 코로나와 러시아-우크라이나 전쟁 등의 외부충격으로 인한 $S M P$ 급등이 없었다면 현물 시장 참여 태양광 발전의 풋옵션 가치는 높지 않았을 것으로 보인다. 다만, 이 경우 $(M + R)_{0}$ 이 낮아져서 풋옵션 가치가 증가하는 효과가 복합적으로 작용할 수 있다.

추가적으로 REC 가중치(𝜇)가 달라질 경우 즉, 태양광 설비용량과 유형별 풋옵션의 가치를 비교한다. 시나리오는 총 4개로, 일반부지의 경우 태양광 설비용량에 따라 0.8~1.2의 가중치를 가정하였고 건축물의 경우 중소규모에 적용되는 1.5 가중치를 기준으로 설정하였다. 가중치가 변화할 경우 수익의 현금흐름 뿐만 아니라 자산가격 변동성 즉, 𝜎도 달라지기 때문에 이를 고려하였다. 분석결과 REC 가중치가 커질수록 풋옵션의 가치가 증가하는 것으로 나타났다(Table 8). 이는 REC 가중치가 커질수록 자산가격 변동성이 커지기 때문이다. 이 때문에 REC 가중치가 가장 큰 건축물 태양광 발전사업자가 가지는 풋옵션의 가치가 일반부지 태양광 발전사업자에 비해 큰 것으로 분석되었다.

Table 8.

Results of Put Option Valuation under REC Multiplier (𝜇) Scenarios

Scenario	Notes	REC Multiplier (𝜇)	Put Option Value	Ratio to Asset Price (𝜌)
Base	100~3000 kW Land	1.0 (𝜎=0.291)	208.0	6.7%
Large	3,000 kW~ Land	0.8 (𝜎=0.287)	182.7	6.4%
Small	~100 kW Land	1.2 (𝜎=0.297)	235.5	7.0%
Roof-top	~3,000 kW Roof-top	1.5 (𝜎=0.305)	279.4	7.4%

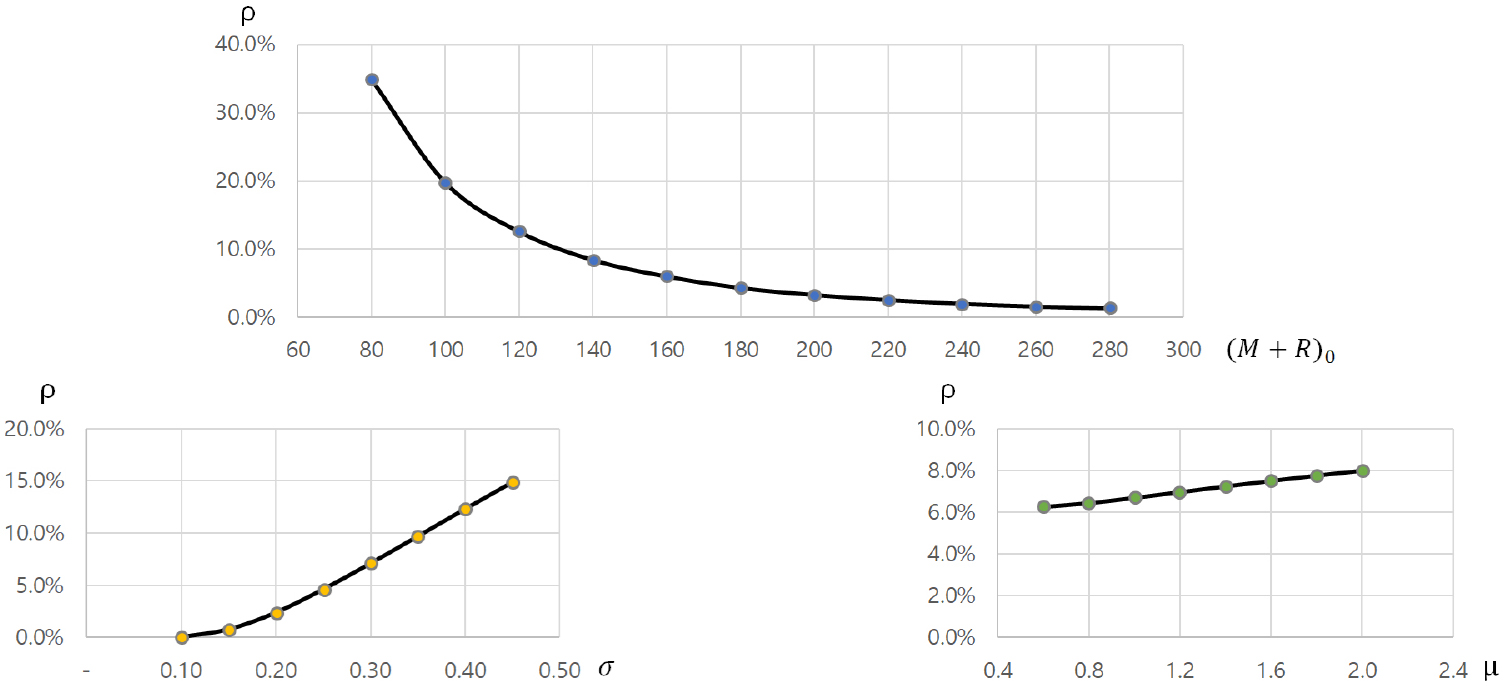
주요 변수들을 대상으로 한 민감도 분석 결과는 Fig. 1과 같다. $(M + R)_{0}$ 과 변동성 𝜎에 따른 민감도는 상대적으로 높은 반면, REC 가중치(𝜇)에 따른 민감도는 상대적으로 낮은 것으로 나타났다.

https://cdn.apub.kr/journalsite/sites/ksmer/2024-061-05/N0330610503/images/ksmer_61_05_03_F1.jpg

Fig. 1.

Sensitivity Analysis of the Ratio to Asset Price (𝜌) with Key Variables.

분석 결과 RPS 현물 시장의 발전사업자가 누리는 아메리칸 풋옵션의 가치는 기준시나리오(Base Case)에서 208.0원으로 나타났는데, 이는 0기의 자산가격 3,112.4원의 약 6.7%에 달한다. 앞서 밝힌 바와 같이 태양광 발전사업자는 해당 옵션에 대한 프리미엄을 지불하지 않는다. 따라서 RPS 제도는, 진입 여건에 따라 차등적이긴 하지만, 현물 시장에 참여하는 발전사업자에게 전체 수익의 7%에 가까운 가치를 가지는 옵션을 무료로 제공하고 있는 것이다. 이러한 상황은 태양광 발전사업자의 시장진입을 촉진한다는 점에서 긍정적이다. 다만, 그들로 하여금 수익의 변동성이 높더라도 이를 수용하고 현물 시장으로 우선 진입하여 높은 수익을 추구하는 전략을 선호하도록 만드는 문제점이 있다. 이러한 상황은 태양광 정산비용 증가와 전기소비자 부담으로 이어진다.

실제로 현물 시장 $S M P + R E C$ 합산가격이 고정가격계약 상한가 보다 낮아졌던 2020년과 2021년에는 고정가격계약 입찰 물량이 모두 소진된 반면, 현물 시장 $S M P + R E C$ 합산가격이 고정가격계약 보다 높아진 2022년과 2023년에는 공고물량 2,000 MW 중 각각 1,354.9 MW, 331.8 MW만이 고정가격계약에 낙찰되었고 입찰 경쟁률도 급락하였다(Table 2). 특히, 2023년 하반기 고정가격계약의 실질 경쟁률은 0.06:1에 불과했다.

결 론

본 논문은 다양한 세부 시장이 존재하는 RPS 제도 하에서 태양광 발전사업자가 누리는 풋옵션의 가치를 추정하였다. 현물 시장의 $S M P + R E C$ 합산가격이 고정가격계약 상한가와 동일한 수준인 상황을 가정하여 분석한 결과 기준시나리오에서 해당 옵션의 가치가 전체 수익의 6.7%에 달하는 것으로 나타났다. 고정가격계약 상한가 153.5 원/kWh과 SMP 기준가격 86.4 원/kWh을 고려할 때 고정가격계약의 1REC 가격은 67.1 원/kWh로 볼 수 있다. 따라서 수익의 6.7%는 가중치 기준으로 환산하면 대략 0.15에 해당 수준으로 추정할 수 있다. 하지만 앞서 밝혔듯이 태양광 발전사업자는 고정가격계약으로 전환할 수 있는 이러한 옵션을 별도의 프리미엄을 구매하거나 지불하지 않은 채 원하는 시기에 행사 여부를 선택할 수 있다. 현물 시장은 SMP와 REC의 이중 불확실성이 존재하는 시장이고 이러한 이중 불확실성은 시장참여자의 시장 진입 의사결정을 지연시키거나 무산시킬 수 있다. 만약 시장에 진입한다 하더라도 시장참여자는 일정 수준의 리스크 프리미엄에 노출된다. 따라서, 일반적으로 현물 시장의 가격은 고정가격계약의 그것에 비해 높은 것이 합리적이다. 현물 시장의 가격 하락 시 고정가격계약으로 전환할 수 있는 풋옵션의 존재는 불확실성 대응에 기여할 수 있다.

다만, 이러한 상황은 두 가지 문제점을 야기시킨다. 첫 번째, 태양광 발전사업자는 옵션의 가치에 상응하는 프리미엄을 지불하지 않는데, 이것이 세부 시장간 최적 포트폴리오 구성을 저해한다는 것이다. 옵션 프리미엄을 요구하지 않는 현재의 상황은 현물 시장의 선호를 증가시키고 현물 시장과 고정가격계약 시장 간의 최적 포트폴리오 구성을 저해하게 된다. 즉, RPS 제도 설계 당시 밸런싱 시장 역할을 할 것으로 기대했던 현물 시장의 비중이 과도하게 증가하여 본래의 목적에 부합하지 않게 운영될 가능성이 커진다는 것이다. 두 번째, 발전사업자가 지불하지 않는 옵션 프리미엄이 전기소비자에게 전가된다는 것이다. 태양광 발전사업자는 프리미엄을 지불하지 않은 풋옵션을 보유한 채 현물 시장에 참여하여 수익성을 극대화하는 전략을 취하게 된다. 이는 전반적인 태양광 가격, 혹은 태양광 정산비용의 증가로 이어지게 되고 결과적으로 전기소비자의 비용 증가로 이어진다. 시나리오 분석에서 제시한 바와 같이 현물 시장 가격이 고정가격계약에 비해 높아질수록 풋옵션의 가치는 감소한다. 그러나 현물 시장 가격 자체가 높아졌기 때문에 전기소비자의 실제 부담이 감소한다고 보기 어렵다.

이러한 상황을 해결하기 위해 필요한 제도적 개선방안은 크게 두 가지로 구분할 수 있다. 첫 번째, 현물 시장 참여자로 하여금 풋옵션의 가치에 상응하는 프리미엄을 지불하게 하는 것이다. 이를 통해 신규 태양광 발전사업자로 하여금 보다 안정적인 수익을 보장받을 수 있지만 가격 수준은 상대적으로 낮은 고정가격계약에 대한 선호를 증가시킬 수 있다. 현물 시장 참여자가 지불한 프리미엄은 RPS 정산에 활용함으로써 정산비용을 하락시켜 전기소비자의 부담을 완화시킬 수 있을 것이다. 두 번째는, 장기적으로 현물 시장을 일몰하고 고정가격계약으로 시장을 통합하는 것이다(Cho and Lee, 2017). 고정가격계약의 장점은 발전사업자에게는 수익의 안정성을 보장하고 전기소비자에게는 비용 감소의 편익을 제공한다는 점이다. 당초 고정가격계약을 도입한 이유도 위와 같은 장점에 주목했기 때문이다.

한편, 본 논문은 다음과 같은 한계가 존재한다. 우선, 본 논문에서 제시한 옵션의 가치는 과다 추정되었을 가능성이 존재한다. 그 이유는 현물 시장에서의 $S M P + R E C$ 합산가격이 고정가격계약의 상한가보다 낮아져서 풋옵션을 실현하고자 하더라도 입찰가를 높게 제시할 경우 낙찰되지 않을 가능성이 존재하기 때문이다. 보다 면밀한 분석을 위해서는 풋옵션을 행사하지만 수용되지 않는 상황까지 고려한 모형을 구축할 필요가 있다. 하지만 최근의 정부의 정책 방향이 고정가격계약을 장려한다는 점, 본 논문에서는 옵션의 행사를 1년에 한 번 만 가능한 것으로 가정했지만 실제로는 추가적으로 한 번의 기회가 더 주어질 수 있다는 점, 그리고 경쟁률이 높을 경우 차기 입찰물량을 상향시켜온 그간의 운영 방식까지 고려하면 그 차이는 유의미하지 않을 것으로 판단된다. 해당 논의는 추후 연구로 남겨둔다.

두 번째로 시장 진입 시점에 따라 풋옵션의 가치가 변화할 수 있다는 점이다. 이는 진입 시점에 따라 현물 시장의 $S M P + R E C$ 합산가격이 차별적이기 때문에 자연스러운 결과이긴 하지만 합리적 초기값 설정과 이에 따라 추정된 옵션 가치의 적정성에 대한 논의가 제기될 수 있다. 이러한 초기값에 따른 옵션 가치의 변화 가능성을 제어, 혹은 반영할 수 있는 방안에 대해서는 향후 추가적인 논의가 필요할 것이다.

Acknowledgements

본 논문은 에너지경제연구원의 지원을 받아 수행된 연구입니다(기본연구보고서, 신재생에너지 공급인증서(REC) 가격 결정요인 분석을 통한 REC 시장 효율성 제고 방안 연구).

References

Black, F. and Scholes, M., 1973. The pricing of options and corporate liabilities, Journal of Political Economy, 81(3), p.637-654.

10.1086/260062

Chang, Y. and Cho, I.H., 2023. Assessment of setback regulation policies on solar photovoltaic deployment, Korea Energy Economics Institute Basic Research, 23-04, KEEI, Seoul, Korea, 126p.

Cho, S. and Lee, S.H., 2017. A study on the introduction of an auction system for the improvement of the RPS scheme, Korea Energy Economics Institute Basic Research, 17-22, KEEI, Seoul, Korea, 124p (in Korean).

Cho, S., 2024. Renewable Energy Deployment Policy Reform. Presentation materials of the Renewable Energy Deployment Policy Reform Research Interim Results Conference, KEA-KEEI, Seoul, Korea, p.1-17 (in Korean).

Choi, S.H. and Kim, K.T., 2003. Investment valuation using real options for large-scale long-term multi-stage energy projects, The Korean Operations Research and Management Science Society, 2003.05a, p.612-619 (in Korean).

Cox, J.C., Ross, S.A., and Rubinstein, M., 1979. Option pricing: A simplified approach, Journal of Financial Economics, 7(3), p.229-263.

10.1016/0304-405X(79)90015-1

Kim, K.S., 2021. Real options analysis for the Eco-Environment Area Project in Saemangeum, Korean Journal of Construction Engineering and Management, 22(1), p.90-97.

Kim, M.J., Myung H.S., and Lim, S.H., 2019. Analysis of flexible resource requirements to increase renewable energy acceptance in power system, Journal of the Korean Institute of Illuminating and Electrical Installation Engineers, 33(11), p.63-70.

10.5207/JIEIE.2019.33.11.063

Kim, M.S. and Li, Q.Z., 2021. A study on the optimal exercise of offshore wind power projects using real options, Korean Journal of Financial Engineering, 20(4), p.117-136.

Kim, S.H. and Jeon, W.Y., 2022. Estimating the investment value of fuel cell power plant under dual price uncertainties based on real options methodology, Environmental and Resource Economics Review, 31(4), p.645-668.

Korea New and Renewable Energy Center, 2024.08.29., https://www.knrec.or.kr/biz/pds/notice/list.do

Kozlova, M., 2017. Real option valuation in renewable energy literature: Research focus, trends, and design, Renewable and Sustainable Energy Reviews, 80, p.180-196.

10.1016/j.rser.2017.05.166

Lee, D.S., Yun, S.J., Kim, S.M., and Jung, K.H., 2012. Economic evaluation of offshore wind power demonstration project by the real option method, Korea Energy Economic Review, 11(2), p.1-26.

Lee, G.D. and Lim, D.O., 2023. Establishment and operation of long-term LCOE forecast system for expansion of renewable energy(4/5), Korea Energy Economics Institute Basic Research, 23-22, KEEI, Seoul, Korea, 116p.

Park, H.J., Jang H.S., and Lee J.H., 2020. Real option analysis of solar power energy grid cost under electricity price uncertainty, Journal of the Korean Society of Mineral and Energy Resource Engineering, 57(1), p.77-85.

10.32390/ksmer.2020.57.1.077

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Estimation of the Put Option Value for Solar Power Plant Operators Participating in the Renewable Portfolio Standard (RPS) Spot Market

ABSTRACT

MAIN

Table 1.

Proportion of Transaction by RPS Sub-markets

Table 2.

Results of Fixed-price Contract Bidding Implementation

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Table 3.

Description and Initial Values of Key Variables

Table 4.

Binomial Lattice Tree Expansion Results of (M+R)n

Table 5.

Binomial Lattice Tree Expansion Results of Sn, Pn

Table 6.

Results of Put Option Valuation under SMP+REC ((M+R)0) Scenarios

Table 7.

Results of Put Option Valuation under Volatility (𝜎) Scenarios

Table 8.

Results of Put Option Valuation under REC Multiplier (𝜇) Scenarios

Fig. 1.

Sensitivity Analysis of the Ratio to Asset Price (𝜌) with Key Variables.

Acknowledgements

References

Binomial Lattice Tree Expansion Results of $(M + R)_{n}$

Binomial Lattice Tree Expansion Results of $S_{n}$ , $P_{n}$

Results of Put Option Valuation under SMP+REC ( $(M + R)_{0}$ ) Scenarios