A Study on Parallel 3D Elastic Wave Modeling Using Flux-corrected Transport

Ju-Won Oh; Dae-Sik Kim; Won-Ki Kim

doi:10.32390/ksmer.2022.59.1.042

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 28 February 2022. 42-58
https://doi.org/10.32390/ksmer.2022.59.1.042

A Study on Parallel 3D Elastic Wave Modeling Using Flux-corrected Transport

플럭스 보정기법을 이용한 병렬 3차원 탄성파 모델링 연구

Ju-Won Oh¹

Dae-Sik Kim²³

Won-Ki Kim⁴^*

오 주원¹

김 대식²³

김 원기⁴^*

¹Associate Professor, Department of Mineral Resources and Energy Engineering, Jeonbuk National University, Jeonju, Korea

²M.S Course, Department of Mineral Resources and Energy Engineering, Jeonbuk National University, Jeonju, Korea

³M.S Course, KIGAM Pohang Branch, Korea Institute of Geoscience and Mineral Resources, Pohang, Korea

⁴Senior Researcher, Maritime Technology Research Institute, Agency for Defense Development, Changwon, Korea

¹전북대학교 자원․에너지공학과 부교수

²전북대학교 자원․에너지공학과 석사과정

³한국지질자원연구원 포항지질자원실증연구센터 석서과정

⁴국방과학연구소 해양기술연구원 선임연구원

^{*Corresponding Author}

ABSTRACT

In this study, we propose an efficient parallel 3D elastic wave modeling algorithm that is suitable for simulating large-scale 3D ocean-bottom seismic data. The proposed parallel 3D seismic modeling algorithm, which is based on domain decomposition using high-performance computing techniques in multi-node and multi-core cluster environments, can provide numerical solutions efficiently. By integrating flux-corrected transport in parallel 3D elastic wave modeling, our algorithm provides kinematically reliable S-wave motions with less numerical dispersions using larger grid sampling, which enables simulating large-scale 3D elastic wave propagations. We first demonstrate the mechanism of the flux-corrected transport in 2D elastic wave propagation and then extend the proposed methods to large-scale 3D elastic problems on a two-layered model. Finally, we verify the applicability of the proposed algorithm to a more realistic 3D elastic Earth model constructed from the Volve oilfield in the North Sea.

Keywords

3D elastic wave modeling

flux-corrected transport (FCT)

numerical dispersion

high performance computing (HPC)

본 연구에서는 대규모 3차원 해저면 탐사자료 구현을 위한 효율적인 병렬 3차원 탄성파 모델링 알고리듬을 제안한다. 제안된 병렬 탄성파 모델링 기술은 다중노드-다중코어 클러스터 환경에서 영역분할법 기반의 고성능 컴퓨팅 기술을 기반으로 3차원 탄성파동방정식의 수치해를 계산하고, 플럭스 보정기법을 적용하여 상대적으로 큰 공간격자를 사용하더라도 P파와 S파의 운동학적 특성(도달시간)을 정확하게 구현할 수 있다는 장점이 있어서 대규모 3차원 다성분 해저면 탐사자료를 구현하기에 적합하다. 2차원 모델에 대해서 플럭스 보정기법의 원리를 소개하고, 3차원 2층 모델에 대한 적용성을 검토하였다. 마지막으로 북해 볼브 유전 지역의 속도 모델에 대해 제안한 기술을 적용함으로써 대규모 3차원 해저면 탐사자료 구현에 활용가능한지 검토하였다.

키워드

3차원 탄성파 모델링

플럭스 보정 기법

수치 분산

고성능 컴퓨팅

MAIN

서 론
병렬 3차원 탄성파동방정식 모델링
엇격자 유한차분법을 이용한 3차원 탄성파동방정식 모델링
영역 분할법을 이용한 병렬 모델링 알고리듬
플럭스 보정기법을 이용한 3차원 탄성파 모델링
플럭스 보정기법(Flux-corrected transport)
플럭스 보정기법의 원리 및 병렬화
3차원 2층 모델에 대한 적용성 검토
북해 볼브 유전지역 3차원 탄성파동방정식 모델링
결 론

서 론

탄성파 모델링은 탄성파 자료의 해석에 활용하기 위한 인공 탄성파 자료를 생성하는 기법으로 다양하게 활용되고 있다. 최근에는 야외에서 획득한 탄성파 자료의 해석을 위한 자료로 활용할 뿐만 아니라, 탄성파 모델링 기법을 이용하여 지층의 물성구조 및 경계면을 효과적으로 영상화하기 위한 완전파형역산(Full Waveform Inversion, FWI) 및 역시간 구조보정(Reverse Time Migration, RTM) 연구가 활발히 진행되고 있다(Operto et al., 2006; Zhang et al., 2007; Brossier et al., 2009; Fletcher et al., 2009; Kim and Min, 2014; Oh et al., 2018; Zhou et al., 2018).

탄성파 모델링 기법을 활용한 완전파형역산과 역시간 구조보정 등의 결과의 신뢰성을 확보하기 위해서는 탄성파 모델링의 정확성이 매우 중요하다. 뿐만 아니라, 과거에는 P 파만을 이용하여 이러한 연구가 주로 진행되었다면, 최근 주목받고 있는 해저면 탐사로 S파까지 기록이 가능해지고, 다양한 모델링 기법의 개발 및 컴퓨터 수준이 발전함에 따라 P 파 뿐만 아니라 S 파까지 고려한 연구를 수행하는 추세이며(Zhao et al., 1992; Xia et al., 2009; Oh and Alkhalifah, 2019), 3차원 모델링 기법까지 확장되어 적용되고 있다(Min et al., 2006; Cho and Son, 2012).

탄성 파동방정식을 기반으로 하는 수치 모델링 기법은 P 파 보다 속도가 느린 S 파까지 고려를 해주어야 한다. 따라서 분산조건에 취약한 특성이 있다. 이러한 수치적 분산을 극복하기 위해서는 더 작은 격자 간격을 적용함으로써 극복할 수 있지만(Alford et al., 1974), 계산 량이 크게 늘어난다는 문제점이 있다. 특히 3차원 모델링을 수행할 경우 계산 량이 기하 급수적으로 증가하게 되어 완전파형역산이나 역시간 구조보정과 같은 지하 영상화 기술에 적용하기 위해서는 슈퍼컴퓨터 급의 대규모 클러스터가 요구된다. 따라서 국내 소규모 클러스터로 S파까지 활용한 3차원 영상화 연구를 수행하기에는 환경적인 제약이 존재한다.

이러한 수치적 분산을 피하기 위한 공간격자의 제한을 완화시키고 정확도 및 효율성을 향상시키기 위한 시간-공간영역 또는 주파수-공간영역에서 유한차분법 및 유한요소법 등의 다양한 수치 근사법을 활용한 모델링 기법이 개발되었다(Kelly et al., 1976; Kosloff and Baysal, 1982; Marfurt, 1984; Fornberg, 1987; Štekl and Pratt, 1998; Min et al., 2004). 수치적 분산을 극복하여 정확성을 향상시킬 수 있는 기법 중 플럭스 보정기법(Flux Corrected Transport, FCT)은 유체역학에서 연속방정식의 정확한 해를 얻기 위해 고안되었다(Boris and Book, 1973; Book et al., 1975). 이 기법은 유한차분식의 해를 수치적 분산 없이 얻을 수 있는 효과적인 기법으로 탄성파동 모델링 기법에도 적용한 사례가 있다. Fei and Larner(1995)는 플럭스 보정기법을 고차 유한차분법에 적용하여 수치 분산을 극복하였고, Zhao et al.(2014)는 플럭스 보정기법을 적용하여 유체로 포화된 매질에서 탄성파는 수층에서 보다 더 급격히 감쇄되는 것을 확인하였다. Wang et al.(2014)은 등방성 및 이방성 매질에서의 3차원 탄성파 모델링을 위해 플럭스 보정기법을 적용하여 각 매질에서의 탄성파 전파를 효과적으로 모델링 하였다. 또한 Kalita and Alkhalifah(2019)는 플럭스 보정기법을 FWI에 적용하였다.

본 연구에서는 영역분할법(Domain decomposition; Bohlen, 2002)으로 병렬화 된 3차원 탄성파 파동방정식 기반의 수치 모델링 기법에 플럭스 보정기법을 추가적으로 적용하여 대규모 3차원 해저면 탐사자료를 시뮬레이션 할 때 발생하는 S파의 수치적 분산 문제를 극복하고자 한다. 먼저 엇격자 유한차분법(Staggered-grid finite-difference method: Graves, 1996)을 이용한 3차원 탄성 파동방정식의 수치모델링에 대해 논의하고 다음으로 공간영역에 대한 고성능 컴퓨팅을 적용하는 영역분할법의 원리에 대해 설명한다. 그 다음으로 분산 조건에 취약한 3차원 탄성 파동방정식 기반의 수치 모델링 알고리듬의 효율성을 증대시키는 플럭스 보정기법에 대해 소개한다. 2차원, 3차원 수치예제를 통해, 기존방법과 비교하여 플럭스 보정기법의 원리와 활용가능성을 비교한다. 마지막으로 북해 볼브 유전 지역의 3차원 속도모델에 대한 적용을 통하여 대규모 3차원 해저면 탐사자료 구현에 대한 적용성을 검토한다.

병렬 3차원 탄성파동방정식 모델링

엇격자 유한차분법을 이용한 3차원 탄성파동방정식 모델링

등방성 매질에 대한 3차원 탄성파동방정식은 뉴턴의 운동방정식과 일반화된 훅의 법칙으로 구성되며 각각 다음과 같이 표현된다(Graves, 1996).

(1)

ρ \frac{\partial^{2} u_{x}}{\partial t^{2}} = \frac{\partial τ_{x x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} + \frac{\partial τ_{x z}}{\partial z} + f_{x}

(2)

ρ \frac{\partial^{2} u_{y}}{\partial t^{2}} = \frac{\partial τ_{x y}}{\partial x} + \frac{\partial τ_{y y}}{\partial y} + \frac{\partial τ_{y z}}{\partial z} + f_{y}

(3)

ρ \frac{\partial^{2} u_{z}}{\partial t^{2}} = \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial τ_{z z}}{\partial z} + f_{z}

(4)

(\begin{matrix} τ_{x x} \\ τ_{y y} \\ τ_{z z} \\ τ_{y z} \\ τ_{x z} \\ τ x y \end{matrix}) = (\begin{matrix} C_{33} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{13} & C_{33} & C_{13} & 0 & 0 & 0 \\ C_{13} & C_{13} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{55} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & C_{55} \end{matrix}) (\begin{matrix} \partial_{x} u_{x} \\ \partial_{y} u_{y} \\ \partial_{z} u_{z} \\ (\partial_{x} u_{x} + \partial_{x} u_{x}) \\ (\partial_{z} u_{x} + \partial_{x} u_{z}) \\ (\partial_{y} u_{x} + \partial_{x} u_{y}) \end{matrix}) + (\begin{matrix} f_{p} \\ f_{p} \\ f_{p} \\ 0 \\ 0 \\ 0 \end{matrix})

이 때, $u_{i}$ 는 $i$ 방향으로 움직이는 입자의 변위, $τ_{i j}$ 는 $j$ 축에 수직인 면에 대해 $i$ 방향으로 작용하는 응력을 의미하며 ( $τ_{x x}, τ_{y y}, τ_{z z}$ )는 수직응력, ( $τ_{y z}, τ_{x z}, τ_{x y}$ )는 전단응력이다. $f_{x}, f_{y}, f_{z}$ 는 각각 육상탐사에서 사용되는 x, y, z 방향에 대한 체적력 송신원을, $f_{p}$ 는 해양탐사에서 사용되는 압력 송신원을 의미한다. 모델의 물리적 특성인 $C_{i j}$ 는 P파 속도, S파 속도, 밀도, 라메상수(𝜆와 𝜇)에 의해 다음과 같이 표현될 수 있다.

(5)

C_{33} = λ + 2 μ = ρ v_{p}^{2}

(6)

C_{13} = λ = ρ (v_{p}^{2} - 2 v_{s}^{2})

(7)

C_{55} = μ = ρ v_{s}^{2}

위의 탄성파동방정식에서 각 응력성분과 변위성분은 공간 1차미분의 관계에 있으며, 변위를 계산하기 위해서는 응력 값이, 응력을 계산하기 위해서는 변위 값이 요구된다. 따라서 시간적으로도 공간적으로도 격자가 엇갈려 있는 엇격자 유한차분법을 이용하여 각 성분을 격자점에 정의하면, 평균값 계산없이 파동방정식의 수치해를 추정하는 것이 가능하다(Fig. 1).

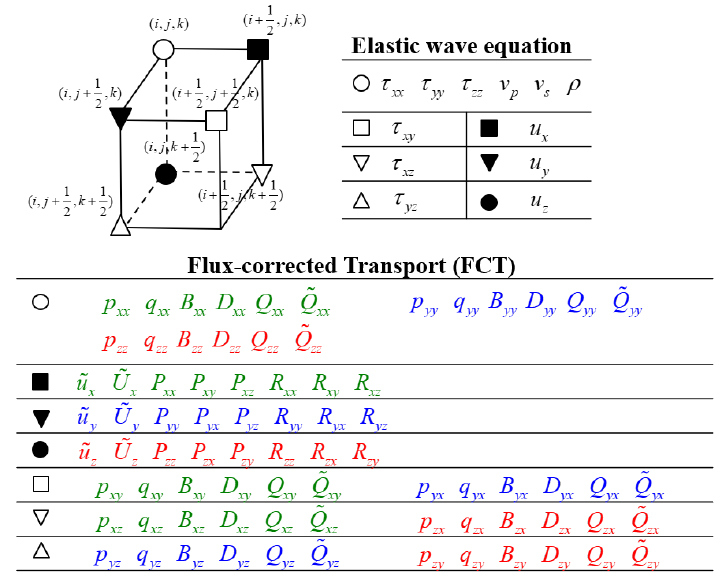
https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F1.jpg

Fig. 1.

Grid layout of a standard staggered-grid formulation (modified from Graves, 1996). A unit cell consists of particle displacements and normal and shear stresses. The variables of flux-corrected transport are also defined on the staggered-grid. The green, blue, and red colors denote the variables required for the flux-corrected transport of particle displacements along x, y, and z directions, respectively.

영역 분할법을 이용한 병렬 모델링 알고리듬

3차원 탄성파동방정식의 해를 수치해석적으로 구하기 위해서는 방대한 메모리가 요구된다. 마지막 수치예제인 북해 볼브 유전 모델을 예로 들면, 10 m 격자를 사용할 경우 모델의 공간격자 수가 1125 × 620 × 450개이며 P파 속도 값 하나를 배열에 저장하는 데에도 약 1 GB의 메모리가 요구된다. 따라서 3차원 탄성파동방정식을 계산하는 필요한 변수의 수와 시간격자의 수, 향후 탄성파 완전파형역산이나 역시간 구조보정 기술로의 확장 가능성을 고려한다면, 다중노드-다중코어 클러스터 환경에서의 모델링 알고리듬의 병렬화가 필수적이다. 그러므로 대규모 3차원 탄성파 모델링 문제에서 MPI(Message Passing Interface) 기반의 영역분할법은 알고리듬의 효율성을 향상시키기 위하여 필수적으로 적용되고 있다(Bohlen, 2002; Oh, 2020).

영역분할법은 전체 3차원 모델 영역(global domain)을 활용가능한 코어 수에 맞게 소 영역(subdomain)으로 나누어 각각의 코어가 할당 받은 소 영역의 파동방정식을 동시에 계산하는 방법이다. 이 때 각각의 코어는 소 영역의 경계에서 파동장의 값을 계산할 때 인접 격자의 이전 시간 파동장 정보가 없는 상태이기 때문에, 인접 소 영역을 할당 받은 코어와 정보를 교환해야 한다. 이를 위한 대표적인 정보교환 방법이 MPI로 MPI_send와 MPI_recv 명령어를 이용하여 소 영역의 경계의 파동장 값을 서로 교환할 수 있다. Fig. 2는 x방향과 y방향으로 2개씩 총 4개의 소 영역으로 병렬화하였을 때 파동방정식의 각 변수가 어떻게 교환되어야 하는지를 보여준다. 각 소 영역의 경계에서 패딩영역(Padding area)을 설정하고, 인접 코어에서 받은 파동장 값을 패딩영역에 저장하면, 소 영역의 경계에서도 마치 모델이 연속적으로 연결된 것처럼 모델링을 수행할 수 있다. 따라서 충분한 코어만 확보된다면, 빠른 시간에 대규모의 3차원 탄성파 모델링이 가능하다. 본 연구에서는 두 줄의 패딩영역을 설정하여 공간 4차 미분 유한차분법을 적용하였다.

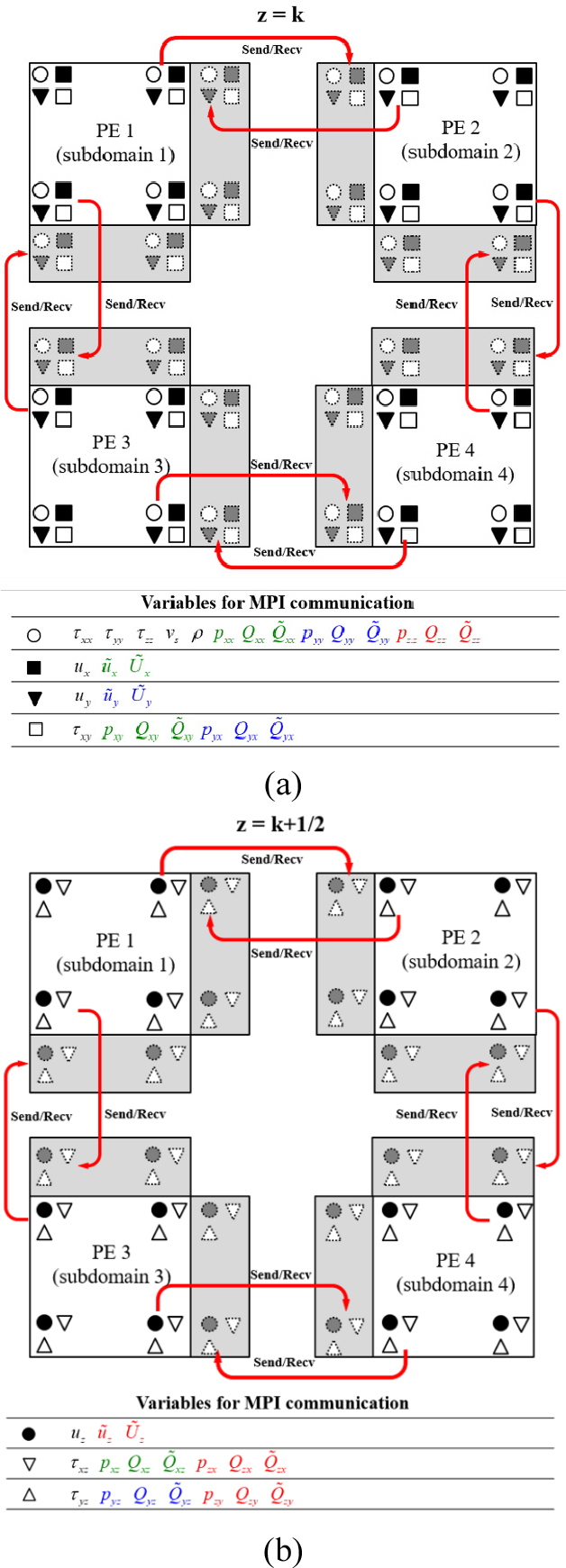
https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F2.jpg

Fig. 2.

The mechanism of domain decomposition at (a) z = k and (b) z = k+1/2 with 4 processing elements (PE). The wavefields at the boundaries of each subdomain are interchanged using an MPI along red arrows and are stored in the gray padding areas (modified from Bohlen, 2002 and Oh, 2020). The green, blue, and red colors denote the additional variables required for the flux-corrected transport of particle displacements along x, y, and z directions, respectively.

플럭스 보정기법을 이용한 3차원 탄성파 모델링

플럭스 보정기법(Flux-corrected transport)

다양한 물리적인 방정식의 수치해석 분야에서 활용되고 있는 플럭스 보정기법은 탄성파 모델링 분야에서 공간격자가 너무 클 경우에 발생하는 수치적인 분산을 제거하기 위한 목적으로 적용되고 있다(Fei and Larner, 1995; Zhao et al., 2014; Wang et al., 2014). 특히 S파까지 고려한 탄성파 모델링에서는 파장이 짧은 S파의 수치분산을 피하기 위해서는 더 작은 공간격자가 요구되는데, 마지막 수치예제인 북해 볼브 유전 지역과 같이 연약한 해저환경에서는 S파 속도가 300 m/s 정도로 느리기 때문에 최대주파수 20Hz로 모델링을 하더라도 약 2.5 m 정도의 공간격자가 요구된다. 이를 위한 공간격자 수는 4500 × 2480 × 1800개로 영역분할법으로 병렬화한다 하더라도 국내의 계산 클러스터 규모를 고려하면 현실적으로 불가능한 수치이다. 따라서 대규모 3차원 탄성파 모델링에서 이론적으로 가능한 가장 큰 공간격자를 설정하더라도 수치분산을 효율적으로 제거해줄 수 있는 플럭스 보정기법을 적용하는 것이 필요하다.

플럭스 보정기법은 확산플럭스(diffusion flux) 보정 단계와 확산방지플럭스(anti-diffusion flux) 보정 단계로 구분된다. 확산플럭스 보정 단계는 전체적으로 파동장을 평활화(smoothing)하는 효과를 주어 수치분산을 제거해주는 단계로 수치분산은 제거가 되지만 진폭과 분해능 손실이 발생한다. 이러한 진폭과 분해능 손실을 일부 복원해주기 위한 단계가 확산방지플럭스 보정 단계이다. 3차원 탄성파 모델링에서 플럭스 보정기법은 각각의 입자 변위 성분에 대해서 적용되는데, 본문에서는 x방향의 입자변위에 대한 보정식 위주로 설명하고, y방향과 z방향 입자변위에 대한 보정식은 각각 부록 A, B에 수록하였다. 본 논문에서는 엇격자 상에서 정의되는 플러스 보정기법을 간략한 수식으로 표현하기 위해서 임시 변수를 사용하였지만, 실제 알고리듬에서는 메모리 절약을 위해서 임시 변수를 저장하지 않는 것이 바람직하다.

먼저 x방향 입자변위에 대해 1단계인 확산플럭스 보정을 적용하기 위해서는 다음 수식과 같이 확산플럭스( $P_{x x}^{t}, P_{x y}^{t}, P_{x z}^{t}$ )를 계산한다.

(8)

P_{x x}^{t} (i, j, k) = ξ_{1} [D_{x x}^{t} (i, j, k) - D_{x x}^{t - ∆ t} (i, j, k)]

(9)

P_{x y}^{t} (i + h, j + h, k) = x i_{1} [D_{x y}^{t} (i + h, j + h, k) - D_{x y}^{t - ∆ t} (i + h, j + h, k)]

(10)

P_{x z}^{t} (i + h, j, k + h) = ξ_{1} [D_{x z}^{t} (i + h, j, k + h) - D_{x y}^{t - ∆ t} (i + h, j, k + h)]

첫 번째 아래첨자는 입자변위의 진동방향, 두 번째 아래첨자는 공간미분의 방향을 의미한다. 이 때, 임시변수 D는 다음과 같으며 파동방정식을 통해서 계산된 이전 시간의 입자변위 성분의 공간 변화량이다.

(11)

D_{x x}^{t} (i, j, k) = u_{x}^{t} (i + h, j, k) - u_{x}^{t} (i - h, j, k)

(12)

D_{x y}^{t} (i + h, j + h, k) = u_{x}^{t} (i + h, j + 2 h, k) - u_{x}^{t} (i + h, j, k)

(13)

D_{x z}^{t} (i + h, j, k + h) = u_{x}^{t} (i + h, j, k + 2 h) - u_{x}^{t} (i + h, j, k)

$h$ 는 공간격자 간격의 절반크기를 의미하며, $ξ_{1}$ 은 확산플럭스 보정의 가중치이다. 큰 값을 사용할수록 확산플러스 보정이 강하게 적용되는데 0.2 이상의 너무 큰 값을 사용하면 수치해석적인 오류를 유발할 수 있다. 계산된 확산플럭스의 공간 변화량을 이용하여 식 (14)와 같이 파동방정식으로 계산된 예측한 시간의 입자변위를 보정해주면 확산플럭스가 보정된 파동장 U를 구할 수 있다.

(14)

{\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k) = u_{x}^{t + ∆ t} (i + h, j, k) + [P_{x x}^{t} (i + h, j, k) + P_{x y}^{t} (i + h, j, k) + P_{x z}^{t} (i + h, j, k)]

이 때, 임시 변수 P는 계산된 확산플럭스의 공간 변화량으로 다음과 같다.

(15)

P_{x x}^{t} (i + h, j, k) = p_{x x}^{t} (i + 2 h, j, k) - p_{x x}^{t} (i, j, k)

(16)

P_{x y}^{t} (i + h, j, k) = p_{x y}^{t} (i + h, j + h, k) - p_{x y}^{t} (i, j - h, k)

(17)

P_{x}^{t} z (i + h, j, k) = p_{x}^{t} z (i + h, j, k + h) - p_{x}^{t} z (i + h, j, k - h)

앞서 언급했듯이, 확산플럭스 보정 단계는 수치분산을 제거해주지만, 진폭과 분해능 손실을 유발하기 때문에, 확산방지플럭스 보정 단계가 추가적으로 요구된다. 대규모 3차원 병렬 탄성파 모델링에서는 플럭스 보정기법을 적용하는데 상당한 시간이 소요되기 때문에, 추가적인 진폭과 분해능 손실이 발생하더라도 단순히 수치분산을 제거하는 것이 목적이라면 확산방지플럭스 보정 단계는 생략 가능하다.

확산방지플럭스 보정단계를 적용하기 위해서는 먼저 예측한 시간과 현재시간의 임시변수 D를 이용하여 다음 식과 같이 확산플럭스를 계산한다.

(18)

q_{x}^{t + ∆ t} x (i, j, k) = ξ_{2} [D_{x x}^{t + ∆ t} (i, j, k) - D_{x x}^{t} (i, j, k)]

(19)

q_{x y}^{t + ∆ t} (i + h, j + h, k) = ξ_{2} [D_{x y}^{t + ∆ t} (i + h, j + h, k) - D_{x y}^{t} (i + h, j + h, k)]

(20)

q_{x z}^{t + ∆ t} (i + h, j, k + h) = ξ_{2} [D_{x z}^{t + ∆ t} (i + h, j, k + h) - D_{x z}^{t} (i + h, j, k + h)]

$ξ_{2}$ 은 확산방지플럭스 보정의 가중치로, 확산플럭스 보정의 가중치( $ξ_{1}$ )보다 10 ~ 15% 큰 값을 사용할 것을 권고하고 있다(Fei and Larner, 1995). 확산플럭스가 보정된 파동장(U)을 이용하여, 다시 한번 확산플럭스를 계산한다.

(21)

Q_{x x}^{t + ∆ t} (i, j, k) = [B_{x x}^{t + ∆ t} (i, j, k) - D_{x x}^{t} (i, j, k)]

(22)

Q_{x y}^{t + ∆ t} (i + h, j + h, k) = [B_{x y}^{t + ∆ t} (i + h, j + h, k) - D_{x y}^{t} (i + h, j + h, k)]

(23)

Q_{x z}^{t + ∆ t} (i + h, j, k + h) = [B_{x z}^{t + ∆ t} (i + h, j, k + h) - D_{x z}^{t} (i + h, j, k + h)]

이 때, 임시변수 B는 확산플럭스가 보정된 파동장의 공간 변화량이다.

(24)

B_{x x}^{t + ∆ t} (i, j, k) = {\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k) - {\tilde{U}}_{x}^{t + ∆ t} (i - h, j, k)

(25)

B_{x y}^{t + ∆ t} (i + h, j + h, k) = {\tilde{U}}_{x}^{t + ∆ t} (i + h, j + 1, k) - {\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k)

(26)

B_{x z}^{t + ∆ t} (i + h, j, k + h) = {\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k + 2 h) - {\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k)

다음 단계는 확산방지플럭스가 보정되어야 하는 영역과 보정되지 않아도 되는 영역을 탐지하는 단계로 다음 수식에 의해 결정될 수 있다.

(27)

{\tilde{Q}}_{x x}^{t + ∆ t} (i, j, k) = s_{x} \cdot \max \{0, \min [s_{x} \cdot Q_{x x}^{t + ∆ t} (i - 2 h, j, k), | q_{x x}^{t + ∆ t} (i, j, k) |, s_{x} \cdot Q_{x x}^{t + ∆ t} (i + 2 h, j, k)]\}

(28)

{\tilde{Q}}_{x y}^{t + ∆ t} (i + h, j + h, k) = s_{y} \cdot \max \{0, \min [s_{y} \cdot Q_{x y}^{t + ∆ t} (i + h, j - h, k), | q_{x y}^{t + ∆ t} (i + h, j + h, k) |, s_{y} \cdot Q_{x y}^{t + ∆ t} (i + h, j + 3 h, k)]\}

(29)

{\tilde{Q}}_{x z}^{t + ∆ t} (i + h, j, k + h) = s_{z} \cdot \max \{0, \min [s_{z} \cdot Q_{x z}^{t + ∆ t} (i + h, j, k - h), | q_{x z}^{t + ∆ t} (i + h, j, k + h) |, s_{z} \cdot Q_{x z}^{t + ∆ t} (i + h, j, k + 3 h)]\}

이 때,

(30)

s_{x} = sign (q_{xx}^{t + ∆ t} (i, j, k))

(31)

s_{y} = sign (q_{xy}^{t + ∆ t} (i + h, j + h, k))

(32)

s_{z} = sign (q_{xz}^{t + ∆ t} (i + h, j, k + h))

이렇게 추정된 보정치를 이용하여 확산플럭스가 보정되었던 파동장 U를 다시 한 번 보정해주면, 플럭스가 보정되어 진폭과 분해능 손실이 발생했던 지점의 일부 복원할 수 있다. 마지막으로 플럭스가 보정된 입자변위( ${\tilde{u}}_{x}^{t + ∆ t}$ )로 지속적으로 이전 시간의 입자변위를 갱신해가면서 파동을 전파시키면 수치분산이 제거된 파동장을 구현할 수 있다.

(33)

{\tilde{u}}_{x}^{t + ∆ t} (i + h, j, k) = {\tilde{U}}_{x}^{t + ∆ t} (i + h, j, k) - [R_{x x}^{t + ∆ t} (i + h, j, k) + R_{x y}^{t + ∆ t} (i + h, j, k) + R_{x z}^{t + ∆ t} (i + h, j, k)]

(34)

R_{x x}^{t + ∆ t} (i + h, j, k) = {\tilde{Q}}_{x x}^{t + ∆ t} (i + 2 h, j, k) - {\tilde{Q}}_{x x}^{t + ∆ t} (i, j, k)

(35)

R_{x y}^{t + ∆ t} (i + h, j, k) = {\tilde{Q}}_{x y}^{t + ∆ t} (i + h, j + h, k) - {\tilde{Q}}_{x y}^{t + ∆ t} (i + h, j - h, k)

(36)

R_{x z}^{t + ∆ t} (i + h, j, k) = {\tilde{Q}}_{x z}^{t + ∆ t} (i + h, j, k + h) - {\tilde{Q}}_{x z}^{t + ∆ t} (i + h, j, k - h)

플럭스 보정기법의 원리 및 병렬화

확산플럭스 보정 단계와 확산방지플럭스 보정 단계의 영향을 검토하기 위하여, 2차원 탄성파동방정식 모델링 알고리듬을 이용하여, 균질매질에 대한 시뮬레이션을 수행하였다. 송신원 함수는 최대주파수가 10 Hz인 리커함수를 사용하였으며, S파가 발생할 수 있도록 수직방향의 체적력을 가정하였다. P파 속도는 1.5 km/s, S파 속도는 1 km/s 또는 0.3 km/s, 밀도는 1g/cm³으로 가정하였다. 공간격자는 20 m로 설정하였는데, Fig. 3a에서 확인할 수 있듯이 S파 속도(1 km/s)가 충분히 빠른 경우에는 주어진 조건에서 공간 4차 미분 유한차분법으로 수치분산의 영향을 최소화할 수 있는 것을 보여준다. 하지만, 연약한 해저지반과 같이 S파 속도가 느린 경우에는 구현된 S파가 수치분산에 의해 심하게 왜곡되는 것을 확인할 수 있다(Fig. 3b). 따라서 S파 속도가 느려지는 경우에는 더 작은 공간격자를 사용해야 하며, Fig. 3c에서 확인할 수 있듯이 5m의 공간격자를 사용해야 S파의 수치분산을 제거할 수 있다. 하지만 시간영역 3차원 탄성파 모델링 문제에서 공간격자를 2배 줄일 경우, 소요 계산시간은 16배 이상, 요구 메모리는 8배 이상으로 증가된다. 따라서 기존의 방법으로는 연약한 해저면을 고려한 대규모 3차원 탄성파 모델링을 수행하여 수치분산 영향 없는S파를 구현하는 것이 현실적으로 불가능한 상황이다.

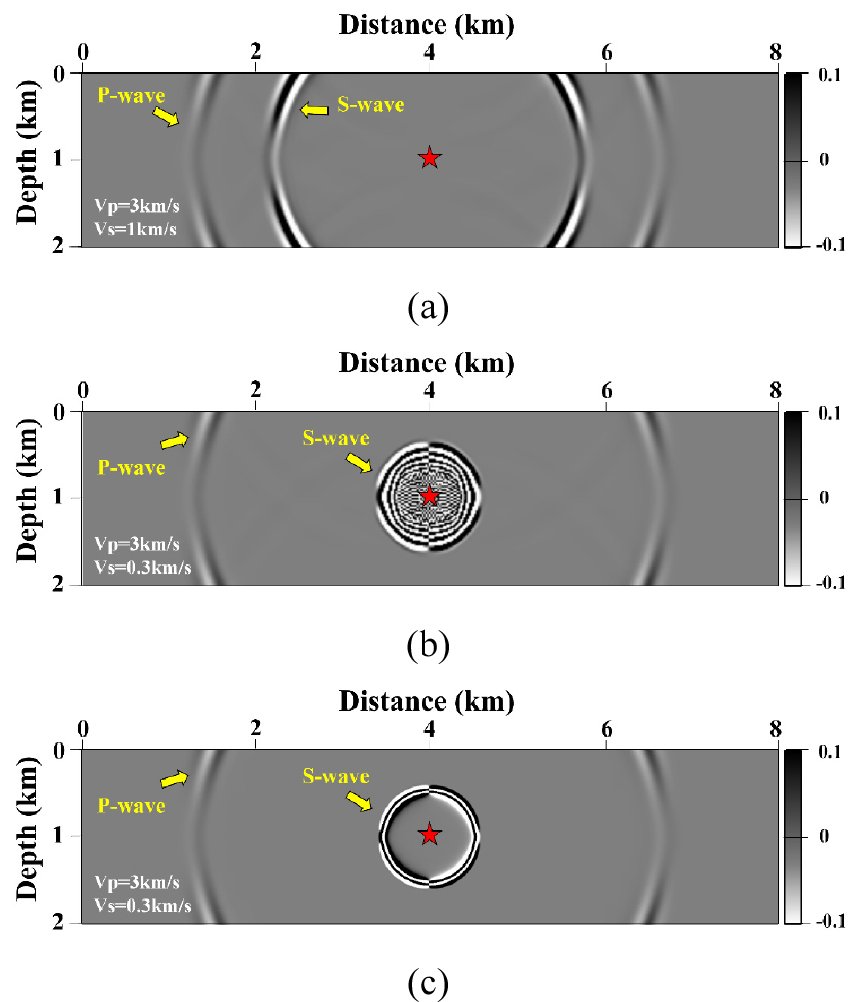
https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F3.jpg

Fig. 3.

Snapshots of horizontal particle displacement at 2 s on the homogeneous elastic media: (a) high S-wave velocity (1 km/s) to avoid numerical dispersion of S-wave. (b) slower S-wave velocity (0.3 km/s) with large grid sampling (0.02 km) and (c) slower S-wave velocity (0.3 km/s) with small grid sampling (0.005 km) to avoid numerical dispersion. Red star indicates the location of the vertical body force.

Fig. 4는 동일한 문제에 대하여 플럭스 보정기법을 적용한 결과를 보여준다. 플럭스 보정기법의 확산플럭스 보정 단계만을 수행하였을 때( $ξ_{1}$ =0.005), 진폭과 분해능이 일부 손실되면서 S파의 수치분산이 제거되지만 너무 큰 보정치를 사용하면( $ξ_{1}$ =0.03) 더 큰 손실을 유발하는 것을 확인할 수 있다(Fig. 4c). 이러한 진폭과 분해능 손실은 추가적인 확산방지플럭스 보정 단계를 거쳐서 일부 복원될 수 있지만, 작은 격자로 모델링한 결과(Fig. 3c)와 비교했을 때 정확한 복원은 어렵기 때문에, S파의 정확한 진폭과 주파수 스펙트럼 정보가 요구되는 정밀한 모델링에서는 주의가 필요하다. 하지만 위상 기반의 탄성파 역산이나, 정성적인 역시간 구조보정에서는 플럭스 보정기법이 충분히 적용되어 S파 속도 정보를 활용하는데 도움이 될 것으로 판단된다.

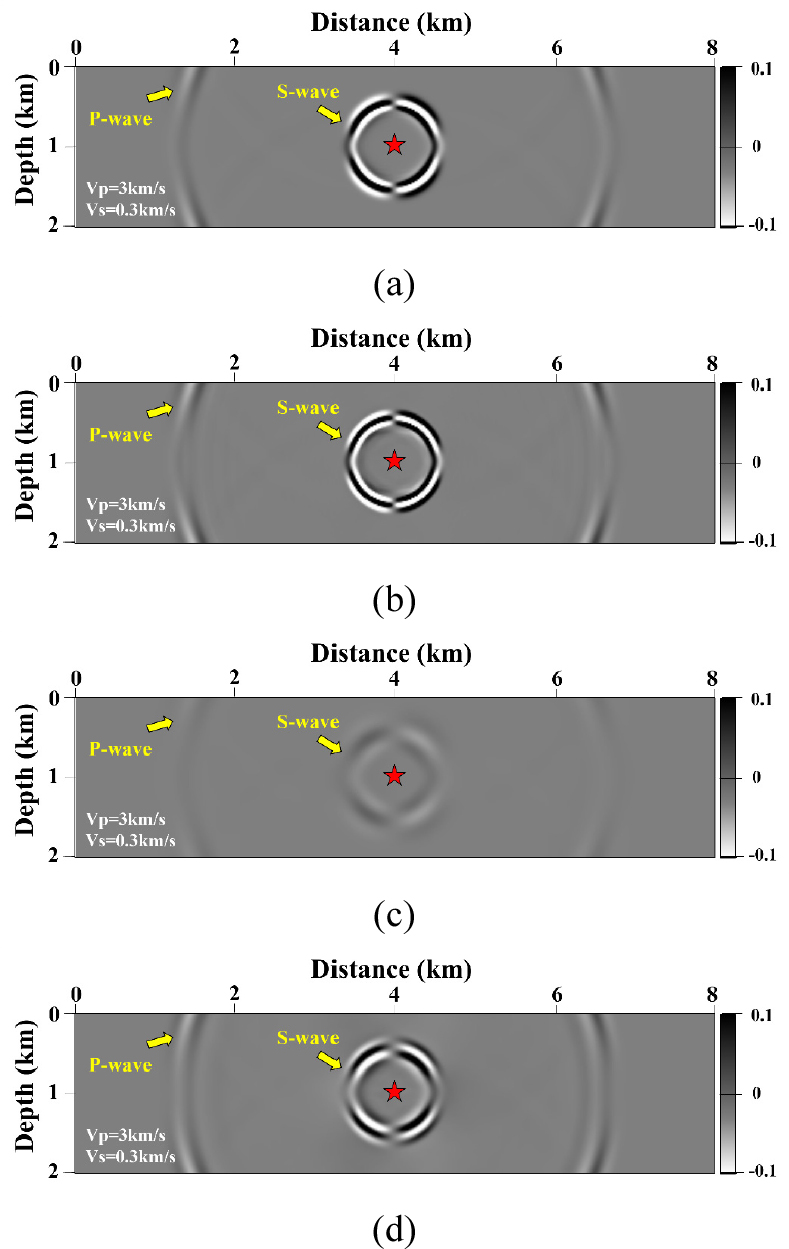
https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F4.jpg

Fig. 4.

Snapshots of horizontal particle displacement at 2 s on the homogeneous elastic media with large grid sampling (0.02 km): (a) after FCT with only diffusion flux ( $ξ_{1}$ =0.005) and (b) with additional anti-diffusion flux ( $ξ_{2}$ =0.0055). (c) after FCT with only diffusion flux ( $ξ_{1}$ =0.03) and (d) with additional anti-diffusion flux ( $ξ_{2}$ =0.033). Red star indicates the location of the vertical body force.

영역분할법 기반의 병렬 3차원 탄성파 모델링 알고리듬에서는, 공간 변화량을 주로 측정하는 플럭스 보정기법 적용하기 위하여 소 영역의 경계에서 자료교환이 이루어져야 한다. 따라서 Fig. 2에서 보여주는 것처럼 엇격자 상에서 정의된 플럭스 보정기법에 사용된 변수들을 인접 소 영역의 코어와 적절하게 교환하는 것이 필요하며, 이는 영역분할법을 위해 수행된 MPI 기반 자료교환과 동일하기 때문에 생략한다.

3차원 2층 모델에 대한 적용성 검토

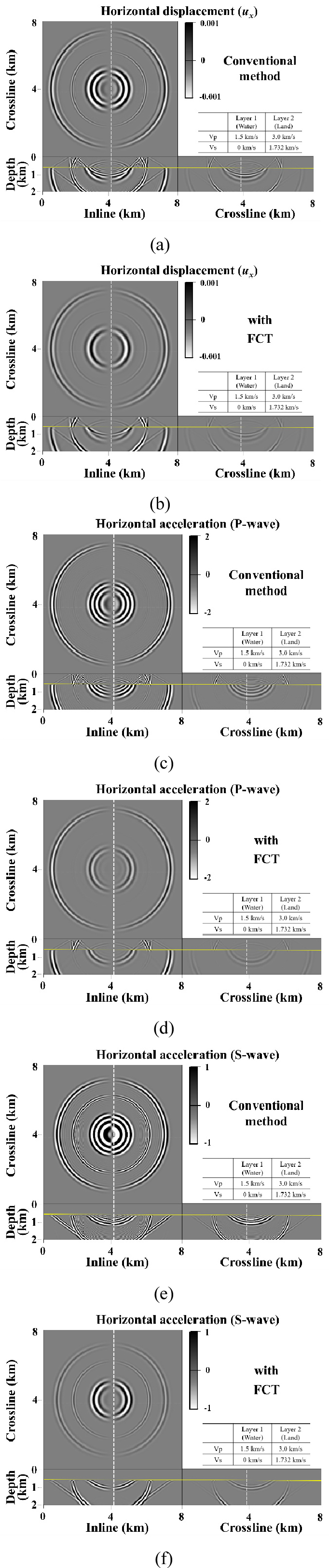
대규모 3차원 탄성파 모델링에서의 플럭스 보정기법의 적용성을 검토하기 위하여, 2층 속도모델에 대한 시뮬레이션을 수행하였다. 모델 크기는 8 km × 8 km × 2 km이며, 20 m 공간격자를 사용하였다. 1층과 2층의 P파 속도와 S파 속도는 각각 (1.5, 0)과 (3.0, 1.732) km/s이며, 1층의 두께는 600 m이다. 밀도는 1g/cm³으로 균질한 모델을 가정하였다. 최대 주파수 20 Hz인 리커함수로 해수면 중앙에서의 압력 송신원을 구현하였으며, S파의 수치분산 현상을 잘 관측하기 위해서 x방향의 수평성분 변위만을 도시하였다. 또한 다양한 모드 변환파 사이에서 P파와 S파를 잘 구분하기 위하여 계산된 변위 성분에 Helmholtz분해법(Helmholtz decomposition)을 적용하여, 입자가속도 성분으로 P파와 S파를 분해하여 도시하였다. 플럭스 보정기법의 가중치는 확산플럭스 보정과 확산방지플럭스 보정을 위하여 각각 $ξ_{1}$ =0.005와 $ξ_{2}$ =0.0055을 이용하였다.

Fig. 5는 플럭스 보정기법 적용 전(b, d, f)과 후(a, c, e)의 파동전파 차이를 보여주는데 설정된 주파수에 비해 공간격자가 너무 크기 때문에, 수치분산이 발생하는 것을 확인할 수 있다. 플럭스 보정기법을 적용했을 때, 이러한 수치분산이 잘 제거되는 것을 확인할 수 있으며 이러한 개선효과는 P파와 S파 만을 분리한 영상에서 더 명확하게 확인할 수 있다. 수치분산이 제거됨과 동시에 일부 진폭과 분해능이 손실되는 것도 확인되지만, 공간격자를 줄이면서 발생하는 추가적인 계산량을 고려한다면, 대규모 3차원 탄성파 모델링에서는 플럭스 보정기법을 적용하는 것이 상황에 따라서는 충분히 효율적인 전략일 수 있다.

https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F5.jpg

Fig. 5.

Snapshots at 1.6 s using the two-layered model for the horizontal particle displacements (a and b) and horizontal particle accelerations of P-wave (c and d) and S-wave (e and f): conventional method (a, c, and e) and FCT (b, d, and f). Yellow lines indicate the seabed.

북해 볼브 유전지역 3차원 탄성파동방정식 모델링

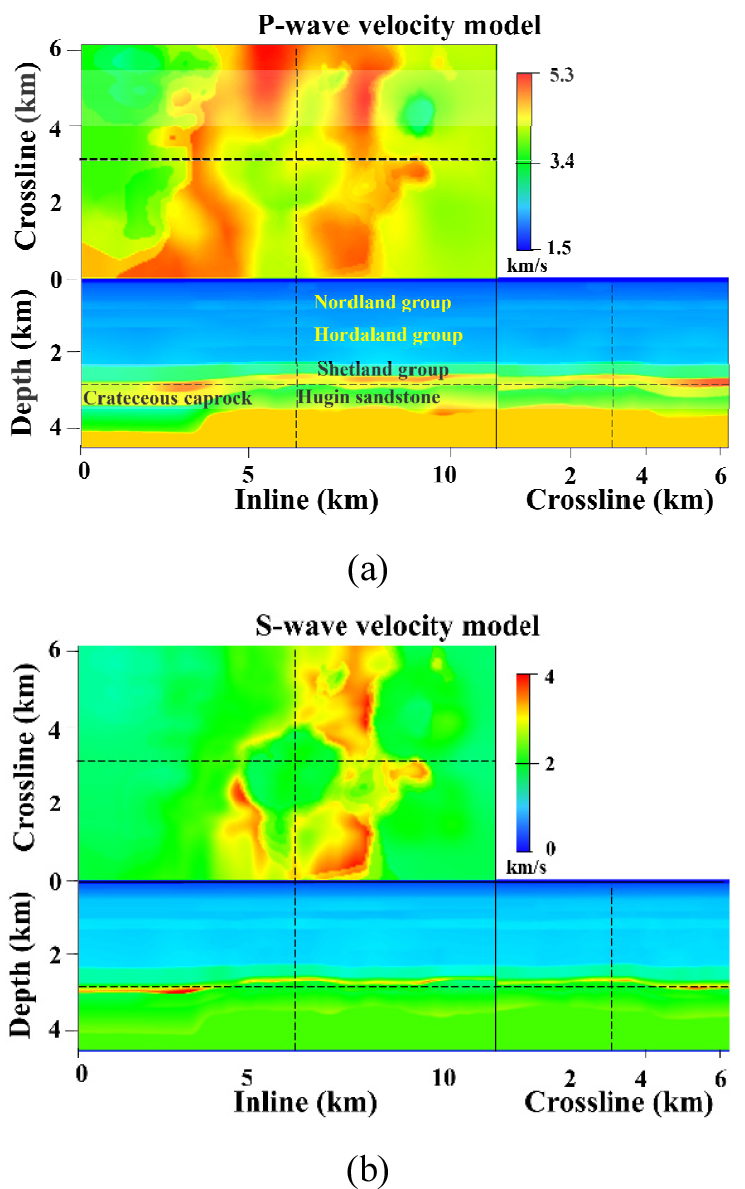
실제와 유사한 더 복잡한 3차원 지질구조와 연약한 해저지반을 가지는 지역에 대한 플럭스 보정기법 기반의 대규모 3차원 탄성파 모델링 기술의 적용성을 검토하기 위하여, 노르웨이의 국영석유회사 Equinor에서 공개한 북해 볼브 유전지역의 3차원 모델을 활용하였다(Szydlik et al., 2007; Oh et al., 2018; Oh and Alkhalifah, 2019). 북해 볼브 유전지역의 고품질의 3차원 4성분 해저면 탄성파 탐사자료가 2018년에 대중에게 공개된 상황이기 때문에, 북해 볼브 유전지역은 앞으로 국내에서 수행될 다성분 해저면 탐사자료 처리 및 영상화 연구에 활용될 가치가 충분한 지역이다. 3차원 모델의 크기는 11.25 km × 6.2 km × 4.5 km이며, 25 m 공간 격자를 사용하여 총 공간격자의 수는 450 × 248 × 180개이며, 기록시간은 5초, 시간간격 2 ms로 설정하여 총 시간 격자수는 2501개로 대규모의 3차원 문제에 해당된다(Fig. 6). S파 속도는 해저면 부근에서 300 m/s정도이며, 최대주파수가 30 Hz인 리커함수를 해수면 중앙의 압력송신원으로 설정하여 P파와 S파 모두 수치분산이 발생하도록 설정하였다. 밀도는 1g/cm³으로 가정하였다. 플럭스 보정기법의 가중치는 확산플럭스 보정과 확산방지플럭스 보정을 위하여 각각 $ξ_{1}$ =0.005와 $ξ_{2}$ =0.0055을 이용하였다.

https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F6.jpg

Fig. 6.

(a) P- and (b) S-wave velocity models of Volve oilfield located in the North Sea.

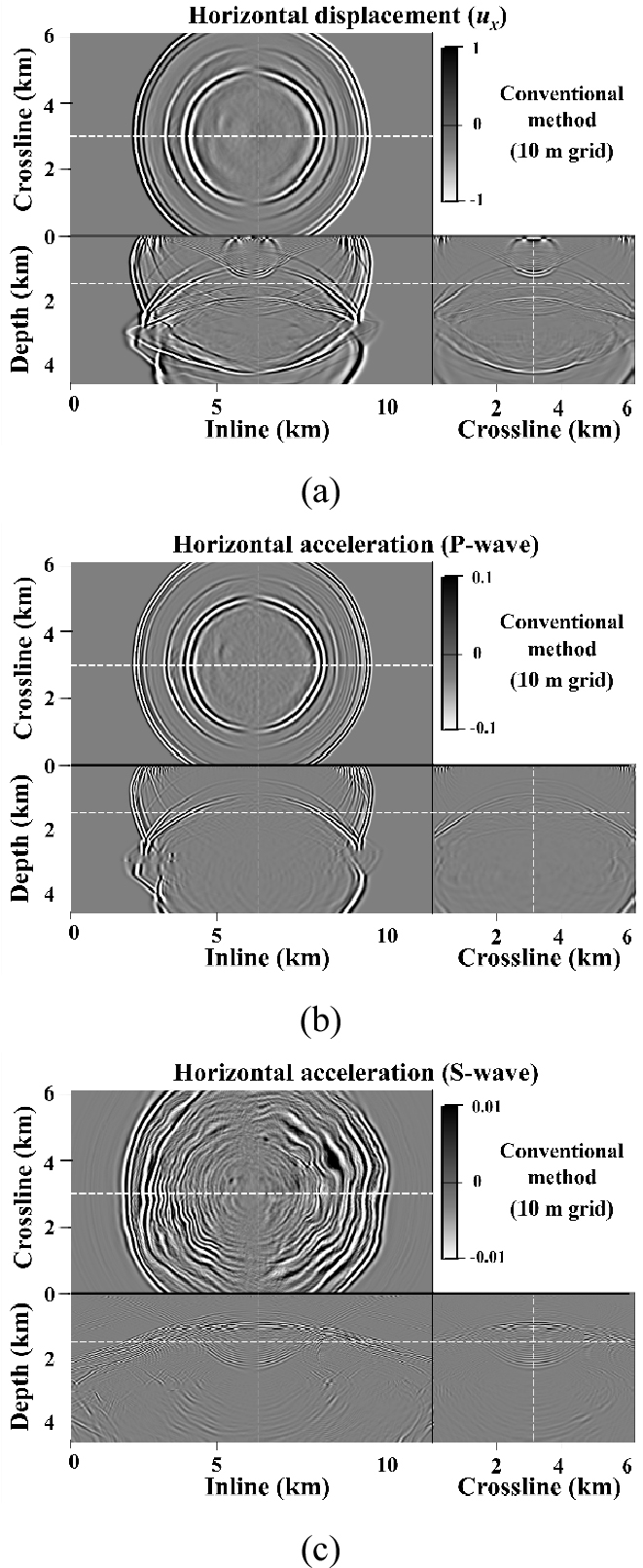
Fig. 7은 볼브 유전 지역 속도모델에서 획득된 탄성파 거동의 플럭스 보정기법 적용 전(왼쪽)과 후(오른쪽)의 차이를 보여주는데, 주어진 계산환경에서 현실적으로 사용가능한 큰 공간격자를 사용하였기 때문에, 기존 방법으로는 P파와 S파 모두 수치분산이 심하게 발생하는 것을 확인할 수 있다. 하지만 플럭스 보정기법을 적용함으로써 이러한 수치분산이 잘 제거되고, 진폭과 분해능 손실은 있지만 각 P파와 S파의 운동학적 특성은 잘 구현되는 것을 확인할 수 있다. Fig. 8은 기존의 방법으로 10 m의 더 작은 공간격자를 사용하여 수치분산을 줄인 결과이다. 해저면 부근의 S파 속도가 300 m/s 수준인 것을 고려하면 10 m의 격자도 여전히 얕은 심도에서 S파의 수치분산을 유발한다.

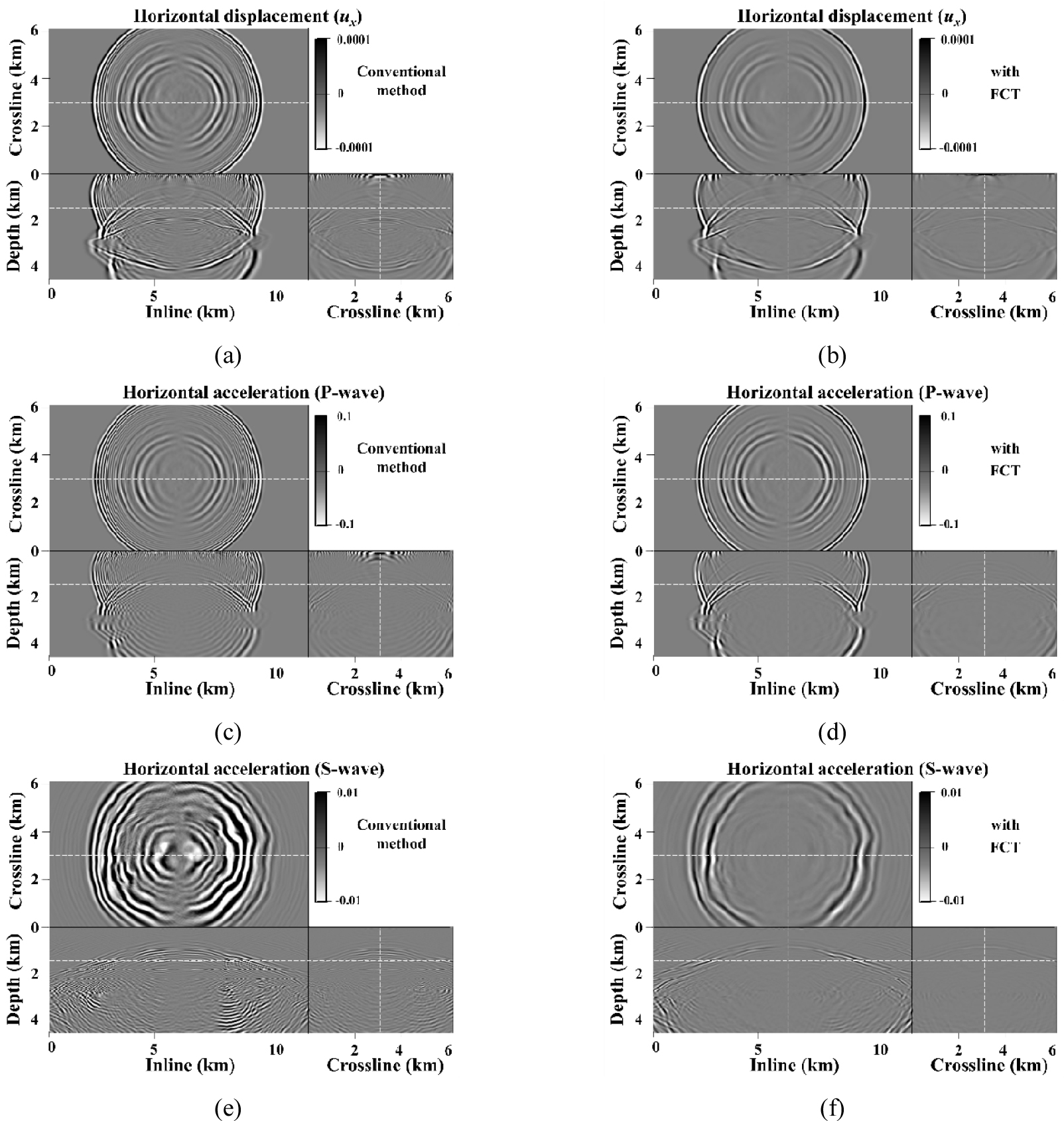
https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F7.jpg

Fig. 7.

Snapshots at 2 s (a, b, c, and d) and 3.2 s (e and f) of the velocity models of Volve oilfield capturing the horizontal particle displacements (a and b) and horizontal particle accelerations of P-wave (c and d) and S-wave (e and f): conventional method (a, c, and e) and FCT (b, d, and f). For mode-separated S-wave, snapshots at later time are also presented to clearly demonstrate the numerical dispersions of converted PS waves from the caprock.

https://cdn.apub.kr/journalsite/sites/ksmer/2022-059-01/N0330590105/images/ksmer_59_01_05_F8.jpg

Fig. 8.

Snapshots at 2 s (a and b) and 3.2 s (c) of the velocity models of Volve oilfield capturing the (a) horizontal particle displacements and (b) horizontal particle accelerations of P-wave and (c) S-wave using the conventional method with a smaller grid spacing (10 m).

10 m 격자를 사용할 경우, 에어건에서 발생하여 해저면에서 S파로 모드전환된 PS파가 25 m 격자를 사용했을 때보다 더 강하게 구현되는 것을 확인할 수 있는데(Fig. 7e와 Fig. 8c 비교), 해저면에서 변환된 S파는 매우 느리게 전파되어(Fig. 8c) 수치분산이 심하게 발생하는 것을 확인할 수 있다. 25 m 격자의 탄성파 모델링에서 이러한 해저면 PS파는 강하게 시뮬레이션 되지 않아서 플럭스 보정기법을 적용한 영상에서(Fig. 7f) 잘 나타나지는 않지만, 반사법 탐사에서 중요한 하부 덮개암과 저장층에서 변환된 PS파의 거동은 10 m 격자를 사용한 결과(Fig. 8c)와 비교하면 수치분산 없이 비교적 정확하게 구현되는 것을 확인할 수 있다. Table 1은 각 방법 별 계산시간을 비교한 것이다. 25 m 격자를 기준으로, 플럭스 보정기법을 적용했을 때 확산플럭스 보정단계, 확산방지플럭스 보정단계에서 각각 유한차분법 계산량에 소요된 시간만큼 추가 소요시간이 발생하여, 대략 3배정도 계산속도가 더 느린 것을 확인할 수 있다. 하지만 기존 방법에서는 수치분산을 줄이기 위하여 10 m 공간격자를 사용했을 때, 약 39배(2.5⁴)의 시간이 더 걸린 것을 통해 추정해보면, 수치분산을 완전히 제거하기 위한 2.5 m(공간격자 수 = 4500 × 2480 × 1800)의 공간격자를 사용했을 때에는 약 10,000배(10⁴)의 시간이 더 걸릴 것이며, 식 (4)의 한 응력 성분만을 저장하는데도 75 GB의 메모리가 필요하기 때문에, 국내 연구기관에서 보유하고 있는 소규모 클러스터에서는 불가능하다. 따라서 대규모 3차원 탄성파 모델링에서 S파의 수치분산을 제거하기 위한 목적으로는 플럭스 보정기법을 활용하는 것이 더 현실적인 선택으로 판단된다. 그렇지 않다면, 수치분산을 피하기 위해 매우 낮은 주파수의 송신원 함수를 이용해서 모델링을 해야 하며, 파장이 길어짐에 따라 송신원 함수의 중심에너지가 지연되어, 정확한 도달 시간을 추정하기 어렵다. 결론적으로, 플럭스 보정기법을 적용하면 진폭과 분해능의 손실은 발생하지만, 대규모 3차원 해저면 탐사자료에 대한 위상기반의 파형역산을 통한 P파, S파 속도 추정 문제나, PS 반사면의 정성적인 역시간 구조보정 문제에서 수치분산의 영향 없이 S파의 도달시간 정보를 활용할 수 있을 것으로 기대된다.

Table 1.

Comparison of computing time for solving wave equation, data communication with MPI and applying FCT.

	Conventional (25 m grid)	FCT (Diffusion flux)	FCT (Diffusion + Anti-diffusion flux)	Conventional (10 m grid)
Number of grids (including PML)	480 × 280 × 200 × 2501			1205 × 700 × 500 × 6251
Time (sec) (FDM)	453	414	442	17307
Time (sec) (MPI)	59	79	57	812
Time (sec) (FCT)	0	584	1121	0

결 론

본 연구에서는 대규모 3차원 탄성파동방정식 모델링 과정에서 수치 분산을 제거하기 위해 플럭스 보정기법을 적용한 병렬 3차원 탄성파 모델링 알고리듬을 제안하였다. 먼저 3차원 탄성파동방정식 모델링의 MPI기반 병렬화 알고리듬을 소개하고, 플럭스 보정기법의 이론과 원리를 2차원 시뮬레이션 결과를 기반으로 설명하였다. 다음으로 플럭스 보정기법 적용에 필요한 변수를 엇격자 상에 정의시키면서 MPI 기반 3차원 병렬 탄성파 모델링 알고리듬에 적용하였다. 3차원 2층 모델에 대한 시뮬레이션 결과 비교를 통하여, 플럭스 보정기법이 진폭과 분해능의 손실을 유발하지만, 큰 공간격자로도 S파의 운동학적인 정보를 구현할 수 있는 것을 확인하였다. 보다 현실적인 지층모델인 북해 볼브 유전 지역 속도모델에 대한 시뮬레이션 결과, 플럭스 보정기법으로 더 큰 격자로도 수치분산 없이 덮개암에서 반사된 PS파의 전파 거동이 구현되는 것을 확인할 수 있었다. 이는 국내 소규모의 클러스터 환경에서도 북해 볼브 유전지역에서 획득한 4성분 해저면 탐사자료를 활용하여 위상기반 파형역산을 통한 S파 속도 추정 연구나, 정성적인 역시간 구조보정을 통한 PS 반사면 추정 연구를 수행할 수 있는 가능성을 제시하는 결과이다. 하지만 이를 위해서는 플럭스 보정기법이 파동방정식의 수반 특성(adjoint state)를 유지시킬 수 있는지에 대한 세심한 주의가 필요하다. 연구 초기에는 플럭스 보정기법이 파동장에 평활화효과를 주어 분해능을 떨어뜨리기 때문에, 구조보정이나 파형역산과 같은 영상화 과정에서 수치분산을 피할 수 있는 저주파성분만을 모델링하는 것과 큰 차이가 없을지도 모른다는 우려가 제기되었다. 하지만 기존 방법은 수치분산에 의해 고주파 성분의 신호가 왜곡되지만, 플럭스 보정기법을 적용하면 고주파 성분의 신호에서도 수치분산의 영향이 줄어드는 것을 확인하였고, 이는 개선된 고주파 성분을 이용하여, 저주파 성분만을 이용했을 때보다 영상화의 분해능을 높일 수 있음을 지시한다. 이에 대한 후속연구가 활발하게 진행중이며, 향후 국내에서 취득될 3차원 해저면 탐사자료에 적용된다면 국내 이산화탄소 지중저장소 탐사나 유가스전 탐사에서 S파 속도 정보를 활용할 수 있을 것으로 기대된다.

부록 A: Y방향 변위에 대한 플럭스 보정 기법 유한차분식

부록 A에서는 Y방향 변위에서 대한 확산플럭스 보정 수식을 수록하였다. 플럭스 보정기법이 엇격자 유한차분법 기반의 병렬 탄성파 모델링에 적용되기 때문에, 엇격자 상에서 정확하게 정의하여 차분하는 것이 필수적이다. 1단계인 확산플럭스 보정을 위해, Y방향 변위에 대한 확산플럭스는 다음과 같이 계산될 수 있다.

(A-1)

p_{y x}^{t} (i + h, j + h, k) = ξ_{1} [D_{y x}^{t} (i + h, j + h, k) - D_{y x}^{t - ∆ t} (i + h, j + h, k)]

(A-2)

p_{y y}^{t} (i, j, k) = ξ_{1} [D_{y y}^{t} (i, j, k) - D_{y y}^{t - ∆ t} (i, j, k)]

(A-3)

p_{y z}^{t} (i, j + h, k + h) = ξ_{1} [D_{y z}^{t} (i, j + h, k + h) - D_{y z}^{t - ∆ t} (i, j + h, k + h)]

이 때,

(A-4)

D_{y x}^{t} (i + h, j + h, k) = u_{y}^{t} (i + 2 h, j + h, k) - u_{y}^{t} (i + h, j + h, k)

(A-5)

D_{y y}^{t} (i, j, k) = u_{y}^{t} (i, j + h, k) - u_{y}^{t} (i, j - h, k)

(A-6)

D_{y z}^{t} (i, j + h, k + h) = u_{y}^{t} (i, j + h, k + 2 h) - u_{y}^{t} (i, j + h, k)

파동방정식으로 추정한 $y$ 방향 변위는 식 (A-7)에 의해 확산플러스 보정 단계가 수행될 수 있다.

(A-7)

{\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k) = u_{y}^{t + ∆ t} (i, j + h, k) + [P_{y x}^{t} (i, j + h, k) + P_{y y}^{t} (i, j + h, k) + P_{y z}^{t} (i, j + h, k)]

(A-8)

P_{y x}^{t} (i, j + h, k) = p_{y x}^{t} (i + h, j + h, k) - p_{y x}^{t} (i - h, j + h, k)

(A-9)

P_{y y}^{t} (i, j + h, k) = p_{y y}^{t} (i, j + 2 h, k) - p_{y y}^{t} (i, j, k)

(A-10)

P_{y z}^{t} (i, j + h, k) = p_{y z}^{t} (i, j + h, k + h) - p_{y z}^{t} (i, j + h, k - h)

확산방지플럭스 보정단계는 X방향 변위와 마찬가지로,

(A-11)

q_{y x}^{t + ∆ t} (i + h, j + h, k) = ξ_{2} [D_{y x}^{t + ∆ t} (i + h, j + h, k) - D_{y x}^{t} (i + h, j + h, k)]

(A-12)

q_{y y}^{t + ∆ t} (i, j, k) = ξ_{2} [D_{y y}^{t + ∆ t} (i, j, k) - D_{y y}^{t} (i, j, k)]

(A-13)

q_{y z}^{t + ∆ t} (i, j + h, k + h) = ξ_{2} [D_{y z}^{t + ∆ t} (i, j + h, k + h) - D_{y z}^{t} (i, j + h, k + h)]

확산플러스 보정 단계가 적용된 파동장(U)에 대한 확산플럭스는 다음과 같이 계산된다.

(A-14)

Q_{y x}^{t + ∆ t} (i + h, j + h, k) = [B_{y x}^{t + ∆ t} (i + h, j + h, k) - D_{y x}^{t} (i + h, j + h, k)]

(A-15)

Q_{y y}^{t + ∆ t} (i, j, k) = [B_{y y}^{t + ∆ t} (i, j, k) - D_{y y}^{t} (i, j, k)]

(A-16)

Q_{y z}^{t + ∆ t} (i, j + h, k + h) = [B_{y z}^{t + ∆ t} (i, j + h, k + h) - D_{y z}^{t} (i, j + h, k + h)]

이 때,

(A-17)

B_{y x}^{t + ∆ t} (i + h, j + h, k) = {\tilde{U}}_{y}^{t + ∆ t} (i + 2 h, j + h, k) - {\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k)

(A-18)

B_{y y}^{t + ∆ t} (i, j, k) = {\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k) - {\tilde{U}}_{y}^{t + ∆ t} (i, j - h, k)

(A-19)

B_{y z}^{t + ∆ t} (i, j + h, k + h) = {\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k + 1) - {\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k)

확산방지플럭스를 적용할 영역은 다음 식에 의해 탐지될 수 있다.

(A-20)

{\tilde{Q}}_{y x}^{t + ∆ t} (i + h, j + h, k) = s_{x} \cdot \max \{0, \min [s_{x} \cdot Q_{y x}^{t + ∆ t} (i - h, j + h, k), | q_{y x}^{t + ∆ t} (i + h, j + h, k) |, s_{x} \cdot Q_{y x}^{t + ∆ t} (i + 3 h, j + h, k)]\}

(A-21)

{\tilde{Q}}_{y y}^{t + ∆ t} (i, j, k) = s_{y} \cdot \max \{0, \min [s_{y} \cdot Q_{y y}^{t + ∆ t} (i, j - 2 h, k), | q_{y y}^{t + ∆ t} (i, j, k) |, s_{y} \cdot Q_{y y}^{t + ∆ t} (i, j + 2 h, k)]\}

(A-22)

{\tilde{Q}}_{y z}^{t + ∆ t} (i, j + h, k + h) = s_{z} \cdot \max \{0, \min [s_{z} \cdot Q_{y z}^{t + ∆ t} (i, j + h, k - h), | q_{y z}^{t + ∆ t} (i, j + h, k + h) |, s_{z} \cdot Q_{y z}^{t + ∆ t} (i, j + h, k + 3 h)]\}

이 때,

(A-23)

s_{x} = sign (q_{yx}^{t + ∆ t} (i + h, j + h, k))

(A-24)

s_{y} = sign (q_{yy}^{t + ∆ t} (i, j, k))

(A-25)

s_{z} = sign (q_{yz}^{t + ∆ t} (i, j + h, k + h))

마지막으로, 확산방지플럭스 보정 단계는 확산플럭스가 보정된 파동장(U)에 대해 다음과 같이 적용된다.

(A-26)

{\tilde{u}}_{y}^{t + ∆ t} (i, j + h, k) = {\tilde{U}}_{y}^{t + ∆ t} (i, j + h, k) - [R_{y x}^{t + ∆ t} (i, j + h, k) + R_{y y}^{t + ∆ t} (i, j + h, k) + R_{y z}^{t + ∆ t} (i, j + h, k)]

이 때,

(A-27)

R_{y x}^{t + ∆ t} (i, j + h, k) = {\tilde{Q}}_{y x}^{t + ∆ t} (i + h, j + h, k) - {\tilde{Q}}_{y x}^{t + ∆ t} (i - h, j + h, k)

(A-28)

R_{y y}^{t + ∆ t} (i, j + h, k) = {\tilde{Q}}_{y y}^{t + ∆ t} (i, j + 2 h, k) - {\tilde{Q}}_{y y}^{t + ∆ t} (i, j, k)

(A-29)

R_{y z}^{t + ∆ t} (i, j + h, k) = {\tilde{Q}}_{y z}^{t + ∆ t} (i, j + h, k + h) - {\tilde{Q}}_{y z}^{t + ∆ t} (i, j + h, k - h)

부록 B: Z방향 변위에 대한 플럭스 보정 기법 유한차분식

Z방향 변위에 대한 확산플럭스는 다음과 같이 계산될 수 있다.

(B-1)

p_{z x}^{t} (i + h, j, k + h) = ξ_{1} [D_{z x}^{t} (i + h, j, k + h) - D_{z x}^{t - ∆ t} (i + h, j, k + h)]

(B-2)

p_{z y}^{t} (i, j + h, k + h) = ξ_{1} [D_{z y}^{t} (i, j + h, k + h) - D_{z y}^{t - ∆ t} (i, j + h, k + h)]

(B-3)

p_{z z}^{t} (i, j, k) = ξ_{1} [D_{z z}^{t} (i, j, k) - D_{z z}^{t - ∆ t} (i, j, k)]

이 때,

(B-4)

D_{z x}^{t} (i + h, j, k + h) = u_{z}^{t} (i + 2 h, j, k + h) - u_{z}^{t} (i + h, j, k + h)

(B-5)

D_{z y}^{t} (i, j + \frac{1}{2}, k + \frac{1}{2}) = u_{z}^{t} (i, j + 2 h, k + h) - u_{z}^{t} (i, j, k + h)

(B-6)

D_{z z}^{t} (i, j, k) = u_{z}^{t} (i, j, k + h) - u_{z}^{t} (i, j, k - h)

파동방정식으로 추정한Z방향 변위에 아래와 같이 확산플러스 보정을 수행한다.

(B-7)

{\tilde{U}}_{z}^{t + ∆ t} (i, j, k + h) = u_{z}^{t + ∆ t} (i, j, k + h) + [P_{z x}^{t} (i, j, k + h) + P_{z y}^{t} (i, j, k + h) + P_{z z}^{t} (i, j, k + h)]

이 때,

(B-8)

P_{z x}^{t} (i, j, k + h) = p_{z x}^{t} (i + h, j, k + h) - p_{z x}^{t} (i - h, j, k + h)

(B-9)

P_{z y}^{t} (i, j, k + h) = p_{z y}^{t} (i, j + h, k + h) - p_{z y}^{t} (i, j + h, k - h)

(B-10)

P_{z z}^{t} (i, j, k + h) = p_{z z}^{t} (i, j, k + 2 h) - p_{z z}^{t} (i, j, k)

확산방지플럭스 보정은 X방향, Y방향 변위와 마찬가지로, 아래와 같이 수행된다.

(B-11)

q_{z x}^{t + ∆ t} (i + h, j, k + h) = ξ_{2} [D_{z x}^{t + ∆ t} (i + h, j, k + h) - D_{z x}^{t} (i + h, j, k + h)]

(B-12)

q_{z y}^{t + ∆ t} (i, j + h, k + h) = ξ_{2} [D_{z y}^{t + ∆ t} (i, j + h, k + h) - D_{z y}^{t} (i, j + h, k + h)]

(B-13)

q_{z z}^{t + ∆ t} (i, j, k) = ξ_{2} [D_{z z}^{t + ∆ t} (i, j, k) - D_{z z}^{t} (i, j, k)]

확산플럭스가 보정된 Z방향 파동장에 대한 확산플럭스는 아래와 같이 계산된다.

(B-14)

Q_{z x}^{t + ∆ t} (i + h, j, k + h) = [B_{z x}^{t + ∆ t} (i + h, j, k + h) - D_{z x}^{t} (i + h, j, k + h)]

(B-15)

Q_{z y}^{t + ∆ t} (i, j + h, k + h) = [B_{z y}^{t + ∆ t} (i, j + h, k + h) - D_{z y}^{t} (i, j + h, k + h)]

(B-16)

Q_{z z}^{t + ∆ t} (i, j, k) = [B_{z z}^{t + ∆ t} (i, j, k) - D_{z z}^{t} (i, j, k)]

이 때,

(B-17)

B_{z x}^{t + ∆ t} (i + h, j, k + h) = {\tilde{U}}_{z}^{t + ∆ t} (i + 2 h, j, k + h) - {\tilde{U}}_{z}^{t + ∆ t} (i, j, k + h)

(B-18)

B_{z y}^{t + ∆ t} (i, j + h, k + h) = {\tilde{U}}_{z}^{t + ∆ t} (i, j + 2 h, k + h) - {\tilde{U}}_{z}^{t + ∆ t} (i, j, k + h)

(B-19)

B_{z z}^{t + ∆ t} (i, j, k) = {\tilde{U}}_{z}^{t + ∆ t} (i, j, k + h) - {\tilde{U}}_{z}^{t + ∆ t} (i, j, k - h)

확산방지플럭스를 적용할 영역은 다음 식에 의해 탐지될 수 있다.

(B-20)

Q_{z x}^{t + ∆ t} (i + h, j, k + h) = s_{x} \cdot \max \{0, \min [s_{x} \cdot Q_{z x}^{t + ∆ t} (i - h, j, k + h), |q_{z x}^{t + ∆ t} (i + h, j, k + h)|, s_{x} \cdot Q_{z x}^{t + ∆ t} (i + 3 h, j, k + h)]\}

(B-21)

{\tilde{Q}}_{z y}^{t + ∆ t} (i, j + h, k + h) = s_{y} \cdot \max \{0, \min [s_{y} \cdot Q_{z y}^{t + ∆ t} (i, j - h, k + h), |q_{z y}^{t + ∆ t} (i, j + h, k + h)|, s_{y} \cdot Q_{z y}^{t + ∆ t} (i, j + 3 h, k + h)]\}

(B-22)

{\tilde{Q}}_{z z}^{t + ∆ t} (i, j, k) = s_{y} \cdot \max \{0, \min [s_{z} \cdot Q_{z z}^{t + ∆ t} (i, j, k - 2 h), |q_{z z}^{t + ∆ t} (i, j, k)|, s_{z} \cdot Q_{z z}^{t + ∆ t} (i, j, k + 2 h)]\}

이 때,

(B-23)

s_{x} = sign (q_{zx}^{t + ∆ t} (i + h, j, k + h))

(B-24)

s_{y} = sign (q_{zy}^{t + ∆ t} (i + h, j, k + h))

(B-25)

s_{z} = sign (q_{zz}^{t + ∆ t} (i, j, k))

마지막으로, 확산방지플럭스 보정 단계는 확산플럭스가 보정된 파동장(U)에 대해 다음과 같이 적용된다.

(B-26)

{\tilde{u}}_{z}^{t + ∆ t} (i, j, k + h) = {\tilde{U}}_{z}^{t + ∆ t} (i, j, k + h) - [R_{z x}^{t + ∆ t} (i, j, k + h) + R_{z y}^{t + ∆ t} (i, j, k + h) + R_{z z}^{t + ∆ t} (i, j, k + h)]

이 때,

(B-27)

R_{z x}^{t + ∆ t} (i, j, k + h) = {\tilde{Q}}_{z x}^{t + ∆ t} (i + h, j, k + h) - {\tilde{Q}}_{z x}^{t + ∆ t} (i - h, j, k + h)

(B-28)

R_{z y}^{t + ∆ t} (i, j, k + h) = {\tilde{Q}}_{z y}^{t + ∆ t} (i, j + h, k + h) - {\tilde{Q}}_{z y}^{t + ∆ t} (i, j - h, k + h)

(B-29)

R_{z z}^{t + ∆ t} (i, j, k + h) = {\tilde{Q}}_{z z}^{t + ∆ t} (i, j, k + 2 h) - {\tilde{Q}}_{z z}^{t + ∆ t} (i, j, k)

Acknowledgements

본 연구는 2021년 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20212010200020). 볼브 유전 지역의 3차원 속도모델을 제공해주신 Equinor에 감사드립니다.

References

Alford, R.M., Kelly, K.R., and Boore, D.M., 1974. Accuracy of finite-difference modeling of the acoustic wave equation, Geophysics, 39(6), p.834-842. 10.1190/1.1440470

Bohlen, T., 2002. Parallel 3-D viscoelastic finite difference seismic modelling, Computers & Geosciences, 28(8), p.887-899. 10.1016/S0098-3004(02)00006-7

Book, D.L., Boris, J.P., and Hain, K., 1975. Flux-corrected transport II: Generalizations of the method, Journal of Computational Physics, 18(3), p.248-283. 10.1016/0021-9991(75)90002-9

Boris, J.P. and Book, D.L., 1973. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works, Journal of computational physics, 11(1), p.38-69. 10.1016/0021-9991(73)90147-2

Brossier, R., Operto, S., and Virieux, J., 2009. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion, Geophysics, 74(6), p.WCC105-WCC118. 10.1190/1.3215771

Cho, C.S. and Son, M.K., 2012. Application of ADE-PML boundary condition to SEM using variational formulation of velocity-stress 3D wave equation, Geophysics and Geophysical Exploration, 15(2), p.57-65. 10.7582/GGE.2012.15.2.057

Fei, T. and Larner, K., 1995. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport, Geophysics, 60(6), p.1830-1842. 10.1190/1.1443915

Fletcher, R.P., Du, X., and Fowler, P.J., 2009. Reverse time migration in tilted transversely isotropic (TTI) media, Geophysics, 74(6), p.WCA179-WCA187. 10.1190/1.3269902

Fornberg, B., 1987. The pseudospectral method: Comparisons with finite differences for the elastic wave equation, Geophysics, 52(4), p.483-501. 10.1190/1.1442319

Graves, R.W., 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences, Bulletin of the seismological society of America, 86(4), p.1091-1106.

Kalita, M. and Alkhalifah, T., 2019. Flux-corrected transport for full-waveform inversion, Geophysical Journal International, 217(3), p.2147-2164. 10.1093/gji/ggz105

Kelly, K.R., Ward, R.W., Treitel, S., and Alford, R.M., 1976. Synthetic seismograms: A finite-difference approach, Geophysics, 41(1), p.2-27. 10.1190/1.1440605

Kim, W.K. and Min, D.J., 2014. A new parameterization for frequency-domain elastic full waveform inversion for VTI media, Journal of Applied Geophysics, 109, p.88-110. 10.1016/j.jappgeo.2014.07.015

Kosloff, D.D., and Baysal, E., 1982. Forward modeling by a Fourier method, Geophysics, 47(10), p.1402-1412. 10.1190/1.1441288

Marfurt, K.J., 1984. Accuracy of finite-difference and finite- element modeling of the scalar and elastic wave equations, Geophysics, 49(5), p.533-549. 10.1190/1.1441689

Min, D.J., Kim, H.S., Yoo, H.S., and Kim, K.H., 2006. Three-dimensional time-domain elastic wave modeling using finite-difference method, Journal of the Korean Society for Geosystem Engineering, 43(1), p.65-75.

Min, D.J., Shin, C., and Yoo, H.S., 2004. Free-surface boundary condition in finite-difference elastic wave modeling, Bulletin of the Seismological Society of America, 94(1), p.237-250. 10.1785/0120020116

Oh, J.W., 2020. Parallel elastic wave modeling considering the effects of orthorhombic anisotropy, Journal of the Korean Society of Mineral and Energy Resources Engineers, 57(1), p.86-96 (in Korean with English abstract). 10.32390/ksmer.2020.57.1.086

Oh, J.W. and Alkhalifah, T., 2019. Study on the full‐waveform inversion strategy for 3D elastic orthorhombic anisotropic media: application to ocean bottom cable data, Geophysical Prospecting, 67(5), p.1219-1242. 10.1111/1365-2478.12768

Oh, J.W., Kalita, M., and Alkhalifah, T., 2018. 3D elastic full-waveform inversion using P-wave excitation amplitude: Application to ocean bottom cable field data, Geophysics, 83(2), p.R129-R140. 10.1190/geo2017-0236.1

Operto, S., Virieux, J., Dessa, J.X., and Pascal, G., 2006. Crustal seismic imaging from multifold ocean bottom seismometer data by frequency domain full waveform tomography: Application to the eastern Nankai trough, Journal of Geophysical Research: Solid Earth, p.111(B9). 10.1029/2005JB003835

Štekl, I. and Pratt, R.G., 1998. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators, Geophysics, 63(5), p.1779-1794. 10.1190/1.1444472

Szydlik, T.J., Way, S., Smith, P., Aamodt, L., and Friedrich, C., 2007. June, 3D PP/PS prestack depth migration on the Volve field. In 68th EAGE Conference and Exhibition incorporating SPE EUROPEC 2006 (pp. cp-2), European Association of Geoscientists & Engineers. 10.3997/1365-2397.25.1106.27412

Wang, J., Li, Z., and Steve, T., 2014. October. 3D elastic simulation with flux correction transport (FCT) for general anisotropic media, 84th SEG Technical Program Expanded Abstracts 2014, Society of Exploration Geophysicists, p.3498-3502. 10.1190/segam2014-0571.1PMC4097234

Xia, J., Miller, R. D., Xu, Y., Luo, Y., Chen, C., Liu, J., and Zeng, C., 2009. High-frequency Rayleigh-wave method, Journal of Earth Science, 20(3), p.563-579. 10.1007/s12583-009-0047-7

Zhang, Y., Sun, J., and Gray, S., 2007. Reverse-time migration: amplitude and implementation issues, 77th SEG Technical Program Expanded Abstracts 2007, Society of Exploration Geophysicists, p.2145-2149. 10.1190/1.2792912

Zhao, D., Hasegawa, A., and Horiuchi, S., 1992. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan, Journal of Geophysical Research: Solid Earth, 97(B13), p.19909-19928. 10.1029/92JB00603

Zhao, H., Gao, J., and Zhao, J., 2014. Modeling the propagation of diffusive-viscous waves using flux-corrected transport-finite-difference method, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7(3), p.838-844. 10.1109/JSTARS.2013.2294190

Zhou, W., Brossier, R., Operto, S., Virieux, J., and Yang, P., 2018. Velocity model building by waveform inversion of early arrivals and reflections: A 2D case study with gas-cloud effects, Geophysics, 83(2), p.R141-R157. 10.1190/geo2017-0282.1

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

A Study on Parallel 3D Elastic Wave Modeling Using Flux-corrected Transport

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Fig. 1.

Fig. 2.

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

Fig. 3.

Fig. 4.

Fig. 5.

Snapshots at 1.6 s using the two-layered model for the horizontal particle displacements (a and b) and horizontal particle accelerations of P-wave (c and d) and S-wave (e and f): conventional method (a, c, and e) and FCT (b, d, and f). Yellow lines indicate the seabed.

Fig. 6.

(a) P- and (b) S-wave velocity models of Volve oilfield located in the North Sea.

Fig. 7.

Fig. 8.

Snapshots at 2 s (a and b) and 3.2 s (c) of the velocity models of Volve oilfield capturing the (a) horizontal particle displacements and (b) horizontal particle accelerations of P-wave and (c) S-wave using the conventional method with a smaller grid spacing (10 m).

Table 1.

Comparison of computing time for solving wave equation, data communication with MPI and applying FCT.

(A-1)

(A-2)

(A-3)

(A-4)

(A-5)

(A-6)

(A-7)

(A-8)

(A-9)

(A-10)

(A-11)

(A-12)

(A-13)

(A-14)

(A-15)

(A-16)

(A-17)

(A-18)

(A-19)

(A-20)

(A-21)

(A-22)

(A-23)

(A-24)

(A-25)

(A-26)