Three-Dimensional SART Analysis for Muon Tomography

Sungchul Lee; Yun Gyeong Choi

doi:10.32390/ksmer.2021.58.5.380

Preview

Research Paper (Special Issue)

Journal of the Korean Society of Mineral and Energy Resources Engineers. 31 October 2021. 380-393
https://doi.org/10.32390/ksmer.2021.58.5.380

Three-Dimensional SART Analysis for Muon Tomography

뮤온 토모그래피 적용을 위한 3차원 SART 분석법 연구

Sungchul Lee¹

Yun Gyeong Choi²^*

이 성철¹

최 윤경²^*

¹Professor, Department of Physics, Gangneung-Wonju National University, Gangneung, Korea

²Research Professor, Natural Science Research Institute, Gangneung-Wonju National University, Gangneung, Korea

¹강릉원주대학교 물리학과 교수

²강릉원주대학교 자연과학연구소 연구교수

^{*Corresponding Author}

ABSTRACT

We developed an analysis program using the simultaneous algebraic reconstruction technique (SART) and applied it to projection data constructed using a three-dimensional Shepp–Logan model. To reduce the memory space and speed up the calculations, we used a compressed expression of the matrix, which saves only nonzero data. We compared the reconstructed images of SART with those of the simultaneous iterative reconstruction technique. This SART analysis can be applied to cosmic muon data and seismic data if the matrix is updated by ray tracing in the iteration process

Keywords

Three-dimensional

SART

muon tomography

compressed expression of a matrix

Shepp-Logan model

3차원 투영자료에 대한 SART 분석법을 개발하여 Shepp-Logan 모델 형태의 투영자료에 적용하여 영상재구성을 수행하였다. SART 계산에서 메모리 공간의 절약과 계산 속도를 높이기 위해 행렬의 값이 0이 아닌 경우만 메모리에 저장하는 압축표현 방식을 사용하였다. 재구성된 영상은 SIRT 분석법에 의해 재구성된 영상과 비교하였다. 본 연구에서 개발된 SART 분석법은 코스믹 뮤온 탐사 자료뿐 아니라, 반복과정 중 파선추적을 통해 행렬을 갱신하는 경우 탄성파 탐사 자료에도 적용이 가능하다.

키워드

3차원

SART

뮤온 토모그래피

압축표현 행렬

Shepp-Logan 모델

MAIN

서 론
영상재구성 이론 및 토모그래피 분석법
이미지 재구성 방정식
반복적 풀이방법
ART
SIRT와 SART
컴퓨터 프로그래밍
길이행렬 $A$ 계산 및 희소행렬의 압축표현 저장
3차원 Shepp-Logan 모델 구성 및 투영 자료 계산
분석결과
2차원 모델
3차원 모델
결 론

서 론

입자나 파동이 특정 영역을 통과하면서 발생된 파형이나 입자의 변화 및 통과시간 등을 측정하여 관심 영역의 내부구조나 물성을 구할 수 있다. 지구 내부나 지표 등을 대상체로 하는 물리탐사 분야에서는 송신원으로 탄성파와 전자기파 등이 주로 사용된다. 물리탐사에서 광범위한 영역을 탐사하는 경우 상대적으로 파장이 큰 파동이 사용하는데 반해, 의학 분야 등에서와 같이 정밀한 측정이 필요한 경우는 X-선 등과 같이 파장이 매우 짧은 파동의 송신원이 주로 사용되고 있다. 특히 X-선은 물질 내부를 거의 직선으로 지나기 때문에 굴절이나 회절현상을 고려하지 않아도 되므로 물리탐사에 비해 분석과정이 간단하다. 최근에 우주로부터 자연적으로 발생하여 지표면에 도달하는 뮤온(muon, 또는 뮤(µ)입자)이 물리탐사에 사용되기 시작하였다. 원자로 및 핵폐기물 저장소 탐사(Jonkmans et al., 2012), Scan Pyramids 미션 등과 같은 피라미드 내부 조사(Morishima et al., 2017) 및 화산 활동 모니터링(Bonechi et al., 2020; Tanaka et al., 2010; Tanaka, 2018; D’Alessandro et al., 2018; Marteau et al., 2016) 등의 탐사에 활발하게 사용되고 있으며, 뮤온 검출기가 일반화된다면 더욱 많은 분야의 물리탐사에 뮤온 토모그래피가 적용될 것으로 예상된다. 코스믹 뮤온의 입사궤적과 출사궤적을 모두 측정하는 경우에는 두 궤적의 최근접점(PoCA, Point of Closest Approach)과 충돌각도와 같은 추가적인 정보를 이용하여 3차원 영상재구성에 이용할 수 있다(Jonkmans et al., 2012; Liu et al., 2019). 그러나 코스믹 뮤온을 이용한 탐사는 인위적인 송신원을 사용하는 X-선과는 달리 자연적으로 발생하는 뮤온을 이용하기 때문에 측정되는 뮤온의 개수가 제한되어, 분석에 충분한 입자수를 확보하는 데 어느 정도의 시간이 필요하다. 따라서 실시간 영상재구성이 어렵고 또한 진행방향이 평행하지 않아 전통적인 X-선 단층촬영(Computed Tomography; CT) 기법을 적용하려면 관측된 뮤온 중 동일 평면을 지나는 입자만을 따로 모아서 분석을 하거나 3차원 토모그래피(tomography)를 적용해야 한다.

3차원 대상체를 영상화하기 위해, 전통적인 X-선 단층촬영 분석법은 송신원으로 평행한 X-선 빔을 사용하며, 이 X-선 빔이 지나는 2차원 절편 단면에 대해 각각 2차원 영상을 재구성한 후, 이 영상들을 쌓아서 3차원 영상처럼 보이도록 한다(Ambrose and Hounsfield, 1973; Comack, 1963; Comack, 1964). 2차원 함수로 표현되는 물성값은 각도 $θ$ 와 횡축(transverse) 방향 거리 $t$ 로 표현된 X-선 빔의 투영 자료들을 분석하여 구할 수 있다. 이를 구하는 해석적인 방법으로 투영 자료에 푸리에 변환과 역변환을 이용한 FBP(Filtered Back Projection)이 있고(Shepp and Logan, 1974a; Shepp and Logan, 1974b; Rosenfeld and Kak, 1982), 비해석적인 방법으로 투영 자료로부터 선형 연립 방정식을 구성하고 그 해를 산술적으로 구하는 방법이 있다. 이 경우 일반적으로 연립방정식의 변수가 매우 많아 역행렬을 구하는데 많은 시간이 걸리기 때문에, 초기 시험해를 시작으로 시험해의 결과와 실제 관측 결과의 차이로부터 차기 시험해를 설정하고, 반복 과정을 통해 그 차이를 점차 줄여 해에 접근하는 반복적인 방법(iterative method)을 사용한다. 이러한 방법으로는 전통적으로 켤레기울기법(Conjugate Gradient) (Hestenes and Stiefel, 1952), ART (Algebraic Reconstruction Technique) (Gordon et al., 1970), SIRT(Simultaneous Iterative Reconstruction Technique) (Dines and Lytle, 1979), SART(Simultaneous Algebraic Reconstruction Technique) (Andersen and Kak, 1984) 등이 있고, 이 외에도 MLEM(Maximum-Likelihood Expectation-Maximization) (Dempster et al., 1977) 등 다양한 방법이 적용되고 있다. 이러한 영상 재구성 기법은 회절과 굴절을 고려하면 탄성파 탐사에도 그대로 적용할 수 있기 때문에 물리탐사 분야에도 일찍부터 적용되어 왔다(Dines and Lytle, 1979; Lee, 1990; Hyun et al., 1992). 3차원을 단면으로 잘라 2차원 영상재구성을 하는 방법이 계산 속도에 있어서나 메모리 크기 등에 있어서 유리하고 병렬처리가 쉽기 때문에 2차원 영상 재구성에 비해 3차원 영상 재구성 적용 사례가 많지는 않지만, 원뿔형 빔(Cone- Beam) CT는 collimation(평행광으로 만드는 과정)을 거치지 않은 X-선 빔을 사용하기 때문에, collimation을 거치면서 잃어버리는 빔의 수를 줄일 수 있고, 주사 간격도 크게 할 수 있기 때문에 CT 검사 속도를 줄일 수 있어서 이를 3차원 영상 재구성하는 방법도 많이 연구되어 왔다(Feldkamp et al., 1984). 탄성파 탐사분야에서도 켤레기울기법에 근간을 둔 LSQR 알고리듬을 적용한 3차원 분석법(Paige and Sounders, 1982) 등이 개발되어 적용된 바 있다. 본 논문에서는 일반적인 형태의 3차원 빔을 가정하고 이를 3차원 Shepp-Logan 팬텀(phantom) 형태의 모델에 대해 투영 자료를 구성한 후 영상 재구성을 수행하였다. 영상재구성 방법은 노이즈 제거나 계산 속도를 모두 만족시킬 수 있도록 계산 블록수를 유연하게 조절할 수 있는 SART를 적용하였고, SIRT 결과와 이를 비교하였다.

영상재구성 이론 및 토모그래피 분석법

이미지 재구성 방정식

X-선을 물체에 투영(projection)시키면, X-선이 물체를 통과하면서 감쇠되며, 이 감쇠량으로부터 물성을 파악할 수 있다. 감쇠량이 빔 궤적에 따라 선형적으로 비례한다고 가정하면, 감쇠량은 다음과 같은 1차원 적분식으로 나타낼 수 있다.

(1)

p = \int_{l_{1}}^{l_{2}} f (x, y, z) d l

여기서 $f (x, y, z)$ 는 각 위치에서의 물성을 의미하며, $p$ 는 투사 빔의 측정값을 나타내며, 각 투사 빔마다 하나의 투영식을 구성하게 된다. 3차원에서 투영된 빔을 직선으로 표현하기 위해서는 4개의 값(parameters)이 필요한데, 3차원 직선이 $z = 0$ 인 단면을 지나는 점의 좌표값 $(x, y)$ 를 나타내는 $p_{0}, p_{2}$ 와 이 직선의 방향을 나타내는 벡터 $(p_{1}, p_{3}, 1)$ 의 $x, y$ 값인 $p_{1}, p_{3}$ 이다. 이 4개의 값을 사용하면 3차원 직선상의 임의의 점은

(2)

x = p_{0} + p_{1} t y = p_{2} + p_{3} t z = t

가 되며, 3차원 직선을 1개의 매개변수 $t$ 로 하여 4개의 값 $(p_{0}, p_{1}, p_{2}, p_{3})$ 으로 표현하면, 투영 자료와 물성간의 1차원 적분식인 식 (1)은

(3)

p (p_{0}, p_{1}, p_{2}, p_{3}) = \int_{t_{1}}^{t_{2}} f (p_{0} + p_{1} t, p_{2} + p_{3} t, t) (\frac{d l}{d t}) d t = \int_{z_{1}}^{z_{2}} f (p_{0} + p_{1} z, p_{2} + p_{3} z, z) (\frac{d l}{d z}) d z

로 나타낼 수 있다. 식 (3)의 적분은 델타함수를 이용하여 다음과 같이 3차원 적분으로 나타낼 수 있다.

(4)

p (p_{0}, p_{1}, p_{2}, p_{3}) = \int_{z_{1}}^{z_{2}} \int_{y_{1}}^{y_{2}} \int_{x_{1}}^{x_{2}} f (x, y, z) δ (x - p_{0} - p_{1} z) δ (y - p_{2} - p_{3} z) (\frac{d l}{d z}) d x d y d z

이 적분을 수치계산을 위해 이산 합으로 나타내면

(5)

p (p_{0}, p_{1}, p_{2}, p_{3}) = \sum_{i z = 1}^{N_{z}} \sum_{i y = 1}^{N_{y}} \sum_{i x = 1}^{N_{x}} f (i x, i y, i z) δ_{i x, p_{0} + p_{1} i z} δ_{i y, p_{2} + p_{3} i z} (Δ l)_{i x, i y, i z}

의 꼴이 된다. 여기에서 식 (5)의 우변에 있는 $δ_{i x, p_{0} + p_{1} i z} δ_{i y, p_{2} + p_{3} i z} (Δ l)_{i x, i y, i z}$ 는 투사 빔이 $(i x, i y, i z)$ 번째 셀(cell)을 통과한 길이에 해당되며 빔과 셀에 모두 의존하므로 $l (p_{0}, p_{1}, p_{2}, p_{3}, i x, i y, i z)$ 의 꼴로 표현할 수 있다. 이 값은 빔이 지나간 셀을 제외한 대부분의 셀에 대해 0이 되며 $(p_{0}, p_{1}, p_{2}, p_{3})$ 역시 수치계산을 위해 정수 지표(index)로 구분해 주어야 한다. 이를 위해 투사 빔 벡터의 x, z 성분이 z축과 이루는 각도를 $θ_{x}$ , 벡터의 y, z 성분이 z축과 이루는 각도를 $θ_{y}$ 라 하고, 이 두 각도를 같은 간격으로 나눈 값을 정수지표로 사용한 후, 원점으로부터의 거리를 기준으로 $p$ 를 이산화한다면,

(6)

p_{1} = \tan (θ_{x}) p_{3} = \tan (θ_{y}) p_{0} = \frac{t_{x}}{c o s θ_{x}} p_{2} = \frac{t_{y}}{c o s θ_{y}}

의 관계식으로부터, 투사 빔을 구분하는 정수지표는 각도 $(j a x, j a y)$ 와 횡축방향 거리 $(j t x, j t y)$ 에 따라 4개의 정수지표 $(j a x, j a y, j t x, j t y)$ 로 나타낼 수 있다. 만일 투사 빔을 나타내는 4개의 정수지표와 셀을 나타내는 3개의 정수지표 $(i x, i y, i z)$ 를 모두 직렬화(serialize)하여 각각 다음과 같이 나타낸다면,

(7)

j = (j a y \times N_{j a x} + j a x) \times N_{j t y} \times N_{j t x} + j t y \times N_{j t x} + j t x i = i z \times N_{y} \times N_{x} + i y \times N_{x} + i x

여기서, $j$ 는 총 개수 $N_{p} = N_{a x} \times N_{a y} \times N_{t x} \times N_{t y}$ 인 하나의 투사 빔을 구분하는 정수지표가 되고, $i$ 는 총 개수 $N_{c} = N_{x} \times N_{y} \times N_{z}$ 인 하나의 셀을 구분하는 정수지표가 된다. 직렬화된 이 두 지표를 사용하여 투사 빔과 셀의 물성간의 관계식을 나타내는 투영식은 아래와 같이 된다.

(8)

p (j) = \sum_{i = 1}^{N_{x} \times N_{y} \times N_{z}} l (j, i) f (i)

식 (8)에서 $p (j)$ 와 $f (i)$ 를 열벡터 $p$ 와 $x$ 로 나타내고 $l (j, i)$ 를 $N_{p} \times N_{c}$ 행렬 $A$ 로 나타내면 아래와 같은 선형 연립방정식이 된다.

(9)

p = A x

이를 벡터의 성분으로 나타내면 다음과 같다.

(10)

p_{j} = \sum_{i = 1}^{N_{c}} a_{j i} x_{i}

여기서 행렬 $A$ 는 실험 조건에 따라 파선 추적이나 기하학적으로 계산할 수 있는 값이고, $p_{j}$ 의 개수, 즉 투영식의 개수가 충분하다면 원리적으로는 최소제곱법을 적용하여 다음과 같은 식을 만족한다.

(11)

A^{t} p = A^{t} A x

이 식에서 $A^{t} A$ 는 정사각행렬(square matrix)이기 때문에 이 행렬의 역행렬로부터 셀의 물성 $x$ 를 구할 수 있지만 실제적으로는 행렬의 크기가 매우 크기 때문에 행렬을 곱하거나 역행렬을 구하는데 많은 시간이 소요된다. 따라서 해를 구하기 위해서는 가정된 초기 시험해(trial solution)를 시작으로 하여 반복적으로 해를 갱신하면서 실제해에 접근하는 반복적 풀이방법(iterative method)을 사용한다.

반복적 풀이방법은 시험해 $x^{(k)}$ 로부터 $A x^{(k)}$ 와 투영 자료 $p$ 와의 차이(residual)로부터 차기 시험해 $x^{(k + 1)}$ 을 결정하는 과정을 반복적으로 수행하면서 실제해와의 차이를 줄이는 방법이다. 반복적 풀이방법을 최소제곱 조건을 만족하는 식 (11)에 적용하면 아래와 같이 나타낼 수 있다.

(12)

x^{(k + 1)} = x^{(k)} + B^{(k)} A^{t} (p - A x^{(k)})

여기서 $B^{(k)}$ 는 갱신의 정도를 결정하는 파라미터들의 행렬로 $N_{c} \times N_{c}$ 행렬이 되어야 한다. $B^{(k)}$ 의 꼴은 두 개의 다른 행렬 $M$ 과 $N$ 으로 분리하여 다음과 같이 나타낼 수 있다.

(13)

A^{t} p = (M - N) x

식 (13)의 우변의 두 번째 항을 좌변으로 이항한 후 $x$ 에 대해 나타내면

(14)

x = M^{- 1} N x + M^{- 1} A^{t} p

이 된다. 만일 $x$ 가 실제해라면 식 (14)가 성립하지만, 반복적인 풀이방법을 적용하는 경우 식의 우변의 $x$ 를 현재 시험해 $x^{(k)}$ 로 놓고 좌변의 $x$ 를 차기 시험해 $x^{(k + 1)}$ 로 놓으면 갱신식이 된다.

(15)

x^{(k + 1)} = M^{- 1} N x^{(k)} + M^{- 1} A^{t} p = x^{(k)} + M^{- 1} A^{t} (p - A x^{(k)})

갱신식은 행렬 $M$ 과 $N$ 에 따라 Jacobi 알고리듬, Gauss- Seidel 알고리듬, Richardson 알고리듬 등으로 구분할 수 있다(Sorzano et al., 2017). 이 3가지 갱신 알고리듬은 ${(A^{t} A)}^{- 1}$ 를 직접 계산하는 시간을 줄이기 위하여, $(A^{t} A)$ 를 어떤 형태의 행렬로 대신하는가에 따라 구분된다. 이 중 Jacobi 알고리듬에 의한 갱신식은 $(A^{t} A)$ 대신에 대각행렬 $D$ 로 대치한 형태로 다음과 같다.

(16)

x^{(k + 1)} = x^{(k)} + D^{- 1} A^{t} (p - A x^{(k)})

갱신식 (16)에서 $D^{- 1}$ 는 단순히 $(A^{t} A)$ 의 대각성분의 역수를 취하면 구할 수 있다. 일반적으로 행렬을 열벡터(column vector)들과 행벡터(row vector)들로도 표현할 수 있으므로(Sorzano et al., 2017), $α_{i}$ 가 행렬 $A$ 의 $i$ 번째 열벡터라면 행렬 $A$ 는

(17)

A = (α_{1}, \dots, α_{i}, \dots, α_{N_{c}})

와 같이 표현할 수 있으며 여기서 $α_{i}$ 는 $N_{p}$ 개의 성분을 갖는다. 마찬가지로 $a_{j}^{t}$ 가 행렬 $A$ 의 $j$ 번째 행벡터라면, 행렬 $A$ 는

(18)

A = (\begin{matrix} a_{1}^{t} \\ \dots \\ a_{j}^{t} \\ \dots \\ a_{N_{p}}^{t} \end{matrix})

이고 여기서 $a_{j}^{t}$ 는 $N_{c}$ 개의 성분을 갖는 $a_{j}^{t} = (a_{j 1}, \dots, a_{j i}, \dots, a_{j N_{c}})$ 이다. $(A^{t} A)$ 를 열벡터 $α_{i}$ 의 내적으로 표현하면

(19)

A^{t} A = (\begin{matrix} α_{1}^{t} \cdot α_{1} & \dots & α_{1}^{t} \cdot α_{i} & \dots & α_{1}^{t} \cdot α_{N_{c}} \\ \dots & \dots & \dots & \dots & \dots \\ α_{i}^{t} \cdot α_{1} & \dots & α_{i}^{t} \cdot α_{i} & \dots & α_{i}^{} \cdot α_{N_{c}} \\ \dots & \dots & \dots & \dots & \dots \\ α_{N_{c}^{t}} \cdot α_{1} & \dots & α_{N_{c}}^{t} \cdot α_{i} & \dots & α_{N_{c}}^{t} \cdot α_{N_{c}} \end{matrix})

로 나타낼 수 있으며 대각행렬 $D$ 는 $(A^{t} A)$ 행렬의 대각성분으로 구성된 행렬이므로, 역행렬 $D^{- 1}$ 은 다음과 같다.

(20)

D^{- 1} = (\begin{matrix} \frac{1}{{|α_{1}|}^{2}} & \dots & 0 & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots \\ 0 & \dots & \frac{1}{{|α_{1}|}^{2}} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots \\ 0 & \dots & 0 & \dots & \frac{1}{{|α_{N_{c}}|}^{2}} \end{matrix})

또한 $A x^{(k)}$ 를 행벡터 $a_{j}^{t}$ 로 나타낸 후, 다시 열벡터 $a_{j}$ 의 내적으로 나타내면

(21)

A x^{(k)} = (\begin{matrix} a_{1}^{t} \\ \dots \\ a_{j}^{t} \\ \dots \\ a_{N_{p}}^{t} \end{matrix}) x^{(k)} = (\begin{matrix} a_{1}^{t} x^{(k)} \\ \dots \\ a_{j}^{t} x^{(k)} \\ \dots \\ a_{N_{p}}^{t} x^{(k)} \end{matrix}) = (\begin{matrix} a_{1} \cdot x^{(k)} \\ \dots \\ a_{j} \cdot x^{(k)} \\ \dots \\ a_{N_{p}}^{} \cdot x^{(k)} \end{matrix})

가 되고, $A^{t} (p - A x^{(k)})$ 는 아래와 같다.

(22)

A^{t} (p - A x^{(k)}) = (a_{1}, \dots, a_{j}, \dots, a_{N_{p}}) (\begin{matrix} p_{1} - a_{1} \cdot x^{(k)} \\ \dots \\ p_{j} - a_{j} \cdot x^{(k)} \\ \dots \\ p_{N_{p}} - a_{N_{p}} \cdot x^{(k)} \end{matrix}) = \sum_{j = 1}^{N_{p}} (p_{j} - a_{j} \cdot x^{(k)}) a_{j}

따라서 Jacobi 알고리듬에 의한 갱신식 (16)의 $i$ 번째 성분에 대한 식은

(23)

x_{i}^{(k + 1)} = x_{i}^{(k)} + \frac{1}{| α_{i} |^{2}} \sum_{j = 1}^{N_{p}} (p_{j} - a_{j} \cdot x^{(k)}) a_{j i}

가 되며, SIRT류 중의 한 형태이다.

ART

전통적인 ART는 Kaczmarz 알고리듬을 적용하여 차기 시험해를 결정하는 방법으로, 한 번 갱신할 때 하나의 투영식을 이용한다. 투영식이 총 $N_{p}$ 개 있으므로, $N_{p}$ 번의 갱신 과정을 거쳐야 한 번 반복 과정을 마치게 된다. $j$ 번째 투영식인

(24)

p_{j} = \sum_{i = 1}^{N_{c}} a_{j i} x_{i}

는 이 공간에서의 초평면(hyper-plane)을 나타내는 식에 해당되며, 따라서 선형 연립방정식의 실제해는 총 투영식의 수 $N_{p}$ 개의 초평면들이 만나는 교점이다. $k$ 번째 시험해인 $x^{(k)}$ 는 $N_{c}$ 차원의 수학적 공간상에서 실제해인 초평면들의 교점과 떨어져 있는 임의의 한 점이라고 생각할 수 있고, 이 점에서 $j$ 번째 초평면에 수직 방향으로 이동하면 초평면과 한 점 $x^{(k + 1)}$ 에서 만나게 되는데, $x^{(k)}$ 와 초평면 상의 수선의 발 $x^{(k + 1)}$ , 그리고 실제해는 직각삼각형을 이루게 되고, 파타고라스 정리에 의해 시험해 $x^{(k)}$ 와 실제해 사이의 거리보다 차기 시험해 $x^{(k + 1)}$ 과 실제해 사이의 거리가 항상 가깝게 된다. $x^{(k + 1)}$ 는 $j$ 번째 초평면에 수직인 벡터 $a_{j}$ 로부터 다음과 같이 구할 수 있다.

(25)

x^{(k + 1)} = x^{(k)} + (x \cdot \frac{a_{j}}{|a_{j}|} - x^{(k)} \cdot \frac{a_{j}}{|a_{j}|}) \frac{a_{j}}{| a_{j} |}

$p_{j} = a_{j} \cdot x$ 이므로, 식 (25)은

(26)

x^{(k + 1)} = x^{(k)} + (p_{j} - x^{(k)} \cdot a_{j}) \frac{a_{j}}{{| a_{j} |}^{2}}

와 같이 나타낼 수 있고, 이것을 성분으로 표현하면 다음과 같다.

(27)

x_{i}^{(k + 1)} = x_{i}^{(k)} + \frac{(p_{j} - \sum_{i = 1}^{N_{c}} a_{j i} x_{i}^{(k)}) a_{j i}}{\sum_{i = 1}^{N_{c}} a_{j i}^{2}}

SIRT와 SART

앞에서 설명한 ART법은 1개의 투영식으로 차기 시험해로 갱신하기 때문에, 1회 반복과정만으로도 $N_{p}$ 회 갱신이 이루어져 해의 수렴 속도가 빠르다. 그러나 최종적으로 갱신할 때 사용된 투영식에 문제가 있는 경우, 그 영향이 재구성된 이미지에 노이즈로 나타나게 된다. 그리고 투영식이 어떤 순서로 계산되는가에 따라 재구성 이미지가 달라지는 단점이 있다. 이러한 노이즈를 줄이기 위해서는 각 투영식마다 차기 시험해로 갱신하지 않고, 모든 초평면의 수선방향의 벡터를 다 더해 평균적인 벡터값으로 차기 시험해를 갱신하는 방법을 적용할 수 있다. 각 초평면에 수직인 벡터에 어떤 가중치를 주어 평균을 구하는가에 따라 실제해에 접근하는 수렴 속도가 달라질 수 있는데, 단순히 ART에서 적용되었던 초평면에 대한 수선의 발에 해당하는 벡터들을 모두 더해 갱신식을 구성한다면 그 식은 다음과 같다.

(28)

x^{(k + 1)} = x^{(k)} + \sum_{j = 1}^{N_{p}} (p_{j} - x^{(k)} \cdot a_{j}) \frac{a_{j}}{{| a_{j} |}^{2}}

(29)

x_{i}^{(k + 1)} = x_{i}^{(k)} + \sum_{j = 1}^{N_{p}} (p_{j} - x^{(k)} \cdot a_{j}) \frac{a_{j i}}{| a_{j} |^{2}}

식 (29)와 앞에서 언급한 Jacobi 갱신식 (23)는 형태가 다른데, 식 (29)는 ART를 기반으로 하는 갱신식으로 ${| a_{j} |}^{2}$ 을 나눈 것을 가중치로 곱한 꼴이고, 식 (23)는 초평면에 수직인 벡터 $a_{j}$ 에 단순히 시험해와 측정치의 차이만을 가중치로 곱해서 모두 더한 후, 각 셀을 지나는 투사 빔의 길이를 모두 제곱해서 더한 ${| α_{i} |}^{2}$ 을 나눈다. 이 두 갱신식 모두 SIRT류에 해당하며 일반적인 SIRT는 여기에 완화계수(relaxation paramter) $λ$ 까지 추가하여 다음과 같이 표현된다(Sorzano et al., 2017).

(30)

x_{i}^{(k + 1)} = x_{i}^{(k)} + λ_{k} \frac{1}{γ_{i}} \sum_{j = 1}^{N_{p}} \frac{1}{ρ_{j}} (p_{j} - a_{j} \cdot x^{(k)}) a_{j i}

특히 이 중 수렴성이 증명된 갱신식의 꼴은

(31)

γ_{i} = \sum_{j = 1}^{N_{p}} {| a_{j i} |}^{α}

(32)

ρ_{j} = \sum_{i = 1}^{N_{c}} {| a_{j i} |}^{2 - α}

이며, 여기서, $0 < α ≦ 2, 0 < λ < 2$ 이다(Van der Sluis and Van der Vorst, 1990). $α = 2$ 인 경우는 Jacobi 갱신식 (23)에 해당하며, $α = 0$ 인 경우는 ART를 기반으로 한 SIRT 갱신식 (29)으로, 전자현미경분야에서 영상을 재구성할 때 많이 사용된다(Sorzano et al., 2017). 본 연구에서는 $α = 1$ 인 갱신식을 사용했는데, 이는 Anderson과 Kak의 SART 갱신식에 사용된 형태이다(Andersen and Kak, 1984). 만일 $|α_{i}|$ 를 투사 빔이 지나간 실제 길이와 관계없이 지나가는 경우 1, 그렇지 않은 경우 0으로 놓는다면, $γ_{i}$ 는 $i$ 번째 셀을 지나가는 투사 빔의 총 개수가 되며, 이는 Dines과 Lytle이 제시한 SIRT 갱신식이 된다(Dines and Lytle, 1979).

SIRT법은 모든 투영식을 반영한 평균값으로 갱신을 수행하므로 ART의 단점인 노이즈를 줄일 수 있으나 수렴속도가 느린 단점이 있다. SART는 이 두 방법을 혼합한 것으로 생각할 수 있는데, 투영식을 여러 블록(block)으로 나눈 후 각 블록에 속한 투영식의 평균으로 시험해를 구하여 갱신하는 방법으로, 수학적으로 블록 Kaczmarz 알고리듬에 해당한다(Sorzano et al, 2017).

(33)

x_{i}^{(k + 1)} = x_{i}^{(k)} + \frac{1}{\sum_{j = b_{s}}^{b_{f}} a_{j i}} \sum_{j = b_{s}}^{b_{f}} \frac{(\sum_{i = 1}^{N_{c}} a_{j i} x_{i}^{(k)} - p_{j}) a_{j i}}{\sum_{i = 1}^{N_{c}} a_{j i}}

여기서 $b_{s}$ 과 $b_{f}$ 는 각 블록의 시작과 마지막에 해당하는 투영식의 지표이다. 이 식에서 블록을 한 개로 설정하면 블록 내의 투영식의 개수가 투영식의 총 개수와 같기 떄문에 SIRT 갱신식과 같아지며, 만일 블록의 개수를 총 투사 빔의 개수로 설정하면 한 개의 블록에 한 개의 투영식만 있기 때문에 $α = 0$ 인 경우는 ART식과 같아진다. 즉 SART식은 블록의 수에 따라 SIRT와 ART를 모두 포함시킬 수 있기 때문에 재구성될 이미지의 품질과 재구성 시간 등을 동시에 고려해 블록의 개수를 유연하게 설정할 수 있다. 그러나 블록을 여러 개로 나누기 때문에 투영식들을 어떻게 블록으로 나누고 묶는가에 따라 그리고 블록의 계산순서에 따라 재구성 이미지가 영향을 받게 된다.

컴퓨터 프로그래밍

길이행렬 $A$ 계산 및 희소행렬의 압축표현 저장

반복 풀이방법으로 영상 재구성을 하려면 각 투사 빔이 각 셀을 지나는 길이행렬 $A$ 를 계산해야 하는데, 이 값은 투사 빔이 셀에 들어가는 점과 셀을 나오는 점의 위치로부터 계산할 수 있다. 그러므로 각 셀을 지나는 길이는 셀 간격으로 나눈 3차원 격자면과 $(p_{0}, p_{1}, p_{2}, p_{3})$ 로 표현되는 3차원 직선 투사 빔의 모든 교점을 구하여, 이 교점을 순서대로 정렬한 후, 이 교점들의 차이로부터 행렬 $A$ 를 구할 수 있다. 직선과 격자면의 교점을 각 방향의 격자면의 순서를 따라 차례로 모으는 경우 추후에 교점을 순서대로 정렬을 하는 과정에서 시간이 걸릴 수 있다. 순서정렬 시간을 줄이기 위해, 교점을 모으는 과정에서 교점의 지표를 $(i x, i y, i z)$ 라 할 때, $z$ 가 최소인 교점을 기준 지표값 $(i x_{r e f}, i y_{r e f}, i z_{r e f})$ 로 하여 기준 지표값과 교점 지표와의 차이인 $| i x - i x_{r e f} | + | i y - i y_{r e f} | + | i z - i z_{r e f} |$ 의 위치에 교점을 저장하고 교점이 저장되었음을 나타내는 플래그(flag)를 설정하는 방식을 사용하였다. 그런데 서로 다른 교점이 같은 위치에 들어갈 수 있는 경우는 최대 2개가 되므로 2번째 교점 및 플래그를 저장할 별도의 배열이 하나 더 필요하다. 이러한 경우 저장 위치에 플래그가 모두 설정된 경우인 (2개의 점) 경우에만 2점에 대한 순서정렬을 수행하면 된다.

그런데 행렬 $A$ 는 3차원 셀들 가운데 각 투사 빔이 지나가는 셀에만 길이값이 존재하고 대부분 셀의 길이값은 0이다. 이러한 희소행렬(sparse matrix)을 일반적인 배열변수로 다루면 메모리를 과도하게 필요로 하고, 또한 반복계산 시 필요하지 않은 행렬의 곱까지 계산하기 때문에 프로그램 계산 속도를 현저히 떨어뜨린다. 따라서 길이 행렬값을 효과적으로 저장하고 사용하기 위해서는 희소행렬을 압축행렬 형태로 저장해야 하는데, 압축행렬을 구성하기 위해서는 길이가 0이 아닌 값만을 메모리에 저장하고, 이 저장된 길이값의 셀 지표도 동시에 저장해야 한다. 2차원 희소행렬의 경우 행렬값과 2차원 지표 $(j, i)$ 를 모두 저장하는 것이 일반적이지만, 길이행렬의 첫 번째 지표인 $j$ 는 투사 빔을 나타내는 지표로 모든 투영식에 대해 관심영역 내의 셀을 대부분 하나라도 지나가기 때문에 $j$ 에 대한 지표는 압축표현을 사용하지 않고, 셀을 나타내는 지표 $i$ 에만 압축표현을 사용하였다. 이처럼 한 지표만 압축표현을 사용하는 경우, 압축표현 행렬로부터 원래 행렬의 지표를 복원하는 과정이 간단해지고, $(j, i)$ 의 이중 루프(loop)를 구현하기가 용이해진다. 압축된 행렬표현과 일반 행렬을 사용하는 경우의 메모리 차이를 대략적으로 계산해보면 투영식의 지표를 위한 배열의 크기는 동일하게 $N^{4}$ 이지만, 일반 행렬배열의 셀에 대한 배열의 크기가 $N^{3}$ 인 것에 반해, 압축표현 행렬의 경우 대략 $3 N$ 이므로 $N^{2}$ 배에 가까운 저장 공간을 절약할 수 있으며, 이 차이가 반복계산 시 행렬 곱 계산에도 그대로 반영되게 된다.

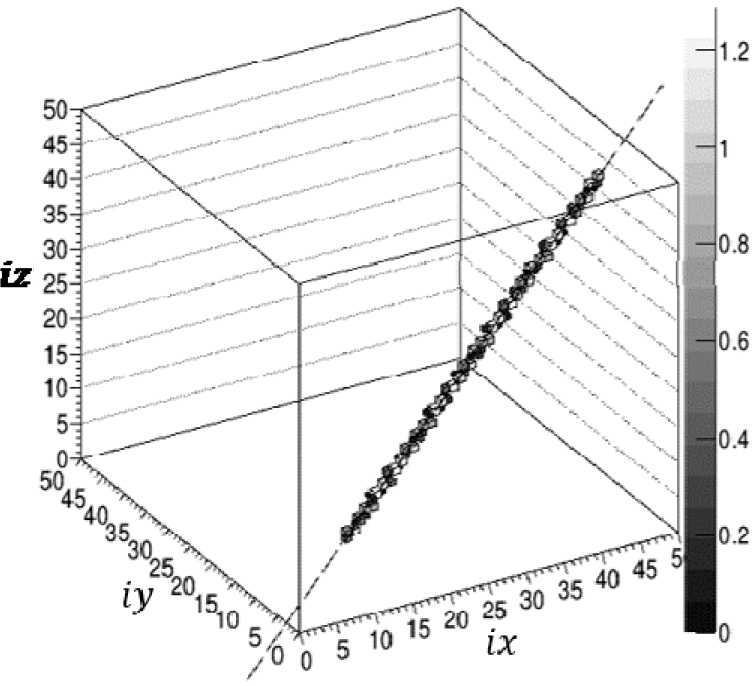
길이행렬 $A$ 의 계산을 검증하기 위해, 임의의 투사 빔의 길이와 이 투사 빔이 지나는 행렬 $A$ 의 값을 비교하였다(Fig.1). 사용한 투사 빔의 $θ_{x}$ 는 55°, $θ_{y}$ 는 30°이며, $p_{0}$ 는 25, $p_{2}$ 는 10인 3차원 직선이다. Fig. 1에서 3차원 투사 빔은 점선으로 표시하였고, 이 투사 빔이 지나는 각 셀의 길이행렬 $A$ 값을 블록의 농도로 나타내었는데, 투사 빔이 지나가는 셀과 $A$ 값이 0이 아닌 셀이 일치하는 것을 확인할 수 있었다. 셀의 크기를 1×1×1로 하였기 때문에 한 셀을 지나는 최대 농도값이 한 셀의 대각선 길이인 $\sqrt{3}$ 보다 작은 값인 것을 확인할 수 있다. 행렬 $A$ 가 제대로 계산되었는지 확인하기 위해서는 대상 영역을 들어가고 나가는 두 교점으로 계산된 투사 빔의 총 길이와 투사 빔이 각 셀을 지나가는 길이의 합을 비교하면 된다. 투사 빔과 대상 영역 전체의 두 교점은 (18.9962, –25, –13.3013)과 (25, –7.21388, 17.5052)로 투사 빔의 총 길이는 56.5778이며, 길이행렬 $A$ 중 이 투사 빔이 지나는 요소의 합과 일치함을 확인하였다. 다른 투사 빔에 대해서도 두 값이 같음을 확인하여 길이행렬이 잘 계산됨을 알 수 있었다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F1.jpg

Fig. 1

Projection line and the values of matrix A that belongs to the projection

3차원 Shepp-Logan 모델 구성 및 투영 자료 계산

SART나 SIRT를 구현하기 위해서는 투영 자료가 필요한데, 주어진 모델로부터 투영 자료를 쉽게 구현하기 위해서 균일한 물성을 갖는 타원체(ellipsoid) 형태로 구성된 3차원 Shepp-Logan 모델을 사용하였다. 균일한 물성의 타원체에 대한 투영 자료는 타원체와 3차원 직선에 만나는 두 교점을 구해 길이를 계산하고 각 타원의 물성을 곱해주면 된다. 중심위치가 $(x_{0}, y_{0}, z_{0})$ 이고, 각 축방향의 길이가 $a, b, c$ 인 타원체와 $(p_{0}, p_{1}, p_{2}, p_{3})$ 로 표현되는 3차원 직선과의 교점은

(34)

\frac{(p_{0} + p_{1} t - x_{0})^{2}}{a^{2}} + \frac{(p_{2} + p_{2} t - y_{0})^{2}}{b^{2}} + \frac{(t - z_{0})^{2}}{c^{2}} = 1

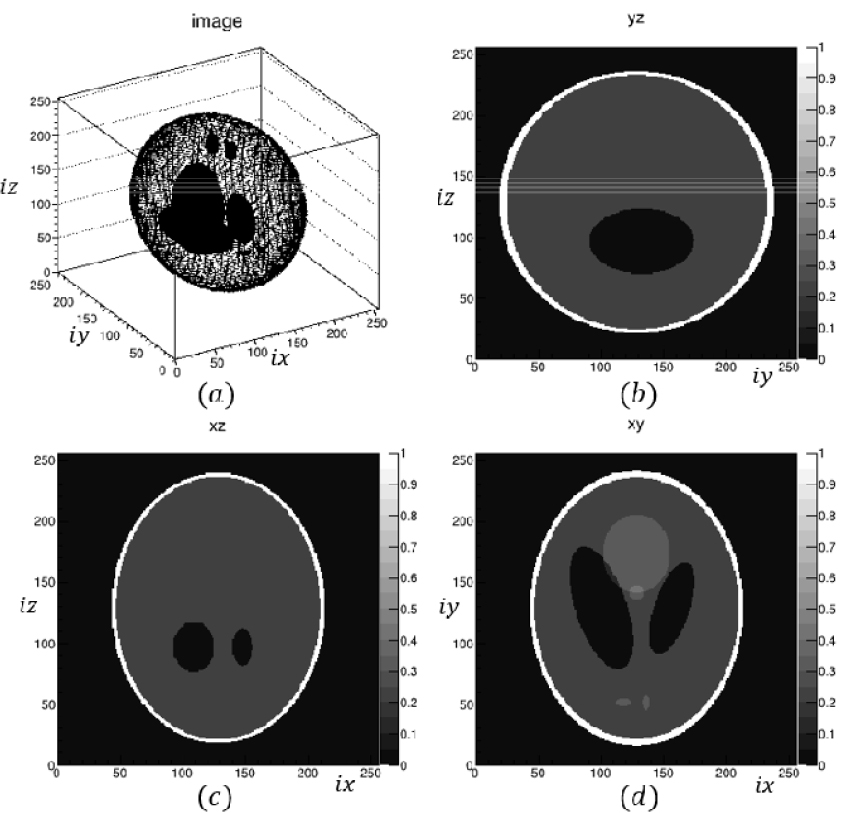
로 주어지며, 이 식은 $t$ 에 대한 2차 방정식이므로, 두 해의 차이인 $Δ t$ 로부터 직선이 타원체를 지나는 길이를 구할 수 있다. 만일 타원체가 회전된 경우에는 좌표계를 타원체의 회전만큼 회전시킨 후 이 회전된 좌표계에서의 직선 표현으로 길이를 구하였다. 물성이 균일한 타원체를 여러 개 합하면 다양한 형태와 물성을 갖는 3차원 모델을 구성할 수 있다. CT의 경우 사람의 머리를 모사한 Shepp-Logan형의 모델을 사용하는데, 본 연구에서도 2차원과 3차원 Shepp- Logan형의 모델을 구성하여 투영 자료를 생성하였다. 3차원 모델의 파라미터는 Table 1과 같으며, 여기서 $α, β, γ$ 는 오일러 각(Euler angle)이다. Fig. 2는 Table 1의 파라미터를 사용한 3차원 모델과 각 축방향의 단면을 그린 그림이다.

Table 1.

Parameters of the three-dimensional Shepp–Logan model ( $- 1 \leq x \leq 1, - 1 \leq y \leq 1, and - 1 \leq z \leq 1$ )

cent_x	cent_y	cent_z	axis_a	axis_b	axis_c	α	β	γ	value
0.0	0.0	0.0	0.69	0.92	0.9	0.0	0.0	0.0	1.0
0.0	0.0	0.0	0.6624	0.874	0.880	0.0	0.0	0.0	-0.8
0.22	0.0	-0.250	0.11	0.31	0.22	-18.0	0.0	0.0	-0.2
-0.22	0.0	-0.250	0.16	0.41	0.21	18.0	0.0	0.0	-0.2
0.0	0.35	-0.250	0.21	0.25	0.50	0.0	0.0	0.0	0.1
0.0	0.1	-0.250	0.046	0.046	0.046	0.0	0.0	0.0	0.1
-0.08	-0.605	-0.250	0.046	0.023	0.020	0.0	0.0	0.0	0.1
0.06	-0.605	-0.250	0.023	0.046	0.020	0.0	0.0	0.0	0.1
0.06	-0.105	0.625	0.040	0.056	0.100	0.0	0.0	0.0	0.1
0.0	0.1	0.625	0.056	0.056	0.100	0.0	0.0	0.0	-0.1

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F2.jpg

Fig. 2

Three-dimensional Shepp–Logan model (nx = ny = nz = 256): (a) 3-D shapes of 10 ellipsoids, (b) yz-plane of ix = 100 (x =−0.22), (c) xz-plane of iy = 128 (y = 0), and (d) xy-plane of iz = 96 (z =−0.25)

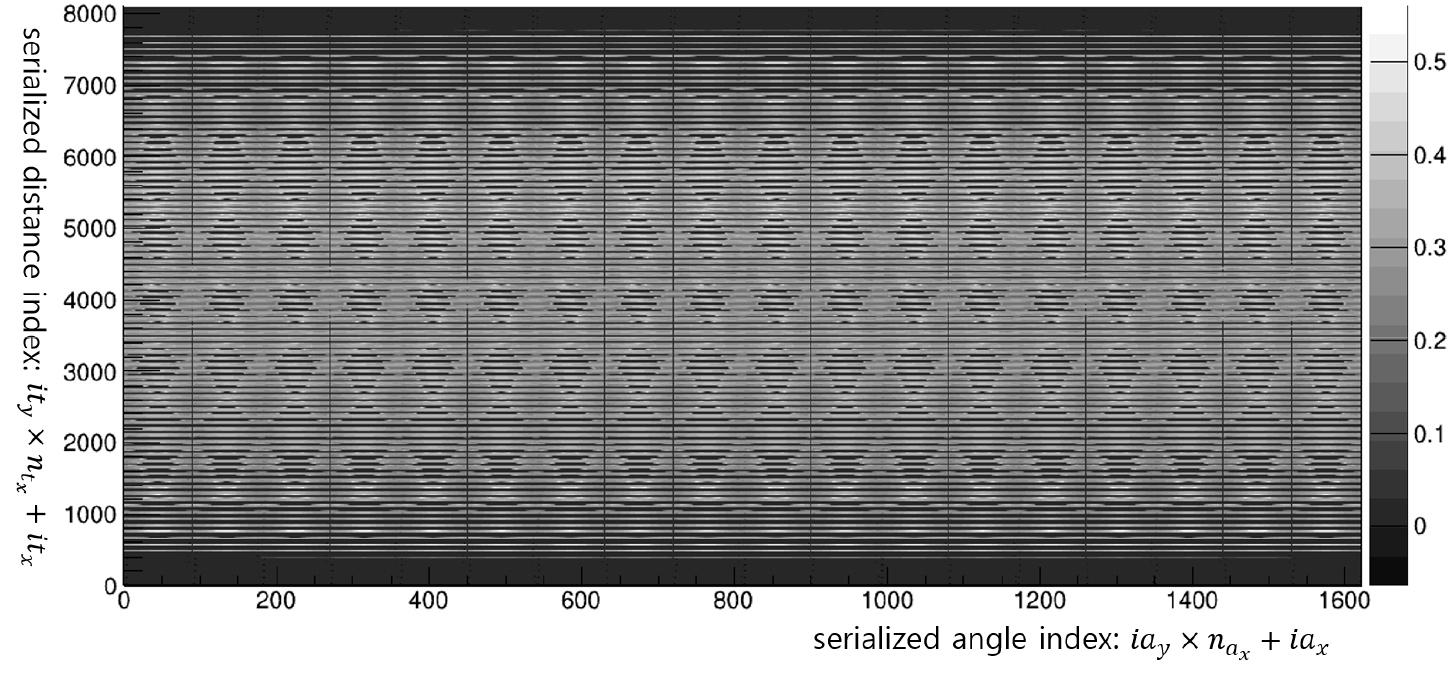
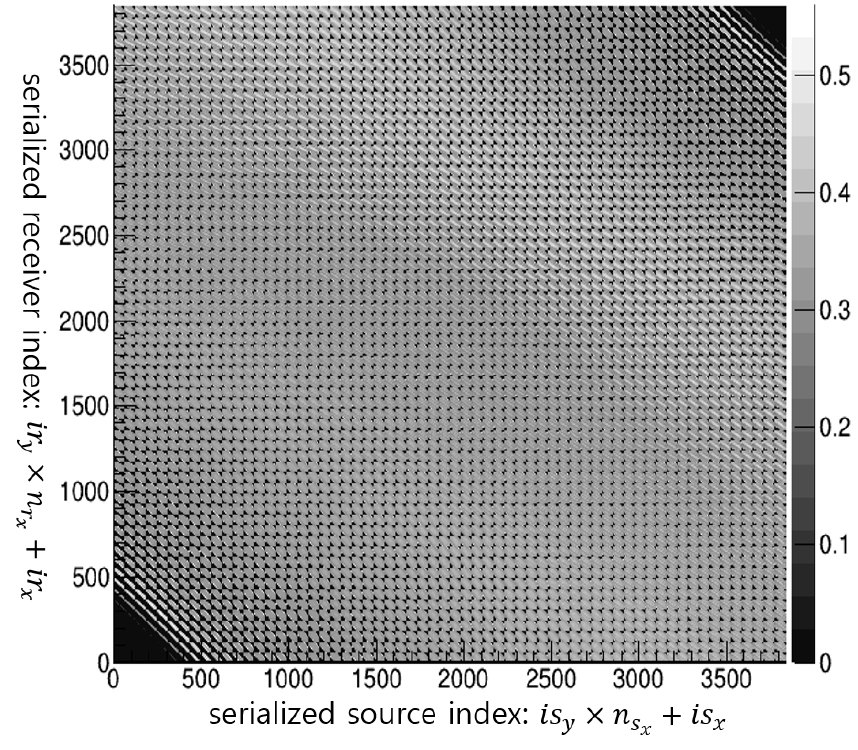
각 투사 빔에 대해 계산된 투영 자료는 파일로 저장하는데, 본 연구에서는 투사 빔을 $(θ, t)$ 로 표현하는 경우와 대상 영역 위와 아래에 위치한 송신점과 수신점의 $(x, y)$ 위치로 표현하는 두 가지 경우를 고려하였다. 첫 번째 자료로 3차원 투영 자료를 $θ$ 와 $t$ 의 정수지표로 하여 계산한 결과를 도시하였다(Fig. 3). 이 그림은 2차원 사이노그램(sinogram)과 같은 역할을 하는 것으로, 가로축은 각도 $θ_{x}$ 와 $θ_{y}$ 를 직렬화해서 나타낸 지표값이고 세로축은 횡축 거리지표 $i t_{x}, i t_{y}$ 를 직렬화한 값이다. 따라서 각 점들은 각각 해당지표에 해당되는 투영식을 나타내고 명암의 크기가 그 투영식에 대한 측정값에 해당하는 $p_{j}$ 를 의미한다. 두 번째 자료로 송신점이 $z = z_{1}$ 인 평면, 수신점은 $z = z_{2}$ 인 평면에 2차원 배열된 경우의 투사 빔 조합에 대한 투영 자료는 Fig. 4에 도시하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F3.jpg

Fig. 3

Calculated projections of the three-dimensional Shepp–Logan model using the serialized angles and distances

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F4.jpg

Fig. 4

Calculated projections of the three-dimensional Shepp–Logan model using the serialized positions of sources and receivers.

분석결과

2차원 모델

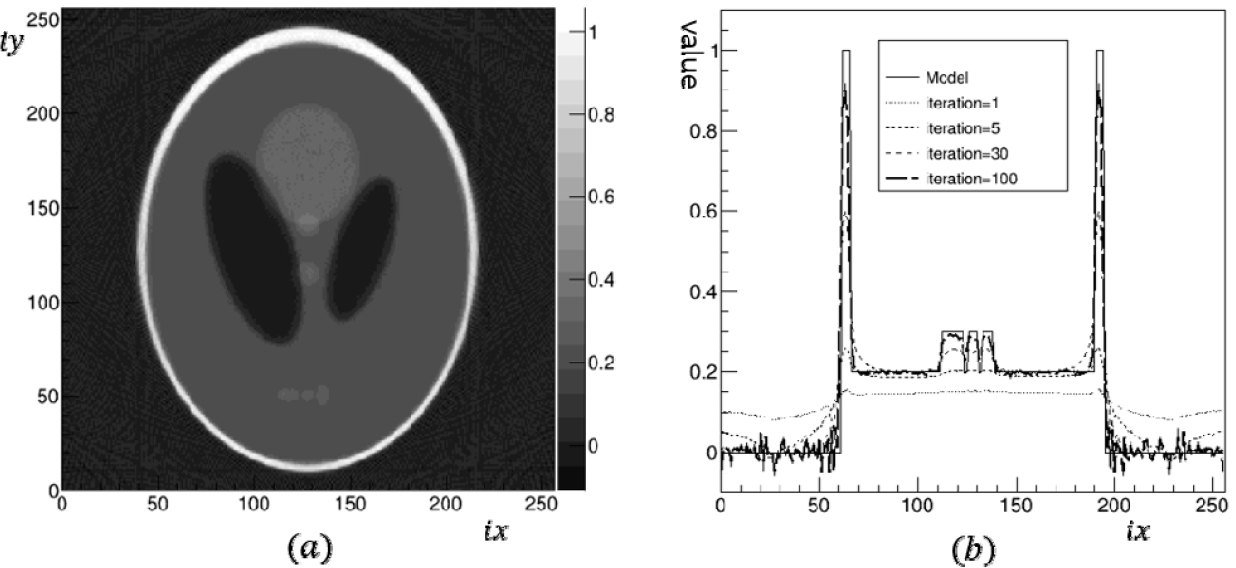
SIRT나 SART법은 행렬로 표현된 선형 연립방정식을 푸는 과정이기 때문에, 투사 빔이 각 셀을 지나는 길이를 계산하는 과정과 셀의 지표를 직렬화하는 과정만 차이가 있을 뿐, 행렬을 직렬화한 이후의 반복적인 풀이 과정은 2차원과 3차원이 차이가 없다. 분석 프로그램의 검증을 위해서 먼저 2차원 Shepp-Logan 모델에 적용한 후 분석 결과와 모델을 비교해 보았다. 10개의 타원으로 만들어진 2차원 Shepp-Logan 모델을 사용하여 투영 자료를 사이노그램 파일로 저장한 후 이 파일을 읽어서 SIRT법으로 영상을 재구성한 결과를 도시하였다(Fig. 5). 투사 빔의 각도는 –90°에서 89°까지 1° 간격으로 총 180개의 각도를 사용하였고, 횡축방향 거리 $t$ 는 256개로 나누었다. 재구성된 영상의 화소수도 횡축방향의 분해능과 유사하게 256×256으로 하였다. (a)는 재구성된 이미지이며 (b)는 재구성된 이미지에서 작은 타원이 3개가 있는 $y = - 0.605 (i y = 50)$ 위치에서 $x$ 방향의 프로파일로써, 1번, 5번, 30번, 그리고 100번 반복 후 재구성된 결과들을 그린 것이다. 가는 실선으로 그린 그래프가 원래 모델의 값이며, 재구성된 이미지는 점선으로 표시하였는데, 1번 반복 재구성 결과는 절대적인 값과 상대적인 값이 모두 모델과 차이가 있는 것을 볼 수 있으며, 30번 반복 후 작은 타원 3개가 모두 구분이 되나 절대적인 값은 차이가 나는 것을 볼 수 있다. 마지막으로 100번 반복하여 재구성된 결과는 실제 모델에 접근하였음을 볼 수 있었다. 계산에 사용된 컴퓨터의 사양으로, CPU는 Intel Core i7-8550U이며, clock 속도는 1.99GHz, Ram은 16GB(Gigabyte)이며, Windows10Pro 64bit 운영 체제이며, OS(Operating System)는 WSL(Window System for Linux)2에서 작동하는 Ubuntu 20.04.2 Linux 배포용을 설치하여 사용하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F5.jpg

Fig. 5

Result of SIRT (2-D Shepp–Logan model, nx = ny = 256): (a) reconstructed image and (b) line plots through three small ellipses for iy = 50 (iteration=1, 5, 30, and 100).

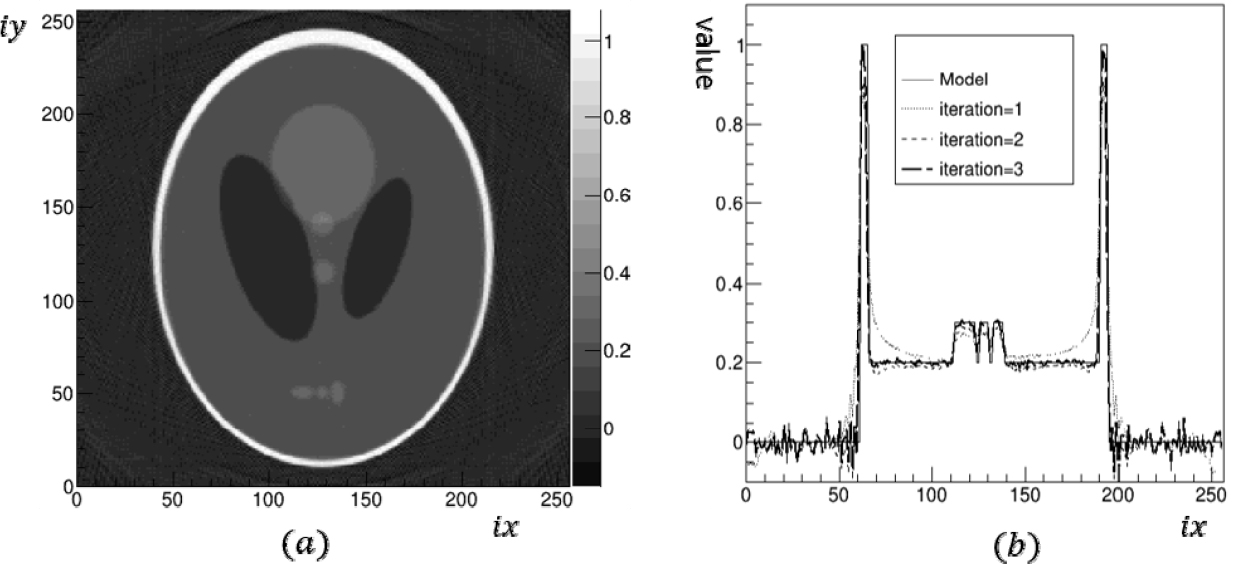
동일한 자료에 대해 SART로 영상을 재구성하였으며, 블록수와 반복회수는 다음과 같이 결정하였다. 반복회수와 블록의 개수의 곱이 SART의 갱신횟수가 되므로, 영상 재구성에 충분한 갱신회수는 SIRT의 수렴 반복회수를 초과하면 충분하므로 100에서 200 사이의 값이 되도록 하였다. 블록의 수는 투영식의 수를 블록수로 나누었을 때 정수가 되는 임의의 값을 택해도 상관은 없지만, 본 연구에서는 각도의 개수 180이 정수로 나누어지도록 정하여, 블록의 수를 45로 하였고, 반복회수를 3회로 설정하여 총 45×3=135번의 갱신과정을 거치도록 하였다. Fig. 6은 SART의 분석결과로서 (a)는 재구성된 이미지이다. 전체적인 이미지 형태는 SIRT와 큰 차이는 없지만, SIRT에 비해 노이즈가 많아 재구성된 셀의 최소값은 더 작아지고 최대값은 더 커져서 물성값의 범위가 더 커진 것을 볼 수 있다. (b)는 Fig. 5 (b)와 같은 위치의 프로파일로서 첫 번째 반복부터 셀값이 모델값에 근접한 것을 볼 수 있고, 3회 반복한 경우 배경 노이즈가 다소 증가하지만, 작은 타원 3개는 잘 구분되어 SIRT 결과와 거의 일치하는 것을 볼 수 있었다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F6.jpg

Fig. 6

Result of SART (2-D Shepp–Logan model, nx = ny = 256): (a) reconstructed image and (b) line plots through three small ellipses for iy = 50 (iteration=1, 2, and 3).

압축표현 효과의 유무와 두 영상 재구성 방법의 계산시간과 메모리 사용량을 비교한 결과를 Table 2에 정리하였다. SIRT와 SART의 메모리 사용량은 거의 비슷하다. 두 경우 모두 압축표현 행렬을 사용하지 않는 경우인 normal expression의 메모리 사용량이 압축표현 행렬을 사용하는 경우인 compressed expression의 메모리 사용량의 약 30배 더 많이 필요했다. 계산시간은 SIRT의 경우 100회 반복하는 데 압축표현 행렬을 사용하지 않은 경우 309분 13.27초 걸렸고, 압축표현 행렬을 사용하면 57.51초가 되어, 321.49배 빨라졌다. SART의 경우 3회 반복동안 압축표현 행렬을 사용하지 않는 경우 1분 36.8초 걸린 반면, 압축표현 행렬을 사용하면 3.0초가 걸려, 32.27배 빨라졌다. SART가 SIRT에 비해 압축표현 행렬을 사용할 때 시간단축 효과가 상대적으로 적은 것처럼 보이지만, 계산시간에 압축표현과 상관없는 길이 행렬 $A$ 를 구하는 시간이 포함되기 때문에 생긴 현상으로 보인다.

Table 2.

Comparison of calculation times and used memories of SIRT and SART of 2D Shepp–Logan model (256×256)

	SIRT		SART
expression	normal	compressed	normal	compressed
Memory	11.5 GBytes	412 MBytes	11.5 GBytes	404 MBytes
CPU time	309 min 13.27 sec	57.71 sec	1 min 36.8 sec	3.0 sec

3차원 모델

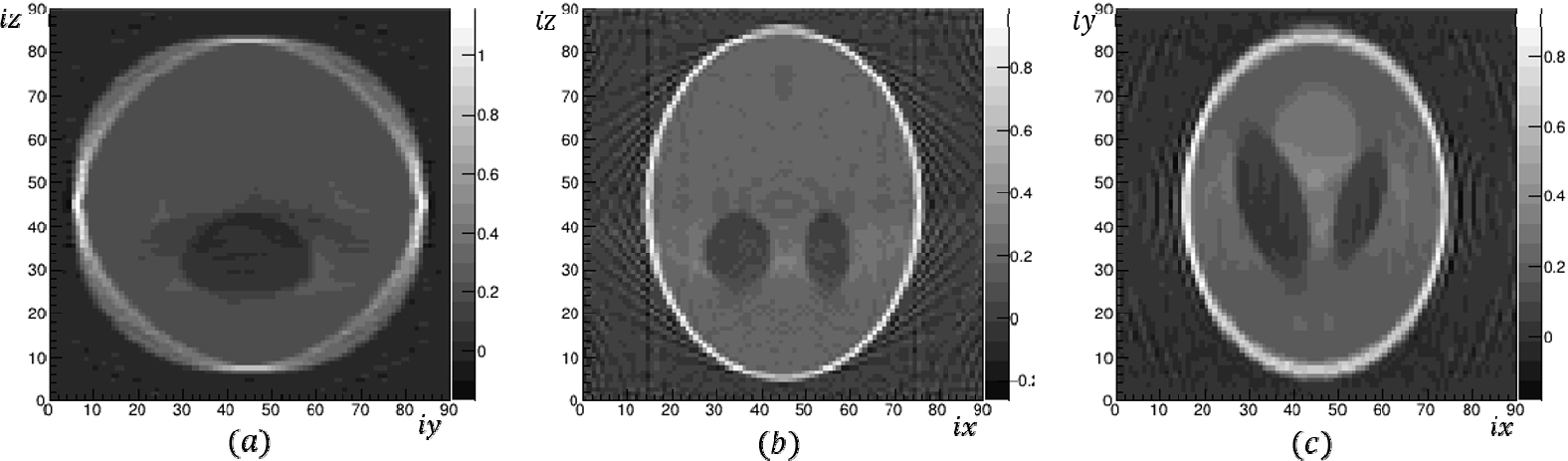
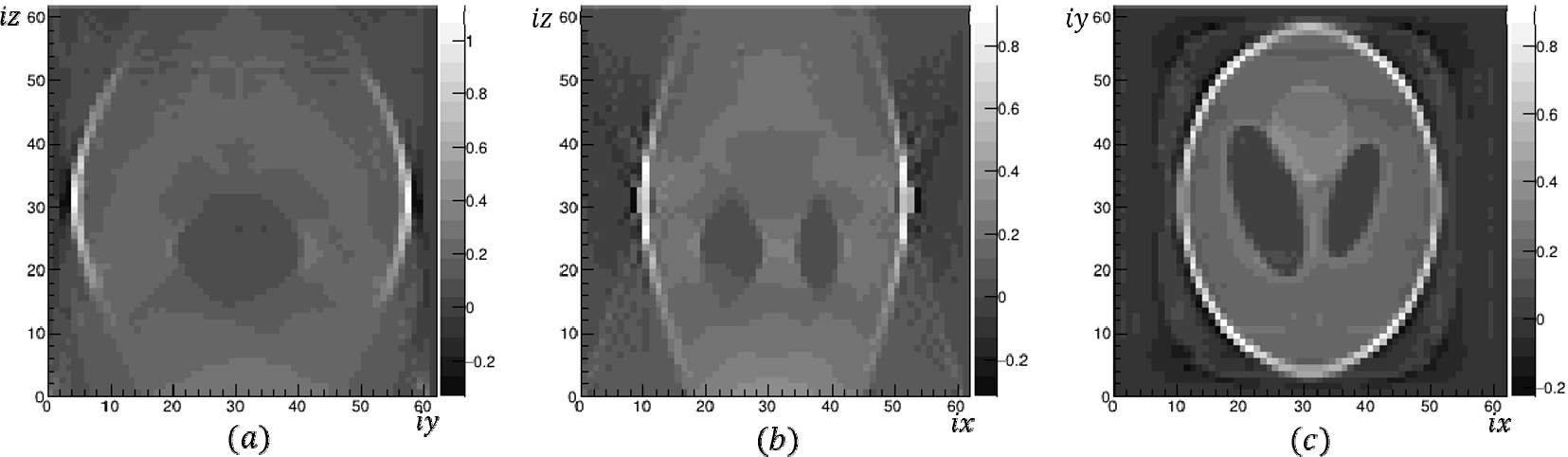
3차원 SART는 2차원과 달리 방대한 메모리를 필요로 하므로, 배열을 크게 할당하기는 쉽지 않아, 투사 빔의 각도 $θ_{x}$ 는 –90°에서 88°까지 2° 간격으로 총 90개를 사용하였고, $θ_{y}$ 는 –9°에서 8°까지 1° 간격으로 총 18개를 사용하였다. 각 각도마다 횡축방향 거리인 $t_{x}, t_{y}$ 의 개수를 모두 90개로 설정하였고, 셀의 개수도 90×90×90으로 하였다. 이 경우 배열의 자료형을 실수(float)로 했을 때 사용된 총메모리가 거의 12GB가 되었다. Fig. 7은 3차원 Shepp-Logan 모델 자료에 SIRT를 100회 반복하여 각 축 방향의 재구성 영상 단면을 나타낸 그림이다. (a)는 Table 1의 4번째 타원체의 정중앙인 $x = - 0.22$ 를 수직으로 지나는 단면의 재구성 영상이고, (b)는 $y = 0$ 를 지나는 단면의 재구성 영상이며, (c)는 Table 1의 3번째부터 8번째까지의 타원체의 중심의 공통 $z$ 값인 $z = - 0.25$ 를 수직으로 지나는 단면의 영상재구성 결과이다. 3차원 SIRT의 결과는 2차원 자료보다 각 셀을 지나는 투영식의 개수와 재구성 영역의 분해능을 작게 했기 때문에, 2차원 SIRT보다는 선명함이 떨어지지만 각 방향의 이미지 재구성이 잘 수행됨을 알 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F7.jpg

Fig. 7

Reconstructed results of SIRT using projections of angles and distances (3-D Shepp–Logan model): (a) yz-plane of ix = 35 (x =−0.22), (b) xz-plane of iy = 45 (y = 0), and (c) xy-plane of iz = 33 (z =−0.25).

Fig. 8은 블록 수를 45로 하여 3회 반복한 SART의 재구성 이미지이며, 사용된 투영 자료는 SIRT의 자료와 같다. 2차원 SART와 마찬가지로 전체 투영식에 대한 반복은 3회 수행했지만 각 블록마다 갱신이 수행되므로 총 45×3회의 갱신과정을 거친 결과이다. 이미 언급된 대로 SART의 경우 영상 재구성 결과가 한 블록 내에서의 투영식들의 계산 순서 및 블록의 순서 등에 영향을 받기 때문에 투영식의 순서를 다음과 같이 재조정하였다.

(35)

p_{- 1 + l}, p_{N_{p} - l}, p_{N_{p} / 2 - l}, p_{N_{p} / 2 - 1 + l}, 여기서 l = 1, 2, \dots, \frac{N_{p}}{4} .

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F8.jpg

Fig. 8

Reconstructed results of SART using projections of angles and distances (3-D Shepp–Logan model): (a) yz-plane of ix = 35 (x =−0.22), (b) xz-plane of iy = 45 (y = 0), and (c) xy-plane of iz = 33 (z =−0.25).

이는 전체투영식의 양끝 두 식과 중간 두 식부터 시작하여 순차적으로 하나씩 감소 및 증가시켜 공간적인 대칭성을 유지하면서 전체 투영식을 선택하기 위한 것이다. 이러한 순서 재조정 없이 SART를 수행하면, 처음 블록을 사용하여 생성된 yz 단면에서의 이미지가 특정 방향으로 일그러졌는데, 이 일그러진 재구성 이미지가 마지막 블록에서는 반대 방향으로 일그러지는 현상이 나타났으나, 순서 재조정을 하여 특정 방향으로 이미지가 일그러짐을 피할 수 있었다. 이 SART 결과(Fig. 8)를 SIRT의 결과(Fig. 7)와 비교하면 SART의 총 반복횟수가 3회에 불과하지만, 100회 반복한 SIRT의 이미지와 유사한 것을 확인할 수 있다. 기본적으로는 최소 한 방향만이라도 각도영역이 충분하다면, 투영 자료에 SART분석법을 적용하는 경우 3차원 이미지 재구성에 문제가 없음을 확인하였다. 3차원에서는 압축표현 행렬을 사용하지 않는 경우 방대한 메모리가 필요하여 PC상에서 구현이 불가능하기 때문에 2차원과 같이 두 경우를 비교할 수 없었다. 압축표현 행렬을 사용한 SIRT의 100회 반복 계산시간은 112분 56.10초이며, SART의 3회 반복 계산시간은 8분 37.18초가 되어, 비슷한 품질의 영상을 얻는 데에 SART가 13.1배 빠르다고 생각할 수 있다.

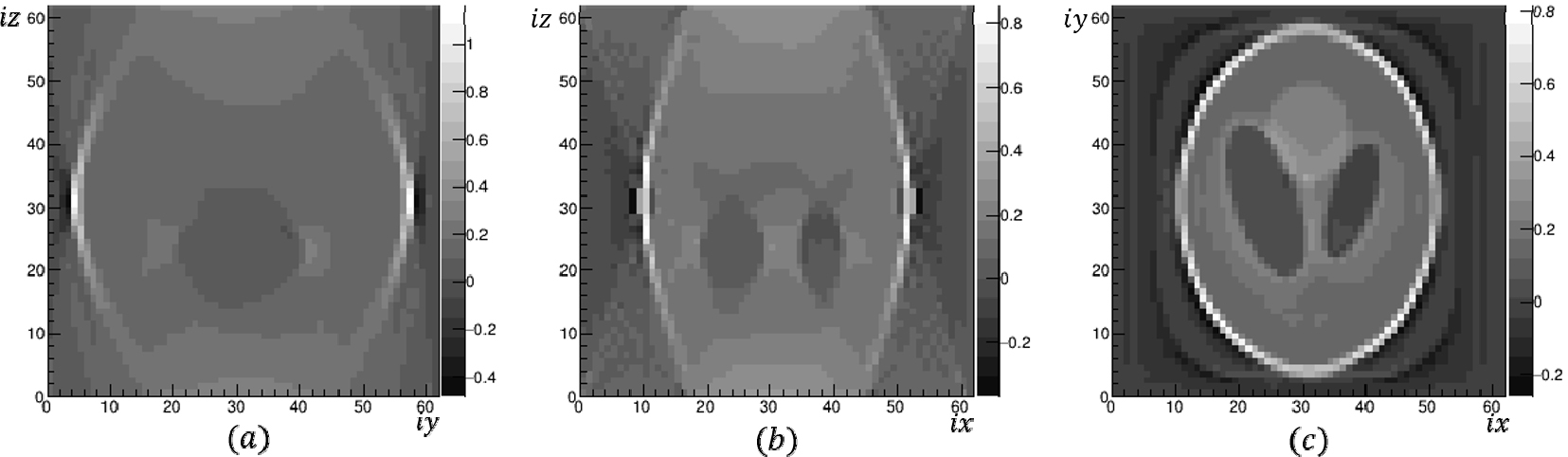
그러나 실제 실험 상황에서는 송신원으로 코스믹 뮤온을 사용하는 경우와 같이 모든 각도에 대한 투영 자료를 충분히 얻을 수 없는 경우도 있다. 한 예로 송신점과 수신점이 서로 다른 높이로 각각 2차원 배열을 이루는 경우, 수평 방향의 투영 자료가 없기 때문에 $z$ 방향의 이미지의 분해능이 떨어질 것으로 예측할 수 있다. Fig. 9와 Fig. 10은 송신점과 수신점이 서로 다른 높이에 2차원 배열로 설치된 경우의 투영 자료를 사용하여 3차원 SIRT(Fig. 9)와 3차원 SART (Fig. 10)로 영상을 재구성한 결과이다. 송신점과 수신점의 배열 개수는 모두 62×62이고 대상 영역도 62×62×62로 나누었다. SIRT는 총 100회의 반복과정을 거쳤으며, SART의 경우 전체 투영식을 31개의 블록으로 나누었고 4회 반복하였다. 앞의 경우와 같이 투영식의 순서를 재조정하여 공간 대칭성을 유지하도록 하였다. 영상재구성 결과는 SIRT와 SART가 유사하며 수평방향에 가까운 각도의 투영 자료가 없기 때문에, $z$ 방향의 분해능이 $x, y$ 방향의 분해능에 비해 떨어지는 것을 볼 수 있다. 이러한 분해능의 저하는 SART나 SIRT의 방법론적 문제라기보다 측정 범위의 제한 때문에 발생하는 것으로서 SART나 SIRT와 같이 산술적인 영상 재구성 방법의 경우, 다른 측정 정보들로부터 산술식에 제한(constraint)을 주거나 산술식을 추가함으로, $z$ 방향의 분해능을 향상시킬 수 있을 것이다. SIRT의 100회 반복 계산시간은 112분 30.68초이며, SART의 3회 반복 계산시간은 8분 46.85초가 되어, 각도 자료를 사용한 경우와 유사한 결과를 보여준다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F9.jpg

Fig. 9

Reconstructed results of SIRT using projections of sources and receivers (3-D Shepp–Logan model): (a) yz-plane of ix = 24 (x =−0.22), (b) xz-plane of iy = 31 (y = 0), and (c) xy-plane of iz = 23 (z =−0.25).

https://static.apub.kr/journalsite/sites/ksmer/2021-058-05S/N0330580502/images/ksmer_58_05_02_F10.jpg

Fig. 10

Reconstructed results of SART using projections of sources and receivers (3-D Shepp–Logan model): (a) yz-plane of ix = 24 (x =−0.22), (b) xz-plane of iy = 31 (y = 0), and (c) xy-plane of iz = 23 (z =−0.25).

결 론

3차원 투영 자료를 이용하여 영상을 재구성할 때 선형연립 방정식을 이루는 행렬의 크기가 매우 크기 때문에 행렬 값을 저장하기 위해 메모리 용량이 많이 필요하고, 반복적인 계산법으로 해를 구하는 데에도 시간이 많이 소요된다. 그런데 이 행렬은 일부분을 제외하고는 대부분의 값이 0인 희소행렬에 해당되므로, 0이 아닌 값만을 메모리에 저장하는 행렬의 압축표현 방식을 사용하여, 필요로 하는 메모리의 용량을 크게 줄일 수 있었으며 반복 계산과정의 루프의 수도 크게 줄기 때문에 계산 시간도 크게 단축시킬 수 있었다. 전체 투영 자료를 모두 계산에 사용하여 셀값을 갱신하는 SIRT류의 분석법은 재구성된 이미지의 노이즈를 줄일 수 있는 장점이 있으나 실제해에 접근하기 위해서 많은 반복 계산과정이 필요하다. 본 연구에서는 3차원 이미지 재구성 방법으로 SART분석법이 적합할 것으로 판단하였으며, 실제 이 방법을 적용하여 SIRT와 비교한 결과 노이즈를 어느 정도 줄이면서 계산 속도도 크게 높일 수 있었다. 프로그램 검증을 위하여, 이미 잘 알려진 2차원 Shepp-Logan 모델로부터 투영 자료를 합성하여, 개발된 SART 분석법을 적용하여 2차원 이미지를 재구성하였고, 프로그램이 잘 작동함을 확인하였다. SART 분석법을 3차원에 적용하기 위해, 10개의 타원체로 구성된 3차원 Shepp-Logan 모델로부터 투사 빔의 각도 범위가 충분한 자료인 각도와 횡축방향 거리에 따라 생성한 자료와, 투사 빔의 각도 범위가 충분치 못한 자료인 송신점과 수신점의 2차원 배열을 가정하여 생성한 두 투영 자료를 사용하였다. SART 분석법은 계산 루프를 수행할 때 투영식의 순서와 블록의 순서에 영향을 받기 때문에 공간적인 대칭이 유지되도록 투영식의 순서를 재조정하였다. 투사 빔의 각도의 범위가 충분한 자료의 경우 $x, y, z$ 각 방향으로 이미지 재구성이 효과적으로 수행되는 것을 확인하였으나, 송신점과 수신점의 2차원 배열의 경우, 수평 방향의 측정 자료가 충분하지 못하여 $z$ 방향의 분해능이 떨어지지만, SART로 재구성된 이미지가 SIRT로 재구성된 이미지와 유사함을 확인할 수 있었다. 결론적으로 압축표현 방식의 행렬의 적용과 수렴 속도가 빠른 SART를 사용함으로써 3차원 영상 재구성을 효과적으로 수행할 수 있었다. 본 연구에서 개발된 압축표현 행렬을 사용한 SART 분석법은 코스믹 뮤온을 이용한 지하구조 탐사뿐 아니라, 굴절과 회절을 고려하여 행렬을 재계산하면 탄성파 토모그래피에도 적용이 가능하다.

References

Ambrose, J. and Hounsfield, G., 1973. Computerized transverse axial tomography, British Journal of Radiology, 46, p.148-149. 10.1259/0007-1285-46-552-10164757352

Andersen, A.H. and Kak, A.C., 1984. Simultaneous algebraic reconstruction technique(SART): A superior implementation of the art algorithm, Ultrasonic Imaging, 6, p.81-94. 10.1177/0161734684006001076548059

Bonechi, L., D'Alessandro, R., and Giammanco, A., 2020. Atmospheric muons as an imaging tool, Reviews in Physics, 5, 100038p. 10.1016/j.revip.2020.100038

Comack, A.M., 1963. Representation of a function by its line integrals with some radiological application, Journal of Applied Physics, 34, p.2722-2727. 10.1063/1.1729798

Comack, A.M., 1964. Representation of a function by its line integrals with some radiological application II, Journal of Applied Physics, 35, p.2908-2913. 10.1063/1.1713127

D'Alessandro, R., Ambrosino, F., Baccani, G., Bonechi, L., Bongi, M., Caputo, A., Ciaranfi, R., Cimmino, L., Ciulli, V., D'Errico, M., Giudicepietro, F., Gonzi, S., Macedonio, G., Masone, V., Melon, B., Mori, N., Noli, P., Orazi, M., Passeggio, P., Peluso, R., Saracino, G., Scognamiglio, L., Strolin, P., Vertechi, E., and Viliani, L., 2018. Volcanoes in Italy and the role of muon radiography, Philosophical Transactions a Royal Society A, 377(2137):20180050. 10.1098/rsta.2018.005030530551PMC6335311

Dempster, A.P., Laird, N.M., and Rubin, D.B., 1977. Maximum likelihood from incomplete data via the EM algorithm, Journal of the Royal Statistical Society B, 39(1), p.1-38. 10.1111/j.2517-6161.1977.tb01600.x

Dines, K.A. and Lytle.R.J., 1979, Computerized geophysical tomography, Proc. IEEE, 67, p.1065-1073. 10.1109/PROC.1979.11390

Feldkamp, L.A., Davis, L.C., and Kress, J.W., 1984. Practical cone-beam algorithm, Journal of the Optical Society of America A, 1(6), p.612-619. 10.1364/JOSAA.1.000612

Gordon, R., Bender, R., and Herman, G.T., 1970. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography, Journal of Theoretical Biology, 29(3), p.471-481. 10.1016/0022-5193(70)90109-8

Hestenes, M.R. and Stiefel, E., 1952. Methods of Conjugate Gradients for Solving Linear Systems, Journal of Research of the National Bureau of Standards, 49(6), p.409-436. 10.6028/jres.049.044

Hyun, B.K., Lim, H.R. and Lee, H.Y., 1992. Applicability of the Seismic Sraight Ray Tomography for the Image Reconstruction of the Subsurface Structure, Journal of The Korean Institute of Mineral and Energy Resources Engineers, 29, p.245-254.

Jonkmans, G., Anghel, V.N.P., Jewett, C., and Thompson, M., 2012. Nuclear Waste Imaging and Spent Fuel Verification by Muon Tomography, Annals of Nuclear Energy, 53, p.267-273. 10.1016/j.anucene.2012.09.011

Lee, H.Y., 1990. Geotomographic Inversion using CG, SIRT and DLSQ Methods, Journal of The Korean Institute of Mineral and Energy Resources Engineers, 27, p.222-233.

Liu, Z., Chatzidakis, S., Scaglione, J.M., Liao, C., Yang, H., and Hayward, J.P., 2019, Muon tracing and image reconstruction algorithms for cosmic muon computed tomography, IEEE Transactions on Image Processing, 28(1), p.426-435. 10.1109/TIP.2018.286966730222560

Marteau, J., Carlus, B., Gibert, D., Ianigro, J.C., Jourde, K., Kergosien, B., and Rolland P., 2016. Muon tomography applied to active volcanoes, Proceedings of Science, International Conference on New Photo-detectors, PhotoDet2015, 6-9 Jul 2015, Moscow, Russia. 10.22323/1.252.000427117017

Morishima, K., Kuno M., Nishio, A., Kitagawa, N., Manabe, Y., Moto, M., Takasaki, F., Fujii, H., Satoh, K., Kodama, H., Hayashi, K., Odaka, S., Procureur, S., Attié, D., Bouteille, S., Calvet, D., Filosa, C., Magnier, P., Mandjavidze, I., Riallot, M., Marini, B., Gable, P., Date, Y., Sugiura, M., Elshayeb, Y., Elnady, T., Ezzy, M., Guerriero, E., Steiger, V., Serikoff, N., Mouret, J.B., Charlès, B., Helal, H., and Tayoubi, M., 2017. Discovery of a big void in Khufu's Pyramid by observation of cosmic-ray muons, Nature, 552, p.386-390. 10.1038/nature2464729160306

Paige, C.C. and Saunders, M.A., 1982. LSQR: An algorithm for sparse linear equations and sparse least squares, ACM Transactions on Mathematical Software, 8, p.43-71. 10.1145/355984.355989

Rosenfeld, A. and Kak, A.C., 1982. Computer Science and Applied Mathematics: Digital Picture Processing(2nd Ed.), Vol. 1, Academic Press, Orlando, USA, p.353-413.

Shepp, L.A., and Logan, B.F., 1974a. The Fourier reconstruction head section Transmissions, IEEE Transactions on Nuclear Science, 21(1), p.21-43. 10.1109/TNS.1974.6499235

Shepp, L. A., and Logan, B. F., 1974b. Reconstructing interior head tissue from X-ray transmissions, IEEE Transactions on Nuclear Science, 21(1), p.228-236. 10.1109/TNS.1974.4327466

Sorzano, C.O.S., Vargas, J., Oton, J. de la Rosa-Trevin, J.M., Vilas, J.L., Kazemi, M., Melero, R., del Caño, L., Cuenca, J., Conesa, P., Gómez-Blanco, J., Marabini, R. and Carazo, J.M., 2017. A survey of the use of iterative reconstruction algorithms in electron microscopy, BioMed Research International, 2017, 6482567. 10.1155/2017/648256729312997PMC5623807

Tanaka, H.K.M., 2018. Japanese volcanoes visualized with muography, Philosophical Transactions a Royal Society A, 377:20180142. 10.1098/rsta.2018.014230530547

Tanaka, H.K.M., Taira, H., Uchida, T., Tanaka, M., Takeo, M., Ohminato, T., Aoki, Y., Nichitama, R., Shoji, D., and Tsuiji, H., 2010. Three-dimensional computational axial tomography scan of a volcano with cosmic ray muon radiography, Journal of Geophysical Research, 115, B12332p. 10.1029/2010JB007677

Van der Sluis, A. and van der Vorst, H.A., 1990. SIRT- and CG-type methods for iterative solution of sparse linear least-squares problems, Linear Algebra and its Applications, 120, p.257-303. 10.1016/0024-3795(90)90215-X

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Three-Dimensional SART Analysis for Muon Tomography

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

Fig. 1

Projection line and the values of matrix A that belongs to the projection

(34)

Table 1.

Parameters of the three-dimensional Shepp–Logan model (-1≤x≤1, -1≤y≤1, and -1≤z≤1)

Fig. 2

Three-dimensional Shepp–Logan model (nx = ny = nz = 256): (a) 3-D shapes of 10 ellipsoids, (b) yz-plane of ix = 100 (x =−0.22), (c) xz-plane of iy = 128 (y = 0), and (d) xy-plane of iz = 96 (z =−0.25)

Fig. 3

Calculated projections of the three-dimensional Shepp–Logan model using the serialized angles and distances

Fig. 4

Calculated projections of the three-dimensional Shepp–Logan model using the serialized positions of sources and receivers.

Fig. 5

Result of SIRT (2-D Shepp–Logan model, nx = ny = 256): (a) reconstructed image and (b) line plots through three small ellipses for iy = 50 (iteration=1, 5, 30, and 100).

Fig. 6

Result of SART (2-D Shepp–Logan model, nx = ny = 256): (a) reconstructed image and (b) line plots through three small ellipses for iy = 50 (iteration=1, 2, and 3).

Table 2.

Comparison of calculation times and used memories of SIRT and SART of 2D Shepp–Logan model (256×256)

Fig. 7

Reconstructed results of SIRT using projections of angles and distances (3-D Shepp–Logan model): (a) yz-plane of ix = 35 (x =−0.22), (b) xz-plane of iy = 45 (y = 0), and (c) xy-plane of iz = 33 (z =−0.25).

(35)

Fig. 8

Reconstructed results of SART using projections of angles and distances (3-D Shepp–Logan model): (a) yz-plane of ix = 35 (x =−0.22), (b) xz-plane of iy = 45 (y = 0), and (c) xy-plane of iz = 33 (z =−0.25).

Fig. 9

Reconstructed results of SIRT using projections of sources and receivers (3-D Shepp–Logan model): (a) yz-plane of ix = 24 (x =−0.22), (b) xz-plane of iy = 31 (y = 0), and (c) xy-plane of iz = 23 (z =−0.25).

Fig. 10

Reconstructed results of SART using projections of sources and receivers (3-D Shepp–Logan model): (a) yz-plane of ix = 24 (x =−0.22), (b) xz-plane of iy = 31 (y = 0), and (c) xy-plane of iz = 23 (z =−0.25).

References

Parameters of the three-dimensional Shepp–Logan model ( $- 1 \leq x \leq 1, - 1 \leq y \leq 1, and - 1 \leq z \leq 1$ )