서 론
물리검층의 개요 및 종류
비저항검층
자연전위검층
감마선검층
밀도검층
중성자검층
음파검층
신경망 기법의 개요
물리검층 분야 신경망 기법 적용사례
저류층 암상 추정
유체유동인자 추정
지질역학인자 추정
합성로그 생성
결 론
서 론
가스하이드레이트(gas hydrate)는 비전통 탄화수소 자원이자 지속가능한 미래 에너지원으로 평가받는다. 고체 상태의 가스하이드레이트는 단위 부피 대비 약 170배의 메탄가스를 포획할 수 있을 뿐만 아니라 가스하이드레이트로부터 얻을 수 있는 탄소량은 화석연료로부터 얻을 수 있는 탄소량의 약 두 배 이상으로 추정되기에 잠재력 측면에서 긍정적인 평가를 받는다(Kil et al., 2009). 또한, 석유와 같은 전통 탄화수소 자원과 비교하였을 때 상대적으로 이산화탄소를 적게 배출한다는 이점이 있기에 환경적 측면에도 기여할 수 있을 것으로 기대된다(Ryu, 2018). 이에 세계 각국은 기후 변화에 대응하기 위한 새로운 대체 에너지원으로서 가스하이드레이트를 주목하기 시작하였다.
가스하이드레이트 개발 및 생산 연구는 미국, 일본, 인도 등 세계 각국에서 1970년대부터 활발히 진행되어왔으며 국내의 경우 1996년 동해 울릉분지 남서부 해역에서 해저모방반사면(bottom-simulating reflector)을 확인하면서 본격적으로 시작되었다(Huh and Lee, 2017). 가스하이드레이트의 개발 및 생산은 상평형 이동을 유도한 해리를 의미하므로 지질학, 열역학 및 공학 기술을 복합적으로 반영한 시뮬레이션 과정이 필수다. 시뮬레이션은 공학자로 하여금 신속한 의사결정을 내리도록 돕는 역할을 하며 이때 사용하는 시뮬레이션 모델은 저류층 공간 물성 분포를 바탕으로 이루어진다(Avansi and Schiozer, 2015). 따라서 신뢰성 높은 저류층 공간 물성 분포를 생성하기 위해서는 공극률(porosity, PHI), 유체투과율(permeability, k), 포화도 등 저류층의 물리적 특성 파악 및 저류층 특성화 작업이 선행되어야 한다.
저류층 특성화에는 물리검층(geophysical logging) 및 코어분석(core analysis) 자료와 같은 유정 자료기반의 지구통계학 모델링이 활용되어 왔다(Ochie and Rotimi, 2018). 지구통계학 모델링이란 기지점에서 취득한 자료의 공간적 분포 특징을 분석하여 미지점에서의 정보를 예측하는 기법이다. 저류층 특성화 모델의 정확도는 저류층이 불균질할수록 감소하므로 더 많은 유정 자료가 확보되어야 하지만 막대한 탐사 및 시추 비용이 요구되기에 충분한 표본을 확보하기에는 현실적으로 어려움이 있다. 대표적으로 동해 울릉분지 가스하이드레이트(UBGH)의 경우 다양한 퇴적 상태가 혼재되어있는 특수성으로 인해 퇴적상 및 물성이 불균질하게 분포되어 있어 한정된 유정 자료로 신뢰성 높은 저류층을 재현하기에는 한계가 있다(Lee et al., 2013a).
최근에는 유정 자료의 양적·질적 한계를 보완하기 위해 심층학습(deep learning) 모델 개발 연구가 활발하게 시도되는 추세이다(Chaki et al., 2018; Miah et al., 2020). 취득한 물리검층 자료의 복잡한 패턴을 인식하거나 주요 특징을 추출하기 위하여 인공신경망(artificial neural network, ANN)을 활용한 모델 개발은 저류층 물성 추정, 합성로그 생성 등 다양한 방면으로 활용된다(Mahmoudi and Mahmoudi, 2014; Akinnikawe et al., 2018; Onalo et al., 2018). 이와 같은 노력은 다양한 저류층을 대상으로 이루어지고 있으나(Tang et al., 2011; Mukherjee and Sain, 2019; Zhu et al., 2019), 가스하이드레이트 저류층을 대상으로 한 연구는 상대적으로 적은 실정이다. 이는 가스하이드레이트가 전통 탄화수소 대비 기술성과 생산성이 덜 확보되어 상업 생산까지 이어지는 경우가 드물기 때문이다(Huh and Lee, 2017). 특히 국내의 경우, UBGH를 대상으로 한 심층학습 관련 연구는 한정된 물리검층 자료 및 시험생산 중단으로 인하여 연구의 범위가 제한적일 뿐만 아니라(Lee et al., 2013b; Jeong et al., 2014; Lee et al., 2017), 물리검층 자료를 활용한 심층학습 관련 연구 또한 기초단계에 머물고 있는 실정이다(Lim, 2003; Lim and Park, 2005). 따라서 국내 가스하이드레이트 개발 수준 및 글로벌 연구 동향을 고려할 때, 물리검층 자료를 활용한 연구에 심층학습법을 적극 활용할 필요가 있다. 심층학습법을 기반으로 하여 미지점에서의 유정 자료를 추정하고 보다 정확한 저류층 물성 분포를 모델링할 수 있을 것으로 기대된다.
본 연구는 향후 국내에서 수행할 가스하이드레이트 저류층에 대한 심층학습 모델 개발 연구의 기반을 제공하기 위한 목적으로 한다. 가스하이드레이트 저류층 뿐만 아니라 다양한 저류층에서 획득한 물리검층 자료에 신경망 기법을 적용한 주요 선행연구를 조사하여 최신 기술동향을 분석한다. 연구사례들은 지도학습법을 중심으로 조사하였으며 신경망 모델의 출력자료에 따라 네 가지 유형으로 분류하였다. 기술동향 분석에 앞서, 물리검층의 개요 및 종류와 신경망 기법에 대해 간략히 설명한다.
물리검층의 개요 및 종류
물리검층은 석유 탐사 단계의 핵심 과정 중 하나로 코어, 탄성파와 함께 지질구조 해석과 부존량 평가 등 저류층 특성화의 기초 자료를 제공한다(Seo et al., 2010). 저류층의 비균질성이 커질수록 저류층 물성 간 상관관계 분석이 어렵기 때문에 확보한 코어, 물리검층, 탄성파 자료를 함께 통합분석하는 연구가 수행되어 왔다(Adams, 2005; Ashraf et al., 2019; Mohamed et al., 2019). 또한, 물리검층 자료는 일부 저류층 구간 또는 유정에서 장비 손상, 해석 오차, 불량한 검층 조건 등 다양한 이유로 미확보되는 경우가 발생할 수 있다(Pham and Naeini, 2019). 이에 자료가 부분적으로 소실된 저류층 구간이나 물리검층을 수행하지 못한 유정의 특정 심도에서 검층 결과를 추정하고자 하는 연구가 수행되어 왔다(Zhang et al., 2018; Chen and Zhang, 2020). 물리검층 분야 연구들은 과거 단순 통계기반에서 IT 산업 기술의 발달과 함께 심층학습 기반의 연구로 확장되는 추세이다(Mukherjee and Sain, 2019; Al Khalifah et al., 2020).
물리검층 분야에서 심층학습 기반 주요 연구사례들은 추정하고자 하는 출력자료(암상 추정, 저류층 물성 추정, 결측 구간 물리검층 추정 등)에 따라 여러 물리검층 자료를 조합하여 입력자료로 사용하고 있다. 신경망 모델의 입출력으로 사용된 물리검층 자료는 방사능검층, 전기검층, 전자유도검층 등 측정하고자 하는 저류층 물성에 따라 그 종류가 다양하다. 대표적으로 비저항검층(resistivity log, RT), 자연전위검층(spontaneous potential log, SP), 감마선검층(gamma-ray log, GR), 밀도검층(density log, DEN), 중성자검층(neutron log, NEU), 음파검층(sonic log, DT) 등이 사용되며, 각 물리검층 자료의 특징을 간략히 설명한다.
비저항검층
RT는 유・가스 저류층에서 암상 및 탄화수소 함유 영역을 식별하고 해저모방반사면과 같은 석유물리학적 특성을 추정하는데 사용한다(Jafari Kenari and Mashohor, 2013). RT는 검층방법(재래식, 전류직속식, 전자유도식, 미소식 등)과 탐사심도에 따라 RS(shallow resistivity), RD(deep resistivity), ILM(induction medium resistivity), ILD(induction deep resistivity), LLS(shallow laterolog resistivity), LLD(deep laterolog resistivity), LL8(shallow laterolog resistivity), MSFL(microspherically focused log resistivity) 등 다양한 약어로 표현한다. 수포화도가 높은 지층의 경우 상대적으로 낮은 RT를 보이는 반면 탄화수소 포화도가 높은 지층은 탄화수소의 비전도성으로 인해 상대적으로 높은 RT를 보인다(Varhaug, 2016). 가스하이드레이트 저류층 또한 가스하이드레이트가 절연체로 작용하여 높은 RT를 보이는 특징이 있다(Majumder, 2009). 따라서 RT는 가스하이드레이트 부존량 평가를 위한 주요 물리검층 중 하나이다(Guerin and Goldberg, 2002).
자연전위검층
SP는 투수층과 불투수층을 구분하기 위한 목적으로 수행되며 지층 내에서 자연적으로 발생하는 전극과 지표에 고정시켜놓은 전극 사이의 전압차를 측정한다(Jafari Kenari and Mashohor, 2013). SP 곡선은 유체투과율, 공극률, 지층수 염분, 이수 침투 등 다양한 인자에 영향을 받으며 불투수성 셰일에서의 SP 값을 기준선으로 설정하였을 때, 음의 SP와 상대적으로 높은 RT를 보이면 탄화수소를 포함할 가능성이 더 높다고 해석할 수 있다(Varhaug, 2016). 가스하이드레이트층 하부에 가스층이 존재하는 경우, 가스하이드레이트층이 상대적으로 더 높은 음의 SP 값을 보인다(Collet, 1992).
GR은 지층에서 자연적으로 발생하는 방사능을 측정하여 암상을 판별한다. 셰일과 점토는 주로 포타슘(potassium, K), 우라늄(uranium, U), 토륨(thorium, Th) 등의 방사성 원소를 방출하기 때문에 GR은 지층의 주요 암상(셰일, 점토, 사암, 탄산염암)을 구분하는데 유용하다(Jafari Kenari and Mashohor, 2013). 전형적으로 탄화수소는 사암층 또는 탄산염암층에 부존하므로 GR이 상대적으로 낮을수록 탄화수소 부존 가능성이 높다(Varhaug, 2016). 가스하이드레이트 저류층 또한 주변 지층에 비해 상대적으로 낮은 GR을 보인다(Wang et al., 2014).
밀도검층
DEN은 밀도 공극률(density porosity, DPHI) 추정 등에 활용되는 검층 자료로 공극률과 역수 관계를 보인다(Jafari Kenari and Mashohor, 2013). RHOB(bulk density log)로 나타내기도 한다. DEN은 검층 장치에서 인위적으로 방출시킨 감마선을 이용하여 지층의 전자 밀도를 도출한다. 탄화수소는 유기물로 이루어져 있어 암석에 비해 밀도가 낮으므로 DEN이 상대적으로 낮을수록 탄화수소 부존 가능성이 높다(Wang et al., 2019). 가스하이드레이트 저류층의 밀도는 물로 포화된 지층의 밀도보다 작으므로 DEN이 감소한 구간에서 가스하이드레이트의 부존 가능성이 있다. 그러나 가스층의 경우 더 작은 밀도를 보이므로 주의가 필요하다(Pandey et al., 2020). 한편, 영구동토층(permafrost)과 같이 얼음이 부존한 지층의 경우 가스하이드레이트 저류층과 유사한 밀도를 보이기 때문에 DEN만으로 가스하이드레이트 부존 가능성을 식별하기는 어렵다(Collet, 1992).
중성자검층
NEU는 수소 원자의 농도(hydrogen index)를 측정하여 중성자 공극률(neutron porosity, NPHI) 추정 등에 활용하는 검층 자료이다(Jafari Kenari and Mashohor, 2013). 검층장비에 따라 CNL(compensated neutron log), SNP(sidewall neutron porosity tool), GNT(gamma-ray neutron tool) 등으로 나타내기도 한다. 수소원자의 양이 많으면 NEU가 상대적으로 낮게 측정되므로 공극이 물 또는 석유로 포화되어 있을 경우 상대적으로 높은 NPHI를 보인다. 따라서 NEU가 낮거나 NPHI가 높으면 탄화수소 부존 가능성이 높다(Varhaug, 2016). 만약, 공극이 가스로 포화되어 있을 경우 수소원자의 양이 적어 NPHI가 낮게 측정된다. 따라서, 가스하이드레이트 안정영역 하부에 가스로 포화된 퇴적층이 위치할 경우 높은 NPHI를 보이다가 해저모방반사면을 기준으로 NPHI가 감소하는 양상을 보인다(Collet, 1992)
음파검층
DT는 지층을 통과하는 압축 및 전단 음파 전파시간차를 측정하여 음파검층 공극률(sonic porosity, SPHI) 추정 등에 활용되는 검층 자료이다(Jafari Kenari and Mashohor, 2013). AC(acoustic log), DTCO(compressional wave sonic transit time), DTSM(shear wave sonic transit time) 등으로 나타내기도 한다. DT는 속도와 역수 관계에 있으므로, DTCO 및 DTSM으로부터 압축파 속도(compressional wave velocity, vp) 및 전단파 속도(shear wave velocity, vs)를 계산할 수 있다. 암상과 공극률은 음파 속도에 직접적인 영향을 끼친다. 음파 속도는 압밀된 지층일수록 빠르며, 유체로 채워진 공극에서는 느리다(Varhaug, 2016). 따라서 탄화수소 부존 구간에서는 음파 속도는 감소하고 DT는 증가한다(Wang et al., 2019). 가스하이드레이트 부존 구간에서 DT는 물 또는 가스로 포화된 지층과 비교하였을 때 감소한다. 그러나 얼음이 부존한 지층의 경우 가스하이드레이트 저류층과 유사한 DT를 보이기 때문에 DT만으로 가스하이드레이트 부존 가능성을 식별하기는 어렵다(Collet, 1992).
Table 1은 대규모 하이드레이트 저류층(massive hydrate), 하이드레이트를 함유한 퇴적층(deposit containing hydrate), 물로 포화된 퇴적층(deposit saturated with water), 가스를 함유한 퇴적층(deposit containing gas)에 대하여 SP를 제외한 물리검층 자료의 일반적인 검층값 범위를 나타낸다(Xu et al., 2007). 상기 검층 범위는 물리검층과 심층학습을 결합한 연구에서 신경망학습시 정규화 및 표준화의 참고자료로 활용가능하다. 물리검층은 종류별로 서로 상이한 특징을 보이며 비전통 저류층에 해당할수록 물리검층을 통한 저류층 부존 특성 파악은 단일한 검층결과가 아닌 다양한 종류의 검층 결과를 종합적으로 해석해야 한다. 따라서 예측하고자 하는 출력자료를 결정하고 나면 매개변수 간 상관관계 분석, 민감도 분석 등을 통하여 출력하고자 하는 자료와 상관성이 높은 물리검층 자료를 입력자료로 선별하는 과정이 필요하다.
Table 1.
Typical range of geophysical logs (Xu et al., 2007)
신경망 기법의 개요
심층학습의 가장 핵심적인 기술인 ANN은 인간의 뉴런을 모방하여 만들어진 알고리듬으로 입력 및 출력 간 비선형 복합관계를 보이는 모델 설계 시 유용하다(Saputro et al., 2016). ANN은 한 개의 입력층, 한 개 이상의 은닉층, 한 개의 출력층으로 구성되며 각 층은 다수의 노드로 이루어져 있으며, 인접층의 노드들끼리는 가중치 로 상호연결되어 있다. 현재층의 노드에 할당되는 값들은 이전층의 노드들의 값들에 가중치 를 곱한 후, 활성화함수(activation function)를 적용한 값이 된다. ANN의 학습은 입력자료와 출력자료를 적절히 대응시킬 수 있도록 가중치 배열 를 조정하는 과정을 의미한다(Karimpouli et al., 2010).
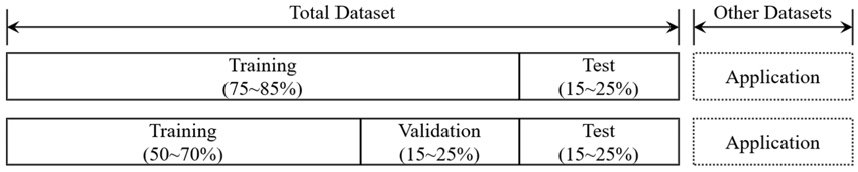
Fig. 1은 신경망 설계에서의 자료구성을 나타낸다. 신경망 설계에 사용되는 자료는 목적에 따라 학습자료(training dataset), 검증자료(validation dataset), 시험자료(test dataset)로 세분화할 수 있다. 일반적으로 전체자료의 50-70%는 학습자료로 구성하여 모델을 학습하는데 사용하며, 15-25%는 검증자료로 학습자료와 함께 신경망의 일반화 성능을 평가하는데 사용한다. 나머지 15-25%는 시험자료로 학습이 완료된 후 모델의 예측성능을 평가하는데 사용한다. 빅데이터를 다루는 심층학습에서는 검증단계를 생략하고 학습과 시험 단계로 자료를 구성하는 경우도 있다(Tang et al., 2011; Wang et al., 2019). 학습, 검증, 시험 단계를 거쳐 신경망 설계를 완료하고 난 후 설계단계에서 사용하지 않은 전혀 다른 자료를 가지고 동일한 신경망에 적용할 수 있으며 본 연구에서는 적용자료(application dataset)라 칭한다.
ANN 학습이 완료되고 나면 해당 ANN이 입력 및 출력 간 비선형 복합관계를 충분히 이해하였는지 예측성능을 평가해야 한다. 예측 성능은 문제 설정에 따라 구분지어 산출한다. 분류 문제(classification)의 예측 성능을 평가하기 위한 성능지표(performance indicator)로는 정확도(accuracy), 정밀도(precision), 재현률(recall), F1-score 등을, 회귀 문제(regression)의 예측 성능을 평가하기 위한 성능지표로는 평균제곱근오차(root mean square error, RMSE), 피어슨 상관계수(Pearson’s correlation coefficient, ) 또는 결정계수(coefficient of determination, )를 주로 사용한다(Cheng et al., 2014).
활성화함수로 sigmoid 또는 tanh 함수를 사용하는 전통적인 ANN은 다수의 은닉층으로 구성한 경우 기울기 소실(vanishing gradient), 과적합(overfitting), 방대한 계산량 등의 문제가 발생하여 학습성능이 현저히 감소하는 문제가 있었다. 전통적인 ANN의 문제점들은 ReLU(rectified linear unit), Leaky ReLU 등의 활성화함수를 활용하고 드롭아웃(dropout)과 정칙화를 적용하는 등 다양한 개선 방안들을 이용하여 개선되면서 DNN이 발전하였다(Min et al., 2020). 그 후 DNN은 주어진 문제에 적합한 형태로 변형되면서 오토인코더(autoencoder, AE), 합성곱신경망(convolutional neural network, CNN), 순환신경망(recurrent neural network, RNN), 장단기메모리(long short-term memory, LSTM), 생성적적대신경망(generative adversarial network, GAN) 등 다양한 형태의 DNN으로 분화되었다. 최근 각광받는 심층학습 기술은 다양한 분야에서 기본적인 이론과 적용사례를 소개하고 있으므로 참고문헌으로 대체하고 생략한다(Yi, 2019; Min et al., 2020).
물리검층 분야 신경망 기법 적용사례
물리검층 분야에서 신경망의 학습에 사용하는 입출력자료에는 물리검층 자료뿐만 아니라 코어 자료가 함께 사용되기도 한다. 그러나 코어 자료는 물리검층 자료에 비해 취득비용이 비싸므로 물리검층 자료만 사용하여 신경망 모델을 설계하기도 한다(Pandey et al., 2020). 입력자료로는 다양한 종류의 물리검층 자료가 가능한데, 출력하고자 하는 자료와 상관성이 높은 주요 물리검층 자료를 입력자료로 선정하는 것이 신경망 성능에 큰 영향을 끼친다(Tang et al., 2011). 출력자료로는 예측하고자 하는 저류층 인자에 따라 다양하며 이 연구에서는 다음과 같이 크게 네 가지 유형으로 분류하였다. (1) 사암, 실트질암, 점토질암 등의 암상 종류 추정, (2) 공극률, 유체투과율, 포화도 등의 유체유동인자 추정, (3) 탄성파 속도, 영률, 일축압축응력 등의 지질역학인자 추정, (4) 합성로그 생성. 한편, 최근 물리검층 분야에서는 시계열 자료 처리에 적합하다고 알려진 RNN 또는 LSTM이 주요 심층신경망으로 활용되고 있는 추세이다(Chen and Zhang, 2020).
Tables 2, 3, 4 and 5는 출력자료에 따라 상기 네 가지 유형별 사례들을 각각 요약한 종합표이다. 저자명과 출판연도, 방법론, 입력자료, 신경망 구조, 출력자료, 필드 위치, 자료 수, 학습/검증/시험 자료비율, 최적화 알고리듬, 성능 순으로 작성하였다. 조사한 연구사례에서 제공하지 않는 내용들은 가독성을 위해 N/A(not available)로 표시하였으며 각 논문에서 사용하고 있는 약어 및 기호들은 통일하여 표기하였다. 일례로, 각 논문의 원문에서 예측 성능 지표로 또는 을 제시한 경우 본문에는 원문에 따라 서술하고 종합표에는 모두 으로 환산하여 표기하였다. 원문에서 또는 을 제공하지 않는 경우 원문에서 제공하고 있는 다른 성능 지표로 대체하였다.
저류층 암상 추정
물리검층 자료로 암상을 추정하는 방법은 직접 추정하는 방법과 간접 추정하는 방법이 있다. 직접 추정은 신경망 모델을 분류 문제로 설계하여 출력자료로 암상을 추정하는 방법이며, 간접 추정은 신경망 모델을 회귀 문제로 설정하여 출력자료로 TOC(total organic carbon), S1(volatile hydrocarbon), S2(remaining hydrocarbon) 등을 먼저 예측하여 간접 추정하는 방법이다. TOC, S1, S2는 셰일층에서 생성되는 탄화수소 양을 평가하는데 사용되는 지표이며 암상 추정은 석유물리학적 특성 분석에 가장 기본적으로 활용된다. 한편, 암상 추정을 분류 문제로 설계하는 경우 예측결과에 대한 불확실성을 정량화하기 위해 확률로 나타내는 방법을 사용하기도 한다(Tang et al., 2011). 아래의 유가스전 사례 5건과 가스하이드레이트 저류층 사례 1건을 요약 및 정리한 후 Table 2에 종합하였다.
Table 2.
Summary for the estimation of reservoir lithofacies using neural networks with log data
|
Authors (year) | Method | Inputs |
Nn (Nh)*a | Outputs |
Field (Nw) *b |
Nd *c |
Data Split Ratio |
Optimizer *d | Performance | ||||
| Indicator | Train | Valid. | Test | Appl. | |||||||||
| Tang et al. (2011) | PNN |
GR, SP, DT, RHOB, NPHI, PE, RT |
N/A (2) |
8 facies |
Wafra, Saudi Arabia (1) | N/A | 25:0:75 | N/A | Accuracy | N/A | N/A | 74% | N/A |
| Alizadeh et al. (2012) | ANN |
GR, SGR, CGR, K, Th, NPHI, DT |
7-5-1 (1) | TOC |
South SouthPars, Iran (3) | 54 | 70:15:15 | LM | R2 | 0.72 | 0.79 | 0.77 | N/A |
| Wang et al. (2019) | CNN |
RT, DT, DEN, NEU |
4-3-2- 10-10-3 (2, 2) | TOC |
Shengli, China (1) | 125 | 80:0:20 | SGD | R2 | 0.83 | N/A | 0.82 | N/A |
| S1 | 0.80 | N/A | 0.73 | N/A | |||||||||
| S2 | 0.85 | N/A | 0.83 | N/A | |||||||||
| Zhu et al. (2019) |
Fully CNN |
GR, DT, DEN, NEU, LLD, LLS |
6-12-12- 24-24 -48-48- 96-96-1 (8) | 2 facies |
Central Ordos Basin, China (228) | 399 | 75:0:25 | Adam | Accuracy | N/A | N/A | N/A | 87.5% |
| Pandey et al. (2020) | DNN |
GR, RT, Rxo, RHOB, NPHI |
5-16- 16-1 (2) | 3 facies |
Cauvery Basin, India (2) | 98 | 70:20:10 | N/A | R2 | 0.98 | N/A | N/A | N/A |
| Singh et al. (2020) | BNN |
DEN, NPHI, GR, RT, DT |
5-7-5 (1) | Probability for 5 facies |
NGHP Exp-01, India *e (3) | 508 | 50:25:25 | N/A | R2 | 0.98 | N/A | N/A | N/A |
|
5-9-4 (1) |
Probability for 4 facies | 560 | 0.98 | N/A | N/A | N/A | |||||||
|
5-9-4 (1) |
Probability for 4 facies | 620 | 0.98 | N/A | N/A | N/A | |||||||
Tang et al.(2011)은 8가지 암상(증발암, 셰일, 이암, 와케질 석회암, 플로트스톤, 머드가 풍부한 혼편 석회암, 머드가 적은 혼편 석회암, 입자암)을 분류하기 위하여 확률신경망(probabilistic neural network, PNN)을 적용하였다. PNN은 분류 및 패턴 인식 문제에 널리 사용되는 확률 신경망으로 예측결과에 대한 불확실성을 정량화하여 확률로 나타낼 수 있다는 장점이 있다. 입력자료로 GR, SP, DT, RHOB, NPHI, PE(photoelectric effect), RT 등 7가지 검층 자료를 사용하였고, 사우디아라비아 Wafra 탄산염암 유전에 위치한 2개의 유정에서 획득한 지점자료(data points)를 학습자료 및 시험자료로 나누어 사용하였다. 신경망의 학습을 위해서는 충분히 많은 자료를 확보하는 것뿐만 아니라 독립적이면서 다양한 자료를 사용하는 것이 중요하다. 해당 논문에서는 학습자료 비율이 25%에서 75%까지 증가할수록 시험자료의 예측 정확도가 증가함을 보였다. 또한, 다양한 종류의 검층자료를 함께 사용할수록 예측 정확도가 48%에서 69%까지 증가하나, 추가된 검층자료가 항상 같은 비율의 성능향상을 보이지는 않음을 제시하였다. 유정 1개의 지점자료 25%로 학습하고 나머지 자료에 대해 시험한 결과 예측 정확도는 74%로 나타났다. 상기 연구는 Wafra 유전 중 Maastrichtian 저류층의 15개 유정의 암상을 예측하여 공간 분포 모델링에 적용할 수 있다는 장점이 있으나 학습자료에 포함되지 않은 암상 예측이 어렵다는 한계가 있다. 이는 신경망 분류 문제의 고질적인 한계에 해당한다.
Alizadeh et al.(2012)은 TOC를 예측하기 위하여 ANN을 적용하였다. 입력자료로는 GR, SGR(spectral gamma-ray), CGR(corrected gamma-ray), K, Th, NPHI, DT 등 7가지 검층 자료를 사용하였으며, 이는 이 0.01 보다 작아 TOC와의 상관관계가 거의 없는 것으로 판단되는 LLD, RHOB, PE를 제외하고 선정한 결과이다. 해당 논문에서는 이란 South Pars 가스전에 위치한 유정 3개에서 획득한 54개 지점자료를 활용하였다. 학습, 검증, 시험자료에 대하여 예측을 수행한 결과, 은 각각 0.85, 0.89, 0.88을 보였다. 추정한 TOC는 군집분석(cluster analysis)을 통해 자료의 유사성에 따라 5가지 암상(Zones 1, 2, 3, 4, 5)으로 분류하였다. 입력자료 중 GR, DT, NPHI가 증가할 때 TOC 또한 증가하는 경향을 보였다. 상기 연구는 입력자료로 사용한 물리검층 자료가 LWD일 경우 시추와 동시에 검층이 진행되기 때문에 바로 암상을 추정할 수 있다는 장점이 있다. 그러나 지질학적 특성이 상이한 저류층에 바로 적용하기에는 한계가 있다. 이 역시 신경망 문제의 고질적인 한계에 해당한다.
2012년 이미지넷(ImageNet) 대회 이후 심층신경망의 성능이 각광을 받으며 2010년대 중반부터 물리검층 분야에서도 심층신경망을 활용한 연구들이 발표되어 왔다. Wang et al.(2019)은 TOC, S1, S2를 예측하기 위하여 CNN을 적용하고 그 성능을 ANN의 성능과 비교하였다. 해당 논문에서는 세 가지 지표를 일정한 기준에 따라 탄화수소 부존 가능성이 높은 TypeⅠ(TOC>4%, S1>8 mg/g, S2>15 mg/g)과 부존 가능성이 보통인 TypeⅡ(TOC=2-4%, S1=2-8 mg/g, S2=10-15 mg/g)로 지층을 구분하였다. 입력자료로는 RT, DT, DEN, NEU를 사용하였으며, TOC와의 상관관계가 거의 없는 GR은 제외하였다. 중국 Shengli 유전에 위치한 1개 유정에서 획득한 125개 지점자료를 학습자료 및 시험자료로 나누어 수행하였다. TOC, S1, S2에 대한 CNN의 학습 결과, 은 각각 0.83, 0.80, 0.85이고 시험 은 0.82, 0.73, 0.83이다. 이는 ANN의 학습결과(0.77, 0.72, 0.85) 및 시험결과(0.75, 0.46, 0.66) 보다 우수하다. 상기 연구는 CNN으로 오일을 생성하는 근원암의 깊이를 추정할 수 있으나, 이를 위해서는 상대적으로 많은 학습자료가 필요하다는 한계가 있다.
Zhu et al.(2019)은 가스층을 판별하기 위해 Fully CNN을 적용하고 그 성능을 기존의 경험적 접근방식(conventional empirical approach, EMA)과 비교하였다. Fully CNN은 일반적인 CNN 구조와는 다르게 후반부 심층신경망 단계 없이 전반부 합성곱 단계만으로 결과를 도출하는 신경망이다. 입력자료로 GR, DT, DEN, NEU, LLD, LLS 등 6가지 검층 자료를 사용하였다. 원시자료를 정규화한 후 2D 회색조 맵(grey map)으로 변환하여 사용하였으며, 지층 추정결과를 가스 저류층(gas layer)과 가스가 부존하지 않는 지층(dry layer)으로 분류하였다. 중국 Ordos 분지 가스전에 위치한 228개 유정에서 획득한 399개 지층 정보를 지점자료로 활용하여 학습 및 시험을 수행하여 신경망을 설계하였다. 신경망 설계에 사용하지 않은 다른 48개 지층 정보에 대하여 EMA와 Fully CNN을 적용한 결과, 예측 정확도는 각각 75.0%, 87.5%로 나타났다. 이러한 정확도 차이는 매우 얇은 지층에 대하여 EMA는 단편적으로 가스가 부존된 지층으로 판별한 반면, Fully CNN은 전체 지층을 포괄적으로 고려하여 가스 포화도가 거의 없는 지층으로 판별한데에서 기인한 것으로 해석하였다. 이처럼 상기연구는 매우 얇은 지층이 존재하거나 지질학적으로 복잡한 지층일 경우 보다 신뢰성 있는 결과를 제공할 수 있다는 장점이 있다. 그러나 정확한 예측을 위해서는 다른 신경망 모델과 마찬가지로 충분한 양의 학습자료가 필요하다는 한계가 있다.
Pandey et al.(2020)은 탄화수소 함유 지층, 대수층 및 셰일층을 판별하기 위하여 DNN을 적용하였다. 입력자료로는 GR, RT, Rxo(resistivity of the flushed zone), RHOB, NPHI를 사용하였으며, 출력자료로는 탄화수소 함유 지층, 대수층, 셰일층에 각각 10, 20, 30의 lithocode 값을 부여하여 사용하였다. 인도 Cauvery 분지 유가스전에 위치한 7개 유정 중 2개 유정에서 획득한 98개 지점자료를 학습, 검증, 시험 단계에 사용하였고, 학습자료에 대한 예측 결과 은 0.98의 값을 보였으며, 표준오차(standard error)는 0.94~ 1.11의 값을 보였다. 신경망 설계에 사용하지 않은 나머지 5개 유정에 대하여 유정별 탄화수소 함유 지층을 판별한 결과, 1개 유정을 제외한 4개 유정에서 탄화수소 함유 지층이 발견되었으며 표준오차는 0.86~1.36의 값을 보였다. 시험결과로 은 따로 밝히고 있지 않다. 상기 연구에서 제안한 신경망 모델은 인도의 다른 분지에 대해 적용할 수 있으나, 입력자료로 사용된 물리검층 결과를 모두 보유한 유정에 대해서만 적용 가능하다는 한계가 있다.
Singh et al.(2020)은 가스하이드레이트 저류층의 암상을 추정하기 위하여 베이지안 신경망(bayesian neural network, BNN)을 사용하였다. BNN은 입력 변수의 확률분포를 계산하여 과적합 문제 해결에 용이한 신경망으로 알려져 있다. 암상 추정을 위한 입력자료로는 DEN, NPHI, GR, RT, DT를 사용하였다. 개발한 기법은 인도의 Krishna–Godavari 해상분지(NGHP Exp-01)에 위치한 유정 3개에서 획득한 지점자료(508개, 560개, 620개)에 적용하여 신경망을 설계하였다. 암상 종류의 개수는 유정마다 다르게 설정하였으며, 이는 k-평균 알고리즘을 포함한 7가지 비지도학습 분류 방법을 적용한 결과이다. 1개의 유정은 5가지 암상(점토, 실트질 점토, 실트, 모래, 가스하이드레이트)에 따라, 나머지 2개 유정은 4가지 암상(점토, 실트, 모래, 가스하이드레이트)에 따라 분류하였다(Fig. 2). 가스하이드레이트는 모래를 제외한 점토, 실트질 점토, 실트 암상에 분포하나 별도의 암상으로 분류하지 않으면 예측 오차가 발생할 수 있음을 강조하며 별도의 암상으로 가스하이드레이트를 추가하였다. 각 유정에 대한 예측성능 은 모두 0.99 수준으로 매우 양호한 결과를 얻었다. 상기 연구는 이러한 암상 예측 결과를 통해 가스하이드레이트 포화도(Sgh) 및 유체투과율을 계산할 수 있으나, 유정별 암상 분류 개수를 사전에 명확히 해야한다는 번거로움이 있다.
유체유동인자 추정
공극률, 유체투과율, 포화도 등의 유체유동인자는 다양한 물리검층 조합을 통해서 추정할 수 있다. 일반적으로 공극률은 유체투과율과 로그 선형관계에 있으나 저류층의 비균질성이 커질수록 선형성이 약해진다. 이처럼 비선형 관계를 보이는 저류층에서 획득한 물리검층 자료의 경우 신경망 모델을 통하여 직접 측정되지 않는 유체유동인자를 예측할 수 있다. 유체투과율 및 포화도를 추정하는 경우 물리검층 자료로부터 추정한 공극률을 입력자료로 활용하는 경향이 있으며 신경망 모델은 주로 ANN 또는 DNN 구조를 사용하는 것으로 조사되었다. 아래의 유가스전 사례 5건과 가스하이드레이트 저류층 사례 3건을 요약 및 정리한 후 Table 3에 종합하였다.
Table 3.
Summary for the estimation of fluid flow parameters using neural networks with log data
|
Authors (year) | Method |
Inputs |
Nn (Nh) *a | Outputs |
Field (Nw)*b |
Nd *c |
Data Split Ratio | Optimizer*d | Performance | ||||
| Indicator | Train | Valid. | Test | Appl. | |||||||||
| Karimpouli et al. (2010) | SCMNN |
SGR, RT, Sw, TPHI, secPHI, Lim, Dolo, Sand, Shale, Depth |
10-23-1 (1) | k |
Southwestern Petroleum Reservoir, Iran (3) | 220 | 80:0:20 | LM | R2 | N/A | N/A | 0.97 | N/A |
| Mahmoudi and Mahmoudi (2014) | ANN |
CALI, DT, NEU, RHOB, EPHI |
5-22-1 (1) | PHI |
Oil Field, Iran (3) | N/A | 70:0:30 | LM | R2 | N/A | N/A | 0.64 | N/A |
| 5-25-1 (1) | Sw | N/A | N/A | 0.84 | N/A | ||||||||
| Saputro et al. (2016) | DNN |
GR, DT |
N/A (10) | PHI |
N/A (1) | N/A | 70:15:15 | LM | R2 | N/A | N/A | 0.93 | 0.75 |
| Al Khalifah et al. (2020) | DNN |
PHI, dPT, F |
3-1-1-1 (2) | k |
Portland Formation, England (N/A) | 130 | 77:0:23 | Adam | R2 | 0.90 | N/A | 0.88 | N/A |
| Miah et al. (2020) | DNN |
DT, GR, NPHI, PE, RHOB, RT |
6-5- 3-1 (2) | Sw |
Bengal Basin, India (N/A) | 182 | 70:15:15 | LM | R2 | 1.00 | N/A | 0.99 | N/A |
| BR | 0.99 | N/A | 0.99 | N/A | |||||||||
| SCG | 0.91 | N/A | 0.95 | N/A | |||||||||
| Lee et al. (2013b) | ANN |
2 seismic attributes |
N/A (N/A) | PHI |
UBGH, Korea*e (3) | N/A | N/A | N/A | R2 | N/A | N/A | N/A | 0.72 |
|
4 seismic attributes | Sgh | N/A | N/A | N/A | 0.27 | ||||||||
| Mukherjee and Sain (2019) | DNN |
RT, RHOB, vp |
3-4- 4-1 (2) | PHI |
NGHP Exp-02, India *e (3) | 442 | 70:15:15 | GDA | R2 | 0.98 | 0.98 | 0.98 | 0.98 |
|
RT, RHOB, vp, DPHI |
4-5- 5-1 (2) | Sgh | 0.92 | 0.94 | 0.92 | 0.79 | |||||||
| Singh et al. (2021) | 12 types of ML |
24 combination of GR, NPHI, DPHI, RHOB, RT, vp |
N/A (N/A) | Sgh |
Alaska North Slope, US*e (2) | 1,953 | N/A | N/A | NAS | N/A | N/A | N/A | 0.83 |
Karimpouli et al.(2010)은 유체투과율을 예측하기 위하여 세 개의 ANN을 합성한 SCMNN(supervised committee machine neural network) 구조를 제안하였다. SCMNN은 높은 유체투과율에 대하여 설계된 신경망, 낮은 유체투과율에 대하여 설계된 신경망, 유체투과율을 크기에 따라 두 개의 집단으로 분류하는 신경망으로 구성된다. 입력자료로는 SGR, RT, Sw(water saturation), TPHI(total porosity), secPHI(secondary porosity) 등 5가지 검층자료와 석회암(limestone, Lim), 백운암(dolomite, Dolo), 사암(sandstone, Sand), 셰일 등 4가지 암상자료 및 깊이 자료를 사용하였다. 이란 남서부에 위치한 유정 3개에서 획득한 220개 지점자료를 두 집단으로 나누어 한 집단은 학습자료로 사용하고 나머지 다른 한 집단은 시험 단계에 사용하였다. 서로 다른 30개의 SCMNN을 구성하였을 때 평균적인 시험 결과 은 0.90의 값을 보였으며, 예측한 출력자료의 평균을 최종 출력자료로 도출하였을 때 시험 결과 은 0.97로 향상되었다. 상기 연구에서 제안한 SCMNN은 독립된 세 개의 ANN을 각각 수행할 때보다 시간비용을 줄일 수 있다는 장점이 있으나 유체투과율을 크기에 따라 분류하는 신경망 성능에 전체 성능이 좌우된다는 한계가 있다.
Mahmoudi and Mahmoudi(2014)는 PHI 및 Sw를 예측하기 위해 ANN을 적용하였다. 입력자료로는 CALI(caliper log), DT, NEU, RHOB, EPHI(effective porosity) 등 5가지 물리검층 자료를 사용하였다. 이란 내 유전에 위치한 유정 3개에서 획득한 자료를 학습자료 및 시험자료로 나누어 신경망 설계를 수행하였으며, BR(bayesian regulation), GD (gradient descent), GDA(gradient descent with adaptive learning rate), LM(levenberg marquardt), RP(resilient backpropagation), SCG(scaled conjugate gradient) 등을 비롯하여 총 13가지 학습 알고리듬에 대한 시험 결과를 과 MSE(mean squared error)로 제시하였다. PHI 및 Sw에 대한 학습 알고리듬으로 LM을 사용한 경우 시험 성능 은 각각 0.80, 0.92이고 MSE는 1.82E-02, 9.5E-03으로 제시한 학습 알고리듬 중 가장 높은 예측 성능을 보였다. 상기 연구를 통해 다양한 학습 알고리듬 중 PHI 및 Sw 예측에 LM이 가장 적합하다는 사실을 확인하였다. 다만, 이 연구는 학습에서 제외된 타 저류층 적용을 통한 개발기술의 일반화 성능 검증을 수행하지는 않았다.
Saputro et al.(2016)은 PHI를 예측하기 위하여 DNN을 적용하였으며, 입력자료로 GR과 DT를 사용하였다. 입출력자료 간의 상관관계를 해석한 결과, GR은 이 0.76을 보인 반면, DT는 이 0.17로 낮은 선형관계를 보였다. 그럼에도 불구하고 DT를 입력자료로 선정한 이유는 DT가 음파 속도와 직접적인 관련이 있는 물리검층 자료이기 때문이다. 상기 DNN은 현장을 명확히 밝히지는 않았으나 현장에서 가용한 3개 유정 중 1개 유정에서 획득한 지점자료를 사용하여 학습, 검증, 시험을 진행하였다. 신경망 설계를 완료한 후 나머지 유정 2개에 대해 적용하여 그 예측 성능을 확인하였다. 또한, 은닉층의 수를 바꿔가며 실험적으로 예측 성능을 비교한 결과, 은닉층 수가 10개인 경우가 5개인 경우보다 우수한 성능을 보였다. 그러나 은닉층 수가 10개 이상인 경우 성능 차이가 미미하여 은닉층의 수는 10개로 설정하였다. 신경망 설계에 사용된 유정에 대해 예측한 결과 및 MSE는 각각 0.93, 5.67E-04의 값을 보였다. 나머지 유정 2개에 대해 예측한 결과 은 0.82, 0.75, MSE는 9.53E-04, 1.1E-03의 값을 보였다. 상기 연구를 통해 GR 및 DT는 PHI 예측에 사용되기 적합한 조합이라는 것을 확인하였다. 다만, 이 연구 또한 Mahmoudi and Mahmoudi(2014)와 마찬가지로 학습에서 제외된 타 저류층 적용을 통한 개발기술의 일반화 성능 검증을 수행하지는 않았다.
Al Khalifah et al.(2020)은 치밀 탄산염암 저류층의 유체투과율을 예측하기 위하여 DNN 및 유전 알고리듬(genetic algorithm, GA)을 적용하고 그 성능을 7가지 유체투과율 추정 방정식(RGPZ(Revil, Glover, Pezard, and Zamora) Generic, RGPZ carbonate, RGPZ approximate, RGPZ exact, Van Baaren, Kozeny-Carman, Berg)과 비교하였다. 입력자료로는 PHI, dPT(pore throat size), F(formation resistivity factor)를 사용하였다. 잉글랜드 포틀랜드 지층에서 획득한 130개 지점자료를 학습자료 및 시험자료로 나누어 신경망 설계를 수행하였으며, 총 9가지 기법에 대한 예측 성능을 보였다. DNN의 학습 및 시험 결과 은 각각 0.90, 0.88이고 RMSE는 3.5E-01, 3.8E-01로 9가지 기법 중 가장 높은 예측 결과를 보였다. 상기 연구를 통해 치밀 탄산염암 저류층에서 유체투과율을 예측하기에는 DNN이 전통적인 경험식 및 GA에 비해 우수한 결과를 보인다는 사실을 확인하였다. 한편, 입력자료로 코어자료뿐만 아니라 다른 물리검층 자료를 추가하면 더 향상된 결과를 얻을 수 있을 것으로 사료된다.
Miah et al.(2020)은 Sw를 예측하기 위하여 기계학습법을 적용한 연구사례를 조사하고, Sw 예측에 DNN을 적용하였다. 선행연구사례들은 다양한 기계학습법 중 비교적 간단하고 높은 수렴 안정성을 보이는 ANN과 SVM(support vector machine)을 사용하였다. 한편, 많은 연구자들이 Sw 예측에 있어 입력자료를 단편적으로 선정하였다는 한계가 있다. 선행연구의 한계를 극복하기 위해 Miah et al.(2020)은 성능평가 관련 통계지표(RMSE, AAPE(average absolute percentage error), MAPE(maximum average percentage error), , PI(performance index) 등)에 따라 입력자료의 기여도를 평가하고 특징 순위(feature ranking) 방법을 통해 중복변수를 체계적으로 줄여 핵심변수를 추출하고자 하였다. 입력자료로 DT, GR, NPHI, PE, RHOB, RT 등 6가지 검층자료를 사용하였으며, 인도의 벵갈 분지(Bengal Basin)에서 획득한 182개 지점자료를 사용하여 학습, 검증, 시험을 진행하였다. DNN의 학습 알고리듬으로 LM, BR, SCG 등 세 가지 학습 알고리듬을 이용하여 DNN을 수행한 결과, 시험결과 은 각각 0.99, 0.99, 0.95, RMSE는 3.62E-04, 6.79E-07, 1.37E-02의 값을 보였다. 세 가지 학습 알고리듬 중 LM을 사용하였을 때 학습 시간이 가장 짧으면서도 성능은 가장 높게 나타났다. 또한, 입력 변수의 영향도를 분석한 결과 RT, RHOB, NPHI, PE, GR, DT 순으로 Sw 예측에 큰 영향을 끼치는 것으로 나타났다. 상기 연구는 DNN은 구조 최적화된 결과로 높은 성능을 보일 뿐만 아니라 입력 변수의 영향도를 확인할 수 있다는 장점이 있다. 한편, 상기 연구를 DNN에 국한되지 않고 CNN, LSTM과 같은 다양한 신경망 기법까지 확장될 수 있을 것으로 기대한다.
Lee et al.(2013b)은 PHI와 Sgh를 예측하기 위하여 ANN을 적용하였다. PHI를 예측하는 경우 입력자료로 두 가지 탄성파 속성자료(1/impedance, cosine instantaneous phase)를, Sgh를 예측하는 경우 네 가지 탄성파 속성자료(impedance2, integrated absolute amplitude, amplitude weighted frequency, dominant frequency)를 사용하였다. 출력자료인 Sgh는 Lee (2008)가 제안한 STPBE(simplified three-phase Biot-type equation) 방정식을 이용하여 계산하였다. 동해 울릉분지에 위치한 유정 3개에 대하여 신경망 설계단계에 유정 2개, 적용단계에 유정 1개를 교차 수행한 결과, 예측한 Sgh는 전반적으로 참조 곡선의 경향을 따르고 있으나 그 성능은 다소 낮게 나타났다(Fig. 3). PHI 및 Sgh에 대한 예측 결과 은 각각 0.85, 0.52이다. 상기 연구는 가스하이드레이트 저류층에서 수행된 연구라는 의의가 있다. 다만, Sgh에 대한 예측 결과가 높지 않고 입력자료로 물리검층 자료가 아닌 탄성파 자료를 활용한 연구라는 차이가 있다.
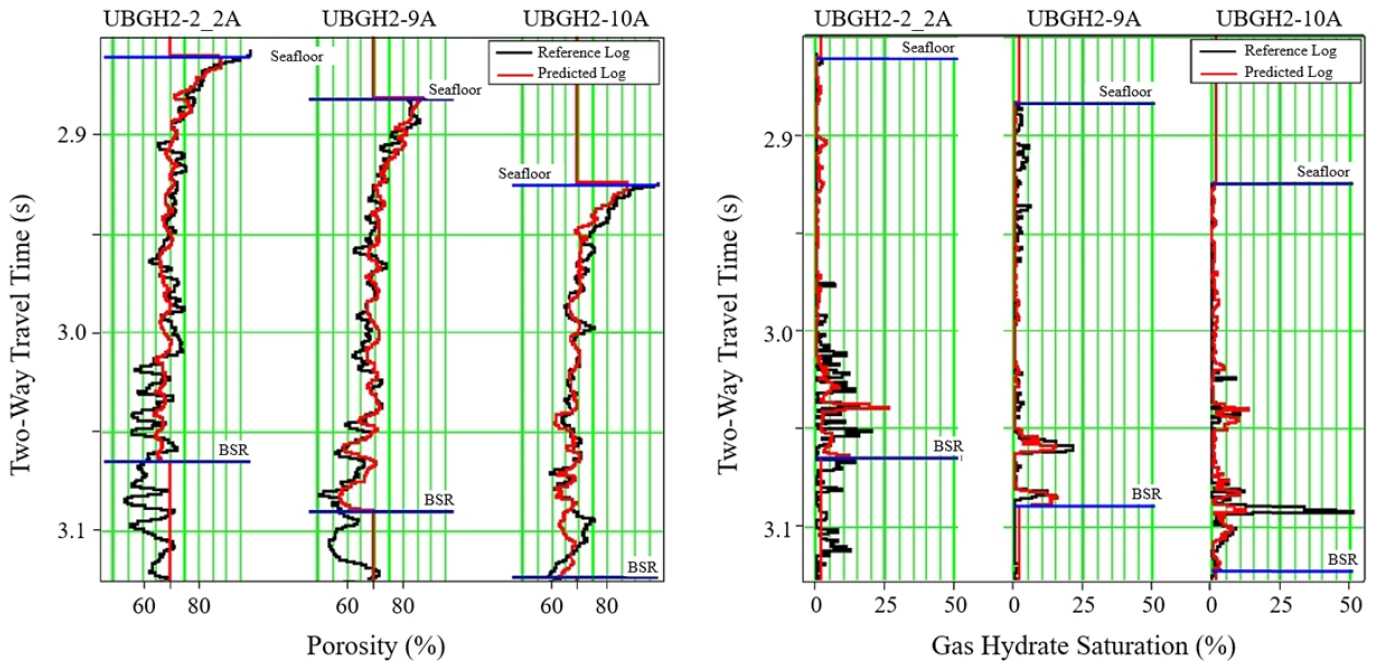
Fig. 3.
Porosity and gas hydrate saturation estimated using ANN for three wells in UBGH field (Lee et al., 2013b).
Mukherjee and Sain(2019)은 PHI와 Sgh를 예측하기 위하여 DNN을 적용하였다. PHI를 예측하는 경우 입력자료로 RT, RHOB, vp를 사용하였으며, 출력자료인 PHI는 RHOB로부터 계산한 값을 사용하였다. Sgh를 예측하는 경우 입력자료로 RT, RHOB, vp, DPHI를 사용하였으며, 출력자료인 Sgh는 Archie’s equation을 이용하여 계산한 값을 사용하였다. 인도의 Krishna–Godavari 해상분지(NGHP Exp-02)에 위치한 유정 3개에서 획득한 442개의 지점자료를 사용하여 1개의 유정으로 신경망을 설계하고 나머지 2개 유정에 대하여 적용하였다. 신경망은 추정하고자 하는 출력자료에 따라 독립적으로 설계되었다. 신경망 설계에 사용한 유정 1개에 대하여 학습, 검증, 시험을 수행한 결과 PHI에 대한 은 모두 0.99이고, Sgh에 대한 은 0.96, 0.97, 0.96이다. 학습에 사용하지 않은 유정 2개에 대하여 예측을 수행한 결과 PHI에 대한 은 모두 0.99이고, Sgh에 대한 은 0.89, 0.95이다. Fig. 4는 Sgh를 예측 결과를 코어자료와 함께 나타낸 것으로, 예측값은 추정값과 유사하며 높은 성능을 보이나 코어자료의 값과는 차이를 보인다는 한계가 있다.
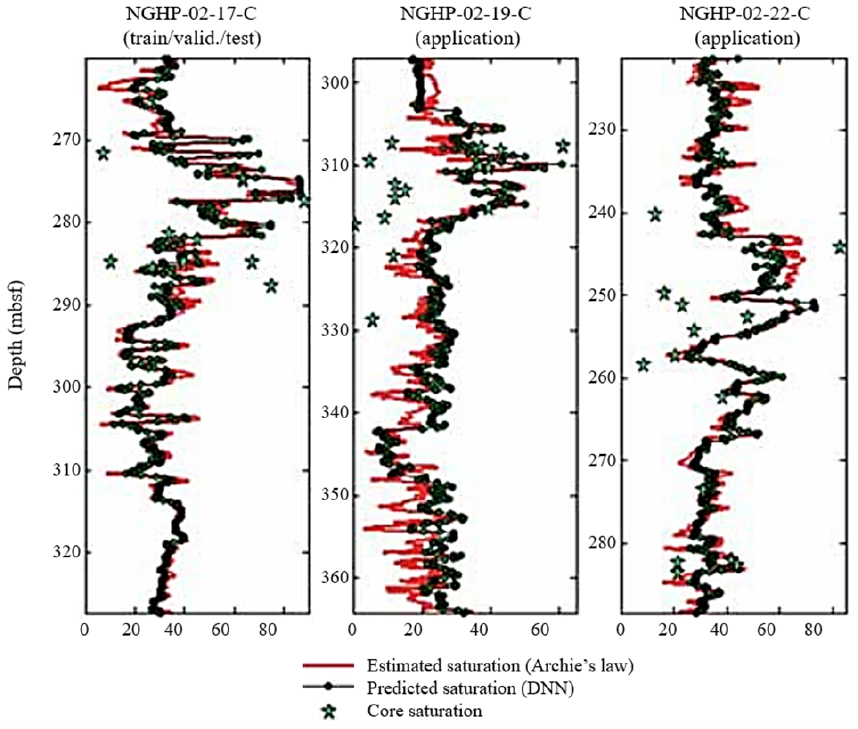
Fig. 4.
Gas hydrate saturation estimated using DNN for three wells in the NGHP Exp-02 field (Mukherjee and Sain, 2019).
Singh et al.(2021)은 Sgh를 예측하기 위하여 신경망 기법을 포함한 12가지 기계학습법에 다양한 입력자료 조합을 사용하고 예측 정확도에 따라 순위를 제시하였다. 입력자료는 GR, NPHI, DPHI, RHOB, RT, vp에 대하여 24개의 조합을 임의로 생성해서 사용하였고, 출력자료 Sgh는 DPHI 및 MPHI(nuclear magnetic resonance-density porosity)로부터 계산하였다. 미국 Alaska North Slope에 위치한 유정 2개에서 획득한 지점자료(각각 822개, 1,131개)로 신경망 설계하고 적용하였다. 이때 신경망 설계에 유정 1개를, 나머지 유정 1개를 적용단계에 사용하였다. 첫 번째 유정을 신경망을 설계에 사용하고 두 번째 유정을 적용단계에 사용한 경우를 Case 1, 그 반대로 유정을 사용한 경우를 Case 2로 나누어 수행하였다. Case 1 및 Case 2의 입력자료에 노이즈를 추가한 경우와 그렇지 않은 경우에 대하여 예측 정확도 NAS(normalized accuracy score)를 계산하였으며, 그 평균값을 기준으로 24개 입력조합에 대한 순위를 제시하였다. 예측 정확도 1순위에서 11순위까지는 유사한 성능(0.81~0.83)을 보이므로 가용한 물리검층 자료에 따라 해당 순위 내에서 입력자료 조합을 선택하여 Sgh를 예측할 수 있었다. 특히, vp 단 하나의 인자만을 사용하였을 때의 입력조합이 3순위에 해당하는 결과를 보였다. 상기 연구를 통해 같은 분지 내 유정에서의 Sgh 예측은 vp만으로도 충분히 가능하다는 사실을 확인하였다. 한편, 지질학적으로 복잡한 분지나 타분지에 위치한 유정에 대하여 Sgh 예측을 수행한다면 다양한 입력자료 조합을 적용하여야 할 것으로 보인다.
지질역학인자 추정
지질역학인자로는 vp, vs, 영률(Young’s modulus, E), 일축압축응력(unconfined compressive strength, UCS), 공극압력(pore pressure, PP) 등이 있으며 저류층의 생산성 분석, 시추공 안정성 확보 및 수압파쇄 설계 등에 필수적인 물성이다. 지질역학인자는 DT로부터 추정할 수 있으나 DT는 RT, DEN, NEU와 같은 일반적인 물리검층과 비교하였을 때 상대적으로 획득이 어려운 것으로 알려져 있다(Chen and Zhang, 2020). 따라서, 지질역학인자 추정을 위해서는 누락된 DT 추정이 선행될 필요가 있다. 본 연구의 조사에 따르면 지질역학인자를 추정하는 경우 신경망 모델로 ANN, DNN 및 LSTM 구조를 주로 사용하고 있다. 아래의 유가스전 사례 5건과 가스하이드레이트 저류층 사례 1건을 요약 및 정리한 후 Table 4에 종합하였다.
Table 4.
Summary for the estimation of geomechanical parameters using neural networks with log data
|
Authors (year) | Method | Inputs |
Nn (Nh)*a | Outputs |
Field (Nw)*b |
Nd *c |
Data Split Ratio | Optimizer*d | Performance | ||||
| Indicator | Train | Valid. | Test | Appl. | |||||||||
| Akinnikawe et al. (2018) | DNN |
19 petrophysical parameters |
19-10- 5-3-1 (3) | UCS |
- (14) | 4,764 | 70:0:30 | N/A | MSE | 309.2 | N/A | 320.2 | N/A |
| Onalo et al. (2018) | ANN |
GR, RHOB, Vsh |
3-3-2 (1) |
DTCO, DTSM |
Offshore West Africa (1) | N/A | 70:15:15 | LM | R2 | 0.99 | 0.99 | 0.99 | N/A |
| Pham and Naeini (2019) |
LSTM -FCNN |
GR, RHOB, vp, RT, Vsh, Sw, NPHI, Depth |
8-200-300 -400-2,048 -1,024-512-1 (3, 3) | vs |
Central North Sea (32) | N/A | N/A | N/A | R2 | N/A | N/A | N/A | 0.88 |
| Pham et al. (2020) |
Conv LSTM -FCNN |
GR, DEN, NPHI |
3-16-32 -64-1,024 -512-128-1 (3, 3) | DT |
UKCS (177) | 26,062 | 90:0:10 | N/A | R2 | 0.77 | N/A | N/A | 0.84 |
| Chen and Zhang (2020) |
PC -LSTM |
TVD, GR, RT, DEN |
4-50-50-25 -2-10-10 (2, 3) | νv, νh, T0, C, Ev, Eh, UCS, μ, vp, vs |
North Dakota, US (39) | N/A | 70:0:30 | N/A | MAE | N/A | N/A | 3.7% | N/A |
| Singha et al. (2014) | ANN |
RHOB, 3 seismic attributes |
4-5-1 (1) |
PP for line-X |
NGHP Exp-01, India *e (4) | N/A | N/A | SAGRAD | MSE | 0.17 | N/A | N/A | 0.24 |
|
PP for line-Y | 0.18 | N/A | N/A | 0.26 | |||||||||
Akinnikawe et al.(2018)은 UCS를 예측하기 위해 DNN을 적용하였다. 입력자료로 GR, NPHI, DPHI, Vclay(clay volume), PE, DTCO, DTSM, Es(static Young’s modulus), Ed(dynamic Young’s modulus) 등을 포함한 19가지 검층자료를 사용하였다. 상기 입력자료 유형은 다수의 검층 자료에 대해 변수 군집분석(variable clustering)을 수행하여 중복되는 인자를 제거하고 선별한 결과이다. 선별한 입출력자료는 각각 0-1 사이의 값으로 정규화한 후 DNN에 사용하였으며, 14개 유정에서 획득한 4,764개 지점자료를 학습 및 시험자료로 나누어 신경망을 설계하였다. 학습 및 시험 결과, MSE는 각각 309.2, 320.2의 값을 보였다. 상기 연구는 또는 을 제공하지는 않았다.
Onalo et al.(2018)은 기계학습법을 적용하여 DTCO, DTSM 또는 vp, vs를 예측한 연구사례를 조사하였고, 이를 바탕으로 DTCO와 DTSM을 동시에 예측하기 위해 ANN을 적용하였다. 조사한 선행연구를 토대로 입력자료로 GR, RHOB, Vsh(shale volume)을 사용하였다. 사용한 자료는 서부 아프리카 해상에 위치한 셰일성 사암 유가스전에서 확보한 1개 유정 심도 7,100-8,400 ft에 해당하는 물리검층 자료를 활용하였으며, 지점자료의 개수는 명확히 밝히고 있지 않다. 학습, 검증, 시험자료에 대하여 예측을 수행한 결과, 은 모두 0.99의 값을 보였다. DTCO 및 DTSM의 예측 결과에 대한 RMSE는 각각 2.62, 5.29이다. 이때, DTCO의 RMSE가 DTSM의 RMSE 보다 작은 이유는 입력자료로 사용한 RHOB의 영향으로 해석되었다. 이는 RHOB가 DTCO와 마찬가지로 매질과 공극에 포화된 유체 모두에게 영향을 받기 때문이다. 또한, 예측한 DTCO 및 DTSM를 이용하여 영률, 체적탄성계수, 전단계수, 공극률, 샌딩 포텐셜(sanding potential) 등의 지질역학인자를 추정하였다. 한편, 상기 연구는 특정 유정의 특정 심도 내에서 학습, 검증, 시험 단계가 이뤄져 높은 예측 수행 결과를 제시하였으나 해당 신경망 모델의 일반화 성능을 검증하기 위해서는 다른 유정에 적용해볼 필요가 있다.
Pham and Naeini(2019)는 vs를 예측하기 위하여 양방향 LSTM(bidirectional LSTM)과 FCNN(fully connected neural network)을 합성한 신경망(LSTM-FCNN)을 제안하였다. 입력자료는 GR, RHOB, vp, RT, Vsh, Sw, NPHI, 깊이 등 8가지 인자를 사용하였다. 북해 중앙부에 위치한 유정 32개에서 획득한 자료로 신경망 설계를 완료한 후 신경망 설계에 사용하지 않은 유정 3개에 대해 예측을 수행하였다. 적용단계에 대한 예측 결과 은 0.94의 값을 보였다. 상기 연구는 드롭아웃과 몬테카를로 방법을 사용하여 불확실성을 정량화하였다는 특징이 있으나 학습, 검증, 시험단계에 대한 예측 결과는 따로 밝히고 있지 않다.
Pham et al.(2020)은 DT를 예측하기 위하여 양방향 ConvLSTM과 FCNN을 합성한 신경망(ConvLSTM-FCNN)을 제안하였다. ConvLSTM은 LSTM 셀 내에서 내적연산(dot product) 대신 컨볼루션연산(convolution operator)을 수행하는 신경망이다. 입력자료로 GR, DEN, NPHI를 사용하였으며, 영국 대륙붕(UK continental shelf, UKCS)에 위치한 177개의 유정에서 획득한 26,062개의 지점자료를 학습자료 및 시험자료로 나누어 신경망 설계를 진행하였다. ConvLSTM-FCNN의 성능은 Gardner’s equation을 적용한 경우와 비교하여 그 우수성을 보였다. 한편, Gardner’s equation은 DEN의 분포에 따라 암상을 구분하여 DT를 계산하는 경험식이다. ConvLSTM-FCNN과 Gardner’s equation의 학습 결과 은 각각 0.88과 0.87을 나타내어 제안한 신경망이 더 높은 결과를 보였다. 학습이 완료된 두 모델은 학습에 사용하지 않은 총 6개의 유정에 적용하여 예측 성능을 평가하였다. 3개의 유정은 노르웨이 북해 Volve 저류층에 위치하며 셰일층에서 사암층으로 암상이 바뀌는 구간을 포함한다. Volve 유정에 대한 예측 결과 은 ConvLSTM- FCNN(0.96, 0.96, 0.92)이 Gardner’s equation(0.72, 0.83, 0.83) 보다 높은 값을 보였다. 또 다른 1개의 유정은 학습 유정과 동일한 지층에 위치한 유정으로 매우 낮은 DEN을 보이는 구간을 포함한다. 이에 Gardner’s equation의 경우 낮은 DEN을 보이는 구간에서 예측 성능이 현저히 감소하는 반면 ConvLSTM-FCNN은 예측 결과 이 0.96으로 여전히 높은 정확성을 보였다. 그 외 2개 유정은 각각 캐나다 해상과 미국 Teapot Dome 육상에 위치한 유정으로 학습에 사용된 유정과 다른 지질조건을 보인다. 그럼에도 불구하고 ConvLSTM-FCNN의 예측결과 은 두 유정에서 각각 0.92, 0.95로 높은 예측 값을 보였다. 상기 연구는 다양한 저류층에서 높은 예측결과를 보였다는 사실에 주목할만 하다.
Chen and Zhang(2020)은 상대적으로 유체유동인자에 비하여 측정이 어려운 지질역학인자를 예측하기 위하여 PC-LSTM을 제안하였다. PC-LSTM은 LSTM과 FCNN을 합성한 신경망으로 FCNN 사이에 PC층(physics-constrained layer)을 추가하였다. PC층은 신경망에 물리제약조건을 추가하여 보다 현실성있는 추정치를 산출하기 위한 목적으로 도입되었다. 입력자료는 TVD(true vertical depth)와 3가지 검층 자료(GR, RT, DEN)로 총 4가지 자료를 사용하였다. 입력자료는 LSTM층을 거쳐 FCNN층으로 정보가 전달되고, PC층에 의해 2개의 노드로 압축 및 확장된다. 이때, TVD와 DEN이 PC층과 연결된 FCNN층에 직접 추가되어 νv(vertical Poisson’s ratio), νh(horizontal Poisson’s ratio), T0(tensile strength), C(internal cohesion), Ev(vertical Young’s modulus), Eh(horizontal Young’s modulus), UCS, μ(internal friction coefficient), vp, vs 등 10가지 지질역학인자를 예측한다. 개발한 신경망은 미국 North Dakota에 위치한 39개 유정에 대하여 학습 및 시험단계를 수행하였으며, 시험 성능의 평가에는 MAE(mean absolute error)를 사용하였다. 10개 인자에 대한 MAE는 3.7%이다. 이는 PC층을 추가하고 TVD를 지층별로 최대최소 정규화하여 적용함으로써 지질역학인자 추정의 정확도를 향상시킨 결과이다. 한편, 상기 연구에서 제안한 신경망 모델은 크리깅과 달리 공간 물성 분포 모델링시 기지점과의 거리 정보의 영향을 받지 않는다는 장점이 있다.
Singha et al.(2014)는 가스하이드레이트 저류층의 PP를 예측하기 위하여 ANN을 적용하였다. 입력자료는 RHOB와 세 가지 탄성파 속성자료(P impedance, S impedance, vp/vs)를 사용하였으며, 출력자료인 PP는 DT로부터 추정 가능한 방정식(Eaton's equation)으로 계산한 값 또는 코어자료를 사용하였다. 인도의 Krishna–Godavari 해상분지(NGHP Exp-01)에 위치한 유정 2개(03A, 10A)에 대하여 학습을 수행하여 신경망 설계를 완료한 후 신경망 설계에 사용되지 않은 다른 유정 2개(10D, 12A)에 대하여 적용한 결과, GHSZ(gas hydrate stability zone)에서는 정수압 구배를 유지하는 예측 결과를 보였다. Fig. 5는 탄성파 측선 line-X에서의 PP 학습 및 적용 결과를 나타낸다. line-X 및 line-Y에서의 학습결과에 대한 MSE는 각각 0.17, 0.18이며, 적용결과에 대한 예측 MSE는 0.24, 0.26이다. 학습결과에 대한 교차상관은 line-X의 경우 0.96, line-Y의 경우 0.95를 보였다. 상기 연구는 가스하이드레이트 저류층에서 수행된 연구라는 점에서 주목할만하다. 이때, 입력자료로 물리검층 자료에 탄성파 자료를 함께 활용한 연구라는 점을 고려할 필요가 있다.
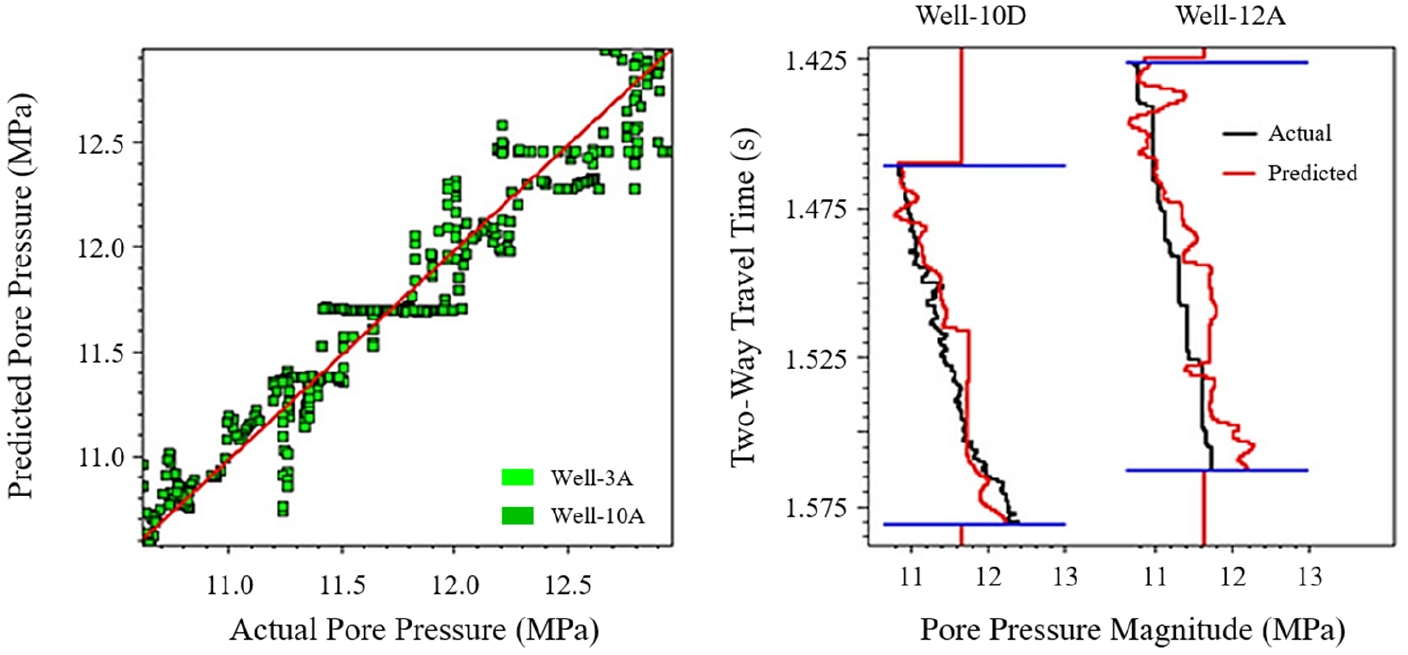
Fig. 5.
Pore pressure for line-X estimated using ANN for two wells in NGHP Exp-01 field (Singha et al., 2014).
합성로그 생성
물리검층 자료는 장비 손상, 불량한 검층 조건 등의 이유로 일부 구간 또는 일부 유정에서 미확보될 수 있다. 기확보한 검층 및 코어 자료를 활용하여 미확보 구간 또는 유정에 대하여 합성로그를 생성하여 저류층 물성 분석에 활용한다. 합성로그 생성은 넓은 의미에서 유체유동인자 및 지질역학인자 추정 또한 포함하나, 본 논문에서는 유체유동인자 및 지질역학인자 추정과 구분하였다. 한편, 현재까지 합성로그 생성과 관련한 가스하이드레이트 저류층 사례는 없는 것으로 파악된다. 이에, 아래에서는 RT, DEN, NEU와 같은 일반적인 물리검층 자료를 추정한 유가스전 사례 5건을 요약 및 정리한 후 Table 5에 종합하였다.
Table 5.
Summary for the generation of synthetic logs using neural networks with log data
|
Authors (year) | Method | Inputs |
Nn (Nh)*a | Outputs |
Field (Nw)*b | Nd*c |
Data Split Ratio | Optimizer*d | Performance | ||||
| Indicator | Train | Valid. | Test | Appl. | |||||||||
| Rolon et al. (2009) | GRNN |
ID, GR, DEN, NEU, LAT, LON, Depth |
7-7,000-1 (1) | RT |
Southern Pennsylvania, US (3) | N/A | 85:15:0 | N/A | R2 | N/A | N/A | N/A | 0.9 |
|
ID, GR, NEU, RT, LAT, LON, Depth | DEN | N/A | N/A | N/A | 0.6 | ||||||||
|
ID, GR, DEN, RT, LAT, LON, Depth | NEU | N/A | N/A | N/A | 0.8 | ||||||||
| Salehi et al. (2017) | DNN |
Rxo, Sw, Sxo |
3-7-3-2-1 (3) | RT |
Mansouri, Iran (3) | 3,000 | 70:15:15 | LM | R2 | 0.98 | 0.98 | 0.98 | N/A |
|
Rxo, RHOB, NPHI |
3-8- 5-4-1 (3) | DT | 0.92 | 0.96 | 0.94 | N/A | |||||||
| LLD, MSFL | 2-7-5-1 (2) | LLS | 0.96 | 0.90 | 0.84 | N/A | |||||||
| Akinnikawe et al. (2018) | ANN |
GR, ILD, NPHI, DPHI, Vclay, DPNPD |
N/A (N/A) | PE |
N/A (over 100) | N/A | 70:0:30 | N/A | MSE | 0.37 | N/A | 0.38 | N/A |
| Zhang et al. (2018) | Cascaded LSTM |
ΔRT, CALI, SP, GR |
N/A (2, 2) | DTh, DTb, DEN |
Daqing, China (6) | 35,110 | N/A | N/A | MSE | N/A | N/A | N/A | 1.10 |
| Kim et al. (2020) | DNN |
DT, LAT, LON, Depth |
4-45- 14-1 (2) | RHOB |
SLVP Form., Canada (23) | 8,684 | 85:15:0 | RP | R2 | N/A | N/A | N/A | 0.33 |
|
SLVP Form. and Golden Field (28) |
over 9,000 | 85:15:0 | N/A | N/A | N/A | 0.31 | |||||||
Rolon et al.(2009)은 RT, DEN, NEU를 예측하기 위하여 GRNN(generalized regression neural network)을 적용하였다. GRNN은 연속 자료를 처리하기 위해 분류 및 패턴 인식 문제에 널리 사용되는 확률 신경망 PNN을 변형한 신경망이다. RT를 예측하기 위한 입력자료로 ID(well id), GR, DEN, NEU, LAT(latitude), LON(longitude), 깊이를 사용하였으며(조합 A), DEN을 추정하기 위한 입력자료로 ID, GR, NEU, RT, LAT, LON, 깊이를(조합 B), NEU를 추정하기 위한 입력자료로 ID, GR, DEN, RT, LAT, LON, 깊이를 사용하였다(조합 C). 미국 펜실베니아 남부에 위치한 유정 4개에서 획득한 지점자료를 지층 및 암상을 고려하여 상부(1,000-2,000 ft)와 하부(2,500-3,500 ft)로 나누고 각각 유정 3개로 학습 및 검증 단계를 거쳐 신경망 설계를 완료한 후 남은 유정 1개에 설계한 신경망을 적용하여 예측을 수행하였다. 모든 유정에 대해서 돌아가면서 신경망 설계 및 예측을 수행한 결과, 학습, 검증, 시험 단계에 대하여 예측 결과를 밝히고 있지는 않으나, 적용 단계에서 조합 A(0.9), 조합 C(0.8), 조합 B(0.6) 순으로 높은 결과를 보였다. 한편, 상기 연구는 신경망 모델을 사용하기 전 물리검층 자료를 지층 및 암상을 고려하여 구간을 나누는 과정을 엔지니어가 직접 수행해야한다는 한계가 있다.
Salehi et al.(2017)은 RT, DT, LLS를 각각 예측하기 위하여 DNN을 적용하였다. 첫째, RT를 예측하기 위한 입력자료로 Rxo, Sw, Sxo(water saturation of the flushed zone)를 사용하였다. 이란 남서부 Mansouri 저류층 유정 3개에서 획득한 3,000개 지점자료로 신경망을 설계한 결과 RT 예측에 대한 높은 성능을 보였다. 학습, 검증, 시험자료에 대한 MSE는 각각 1.0E-04, 1.5E-04, 9.0E-05이고 은 모두 0.99이다. 둘째, DT를 예측하기 위한 입력자료로 Rxo, RHOB, NPHI를 사용하였다. 동일한 지점자료로 학습, 검증, 시험을 수행한 결과 DT의 MSE는 4.0E-03, 1.6E-03, 3.5E-03이고 은 0.96, 0.98, 0.97의 값을 보였다. 셋째, LLS를 예측하기 위한 입력자료로 LLD, MSFL을 사용하였다. LLS의 MSE는 1.0E-03, 2.7E-03, 4.0E-03이고 은 0.98, 0.95, 0.92의 값을 보였다. 밀도와 비저항 검층 자료는 저류층 암상 및 탄화수소 부존을 파악하고 공극률 및 수포화도를 계산하는 등 저류층 평가에서 기본적으로 활용되는 자료이다. 따라서 밀도와 비저항 검층 자료 일부에 결함이 있는 경우 상기와 같은 입력자료를 활용하여 소실된 자료를 예측할 수 있다. 한편, 상기 연구에서 제안한 신경망 모델의 일반화를 확인하기 위해서는 다른 분지에 위치한 유정에 대해 적용해 볼 필요가 있다.
Akinnikawe et al.(2018)은 PE를 추정하기 위하여 ANN을 적용하였다. 입력자료로 GR, ILD, NPHI, DPHI, Vclay 등 5가지 검층 자료에 중성자 및 밀도 공극률의 차이(DPNPD = │NPHI – DPHI│)를 하나의 변수로 추가하여 총 6가지 변수를 사용하였다. PE에 대한 입력 변수의 중요도는 DPHI, NPHI, GR, DPNPD, Vclay, ILD 순으로 큰 영향을 끼치는 것으로 나타났다. 한편, 출력변수 PE에 대한 입력 변수들의 상관관계를 살펴본 결과 모두 이 0.2 미만으로 뚜렷한 선형관계를 보이지 않았다. 100개가 넘는 유정에서 획득한 지점자료를 사용하여 학습 및 시험을 수행한 결과, MSE는 각각 3.77E-01, 3.80E-01의 값을 보였다. 그러나 상기 연구는 또는 을 제공하지 않았다.
Zhang et al.(2018)은 DTh(high-resolution acoustic log), DTb(borehole compensated sonic log), DEN을 예측하기 위하여 Cascaded LSTM을 적용하였다. Cascaded LSTM은 출력자료를 다시 입력자료로 추가하여 사용하도록 설계된 계단식 LSTM으로 상대적으로 예측이 어려운 인자를 후순 배치하여 선 예측한 인자를 함께 입력자료로 활용할 수 있다는 장점이 있다. 먼저 입력자료로 ΔRT, CALI, SP, GR를 사용하여 DTh를 예측한다. 예측된 DTh는 ΔRT, CALI, SP, GR와 함께 DTb를 예측하는데 사용한다. 마지막으로 예측된 DTh, DTb는 ΔRT, CALI, SP, GR와 함께 DEN을 예측하는데 사용한다. 중국 대경유전(Daqing Oilfield)의 유정 6개에서 획득한 35,110개 지점자료를 활용하였다. 유정 5개로 신경망 설계를 완료한 후 남은 유정 1개에 적용하여 예측을 수행하였다. 모든 유정에 대해서 돌아가면서 신경망 설계 및 예측을 수행한 결과, 가장 낮은 MSE는 3.9E-01의 값을 보인 반면 가장 높은 MSE는 1.1E+00의 값을 보였다. 상기 연구는 Cascaded LSTM은 FCNN과 달리 예측하고자 하는 깊이에 해당하는 입력자료뿐만 아니라 이전 깊이에 대한 입력자료도 고려하여 높은 예측성능을 보였다는 장점이 있으나 또는 을 제공하지 않았다.
Kim et al.(2020)은 RHOB를 예측하기 위하여 DNN을 적용하였다. 입력자료로는 DT, LAT, LON, 깊이를 사용하였으며 캐나다 Golden 저류층에 위치한 유정을 예측하고자 하였다. 그러나 입력자료로 사용된 물리검층 자료는 위치 정보를 제외하면 DT 1개이고 Golden 저류층에서 가용한 유정이 5개뿐이라 학습의 정확도를 높이기 위하여 타 지역의 유정을 추가로 사용하였다. 이때 Golden 저류층과 물리적으로 가까운 유정을 선택하기보다 SLVP(Slave Point) 지층 중 동일한 지질환경을 보이는 지역의 유정을 선별하였다. 또한, 지질학적으로 적절한 학습 자료를 추가하는 것이 중요하다는 사실을 확인하기 위해 다음과 같이 두 가지 경우로 나누어 결과를 비교하였다. Case 1에서는 SLVP 지층에 위치한 24개 유정 중 23개 유정에서 획득한 8,684개의 지점자료를 학습 및 검증단계에, 나머지 1개 유정을 시험단계에 사용하였다. 그리고 Golden 저류층에 위치한 유정 5개를 적용단계에 사용하였다. Case 2에서는 SLVP 지층에 위치한 24개 유정뿐만 아니라 Golden 저류층에 위치한 유정 4개에서 획득한 9,000개 이상의 지점자료를 학습 및 검증단계에 사용하였으며, 신경망 설계단계에서 사용하지 않았으면서도 Golden 저류층에 위치한 유정 1개를 적용단계에 사용하였다. 이때 설계 및 적용단계에 사용한 Golden 저류층 유정을 교차 수행한 결과 Case 1의 과소추정되는 경향이 Case 2에서 완화되는 것으로 나타났다. Golden 저류층의 5개 유정에 대한 Case 1의 RMSE는 1.19E+02, 1.21E+02, 1.29E+02, 1.07E+02, 1.39E+02인 반면 Case 2의 RMSE는 6.8E+01, 5.7E+01, 4.8E+01, 6.1E+01, 8.8E+01로 모두 감소하였다. 이는 단순히 신경망 설계에 사용된 자료의 수가 증가한 것 뿐만 아니라 예측하고자 하는 유정과 유사한 지질환경을 보이는 유정을 신경망 설계 자료에 추가하였기 때문이다. 한편, 의 값은 Case 1(0.58, 0.39, 0.36, 0.53, 0.50)과 Case 2(0.56, 0.39, 0.17, 0.51, 0.49)에서 큰 차이를 보이지 않았다. 상기 연구는 Rolon et al.(2009)과 비교하였을 때 다양한 유형의 물리검층 자료를 충분히 확보하는 경우 보다 개선된 결과를 도출할 수 있을 것으로 기대한다.
결 론
이 연구는 향후 국내에서 수행될 가스하이드레이트 저류층에 대한 심층학습 모델 개발 연구의 기반을 제공하기 위하여 상대적으로 적은 가스하이드레이트 저류층 사례 뿐만 아니라 사암층, 탄산염암층 등 다양한 유·가스 저류층을 대상으로 물리검층 분야에서 신경망기법을 적용한 최신 기술동향을 분석하였다. 조사한 사례들은 저류층 암상 추정, 유체유동인자 추정, 지질역학인자 추정, 합성로그 생성 등 출력자료에 따라 네 가지 유형별로 분류한 후 각 유형별로 종합표(Tables 2, 3, 4 and 5)를 제시하였다.
(1) 저류층 암상 추정의 경우, 암상을 직접 추정하거나 TOC, S1, S2의 추정을 통하여 간접적으로 암상을 추정하는 방법이 있으며 PNN, ANN, CNN, DNN, BNN 등의 신경망 기법을 적용하였다. 신경망 모델에 군집분석을 함께 적용하거나 불확실성을 확률적으로 정량화하는 기법을 사용하기도 하였다. 다른 유형에 비해 상대적으로 적은 지점자료가 사용되었으며, 조사한 연구사례 중 최대 지점자료 수는 620개이다.
(2) 유체유동인자 추정의 경우, 공극률, 유체투과율, 수포화도를 추정하고자 하며 주로 ANN 또는 은닉층이 2개인 DNN이 적용되었으며 경험식과 성능 비교를 제시하거나 신경망 최적화 과정을 제시하였다. 학습 알고리듬으로는 주로 LM을 사용하였으며, 조사한 연구사례 중 최대 지점자료 수는 1,953개이다.
(3) 지질역학인자 추정의 경우, DT, vp, vs, E, UCS, PP 등 다양한 인자를 추정하고자 하며 ANN, DNN 뿐만 아니라 시계열 자료 처리에 용이한 LSTM 등의 기법이 적용되었다. 조사한 연구사례 중 최대 지점자료 수는 26,062개이다.
(4) 합성로그 생성의 경우, RT, DEN, NEU 등 다양한 검층 자료를 생성하고자 하였으며, 입력자료로 위도, 경도, 깊이 자료가 포함되기도 하는 것으로 조사되었다. 이 유형에는 GRNN, ANN, DNN, LSTM 등 다양한 신경망 기법이 적용되었다. 조사한 연구사례 중 최대 지점자료 수는 35,110개이다. 한편, 현재까지 가스하이드레이트 저류층 사례는 없는 것으로 파악하였다.
조사한 연구사례들은 신경망 기법 중에서도 지도학습에 해당하는 사례에 한정하여 수행하였으며 조사한 사례들이 같은 유형이더라도 서로 다른 입력자료 조합과 신경망 기법을 적용하였기 때문에 직접적인 성능 비교가 어렵다는 한계가 있다. 한편, 가스하이드레이트 저류층 대상 연구의 경우 최근 5년 이내 국내에서 수행된 연구는 보고되지 않았다. 이는 국내 동해 울릉분지의 시험생산 중단, 불균질한 퇴적 특성, 한정된 물리검층 자료 등이 원인인 것으로 사료된다. 가스하이드레이트가 기후변화 대응을 위한 새로운 대체 에너지원으로 부상하고 심층학습법이 글로벌 연구 트렌드로 정착함에 따라 국내 가스하이드레이트 연구 또한 심층학습법을 접목하여 미지점에서의 물리검층 자료를 추정하고 확보한 추가 자료를 통해 다양한 연구로 확장할 수 있을 것으로 기대한다.