Review of 3D Anisotropic Seismic Imaging Technology

Ju-Won Oh

doi:10.32390/ksmer.2022.59.2.240

Preview

General Remarks

Journal of the Korean Society of Mineral and Energy Resources Engineers. 30 April 2022. 240-258
https://doi.org/10.32390/ksmer.2022.59.2.240

Review of 3D Anisotropic Seismic Imaging Technology

3차원 이방성 탄성파 영상화 기술 동향

Ju-Won Oh¹²^*

오 주원¹²^*

¹Associate Professor, Department of Mineral Resources and Energy Engineering, Jeonbuk National University, Jeonju, Kroea

²Associate Professor, Department of Environment and Energy, Jeonbuk National University, Jeonju, Kroea

¹전북대학교 자원·에너지공학과 부교수

²전북대학교 환경에너지융합학과 부교수

^{*Corresponding Author}

ABSTRACT

Recently, 3D seismic imaging techniques have been highlighted with increasing international demands on the discovery of new oil fields as well as the site characterization and CO₂ monitoring in carbon capture and storage. Because 3D seismic data can be distorted by various types of seismic anisotropy, a 3D anisotropic seismic imaging technique is required. In this study, we explain the geological reasons for seismic anisotropy and the influence of seismic anisotropy on 3D seismic data. Then, we introduce international research trends in anisotropic seismic imaging depending on seismic modeling, full-waveform inversion, and reverse-time migration. Finally, we introduce the current status and future trends in Korean 3D anisotropic seismic imaging technology.

Keywords

seismic anisotropy

3D seismic survey

3D seismic imaging

carbon capture and storage

최근 3차원 탄성파 영상화 기술이 신규 유전 개발과 이산화탄소 지중저장소 탐사 및 모니터링에 대한 국제 사회의 수요가 증가함에 따라 큰 주목을 받고 있다. 3차원 탄성파 탐사자료는 다양한 형태의 탄성파 이방성에 의해 왜곡될 수 있기 때문에 이를 고려할 수 있는 이방성 탄성파 영상화 기술이 요구된다. 본 총설에서는 다양한 형태의 탄성파 이방성의 원인과 탐사 자료에 미치는 영향을 설명하고, 모델링, 완전파형역산, 역시간 구조보정 기술을 중심으로 이방성 영상화 기술 개발 동향을 소개한다. 마지막으로 3차원 이방성 탄성파 영상화 기술의 국내 개발 현황과 앞으로의 전망을 소개한다.

키워드

탄성파 이방성

3차원 탄성파 탐사

3차원 탄성파 영상화

이산화탄소 지중저장

MAIN

서 론
탄성파 이방성의 원인과 영향
탄성파 이방성의 원인
이방성 변수
탄성파 이방성의 영향
이방성 탄성파 모델링 기술 연구 동향
이방성 탄성파동방정식
이방성 음향파동방정식
이방성 완전파형역산 기술 연구 동향
다변수 완전파형역산의 기본 원리
이방성 음향 완전파형역산
이방성 탄성 완전파형역산
이방성 역시간 구조보정 기술 연구 동향
국내 3차원 이방성 탄성파 영상화 기술 개발 현황
결론 및 향후 전망

서 론

최근 지구온난화 문제와 2050 탄소중립 선언과 함께 자원개발 분야에도 큰 변화의 바람이 불고 있다. 화석연료를 이용하여 수소를 생산하지만, 탄소가 배출되는 그레이 수소 방식보다는 수소 생산 중 발생한 이산화탄소를 이산화탄소 지중저장 기술(Carbon Capture and Storage, CCS)로 처리하는 블루 수소 방식이 주목을 받고 있다. 2050 탄소중립을 달성하기 위해서는 2050년까지 화석연료를 완전히 탈피한 신재생에너지로의 전환이 이루어져야 하지만 단기적으로는 여전히 화석연료에 의존할 수 밖에 없는 실정이다. 따라서 기존에 2차원 탐사로 발견하지 못했던 복잡한 3차원 지질구조를 가지는 지역에 대한 정밀 3차원 탄성파 탐사를 통해 신규 유전을 발견함으로써 에너지 전환이 원활히 이루어지도록 유예기간을 확보해야 한다.

또한 2021년 10월 18일에 정부가 발표한 2050 탄소중립 시나리오 B안(LNG 일부 잔존 가정)에 따르면, 에너지 전환이 이루어진 이후에도 CCS 기술로 연간 6,000만 톤의 이산화탄소를 CCS 기술로 처리해야 하는데 이 중 3,000만 톤은 국내 저장소에서 나머지 3,000만 톤은 해외 저장소에서 처리하는 것을 계획하고 있다. 2021년 11월 3일에 열린 ‘한국 CO₂ 저장소 유망구조 및 저장용량 종합평가 심포지엄’에서의 논의 결과에 따르면, 우리나라의 해양 CCS 유망 저장소는 7.3억 톤으로 추정되는데, 이는 연간 2,430만 톤의 이산화탄소를 30년 간 저장할 수 있는 양이다. 따라서 신규 저장소 확보 및 유망 저장소의 안전성을 재검토하기 위한 3차원 탄성파 탐사 기술과 3차원 탄성파 영상화 기술에 대한 수요가 증가하고 있다.

또한 동해가스전을 시작으로 앞으로 국내 퇴적분지에 본격적인 이산화탄소 주입이 이루어질 계획이므로, 노르웨이 슬라이프너(Sleipner) 프로젝트의 사례처럼 신뢰성 있는 4차원 탄성파 모니터링 기술이 확보되어야 한다. 4차원 탄성파 모니터링은 반복적인 3차원 탄성파 영상화를 통해 주입 이산화탄소에 의한 지하 물성 변화를 추정하는 방법으로, 국내 CCS 기술의 국제적 수용성을 확보하기 위해서는 신뢰성 있는 3차원 탄성파 영상화 기술의 확보가 시급하다.

하지만 3차원 탄성파 탐사자료의 영상화는 오랜 시간과 방대한 계산자원이 요구되는 물리탐사 분야의 가장 어려운 문제 중 하나이다. 특히 지구는 이방성 매질이므로 탐사 지역에 따라 다양한 형태의 이방성이 나타나 탐사 자료가 왜곡될 수 있다. 이미 3차원 탄성파 영상화에서 등방성 영상화 기술의 한계는 충분히 인식되어 왔으며, 대형 석유기업과 해외 대학에서는 이를 극복하기 위한 이방성 영상화 기술 개발이 활발한 상황이다. Shin et al.(2021)이 물리탐사 분야의 대표적인 학술지를 기반으로 최근 5년간 연구주제를 분석한 결과에 따르면, 탄성파 탐사 분야에서 역산(inversion), 이방성(anisotropy), 영상화(imaging), 모델링(modeling)의 키워드가 최상위에 분포하고 있으며, 이는 이방성 탄성파 영상화 분야가 현재 물리탐사 학계의 큰 주목을 받고 있음을 의미한다. 그럼에도 불구하고, 3차원 이방성 탄성파 영상화는 기술적 어려움으로 인해 특정 연구 그룹을 중심으로 제한적으로 연구가 수행되고 있다.

이러한 사회적 분위기에 맞추어, 본 총설에서는 3차원 이방성 탄성파 영상화 기술의 국내외 개발 현황을 소개하고 앞으로의 전망을 논의해보고자 한다. 먼저 3차원 탄성파 탐사자료 획득 시 나타날 수 있는 다양한 탄성파 이방성의 원인을 설명하고, 이방성 변수가 3차원 탄성파 탐사자료에 미치는 영향을 논의한다. 그리고 이를 극복하기 위한 기술 개발 사례를 모델링, 완전파형역산, 역시간 구조보정 기술로 구분하여 소개하고, 국내 기술 개발 현황 및 앞으로의 전망을 논의할 것이다.

탄성파 이방성의 원인과 영향

탄성파 이방성의 원인

탄성파 이방성이란 균질한 매질 내에서 방향에 따라 탄성파의 속도가 달라지는 현상을 의미한다. 탄성파 탐사 자료처리를 통한 영상화가 정확하게 수행되려면 탄성파의 도달 시간이 정확하게 예측되어야 하기 때문에, 전파 방향에 따라 탄성파의 속도를 복잡하게 변화시키는 탄성파 이방성은 때때로 지하 영상의 품질을 저하시킨다. 따라서 탄성파 이방성이 강한 지역에서는 탐사 자료 처리 시, 이방성에 의해 심하게 왜곡된 부분을 배제하거나 이방성을 구현한 영상화 기법을 이용하여 이방성에 의한 영향을 적절하게 고려해주어야 한다. 자료처리 과정에서 이를 판단하기 위해서는 탄성파 이방성이 나타나는 원인을 이해하고, 해당 지역에서 이러한 이방성이 나타날 수 있는지 사전에 분석하는 것이 중요하다.

탄성파 이방성은 지구의 지각, 맨틀, 내핵을 포함하여 전지구적으로 나타나는 현상이다(Babuska and Cara, 1991). 하지만 본 총설에서는 퇴적분지 내의 수 km 깊이의 지질구조를 규명하기 위한 탄성파 탐사 과정에서 나타나는 이방성만 다룰 것이다. 퇴적분지에서 탄성파의 이방성을 유발하는 대표적인 세 가지 원인은 수평적으로 퇴적된 셰일과 같이 암석이 가지는 고유의 이방성, 수직 분해능보다 작은 규모에서 지층이 수평적으로 얇게 교호할 때 발생하는 겉보기 이방성, 수평 분해능보다 작은 규모에서 균열망이 수직으로 나란히 발달할 때 발생하는 이방성이 있다(Oh, 2020). 처음 두 가지 원인은 지층에 수직인 대칭축을 기준으로, 탄성파의 수평방향과 수직 방향의 속도 차이를 유발하기 때문에 횡등방성(Vertically Transverse Isotropy, VTI) 매질의 대표적인 형태이며, 마지막 원인은 균열망에 수직인 대칭축을 기준으로 균열에 평행한 방향과 수직인 방향의 속도 차이를 유발하기 때문에 종등방성(Horizontally Transverse Isotropy, HTI) 매질의 대표적인 형태이다. 이 두가지 형태의 이방성이 결합된 보다 복잡한 이방성 매질을 사방정계 형태의 이방성 매질(Orthorhombic anisotropy, ORT)이라고 한다(Fig. 1). ORT 매질에서는 세 개의 축( $x, y, z$ )을 따라 P파 속도가, 이를 가로지르는 세 개의 면( $y z, x z, x y$ )을 따라 S파 속도가 달라진다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F1.jpg

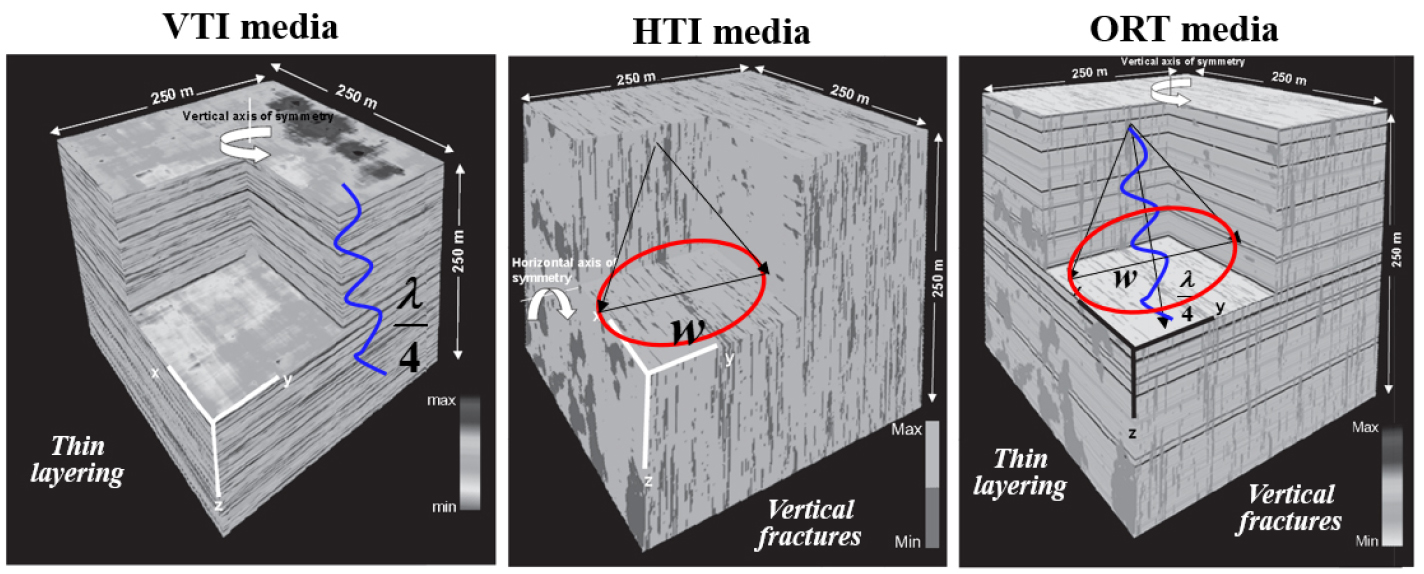
Fig. 1.

Vertical resolution (related to blue lines) and horizontal resolution (related to red circles) of seismic waves causing seismic anisotropy in VTI, HTI, and orthorhombic models (Ikelle and Amundsen, 2005; Oh, 2020).

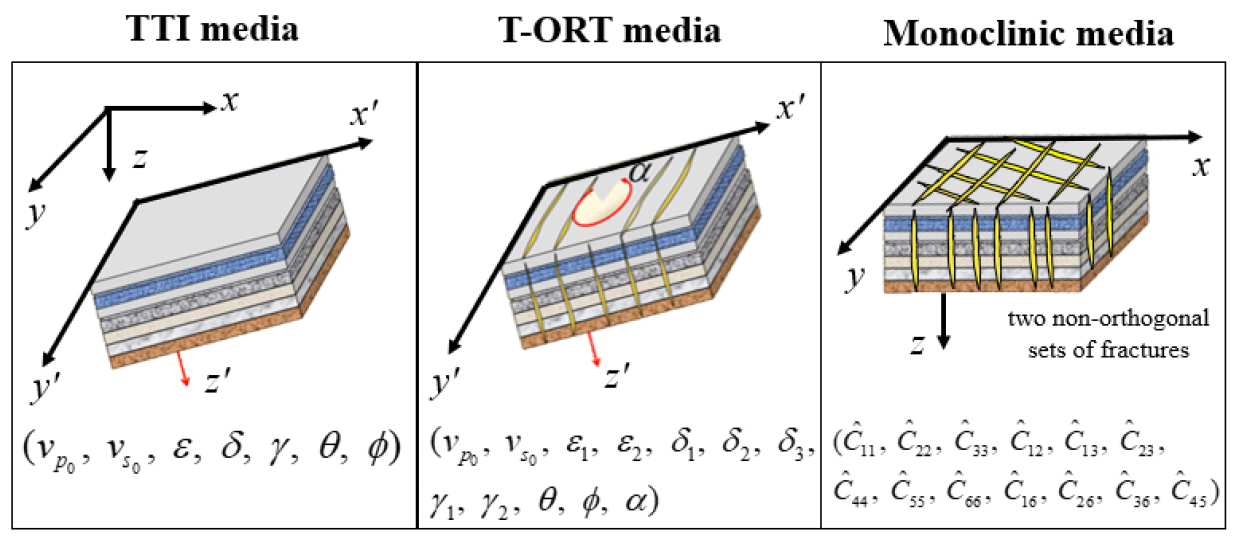
하지만 위의 세 가지 이방성 매질은 실제 퇴적분지에서 존재할 수 있는 이방성을 단순화시킨 모델이다. 암염돔이나 과거의 지구조적 변동으로 인한 습곡이 존재하여 지층의 경사에 변화가 생기거나 퇴적 과정에서 경사층이 형성될 경우, Fig. 2와 같이 이방성의 대칭축은 지역적으로 회전될 수 있다(Tilted Transverse Isotropy, TTI). 따라서 이러한 복잡한 지질구조를 가지는 이방성 지역에서 탄성파 탐사를 할 경우, 지역적으로는 TTI의 영향을 받을 수 있다. 또한 수직으로 발달된 균열망이 탐사 측선에 대해 완전히 평행하거나 수직하지 않기 때문에 일반적으로 HTI나 ORT 매질은 탐사 측선에 대해 방위각 방향으로 회전되어 있다. 따라서 방위각 방향으로의 회전(z축 중심), $x z$ 면상에서의 회전( $y$ 축 중심), $y z$ 면상에서의 회전(x축 중심)이 모두 결합된 T-ORT(Tilted Orthorhombic anisotropy) 매질이 존재할 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F2.jpg

Fig. 2.

Comparison of TTI, T-ORT, and monoclinic media (Modified from Li et al., 2012).

하지만 T-ORT 매질은 여전히 서로 직교하는 세 개의 축을 따라 탄성파의 속도가 정의될 수 있는 단순화된 형태이다. 예를 들어 두 그룹의 균열망이 서로 직교하지 않는 방향으로 발달될 경우, $x y$ 면상에서 두 대칭축이 서로 수직하지 않는(Fig. 2) 단사정계 형태의 이방성(Monoclinic anisotropy)이 나타날 수 있다(Far et al., 2013). 또한 지층이 경사져서 TTI 매질이 형성된 이후, 지구조적 장력에 의해 수직으로 균열망이 발달한다면 $y z, x z$ 면상에서도 각각 단사정계 형태의 이방성이 발생할 수 있기 때문에, 이 모든 효과들이 결합된다면 모든 대칭축이 서로 직교하지 않는 가장 복잡한 형태의 이방성 매질인 삼사정계 형태의 이방성 매질(Triclinic anisotropy)이 형성될 수 있다.

이방성 변수

탄성파 탐사자료에 대한 탄성파 이방성의 영향을 가늠하기 위해서는 이방성의크기를 정량화하는 것이 중요하다. 탄성파 탐사 자료처리에서는 Thomsen(1986)이 제안한 이방성 변수( $ε, δ, γ$ )가 널리 사용되고 있다. 이를 이해하기 위하여 먼저 탄성파동방정식을 살펴보면, 삼사정계 형태의 이방성 매질에 대한 3차원 탄성파동방정식은 뉴턴의 운동방정식과 응력-변형률 관계에 의해 다음과 같이 표현된다.

(1)

ρ \frac{\partial^{2} u_{x}}{\partial t^{2}} = \frac{\partial τ_{x x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} + \frac{\partial τ_{x z}}{\partial z} + f_{x}

(2)

ρ \frac{\partial^{2} u_{y}}{\partial t^{2}} = \frac{\partial τ_{x y}}{\partial x} + \frac{\partial τ_{y y}}{\partial y} + \frac{\partial τ_{y z}}{\partial z} + f_{y}

(3)

ρ \frac{\partial^{2} u_{z}}{\partial t^{2}} = \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial τ_{z z}}{\partial z} + f_{z}

(4)

(\begin{matrix} τ_{x x} \\ τ_{y y} \\ τ_{z z} \\ τ_{y z} \\ τ_{x z} \\ τ_{x y} \end{matrix}) = (\begin{matrix} {\bar{C}}_{11} & {\bar{C}}_{12} & {\bar{C}}_{13} & {\bar{C}}_{14} & {\bar{C}}_{15} & {\bar{C}}_{16} \\ {\bar{C}}_{12} & {\bar{C}}_{22} & {\bar{C}}_{23} & {\bar{C}}_{24} & {\bar{C}}_{25} & {\bar{C}}_{26} \\ {\bar{C}}_{13} & {\bar{C}}_{23} & {\bar{C}}_{33} & {\bar{C}}_{34} & {\bar{C}}_{35} & {\bar{C}}_{36} \\ {\bar{C}}_{14} & {\bar{C}}_{24} & {\bar{C}}_{34} & {\bar{C}}_{44} & {\bar{C}}_{45} & {\bar{C}}_{46} \\ {\bar{C}}_{15} & {\bar{C}}_{25} & {\bar{C}}_{35} & {\bar{C}}_{45} & {\bar{C}}_{55} & {\bar{C}}_{56} \\ {\bar{C}}_{16} & {\bar{C}}_{26} & {\bar{C}}_{36} & {\bar{C}}_{46} & {\bar{C}}_{56} & {\bar{C}}_{66} \end{matrix}) (\begin{matrix} \partial_{x} u_{x} \\ \partial_{y} u_{y} \\ \partial_{z} u_{z} \\ \partial_{z} u_{y} + \partial_{y} u_{z} \\ \partial_{z} u_{x} + \partial_{x} u_{z} \\ \partial_{y} u_{x} + \partial_{x} u_{y} \end{matrix})

이 때, ( $τ_{x x}, τ_{y y}, τ_{z z}, τ_{y z}, τ_{x z}, τ_{x y}$ )은 각각 $x, y, z$ 방향의 수직응력과 $y z, x z, x y$ 단면상에서의 전단응력을 의미하며, ( $u_{x}, u_{y}, u_{z}$ )는 각각 $x, y, z$ 방향에 따른 입자의 변위이다. ( $f_{x}, f_{y}, f_{z}$ )는 각 방향에 따른 체적력 송신원이다. 𝜌는 밀도이며, ${\bar{C}}_{i j}$ 는 탄성계수로 매질의 탄성 이방성을 결정한다. 보다 근사된 이방성인 $x y$ 면상에서의 단사정계 형태의 이방성 매질에 대한 탄성 계수 행렬은 다음과 같다.

(5)

C_{x}^{M o n o c l i n i c} = (\begin{matrix} {\tilde{C}}_{11} & {\tilde{C}}_{12} & {\tilde{C}}_{13} & 0 & 0 & {\tilde{C}}_{16} \\ {\tilde{C}}_{12} & {\tilde{C}}_{22} & {\tilde{C}}_{23} & 0 & 0 & {\tilde{C}}_{26} \\ {\tilde{C}}_{13} & {\tilde{C}}_{23} & {\tilde{C}}_{33} & 0 & 0 & {\tilde{C}}_{36} \\ 0 & 0 & 0 & {\tilde{C}}_{44} & {\tilde{C}}_{45} & 0 \\ 0 & 0 & 0 & {\tilde{C}}_{45} & {\tilde{C}}_{55} & 0 \\ {\tilde{C}}_{16} & {\tilde{C}}_{26} & {\tilde{C}}_{36} & 0 & 0 & {\tilde{C}}_{66} \end{matrix})

삼사정계 또는 단사정계 형태의 이방성은 매우 복잡한 파동 전파 특성을 가지기 때문에, 자료 처리 과정에서는 거의 고려되고 있지 않다. 따라서 서로 직교하는 세 방향으로의 이방성을 갖는 ORT 매질이 회전된 형태인 T-ORT 매질로 근사하면, 식 (4)의 탄성계수 행렬은 $x$ 축, $y$ 축, z축 중심에 대한 회전에 대해 각각 다음과 같이 표현될 수 있다.

(6)

C_{x}^{T - O R T} = M_{x} (ϕ) C^{O R T} M_{x}^{T} (ϕ)

(7)

C_{y}^{T - O R T} = M_{y} (θ) C^{O R T} M_{y}^{T} (θ)

(8)

C_{z}^{T - O R T} = M_{z} (α) C^{O R T} M_{z}^{T} (α)

이 때, $C^{O R T}$ 는 회전되지 않은 사방정계 형태의 이방성 매질에 대한 탄성계수 행렬이며, 행렬 $M_{x} (ϕ), M_{y} (θ), M_{z} (α)$ 은 $x$ 축, $y$ 축, $z$ 축 중심에 대해 각각 𝜙, 𝜃, 𝛼만큼 회전 변환을 해주는 Bond 변환 행렬이다(Auld, 1973; Ivanov and Stovas, 2016). 탄성 ORT 매질에 대한 탄성계수 행렬은 다음과 같다.

(9)

C_{e l a s t i c}^{O R T} (\begin{matrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{matrix})

ORT 매질에서 각 탄성계수는 Thomsen의 이방성 변수를 이용하여 다음과 같이 표현될 수 있다(Tsvankin, 1997; Oh, 2020).

(10)

V_{P 0} = \sqrt{\frac{C_{33}}{ρ}}

(11)

V_{S 0} = \sqrt{\frac{C_{55}}{ρ}}

(12)

ε_{1} = \frac{C_{11} - C_{33}}{2 C_{33}}

(13)

ε_{2} = \frac{C_{22} - C_{33}}{2 C_{33}}

(14)

γ_{1} = \frac{C_{66} - C_{55}}{2 C_{55}}

(15)

γ_{2} = \frac{C_{66} - C_{44}}{2 C_{44}}

(16)

δ_{1} = \frac{(C_{13} + C_{55})^{2} - (C_{33} - C_{55})^{2}}{2 C_{33} (C_{33} - C_{55})}

(17)

δ_{2} = \frac{(C_{23} + C_{44})^{2} - (C_{33} - C_{44})^{2}}{2 C_{33} (C_{33} - C_{44})}

(18)

δ_{3} = \frac{(C_{12} + C_{66})^{2} - (C_{11} - C_{66})^{2}}{2 C_{11} (C_{11} - C_{66})}

이 때 $V_{P 0}$ 와 $V_{S 0}$ 는 각각 z축 방향으로 전파하는 수직 P파 속도와 $x z$ 면상에서 $x$ 축 방향으로 입자 운동하며 $z$ 축 방향으로 전파하는 수직 S파 속도를 의미한다. $γ_{1}$ 과 $γ_{2}$ 는 각각 $y z$ 면과 $x z$ 면상에서의 SH파의 전파 방향에 따른 속도 변화를 결정한다. 탄성 ORT 매질에서의 SV파와 SH파의 전파 거동은 매우 복잡하기 때문에, 현재까지의 탄성파 영상화 연구에서는 크게 고려되고 있지 않아서 본 논문에서는 이를 자세히 다루는 것을 생략할 것이다.

T-ORT 매질은 세 축이 직교한 ORT 매질이 방향에 따라 단순히 회전한 형태이기 때문에, ORT 매질에서의 각 방향에 따른 탄성파 속도를 이해하는 것이 중요하다. ORT 매질에서 $z$ 축 방향으로 전파하는 수직 P파 속도와 $x$ 축, $y$ 축 방향으로 전파하는 수평 P파 속도의 비는 각각 $ε_{1}$ 과 $ε_{2}$ 에 의해 정의된다. $δ_{1}$ 과 $δ_{2}$ 은 각각 $x z$ 와 $y z$ 면상에서의 입사각도에 따른 P파 속도의 변화를 결정하며, $δ_{3}$ 는 방위각에 따른 P파 속도의 변화를 결정한다. ORT 매질에서 입사각( $θ_{i}$ )과 방위각( $ϕ_{i}$ )에 따른 P파의 위상 속도는 다음과 같이 정의된다(Tsvankin, 1997).

(19)

V_{p} (θ_{i,} ϕ_{i}) = V_{p 0} [1 + δ (ϕ_{i)} \sin^{2} θ_{i} \cos^{2} θ_{i} + ε (ϕ_{i}) \sin^{4} θ_{i}]

(20)

ε (ϕ_{i}) = ε_{2} \sin^{4} ϕ_{i} + ε_{1} \cos^{4} ϕ_{i} + (2 ε_{1} + δ_{3}) \sin^{2} ϕ_{i} \cos^{2} ϕ_{i}

(21)

δ (ϕ_{i}) - δ_{1} \sin^{2} ϕ_{i} + δ_{2} \cos^{2} ϕ_{i}

탄성 VTI 매질과 y방향으로 평행한 균열망을 가진 HTI 매질에 대한 탄성계수 행렬은 각각 식 (22)와 (23)과 같으며, 최종적으로 모든 방향으로 탄성파 속도가 같은 등방성(Isotropic, ISO) 탄성 매질과 등방성 음향 매질에서는 각각 식 (24)와 식 (25)와 같이 표현된다.

(22)

C_{e l a s t i c}^{V T I} = (\begin{matrix} C_{11} & C_{11} - 2 C_{66} & C_{13} & 0 & 0 & 0 \\ C_{11} - 2 C_{66} & C_{11} & C_{13} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{55} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{matrix})

(23)

C_{e l a s t i c}^{H T I (y)} = (\begin{matrix} C_{11} & C_{13} & C_{13} & 0 & 0 & 0 \\ C_{13} & C_{33} & C_{33} - 2 C_{44} & 0 & 0 & 0 \\ C_{13} & C_{33} - 2 C_{44} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{matrix})

(24)

C_{e l a s t i c}^{I S O} = (\begin{matrix} C_{33} & C_{33} - 2 C_{55} & C_{33} - 2 C_{55} & 0 & 0 & 0 \\ C_{33} - 2 C_{55} & C_{33} & C_{33} - 2 C_{55} & 0 & 0 & 0 \\ C_{33} - 2 C_{55} & C_{33} - 2 C_{55} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{55} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{matrix})

(25)

C_{a c o u s t i c}^{I S O} = (\begin{matrix} C_{33} & C_{33} & C_{33} & 0 & 0 & 0 \\ C_{33} & C_{33} & C_{33} & 0 & 0 & 0 \\ C_{33} & C_{33} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix})

VTI 매질에서는 $ε_{2} = ε_{1}, δ_{2} = δ_{1}, δ_{3} = 0$ 이기 때문에 식 (19)와 식 (20)이 각각 $ε (ϕ_{i}) = ε_{1}$ 과 $δ (ϕ_{i}) = δ_{1}$ 이 되어 모든 방위각에 따른 P파의 거동이 같아, 2차원 탐사에서 측선의 방향에 무관하게 항상 횡등방성이 나타난다. 또한 $ε_{1} = δ_{1}$ 인 경우, P파의 파면이 완전한 타원형을 이루기 때문에 이를 타원형 이방성(elliptical anisotropy)이라고 한다. 하지만 HTI 매질에서 2차원 탐사를 수행할 경우, 측선이 균열망에 평행할 경우에는 등방성처럼, 균열망에 수직일 경우에는 횡등방성처럼 나타날 수 있다. 이는 식 (23)을 각각 yz, xz 단면에서의 2차원으로 근사하면 이해하기 쉽다.

탄성파 이방성의 영향

삼사정계 형태의 이방성 매질은 퇴적분지에서 존재할 수 있는 가장 복잡한 형태의 이방성 매질로 퇴적분지의 이방성 특성을 가장 정확하게 반영하지만, 탄성파 영상화 과정에서 이를 구현하는 것은 매우 어려운 일이며, 대부분의 경우 이러한 복잡한 이방성을 고려하는 것이 불필요하다. 따라서 탐사 지역에 복잡하고 강한 이방성이 존재한다고 하더라도, 실제로 획득된 탐사 자료가 이러한 이방성에 의해 얼마나 왜곡될 수 있는가를 판단하는 것이 중요하다.

탄성파 탐사에서 이방성의 영향은 각 이방성 변수의 방사패턴을 추정함으로써 분석될 수 있다(Operto et al., 2013; Oh and Alkhalifah, 2016a; Oh and Alkhalifah, 2016b; He and Plessix, 2017). 이방성 변수의 방사패턴은 이방성 변수 추정을 위한 다변수 완전파형역산(multi-parameter full-waveform inversion)을 목적으로 10여년 전부터 활발하게 연구되어 왔다. 이에 대한 자세한 설명은 뒤에 이방성 완전파형역산 기술 동향에서 다시 다룰 것이다. He and Plessix(2017)은 이방성 변수의 방사패턴을 회절패턴(diffraction radiation pattern), 반사패턴(reflection radiation pattern), 투과패턴(transmission radiation pattern)으로 구분하여 분석하였는데, 이러한 분류 기준은 탐사 특성에 맞게 이방성 변수의 영향을 예측하는데 큰 도움을 주었다.

Fig. 3은 탄성 ORT 매질에서의 이방성 변수의 반사각에 따른 반사패턴을 보여준다(Oh and Alkhalifah, 2019). 예를 들어, 반사각 0°는 수직 반사파에 대한 영향을, 반사각 180°는 다이빙파와 같은 굴절파에 대한 영향을 의미한다. 이방성 변수의 반사패턴은 식 (19), (20), (21)의 ORT 매질에서의 P파의 위상속도 식과 연관지어 해석할 필요가 있다. P파의 위상속도 식에서 확인할 수 있듯이, $ε_{1}$ 과 $ε_{2}$ 는 각각 $x$ 축 방향(방위각 0°)과 $y$ 축 방향(방위각 90°)으로의 입사각이 클수록(수평 전파) P파의 위상속도에 큰 영향을 준다. 따라서 Fig. 3에서 $ε_{1}$ 과 $ε_{2}$ 는 각각 방위각 0°와 90° 방향에서 반사각이 커질수록 그 영향이 커지게 된다. 반면에 $δ_{1}$ 과 $δ_{2}$ 는 45° 방향으로 입사하는 P파의 위상속도에 큰 영향을 주기 때문에 각각 방위각 0°와 90° 방향을 따라 90°의 각도로 반사되는 파에 가장 큰 영향을 미치게 된다. $δ_{3}$ 는 식 (20)에서 확인할 수 있듯이 방위각 45°에서 가장 영향이 크며, 식 (19)에서 확인할 수 있듯이 입사각이 클수록 영향이 크기 때문에 Fig. 3과 같은 반사패턴을 가지게 된다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F3.jpg

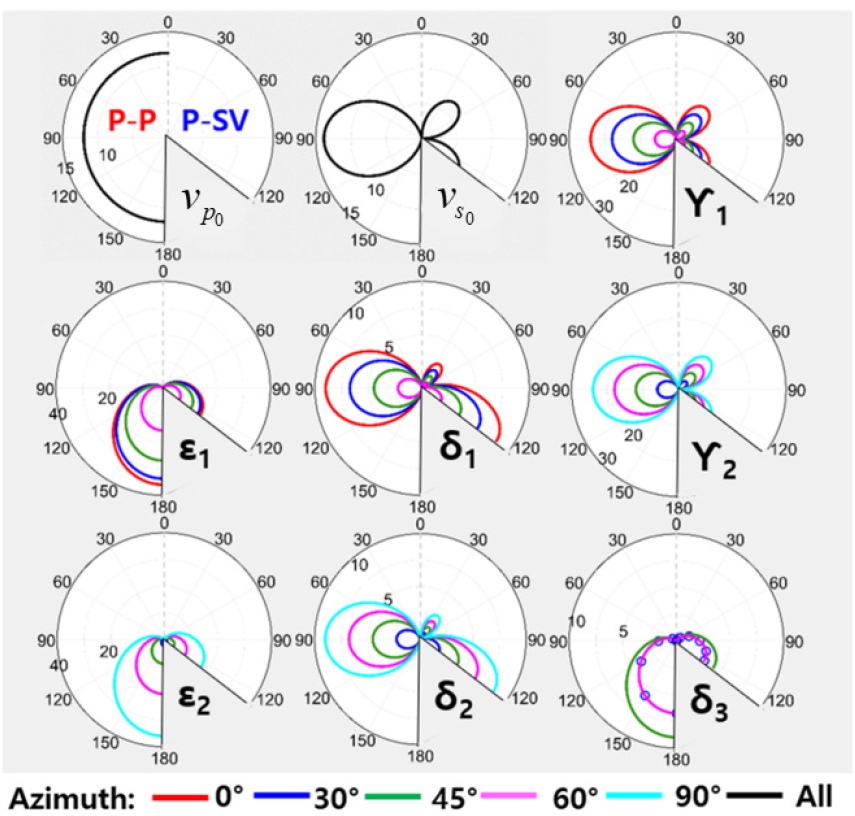
Fig. 3.

P-P and P-SV reflection radiation patterns of elastic orthorhombic parameters (modified from Oh and Alkhalifah, 2019). The angles outside circles indicate the reflection angle (or the opening angle) satisfying the Snell’s law from a horizontal reflector.

T-ORT 매질에서는 방위각 방향으로 이방성 축이 회전될 경우, 단순히 반사패턴이 회전되기 때문에 ORT 매질에 대한 반사패턴 분석이 유효하지만, 경사 방향으로 이방성 축이 회전될 경우 수평층에 대한 근사가 더 이상 유효하지 않아서 더욱 복잡해진다. 단사정계 형태의 이방성 변수의 반사패턴은 보다 복잡하며(Fig. 4), 식 (5)에서 추가된 4개의 변수( ${\tilde{C}}_{16}, {\tilde{C}}_{26}, {\tilde{C}}_{36}, {\tilde{C}}_{45}$ )의 반사패턴은 방위각 방향으로의 위상 변화가 특징적이다. 하지만 각도에 따른 에너지를 기반으로 한 기존의 해석적인 반사패턴으로는 이를 완벽하게 구분할 수 없다. 예를 들어 ${\tilde{C}}_{16}, {\tilde{C}}_{26}, {\tilde{C}}_{36}, {\tilde{C}}_{45}$ 와 ${\tilde{C}}_{16}$ 의 이론적인 반사패턴이 유사하여 두 변수가 비슷한 영향을 미치는 것처럼 보이나, ${\tilde{C}}_{16}$ 는 위상 변화를 유발한다. 따라서 이방성 축이 회전된 복잡한 이방성 매질에서는 수치모델링을 기반으로 한 반사패턴 분석도 병행될 필요가 있다. 하지만 회전되지 않은 이방성 매질에서는 이방성 변수의 반사패턴에 대한 해석적인 분석만으로도 이방성 변수가 어떤 반사각도의 신호에 영향을 미치는지 예측할 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F4.jpg

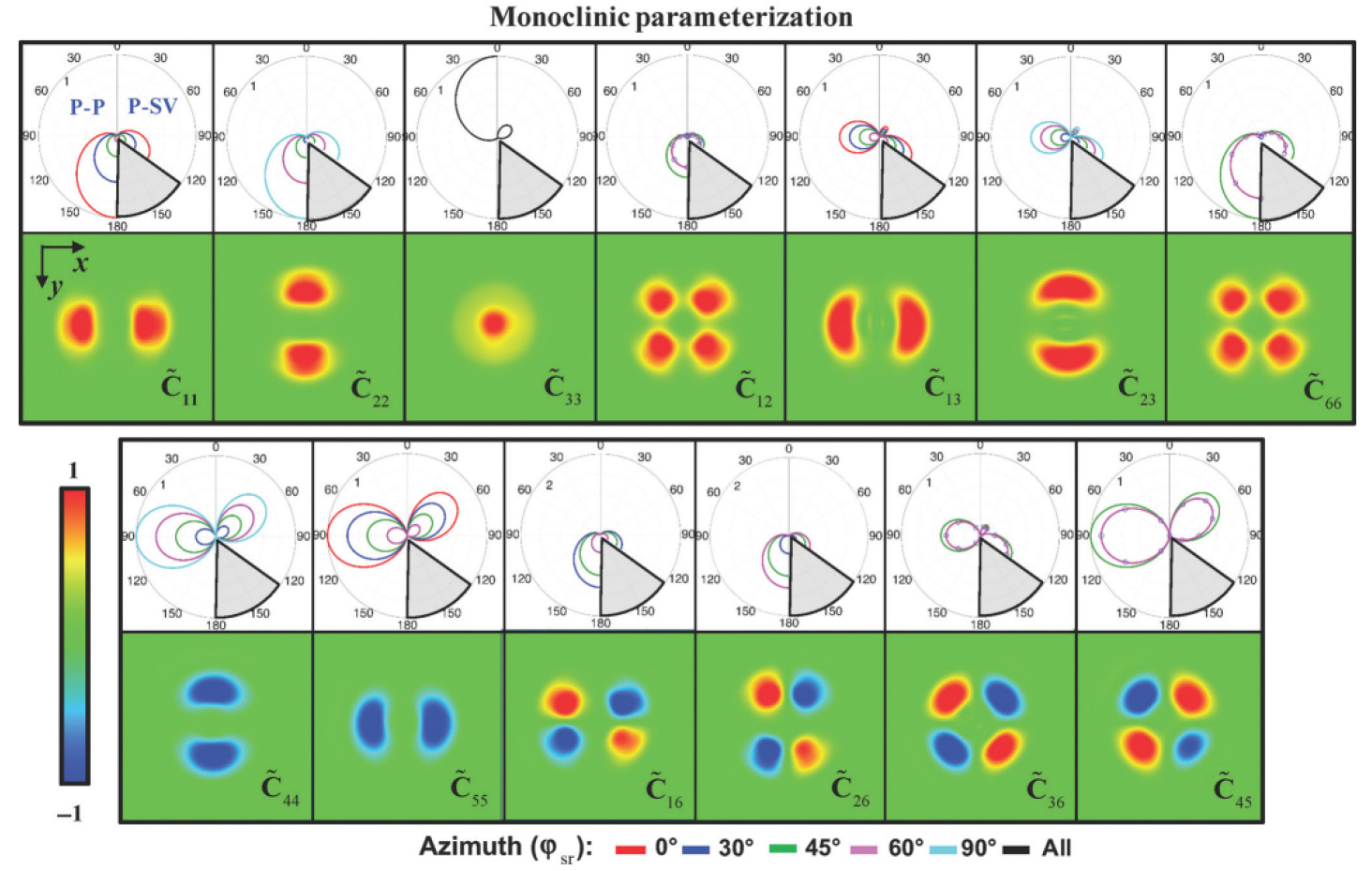
Fig. 4.

P-P and P-SV reflection radiation patterns of monoclinic parameters specified in Eq. (5) (Oh and Alkhalifah, 2018a). Top circles indicate the theoretical radiation patterns assuming a horizontal reflector, and bottom snapshots indicate the numerical radiation patterns in the xy plane at the upper boundary of the horizontal reflector.

이방성이 실제 탄성파 탐사자료에 미치는 영향을 이해하기 위해서는 방위각 방향에 따른 오프셋 대 깊이의 비(offset-to-depth ratio)를 함께 고려하는 것이 중요하다. 앞서 반사패턴 분석 결과에서 확인하였듯이, 이방성 변수 ( $ε_{1}, δ_{1}$ )와 ( $ε_{2}, δ_{2}$ )는 각각 종방향 측선(inline)과 횡방향 측선(crossline)에 따른 먼 오프셋 자료에, $δ_{3}$ 는 중간 방위각의 먼 오프셋 자료에 주로 영향을 미치게 된다. 따라서 탐사 대상이 얕은 심도에 있고 그 상부에 이방성의 원인이 존재하는 지역에서 원거리 탐사를 수행한다면, 먼 오프셋 자료는 이방성에 의해 왜곡될 수 있다. 이러한 경우, 먼 오프셋의 자료를 영상화에서 배제한다면 이방성의 영향을 최소화할 수 있다. 하지만 이방성을 고려한 영상화 기술을 통해 먼 오프셋의 자료까지 영상화에 활용한다면, 보다 많은 자료를 중합(stack)할 수 있기 때문에 영상의 신호 대 잡음비를 향상시킬 수 있다. 반면에 이방성 층이 깊은 심도에 있고, 오프셋이 충분히 짧게 설정되었다면 기존의 등방성 영상화 기술로도 충분하다. 따라서 탐사지역의 지질학적 연구를 통한 이방성의 존재 가능성과 탐사 배열 분석을 통한 이방성의 왜곡 가능성을 분석하여 최적의 이방성 모델을 도출하고, 이를 기반으로 이방성 탄성파 영상화를 수행하는 것이 바람직하다. 또한 이방성 탄성파 영상화는 방대한 계산량이 요구되기 때문에 주어진 계산환경을 고려하여 최선의 이방성 탄성파 영상화 기술을 선정한 뒤, 고려할 수 없는 방위각/오프셋 자료는 영상화에서 배제시키는 것이 바람직하다.

이방성 탄성파 모델링 기술 연구 동향

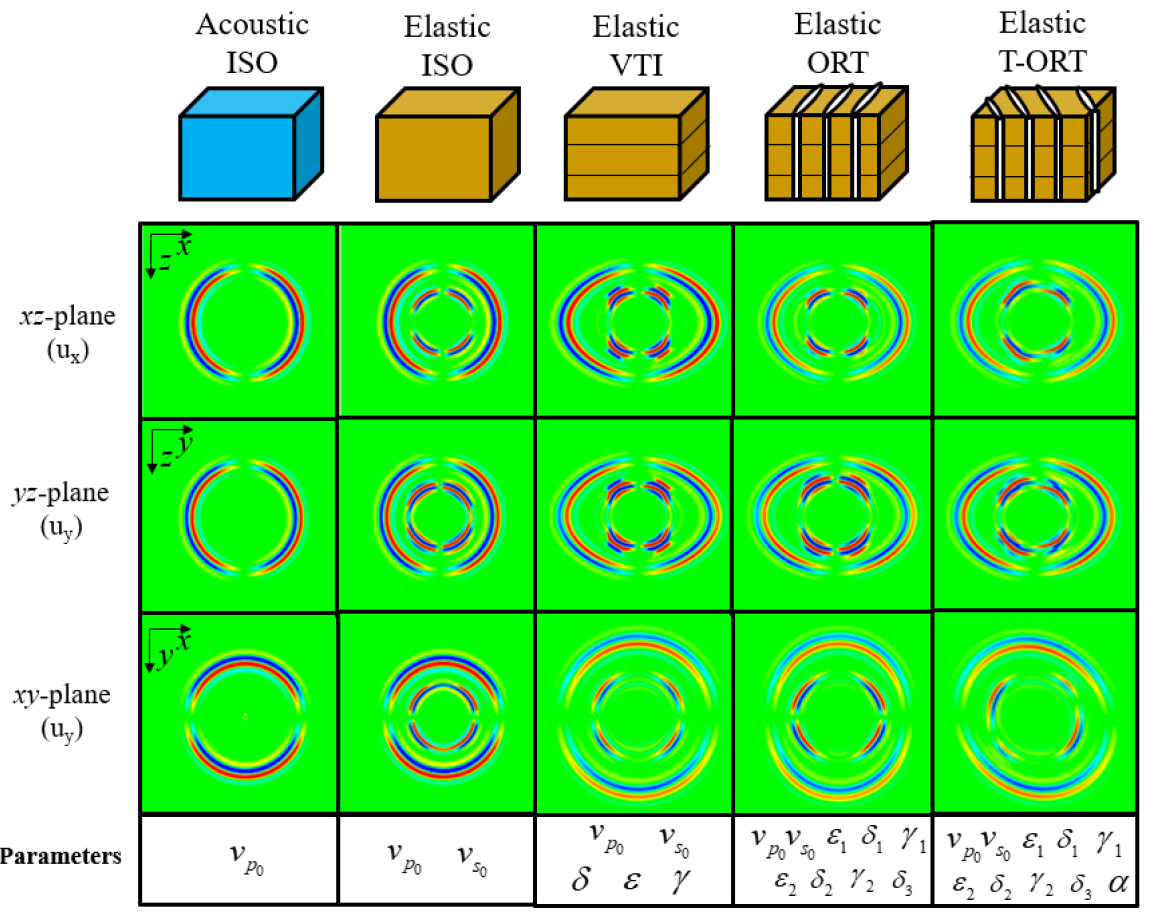
이방성 탄성파 모델링 기술은 이방성 매질에서의 탄성파의 거동을 이해하고, 실제 탄성파 탐사자료의 이방성 특성을 규명하는데 활용될 수 있다. 또한 수치모델링을 기반으로 한 영상화 기술인 완전파형역산과 역시간 구조보정 연구에서는 이방성을 고려할 수 있는 최적의 모델링 알고리듬을 확보하는 것이 필수적이다. Fig. 5는 식 (8), 식 (9), 식 (22), 식 (24), 식 (25)와 같이 탄성계수 행렬이 다른 다양한 형태의 이방성 매질에서의 탄성파 전파 양상을 보여준다. 보다 정확한 이방성 매질을 구현하기 위해서는 점점 더 많은 이방성 변수를 고려해야 하기 때문에, 물리적으로 더 정확한 이방성 모델을 가정할수록 더 많은 계산량이 요구된다. 따라서 이를 극복하기 위한 이방성 탄성파 모델링 기술의 최근 연구 동향을 살펴볼 필요가 있다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F5.jpg

Fig. 5.

Snapshot examples of wave propagations in different anisotropic media. Note that we require more parameters to simulate a more accurate anisotropic model.

이방성 탄성파동방정식

식 (1), (2), (3), (4)로 표현되는 탄성파동방정식의 해는 다양한 수치해석 방법을 이용하여 계산할 수 있으며, 탄성계수 행렬의 근사도에 따라 다양한 이방성을 구현할 수 있다. 3차원 탄성파동방정식의 모델링 연구는 엇격자 유한차분법을 기반으로 초기에는 등방성을 가정하여 수행되었다(Randall, 1988; Graves, 1996). 3차원 이방성 매질을 고려한 연구로는 Carcione et al.(1992)가 TI 매질과 T-ORT 매질에 대한 탄성파 모델링, Igel et al.(1995)가 삼사정계 형태의 이방성 매질에 대한 모델링을 수행한 바 있으며, Bansal and Sen (2008)은 회전된 엇격자 유한차분법을 이용하여 단사정계 형태의 이방성 매질에 대한 모델링을 수행하였다.

3차원 탄성파동방정식 모델링은 방대한 계산량이 요구되는 문제로, 대규모 3차원 이방성 탄성파 영상화에 적용되기 위해서는 현실적으로 여러가지 어려움이 존재한다. 따라서 고성능 컴퓨팅 기반의 병렬화가 필수적이며, 클러스터 환경에서 MPI(Message Passing Interface)를 이용한 영역분할법과 같은 기술이 적용될 필요가 있다(Bohlen, 2002). Weiss and Shragge(2013)은 영역분할법 기반의 GPU (Graphics Processing Unit)를 이용한 3차원 이방성 파동방정식의 병렬화 연구를 수행한 바 있다. 하지만 S파 속도가 매우 느린 매질에서는 공간 격자를 더 작게 사용해야 하기 때문에 수치모델링에 필요한 계산량이 기하급수적으로 늘어날 수 있다. 이를 극복하기 위하여 큰 공간 격자를 사용하면서 발생하는 수치분산을 제거하기 위한 플럭스 보정기법(Flux-Corrected Transport, FCT)을 적용할 수 있으나(Fei and Larner, 1995; Wang et al., 2014; Oh et al., 2022), 진폭과 분해능 손실이 발생하니 탄성파 영상화에 적용 시 주의가 필요하다.

이방성 음향파동방정식

3차원 해양탐사자료와 같이 P파만을 이용한 탄성파 영상화 과정에서 이방성을 구현하기 위하여 탄성매질을 가정하는 것은 매우 비효율적이다. 따라서 이방성 매질에서의 P파만을 구현하기 위한 이방성 음향파동방정식이 활발하게 개발되어 왔다. P파의 이방성을 구현하기 위하여 Alkhalifah (2000)은 유사미분연산자를 이용하여 VTI 매질에 대한 유사음향파동방정식(pseudo-acoustic wave equation)을 다음과 같이 제안하였다.

(26)

\frac{\partial^{2} P}{\partial t^{2}} - \frac{ν_{P 0}^{2}}{2} ((1 + 2 ε) \frac{\partial^{2}}{\partial h^{2}} + \frac{\partial^{2}}{\partial z^{2}} + Q) P = 0

이 때, P는 P파의 압력파동장이고, $\partial^{2} / \partial h^{2} = \partial^{2} / \partial x^{2} + \partial^{2} / \partial y^{2}$ 이며, $Q$ 는 다음과 같다.

(27)

Q = \sqrt{((1 + 2 ε) \frac{\partial^{2}}{\partial h^{2}} + \frac{\partial^{2}}{\partial z^{2}}) - 8 (ε - δ) \frac{\partial^{2}}{\partial h^{2}} \frac{\partial^{2}}{\partial z^{2}}}

위 식은 공간 4차 미분항의 처리가 어렵기 때문에, Duveneck et al.(2008)은 식 (22)의 VTI 매질에 탄성계수 행렬에 $C_{55} = 0, C_{66} = 0$ 을 대입하여, P파만을 구현하였다. 하지만 $ε \neq δ$ 인 비타원형(anelliptical) 횡등방성의 경우, 송신원 주변에서 S파 잡음이 발생하는데(Grechka et al., 2004), Duveneck et al.(2008)은 송신원 주변에 얇은 타원형 이방성 층을 할당하여 이 문제를 해결하였다.

Xu and Zhou(2014)는 Alkhalifah(2000)식의 공간 4차 미분항을 제거하기 위하여, 주파수-파수 영역에서 미분연산자를 재정렬하고, 다시 시간-공간 영역으로 역푸리에변환 함으로써 다음과 같은 순수음향파동방정식(pure acoustic wave equation)을 유도하였다.

(28)

\frac{\partial^{2} P}{\partial t^{2}} - \nabla ∙ (ν_{p 0}^{2} S \nabla P) = 0

이 때,

(29)

S = \frac{1}{2} ((1 + 2 ε) n_{h}^{2} + n_{z}^{2} + \sqrt{{((1 + 2 ε) n_{h}^{2} + n_{n}^{2})}^{2} - 8 (ε - δ) n_{h}^{2} n_{n}^{2}})

이며, 위상 방향 벡터(phase direction vector)는 $\vec{n} = \nabla P / |\nabla P|$ 로 근사되어, 매시간 간격에서의 파동장 p에 의해 계산될 수 있다. 식 (28)의 순수음향파동방정식은 다음과 같이 등방성 파동방정식과 이방성 보정항으로 분리될 수 있다.

(30)

\frac{\partial^{2} P}{\partial t^{2}} = ν_{p 0}^{2} \nabla^{2} P + ν_{p 0}^{2} \nabla ∙ (∆ S \nabla P)

(31)

∆ S = \frac{1}{2} (\sqrt{{((1 + 2 ε) n_{h}^{2} + n_{z}^{2})}^{2} - 8 (ε - δ) n_{h}^{2} n_{z}^{2}} + 2 ε n_{h}^{2} - 1)

Xu et al.(2015)는 위의 식을 파면이 구형인 등방성 성분과 이방성의 효과가 분리되었다는 의미에서 구형분리 기반의(spherical decomposition) 음향파동방정식이라 정의하고, 이를 개선하기 위하여 다음과 같은 타원형분리 기반의(elliptical decomposition) 음향파동방정식을 제안하였다.

(32)

\frac{\partial^{2} P}{\partial t^{2}} = (ν_{p 0}^{2} \frac{\partial^{2} P}{\partial z^{2}} + (1 + 2 ε) ν_{p 0}^{2} \frac{\partial^{2} P}{\partial h^{2}}) (1 + ∆ S_{e})

(33)

∆ S_{e} = \frac{1}{2} (\sqrt{1 - \frac{8 (ε - δ) n_{h}^{2} n_{z}^{2}}{{((1 + 2 ε) n_{h}^{2} + n_{z}^{2})}^{2}} - 1})

구형분리 기반의 음향파동방정식과 달리 식 (32)는 타원형 이방성 성분과 $∆ S_{e}$ 로 정의되는 비타원형 보정항이 분리되어 있는 형태로, 배경모델의 𝜀과 𝛿값에 따라 횡등방성과 타원형 이방성을 조절할 수 있기 때문에 탄성파 영상화에서 편의성이 높다. 또한 이방성이 강한 매질에서는 특히 수평방향에서 등방성 파면과 이방성 파면의 오차가 타원형 파면과 비타원형 파면의 오차보다 훨씬 크기 때문에 더 정확한 근사치를 제공할 수 있다(Xu et al., 2015).

Xu et al.(2015)가 제안한 타원형분리 기반의 순수음향파동방정식은 음향 ORT 매질로 쉽게 확장될 수 있으며(Xu and Zhou, 2014), TTI나 T-ORT와 같이 회전된 이방성 매질에 대해서도 확장될 수 있다(Zhang et al., 2011). 이외에도 low-rank 근사법(Song and Alkhalifah, 2013; Zhang et al., 2019) 등이 개발되었지만, 공간 푸리에 변환이 요구되기 때문에 영역분할법 기반의 대규모 3차원 탄성파 영상화에서는 부적합하다. 3차원 이방성 탄성파동방정식과 달리 이방성 음향파동방정식은 요구 메모리가 상대적으로 적어 주파수영역 모델링으로도 가능하기 때문에(Operto et al., 2009; Operto et al., 2014), 적은 수의 주파수 자료만으로도 가능한 3차원 이방성 완전파형역산 연구에서 활용될 수 있다.

이방성 완전파형역산 기술 연구 동향

이방성 구조보정을 통한 지층 영상화를 위해서는 앞서 언급한 이방성 변수를 추정해야 한다. 이에 따라 기존의 P파 속도 추정을 위한 등방성 음향 완전파형역산을 확장하여 이방성 모델링을 기반으로 이방성 변수까지 역산으로 추정하는 다변수 완전파형역산(multi-parameter full waveform inversion) 기술에 대한 연구가 활발히 진행되고 있다. 다변수 완전파형역산에서는 이방성 변수를 어떻게 변수화하느냐에 따라서 각 변수 별 방사패턴이 달라지고, 이에 따라 역산 민감도가 변하기 때문에 최적의 변수화 방법을 찾기 위한 연구가 중심이 되어 왔다(Operto et al., 2013).

다변수 완전파형역산의 기본 원리

다변수 완전파형역산의 기본 원리는 P파 속도 추정을 위한 기존의 등방성 음향 완전파형역산(Virieux and Operto, 2009)과 같으나, 모델의 물성 변화 추정치인 그래디언트(gradient) 벡터가 모델 변수의 수만큼 커지게 된다. 추정할 모델 변수의 종류를 $n p$ , 모델 내 격자점의 수를 $n$ 이라고 하면 $n p \times n$ 만큼의 그래디언트를 추정해야 한다. $i$ 번째 격자점에 위치한 $j$ 변수( $m_{i, j}$ )의 그래디언트( $\nabla E_{m_{i, j}}$ )는 각 관측 자료( $d_{o}$ )와 모델링 자료( $d_{c}$ )의 차이로 정의되는 잔차(residual, $∆ d = d_{c} - d_{o}$ )와 해당 변수의 변화에 의해 유발되는 편미분파동장(partial derivative wavefields)을 이용하여 다음과 같이 계산될 수 있다.

(34)

\nabla E_{m_{i, j}} = \sum_{s}^{} \sum_{r}^{} \sum_{t}^{} \frac{\partial d_{c} (s, r, t)}{\partial m_{i, j}} ∆ d (s, r, t)

이 때, $s$ 와 $r$ 은 송신원과 수신기를 의미한다. 최종적으로 지하의 물성 모델 벡터( $m$ )는 수렴할 때까지 다음 수식에 의해 반복적으로 갱신된다.

(35)

m = m_{0} = β H^{- 1} \nabla E_{m}

이 때, $m_{0}$ 는 초기 물성 모델 벡터, 𝛽와 $H$ 는 갱신 크기(steplength)와 헤시안(Hessian)을 의미한다.

하나의 물성 변수를 추정하는 등방성 음향 완전파형역산과 비교하면, 다변수 완전파형역산은 동일한 탐사자료로부터 여러 물성 변수를 추출해야 하므로 더 복잡한 문제이다. 따라서 각 변수간 방사패턴을 분석하여 변수 간 트레이드오프가 적고 모델 갱신에 유리한 변수화 방법을 찾는 것이 중요하다. 가장 단순한 형태의 다변수 완전파형역산은 식 (36)으로 표현되는 밀도까지 고려한 음향파동방정식을 이용하여, 속도와 밀도(𝜌) 두 가지 정보를 추정하는 것이다(Operto et al., 2013). 따라서 이를 기반으로 다변수 완전파형역산에서 변수화 방법 선택의 중요성을 설명하고, 이를 더 복잡한 형태의 이방성 다변수 완전파형역산으로 확장할 것이다.

(36)

\frac{1}{ρ ν_{p}^{2}} \frac{\partial^{2 P}}{\partial t^{2}} = \frac{\partial}{\partial x} (\frac{1}{ρ} \frac{\partial P}{\partial x}) + \frac{\partial}{\partial z} (\frac{1}{ρ} \frac{\partial P}{\partial z})

위의 밀도를 고려한 음향파동방정식을 P파 속도와 P파 임피던스로 표현하면 다음과 같이 변수화 될 수 있다.

(37)

\frac{1}{ν_{p} I_{p}} \frac{\partial^{2 P}}{\partial t^{2}} = \frac{\partial}{\partial x} (\frac{ν_{p}}{I_{p}} \frac{\partial P}{\partial x}) + \frac{\partial}{\partial z} (\frac{ν_{p}}{I_{p}} \frac{\partial P}{\partial z})

식 (36)과 (37)의 해는 같지만, 변수화 방법을 바꿈에 따라 각 변수의 방사패턴이 변화하고 수신기에 기록된 자료에 대한 역산 민감도가 달라지게 된다(Fig. 6). 이는 Fig. 7의 각 변수화 방법에 따른 역산 변수의 방사패턴에서 확인할 수 있다. 식 (36)과 같이 속도-밀도로 변수화한 경우, P파 속도는 등방적인 방사패턴을 가지므로 P파 속도의 변화는 표면에 위치한 모든 수신기에 민감하고, 이는 모든 수신기의 자료가 P파 속도를 역산하는데 영향을 미친다는 것을 의미한다. 반면 밀도는 송신원 방향으로 후방 산란(back scattering)되는 방사패턴을 가지는데 이는 송신원 주변의 오프셋이 작은 자료가 밀도를 역산하는데 영향을 미친다는 것을 의미한다. 따라서 속도-밀도 변수화 방법은 모든 자료를 이용하기 때문에, P파 속도를 추정하기 용이하지만 밀도는 반사각이 작은 자료 위주로 역산이 되어 단파장의 모델이 추정된다(Fig. 6d의 수식 참고). 또한 두 변수의 방사패턴이 작은 열림 각도(opening angle)에서 완전히 겹치는데, 이는 작은 오프셋 자료에서의 잔차를 이용하여 P파 속도와 밀도의 변화가 동시에 추정됨을 의미한다. 즉 두 변수 사이에는 역산 과정에서 트레이드오프가 존재하며, 밀도 역산은 초기 P파 속도의 오차에 큰 영향을 받게 된다. 반면 P파 속도의 역산은 밀도의 방사패턴과 겹치지 않는 먼 오프셋 자료까지 사용하므로 밀도 오차의 영향을 상대적으로 덜 받는다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F6.jpg

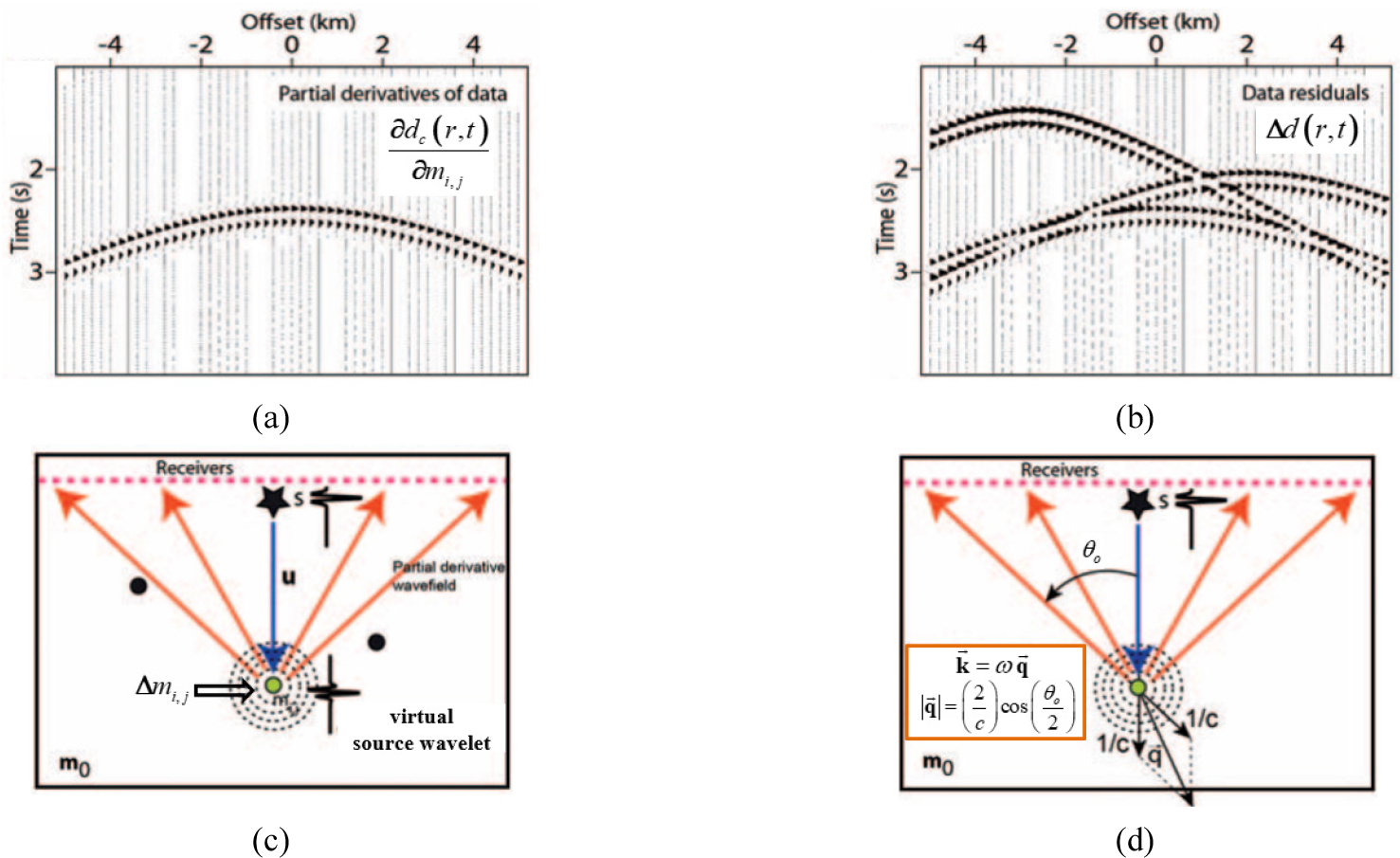
Fig. 6.

Physical interpretation of the gradient specified in Eq. (34) for the model parameter (j) at the ith nodal point (modified from Operto et al., 2013). (a) Partial derivative wavefields from the model parameter perturbation ( $∆ m_{i, j}$ ) as a virtual source, (b) data residuals between calculated and observed data, (c) propagation of partial derivative wavefields from the virtual source to the receivers, and (d) expressions in the wavenumber domain with the wave speed (c) and opening angle ( $θ_{o}$ ).

반면에, 식 (37)과 같은 속도-임피던스 변수화 방법을 이용하면(Fig. 7c, 7d), 속도와 임피던스의 방사패턴이 완전히 분리되기 때문에 속도는 큰 열림 각도(먼 오프셋), 임피던스는 작은 열림 각도(작은 오프셋) 자료를 이용하여 추정되게 된다. 따라서 속도와 임피던스 사이에는 트레이드오프가 적다. 하지만 일반적으로 속도와 임피던스 모델은 비슷한 구조를 갖지만, Fig. 6d의 수식에 따라 속도 모델은 장파장(큰 열림 각도), 임피던스 모델은 단파장(작은 열림 각도)으로 추정되기 때문에 이에 대한 주의가 필요하다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F7.jpg

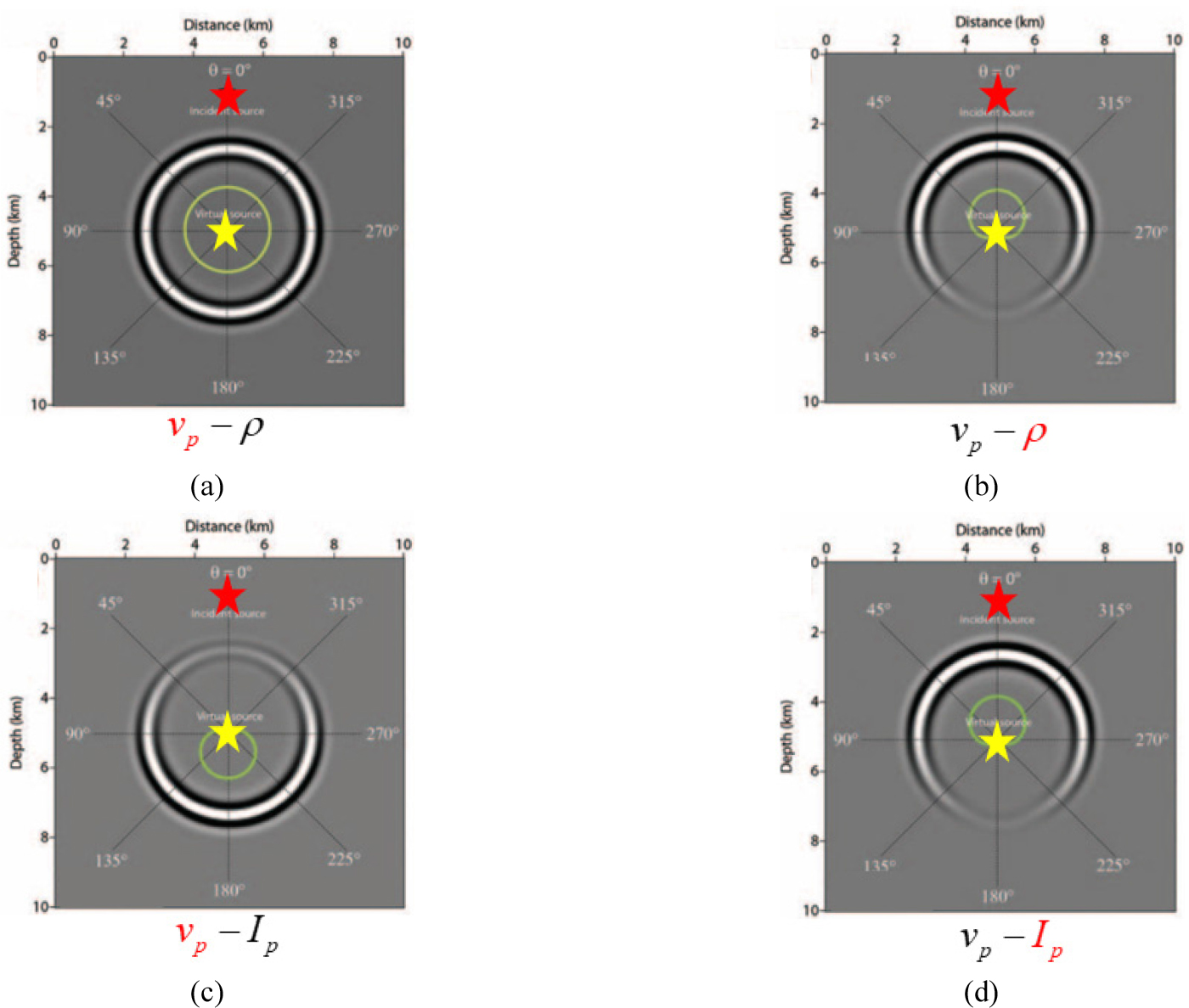
Fig. 7.

Radiation patterns of the partial derivative fields from the model parameter perturbations with two different parameterizations (modified from Operto et al., 2013). Red and yellow stars indicate the seismic sources and virtual sources, respectively.

이방성 완전파형역산은 밀도를 배제하더라도 어느 수준의 이방성 모델까지 구축할 것인가에 따라 추정해야 하는 변수가 21개까지 늘어날 수 있다. 역산에서 고려해야 하는 독립 변수는 2차원 음향 VTI 매질에서는 3개, 2차원 탄성 VTI 매질에서는 4개, 탄성 ORT 매질에서는 9개, 3방향 모두 회전된 탄성 T-ORT 매질에서는 12개, 삼사정계 이방성 매질에서는 21개이다. 따라서 다양한 변수화 방법이 가능하며, 변수 간 트레이드 오프가 나타나는 양상이 다양하기 때문에 최적의 변수화 방법을 설정하는 것이 중요하다. 이를 위한 기존의 연구사례를 소개하고자 한다.

이방성 음향 완전파형역산

이방성 음향 완전파형역산은 가장 단순한 형태인 2차원 음향 VTI 매질을 가정하여 시작되었다(Gholami et al., 2013a; Gholami et al., 2013b). Gholami et al.(2013a)은 2차원 음향 VTI 매질에서 가능한 6가지 변수화 방법에 대하여, 각 변수 별 방사패턴을 분석하여 역산 민감도와 트레이드오프를 비교하였고, Gholami et al.(2013b)은 이를 실제 합성자료와 현장자료 역산에 적용하여 역산 성능의 차이를 검토하였다. 이 두 연구는 어떤 변수화 방법을 사용하느냐에 따라 역산 결과가 크게 달라질 수 있고, 역산을 통한 이방성 변수 추정으로 구조보정 결과가 개선될 수 있다는 것을 증명하였다. 이는 물리탐사 학계의 연구자들에게 큰 영감을 준 선도적인 연구였으며, 이 후 이방성 완전파형역산 연구가 크게 증가하였다.

Alkhalifah and Plessix(2014)는 방사패턴을 기반으로 밀도까지 고려한 2차원 음향 VTI 매질에서의 변수화 방법을 분석하였으며, Wu and Alkhalifah(2016)와 Djebbi and Alkhalifah(2019)는 2차원 음향 VTI 매질을 가정한 현장자료에 대한 주파수 영역 역산을 수행하였다. Masmoudi and Alkhalifah(2018)은 수평 속도 기반의 음향 ORT 매질에서의 최적의 변수화 방법을 제안하였다. Shin et al.(2019)은 압력파동장 기반의 음향 다변수 완전파형역산의 방사패턴 구현 과정에서의 오류를 개선하기 위하여 변환된 벡터 파동장을 이용한 2차원 음향 VTI 역산 전략을 제안하였으며, Li and Alkhalifah(2020)은 2차원 음향 VTI 매질을 가정한 반사파 파형역산(Reflection waveform inversion, RWI)을 수행하여 다변수 완전파형역산이 가지는 각 변수 별 분해능 차이 문제를 해결하고자 하였다.

이방성 탄성 완전파형역산

탄성 완전파형역산은 등방성 가정으로도 P파 속도, S파 속도, 밀도의 3가지 변수가 존재하는 다변수 완전파형역산이다. Tarantola(1986)은 방사패턴을 기반으로 등방성 탄성 완전파형역산에서의 변수화 방법에 대해 연구하였다. 이방성 탄성 완전파형역산에서의 변수화 방법 연구는 2016년부터 활발하게 수행되어 왔다. S파 속도와 S파와 관련된 이방성 변수까지 존재하는 탄성 이방성 매질에서는 더 많은 변수와 P-SV파 등의 모드변환파까지 고려해야하기 때문에 방사패턴 분석이 더 복잡하다.

Kamath and Tsvankin(2016)은 2차원 탄성 VTI 매질에서 세 가지 P파 속도를 기반으로 한 변수화 방법을 제안하였으며, He and Plessix(2017)는 2차원 탄성 VTI 매질에서의 변수화 방법을 회절패턴, 반사패턴, 투과패턴에 따라 더 체계적으로 비교하였다. Pan et al.(2016)은 보다 정확한 헤시안을 이용한 탄성 HTI 매질에서의 다변수 완전파형역산 전략을 제시하였고, Oh et al.(2020)은 탄성 TTI 매질에서 이방성 축의 경사방향 회전각 역산을 위한 다단계 역산 전략을 제안하였다. Oh and Alkhalifah(2016b)는 3차원 탄성 ORT 매질에서의 수평 P파 속도와 수직 S파 속도, 이방성 변수로 구성된 계층적 변수화 방법(hierarchical parameterization)을 제안하였고, 이를 확장하여 방위각 방향으로 회전된 T-ORT 매질에 대한 변수화 방법을 제안하였다(Oh and Alkhalifah, 2018a). Podgornova et al.(2015)과 Kazei and Alkhalifah(2018)는 특이점 분석, 분해능 행렬을 이용하여 각각 탄성 VTI, 탄성 ORT 역산에서의 각 변수 별 분해능 한계를 더 체계적으로 분석하였다. Köhn et al.(2015)은 21개 삼사정계 형태의 이방성 변수에 대한 역산 민감도 분석을 수행하였다. Singh and Tsvankin(2022)는 Kamath and Tsvankin(2016)이 제안한 속도 기반의 변수화 방법을 탄성 ORT 매질로 확장하여 민감도 분석을 수행하였으며, Stovas(2021)는 단사정계 형태의 이방성 매질에 대한 변수화 방법을 연구하였다.

이방성 음향 완전파형역산에 비해 이방성 탄성 완전파형역산은 더 어려운 문제이기 때문에 현장자료에 대한 연구는 상대적으로 적다. Owusu et al.(2016)은 VSP(Vertical Seismic Profiling) 자료에 대해 탄성 VTI 완전파형역산을 적용하였고, Oh and Alkhalifah(2019)는 3차원 해저면 탐사자료에 대한 탄성 ORT 완전파형역산의 성능을 검토하였다.

이방성 음향 및 탄성 매질을 가정하여 변수화 방법에 대한 연구가 수행되어왔고, 그 동안의 연구에 따르면 논문에 따라 서로 다른 최적의 변수화 방법을 제안해왔다. 모든 상황에서 항상 최고의 성능을 가진 변수화 방법은 존재하지 않는다. Fig. 7과 Fig. 8에서 확인한 것처럼 다변수 완전파형역산의 변수화 방법이 달라지면, 각 변수 별 방사패턴이 달라지고 이는 해당 변수의 역산 민감도에 영향을 주기 때문에 탐사 지역의 지질학적 특징, 탐사 자료의 기하학적 특징(data acquisition), 각 이방성 변수 별 민감도 분석을 통하여 상황에 맞게 최적의 변수화 방법이 선정되어야 한다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F8.jpg

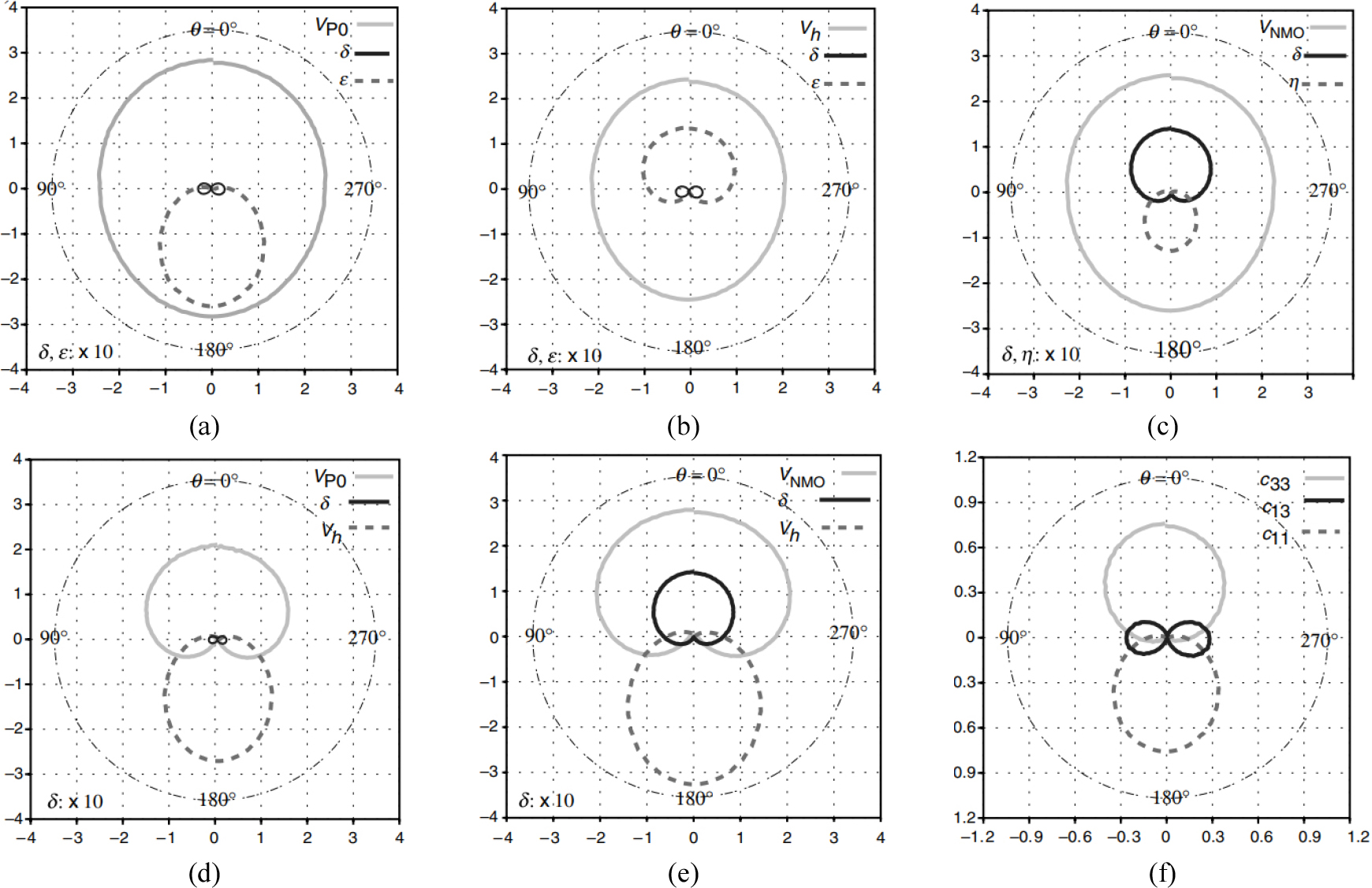
Fig. 8.

Reflection patterns of partial derivative wavefields using six different parameterizations in acoustic VTI full-waveform inversion (Gholami et al., 2013a).

이방성 역시간 구조보정 기술 연구 동향

역시간 구조보정에서 모델 상의 공간(x)에서의 영상화조건(I)은 송신원으로부터 전파한 송신원 파동장(S)과 현장자료를 역시간으로 전파시켜 얻은 수신기 파동장(R)을 영지연 상호상관(zero-lag cross-correlation)하여 계산할 수 있다(Zhou et al., 2018).

(38)

I (x) = \sum_{x}^{} \sum_{t}^{} S (x, t) R (x . t)

이방성 역시간 구조보정은 송신원 파동장과 수신기 파동장의 전파를 위하여 이방성 모델링을 이용하는데, 이방성이 강한 지역에서 획득한 신호의 운동학적 특성을 구현함으로써 도달 시간을 보다 정확하게 추정할 수 있다. 따라서 이방성 역시간 구조보정을 위한 연구는 앞서 모델링 연구사례에서 다루었던, 보다 정확하고 효율적인 이방성 모델링 알고리듬을 개발하는 연구와도 연결된다.

이를 기반으로 이방성 음향 매질에 다양한 역시간 구조보정 기술이 개발되고 실제 현장자료에 적용되어 왔다. 2차원 음향 VTI 역시간 구조보정(Duveneck et al., 2008)부터 2차원 음향 TTI 역시간 구조보정(Du et al., 2007; Fletcher et al., 2009; Huang et al., 2009; Zhang et al., 2011), 3차원 음향 TTI 역시간 구조보정(Zhang and Zhang, 2008), 3차원 음향 ORT/T-ORT 역시간 구조보정(Zhang and Zhang, 2011)까지 다양한 이방성 매질에 대한 역시간 구조보정 기술이 이미 개발되었으며, 앞으로의 연구는 앞서 다루었던 다변수 완전파형역산 기술을 이용하여 역시간 구조보정에 필요한 보다 정확한 이방성 배경 속도 모델을 구축하는 방향으로 진행될 필요가 있다.

음향 매질에서는 P파만이 존재하기 때문에 역시간 구조보정의 영상화조건이 자연스럽게 PP 반사면을 의미한다. 하지만 육상 탐사자료나 해저면 탐사자료를 이용한 탄성 역시간 구조보정에서는 송신원 파동장과 수신기 파동장이 P파와 S파를 모두 포함하기 때문에, 식 (38)의 영상화조건이 다양한 모드변환파의 반사 정보까지 포함하게 되어 정량적인 구조보정이 어렵다. 따라서 이방성 탄성 역시간 구조보정에서는 다양한 형태의 이방성 모델에서 P파와 S파를 분리하여 PP 영상화조건과 PS 영상화조건을 계산하는 연구가 활발하게 수행되어 왔다(Yan and Sava, 2009; Yan and Sava, 2011; Wang et al., 2017; Yang et al., 2019).

역시간 구조보정은 파동방정식의 수치모델링을 기반으로 하기 때문에, 다른 중합전 구조보정 방법과 비교하여 계산량이 많고, 수치분산 문제로 3차원 역시간 구조보정에 사용할 수 있는 주파수대역이 낮아 분해능이 떨어질 수 밖에 없다. 특히 3차원 탄성 역시간 구조보정은 S파의 수치분산을 피하기 위해 더 작은 모델링 격자를 사용해야 하기 때문에, 방대한 계산량이 요구된다. 따라서 3차원 탐사자료에 대한 적용성을 향상시키기 위하여 앞으로의 이방성 탄성 역시간 구조보정 연구는 3차원 탄성 역시간 구조보정의 계산량을 더 줄이는 방향으로 진행될 필요가 있다. 특히 계산자원이 부족한 국내 상황을 고려하면 가장 시급한 연구주제로 생각된다. 또한 이방성 탄성 완전파형역산 기술 개발과 연계하여 탐사지역의 보다 정확한 탄성 이방성 모델을 구축하는 연구도 중요하다.

국내 3차원 이방성 탄성파 영상화 기술 개발 현황

국내에서의 탄성파 탐사는 주로 2차원 탐사가 수행되어 왔다(Lee et al., 2019). 이에 따라 이방성 탄성파 영상화 기술도 주로 2차원을 가정하여 발전되어 왔다. 이방성 수치 모델링 분야의 연구 사례로는 2차원 탄성 VTI 모델링에서의 경계조건 연구(Lee et al., 2008), 2차원 탄성 TTI 모델링에서의 경계조건 연구(Han et al., 2012), 3차원 탄성 TTI 모델링에서의 경계조건 연구(Han et al., 2011), 3차원 탄성 ORT 모델링의 병렬화 연구(Oh, 2020) 등이 있으며, Ha and Shin(2010)은 탄성 VTI 매질을 고려한 축소모형실험 연구를 수행하였다.

이방성 구조보정 분야의 연구 사례로는 2차원 음향 VTI와 TTI 매질에서의 역시간 구조보정(Kwak et al., 2011), GPU를 이용한 3차원 음향 TTI 매질에서의 역시간 구조보정(Kim et al., 2013), GPU를 이용한 2차원 탄성 VTI 매질에서의 역시간 구조보정(Choi et al., 2015), 동해 원거리 해양탄성파 탐사자료의 이방성 자료처리(Joo and Kim, 2020), 북해 해저면 탐사 자료에 대한 음향 VTI 매질에서의 역시간 구조보정 연구(Shin et al., 2021a) 등이 있다.

국내에서 이방성 역산 분야는 과거에는 주로 육상 소규모 탐사자료 해석을 위한 주시 토모그래피에 많이 적용되어 왔다(Jeong and Suh, 2007; Kang et al., 2007). 2010년 전후로 국내에서도 완전파형역산 연구가 주목을 받기 시작하였다. Lee et al.(2010)은 탄성 VTI 매질을 가정한 주파수영역 완전파형역산 연구를 수행하였는데, 이는 앞서 연구동향에서도 확인할 수 있듯이 국제적으로도 이방성 탄성 완전파형역산 분야의 선도적인 연구였다. Kim and Min (2014)은 탄성 VTI 완전파형역산의 성능 개선을 위한 라메상수와 이방성 변수 기반의 새로운 변수화 방법을 제안하였으며, Oh and Min(2014)은 가상송신원의 모멘트 텐서 분석 결과를 기반으로 포아송비를 이용한 탄성 VTI 매질에서의 변수화 방법을 고안하였고, Shin et al.(2021b)은 음향 VTI 매질에서의 변수화 방법에 따른 역산 성능을 비교하였다.

고성능 컴퓨팅 기술이 발달하고 수치모델링 기반의 3차원 영상화에 필요한 메모리를 줄이기 위한 다양한 기술이 개발됨에 따라, 2018년 이후로 국내에서도 3차원 탄성파 영상화 연구가 가능해졌으며, 등방성과 이방성 역산의 성능을 향상시키기 위한 다양한 연구가 수행되고 있다(Oh and Alkhalifah, 2018b; Oh et al., 2018; Oh et al., 2021; Kim et al., 2022). Oh and Alkhalifah(2018a)은 방위각 방향의 회전을 고려한 T-ORT 매질에서 가상으로 획득된 합성 탐사자료에 대해 다변수 완전파형역산을 적용하여 성공적으로 회전각도를 추정하였는데, 이는 세계 최초로 시도된 연구로 주목을 받았다. 이를 기반으로 Oh et al.(2020)은 2차원 탄성 TTI 매질에서 경사 방향의 회전각도를 파형역산을 통해 추정하고자 하였으며, Oh and Alkhalifah(2019)는 북해 볼브 유전(Volve oilfield)에서 획득된 3차원 해저면 탐사자료에 대한 탄성 ORT 완전파형역산의 적용성을 검토하였다.

하지만 이방성 영상화 기술을 현장 자료에 성공적으로 적용하기까지는 여전히 해결해야 할 많은 문제가 존재한다. 특히 이방성 구조보정에 필요한 이방성 변수를 추정하기 위한 이방성 완전파형역산 기술의 현장자료에 대한 적용성을 향상시키기 위한 연구가 지속적으로 수행되어야 한다. 반사파의 도달시간을 보다 정확하게 구현하기 위한 이방성 변수가 완전파형역산을 통해 추정될 수 있다면, 3차원 지층 구조를 개선하는 것이 가능하다.

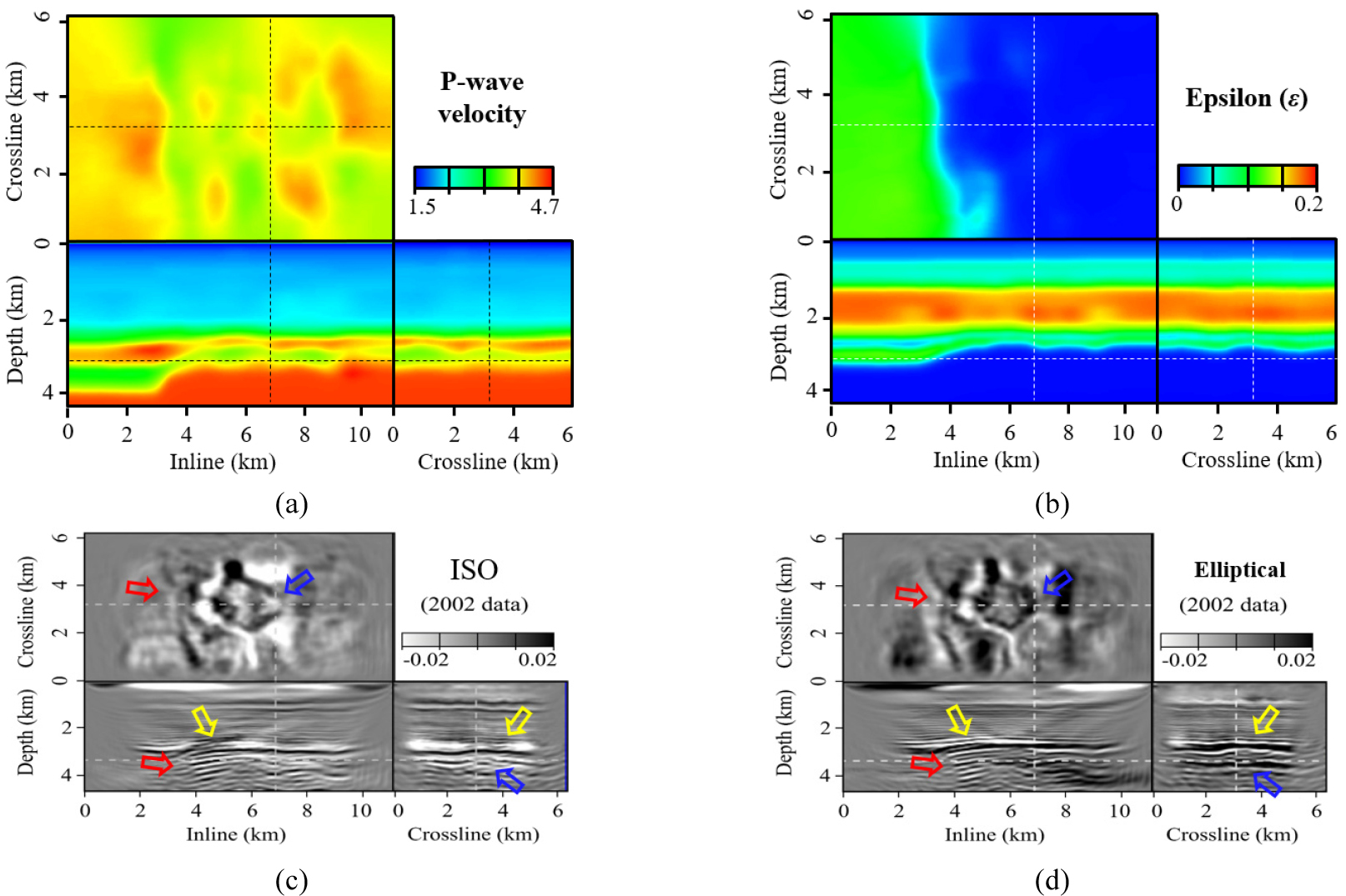
마지막으로, 현재 국내의 3차원 이방성 영상화 기술 수준을 소개하기 위하여 북해 볼브 유전 지역에서 획득한 3차원 해저면 탄성파 탐사자료에 대해 이방성 영상화 기술을 적용하였다. Fig. 9는 북해 볼브 유전 지역의 지질학적 특징과 3차원 해저면 탐사자료의 정보를 보여준다. Fig. 10은 노르웨이의 국영석유회사 이퀴노르(Equinor)가 추정한 이 지역의 P파 속도와 이방성 변수 ε 모델을 평활화하여 3차원 음향 역시간 구조보정을 적용한 결과이다. 볼브 유전 지역은 백악기 덮개암(노란색 화살표) 상부로는 수평층이 발달해 있어 이로 인한 강한 횡등방성(Fig. 10b)이 존재하는 지역으로, 이를 고려하지 않고 등방성 역시간 구조보정을 수행한다면, 저류층의 3차원 지질구조가 왜곡될 수 있다(Fig. 10c). 음향 타원형 이방성(식 (32)에서 $∆ S_{e} = 1$ , 즉 𝜀=𝛿)을 가정한 역시간 구조보정의 계산량은 음향 등방성 역시간 구조보정과 거의 같으므로, 가장 저렴한 계산비용으로 이방성 효과를 구현할 수 있다. Fig. 10c와 10d를 비교해보면, 이방성 역시간 구조보정을 적용함으로써 덮개암의 연속성과 분해능이 개선되고(노란색 화살표), 저류층의 돔 형태의 구조가 개선되었으며(파란색 화살표), 저류층 하부 단층의 연속성이 개선되었다(빨간색 화살표).

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F9.jpg

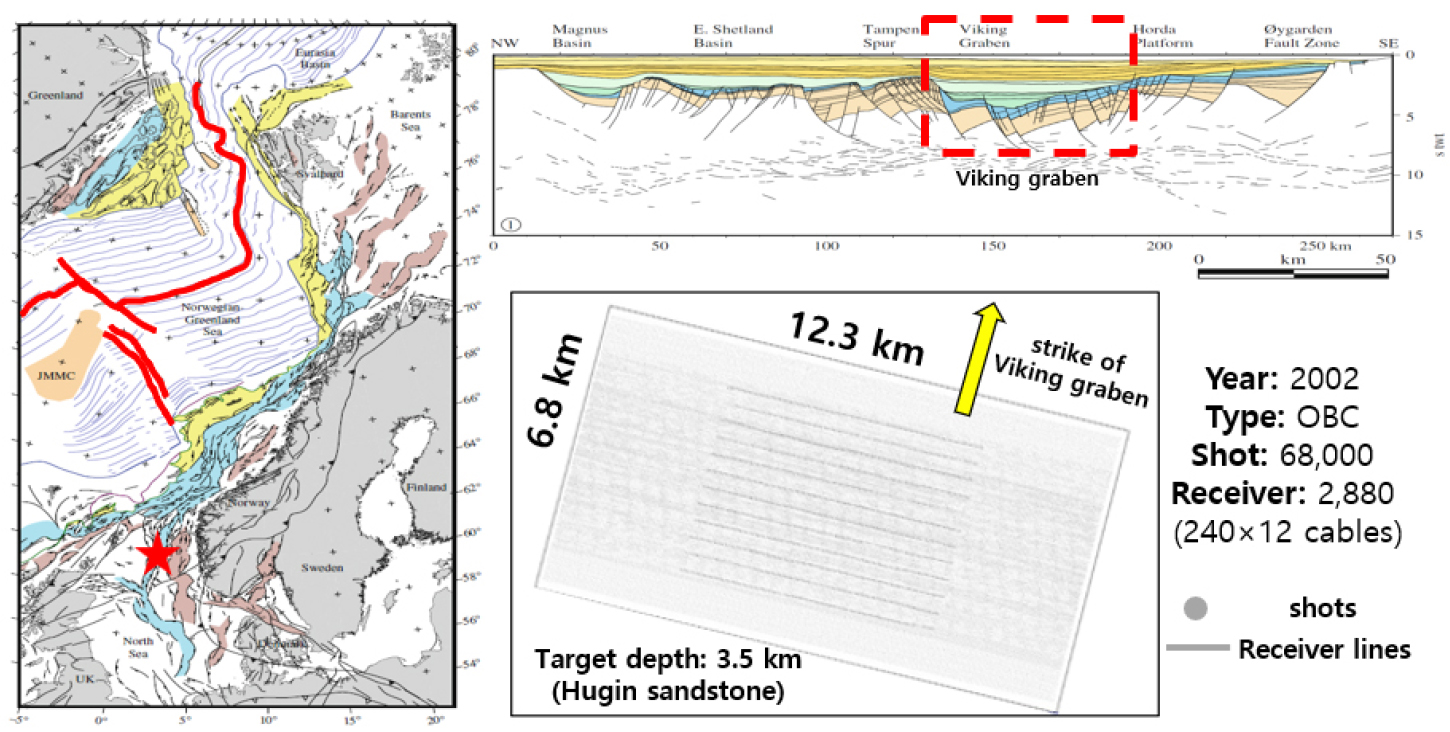
Fig. 9.

Location and geological structures of the Volve oil field in the North Sea (Faleide et al., 2010). Red lines in the left figure indicate the plate boundaries of the area. The right bottom figure shows the geometry information of 3D ocean-bottom seismic data acquired in 2002.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F10.jpg

Fig. 10.

Background model of the (a) P-wave velocity and (b) anisotropic parameter (𝜀). Reverse-time migration images using (a) isotropic acoustic modeling and (b) elliptical anisotropic acoustic modeling. The arrows indicate the area where anisotropic imaging shows better features.

결론 및 향후 전망

앞서 살펴본 것처럼 3차원 이방성 탄성파 영상화 기술은 이방성이 강한 지역에서 획득된 탐사 자료의 영상화 결과를 크게 개선시킬 수 있다. 이러한 이유로 최근 물리탐사 분야에서 이방성 영상화 기술을 개선하기 위한 다양한 모델링, 완전파형역산, 역시간 구조보정 연구가 활발하게 수행되고 있음을 살펴보았다. 이러한 가능성에도 불구하고 국내에서는 3차원 탄성파 탐사를 위한 기반이 부족하였기 때문에, 2차원을 가정한 영상화 연구나 해외자료를 이용한 3차원 탄성파 영상화 연구가 주로 수행되어 왔다.

하지만 최근 국내에서도 고품질의 3차원 탄성파 탐사자료 획득에 대한 기대감이 높아지고 있다. 한국지질자원연구원이 3차원/4차원 해양 탄성파 탐사선(가칭 탐해 3호)을 건조 중이고, 2022년 육상 탄성파 탐사 송신원인 3만 파운드급 바이브로사이즈(GIN30)를 도입하는 등 국내 탄성파 탐사 여건이 크게 개선되고 있다(Fig. 11). 이러한 분위기에 발맞추어 국내에서 획득할 3차원 탄성파 탐사자료에 대한 신뢰성 있는 3차원 탄성파 영상화 기술 확보가 시급하다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590211/images/ksmer_59_02_11_F11.jpg

Fig. 11.

3D/4D seismic survey vessel, Tamhae III (left), and the 30,000 pound-level vibroseis, GIN30 (right), in Korea Institute of Geoscience and Mineral Resources (KIGAM), South Korea (Courtesy of KIGAM).

국내 3차원 탄성파 탐사자료 확보가 제한적인 상황에서도 전북대학교 지질·지구물리연구실은 해외 대학과의 공동연구를 통하여 이를 극복하고, 세계적인 수준의 3차원 이방성 탄성파 영상화 기술을 개발해오고 있다. 이를 기반으로 국내 3차원 이방성 탄성파 영상화 분야의 연구를 선도하고 있으며, 보다 개선된 3차원 탄성파 영상화 기술을 확보하기 위하여 현재에도 해외 대학과 활발하게 공동연구가 진행 중이다. 사우디아라비아의 King Abdullah University of Science and Techonology(KAUST)와 3차원 병렬 이방성 영상화 기술 개발, 캐나다 University of Calgary의 CREWES 팀과 3차원/4차원 육상 탄성파 탐사자료의 이방성 영상화 기술 개발, 노르웨이의 Norwegian University of Science and Technology(NTNU)와 CO₂ 모니터링을 위한 4차원 이방성 탄성파 모니터링 기술 개발, 중국 Tongji University와 해저면 탄성파 탐사 자료처리 기술 개발 연구를 수행하고 있으며, 2022년 하반기에는 Massachusetts Institute of Technology(MIT)와 격자선호 방향성에 따른 이방성 추정을 통한 상부 맨틀의 동역학적 특성 분석, Lawrence Berkeley National Laboratory(NBNL)와 지열 개발 부지의 이방성 영상화 연구를 수행할 예정이다. 3차원 이방성 탄성파 영상화 기술을 선도하는 해외 대학과의 활발한 공동연구를 통하여, 빠른 시일 내에 보다 완성도 있는 3차원 이방성 탄성파 영상화 기술을 확보할 수 있을 것으로 예상된다.

하지만 대형 석유기업이 획득한 해외 탐사자료는 자료의 양과 품질 면에서 이미 상당 부분 검증된 자료이다. 앞으로 국내에서 수행될 이산화탄소 지중저장 프로젝트나 핵폐기물 저장소 탐사 등에 적용하기 위해서는 국내 지질 특성과 탐사 여건을 고려하여 3차원 탄성파 영상화 기술의 현장 적용성을 꾸준히 개선해야 한다. 국내 고유의 3차원 이방성 탄성파 영상화 기술을 탐해 3호와 GIN30이 획득할 국내 3차원/4차원 탄성파 탐사자료의 영상화에 활용할 수 있는 날이 오기를 기대한다.

Acknowledgements

본 연구는 2021년 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20212010200020). 볼브 유전 지역의 3차원 탄성파 탐사자료를 제공해주신 Equinor에 감사드립니다. 논문을 꼼꼼하게 검토해주신 심사위원 분들과 자료 정리에 도움을 준 전북대학교 지질·지구물리연구실 김석한, 노희찬 학생에게도 감사의 말씀을 전합니다.

References

Alkhalifah, T. and Plessix, R.É., 2014. A recipe for practical full-waveform inversion in anisotropic media: An analytical parameter resolution study, Geophysics, 79(3), p.R91-R101. 10.1190/geo2013-0366.1

Alkhalifah, T., 2000. An acoustic wave equation for anisotropic media, Geophysics, 65(4), p.1239-1250. 10.1190/1.1444815

Auld, B., 1973. Acoustic fields and waves in solids: Wiley- Interscience.

Babuska, V. and Cara, M., 1991. Seismic-wave propagation in anisotropic media. In Seismic Anisotropy in the Earth, p.5-38, Springer, Dordrecht. 10.1007/978-94-011-3600-6_2

Bansal, R. and Sen, M.K., 2008. Finite‐difference modelling of S‐wave splitting in anisotropic media, Geophysical Prospecting, 56(3), p.293-312. 10.1111/j.1365-2478.2007.00693.x

Bohlen, T., 2002. Parallel 3-D viscoelastic finite difference seismic modelling, Computers & Geosciences, 28, p.887-899. 10.1016/S0098-3004(02)00006-7

Carcione, J.M., 1992. Anisotropic Q and velocity dispersion of finely layered media1, Geophysical Prospecting, 40(7), p.761-783. 10.1111/j.1365-2478.1992.tb00551.x

Choi, H., Seol, S.J., and Byun, J., 2015. Acceleration of anisotropic elastic reverse-time migration with GPUs, Geophysics and Geophysical Exploration, 18(2), p.74-84. 10.7582/GGE.2015.18.2.074

Djebbi, R. and Alkhalifah, T., 2019. Frequency domain multiparameter acoustic inversion for transversely isotropic media with a vertical axis of symmetry, Geophysics, 84(1), p.C1-C14. 10.1190/geo2017-0564.1

Du, X., Bancroft, J.C., and Lines, L.R., 2007. Anisotropic reverse‐time migration for tilted TI media, Geophysical Prospecting, 55(6), p.853-869. 10.1111/j.1365-2478.2007.00652.x

Duveneck, E., Milcik, P., Bakker, P. M., and Perkins, C., 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration, In 78th SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, p.2186-2190. 10.1190/1.3059320

Faleide, J.I., Bjørlykke, K., and Gabrielsen, R.H., 2010. Geology of the Norwegian continental shelf, In: Petroleum Geoscience, Springer, Berlin, p.467-499. 10.1007/978-3-642-02332-3_22

Far, M.E., Sayers, C.M., Thomsen, L., Han, D.H., and Castagna, J.P., 2013. Seismic characterization of naturally fractured reservoirs using amplitude versus offset and azimuth analysis, Geophysical prospecting, 61(2-Rock Physics for Reservoir Exploration, Characterisation and Monitoring), p.427-447. 10.1111/1365-2478.12011

Fei, T. and Larner, K., 1995. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport, Geophysics, 60(6), p.1830-1842. 10.1190/1.1443915

Fletcher, R.P., Du, X., and Fowler, P.J., 2009. Reverse time migration in tilted transversely isotropic (TTI) media, Geophysics, 74(6), p.WCA179-WCA187. 10.1190/1.3269902

Gholami, Y., Brossier, R., Operto, S., Ribodetti, A., and Virieux, J., 2013a. Which parameterization is suitable for acoustic vertical transverse isotropic full waveform inversion? Part 1: Sensitivity and trade-off analysis, Geophysics, 78(2), p.R81-R105. 10.1190/geo2012-0204.1

Gholami, Y., Brossier, R., Operto, S., Prieux, V., Ribodetti, A., and Virieux, J., 2013b. Which parameterization is suitable for acoustic vertical transverse isotropic full waveform inversion? Part 2: Synthetic and real data case studies from Valhall, Geophysics, 78(2), p.R107-R124. 10.1190/geo2012-0203.1

Graves, R.W., 1996. Simulating Seismic wave propagation in 3D elastic media using staggered-grid finite differences, Bulletin of the Seismological Society of America, 86(4), p.1091-1106.

Grechka, V., Zhang, L., and Rector III, J.W., 2004. Shear waves in acoustic anisotropic media, Geophysics, 69(2), p.576-582. 10.1190/1.1707077

Ha, Y.S. and Shin, S.R., 2010. Seismic anisotropy physical modeling with vertical transversely isotropic media, Geophysics and Geophysical Exploration, 13(4), p.307-314.

Han, B., Seol, S.J., and Byun, J., 2011. Elastic modeling in 3D tilted transversely isotropic (TTI) media with convolutional perfectly matched layer (CPML) boundary conditions, In 81st SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, p.3037-3041. 10.1190/1.3627826

Han, B., Seol, S.J., and Byun, J., 2012. Elastic modelling in tilted transversely isotropic media with convolutional perfectly matched layer boundary conditions, Exploration Geophysics, 43(2), p.77-86. 10.1071/EG12015

He, W. and Plessix, R.É., 2017. Analysis of different parameterisations of waveform inversion of compressional body waves in an elastic transverse isotropic earth with a vertical axis of symmetry, Geophysical Prospecting, 65(4), p.1004-1024. 10.1111/1365-2478.12452

Huang, T., Zhang, Y., Zhang, H., and Young, J., 2009. Subsalt imaging using TTI reverse time migration, The Leading Edge, 28(4), p.448-452. 10.1190/1.3112763

Igel, H., Mora, P., and Riollet, B., 1995. Anisotropic wave propagation through finite-difference grids, Geophysics, 60(4), p.1203-1216. 10.1190/1.1443849

Ikelle, L.T. and Amundsen, L., 2005. Introduction to petroleum seismology: Investigations in Geophysics, Society of Exploration Geophysics, Tulsa, OK. 10.1190/1.9781560801702

Ivanov, Y. and Stovas, A., 2016. Upscaling in orthorhombic media: Behavior of elastic parameters in heterogeneous fractured earth, Geophysics, 81(3), p.C113-C126. 10.1190/geo2015-0392.1

Jeong, C.H. and Suh, J.H., 2007. Seismic traveltime tomography in inhomogeneous tilted transversely isotropic media, Geophysics and Geophysical Exploration, 10(4), p.229-240.

Joo, Y. and Kim, B.Y., 2020. Data processing using anisotropic analysis for the long-offset marine seismic data of the East Sea, Korea, Geophysics and Geophysical Exploration, 23(1), p.13-21.

Kamath, N. and Tsvankin, I., 2016. Elastic full-waveform inversion for VTI media: Methodology and sensitivity analysis, Geophysics, 81(2), p.C53-C68. 10.1190/geo2014-0586.1

Kang, J.S., Cha, Y.H., Lee, K.B., and Jo, C.H., 2007. Seismic traveltime tomography in anisotropic black shale, Geophysics and Geophysical Exploration, 10(4), p.393-398.

Kazei, V. and Alkhalifah, T., 2018. Waveform inversion for orthorhombic anisotropy with P waves: Feasibility and resolution, Geophysical Journal International, 213(2), p.963-982. 10.1093/gji/ggy034

Kim, D., Hwang, J., Min, D.J., Oh, J.W., and Alkhalifah, T., 2022. Two-step full waveform inversion of diving and reflected waves with the diffraction-angle-filtering-based scale-separation technique, Geophysical Journal International, 229(2), p.880-897. 10.1093/gji/ggab522

Kim, W.K. and Min, D.J., 2014. A new parameterization for frequency-domain elastic full waveform inversion for VTI media, Journal of Applied Geophysics, 109, p.88-110. 10.1016/j.jappgeo.2014.07.015

Kim, Y., Cho, Y., Jang, U., and Shin, C., 2013. Acceleration of stable TTI P-wave reverse-time migration with GPUs, Computers & Geosciences, 52, p.204-217. 10.1016/j.cageo.2012.10.013

Köhn, D., Hellwig, O., De Nil, D., and Rabbel, W., 2015. Waveform inversion in triclinic anisotropic media-A resolution study, Geophysical Journal International, 201(3), p.1642-1656. 10.1093/gji/ggv097

Kwak, N.E., Min, D.J., and Bae, H.S., 2011. Reverse-time migration for VTI and TTI media, Geophysics and Geophysical Exploration, 14(3), p.191-202.

Lee, H.Y., Koo, J.M., Min, D.J., Kwon, B.D., and Yoo, H.S., 2010. Frequency-domain elastic full waveform inversion for VTI media, Geophysical Journal International, 183(2), p.884-904. 10.1111/j.1365-246X.2010.04767.x

Lee, H.Y., Koo, N.H., Kim, B.Y., Kang, M., and Park, K.P., 2019. Status of marine seismic exploration technology, Journal of the Korean Society of Mineral and Energy Resources Engineers, 56(1), p.86-106 (in Korean with English abstract). 10.32390/ksmer.2019.56.1.086

Lee, H.Y., Min, D.J., Kwoon, B.D., Lim, S.C., and Yoo, H.S., 2008. Boundary conditions for Time-Domain Finite-Difference Elastic Wave Modeling in Anisotropic Media, Geophysics and Geophysical Exploration, 11(2), p.153-160.

Li, Y. and Alkhalifah, T., 2020. Multi‐parameter reflection waveform inversion for acoustic transversely isotropic media with a vertical symmetry axis, Geophysical Prospecting, 68(6), p.1878-1892. 10.1111/1365-2478.12966

Li, Y., Han, W., Chen, C. S., and Huang, T., 2012. Velocity model building for tilted orthorhombic depth imaging, In 82nd SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, p.1-5. 10.1190/segam2012-1231.1

Masmoudi, N. and Alkhalifah, T., 2018. Full-waveform inversion in acoustic orthorhombic media and application to a North Sea data set Orthorhombic model inversion, Geophysics, 83(5), p.C179-C193. 10.1190/geo2017-0738.1

Oh, J.W. and Alkhalifah, T., 2016a. The scattering potential of partial derivative wavefields in 3-D elastic orthorhombic media: an inversion prospective, Geophysical Journal International, 206(3), p.1740-1760. 10.1093/gji/ggw238

Oh, J.W. and Alkhalifah, T., 2016b. Elastic orthorhombic anisotropic parameter inversion: An analysis of parameterization, Geophysics, 81(6), p.C279-C293. 10.1190/geo2015-0656.1

Oh, J.W. and Alkhalifah, T., 2018a. Optimal full-waveform inversion strategy for marine data in azimuthally rotated elastic orthorhombic media, Geophysics, 83(4), p.R307-R320. 10.1190/geo2017-0762.1

Oh, J.W. and Alkhalifah, T., 2018b. Full waveform inversion using envelope-based global correlation norm, Geophysical Journal International, 213(2), p.815-823. 10.1093/gji/ggy031

Oh, J.W. and Alkhalifah, T., 2019. Study on the full‐waveform inversion strategy for 3D elastic orthorhombic anisotropic media: Application to ocean bottom cable data, Geophysical Prospecting, 67(5), p.1219-1242. 10.1111/1365-2478.12768

Oh, J.W. and Min, D.J., 2014. A new parameterisation with poissons ratio for multi-parametric FWI in isotropic elastic media, In 76th EAGE Conference and Exhibition 2014 (Vol. 2014, No. 1, pp. 1-5). European Association of Geoscientists & Engineers. 10.3997/2214-4609.20141412

Oh, J.W., 2020. Parallel elastic wave modeling considering the effects of orthorhombic anisotropy, Journal of the Korean Society of Mineral and Energy Resources Engineers, 57(1), p.86-96 (in Korean with English abstract). 10.32390/ksmer.2020.57.1.086

Oh, J.W., Cheng, J., and Min, D.J., 2021. Diffraction-angle filtering of gradient for acoustic full-waveform inversion, Geophysics, 86(2), p.R173-R185. 10.1190/geo2019-0801.1

Oh, J.W., Kalita, M., and Alkhalifah, T., 2018. 3D elastic full-waveform inversion using P-wave excitation amplitude: Application to ocean bottom cable field data, Geophysics, 83(2), p.R129-R140. 10.1190/geo2017-0236.1

Oh, J.W., Kim, D.S., and Kim, W.K., 2022. A study on parallel 3D elastic wave modeling using flux-corrected transport, Journal of the Korean Society of Mineral and Energy Resources Engineers, 59(1), p.42-58 (in Korean with English abstract). 10.32390/ksmer.2022.59.1.042

Oh, J.W., Shin, Y., Alkhalifah, T., and Min, D.J., 2020. Multistage elastic full-waveform inversion for tilted transverse isotropic media, Geophysical Journal International, 223(1), p.57-76. 10.1093/gji/ggaa295

Operto, S., Brossier, R., Combe, L., Métivier, L., Ribodetti, A., and Virieux, J., 2014. Computationally efficient three- dimensional acoustic finite-difference frequency-domain seismic modeling in vertical transversely isotropic media with sparse direct solver, Geophysics, 79(5), p.T257-T275. 10.1190/geo2013-0478.1

Operto, S., Gholami, Y., Prieux, V., Ribdetti, A., Brossier, R., Métivier, L., and Virieux, J., 2013. A guided tour of multiparameter full-waveform inversion with multicomponent data: From theory to practice, The Leading Edge, 32, p.1040-1054. 10.1190/tle32091040.1

Operto, S., Virieux, J., Ribodetti, A., and Anderson, J.E., 2009. Finite-difference frequency-domain modeling of viscoacoustic wave propagation in 2D tilted transversely isotropic (TTI) media, Geophysics, 74(5), p.T75-T95. 10.1190/1.3157243

Owusu, J.C., Podgornova, O., Charara, M., Leaney, S., Campbell, A., Ali, S., Borodin, I., Nutt, L., and Menkiti, H., 2016. Anisotropic elastic full‐waveform inversion of walkaway vertical seismic profiling data from the Arabian Gulf, Geophysical Prospecting, 64(1), p.38-53. 10.1111/1365-2478.12227

Pan, W., Innanen, K.A., Margrave, G.F., Fehler, M.C., Fang, X., and Li, J., 2016. Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion, Geophysics, 81(5), p.R275-R291. 10.1190/geo2015-0594.1

Podgornova, O., Leaney, S., and Liang, L., 2015. Analysis of resolution limits of VTI anisotropy with full waveform inversion, In 85th SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, p.1188-1192. 10.1190/segam2015-5876311.1

Randall, C.J., 1988. Absorbing boundary condition for the elastic wave equation, Geophysics, 53(5), p.611-624. 10.1190/1.1442496

Shin, S., Kim, D., Jeong, S., Lee, D., and Chung, W., 2021. Recent research trend analysis in geophysical exploration focused on seismic exploration, Journal of the Korean Society of Mineral and Energy Resources Engineers, 58(5), p.444-463 (in Korean with English abstract). 10.32390/ksmer.2021.58.5.444

Shin, Y., Oh, J.W., Min, D.J., and Hwang, J., 2021a. Pseudo- acoustic anisotropic reverse-time migration of an ocean-bottom cable dataset acquired in the North Sea, Exploration Geophysics, 52(5), p.551-562. 10.1080/08123985.2020.1852877

Shin, Y., Oh, J.W., and Min, D.J., 2021b. An efficient multiparameter acoustic anisotropic full-waveform inversion depending on parameterization, Acta Geophysica, 69(4), p.1257-1267. 10.1007/s11600-021-00609-2

Shin, Y., Oh, J.W., Kim, S., and Min, D.J., 2019. Mono- component multiparameter acoustic full waveform inversion in vertically transverse isotropic media using converted vector wavefields, Journal of Applied Geophysics, 170, p.103816. 10.1016/j.jappgeo.2019.07.010

Singh, S. and Tsvankin, I., 2022. Sensitivity analysis of elastic full-waveform inversion for orthorhombic media, Journal of Seismic Exploration, 31, p.105-130.

Song, X. and Alkhalifah, T., 2013. Modeling of pseudoacoustic P-waves in orthorhombic media with a low-rank approximation, Geophysics, 78(4), p.C33-C40. 10.1190/geo2012-0144.1

Stovas, A., 2021. On parameterization in monoclinic media with a horizontal symmetry plane, Geophysics, 86(1), p.C37-C49. 10.1190/geo2020-0301.1

Tarantola, A., 1986. A strategy for nonlinear elastic inversion of seismic reflection data, Geophysics, 51(10), p.1893-1903. 10.1190/1.1442046

Thomsen, L., 1986. Weak elastic anisotropy, Geophysics, 51(10), p.1954-1966. 10.1190/1.1442051

Tsvankin, I., 1997. Anisotropic parameters and P-wave velocity for orthorhombic media, Geophysics, 62(4), p.1292-1309. 10.1190/1.1444231

Virieux, J. and Operto, S., 2009. An overview of full-waveform inversion in exploration geophysics, Geophysics, 74(6), p.WCC1-WCC26. 10.1190/1.3238367

Wang, J., Li, Z., and Steve, T., 2014. 3D elastic simulation with flux correction transport (FCT) for general anisotropic media, In 84th SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, p.3498-3502. 10.1190/segam2014-0571.1PMC4097234

Wang, J., Meng, X., and Zheng, W., 2017. Elastic-wave-mode separation in TTI media with inverse-distance weighted interpolation involving position shading, Journal of Geophysics and Engineering, 14(5), p.1260-1267. 10.1088/1742-2140/aa7bd1

Weiss, R.M. and Shragge, J., 2013. Solving 3D anisotropic elastic wave equations on parallel GPU devices, Geophysics, 78(2), p.F7-F15. 10.1190/geo2012-0063.1

Wu, Z. and Alkhalifah, T., 2016. Waveform inversion for acoustic VTI media in frequency domain, In SEG Technical Program Expanded Abstracts 2016, p.1184-1189, Society of Exploration Geophysicists. 10.1190/segam2016-13867221.126814890PMC6274342

Xu, S. and Zhou, H., 2014. Accurate simulations of pure quasi-P-waves in complex anisotropic media, Geophysics, 79(6), p.T341-T348. 10.1190/geo2014-0242.1

Xu, S., Tang, B., Mu, J., and Zhou, H. 2015. Elliptic decomposition of quasi-P wave equation, In 77th EAGE Conference and Exhibition incorporating SPE EUROPEC 2015, European Association of Geoscientists & Engineers. p.1-5 10.3997/2214-4609.201413134

Yan, J. and Sava, P., 2009. Elastic wave-mode separation for VTI media, Geophysics, 74(5), p.WB19-WB32. 10.1190/1.3184014

Yan, J. and Sava, P., 2011. Improving the efficiency of elastic wave-mode separation for heterogeneous tilted transverse isotropic media, Geophysics, 76(4), p.T65-T78. 10.1190/1.3581360

Yang, J., Zhang, H., Zhao, Y., and Zhu, H., 2019. Elastic wavefield separation in anisotropic media based on eigenform analysis and its application in reverse-time migration, Geophysical Journal International, 217(2), p.1290-1313. 10.1093/gji/ggz085

Zhang, H. and Zhang, Y., 2008. Reverse time migration in 3D heterogeneous TTI media, In SEG Technical Program Expanded Abstracts 2008, p.2196-2200, Society of Exploration Geophysicists. 10.1190/1.305932219166005

Zhang, H. and Zhang, Y., 2011. Reverse time migration in vertical and tilted orthorhombic media, In SEG Technical Program Expanded Abstracts 2011, p.185-189, Society of Exploration Geophysicists. 10.1190/1.3627568

Zhang, Y., Zhang, H., and Zhang, G., 2011. A stable TTI reverse time migration and its implementation, Geophysics, 76(3), p.WA3-WA11. 10.1190/1.3554411

Zhang, Z.D., Alkhalifah, T., and Wu, Z., 2019. A hybrid finite-difference/low-rank solution to anisotropy acoustic wave equations, Geophysics, 84(2), p.T83-T91. 10.1190/geo2018-0333.1

Zhou, H.W., Hu, H., Zou, Z., Wo, Y., and Youn, O., 2018. Reverse time migration: A prospect of seismic imaging methodology, Earth-science reviews, 179, p.207-227. 10.1016/j.earscirev.2018.02.008

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Review of 3D Anisotropic Seismic Imaging Technology

ABSTRACT

MAIN

Fig. 1.

Vertical resolution (related to blue lines) and horizontal resolution (related to red circles) of seismic waves causing seismic anisotropy in VTI, HTI, and orthorhombic models (Ikelle and Amundsen, 2005; Oh, 2020).

Fig. 2.

Comparison of TTI, T-ORT, and monoclinic media (Modified from Li et al., 2012).

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

Fig. 3.

P-P and P-SV reflection radiation patterns of elastic orthorhombic parameters (modified from Oh and Alkhalifah, 2019). The angles outside circles indicate the reflection angle (or the opening angle) satisfying the Snell’s law from a horizontal reflector.

Fig. 4.

Fig. 5.

Snapshot examples of wave propagations in different anisotropic media. Note that we require more parameters to simulate a more accurate anisotropic model.

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

Fig. 6.

Fig. 7.

Radiation patterns of the partial derivative fields from the model parameter perturbations with two different parameterizations (modified from Operto et al., 2013). Red and yellow stars indicate the seismic sources and virtual sources, respectively.

Fig. 8.

Reflection patterns of partial derivative wavefields using six different parameterizations in acoustic VTI full-waveform inversion (Gholami et al., 2013a).

(38)

Fig. 9.

Location and geological structures of the Volve oil field in the North Sea (Faleide et al., 2010). Red lines in the left figure indicate the plate boundaries of the area. The right bottom figure shows the geometry information of 3D ocean-bottom seismic data acquired in 2002.

Fig. 10.

Background model of the (a) P-wave velocity and (b) anisotropic parameter (𝜀). Reverse-time migration images using (a) isotropic acoustic modeling and (b) elliptical anisotropic acoustic modeling. The arrows indicate the area where anisotropic imaging shows better features.

Fig. 11.

3D/4D seismic survey vessel, Tamhae III (left), and the 30,000 pound-level vibroseis, GIN30 (right), in Korea Institute of Geoscience and Mineral Resources (KIGAM), South Korea (Courtesy of KIGAM).

Acknowledgements

References