서 론
연구방법
다목적 문제로서의 CCS 통합 시스템 설계
파레토 최적(Pareto-optimality)
다목적 최적화 알고리듬
연구결과
CCS 통합 시스템의 다목적 최적화 설정
CCS 통합 시스템의 다목적 최적화 결과
제약조건이 없는 다목적 최적화 결과
결 론
서 론
CCS(carbon capture and storage)는 2050년까지의 탄소 중립 목표를 달성하기 위해 필수적인 기술로 인정받고 있으며, 여러 국가가 이에 대한 정책적 지원과 투자를 확대하고 있다(IEA, 2024). CCS는 배출원에서 CO2를 포집하고 압축한 후 주로 수송관을 통해 고밀도 액체(dense liquid) 또는 초임계(supercritical) 상(phase)으로 운반한 뒤 주입정을 통해 저장층(geological reservoir)에 CO2를 주입하고 저장하는 기술로 정의된다(Middleton and Bielicki, 2009). 대부분의 CO2 지중저장 후보지는 CO2 포집원으로부터 수십에서 수백 km 떨어져 있는 경우가 많다. 해상 CCS의 경우 액화 CO2 운반선을 통해 저장지까지 수송하기도 하지만(Hwang et al., 2023), 지속적인 CO2 주입을 위한 가장 일반적이고 경제적인 수송 방법은 수송관을 활용하는 것이다.
CO2 지중저장 프로젝트는 수송에서부터 저장까지의 전체 시스템을 크게 4단계로 구분할 수 있다. 육상 허브 터미널에서 CO2를 송출하는 단계(송출 단계), 송출된 CO2를 수송하는 단계(수송 단계), 수송된 CO2를 주입하는 단계(주입 단계), 주입된 CO2를 지하 저장층에 저장하는 단계(저장 단계)이다. 육상 허브 터미널의 압축 및 처리 상태는 수송관의 규격과 압력 조건에 직접적인 영향을 미치며, 수송관 내 CO2 유량과 압력은 주입정 주입량과 압력에 영향을 끼친다. 주입정의 규격과 운영조건은 저장층 내 압력 변화와 CO2 분포에 영향을 미치며, 저장층의 동적 특성 변화 또한 주입정과 수송관, 허브 터미널 운영 등 설비에 영향을 끼치는 상호작용을 한다.
따라서 전체 CCS 시스템의 최적 설계를 위해서는 수송, 주입, 저장 전 과정의 통합 모델링에 기반한 분석이 필수이다. 각 단계는 개별적으로 분석하고 최적화할 수 있으나, 그 결과는 전체 시스템의 최적화와 상충될 수 있다(Shokrlu et al., 2020). 전통적으로는 단계별로 다른 도구를 사용하여 모델링하고 분석한 후 명시적 결합(explicit coupling)을 통해 전체 시스템을 분석해왔다(Inoue and Fontoura, 2009; Vissers et al., 2012; Sierra et al., 2015). 하지만 이러한 방식은 단계 간 상호작용을 해석하는 데에 한계가 있을 뿐만 아니라, 시간 흐름에 따른 압력, 유량, 온도의 변화를 모사하는 데에 어려움이 있다(Pathak et al., 2017, 2019). 한 단계를 개별적으로 분석하는 경우, 이전 단계와 이후 단계에 대해 고정된 값을 입력하기 때문이다. 예를 들어 주입정 내 특정 노드(node)에서의 유체 거동을 분석할 때 주입성(injectivity) 및 저장과 관련된 정보는 IPR(inflow performance relationship)과 OPR(outflow performance relationship)의 표와 그래프 형태로 입출력할 수 있다. 다만 시간에 따른 시스템 간의 변화를 모사하기 위해서는 사용자가 계속해서 입력값을 변경해야 하기에 시간 간격에 따른 불연속성이 발생한다. 따라서 전체 시스템으로써 분석해야 지상 설비와 지하 저장층 간 압력에 따른 영향을 현실적이고 연속적으로 고려할 수 있어 전반적인 설계 및 운영의 효율성과 안전성을 높일 수 있다(Dudek et al., 2019; Abdellatif et al., 2023).
CO2 수송-주입-저장 통합 시스템 설계 문제에서, 지질학적 불확실성 및 운영조건의 변동 등 고려해야 하는 모든 변수를 동시에 만족시키는 단일 해를 도출하는 것은 현실적으로 불가능에 가깝다. 특히, CO2 지중저장 프로젝트는 CO2 저장량뿐만 아니라 지질학적 안전성과 프로젝트의 비용 등 세 가지 측면을 함께 고려해야 하므로 다목적 문제로 간주할 수 있다. 세 가지 측면이 상호 연관되어 있으므로 한 측면을 개선할 때 다른 측면들은 약화될 수 있기 때문이다. 따라서 다수의 목적함수를 더 이상 동시에 개선할 수 없는, 즉 목적함수 간 최적의 상충관계(trade-off)를 보이는 등가의 우수해를 다수 도출함으로써 시스템 설계를 위한 의사결정을 지원하는 다목적 최적화를 수행할 필요가 있다.
다목적 최적화는 다수의 목적함수가 상충관계에 있어 더 이상 개선할 수 없는 파레토 최적해의 집합인 파레토 최적면을 탐색하는 것을 목표로 한다(Deb et al., 2002). 다차원 파레토 최적면을 탐색하는 것은 실현 가능한 해 전체 영역에서 서로 비지배 관계(상충관계)에 있는 등가의 우수해, 즉 파레토 최적해들을 찾는 것을 의미한다. 만약 다수의 목적함수를 가중합한 단일 광역 목적함수로 최소화 또는 최대화하는 광역 최적화(global optimization)에 적용하는 경우, 단일 광역 최적해(global optimum)를 향하여 해들이 수렴하기 때문에 가중치에 따라 일부 목적함수에 편향된 최적해가 도출되는 한계가 있다(Min et al., 2014, 2015). 광역 최적화에 비해 다목적 최적화는 파레토 최적면을 구성하는 다수의 파레토 최적해를 제공하여 의사결정 과정에서 특정 사례로 치우치는 편향을 방지할 수 있기 때문에 다기준 의사결정 문제를 푸는 데 있어 효과적이다(Min et al., 2015). 따라서 다목적 최적화 알고리듬은 파레토 최적면으로의 해의 수렴성과 파레토 최적면 내 해의 다양성을 동시에 만족시켜야 한다(Schulze-Riegert et al., 2007; Min et al., 2014, 2016; Kam et al., 2017; Park et al., 2021). 다양한 공학 문제에 적용한 결과, 다목적 최적화는 두 개에서 세 개의 목적함수를 가지는 다목적 문제에서 목적함수 공간의 차원과 해집합 크기(예: 모집단 크기)를 균형 있게 조정하여 파레토 최적면을 탐색하는 데 있어 만족스러운 성능을 보여왔다(Sinha et al., 2013). 이러한 장점을 활용하여 다목적 최적화는 미국 Cranfield에서 CO2 주입 펄스 실험(pulse testing)의 히스토리 매칭(Min et al., 2018), CCUS(carbon capture, utilization, and storage) 공급망 설계(Zhang et al., 2020), 저류층 불확실성을 고려한 대염수층 CO2 지중저장(Park et al., 2021) 등 여러 CCS 연구에 활용됐다. 그러나 기존 연구들은 CO2 주입 조건을 공저(bottomhole)에서부터 설정하여 저장층 내 CO2 유동을 분석하는 저류공학(reservoir engineering) 관점에서 실시되어 왔기 때문에, CO2 송출 지점에서부터 주입정 상단(wellhead)까지에서의 압력 변화를 현실적으로 고려하지 못한 한계가 있다. 또한, 기존 연구들은 지상 설비와 그에 따른 설비 비용을 고려하지 않았다는 한계가 있다.
본 연구는 CO2 송출 및 수송을 위한 지상 설비와 지중저장층을 연계한 통합 모델링을 통해 FEED(front-end engineering design)의 기초가 될 설비 인자와 운영조건의 최적해를 도출하는 방법론을 제시하는 것을 목표로 한다. 본 연구에서는 통합 CCS 모델에 다목적 최적화를 적용하여 통합 시스템 디자인의 실현 가능성(feasibility)을 분석하고 CO2 지중저장 통합 시스템의 기초 설계 단계에서 참고할 수 있는 최적의 설비인자 및 운영조건 조합을 제공하고자 한다. 본 논문은 다음과 같이 구성하였다. 먼저, 다목적 최적화와 이 연구에서 활용한 알고리듬을 소개한다. 그 후, 최적화 대상인 CO2 수송-주입-저장 통합 모델과 다목적 문제를 설명하고, 대염수층 사례에 적용한 최적화 결과를 분석한다. 마지막으로, 연구 결과를 바탕으로 결론을 도출한다.
연구방법
본 연구에서 제안하는 다목적 최적화 기반의 CCS 설비 및 운영 인자 선정 방법론은 다음과 같다. 우선, 포집된 CO2를 저장 및 송출하는 육상 허브 터미널, CO2를 수송하는 해저 수송관, CO2를 주입하는 주입정, 주입 및 저장 대상 지층을 전체 통합 시스템으로써 모델링한다. 이후 선정한 결정변수와 각 결정 변수별 범위를 기반으로 세 가지 목적함수에 대한 다목적 최적화를 진행하여 파레토 최적면을 도출한다. 파레토 최적면을 구성하는 파레토 최적해의 결정변수 분포를 분석함으로써 안정적이고 효율적인 운영을 위한 설비 및 운영 인자의 범위를 도출한다.
다목적 문제로서의 CCS 통합 시스템 설계
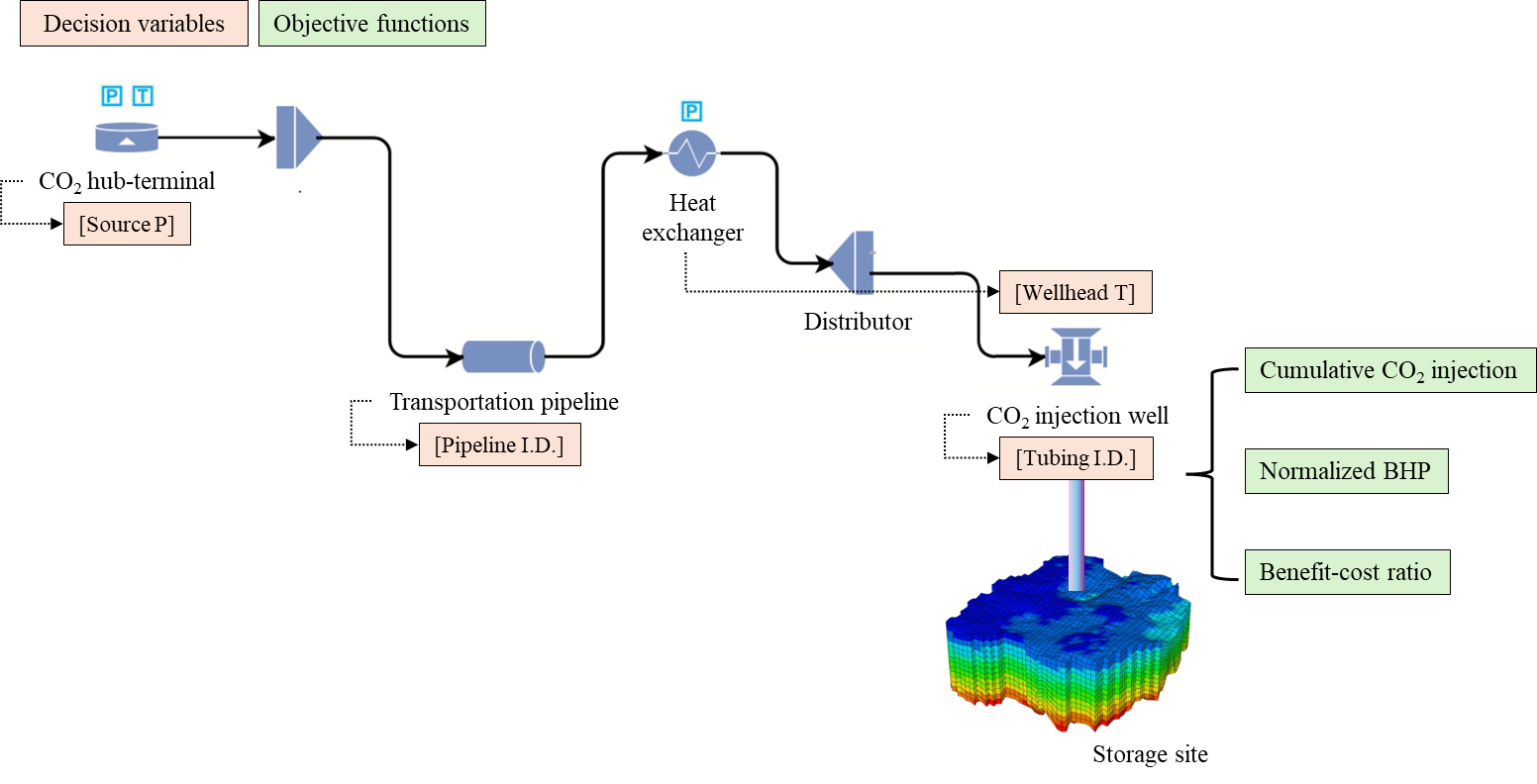
Fig. 1은 CCS 통합 시스템의 개념도이며, 본 연구에서 고려한 결정변수(decision variables)와 목적함수(objective functions)를 함께 표기하였다. 식 (1)은 개의 결정변수를 가진 목적 최적화 문제를 일반화하여 나타낸다.
이때, 는 목적함수들의 집합을, x는 결정변수들의 집합을 나타낸다.
본 연구의 CCS 통합 시스템 설계는 식 (2)와 같이 =4, =3인 다목적 최적화 문제로 설정할 수 있다.
이때, 4개의 결정변수 은 각각 ‘육상 허브 터미널에서의 CO2 송출 압력(discharge pressure; Source P)’, ‘수송관 내경(pipeline inner diameter; Pipeline I.D.)’, ‘주입정 튜빙 내경(tubing inner diameter; Tubing I.D.)’, ‘주입정 상단에서의 CO2 온도(Wellhead T)’이며, 3개의 목적함수 , , 은 각각 CO2 저장이 종료된 시점에서의 누적 CO2 주입량(cumulative CO2 injection), 저장층 최대 주입 허용 압력 대비 주입정 최대 공저압(normalized maximum bottomhole pressure; Normalized maximum BHP), 편익비용비(benefit-cost ratio; BCR)이다. 누적 CO2 주입량은 질량 단위 CO2 톤으로 계산하며, 저장층 최대 주입 허용 압력 대비 주입정 최대 공저압과 편익비용비는 각각 식 (3) 및 식 (4)로 계산한다. 는 시점 에서의 공저압을 의미하고, 은 저장층의 최대 주입 허용 압력(maximum allowable pressure)을 의미한다. BCR에서 는 기간 내 순현금흐름(net cash flow at time period), 은 연간 할인율(annual discount rate)을 의미한다.
본 연구는 탄소 저감을 위해 를 최대화, 주입된 CO2의 누출 방지 등 안전성을 위해 를 최소화, 경제성을 위해 BCR을 최대화하는 방향으로 파레토 최적면을 탐색한다.
파레토 최적(Pareto-optimality)
수학적으로 파레토 최적은 최상의 비지배 상태를 의미한다(Deb et al., 2002). 즉, 임의의 목적함수가 더 개선되기 위해서는 다른 목적함수들이 악화될 수밖에 없는 상충관계를 보이는 최적의 등가 상태이다(Srinivas and Deb, 1994). 이러한 최적의 상충관계를 보이는 최선의 비지배 해들의 집합을 파레토 최적면이라고 한다. 예를 들어, 다목적 최소화 문제에서 해 x1이 x2를 지배한다(즉, 해 x1이 해 x2보다 우월하다)라고 말할 수 있는 경우는 오직 식 (5)의 비지배 관계가 만족될 때이다. 즉, 모든 목적함수에 대해 해 x1의 목적함수 값이 해 x2의 목적함수 값보다 작거나 같으면서, 최소한 한 개 이상의 목적함수에 대해서는 해 x1의 목적함수 값이 해 x2의 목적함수 값보다 작음으로써 우월성을 확보하는 경우이다.
이때, 와 는 각각 임의의 번째와 번째 목적함수 값을 의미한다.
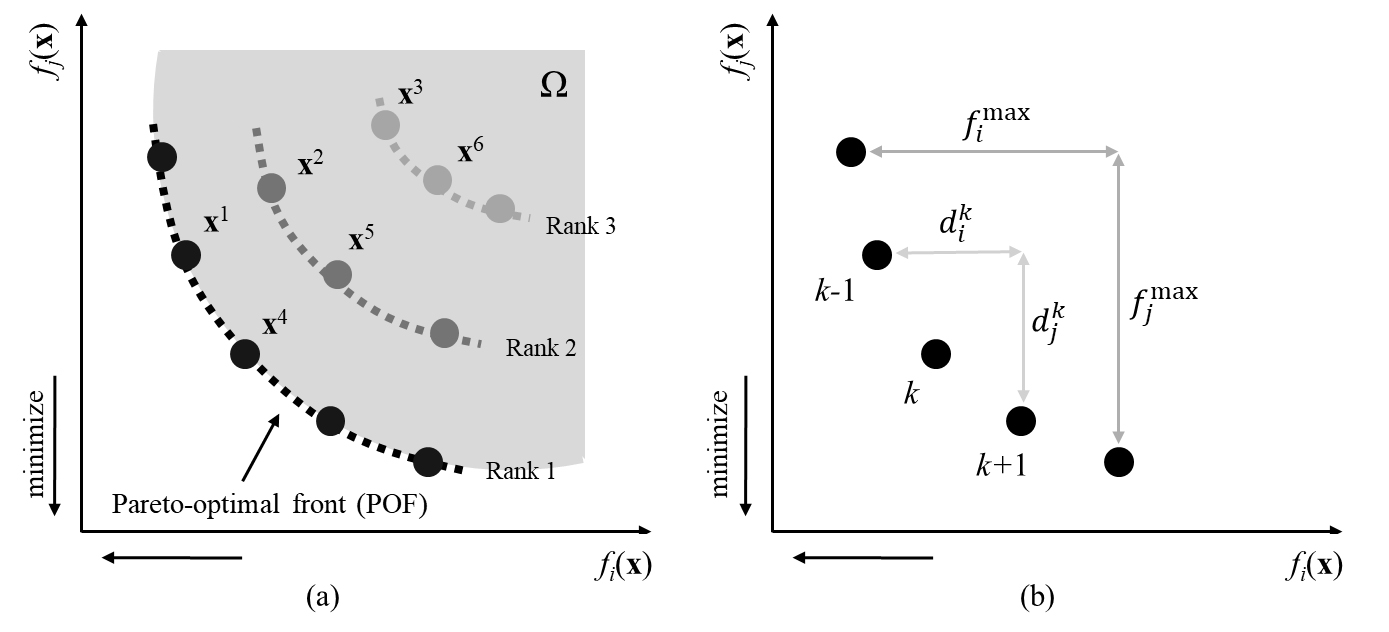
Fig. 2에 나타내듯이 다목적 최적화 알고리듬에서 해들간 우열 결정(sorting) 및 우수해 선택(selection)은 비지배 정렬(non-dominated sorting)과 밀집도 거리 정렬(crowding-distance sorting)에 기반한다. 비지배 정렬은 파레토 최적면으로의 수렴을 위하여, 밀집도 거리 정렬은 파레토 최적해 간 다양성 확보를 위하여 사용한다. 우수 해의 결정과 선택 과정을 순차적으로 표현하면 다음과 같다. 첫째, 비지배 계층 순위(rank)에 따라 해들을 정렬한다(Fig. 2(a)). 둘째, 같은 계층 내에서는 밀집도 거리가 큰 순서대로 정렬한다(Fig. 2(b)). 셋째, 비지배 계층 순위와 밀집도 거리 순위에 따라 모집단 크기만큼의 최상위 해들을 선택하여 다음 세대의 부모 해(parent solutions)로 전달한다. 상기 과정은 다목적 최적화 알고리듬의 각 세대마다 반복되며, 세대를 거듭하는 진화 과정을 통해 다목적 최적화 문제에서 파레토 최적면으로의 수렴과 해의 다양성 보존을 충족할 수 있다.
Fig. 2(a)는 다목적 최적화에서 비지배 정렬을 통해 해들의 우열을 결정하는 방법을 설명한다. Fig. 2(a)는 2개의 목적함수 와 로 구성된 2차원 목적함수 공간에서 x1부터 x6까지 여섯 개 해의 우열을 나타낸 개념도이다. x1은 <이면서 <이기 때문에 x2를 지배한다(우월하다). 또한, x2가 x3을 지배하기 때문에 x1은 x3도 지배한다. 동일한 방식으로, x4는 x5와 x6를 모두 지배한다. 한편, x1과 x4는 <이면서 >임에 따라 서로 비지배하기 때문에 동등한 가치를 갖는다. 요약하자면, x1과 x4는 Fig. 2(a)에서 가장 우등한 1차 비지배해 집합(rank 1)에 속하며, 반면 x3와 x6는 가장 열등한 비지배 해(여기서는 rank 3)에 속한다. 다목적 최적화의 세대에 따른 진화 과정에서 지배하는 해들은 지배당하는 해들보다 생존 확률이 높다. 다목적 최적화가 원활히 수행되는 경우, 최종 세대에서의 1차 비지배해 집합은 실현 가능한 해 영역 Ω에서 파레토 최적면에 충분히 근사할 것으로 간주한다. 현실 문제에서 파레토 최적면의 정확한 형태는 알 수 없으므로, 이 연구에서는 1차 비지배해 집합을 파레토 최적면으로 가정하고 다목적 최적화를 수행한다.
다목적 최적화는 파레토 최적해의 수렴뿐만 아니라 다양성을 함께 확보하기 위해 밀집도 거리 정렬을 함께 사용한다. 개체의 비지배 정렬 순위만으로 우월한 해를 결정하면, 다음 세대의 우월한 해들이 특정 목적함수 공간에 밀집하여 해의 다양성이 저하되기 때문이다. Fig. 2(b)는 밀집도 거리 정렬의 개념을 나타낸다. 동일한 비지배 계층(rank)에 속하는 해들에 대하여 번째 해의 밀집도 거리 는 식 (6)과 같이 계산한다.
이때, 과 는 번째 해에서 가장 가까운 두 개의 이웃 해(neighbors)의 번째 목적함수 값이며, 와 는 번째 목적함수 값의 최댓값과 최솟값이다. 동일한 비지배 계층에 속하는 경우 해의 다양성을 확보하기 위해서 밀집도 거리가 큰 해일수록 우수해로 간주한다.
다목적 최적화 알고리듬
파레토 최적면은 차원 목적함수 공간에서 -1 차원의 초곡면(hypersurface) 형태를 가진다. 이 연구에서는 3차원 목적함수 공간에서 2차원 곡면의 형태를 띠게 된다. 이러한 이유로 다목적 최적화 알고리듬은 NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm-Ⅱ), 다목적 입자 군집 최적화(Multi-Objective Particle Swarm Optimization, MOPSO) 등 비지배 정렬과 밀집도 거리 정렬을 구현한 모집단(population-based method) 기반의 방법을 주로 사용한다. 다목적 최적화의 과정은 다음과 같다. 세대별 모집단 크기(population size)와 세대 수(generation)를 설정한 후, 첫 세대의 모집단을 생성하는 초기화를 수행한다. 초기 해들에 대하여 목적함수를 평가한 후, 비지배 정렬을 시행하여, 각 해의 비지배 계층을 할당한다. 다른 해들에 의해 지배되지 않는 해들에 대해 다시 비지배 해를 찾아 두 번째 계층(rank 2)을 할당한다. 이 과정을 모든 해가 임의의 비지배 계층에 할당될 때까지 반복한다. 따라서, 비지배 정렬이 완료되면, 여러 계층(rank 1, rank 2, ...)의 해집단이 형성된다.
모든 해에 대하여 비지배 정렬을 완료하면 밀집도 거리 정렬을 시행한다. 우선 각 계층 내의 모든 해의 밀집도 거리를 0으로 초기화한다. 그 후, 각 계층에 대해 개별 목적함수 값에 따라 해들을 정렬한다. 그 후 각 목적함수 값에 대해, 가장자리 해의 밀집도 거리는 무한대로 설정하고, 나머지 해들의 밀집도 거리는 이웃 해들의 차이를 계산하여 구한다. 이 차이를 모든 목적함수 값에 대해 합산하여 최종 밀집도 거리를 계산한다. 비지배 정렬과 밀집도 거리 정렬을 조합하여 모집단 크기의 우수한 해들을 선발하면 이 해들을 재조합하여 다음 세대의 모집단을 생성한 후 해들의 품질을 평가한다. 이 과정을 최종 세대에 도달할 때까지 반복하며, 최종 세대의 첫 번째 비지배 계층은 파레토 최적면을 근사함으로 간주한다.
연구결과
CCS 통합 시스템의 다목적 최적화 설정
제안한 연구 방법을 대염수층 대상 CO2 지중저장 통합 시스템 설계에 적용하여 성능을 검증하였다. 파레토 최적해들의 결정변수와 목적함수의 분포를 분석하여 최적의 설비 및 운영인자 범위를 확인하였다. Fig. 1에 나타낸 것처럼 통합 시스템 모델링 시 육상 CO2 허브 터미널, 수송관, 해상 플랫폼에서의 가열 시스템, 주입정과 균질 해상 저장층을 구현하였다. 본 연구에서 활용하는 저장층 모델의 경우, 국내 A 분지를 대상으로 하며 육상과 해상의 특정 지점을 기준으로 육상 CO2 허브 터미널과 해상 저장층을 모델링하였다. 해당 모델은 다양한 시나리오에 따른 저장량 사전 평가를 위해 사용하고 있다. 저장층 모델의 물성은 Table 1과 같다. 모델의 저장층 심도는 해수면으로부터 1,150 m이며 저장층의 두께는 60 m이다. 저장층 내에서는 균질한 분포의 공극률과 유체투과율을 갖는다고 가정하였으며, 공극률은 20%, 유체투과율은 60 md로 설정하였다. 저장층 모델의 초기 압력은 12 MPa, 온도는 50°C이고, 최대 주입 허용 압력은 기 확보한 자료를 참고하여 15 ~ 20 MPa의 값 중 단일 값을 가정하였다. 상기 저장층의 심도, 두께, 공극률, 유체투과율 등 물성들은 향후 시추 과정에서 추가 확보될 자료에 근거하여 수정될 수 있다. 본 연구는 초기 단계에서 운영조건 및 FEED의 설비인자 최적 범위를 산정하는 방법론 제안에 초점을 맞추고 있다.
Table 1.
Properties of reservoir model
| Parameter | Value |
| Reservoir depth [m] | 1,150 |
| Reservoir thickness [m] | 60 |
| Porosity [%] | 20 |
| Permeability [mD] | 60 |
| Initial pressure [MPa] | 12 |
| Reservoir temperature [°C] | 50 |
해저 수송관과 해상 플랫폼, 주입정은 다음에 근거하여 모델링하였다. 본 연구에서는 양호한 물성값을 균질하게 갖는 저장층을 활용하였기 때문에 펌프 스테이션은 설치하지 않았다. 펌프 스테이션은 추후 저장층 및 수송관 내 압력 변화에 따라 설치를 고려할 수 있다(Knoope et al., 2014). 수송관 내에서의 유체 거동 양상은 해저 지형의 영향을 받으므로 이 연구에서는 현실적인 모델링을 위해 GEBCO(General Bathymetric Chart of the Oceans)의 해양 수심 측량도를 기반으로 해저면을 따라 수송관 분포를 구현하였다(GEBCO, 2024). 해상 플랫폼은 대륙붕에 설치하는 상황을 가정하였으며, 대륙붕 평균 수심을 고려하여 주입정의 길이를 설정하였다. CCS 통합 시스템 모델링에는 캐나다 Computer Modelling Group Ltd.(CMG)의 소프트웨어 CoFlowTM를 사용하였다.
다목적 최적화의 결정변수는 식 (2)에서 소개한 것처럼 통합 시스템 설계 시 고려하는 설비 및 운영 인자 4개(, , , )를 설정하였다. 대부분 해상 CCS의 경우, 육상에서 송출된 CO2는 해상 플랫폼에서 보관하지 않고 곧바로 대상 저장층으로 주입된다. 따라서 CO2 수송 및 주입, 저장에 영향을 미치는 육상 허브 터미널에서의 CO2 송출 압력을 결정변수로 선정하였다. 본 연구에서는 육상으로부터 해상 저장층의 거리와 해수면으로부터의 저장층 심도를 고정값을 사용하므로, 주요 설비인자 중 수송관과 주입정 튜빙의 길이는 고정하고, 수송관 내경과 주입정 튜빙 내경을 결정변수로 선정하였다. 주입정 상단에서의 CO2 온도는 압력과 더불어 유체의 상변화에 영향을 미치기 때문에, 안전성과 주입성을 평가하기 위한 결정변수로 선정하였다.
다목적 최적화 수행을 위한 각 결정변수의 최솟값 및 최댓값의 범위는 미국석유협회(American Petroleum Institute, API)의 표준 범위를 참고하였으며 기본값(default)은 각 결정변수의 평균값이다(Trident Steel, 2024). Table 2는 결정 변수별로 기본값, 최댓값, 최솟값, 증감 크기(step size), 개수(number of steps)를 보여준다. 이 결정변수의 조합으로 실현가능한 총 해의 수는 13,377개이다.
Table 2.
Range of decision variables in multi-objective optimization
| Variable | Default | Lower limit | Upper limit | Step size | Number of steps |
| Source P [MPa] | 10 | 7 | 13 | 1 | 7 |
| Pipeline I.D. [inch] | 12 | 6 | 18 | 1 | 13 |
| Tubing I.D. [inch] | 5 | 2 | 8 | 1 | 7 |
| Wellhead T [°C] | 20 | 10 | 30 | 1 | 21 |
다목적 최적화의 목적함수 또한 식 (2)와 같이 CO2 저장량, 안전성, 경제성 세 가지 측면을 고려할 수 있도록 누적 CO2 주입량 최대화, 저장층 최대 주입 허용 압력 대비 주입정 최대 공저압 최소화, 편익비용비 최대화의 문제로 설정하였다. 주입 기간의 주입정 최대 공저압을 저장층 최대 주입 허용 압력으로 나누어 정규화하였으며, 이로써 최대 주입 허용 압력에 대한 안전율의 형태로 목적함수를 설정하였다. 편익비용비는 사업 진행으로 인한 총편익을 총비용으로 나눈 것으로 식 (4)로 계산하며, 계산에 활용한 경제성 인자는 Table 3과 같다. (benefits)에서는 연간 CO2 주입량에 따른 탄소 크레딧을 고려하고, (Costs)는 연간 CO2 주입량에 따른 CO2 주입 비용과 수송관 및 주입정의 설치 및 운영 총비용을 고려하였다. 경제성은 순현재가치(net present value, NPV)로 평가한다. 연간 할인율은 10%로 설정하고, 탄소 크레딧은 국제에너지기구(International Energy Agency, IEA)의 2030년 탄소 크레딧 전망치의 평균값을 활용하였다(IEA, 2018). CO2 주입 비용은 Schmelz et al.(2020)의 해상 CCS 프로젝트 사례로 계산한다. 수송관 및 주입정(튜빙) 총비용의 경우 Parker(2004)의 값을 기반으로 본 케이스에서의 주입정 및 수송관 길이에 맞게 계산하며, 내경에 따라 다른 값을 갖는다. 모든 경제성 인자는 각 문헌의 기준 시점 대비 경제협력개발기구(Organization for Economic Co-operation and Development, OECD) 평균 물가 상승률을 고려하여 2022년 미국 달러로 환산한 값을 활용하였다(OECD, 2024).
Table 3.
Economic parameters used to calculate BCR
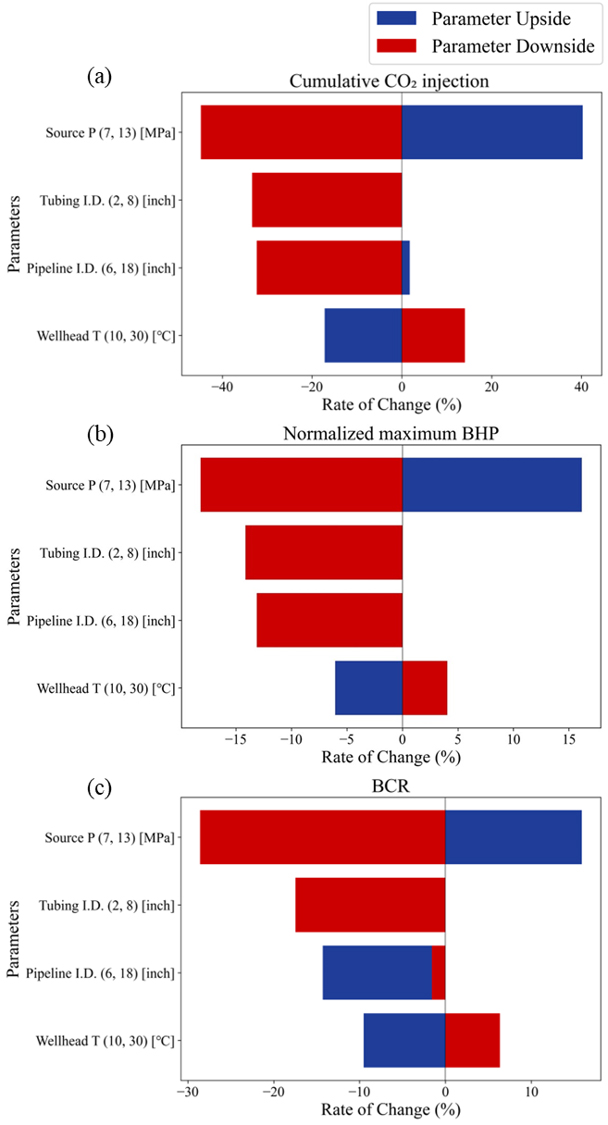
최적화에 앞서, 각 결정변수 별로 목적함수에 대한 민감도 분석을 수행하여 결정변수가 목적함수에 미치는 영향을 확인하였다. 민감도 분석 시에는 OPAAT(One parameter at a time) 방법을 사용하였다. Fig. 3은 민감도 분석의 결과를 시각화한 토네이도 차트(tornado chart)이다. 민감도 분석 시에는 CO2 송출 압력으로 29년간 주입하도록 설정하였다. 설정한 범위 내에서는, 모든 목적함수에 대해 CO2 송출 압력이 가장 큰 영향을 미치고, 주입정 튜빙 내경, 수송관 내경, 주입정 상단에서의 CO2 온도 순으로 영향을 미치는 것을 확인하였다. CO2 송출 압력과 주입정 튜빙 내경은 항상 목적함수와 양의 상관관계를 보이며, 주입정 상단에서의 CO2 온도는 목적함수와 항상 음의 상관관계를 보였다. 각 결정변수 별로 선정한 탐색 범위 내에서는 모든 목적함수에 대해 유의미한 영향을 미치는 것을 확인하여, 4개를 모두 다목적 최적화의 결정변수로 선택하였다.
본 연구의 통합 시스템에서는 육상 CO2 허브 터미널에서의 송출 압력으로 CO2를 수송 및 주입, 저장하도록 설계하였다. 공급되는 CO2 총 유량을 기준으로 주입 조건을 설정하는 선행 연구 대비, 본 연구는 설비 및 운영조건에 따른 누적 주입량의 차이를 비교하기 위해 CO2 허브터미널에서의 송출 압력을 주입 조건으로 설정하였다. 한 개의 실현 가능한 해 조합으로 구성한 케이스들은 29년간의 CO2 주입을 시뮬레이션하도록 설정하였다. 이때, 주입성과 안전성 측면에서 의사결정자의 사전 선호(prior preference)를 제약조건(constraint)으로 설정하고 다목적 최적화를 진행하였다. 즉, 제약조건을 위반한 해들은 식 (5)의 비지배 관계에 무관하게 제약조건을 만족하는 해들보다 열등하다고 설정하였다. 연간 최소 주입량은 대한민국의 국가 온실가스 감축목표(Nationally Determined Contribution, NDC)를 고려하고 중규모 CCS 프로젝트를 가정하여 설정하였으며, 주입정의 공저압이 저장층 최대 주입 허용 압력에 도달하는 경우 주입을 중단하도록 설정하였다. 즉, 주입을 시작한 이래로 공저압이 저장층 최대 주입 허용 압력에 도달하지 않으면 총 29년간 CO2를 주입하고, 공저압이 저장층 최대 주입 허용 압력에 도달하는 경우 그 즉시 주입을 중단하여, 29년보다 짧은 기간 동안 CO2를 주입하는 사례가 된다. 다목적 최적화를 위한 사례별 시뮬레이션은 CMG의 CMOSTTM를 CoFlowTM와 결합하여 수행하였다. 다목적 최적화 알고리듬은 MOPSO를 활용하였으며 MOPSO의 설정값은 Clerc and Kennedy(2002)를 참고하였다(Table 4).
Table 4.
Experimental setting for MOPSO algorithm
| Parameter | Value |
| Number of evaluations | 503 |
| Inertia weight, ω | 0.7298 |
| Cognitive component, c1 | 1.49618 |
| Social component, c2 | 1.49618 |
CCS 통합 시스템의 다목적 최적화 결과
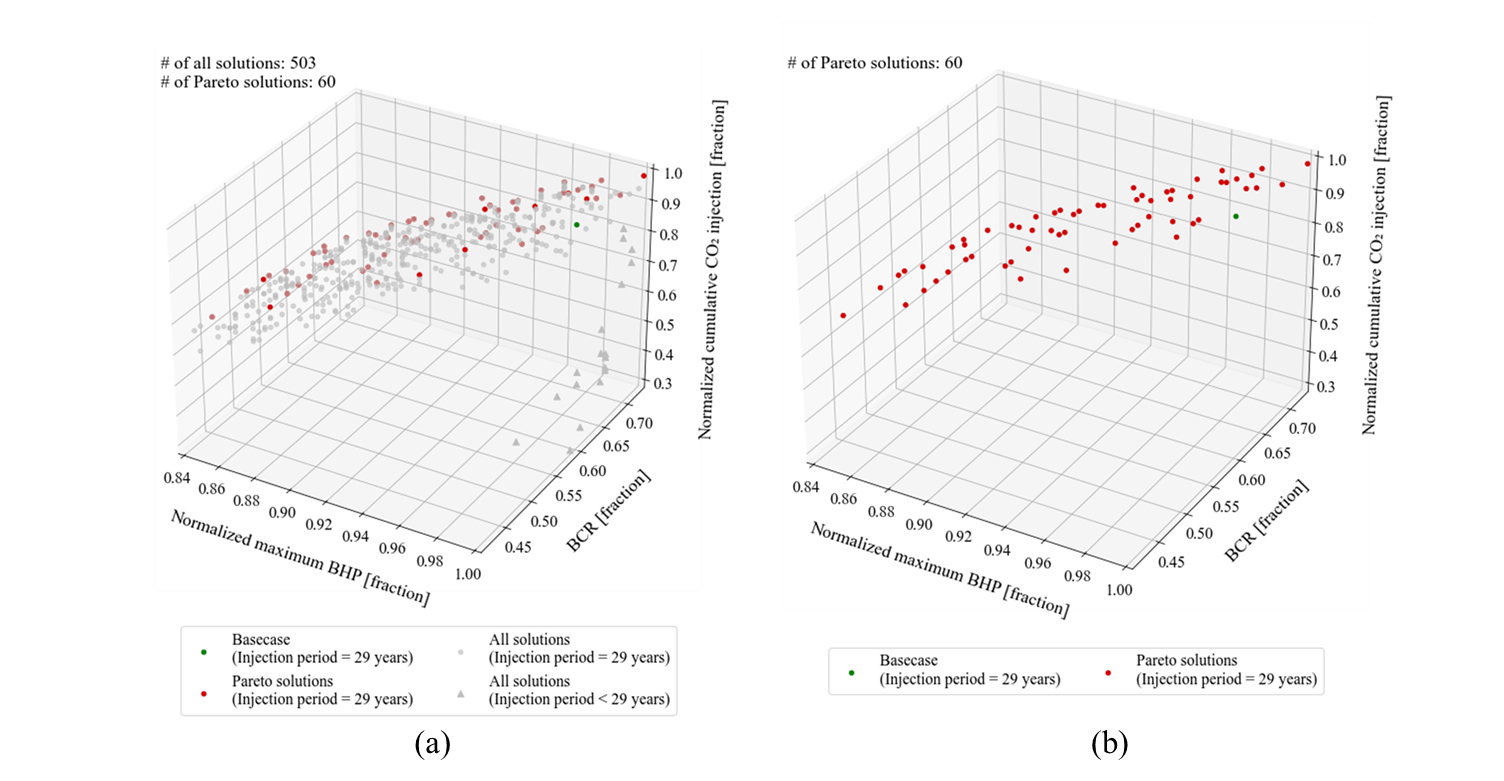
Fig. 4는 3차원 목적함수 공간에서 다목적 최적화를 통해 탐색한 전체 해의 분포(Fig. 4(a))와 1차 비지배 해의 분포(Fig. 4(b))를 보여준다. Fig. 4(a)는 탐색 과정에서 생성된 전체 해 503개의 분포를 시각화하였다. 503개의 해는 인구수(population)와 세대(generation)수를 고려하여 생성되었으며, 이는 전체 실현 가능한 해의 수 13,377 대비 약 3.8%에 해당한다. 누적 CO2 주입량의 경우 다른 두 목적함수 값과의 규모 비교를 용이하게 하기 위해 503개의 시뮬레이션 결과 중 최댓값으로 나누어 정규화하였다. 주입 최대 공저압이 저장층 최대 주입 허용 압력에 도달하는 경우 주입을 중단하여 저장량이 적은 해들도 포함되었음을 확인할 수 있다. Fig. 4(b)는 전체 해 503개 중 1차 비지배해로 선별된 60개를 시각화한 것이다. 특정 목적함수의 편익을 극대화하는 방향으로 치우치지 않고 다양한 우수해를 포함하므로 1차 비지배해가 파레토 최적면을 충분히 근사하는 파레토 최적해로 간주할 수 있음을 확인하였다. 60개의 파레토 최적해는 모두 비지배 관계에 있어 등가의 우수한 해로 간주하므로, 해 간의 우열이 없다. 따라서 의사결정자는 최적해 중 선호에 따라 최적의 설비 및 운영인자를 선택할 수 있다.
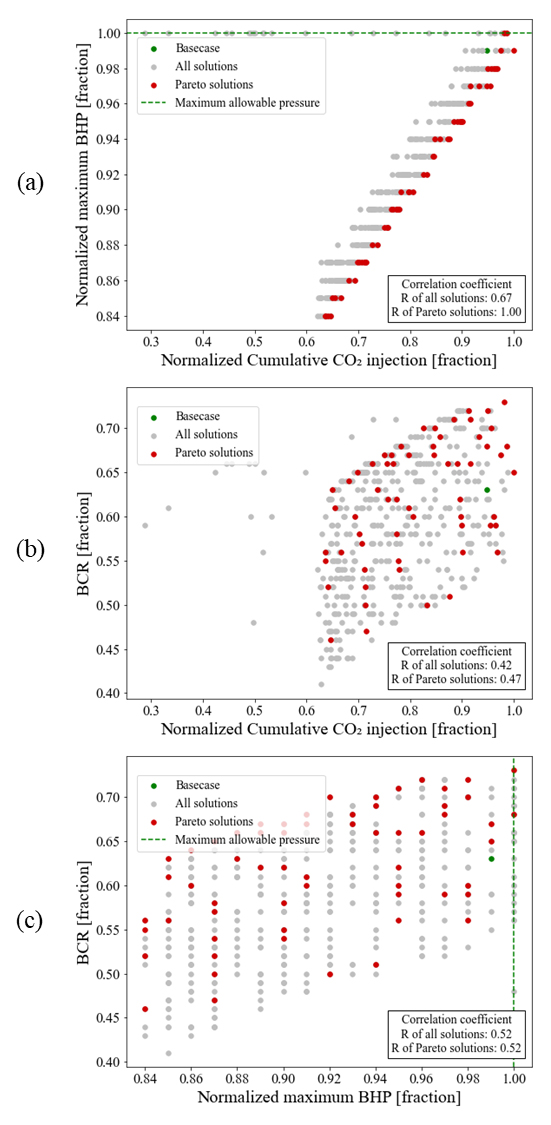
Fig. 5는 2차원 목적함수 공간에서 해의 분포와 해 간의 상관계수(correlation coefficient, R)를 시각화한 것이다. 이를 통해 파레토 최적해는 탐색한 전체 해에 비하여 목적함수 간에 더 큰 상관계수를 가짐을 확인하였다. 특히 Fig. 5(a) 누적 CO2 주입량과 주입정 최대 공저압의 경우, 탐색한 전체 해의 상관계수는 0.67인 반면, 파레토 최적해의 상관계수는 1.00으로 강한 양의 상관관계를 나타낸다. 편익비용비와 다른 두 목적함수에 대한 각각의 조합(Fig. 5(b), Fig. 5(c))에서는 해의 분포에서 확인할 수 있는 상관성은 약간 감소하나, 여전히 파레토 최적해간 상관계수가 전체 해간 상관계수에 비해 같거나 크다. 이 사례의 경우, 누적 CO2 주입량과 주입정 최대 공저압이 매우 강한 선형성을 보이므로 만약 둘 중 하나의 목적함수만을 선택하여 편익비용비와 두 개의 목적함수로 다목적 최적화를 수행했어도 유사한 결과를 얻을 수 있을 것으로 해석할 수 있다. 그럼에도 불구하고, 향후 비균질성과 이방성을 반영한 저장층의 경우 주입정 위치에 따라 결정변수와 목적함수 간의 상관관계가 달라지는 등 문제의 복잡도가 높아지기 때문에 3개의 개별 목적함수를 사용하는 것이 유의미하다.
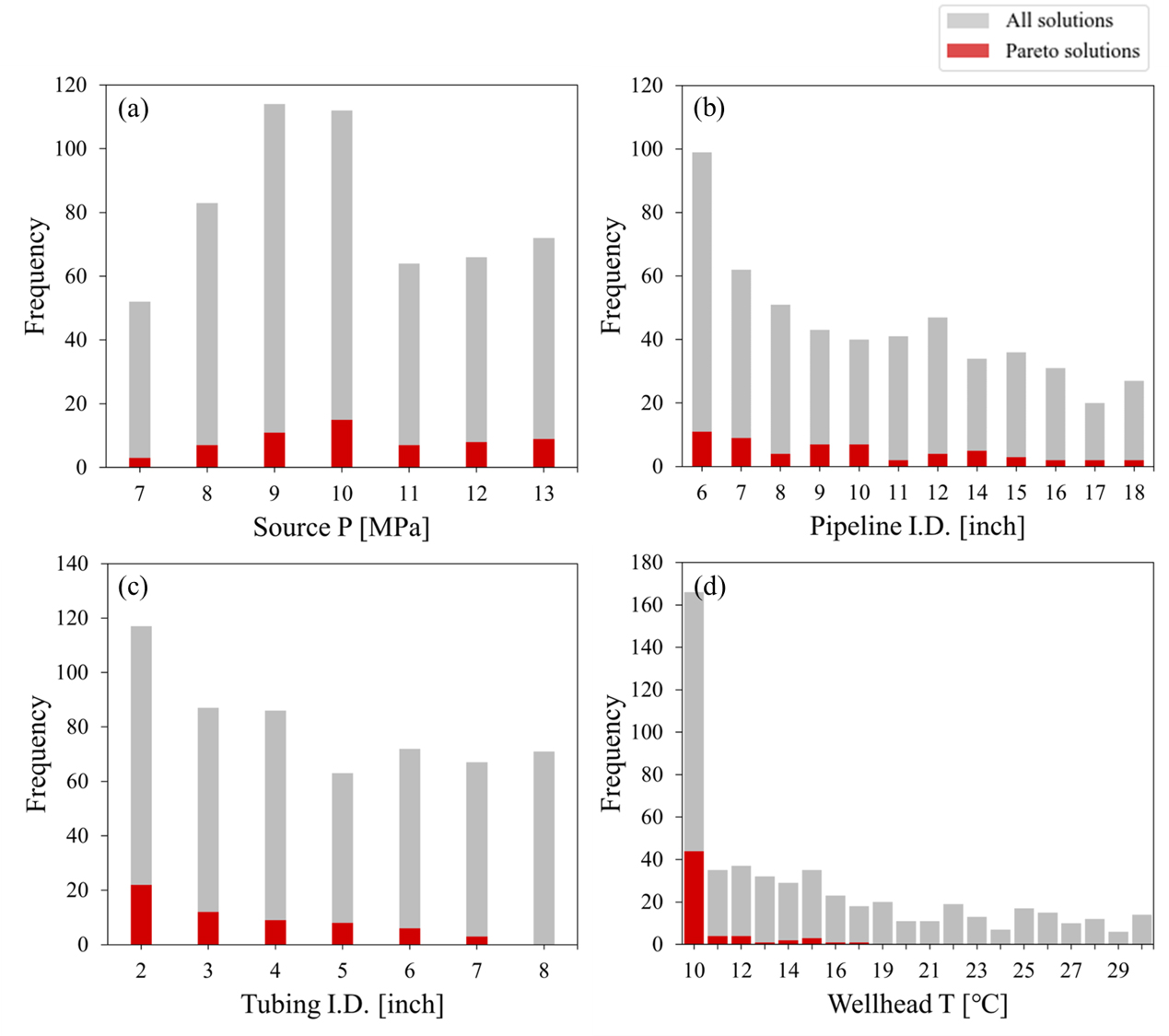
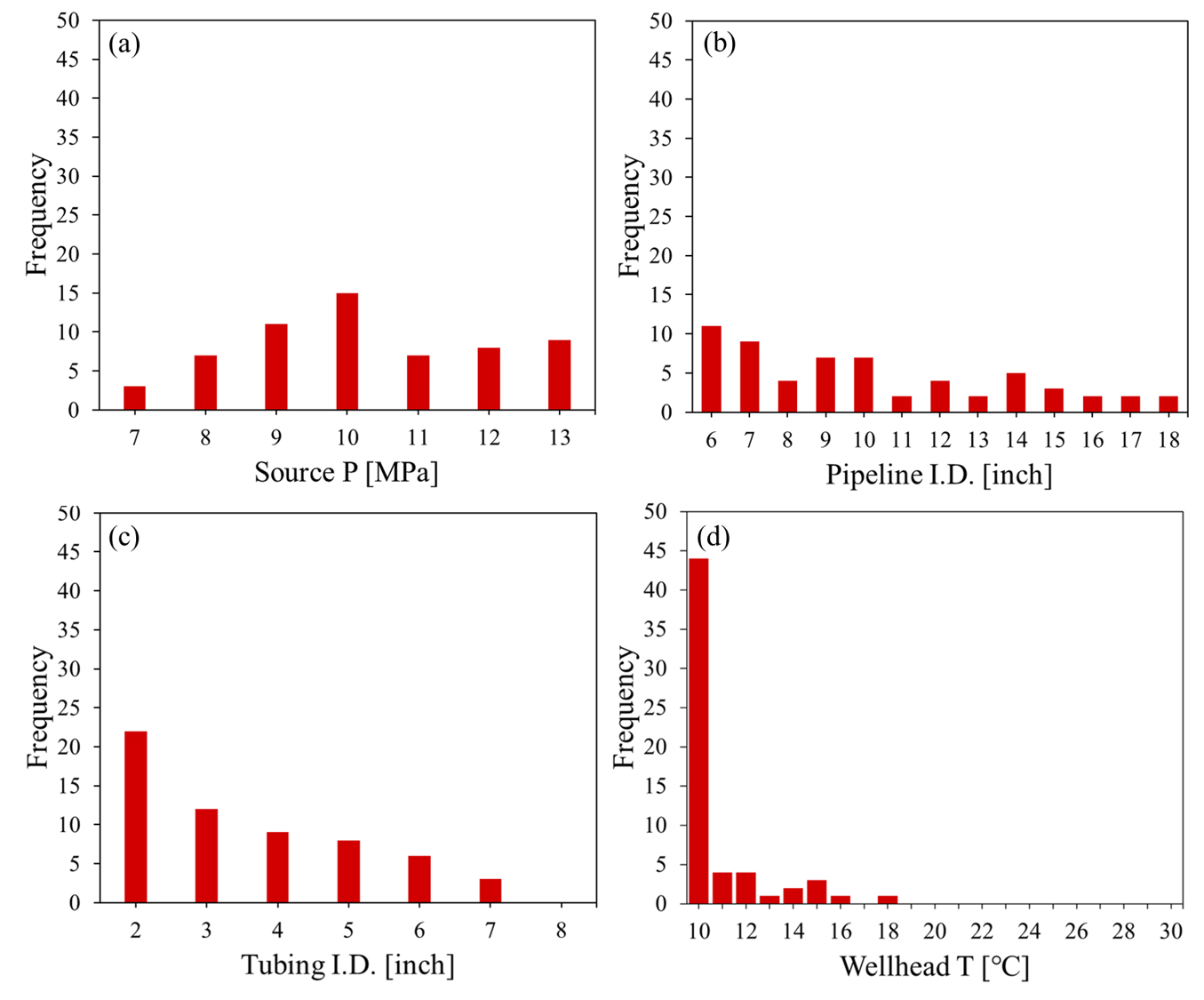
Fig. 6과 Fig. 7은 파레토 최적해를 결정변수 공간에서 시각화한 것이다. Fig. 6은 탐색한 전체 해와 파레토 최적해의 결정 변수별 값의 빈도(frequency)를 나타낸 히스토그램이고, Fig. 7은 Fig. 6에서 최적해의 결정 변수별 값의 빈도만을 추출하여 나타낸 것이다. Fig. 7에서 파레토 최적해는 CO2 송출 압력과 수송관 내경에 대해서는 비교적 균일분포에 가까운 형태를 보이고, 주입정 튜빙 내경과 주입정 상단에서의 CO2 온도의 경우 비교적 로그 정규 분포에 가까운 형태를 보이는 것을 확인하였다. 다목적 최적화는 목적함수 공간 내 파레토 최적면 상에서 균일하게 해가 분포하도록 설계되었으나, 이것이 결정변수 공간에서 균일분포를 의미하지는 않는다. 이 연구에서 4개의 결정변수는 모두 목적함수의 최적 달성에 영향을 미치므로, 4개의 조합으로써 최적값을 해석해야 하며, 높은 빈도가 단적으로 결정변수의 최적값을 의미하지는 않는다는 점을 유의해야 한다.
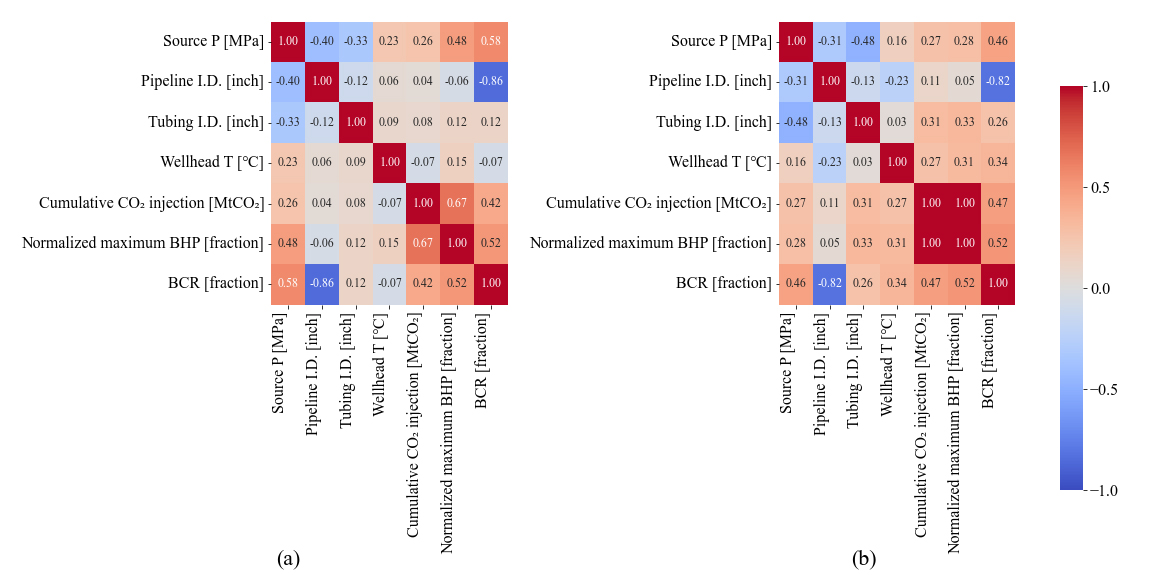
결정변수들과 목적함수 간의 상관계수 행렬을 통해 전체 해집합 대비 파레토 최적해 집합의 우수성을 확인하였다. Fig. 8(a)와 Fig. 8(b)는 각각 503개의 전체 해와 60개의 파레토 최적해에 대한 결정변수들과 목적함수 간의 상관계수 행렬이다. 변수 간의 상관성은 전체 해보다 파레토 최적해에 대해 더 명확히 나타난다. 전체 해의 상관계수는 –0.86에서 0.67 사이의 값을 갖는 것에 비해 파레토 최적해의 상관계수는 –0.82에서 1.00 사이의 값을 가진다. 이는 다목적 최적화를 통해 목적함수 간 파레토 최적을 드러내는 다양한 해를 탐색함으로써 결정변수 간의 상관관계를 포착한 최적해를 도출하였음을 의미한다.
제약조건이 없는 다목적 최적화 결과
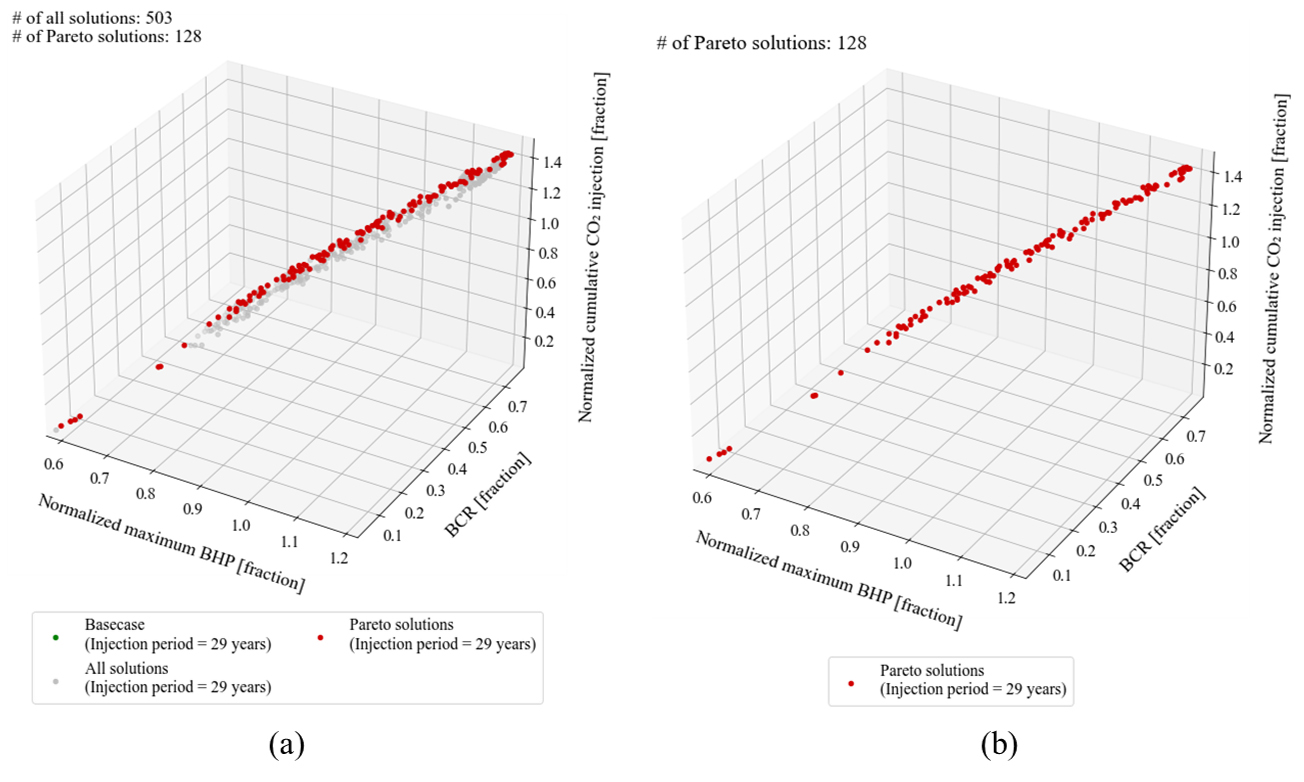
지금까지의 연구 결과는 효율적인 최적화를 위해 의사결정자의 사전 선호를 반영한 제약 다목적 최적화(constrained multi-objective optimization)의 결과이다. 본 연구는 의사결정자의 사전 선호 반영 여부에 따른 최적화 성능을 비교하기 위해 주입성과 안전성에 대한 선호를 사전에 반영하지 않은 비제약 다목적 최적화(unconstrained multi-objective optimization)를 추가로 진행하였다. Table 5는 제약 다목적 최적화와 비제약 다목적 최적화의 시뮬레이션 설정값을 비교하는 표이다. 비제약 다목적 최적화 또한 결정변수 별 탐색 범위와 증감 크기, 목적함수는 제약 다목적 최적화와 동일하게 설정하였다. Fig. 9는 최소 연간 주입량과 최대 주입압력에 대한 사전 선호(제약조건) 없이 진행한 다목적 최적화 결과이다. Fig. 9(a)는 탐색한 503개의 전체 해를 시각화한 것이며, 각 해는 목적함수 공간에서 균일하게 분포된 결과를 보여준다. Fig. 9(b)는 비제약 다목적 최적화를 통해 도출한 128개의 1차 비지배해로 구성된 파레토 최적면을 나타낸 것으로, 목적함수 간 균형을 이루고 있음을 보여준다. 수직 축의 누적 CO2 주입량은 비제약 다목적 최적화의 누적 CO2 주입량을 제약 다목적 최적화 결과 중 누적 CO2 주입량의 최댓값으로 나누어 시각화하였다. 그 결과, 128개의 최적해는 목적함수 공간에서 고르게 분포하며 파레토 최적면을 구성함을 확인하였다. 이때, 최대 주입 허용 압력에 대한 제약 없이 탐색하였으므로 최대 주입 허용 압력에 대한 안전율의 형태로 정의한 두 번째 목적함수인 주입정 최대 공저압이 1을 초과하는 해 또한 탐색 된 것을 확인할 수 있다. 뿐만 아니라, 최소 연간 주입량에 대한 제약조건 없이 탐색하였기 때문에 누적 CO2 주입량과 주입정 최대 공저압 모두 매우 작은 해 또한 탐색 됨을 확인하였다.
Table 5.
Comparison of simulation settings for constrained and unconstrained multi-objective optimization
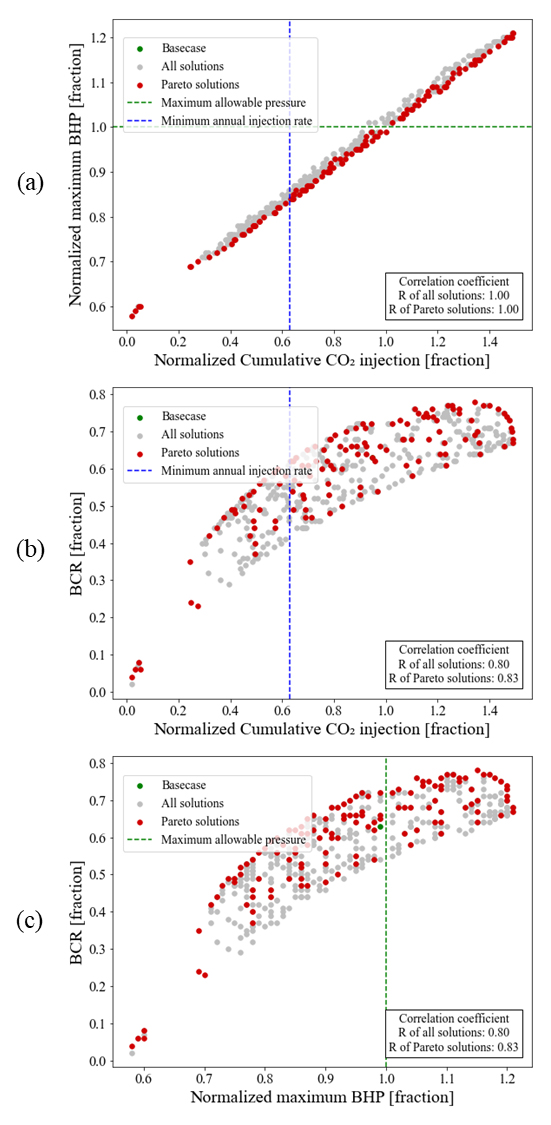
Fig. 10은 비제약 다목적 최적화 결과의 2차원 목적함수 공간에서 2개의 목적함수 조합에 대한 해의 분포를 시각화한 것이다. 사전 선호를 반영하지 않았으므로 비제약 다목적 최적화 결과의 상관계수는 세 목적함수 간 본질적인 물리적 상관성을 나타낸다. 사전 선호를 반영한 Fig. 5와 비교할 때, 두 최적화 결과 모두 파레토 최적해의 목적함수 간 상관계수가 전체 해의 목적함수 간 상관계수보다 높음을 확인할 수 있다. Fig. 5와 대비되는 점은 비제약 다목적 최적화가 제약 다목적 최적화에 비하여 목적함수 간 상관관계를 더욱 명확히 드러낼 수 있다는 것이다. 만약 비제약 다목적 최적화에 사후 선호(posterior preference)를 적용하면 Fig. 10에 초록색 점선으로 표시한 최대 주입 허용 압력 이하, 파란색 점선으로 표시한 최소 연간 주입량 이상의 해들이 의사결정자가 고려할 수 있는 최적해가 된다. 따라서, 128개의 최적해 중 51개의 해만이 실질적으로 고려할 수 있다. 이상의 비교 결과, 다목적 최적화로 파레토 최적해를 도출하는 경우, 의사결정자의 선호를 사전에 반영하는 제약 다목적 최적화가 선호 범위 내에서 더 빠르게 최적해를 탐색할 수 있음을 시사한다. 반면, 의사결정자의 선호는 목적함수 간 물리법칙을 고려하지는 않으므로 목적함수 간 상관관계를 더욱 명확히 규명할 필요가 있는 경우에는 비제약 다목적 최적화를 수행한 후 선호도를 만족하는 해들을 사후에 선별하는 접근법이 더 유용할 수 있다.
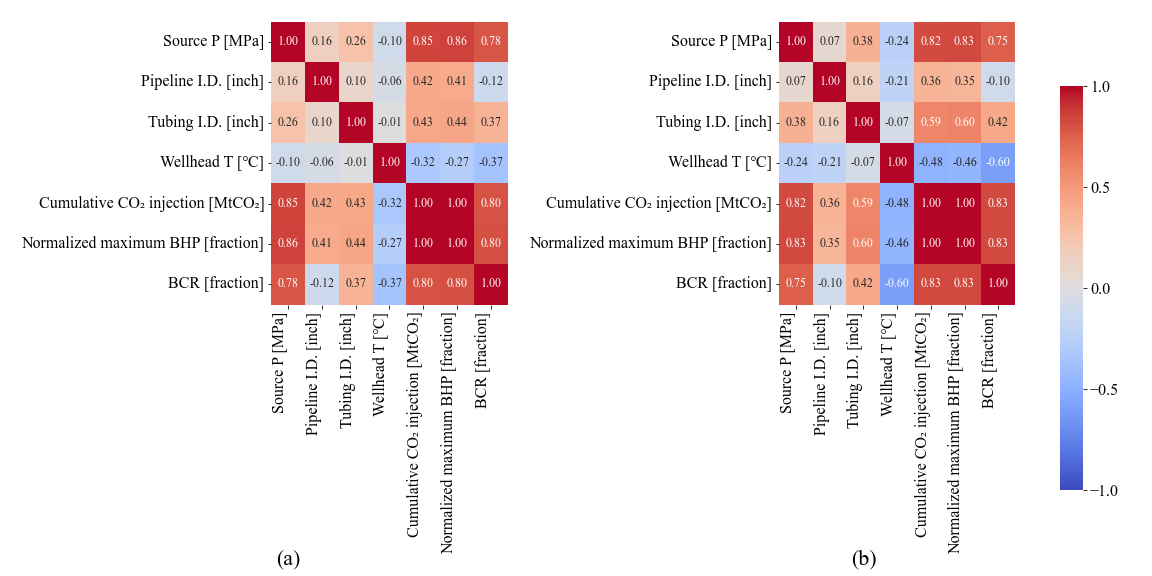
Fig. 11(a)와 (b)의 상관계수 행렬은 비제약 다목적 최적화의 전체 해와 파레토 최적해에 대하여 구성한 것이다. 사전 선호를 반영한 제약 다목적 최적화와 마찬가지로, 사전 선호를 반영하지 않은 비제약 다목적 최적화 결과에서도 탐색한 전체 해 대비 파레토 최적해에서 변수 및 목적함수 간 더 높은 상관계수를 확인하였다. 비제약 다목적 최적화 결과의 상관계수 행렬을 통해 본 문제에서 설정한 결정변수와 목적함수 간의 선형적 관계의 정도와 방향을 알 수 있다. 사전 선호를 반영하지 않은 파레토 최적해의 상관계수 행렬(Fig. 11(b)) 대비 사전 선호를 반영한 파레토 최적해의 상관계수 행렬(Fig. 8(b))을 보면, 수송관 내경과 주입정 상단에서의 CO2 온도 각각의 다른 변수들에 대한 상관관계가 각각 양에서 음으로, 음에서 양으로 전환되었다. 이는 선호를 반영한 최적화 과정에서 특정 변수들이 목적함수에 미치는 영향을 조정하여 발생한 것이다. 상기 결과로부터, 의사결정자의 선호에 따라 특정 결정변수가 목적함수에 긍정적인 영향을 미치도록 조정되었음을 시사한다.
연구 결과를 통해, 다목적 최적화 방법론이 CO2 수송-주입-저장 통합 시스템의 최적 설계를 위한 다수의 우수해를 도출함을 명확히 보여주었다. 통합 모델링을 통해 육상 CO2 허브 터미널에서부터 주입정까지 수송 과정에서의 압력 변화와 주입에 따른 저장층 압력 변화를 연속적으로 모사하여, 더욱 정확한 최적화가 가능했다. 다목적 최적화를 통해 도출한 파레토 최적면은 결정변수와 목적함수 간의 상관관계를 잘 파악한 우수해로 구성되었음을 확인하였다. 따라서 본 연구에서 제안한 방법론은 CO2 지중저장 통합 시스템 설계의 유연성과 신뢰성을 향상시킬 수 있다. 향후 연구에서는 다목적 최적화로 탐색한 전체 해의 결정변수와 목적함수를 각각 입력자료와 출력자료로 하는 예측 모델을 구축하여 더 작은 증감 크기를 갖는 결정변수 조합에 대한 목적함수 값 예측 및 최적해 집합 도출에 활용하고자 한다. 이를 통해 다목적 최적화 과정에서 고려하지 못한 세부 운영조건을 신속히 평가함으로써 더욱 정밀한 최적 설계가 가능할 것으로 기대한다. 제안하는 방법론은 향후 저장층 모델, 설비인자, 운영조건 등이 변경되거나 추가되더라도 확장 적용하여 분석할 수 있다.
결 론
본 연구는 다목적 최적화에 기반하여 CO2 지중저장을 위한 CO2 수송-주입-저장 통합 시스템의 기본 설계 단계에서 활용할 수 있는 설비 및 운영 인자 선정 방법론을 제안하였다. 제안한 방법론을 균질 대수층 대상 해상 CO2 지중저장 통합 시스템 설계에 적용하여 그 성능을 검증하였으며 다음의 결론을 도출하였다.
(1) CO2 지중저장 통합 시스템 전체의 최적 달성을 위해 통합 모델링으로 CO2 수송-주입-저장 시스템을 구현하고 다목적 최적화를 진행하였다. 육상 송출 및 수송 단계와 해상 주입 및 저장 단계 간 상호작용을 동적으로 반영하여 통합 시스템을 분석하였다. 다목적 최적화를 위해 4개의 결정변수와 3개의 목적함수를 선정하였다. 결정변수로는 육상 허브 터미널에서의 CO2 송출 압력, 수송관의 내경, 주입정 튜빙의 내경, 주입정 상단에서의 CO2 온도를 선정하였다. 목적함수로는 저장성 측면에서 누적 CO2 주입량 최대화, 안전성 측면에서 주입정 최대 공저압 최소화, 경제성 측면에서 편익비용비 최대화를 선정하였다.
(2) 구현한 통합 시스템을 대상으로 다목적 최적화를 진행한 결과 전체 실현 가능한 해 대비 3%의 해를 탐색하여 파레토 최적면을 성공적으로 도출하였다. 파레토 최적면을 구성하는 60개의 파레토 최적해는 목적함수 공간과 결정변수 공간에서 모두 광범위하게 분포하는 것으로 나타났으며, 이를 통해 다수의 우수한 해를 도출하는 다목적 최적화가 성공적으로 진행되었음을 확인하였다. 파레토 최적해의 상관계수는 –0.87에서 0.99로 다목적 최적화 과정에서 복잡한 변수 간의 관계와 문제의 특성을 잘 파악하였음을 확인하였다. 또한, 의사결정자의 선호를 사전에 반영한 제약 최적화가 최적해 도출에 효율적임을 확인하였다. 반면 비제약 최적화는 목적함수 간 상관관계를 더욱 명료하게 도출할 수 있으므로 사후 선호를 반영함으로써 유의미한 최적해를 도출할 수 있다.
(3) 향후 도출한 파레토 최적해를 기반으로 단계별 상세 분석을 수행한다면 더욱 정밀한 최적 설계가 가능할 것으로 기대한다. 다목적 최적화 결과를 바탕으로 머신러닝 등을 활용한 예측 모델을 구축한다면 시뮬레이션 기반 최적화에 비해 적은 계산 비용으로 세밀한 결정변수 값의 조합에 대한 목적함수 값을 예측하고 최적해를 도출할 수 있을 것이다.
파레토 최적해는 등가의 최고 비지배 해로써 CO2 지중 저장 통합 시스템 기본 설계의 자료로 활용할 수 있으며, 의사결정자가 선호에 따라 최적 설계안을 선택할 수 있는 기반을 제공한다. 제안한 방법론은 향후 저장층 모델이 업데이트되거나 설비인자 혹은 운영조건이 변경 및 추가되더라도 적용 가능하다는 점에서 범용성을 확보하였다. 이 방법론은 국내외 CO2 지중저장 통합 시스템의 설계안 도출뿐만 아니라, 다수의 우수한 대안을 제공하여 CO2 지중저장 프로젝트의 실효성, 안전성, 경제성 향상에 기여할 수 있을 것으로 기대한다.