서 론
연구방법
랜덤 포레스트(random forest, RF)
베이즈 최적화(Bayesian optimization)
수정 쌍곡선법(modified hyperbolic)
연구내용 및 결과
대상 광구
데이터 전처리(data preprocessing)
입력자료 특성 분석
RF 모델변수 최적화
궁극가채량 예측 RF 모델 적용
RF 모델의 EUR 예측오차 분석
RF 모델의 EUR 예측 신뢰구간 분석
결 론
서 론
전 지구적 기후변화에 대한 위기감 고조로 청정에너지에 대한 중요성 부각과 함께 석유 및 가스와 같은 화석에너지에 대한 개발이 주춤한 상황이다. 그러나, 천연가스는 미래 에너지 전환시대를 달성할 때까지 징검다리 에너지(bridge energy)로서 인식되고 있으며, 셰일가스는 천연가스의 주요 공급원 중 하나로서 중요성이 부각되고 있다(TodayEnergy, 2021). 셰일가스는 수평시추(horizontal drilling) 및 다단계 수압파쇄(multi-stage hydraulic fracturing)를 통해 저류층에서 가스가 이동할 수 있는 통로를 인위적으로 만들어야 경제적 생산이 가능하게 된다. 또한, 셰일 저류층은 매질의 높은 불균질성, 나노 스케일의 유체투과도, 그리고 유체 유동 메커니즘의 복잡성 등으로 인해 저류층 시뮬레이션과 같은 전통적 방법으로 미래 생산성을 예측하는 것에 어려움이 있다(Kothari, 2011).
전통적인 시뮬레이션 기법 적용이 어려운 셰일저류층의 다양한 문제를 해결하기 위해 생산데이터 기반 생산 예측 방법이 사용되고 있으며, 최근들어 딥러닝(deep learning)을 포함한 머신러닝(machine learning)을 활용하는 방법이 널리 활용되고 있다. 머신러닝은 물리적 모델이 아닌 복잡한 데이터를 학습하여 해당 시스템의 패턴을 파악하는 알고리즘이다. 오일 및 가스개발에서는 저류층 특성변수 예측(Iturrar and Parra, 2014; Zerrouki et al., 2014), 암상분류(Silversides et al., 2015), 물리검층자료 복원(Alizadeh et al., 2012), 저류층 히스토리 매칭(Ahn et al., 2018; Kim et al., 2020), 생산압력 복원(Ki et al., 2020) 등의 다양한 분야에서 머신러닝을 활용한 연구가 수행되고 있다.
또한, 궁극가채량(estimated ultimate recovery, EUR) 예측관련 연구분야에서도 머신러닝 기반 연구가 진행되었다. He(2017)는 셰일 저류층의 특성, 수압파쇄 설계인자, 생산량 자료를 사용하는 인공신경망모델(artificial neural network model)을 구축하여 50년 생산기간의 EUR 예측연구를 수행하였다. 또한, 셰일가스 생산성에 대한 주요 입력인자의 영향을 분석하였다. Vyas and Datta-Gupta(2017)은 Eagle Ford에서 수집한 유정완결 데이터와 생산 데이터를 머신러닝 기법인 랜덤 포레스트(random forest, RF), 서포트 벡터머신(support vector machine) 등에 학습시켜 생산감퇴곡선 변수를 예측하는 모델을 개발하였고, 개발된 모델을 통해 예측한 생산감퇴곡선 변수를 사용하여 개발 예정인 생산정의 감퇴곡선과 궁극가채량을 신속하게 예측하였다.
Amr et al.(2018)은 생산정의 특징(feature)을 조합한 자료를 입력 데이터로 설정하고 EUR, 초기 최대 생산량, 그리고 초기 감퇴율을 출력 데이터로 설정하여 머신러닝 알고리즘에 학습시켜 비전통 수평정의 월 생산량을 예측하는 데이터 기반 모델을 제안하였다. Liang and Zhao(2019)는 Eagle Ford의 4,000개 생산정에서 생산량, 물리검층, 수압파쇄 및 지질정보 등 25개의 입력변수를 사용하여 EUR 예측을 위한 RF 모델을 학습시켰으며, EUR 예측에 가장 중요한 영향인자를 확인하였다. Shin et al.(2021)은 셰일 저류층으로부터 수집한 입력자료를 퍼지 클러스터링을 통해 3가지 그룹으로 분류하고 그룹별 생산성의 불확실성을 분석하였다. 또한, 새로운 시추정에 대해서는 기존 생산정의 분류정보를 바탕으로 미래 생산량을 확률적으로 예측하는 방법을 제안하였다.
앞에서 제시한 대부분의 기존 연구에서는 어느 한 시점을 기준으로 머신러닝을 학습시켜 EUR을 예측하는 연구를 수행하였다. 그러나 생산이 진행되면서 가용한 자료가 변할 때 머신러닝 모델의 예측오차 및 신뢰구간 등 예측 신뢰도의 변화 추이를 파악하여 해당 머신러닝 모델의 사용이 적합한지 분석하는 것이 필요하다. 이 연구에서는 생산이 진행됨에 따라 가용한 자료의 종류와 양의 변화에 따른 EUR 예측의 오차와 불확실성 변화 추이를 분석하였다. 특히, 초기 생산이 이루어지지 않아 저류층 정보인 정적자료만 있는 경우, 초기 최대 생산이 이루어지는 지점, 6개월 및 12개월 생산량이 확보된 시점 등을 기준으로 머신러닝의 EUR 예측 신뢰도를 분석하였다.
연구방법
랜덤 포레스트(random forest, RF)
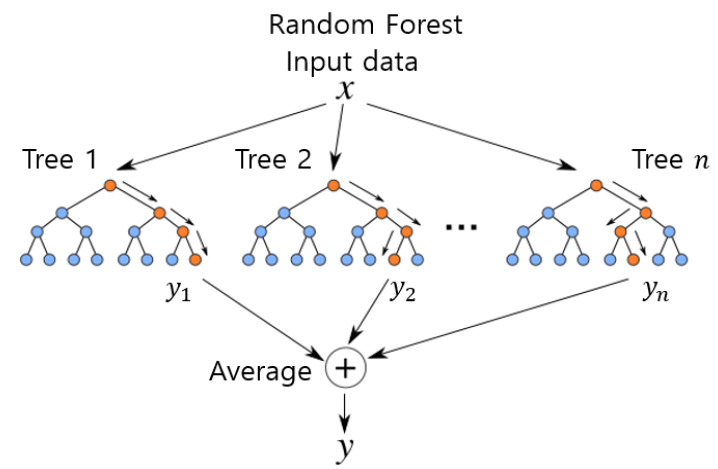
트리 기반 모델들은 성능이 뛰어나 많이 사용되는 지도 학습 알고리즘 중의 하나이다. 이들은 분류와 회귀 문제에 모두 사용이 가능하고, 선형 데이터뿐만 아니라 비선형 데이터에도 쉽게 적용이 가능한 모델이다(Yoon et al., 2018). RF는 많은 수의 서로 상관되지 않은 결정트리(uncorrelated decision tree)들로 구성된 앙상블 기반 머신러닝 알고리즘이다(Breiman, 2001). 앙상블 학습(ensemble learning)은 머신러닝에서 여러 개의 모델을 학습시킨 뒤 그 모델들의 예측 결과들을 이용해 하나의 모델보다 더 나은 결과를 예측하는 것을 말한다. 또한, RF는 CART(classification and regression trees) 알고리즘 기반으로 구성되어 입력 데이터와 출력 데이터의 종류에 제약이 거의 없다. Fig. 1은 RF의 일반적인 구조를 나타낸 것으로 다수의 결정트리로 구성된다.
RF 모델 내의 각각의 결정 트리는 학습 데이터(training data)의 서브샘플과 예측 변수의 서브샘플로 모델링된다. 데이터의 서브샘플은 중복을 허락하는 배깅(bagging)과 중복을 허락하지 않는 페이스팅(pasting)으로 구별되는데, 배깅은 “boostrap aggregating”으로서 샘플 모집단에서 중복을 허락하여 모집단의 개수만큼 샘플링한 후 머신러닝에 사용하는 방법을 의미한다. 결정트리의 학습과정에서는 하위노드에서의 출력변수의 목적함수(objective function)가 최소가 되도록 하는 분기점을 찾아 이를 기준으로 데이터를 분할하여 두 개의 하위노드를 형성한다. 목적함수는 식 (1)을 통해 계산되는데, 각 노드마다 이러한 분할 과정을 거쳐 단말 노드인 리프(leaf)의 크기가 최솟값에 도달하면 번째 트리의 학습이 완료된다.
여기서, 는 번째 트리의 목적함수이며, 은 데이터의 개수, 첨자 와 는 각각 왼쪽과 오른쪽 하위노드를 의미한다. 그리고 는 하위노드에 포함된 번째 샘플의 출력변수에 대한 참값이며, 은 하위노드에 포함되는 데이터의 평균을 의미한다.
위의 과정을 미리 정한 횟수만큼 반복하면 트리 앙상블이 형성되며, 각 트리의 출력값은 모두 입력자료에 대한 예측값으로서의 가능성을 가진다(Vyas et al., 2017; Jeong, 2020). 이 중 대표 예측값은 산술평균(arithmetic mean) 또는 중앙값(median value)으로 결정한다. RF 모델의 성능을 측정하는 지표로는 식 (2)와 식 (3)의 MAE(mean absolute error) 및 MAPE(mean absolute percent error)를 사용한다.
여기서, 는 번째 데이터의 참값, 는 번째 데이터에 대한 RF 예측값이며, 은 데이터의 개수를 의미한다.
RF의 장점 중 하나는 트리기반 모델로서 특성변수의 스케일에 영향을 받지 않기 때문에 데이터의 스케일링 과정이 필요하지 않다는 점이다(Ashan et al., 2021). 또한, 배깅을 사용하는 경우 학습결과에 대한 검증을 위해 따로 데이터를 준비할 필요가 없는 점이다. 배깅은 중복을 허용하여 서브샘플링을 하기 때문에 한 세트의 서브샘플링 후 전체 데이터 중 평균적으로 37%의 데이터는 선택되지 않는데, 이를 oob(out-of-bag) 샘플이라 한다(Geron, 2019). RF 모델은 일반적으로 수백 개의 트리로 구성되며, 트리마다 oob 샘플이 다르기 때문에 RF 모델의 oob 샘플은 결과적으로 학습데이터 전체가 된다. 즉, 충분한 수의 트리로 구성된 RF 모델에서는 oob 샘플을 검증 데이터로 사용하며 교차검증(cross validation)과 동등한 결과로 인정된다(Hastie et. al, 2008). RF는 많은 수의 결정트리의 앙상블 모델이므로 예측 결과에 대한 불확실성 분석이 용이하다. 즉, RF를 구성하는 결정트리의 예측 분포로부터 P10, P50, P90 값을 구할 수 있다. P90와 P10 사이에 실제 값이 존재하는 비율 및 불확실성을 나타내는 P90와 P10을 통해 모델의 예측 성능을 분석할 수 있다.
베이즈 최적화(Bayesian optimization)
머신러닝 모델의 내부변수 즉, 하이퍼 파라메터(hyper- parameter)를 최적화하는 방법의 하나로 베이즈 최적화법이 사용된다. 베이즈 최적화는 베이즈 정리를 기초로 하며, 베이즈 정리는 기존의 관측 데이터로부터 산출한 사전 확률(prior probability)에 새로 관측한 자료의 결과를 결합하여 사후 확률(post probability)를 도출하는 방법으로 식 (4)와 같이 표현된다(Krasser, 2021).
여기서, 는 가 관찰되었을 때 모델 의 사후 확률을 의미하고, 는 가 발생할 확률, 는 모델 의 사전 확률, 그리고 는 모델 가 주어졌을 때 가 발생할 확률인 우도(likelihood)를 나타낸다.
베이즈 최적화는 주어진 자료를 사용하여 구성하는 대리모델(surrogate model)과 조사할 다음 위치를 추천하는 획득함수(acquisition function)로 이루어진다. 대리모델은 주어진 자료의 목적함수를 사용하여 구성되며 미지의 지점에 대한 목적함수 추정을 위해 식 (5)와 같이 확률모델인 가우스과정(Gaussian process)을 사용한다.
여기서, 는 에서 추정하는 목적함수 값이며, 는 에서 평균, 는 와 목적함수 값을 알고 있는 사이의 공분산(covariance)을 의미한다. 은 평균 와 공분산 를 가지는 가우스분포로부터 값이 확률적으로 결정된다는 것을 의미한다.
획득함수는 조사할 다음 위치를 선정하기 위해 사용되는 것으로 기대개선(expected improvement) 방법이 일반적으로 사용된다. 기대개선은 기존에 알려진 목적함수의 최솟값보다 더 작은 목적함수를 획득할 수 있는 위치를 선정하는 것으로 식 (6)을 사용하여 계산된다.
여기서, 는 에서의 기대개선 값이며, 는 기댓값, 는 알려진 위치 중에서 최소의 목적함수를 나타내며, 는 에서의 목적함수를 의미한다. 식 (6)에 의해 여러 위치에 대한 기대개선을 계산한 후 기대개선이 가장 크게 나오는 위치를 다음 조사 위치로 선정하게 된다.
수정 쌍곡선법(modified hyperbolic)
셰일가스 생산의 경우 수압파쇄 등의 유정완결 기술을 적용하여 초기 생산량이 증가한 뒤 급격하게 감소하는 감퇴현상을 보인다. 따라서 초기 감퇴율(initial decline rate) 이 크고 저류층 경계까지 도달하는데 오랜 시간이 걸려 천이유동구간(transient period)이 길어져 감퇴지수(decline exponent) 의 값이 1을 초과하는 특징을 나타낸다. 감퇴지수의 값이 1이 넘지 않는 것을 가정한 전통적인 Arps 감퇴곡선인 식 (7)을 그대로 사용할 경우에 궁극가채량을 과대 산정하거나 실제 생산 프로파일을 반영하지 못하는 한계가 있다(Shin, 2013).
여기서, 는 초기 생산량, 는 시간 시점의 생산량, 는 감퇴지수, 그리고 는 초기 감퇴율을 의미한다.
이와 같은 문제를 해결하기 위한 방법 중 하나로 셰일 저류층의 초기 감퇴율이 높은 생산 프로파일 특징을 반영한 수정 쌍곡선법(Robertson, 1988)이 사용되고 있다. 수정 쌍곡선법은 식 (7)의 Arps 쌍곡선식을 적용하다가 식 (8)로 계산되는 감퇴율이 최소 감퇴율(minimum decline rate) 에 도달하면 지수감퇴곡선인 식 (9)으로 전환하는 것이다.
여기서, 는 시점의 감퇴율을 의미하며, 은 최소감퇴율을 나타낸다. 일반적으로 최소 감퇴율은 경험적으로 5~10%/year를 적용한다.
연구내용 및 결과
대상 광구
이 연구에서는 미국 텍사스 Fort Worth 분지의 북부 지역에 위치한 Newark East Field의 Barnett Shale Gas Play에서 취득한 셰일가스 생산 데이터를 사용하였다(Fig. 2(a)). Fort Worth 분지는 주로 고생대 석탄기인 미시시피기(Mississippian)와 펜실베니아기(Pennsylvanian)에 형성되었다. Barnett Shale Gas Play는 Fig. 2(b)와 같이 상부(upper) Barnett Shale과 하부(lower) Barnett Shale로 나누어지며, 상부층과 하부층은 Forestburg 석회암 층에 의해 분리되어 있다. 하부층은 평균 300ft의 두께를 가지고 있으며, Ellenburger Group과 Viloa 석회암층 사이에 형성된 경사 부정합 위에 위치한다. 상부층의 두께는 평균 150ft이며, 미시시피기에 형성된 Marble Falls 석회암층이 덮여 있다(Bowker, 2007).
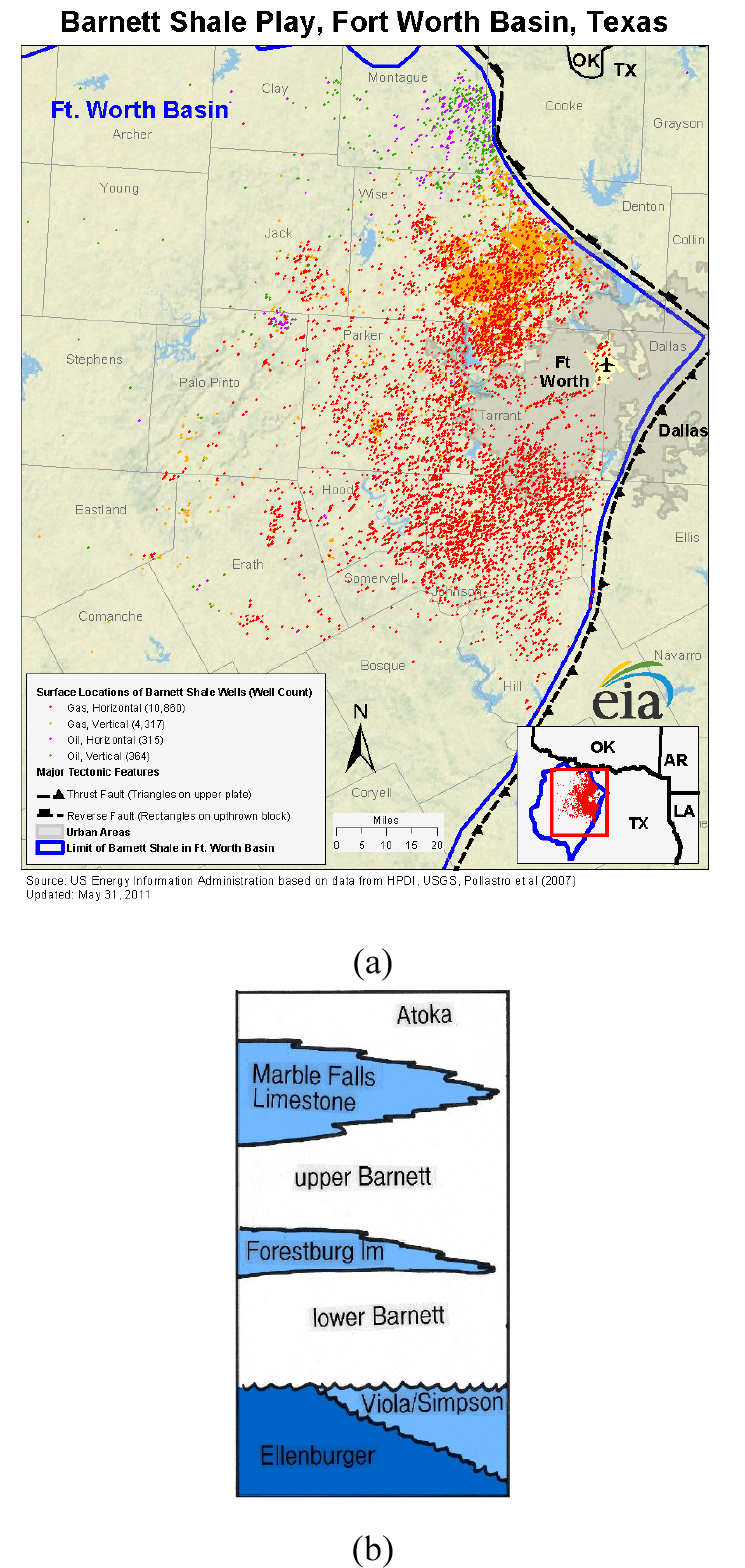
Fig. 2
(a) Location of Barnett Shale Play (b) A section of the stratigraphic in the northern portion of the Fort Wort basin (Bowker, 2007).
데이터 전처리(data preprocessing)
이 연구에서는 Barnett Shale에서 취득한 생산정 중 머신러닝 예측 모델을 개발하기 위해 아래와 같은 조건으로 전처리를 수행하였다.
1. 최소 60개월 이상의 생산량 정보
2. 월 생산량이 최소 1 MMcf/m 이상
3. 하부 Barnett 저류층에서 생산
4. 주 생산유체는 가스
5. 수평정
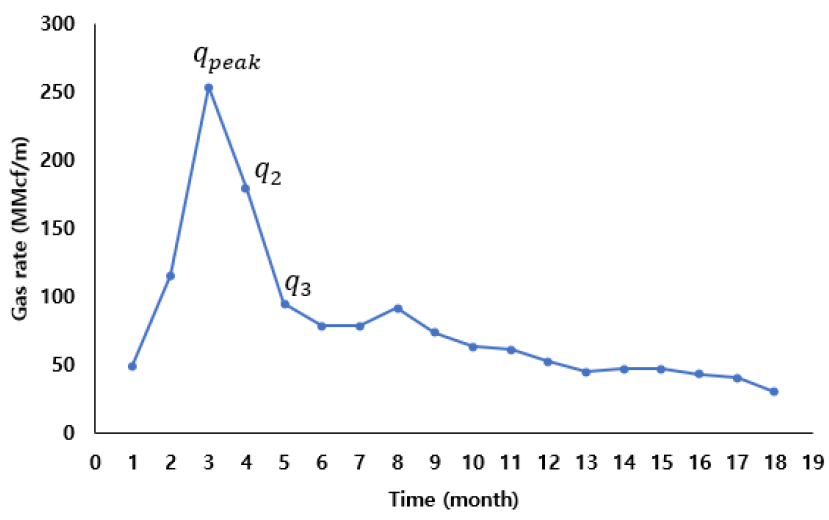
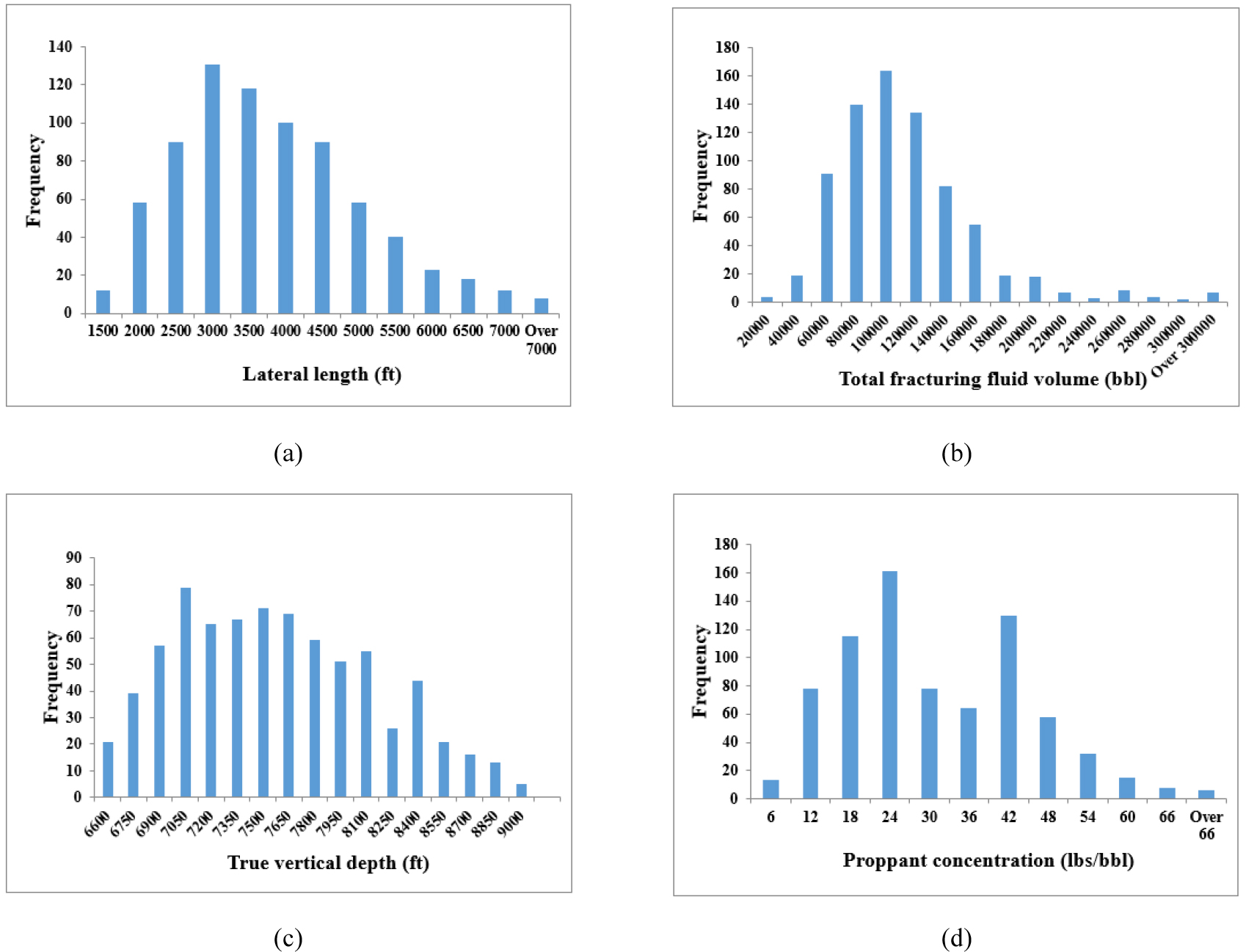
위의 조건을 통해 총 726개의 생산정이 선별되었으며, 가용한 입력 데이터의 종류는 Table 1과 같다. 입력데이터는 크게 정적 데이터와 동적 데이터로 나뉘며, 정적 데이터에는 생산정 정보 데이터, 수압파쇄 관련 완결 데이터, 그리고 저류층 데이터로 구성된다. 동적 데이터인 생산량 정보는 시점에 따라 초기 최대 생산량, 6개월간 월별 생산량, 12개월간 월별 생산량으로 분류하였다. Fig. 3에는 셰일가스 생산프로파일에서 초기 최대 생산량(, 첫 번째 월간 생산량에 해당), 2개월째 생산량() 등을 선정하는 예를 제시하였다. 초기 최대 생산량이 나오기 2~6개월 동안 생산량이 증가하는 지점이 있으나, 이는 수압파쇄의 파쇄수를 배출하는 기간이므로 이 연구에서는 해당 기간을 제외하였다. RF는 입력자료의 표준화가 필요하지 않은 방법이므로 추가적인 변환과정 없이 주어진 값 그대로 입력자료로 사용하였다. Fig. 4는 이 연구에서 사용한 몇가지 주요 정적자료의 분포를 나타낸 것이다.
Table 1.
Available data set for machine learning
| Data type | Input data | Comments |
| Static data | Azimuth (°) | Well information data |
| Longitude (°)1) | ||
| Latitude (°)1) | ||
| Lateral length (ft) | ||
| True vertical depth (ft) | ||
| Total fracturing fluid volume (bbl) | Completion data | |
| Proppant concentration (lbs/bbl) | ||
| Total proppant mass (lbs) | ||
| Lower perforation depth (ft) | ||
| Upper perforation depth (ft) | ||
| Formation thickness (ft) | Reservoir data | |
| Temperature (°F) | ||
| Dynamic data | Production rate (1~12 month) (MMcf/m) |
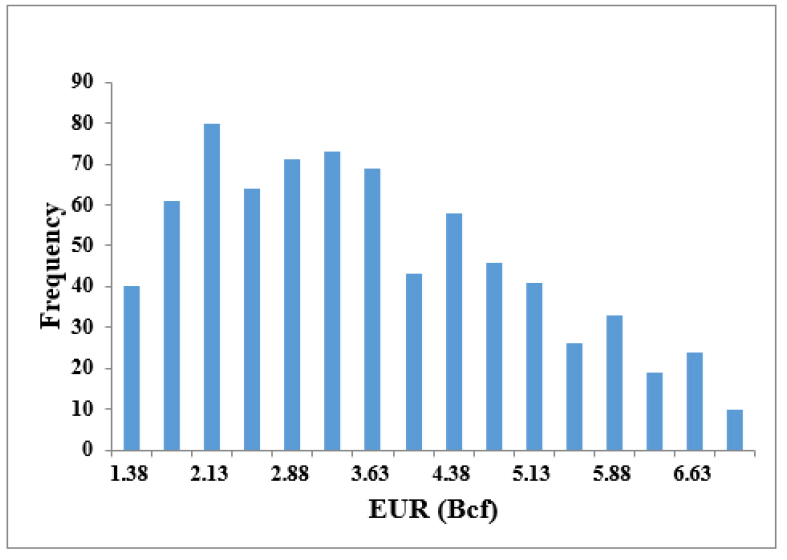
머신러닝의 목표가 되는 출력자료인 EUR을 계산하기 위해 생산정 별 생산량 데이터에 수정 쌍곡선법을 적용하였다. 수정 쌍곡선법 적용 시 생산가능 기간(production period)을 최대 600개월로 가정하였으며 지수감퇴곡선으로 전환하는 기준인 최소 감퇴율은 연간 5%로 설정하였다. Fig. 5는 이렇게 구한 EUR 분포를 나타낸 것으로, 평균 3.41 Bcf와 표준편차 1.47 Bcf로 분석되었다.
입력자료 특성 분석
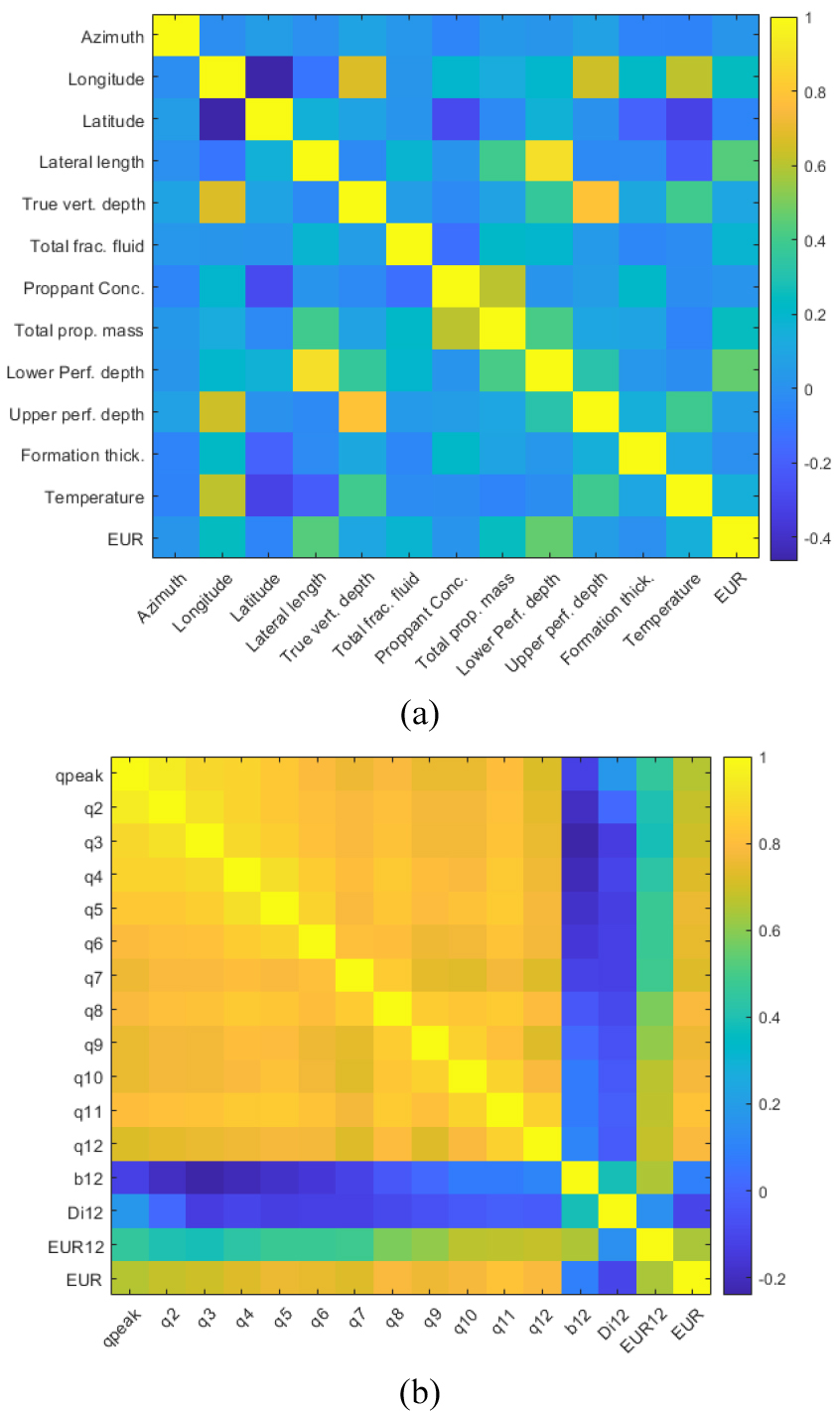
다음은 RF 모델의 입력자료 구성을 위하여 Table 1의 입력자료와 EUR과의 상관관계를 분석하였다(Fig. 6). 이를 위해 피어슨 상관계수(Pearson’s correlation coefficient)인 식 (10)을 사용하였다.
여기서, 는 피어슨 상관계수, 와 는 분석하려는 변량(variable), 와 는 두 변량의 평균, 그리고 은 자료의 개수를 의미한다.
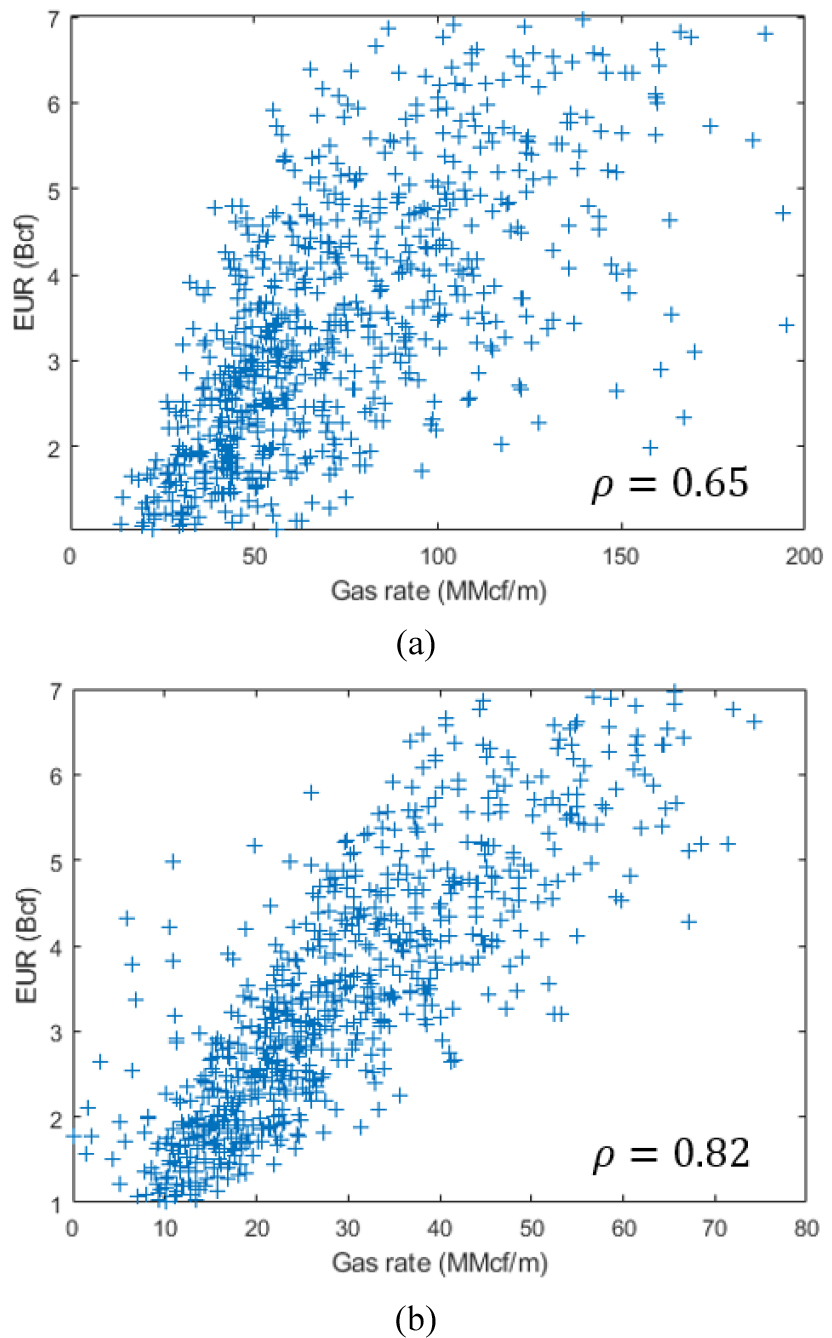
Fig. 6(a)는 Table 1의 정적자료와 EUR의 상관관계를 나타낸 것으로 수평정 길이 및 천공위치 등에서 상관계수 0.45 정도의 상관성을 보였다. 반면, Fig. 6(b)는 월간 생산량 자료와 EUR과의 상관관계로서 월간 생산량 자료와 최소 0.65(초기 최대 생산량 )에서 최대 0.82(11개월째 월간 생산량 )의 높은 상관성을 나타냈다. Fig. 7은 초기 최대 생산량과 11개월째 월간 생산량에 대한 EUR을 나타낸 것으로 초기 최대 생산량보다는 11개월째 생산량이 EUR과 선형적 상관성이 더 큰 것을 볼 수 있다.
Fig. 6(b)에서 생산량 자료 외에 , 그리고 EUR12도 포함되어 있다. 이는 12개월간 생산량 자료만을 사용하여 도출한 DCA(decline curve analysis) 변수 및 궁극가채량을 의미한다. 이와 더불어 6개월간 생산량 자료만을 사용하여 구한 DCA 변수 및 , 그리고 궁극가채량 EUR6도 입력변수로 활용하였다.
위의 상관성 분석을 바탕으로 생산기간에 따른 가용한 입력자료를 사용한 RF 모델의 EUR 예측성능을 분석하기 위해 Table 2와 같이 다양한 형태의 입력자료를 구성하였다. Case 1은 생산자료 없이 Table 1에 제시된 정적자료만 사용한 경우이며, Case 2는 정적자료와 더불어 초기 최대 생산량 값을 입력하는 경우이다. Cases 3~6은 6개월간의 생산량 정보를 다양한 형태로 추가한 것이다. Case 3은 정적자료에 6개월간 생산량 자료를 추가한 것이며, Case 4는 6개월 생산량에 대한 DCA 분석을 통해 도출한 와 를 입력자료로 추가한 것이다. Case 5는 Case 3에 6개월간의 생산량 자료로부터 DCA 분석을 통해 도출한 궁극가채량(EUR6) 정보를 포함시킨 경우이며, Case 6은 Case 4와 5를 결합한 것이다. Case 7에서 Case 10까지는 6개월 대신 12개월 생산량 정보를 사용하여 위의 과정을 반복 구성한 경우이다. 또한, Fig. 6(b)와 같이 월간 생산량 정보가 EUR과 매우 높은 상관관계를 띄고 있어서 Case 11과 12는 정적자료 없이 6개월 및 12개월간의 생산량 정보만 사용한 경우로서 생산량 정보만으로 EUR을 어떻게 예측하는지 분석하였다.
Table 2.
Definition of cases with input data for RF models
| Case | Case 1 | Case 2 | Case 3 | Case 4 |
| Input data | Static data |
Static data + 1) |
Static data + 2) |
Static data + 3) |
| Case | Case 5 | Case 6 | Case 7 | Case 8 |
| Input data |
Static data + + EUR64) |
Static data + + EUR6 |
Static data + |
Static data + 5) |
| Case | Case 9 | Case 10 | Case 11 | Case 12 |
| Input data |
Static data + + EUR126) |
Static data + + EUR12 |
RF 모델변수 최적화
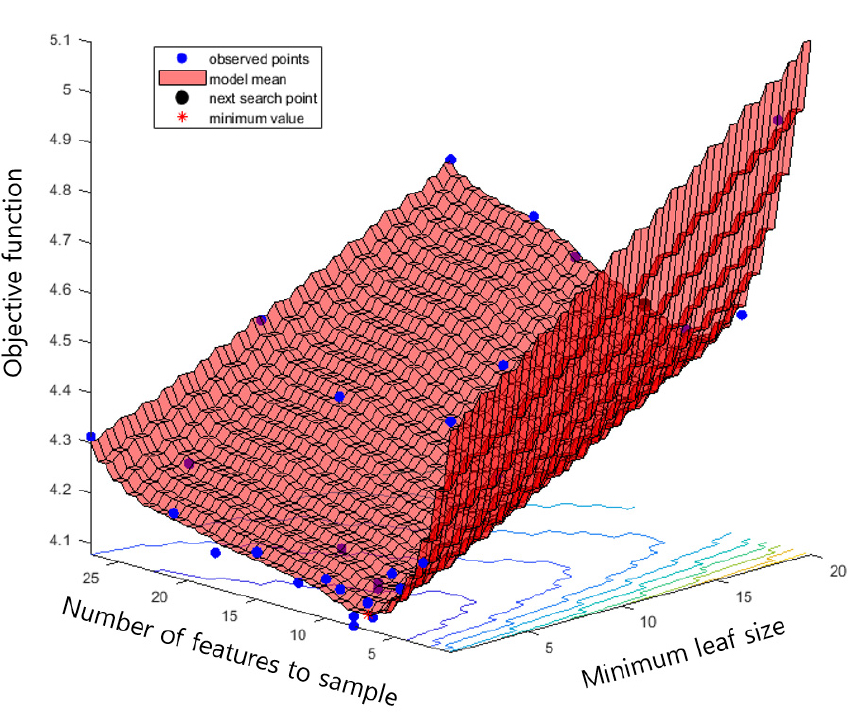
RF 모델을 사용하기 전 모델을 구성하는 내부변수에 대한 최적화를 수행하여 예측오차를 최소화시켰다. RF에서는 결정트리의 마지막 노드인 리프(leaf) 당 관측자료의 최소 개수(minLS)와 각 결정분할에 사용하기 위한 임의로 선택할 입력변수(특성변수)의 개수(numFTS)가 최적화할 주요 내부변수이다. 일반적으로 머신러닝의 내부변수 최적화를 위해 그리드 탐색(grid search), 랜덤 탐색(random search) 등의 방법이 있으나 이 연구에서는 탐색 효율이 뛰어난 베이즈 최적화법을 적용하였다(BorealisAI, 2021).
RF에 베이즈 최적화를 적용하기 위해 주요변수 minLS와 numFTS에 대해 식 (5)의 목적함수인 에 EUR 값에 대한 MAE(식 (2))를 사용하였다. 베이즈 최적화 과정을 30회 반복 수행 결과 Fig. 8과 같이 오차에 대한 3차원 곡면이 그려졌으며 이중 minLS = 1, numFTS = 8일 때 교차검증에 해당하는 oob 샘플에 대한 목적함수는 최솟값인 0.506으로 결정되었다. 즉, EUR을 예측하는 RF에서는 개별 결정트리를 학습시킬 때 리프당 관측값의 최소 개수는 1개, 결정분할에 사용할 입력변수 또는 특성변수의 값은 Table 1에 나열된 특성 중 8개를 임의로 선택하는 것이 최적이라고 분석되었다. 그러나 이 결과는 학습자료의 특성과 목적함수의 지역적 극소점에 따라 달라질 수 있으므로 이 연구에서는 RF 모델 학습 전 내부변수 최적화 과정을 항상 수행하였다.
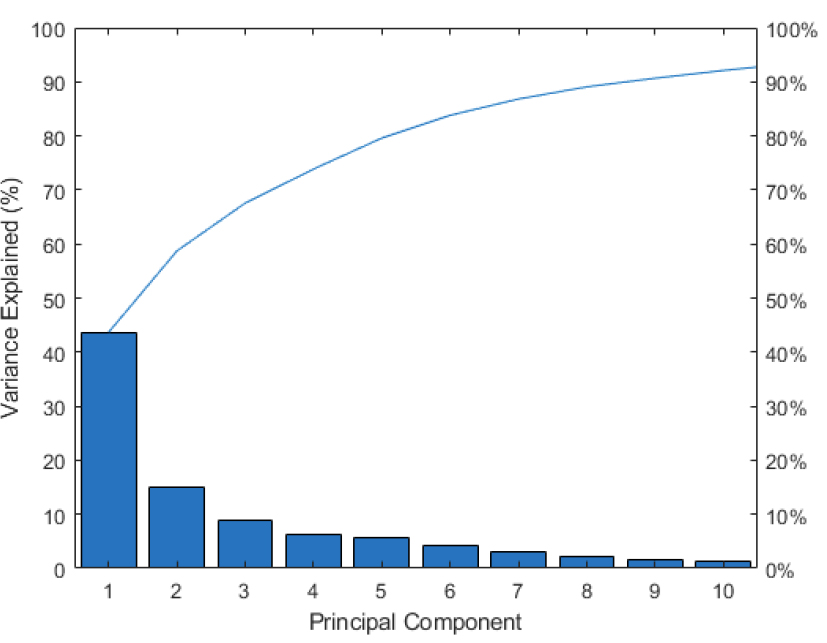
다음으로 RF 모델에 사용되는 입력자료의 주성분 분석(principal component analysis, PCA)을 수행하여 주요 주성분을 RF의 입력자료로 사용할 경우 예측성능이 향상되는지를 검토하였다. 주성분 분석은 특성변수의 종류가 많을 때 즉, 고차원의 특성변수를 저차원의 특성변수로 축소할 때 유용한 것으로 데이터 사이언스 분야에 널리 사용되고 있다(Han, 2015).
이 연구에서도 주성분 분석을 사용하여 입력변수의 차원을 줄일 경우 성능이 향상되는지 분석하였다. Table 1의 입력자료를 모두 사용하여 주성분 분석을 수행한 결과 10개의 주성분을 사용할 경우 입력자료에 대한 총 분산의 92.1%를 설명하는 것으로 나타났다(Fig. 9). 즉, 24차원으로 되어있는 입력자료를 10차원의 주성분 좌표계로 나타내면 전체 분산 중 92.1%를 손실없이 표현할 수 있다는 의미이다.
10차원의 주성분을 입력자료로 사용한 모델의 내부변수를 최적화하기 위해 베이즈 최적화를 적용한 결과 minLS = 1, numFTS = 5일 때 oob 샘플에 대한 목적함수는 0.551로 결정되었다. Table 3과 같이 MAE 오차는 주성분을 사용하는 경우에서 모든 입력자료를 사용하는 것에 비해 약 8.9% 더 크게 나타나 차원 축소에 의해 예측성능이 떨어지는 것으로 분석되었다. 이는 입력변수의 차원이 24차원으로서 머신러닝 학습에 사용하기에 과도한 차원이라 할 수 없고 10차원으로 축소하면서 전체 분산의 7.9%를 소실하게 된 결과라 할 수 있다. 따라서 이 연구에서 사용하는 규모의 자료에 대해서는 차원 축소없이 모든 데이터를 사용하여 머신러닝을 구축하였다.
Table 3.
Comparison of optimization results for hyper-parameters
| 24 input data | 10 principal components | |
| minLS | 1 | 1 |
| numFTS | 8 | 5 |
| MAE (Bcf) | 0.506 | 0.551 |
궁극가채량 예측 RF 모델 적용
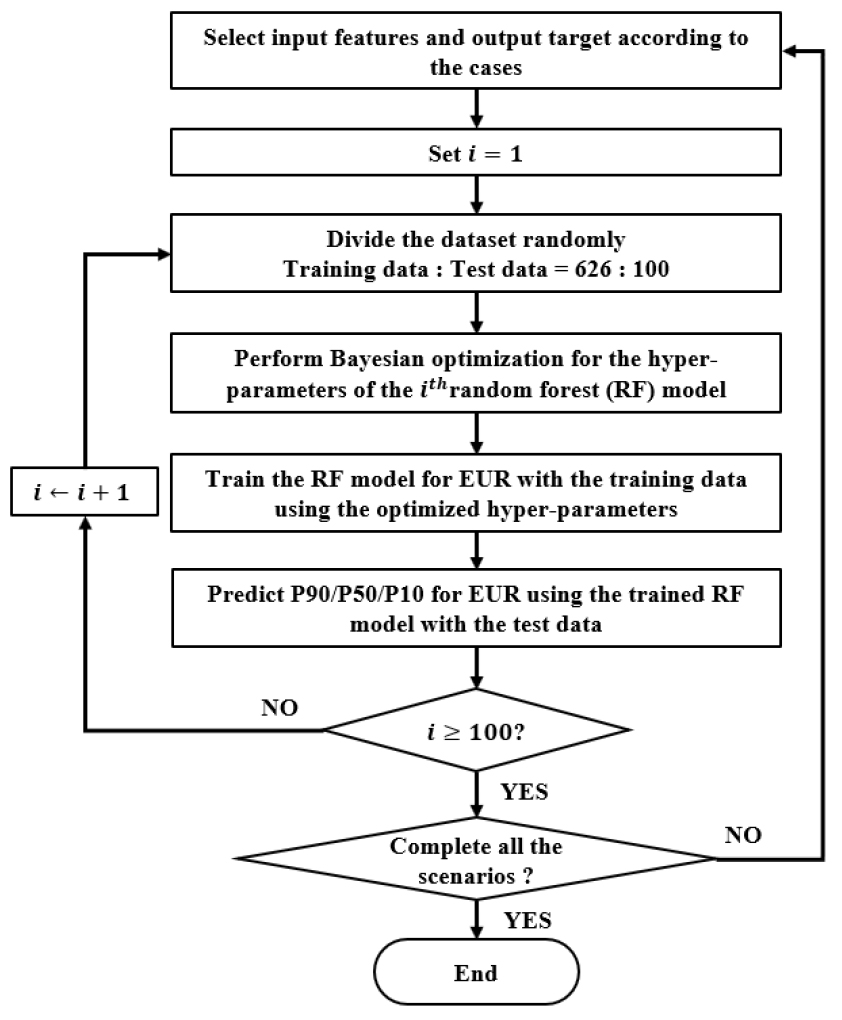
EUR 예측을 위한 RF 학습을 위해 726개의 생산정 자료를 626개의 학습자료와 100개의 시험자료로 나누었으며 이 중 학습자료를 사용하여 RF 모델을 학습시켰다. RF를 구성하는 결정트리 개수를 500개로 설정하고, 각 트리를 위한 학습자료 샘플링은 중복을 허용하는 배깅 방식을 사용하였다. Fig. 10은 이 연구에서 적용한 연구과정 흐름도(flowchart)를 나타낸 것이며, 전반적인 과정은 Table 2의 각 경우에 대해 RF 모델을 100회 반복 구축한 후 학습에 관여하지 않은 시험자료의 결과로부터 불확실성 분석을 수행하는 과정으로 구성된다.
이를 세부적으로 설명하면, 먼저 Table 2의 Case 1에 해당하는 입력특성을 선정한 후, 전체 데이터로부터 학습데이터 626개와 시험데이터 100개를 무작위로 나눈다. RF 모델을 학습시키기 전, 학습데이터에 대한 베이즈 최적화를 적용하여 내부변수인 minLS와 numFTS를 최적화한다. 학습데이터로 모델을 학습시킨 후 시험데이터를 입력하여 EUR을 예측하고 P90/P50/P10 값을 산출한다. 이러한 과정을 100회 반복하여 결과를 얻은 후 Case 2에서 12까지 순차적으로 동일한 과정을 반복한다.
RF 모델의 EUR 예측오차 분석
RF 모델의 예측성능에 대한 객관적인 결과를 얻기 위해 RF 학습 후 학습에 사용되지 않은 100개의 시험자료에 대한 예측성능을 분석하였으며, 그 결과를 Fig. 11과 Table 4에 정리하였다. Fig. 11은 Fig. 10의 흐름도에 따라 학습된 100개의 RF 모델 중 무작위로 선택한 하나의 모델에서 예측한 결과이며, Table 4는 100개의 시험자료에 대해 P50 EUR을 도출하고 절대오차인 MAE를 구하는 과정을 100개의 RF 모델에 대해 반복한 결과를 정리한 것이다. 즉, Table 4에 제시된 “Mean”과 “Standard deviation”은 100회 반복해서 계산된 MAE 값에 대한 평균과 표준편차를 의미한다.
Table 4.
Comparison of MAE of EUR prediction for test data
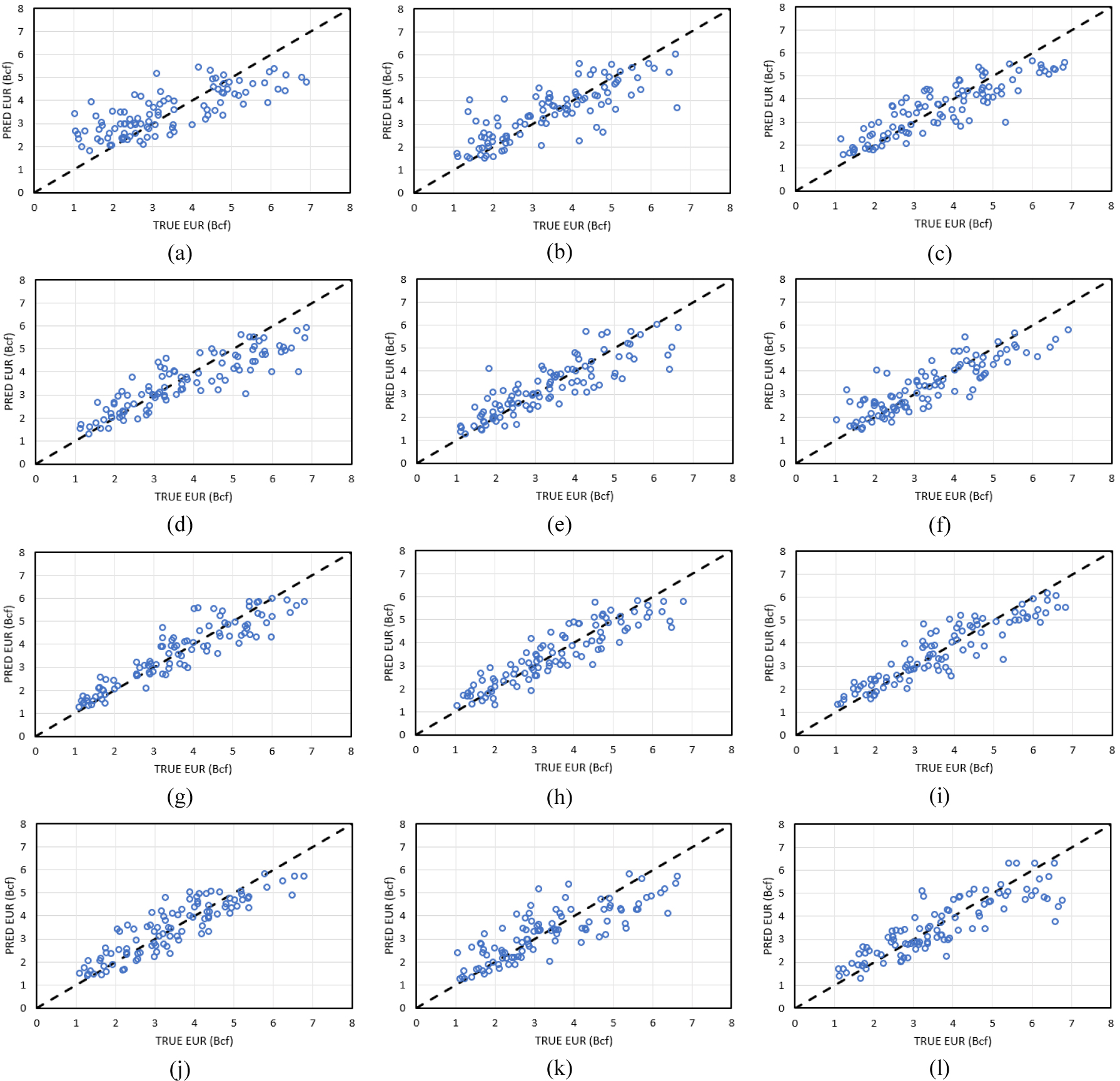
Fig. 11은 Case 1에서 12까지에 대한 시험자료의 예측값과 실제값을 그래프로 나타낸 것으로 점선은 실제값과 예측값이 일치하는 지점을 표시한 것이다. Fig. 11(a)와 같이 정적자료만 사용한 Case 1의 경우 실제값과 모델의 예측값 사이에 MAE = 0.85 Bcf(Table 4)로 다소 크게 나타나는 것을 볼 수 있다. 그러나 Fig. 11(b)와 같이 초기 최대 생산량을 추가로 사용한 경우(Case 2) MAE = 0.68 Bcf, 6개월 생산량 자료를 추가한 경우(Case 3, Fig. 11(c)) MAE = 0.58 Bcf, 그리고 12개월 생산량 자료까지 추가한 경우(Case 7, Fig. 11(g)) MAE = 0.50 Bcf로 나타나 생산자료가 많아질수록 오차가 줄어드는 것을 볼 수 있다.
Table 4에 제시된 바와 같이 6개월 생산량자료, , 그리고 EUR6의 조합을 사용한 경우인 Case 3~6의 MAE가 0.57에서 0.58 범위로 나타나 뚜렷한 성능 개선이 보이지 않았다(Fig. 11(c)~11(f)). 이러한 현상은 12개월 자료를 사용한 경우(Fig. 11(g)~11(j), Case 7~10)에도 동일하게 나타났다. 이는 월별 생산량 자료와 EUR의 상관성이 매우 높아 RF 학습에 크게 영향을 주지만 생산자료에서 파생된 DCA 변수 및 EUR은 영향력이 제한적이기 때문으로 판단된다. 즉, Fig. 6(b)에서 월 생산량 자료와 EUR과의 상관계수는 0.65에서 0.82 사이로 나타나지만, 및 EUR12과 EUR의 상관계수는 각각 0.1, -0.1, 0.64로서 EUR12과를 제외하면 나머지 두 입력자료는 상관관계가 거의 없는 것으로 판명되었다.
Case 11과 12는 정적자료 없이 EUR과 상관성이 매우 높은 6개월 및 12개월 생산량 자료만 사용하여 학습시킨 결과이다(Fig. 11(k)와 11(l)). Case 11의 시험데이터에 대한 MAE는 0.684 Bcf로서 정적자료와 초기 최대 생산량을 사용한 Case 2의 오차와 유사한 수준이다. 그리고 Case 12의 12개월 생산량 자료만 사용한 경우 MAE는 0.567 Bcf이며, 이는 정적자료와 6개월 생산자료 조합을 사용한 Case 3에 가까운 오차이다. 즉, 이 연구에서 수행한 경우들로만 한정한다면 정적자료를 사용하지 않을 경우, Table 4에 나열된 입력자료 중 한 단계 낮은 Case와 유사한 오차수준을 보이는 것으로 나타나 생산량 자료만으로도 상당히 의미있는 수준의 EUR 예측이 가능함을 보였다.
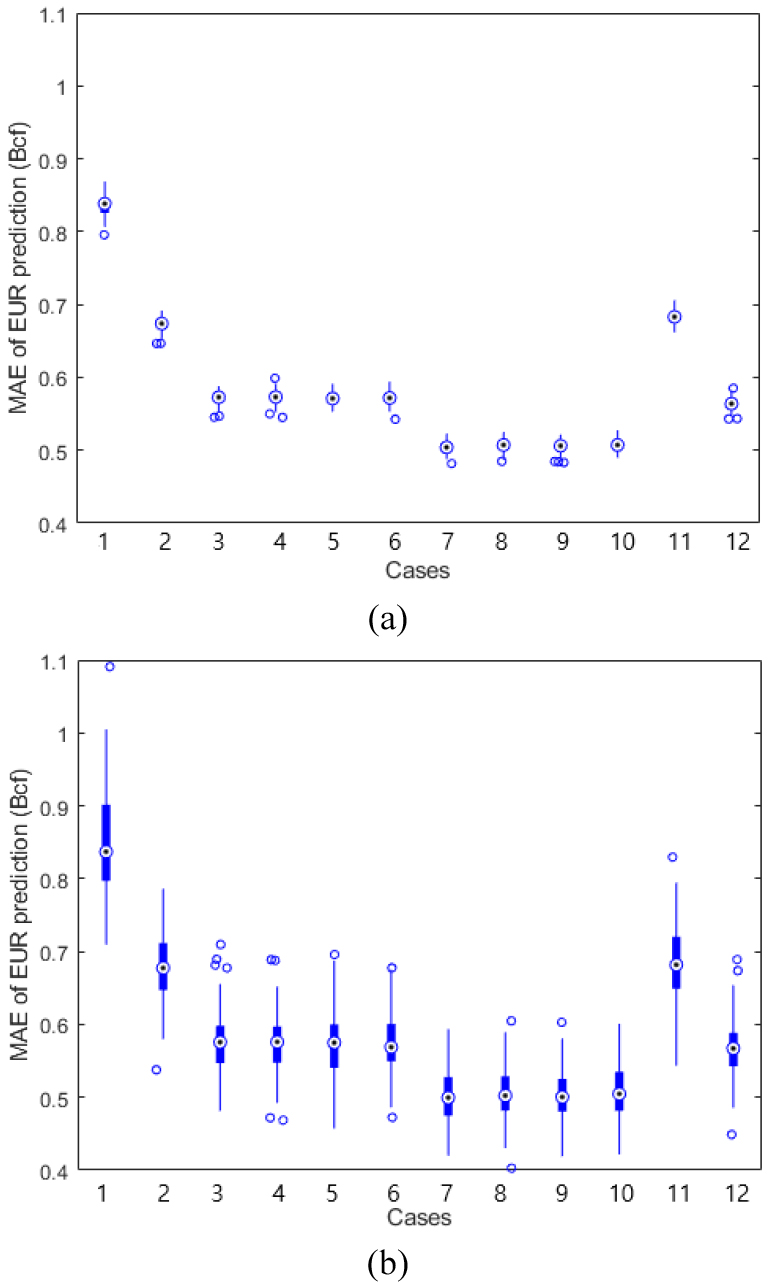
Table 4에는 시험자료뿐만 아니라 교차검증에 해당하는 oob 자료에 대한 MAE의 평균과 표준편차 분포가 제시되어 있으며, Fig. 12에 박스그래프로 표현되어 있다. 두 자료의 평균 MAE를 비교하면 모든 경우에 대해 매우 유사한 결과가 나타나는 반면, 시험자료에 대한 MAE의 표준편차는 oob의 결과보다 4~5배 높게 형성되었다. 그 이유를 다음과 같이 분석할 수 있다. 먼저, oob 자료의 변동성이 매우 낮게 형성되는 이유는 RF의 내부변수 최적화 과정에서 찾을 수 있다. 최적화의 목적은 바로 oob 데이터의 예측오차를 최소화하는 내부변수를 찾는 것이기 때문에 최적화된 RF는 oob 오차를 최솟값으로 수렴하게 한다. 그 결과 oob 자료의 MAE 분포는 일정한 값 주변으로 매우 조밀하게 형성되는 것이다. 시험자료 MAE 값의 변동이 큰 이유는 다음과 같이 유추할 수 있다. 이론적으로 검증자료와 시험자료의 개수가 충분히 크고 통계적으로 동일하다면 두 자료의 예측오차도 동일하게 나타날 것이다. 그러나 이 연구에서 사용한 자료가 제한적이기 때문에 Fig. 12와 같은 결과가 나타난 것이다. Fig. 10의 흐름도에 따라 100회의 RF 반복 생성시 시험자료는 100개의 무작위 샘플로 구성된다. 이때 시험자료의 수가 oob 자료보다 매우 작아 편향된 샘플로 구성될 수 있으며 이때 MAE 변동성이 크게 나타난다.
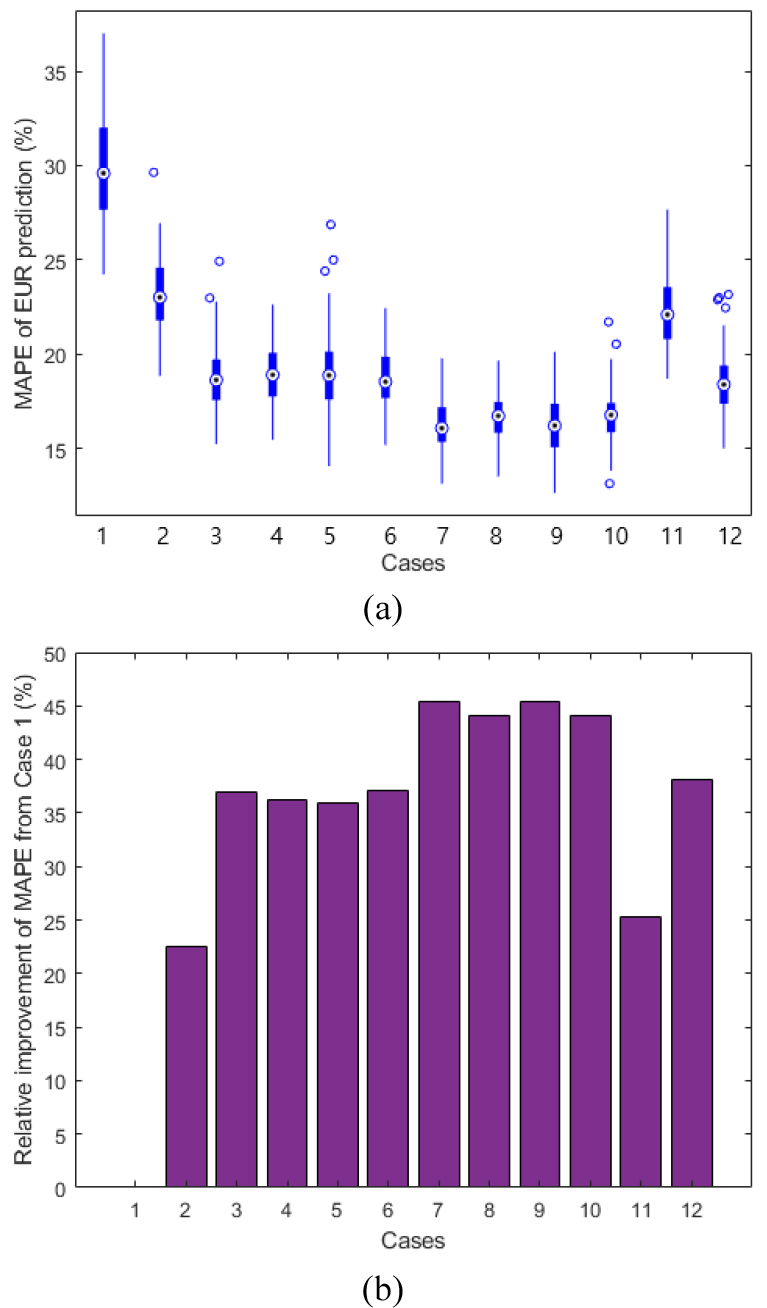
Fig. 13은 시험자료에 대한 EUR 예측정확도를 상대오차인 MAPE로 표현한 것이다. Fig. 13(a)는 100회 반복 실행한 Case 별 MAPE 분포에 대한 박스그래프이며, Fig. 13(b)는 Case 1을 기준으로 다른 Case의 MAPE의 상대적 향상도를 표현한 것이다. 정적자료만 사용한 Case 1의 EUR 예측 MAPE는 약 30%이며, 초기 생산량을 추가한 Case 2는 23%의 MAPE로 Case 1보다 23%[=(30-23)/30 × 100] 향상되었으며, 6개월 생산량 및 관련 정보를 추가한 Case 3에서 6까지의 경우 19%의 MAPE를 보여 Case 1 대비 36% 개선되었다. 12개월 생산량 및 관련 정보를 사용하는 Case 7에서 10까지는 16% MAPE로 45%의 개선효과가 나타났다. Case 11과 Case 12는 정적자료없이 6개월 및 12개월 생산량 자료만 사용한 경우로서 전술한 바와 같이 한단계 이전의 Case와 유사한 결과를 보였다.
RF 모델의 EUR 예측 신뢰구간 분석
이 절에서는 RF 모델의 EUR 예측에 대한 불확실성을 P90/P50/P10 개념을 통해 분석하였다. EUR 예측에 있어서 실제값을 정확히 예측하는 것은 사실상 불가능하므로 P90/P50/P10의 개념을 활용한 확률적인 방법을 적용하는 것이 예측의 불확실성을 평가하는 적절한 방법이다. P90는 실제값이 P90로 제시한 값보다 더 크게 나타날 확률이 90%이며, P10은 실제값이 P90 값보다 더 클 확률이 10%임을 의미한다. 즉 실제값이 P90와 P10 값 사이에 존재할 확률은 80%가 되므로 P10-P90는 80% 신뢰구간(CI, confidence interval)에 해당한다.
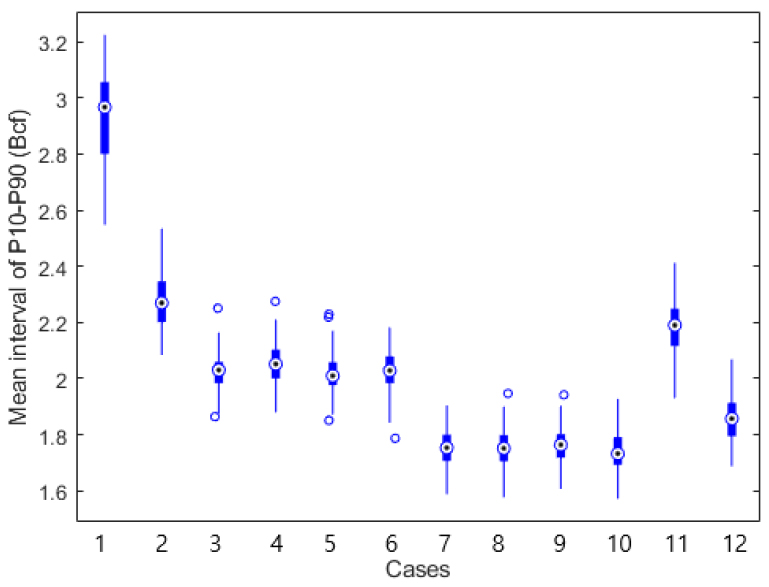
EUR 예측에서 P90/P50/P10을 구하기 위해 각 Case에 대해 RF 모델을 구성하는 500개 결정트리의 예측 분포를 사용하였다. Table 5는 시험자료에 대해 P90와 P10을 추정한 후 80% CI 분포를 계산한 결과이다. Case 1에서는 P90과 P10 사이의 CI값이 2.93 Bcf이며, 초기생산량을 추가한 Case 2에서는 2.27 Bcf, 6개월 생산량 관련 정보를 추가한 Case 3~6에서는 2.02~2.05 Bcf, 그리고 12개월 생산량 관련 자료를 추가한 Case 7~10에서는 1.74~1.76 Bcf로 줄어들었다. 즉 생산량 정보를 추가할수록 EUR을 예측하는 불확실한 구간이 줄어들며, 예측의 신뢰도는 높아졌다. 6개월 생산량 자료만 사용한 Case 11은 2.18 Bcf로 Case 2와 3 사이의 값으로, 12개월 생산량 자료만 사용한 Case 12는 1.86 Bcf로 Case 3과 7 사이의 값으로 계산되었다. 즉, 생산량 정보는 EUR과 매우 높은 상관관계가 있으며, EUR 예측의 불확실성 분석에서도 매우 신뢰도 높은 입력변수임을 확인하였다. Fig. 14는 100개의 시험자료에 대한 평균 CI의 분포를 표시한 그래프이다. Case 1과 같이 정적자료만 사용하는 경우 평균 신뢰구간의 변동폭이 크게 나타나지만, 생산량 자료를 추가하여 적용하는 경우 변동폭이 점차 줄어드는 형태를 보였다.
Table 5.
Comparison of confidence interval between P90 and P10 for the test data
| CI1) | Case | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Mean (Bcf) | 2.93 | 2.27 | 2.02 | 2.05 | 2.02 | 2.03 |
| Standard deviation (Bcf) | 0.15 | 0.10 | 0.07 | 0.08 | 0.07 | 0.07 |
| CI | Case | |||||
| 7 | 8 | 9 | 10 | 11 | 12 | |
| Mean (Bcf) | 1.75 | 1.75 | 1.76 | 1.74 | 2.18 | 1.86 |
| Standard deviation (Bcf) | 0.07 | 0.07 | 0.07 | 0.07 | 0.09 | 0.08 |
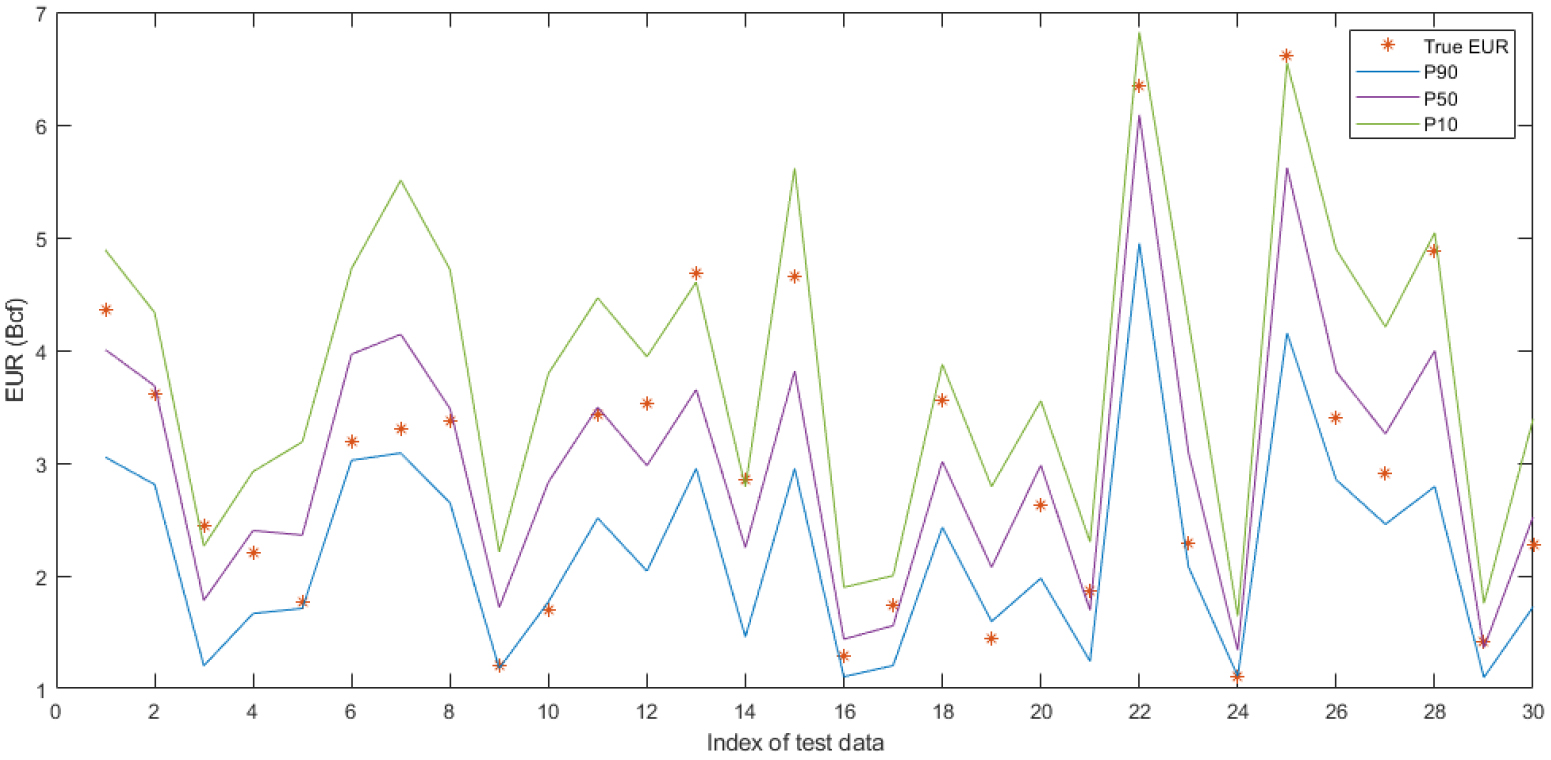
Table 6은 100개의 시험자료에 대해 실제 EUR이 P10과 P90의 신뢰구간 사이에 존재하는 비율, P90보다 작은 비율, 그리고 P10보다 큰 비율을 요약한 것이다. 먼저 실제 EUR이 80% 신뢰구간 내에 존재하는 비율은 모든 Case에 대해 79%~84% 사이에 있으며 평균 82%로 계산되었다. 또한, 실제 EUR이 P90보다 작거나 P10보다 큰 데이터의 비율도 대부분 7.5~10.9% 사이 존재하는 것으로 나타났다. Fig. 15는 100개의 시험자료 중 30개를 임의로 선택하여 실제 EUR과 RF 모델에서 예측한 P90/P50/P10 값을 그래프로 나타낸 것이다. 별표로 표시된 실제 EUR은 P90, P50, 그리고 P10에 각각 근접하여 신뢰구간에 포함된 경우도 있으며, P90보다 작은 경우 및 P10보다 커서 신뢰구간에 포함되지 않는 경우도 관찰된다. 이와 같이 신뢰구간에 대한 분석결과 80% 신뢰구간 내에 평균 82%의 자료가 포함되어 있어 이론상 80%에 매우 근접한 결과를 보였다. 이는 이 연구에서 구축한 RF 모델의 EUR 예측 적합성을 시사하는 것으로 판단된다.
Table 6.
Comparison of ratio of data with true EUR within CI, and out of CI for the test data
다음은 신뢰구간에 포함되지 못한 자료에 대해 분석으로 Table 6에 제시된 바와 같이 7.5~10.9%에 해당하는 시험자료에서는 실제 EUR이 P10-P90의 신뢰구간에 포함되지 않는 결과를 보였다. 이러한 자료에서 실제 EUR은 신뢰구간에서 얼마나 벗어나 있는지 분석하기 위해 실제 EUR이 P90보다 작은 경우 P90와 EUR 간의 상대오차를 계산하고, P10보다 큰 경우 P10과 EUR간의 상대오차를 계산하여 MAPE를 도출하여 Table 7에 요약하였다.
Table 7.
Comparison of MAPE for the difference between the true EUR and CI range for the test data with EUR out of prediction
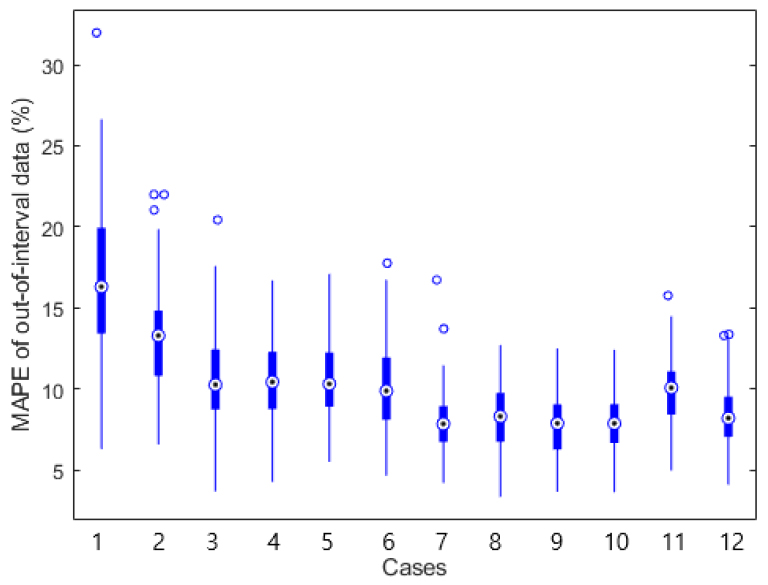
정적자료만 사용한 Case 1에서는 시험자료의 EUR이 신뢰구간을 벗어난 경우, 신뢰구간의 경계점에서 평균적으로 16.8% 떨어져 있는 것으로 분석되었다. 또한, 초기 최대 생산량을 추가한 Case 2에서는 13.0%, 6개월 생산량 관련 정보를 추가한 Case 3에서 6까지의 경우에서는 약 10.5%, 그리고 12개월 생산량 관련 정보를 추가한 Case 7에서 10까지는 약 8.0% 정도 차이가 점차 줄어드는 경향을 보였다. Case 11과 같이 정적자료 없이 6개월 생산량 자료만 사용한 경우는 Case 3에서 6까지의 정적자료 및 6개월 생산자료를 모두 사용한 경우와 통계적으로 매우 근접한 결과를 보였다. 12개월 생산량 자료만 사용한 경우에도 이와 유사하게 Case 7에서 10까지의 결과와 매우 유사한 결과를 보였다. Fig. 16은 100회의 RF 모델 반복 학습을 통해 신뢰구간과 실제 EUR의 상대적 차이인 MAPE의 변동을 박스그래프로 표시한 것이다. Case 별 MAPE의 변동폭이 상당히 크게 나타났으며, 입력자료의 정보량에 따라 평균값의 수준이 달라짐을 확인할 수 있다.
결 론
이 연구에서는 미국 텍사스 주에 위치한 Fort Wort 분지의 Barnett 셰일층에서 취득한 셰일가스 생산데이터를 바탕으로 RF 모델을 사용하여 입력자료의 종류와 양에 따른 EUR 예측의 불확실성을 분석하였다. 생산정의 정적자료, 초기 최대생산량, 6개월 생산정보, 12개월 생산정보 등의 조합을 사용하여 RF의 EUR 예측 오차를 분석하였다.
(1) 본 연구에서는 베이즈 최적화 기법을 통한 RF 내부변수 최적화 및 입력자료의 PCA 분석을 통해 EUR 예측을 위한 RF 모델을 최적화하였다. 또한, 연구결과 분석에 있어서 학습에 사용되지 않은 시험자료만을 사용함으로써 연구결과의 신뢰도를 높였다.
(2) 생산기간에 따라 입력자료의 종류와 양이 증가할수록 예측의 신뢰도가 향상되었고 정적자료의 영향력이 감소하는 것을 확인하였다. 즉, 셰일가스의 EUR 예측 시 초반 생산이 시작되기 전에는 정적자료의 활용이 중요하나, 비교적 단기간인 6개월 또는 12개월의 생산량 자료를 추가하면 정적자료만 사용한 경우 대비 EUR 예측오차를 각각 36%와 45% 개선할 수 있었다. 특히, 정적자료 없이 6개월 생산량 자료 및 12개월 생산량 자료만 사용한 경우에도 매우 우수한 예측성능이 확인되었다.
(3) P10-P90의 신뢰구간 분석에 있어서도 생산기간에 따른 입력자료가 증가할수록 신뢰구간의 개선이 뚜렷하게 나타났으며, 생산자료의 중요성이 다시 한번 확인되었다. 또한, 신뢰구간 내의 시험자료 포함 비율도 이론상 수치인 80%에 가까운 평균 82%로 나타나 EUR 예측을 위한 RF 모델의 적합성을 검증하였다.
(4) 이 연구에서 활용한 RF 모델은 Barnett Shale의 생산정 자료만을 사용하여 결과를 제시하였지만, 다른 셰일분지에 대해 동일한 과정을 수행한다면 범용적으로 적용가능할 것으로 사료된다. 즉, 이 연구에서 제시한 방법론은 초기 자료의 큰 변동성에 따른 DCA의 주관성을 배제할 수 있고, EUR 예측시 적정 신뢰구간을 제시하여 사업 위험도 평가의 유용한 도구로 활용될 수 있다.