서 론

탄성파 탐사는 크게 실체파(Body wave)와 표면파(Surface wave)를 이용하는 탐사법으로 구분할 수 있다. P파(Primary wave)와 S파(Secondary/shear wave)로 나눠지는 실체파를 측정하는 탐사는 매질 내를 전파하는 파의 반사 현상을 이용한 반사법 탐사나 굴절 현상을 이용한 굴절법 탐사를 이용해 지질구조를 파악한다. 표면파 탐사는 표면파의 분산 특성(표면파 탐사)을 이용하여 S파 속도 구조를 파악한다(O’Connel and Turner, 2011). 일반적으로 굴절법 탐사나 반사법 탐사는 능동형 탐사법인 반면, 지표면을 따라 전파하는 표면파 탐사는 송신원 유무에 따라 능동형과 수동형으로 나눌 수 있다. 수신기에서 기록된 파동장은 지구조에서 전파된 배경 잡음, 지진으로 인한 신호, 자동차 등 인공적인 물체들에 의해 만들어진 신호 그리고 인공 송신원에 의한 신호들까지도 포함할 수 있다(Curtis et al., 2006).

탄성파 간섭(seismic interferometry; SI)법은 측정한 트레이스 사이의 간섭현상을 이용하여 지하매질에 관한 정보를 얻는 방법으로 지하구조 영상화와 건축물 안정성 평가 및 손상 탐지, 산사태 예측 그리고 석유 개발 분야 등에 활용되고 있다(Miyazawa et al., 2008; Nakata and Snieder, 2014; Matzel et al., 2017; Zhang et al., 2019;). 탄성파 간섭법은 측정 신호들 사이에 발생하는 가상의 송신원으로부터 새로운 탄성파 신호를 생성하여 굴절법, 반사법, 그리고 미소진동 등 다양한 탄성파 탐사 데이터에 적용할 수 있다(Schuster, 2001; Forghani and Snieder, 2010; Dong et al., 2006). 탄성파 간섭법은 탄성파 잡음(seismic noise)의 자기상관(autocorrelation)을 통해 지층 경계면의 정보를 얻을 수 있다는 사실을 Cleaerbout(1968)가 최초로 밝혀내면서 시작되었다. 이후 시간에 대한 역전파를 통해 파원의 정보를 알아낼 수 있다는 연구(Fink, 1997) 등을 거쳐, Schuster(2001)가 서로 다른 위치의 수신기에서 측정한 탄성파 신호를 교차 상관하여 가상 송신원(virtual source)에 의한 신호를 얻을 수 있다는 것이 밝혀지면서 SI로 불리기 시작했다. 인공 송신원을 이용하는 능동형 탄성파 간섭법의 경우는, 수동형에 비해 비용적 효율성과 탐사 환경의 문제 등 탐사 시 고려해야 할 점이 더 많으므로 탄성파 간섭법에서는 수동 탐사법인 배경잡음 탄성파 간섭법(ambient noise seismic interferometry, ANSI)이 대표적으로 많이 사용되고 있다(이후, 특별한 언급이 없는 한 SI는 ANSI를 통칭) (Boullenger et al., 2015).

기본적인 탄성파 간섭법은 교차상관(cross correlation)을 적용하는 방법이 가장 대표적이며 이에 대한 적용과 이론들이 많이 연구되었다(Larose et al., 2006; Schuster, 2009; Snieder et al., 2009). 곱풀기(deconvolution)를 이용한 방법은 건물을 모니터링하고 손상 부위를 분석하기 위해 많이 사용되며(Curtis et al., 2006; Vasconcels and Snieder, 2008) 결맞음(cross coherence)을 이용한 방법은 지진학(seismology) 분야에서 주로 사용한다(Prieto et al., 2009; Nakata et al., 2011). 그 외에도 지구조 해석(Shapiro et al., 2005), 배경잡음에 간섭법을 이용해 반사파 영상을 획득하는(Draganove et al., 2009) 등의 목적으로 사용한다.

이러한 SI는 지질구조 파악이나 건물 손상 평가 등을 위해 여러 분야에서 활용되고 있으며 국내에서 역시 지진 배경잡음 상관분석을 이용한 신호추출 및 음원의 형태에 대한 연구(Jang et al., 2009; Kang, 2011; Ko and Jang, 2017), 중합전 심도 구조보정(Kim et al., 2011), 간섭법을 이용한 가상반사파의 영상 특성(Kim et al., 2018) 등 다양한 연구들이 진행되었다. 그러나 이론 및 활용분야에 대해 기술보고한 사례가 국내에 없기 때문에 이 기술보고에서는 탄성파 간섭법의 적용 방법과 이를 이용한 실제 탐사 사례들을 소개하고자 한다. 먼저 간섭법의 기본적인 이론인 교차상관과 곱풀기, 결맞음을 이용한 간섭법과 각각의 방법들이 어떻게 쓰일 수 있는지에 대해 서술하고 탄성파 탐사법인 반사법, 굴절법, 표면파 탐사에 적용되는 탄성파 간섭법의 활용에 대하여 기술하였으며 각 분야의 실제 적용사례들을 분석하였다.

탄성파 간섭법 이론

탄성파 간섭법은 두 수신기를 한 쌍으로 생각하고 각 수신기에서 측정한 신호들을 이용한다. 측정한 송수신 신호에 간섭법을 적용하게 되면 기준 수신기 위치에서 마치 새로운 송신이 발생한 것과 같은 가상의 송신원이 생기게 된다. 이 때 발생한 새로운 송수신 신호를 획득하여(Lobkis and Weaver, 2001; Wapenaar et al., 2004), 다양한 탄성파 탐사 데이터를 생성할 수 있다. 이러한 간섭법에는 교차상관, 곱풀기, 결맞음 등을 이용하는 방법이 있다.

상관분석에 기초한 방법

교차상관(cross-correlation)을 이용한 탄성파 간섭법은 가상의 송신원 또는 수신원을 갖는 새로운 탄성파 신호를 만들어서, 지하 매질에 관한 정보를 얻는 것이다. 1 차원의 간섭법에 대해서 간단히 살펴보기 위해, 먼저 xS에 위치한 송신원 s에서 발생한 송신파형(s(t))을 두 개의 수신기 xA와 xB에서 측정한 신호를 다음과 같이 표현한다.

여기서 *는 곱말기(convolution)이고, G는 손실없는 매질에서 스파이크 송신원에 의한(impulsive source) 신호인 그린함수(Green function) 또는 충격함수반응(impulse response function; IRF)이다. 또한, 균질 속도 매질에서 xS 평면파가 발생하여 두 개의 수신 지점(xA와 xB)에서 측정되는 충격함수반응은 각각 다음과 같이 표현할 수 있다(Wapenaar et al., 2010).

여기서 𝛿는 스파이크 송신원의 수학적 표현인 Dirac-delta 함수이고 t_A와 t_B는 x_s에서 xA와 xB까지 평면파가 각각 도달하는 시간이다. xA와 xB의 충격함수반응(식 (3), 식 (4))을 교차상관 하면 송신원이 A에 있을 때, B에서의 충격함수반응(G(xB,xA,t))을 다음과 같이 얻을 수 있다.

여기서 두 번째 항의 시간을 역전하여, 두 충격함수를 곱말기 했으므로 위 식은 두 신호의 교차상관이며, 이를 적분식으로 표현하면 다음과 같다.

이때, 우측항을 델타 함수로 치환하면 다음과 같다.

여기서 c 는 파의 속도이며, 진동수 영역에서 식 (7)을 나타내자면 각 수신기 xA와 xB에서의 그린함수를 GA,GB라고 치환하였을 때 진동수 영역의 충격함수반응 H(ω)은 다음과 같은 식으로 나타나며 GB(ω)¯는 GB(ω)의 켤레(conjugate)이다.

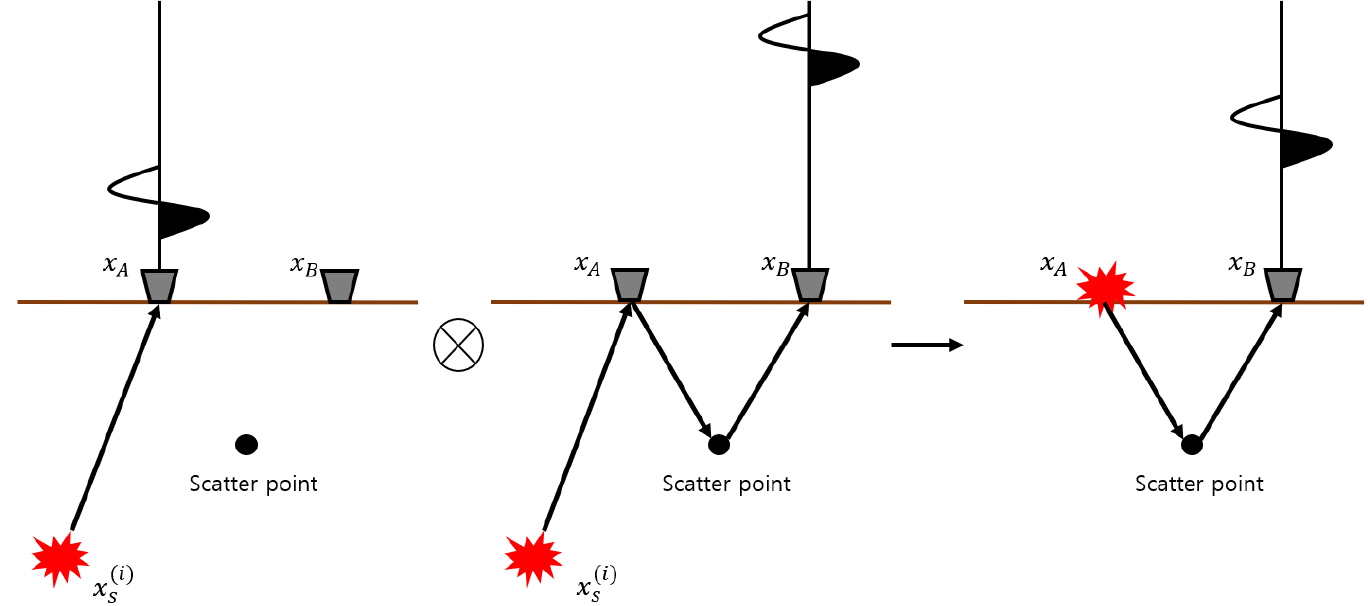
1차원에서 수신점 A와 B에 도달한 파의 경로 중 xS에서 xA까지가 공통인 것처럼 G(xA,xS,t)와 G(xB,xS,t)의 파선 경로에 공통된 구간이 포함되어 있는 경우, 위상차 eiω(tB-tA)는 주시의 차와 같다(Fig. 1). 따라서, 교차상관 후 공통된 경로를 제외한 xA에서 xb로 가는 경로의 주시만 남게 된다. 즉, tB-tA의 주시에 대한 충격 신호로 남게 되며 이 충격 신호는 가상의 송신원 xA에서 발생한 파가 수신기 xB에서 측정된 데이터로 해석할 수 있고, 이는 그린함수 G(xB,xA,t)가 된다(Fig. 1(d)). 만약 t=0 대신 t=tS에서 송신이 발생하게 되더라도 xA와 xB에서 측정한 충격신호가 각각 주시 ts만큼 지연되어 상쇄되기 때문에 xS에 있는 송신원 자체의 정보는 크게 영향을 미치지 않는다. 교차상관분석을 통해 xA에서 xB로 전파된 그린함수는 G(xB,xA,t)가 되고, 1차원 그린함수는 식 (5)와 같이 나타나게 된다.

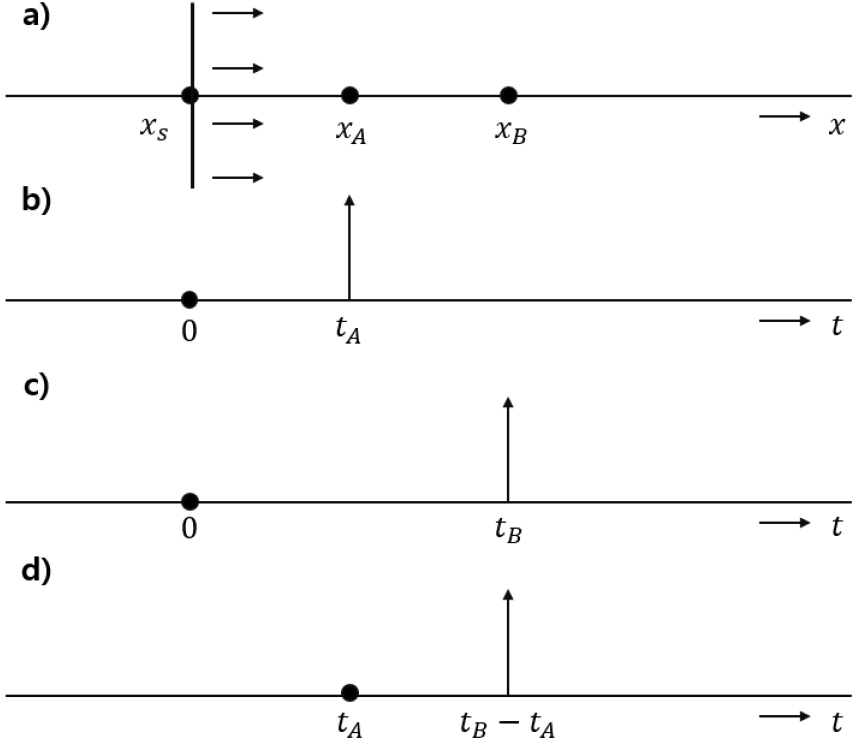
Fig. 1.

One-dimensional example of direct-wave interferometry: a) a right traveling plane wave represented as an impulse function at xs, b) impulse reaching a receiver located at point xA at time tA, c) impulse reaching a receiver located at point xB at time tB, and d) result of cross correlating the impulse functions in b) and c) (modified by Wapenaar et al., 2010).

곱풀기에 기초한 방법

교차상관을 이용한 탄성파 간섭법 방법은 가장 대표적이며 많은 곳에서 적용되고 있지만, 파가 전파될 때 에너지의 손실이 없다는 가정을 하기 때문에 실제 매질에서는 파가 전파할 때 감쇠가 발생하여 교차상관을 이용한 데이터가 맞지 않을 수 있다. 이를 해결하기 위해 교차상관 과정을 곱풀기로 대체하기도 한다(Sneider, 2006; Wapenaar et al., 2011). 곱풀기(deconvolution)를 적용한 기법에서는 교차 상관 분석을 이용한 방법과 마찬가지로 두 개 이상의 수신기를 필요로 하며, 송신원의 스펙트럼 진폭의 변화를 보정하므로 교차상관분석을 이용한 경우보다 더 큰 대역폭으로 파동을 추출할 수 있다(Vasconcelos et al., 2008). 또한, 곱풀기를 이용할 경우에는 경계 조건을 달리해 그린 함수를 획득할 수 있기 때문에 이를 이용하여 최근에는 구조물의 탄성파 전단특성을 추출하기 위해 많이 사용되고 있다(Todorovska and Trifunac, 2008; Nakata and Snieder, 2014; Wen and Kalkan, 2017; García-Macías and Ubertini, 2019). 진동수 영역에서 주어진 파동장 u(xA,B,ω)=G(xA,B,s)S(ω)로 표현할 수 있으며 이때 곱풀기는 다음과 같이 나타낼 수 있다.

여기서 DAB는 진동수 영역에서 곱풀기로 얻어지는 충격함수반응이며 이 경우 송신파형 S(ω)가 제거되므로 송신 파형의 영향을 없앨 수 있다. 이는 u(xB,ω)로 u(xA,ω)의 측정된 데이터를 곱풀기한다는 것을 의미하며 교차상관 간섭법과 같이 xB에서 생성된 가상의 파가 전파되고 xA에서 기록되는 것을 보여준다.

식 (9)에서 G(xA,s)G(xB,s)¯가 위상을 결정하게 되므로 D_AB는 교차상관 간섭법과 비슷하게 표현된다. 하지만 실제로 그린함수의 파워스펙트럼(power spectrum)은 간섭법의 파들이 겹칠 때 진동수에 따라 크게 달라진다. 특히, xA에서 측정된 데이터와 xB에서 측정된 데이터가 동일할 경우, 식 (9)는 DAB=1이 되며 시간영역의 DAB(t)=δ(t)와 같아진다. 이는 δ(t) 함수로 인해 0이 아닌 시간을 제외하고는 곱풀기 결과가 0과 같다고 할 수 있으며 고정된 경계 조건(clamped boundary condition)에 해당된다(Vasconcelos and Snieder, 2008).

결맞음에 기초한 방법

결맞음(cross-coherence)은 정규화 된 교차상관으로 볼 수 있다. 진동수 영역과 시간영역에서 배경잡음장(ambient noise field)과 그린함수 사이 공간적 결맞음(spatial coherency)의 관계성을 표현하여 지질 구조에 대한 정보를 획득할 수 있으며(Prieto et al., 2009) 이를 식으로 표현하면 다음과 같다.

결맞음은 교차상관과 비슷한 결과를 보이지만, 곱풀기를 이용할 때와 같이 송신 파형의 영향은 제거되며 분모의 값으로 인해 진폭에 대한 정보 역시 사라진다. 따라서 각 파동장의 위상에 대한 정보만 남게 되어 계측 상의 문제, 지표 부근에서의 송신원으로 인한 갑작스러운 진폭 변화 발생 등의 상황에 적용할 수 있다(Snieder et al., 2009).

탐사법에 따른 간섭법 활용

탄성파 간섭법은 주로 천부를 탐사하거나 표면파 및 직접파를 재구성하는 데 자주 사용된다(Curtis et al., 2006). 또한, 기존의 반사파 탐사로는 확인하기 힘들었던 복잡한 암염층의 형태 등의 문제를 반사파 데이터에 간섭법을 적용하여 해결하거나 선두파의 SNR을 증가시키기 위해 굴절법 데이터에도 간섭법을 적용할 수 있다(Dong et al., 2006). 여기에서는 표면파 탐사, 반사법 탐사, 굴절법 탐사에 간섭법을 적용하는 방법에 대해서 알아보고자 한다.

반사법 탐사

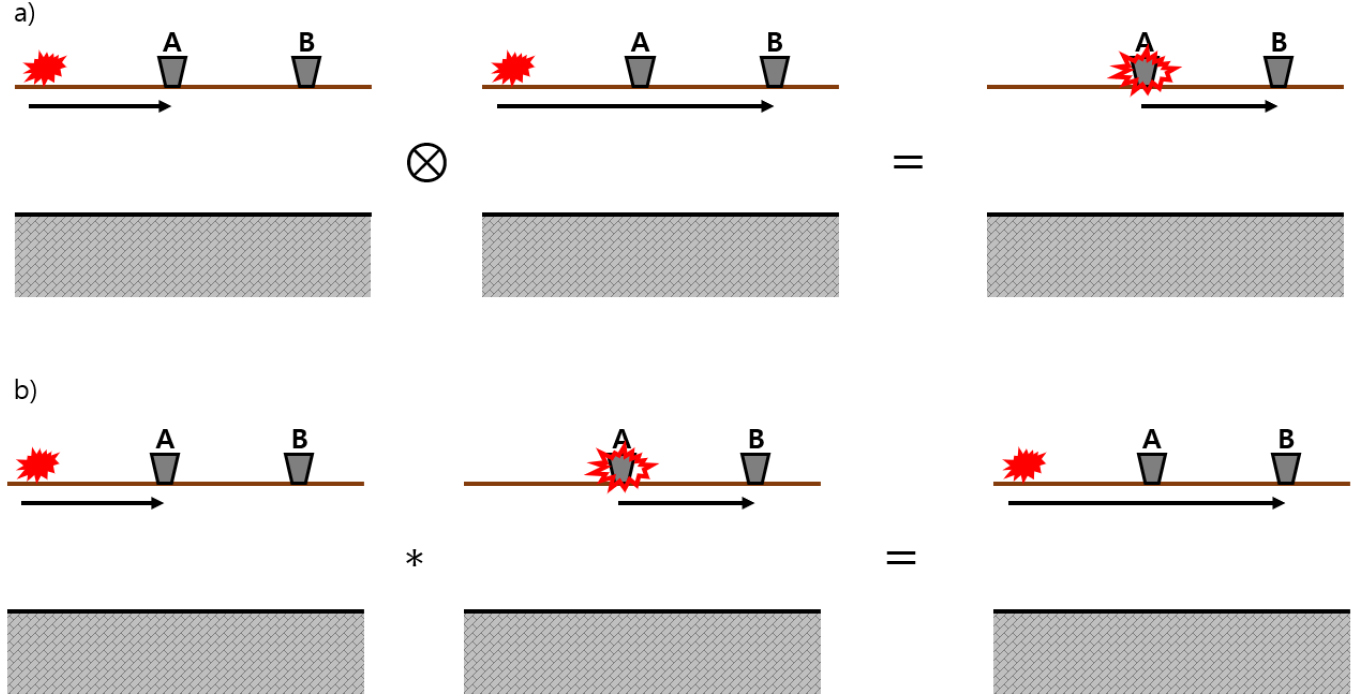
반사파 간섭법 탐사를 수행하면 보다 적은 비용으로 적절한 지질 정보를 얻을 수 있다. 간섭법 이론을 반사파에 적용시킨 반사파 간섭법은 Schuster(2001)가 처음 제안한 방법으로, 실제 송신원에서 발생한 신호가 첫번째 수신기를 지나 다른 수신기에 측정되기 전의 파선 경로 상에서 반사가 발생한 신호를 이용한다. 즉, xS에서 발생된 신호는 지하 구조에 의해 반사되어 첫 번째 수신기에 측정이 된 후에 xB까지 다시 전파되며, xB에서 측정한 신호는 xA에 측정한 신호에 비해 시간이 지연된다. 이 경우에서도 1D 직접파와 유사하게 송신원으로부터 지하 매질을 지나 첫 번째 수신기에 도달하는 공통된 전파경로를 갖게 된다. 즉, 두 신호를 교차상관하면 공통된 경로가 삭제되고 결과적으로 첫 번째 수신기에서 지하 매질에 반사되어 두 번째 수신기로 도달하는 신호만 남게 된다(Fig. 2).

Fig. 2.

Principle of reflected-wave interferometry (Schuster, 2009).

굴절법 탐사

탄성파 굴절법 탐사에서는 초동 발췌가 가장 중요한데, 종종 잡음의 영향으로 초동 발췌가 어려울 때가 있다. 특히 벌림거리가 큰 수신기 데이터의 초동을 확실하게 발췌하기 위해서는 더욱 강한 송신원이 필요하다(Lu and Chávez- Pérez., 2020). 굴절파 간섭법은 일반적으로 잡음의 영향이 크게 작용하는 벌림거리가 큰 데이터의 신호대 잡음비(signal to noise ratio; SNR)를 향상시켜 보다 안정적으로 초동 발췌를 할 수 있도록 해준다(Dong et al., 2006). 또한, 초동에서 입사된 파가 굴절되어 다시 지표로 돌아오는 다이빙파(diving wave)의 유무를 확인하여 굴절 경계의 특성을 평가하는 데에도 활용할 수 있다(Bharadwaj et al., 2012).

굴절파 간섭법에서는 수신기 A, B에 각각 기록된 선두파의 데이터들을 교차상관 시켜 가상의 선두파를 획득한다(Fig. 3a). 이와 같은 과정을 수신기 A, B에 기록된 각 송신 위치에서의 데이터에 반복적으로 적용하여 stacking을 수행하면 SNR은 송신 횟수(N)의 제곱근(N) 만큼 향상된다. 하지만 교차상관만을 이용하게 되면 가상 송신의 발생 시간을 알 수 없으며 송신원과 수신기의 벌림거리를 감소시키게 되므로 교차상관을 적용한 후 곱말기를 통해 가상의 원거리 송신원을 생성해야 한다(Bharadwaj et al., 2012; Lu and Chávez-Pérez, 2020). 실제 원거리 벌림거리 굴절파 데이터와 가상의 굴절파 데이터를 곱말기하여 가상 원거리 벌림거리 굴절파를 획득하게 된다(Fig. 3b).

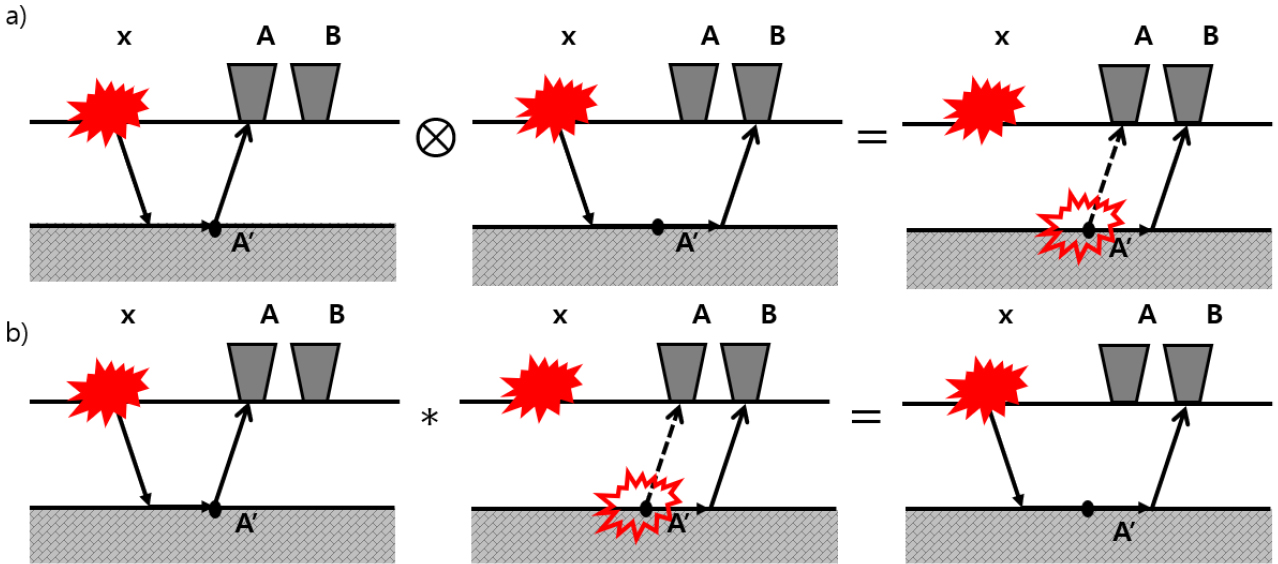
Fig. 3.

Steps for creating 2D super virtual refraction arrivals: a) correlation of the recorded trace at A with that at B for a source at x and b) virtual far-offset refraction arrivals by a combination of both a) correlation and convolution (solid rays are associated with positive travel times and dashed rays are negative travel times) (Bharadwaj et al., 2012).

표면파 탐사

표면파는 분산 특성에 기초하여 매질의 전단 속도를 파악하고 천부 지질의 지반 안정성을 평가하는 데 활발히 이용될 뿐만 아니라 지질구조 특성화, 사이트 반응 분석 및 지진피해 평가 연구 등에도 적용되고 있다(Park et al., 1999; Louie, 2001; O’Connel and Turner, 2011). 그 중 표면파 간섭법은 주로 배경잡음에서 표면파를 획득하고 이를 이용하는 방법으로 사용되고 있다(Campillo and Paul, 2003; Shapiro and Campillo, 2004; Gerstoft et al., 2006).

표면파 간섭법은 굴절법 간섭법과 유사하며 마찬가지로 임의의 수신기 A, B 에서 측정한 탄성파 데이터들에 교차상관을 이용하여 가상의 표면파를 획득한다(Fig. 4a). 간섭법 적용 전에, 측정한 데이터들은 대역통과 필터링과 선형 추세(linear trend) 제거 등의 데이터 전처리 과정을 거쳐 표면파 데이터가 더 쉽게 확인될 수 있도록 한다. 전 처리과정을 거친 데이터는, 가상의 송신원 위치가 될 수신기를 선정하고 두 수신기의 데이터들에 교차상관을 적용하게 된다. 이렇게 교차상관으로 획득한 데이터는 겹쌓기와 진동수-시간 분석(frequency-time analysis; FTAN)을 통해 속도 분산 곡선을 얻어(Fig. 5, 6) 가상의 표면파 데이터를 분석한다(Bensen et al., 2007; Czarny et al., 2018).

Fig. 4.

Schematic diagram of reconstruction of surface waves generated by a) correlation-type interferometry and b) convolution-type interferometry.

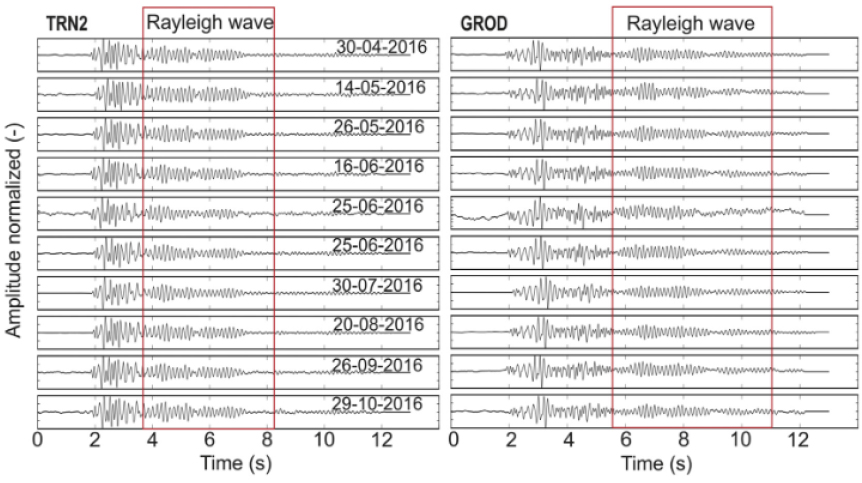
Fig. 5.

Seismograms of the vertical component after preprocessing, recorded by two receivers: the Rayleigh wave can be easily identified (red boxes) (Czarny et al., 2018).

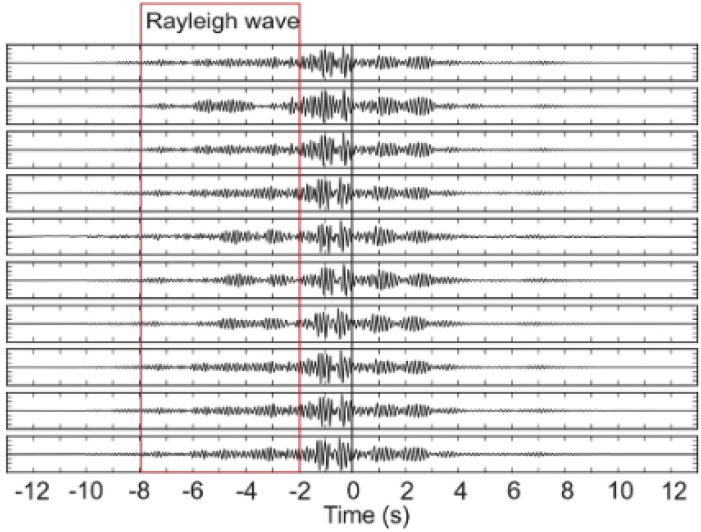
Fig. 6.

Result of cross-correlation: the negative time in the position of the virtual source corresponds to the estimated impulse response between receivers (Czarny et al., 2018).

표면파 간섭법은 refraction microtremor를 사용하는 수동형 MASW 탐사법과 SPAC, f-k method를 이용해 획득한 데이터보다 데이터의 SNR이 더 높다는 장점이 있다(Harba et al., 2019). 또한, 교차상관을 통해 획득한 가상의 표면파 데이터와 기존의 송신원 데이터를 곱말기하여 원거리 표면파 데이터(Fig. 4b)를 생성할 수도 있다(Dalen et al., 2014).

적용 사례

간섭법 적용 분야는 크게 지하구조 영상화와 건축물 안정성 평가로 나눌 수 있다. 탄성파 간섭법을 가장 많이 적용하는 분야로는, 지질 구조 영상화, 단층의 유무 판단, 마그마의 분포와 같은 심부 지질 구조 영상화와 모니터링이다(Miyazawa et al., 2008; Voisin et al., 2016; Guillemot et al., 2020). 한편 건축물 안정성 평가에도 적용되는데, 건축물에 설치한 수신기에서 얻은 반응을 바탕으로 파의 속도나 전단 강도를 분석해 구조물의 손상 정도를 평가할 수 있다.

지질 구조 영상화

간섭법으로 지질 구조를 분석하기 위해 배경잡음이나 지진 발생 시 데이터를 측정하여 산사태 사면 모니터링, 지각속도 구조, 화산 지역의 마그마 분포, 저류층 등 다양한 지질구조 해석 분야에서 사용하고 있다.

도심지 지하 구조 영상화

도심지에서는 교통잡음 등의 다른 잡음들이 많다는 점에서 일반적인 물리탐사를 수행하는 데 어려움이 있으나, 탄성파 간섭법 탐사는 교통잡음을 송신원으로 이용하여 탐사를 수행할 수 있다. 도심지 간섭법에서는 주로 교통잡음과 같은 배경잡음 데이터를 이용하여 천부층 탐사 혹은 기반암이나 대수층을 파악하는 데 이용한다(Zhang et al., 2019; Nilot et al., 2020).

Zhang et al.(2019)은 싱가폴의 도시 개발을 위하여 개발 현장의 지질구조를 파악하고자 간섭법을 활용하였다. 도심지의 환경을 고려해 교통 잡음을 이용한 탄성파 탐사에 간섭법을 적용했으며 총 11개의 4.5 Hz 단일 성분 지오폰을 L 자 형태로 각도를 바꾸어가며 3개 세트를 설치하여 각각 약 15분 동안 데이터를 획득하였다. 이후, 교차 상관과 결맞음 두 가지 간섭법을 적용하여 획득한 표면파의 분산 곡선을 추정하였고 이를 통해 기반암의 깊이를 알 수 있었다. 시추공 탐사 결과와 비교하였을 때 최대 오차가 3 m 이내로 나타났으며 이는 교통 잡음과 짧은 시간만으로도 도심지 내에서의 탐사가 효율적으로 수행 가능함을 보여준다.

도심지에서는 전신주 등의 영향으로 전기전자 탐사를 수행하였을 때 전기적 잡음이 다수 존재하고 화약을 탄성파 탐사 송신원으로 이용하기 어렵기 때문에 깊은 영역에 있는 지하 대수층에 대해서 탐사하기 어렵다. 이와 같은 문제점을 해결하고자 싱가폴에서는 지하 대수층을 파악하기 위해 원지 지진(teleseismic)으로 발생한 배경잡음을 활용해 간섭법 탐사를 수행했다(Nilot et al., 2020). 지진 관측을 위해 설치한 수신기의 데이터와 싱가폴 동부에 설치한 6개의 다중채널 수신기배열에서 측정한 데이터를 이용했으며 교차상관 간섭법을 적용했다. 간섭법을 이용해 표면파 데이터를 획득했으며 이를 이용해 낮은 전단파 속도를 가진 지역의 지하에 대수층이 존재한다고 해석하였다.

지각속도 구조 영상화

지각속도 구조 영상화는 지표의 수 km에서 맨틀에 해당하는 수십 km의 고심도를 목표로 하기 때문에 발파 등과 같은 능동 탐사법으로 지각속도구조를 밝히기에는 매우 어렵다. 발파 등과 같은 송신원은 높은 진동수 특징을 나타내기 때문에 고해상도의 영상을 얻을 수 있지만 파동 에너지의 감쇠가 상대적으로 많아 깊은 심도의 고해상도 영상을 얻기에는 한계가 있다. 또한 지진이 덜 발생하는 지역에서는 수평 및 수직 지진원의 분포가 한정적이고 매우 장기간의 감시가 필요한 지역은 지진데이터를 이용한 지각속도구조 영상화에도 한계를 가지고 있다. 이러한 지역에 지각속도구조를 밝히는 방법으로 탄성파 간섭법을 이용한 지각속도 구조 영상화는 좋은 선택이 될 수 있다.

미국에서는 대륙지각 탄성파 배열에 대한 연구 프로그램(Program for the Array Seismic Studies of the Continental Lithosphere; PACSCAL)과 USArray를 이용한 지각구조 영상화를 위해 탄성파 간섭법을 이용하기도 하였으며 주로 표면파 군속도 또는 위상속도, 감쇠를 이용한 연구가 활발히 수행되었다(Shapiro et al., 2005; Lawrence and Prieto, 2011; Ritzwoller et al., 2011; Luo et al., 2015; Zhao et al., 2019). Shapiro et al.(2005)의 탄성파 간섭법을 이용한 지각구조 연구는 지진학 분야에서 부흥을 이끌었다고 볼 수 있다. Zhao et al.(2020)은 위상 민감도 커널(phase sensitivity kernel)을 이용해 상부 맨틀 구조(upper‐mantle structure)를 잘 도출하고 평가하였다. Luo et al.(2015)은 탄성파 간섭법을 이용한 배경잡음토모그래피(Ambient Noise Tomography; ANT)에서 획득한 분산곡선의 위상속도와 관측소 간의 거리와의 관계에서 관측소 간 거리가 구하고자 하는 위상 속도의 한 파장 보다 긴 경우에 신뢰할 만한 결과를 얻을 수 있다는 결과를 얻었다.

Yao and Van der Hilst(2009)는 티벳지역의 탄성파 간섭법 결과에서 위상속도가 잡음 송신원 에너지분포의 방위각에 따라 다를 때 이방성 정보를 도출 할 수 있음을 보여주었다. Fang et al.(2015)은 타이완의 타이페이 분지(Taipei basin)지역에서 탄성파 간섭법을 이용한 표면파 토모그래피를 수행해서 2 km이내의 천부 속도구조를 잘 도출하고 기존의 지질구조와 비교하여 일치함을 입증하였다. 국내의 경우는 Kim et al.(2016)이 탄성파 간섭법을 이용하여 위상 분산곡선을 구하고 이로부터 베이지안 역산법을 동아시아 지역에 적용하여 지각 구조를 확인하였다. 이때, 판 경계 수렴지역의 back-arc와 관련된 저속도 지역이 화산과 관련될 수도 있다고 주장하였다.

마그마 분포 영상화

마그마는 유체이기 때문에 다른 암석층에 비해 저속도대로 보여지는 특징이 있다(Casas et al., 2020; Plaen et al., 2019). 이러한 특성을 이용해 탄성파 탐사로 마그마 분포를 확인할 수 있다. 영벌림거리(zero offset) 탐지 수행 시 탐사심도가 깊다는 장점이 있으며 이러한 영벌림거리 탐지 데이터에 간섭법을 적용한다면 모호면 부근의 깊은 심도에 위치한 마그마의 분포 영역까지도 확인할 수 있다.

Casas et al.(2020)은 아르헨티나-칠레의 중앙 안데스 산맥의 화산지역에서 1년 동안 기록된 탄성파 데이터와 자기상관 간섭법을 통해 지하 구조의 특징과 화산지역의 마그마 분포를 해석하였다. 해석 결과 낮은 진동수 범위의 모호면의 위치와 섭입대와 하부 맨틀로 인한 저속도대를 확인하였으며, 0.8 ~ 3 Hz에서는 모호면 근처에 위치한 마그마 분포 영역을 파악할 수 있었다.

마그마의 분포와 화산 활동으로 생기는 탄성파 속도의 변화를 감지하는 모니터링 또한 수행이 가능하다. Plaen et al.(2019)은 화산에서 측정된 배경잡음에 자기상관 간섭법을 이용해 약 18개월 동안 3개의 수신기로 모니터링을 수행하였다. 자기 상관과 교차 상관을 이용하였으며 3개의 수신기에서 화산 활동 시에는 나타나는 일정한 탄성파 속도 변화가 관찰되었다.

사면 모니터링

최근 사면 안정성을 파악하기 위해 간섭법을 이용한 모니터링 기법에 관심이 높아지고 있다(Breton et al., 2021). 간섭법을 이용한 사면 모니터링에서는 영구동토층의 암석 빙하의 열화 정도를 모니터링하여 낙석의 위험도를 파악할 수 있다(Guillemot et al., 2020). 주로 봄철의 강한 용해 과정에서 급속한 미세진동이 발생하게 되며, 이는 속도가 급격하게 감소하는 것과 동시에 발생한다. 이 외에도 사면의 안정성에 큰 영향을 미치는 지하수위의 변화에도 탄성파 간섭기법을 사용할 수 있다(Voisin et al., 2016). 산사태 모델에서의 유체 포화도 변화를 통해 제한된 진동수 대역과 탄성파 속도 변화의 진폭을 설명할 수 있다. 탄성파 배경잡음의 교차상관분석은 수포화도 변화에 따른 지하수위 변화에 민감하며, 비파괴 수문학적 모니터링 도구로 사용할 수 있다.

저류층 모니터링

CCS 모니터링이나 지열 발전 혹은 원유 생산 시에도 마찬가지로 배경잡음을 이용한 저류층 탐사가 가능하다(Cheraghi et al., 2017; Matzel et al., 2017; Verdel et al., 2019). 탄성파 간섭법은 원유 생산 과정에서 발생하는 배경잡음을 이용하여 탐사가 가능하다는 장점이 있다.

캐나다의 서스캐처원(Saskatchewan) 주에 있는 이산화탄소 지중저장 현장에서는 배경잡음을 송신원으로 하는 간섭법을 활용해 이산화탄소 저장소 부근의 지질 구조와 모니터링 가능성을 확인하였다(Cheraghi et al., 2017). 배경잡음에 자기상관을 적용시킨 후 가상의 발파로부터 측정되는 표면파의 영향을 줄이기 위해 2 ~ 35 Hz 대역의 대역 필터(band pass filter)와 빔 형성 해석(beam-forming analysis)을 사용하였고, 반사파 에너지의 크기를 키우기 위해 CMP 방법을 사용하였다. 간섭법을 활용한 탐사 결과는 적절한 필터링을 적용한 능동형 탄성파 탐사의 단면과 유사하였으며, 10초와 1일, 13일, 23일의 길이를 가지는 배경잡음 데이터를 각각 이용하여 결과를 비교하였을 때 길이가 길수록 더 다양한 송신원의 잡음들이 획득되어 더 좋은 결과를 획득하였다고 한다.

건축물 안전진단 및 모니터링

건축물에서 파의 전파는 건축물의 강성 변화를 추정하는 데 사용할 수 있으며, 강성의 변화는 건축물 상태 모니터링의 주 목표이다. 건축물의 손상된 부분을 지나는 파는 속도가 느려지게 되는데, 간섭법을 통해 획득한 데이터에서는 파속이 일시적으로 감소했던 부분이 시간지연으로 나타나게 되며 파속이 감소한 부분이 강성이 약화된 부분이다(García-Macías and Ubertini, 2019). 이를 위해 곱풀기를 활용한 간섭법이 건축물의 전단파 전파 속도를 계산하는 데 자주 사용되고 있다. 건축물의 각 위치에 설치한 수신기에서 측정한 탄성파 데이터들에 곱풀기 간섭법을 적용하여 IRF (impulse response function)파형을 획득한다. IRF는 파의 속도, 모드 진동수, 전단 강도의 구조적 매개변수를 식별하는 데 사용할 수 있으며 이를 분석해 구조물의 손상 여부와 위치 등을 평가한다(Nakata and Snieder, 2014; Wen and Kalkan, 2017; Mordret et al., 2017; Lopez-Caballero and Mercerat, 2018; Bulajic et al., 2020).

간섭법을 이용한 건축물 안정성 평가를 수행하기 위해서 일반적으로 수신기는 각 층(높이) 마다 설치되며 기준 수신기를 설정한다. 기준 수신기에서 측정한 신호에 대해 파형을 획득하고자 하는 목표 수신기의 신호를 곱풀기하면 IRF를 획득하게 되며 이 IRF는 기준 수신기에서 발생한 가상의 파형이 건물을 따라 목표 수신기까지 전파한 정보를 포함하고 있다. 기준 수신기는 실제로 파가 진입해 전파되기 시작하는 지표 높이(ground-level)의 수신기를 선택해 실제 탄성파의 데이터를 사용할 수도 있으며, 다른 높이의 수신기를 선택할 수도 있다. 다른 높이의 수신기를 선택할 경우에는 서로 다른 층의 기준 수신기를 선택해 손상을 평가하기도 하지만 IRF가 가장 명확하게 식별되는 최상층의 높이를 선택해 탐사를 수행하기도 한다(Nakata et al., 2013; Lacanna et al., 2019).

건축물 안전진단

탄성파의 속도 변화 및 변형을 기반으로 얻은 시간 지연을 이용해 지진으로 발생한 건물의 손상을 식별할 수 있다. 2002년 미국 Yorba Linda에서 발생한 지진 데이터에 간섭법을 적용하여 Millikan Library건물 모델을 계층화(layering)하고 각 층의 수신기에 도달한 탄성파의 곱풀기 파형에서 도착 시간을 측정해 S파의 속도를 계산했다(Snieder and Safak, 2006; Ebrahimian et al., 2014). 이와 유사한 방법으로 미국 캘리포나아대학교 로스앤제레스 캠퍼스(University of California at Los Angeles; UCLA)의 Factor 건물의 데이터를 활용한 사례가 있으며 Factor 건물의 지진 발생 시와 평상시의 배경잡음에서 추출한 IRF를 이용해 건축물의 손상을 평가했다(Kohler et al., 2007; Prieto et al., 2010).

마찬가지로 건물의 IRF를 이용해 전파하는 파의 속도를 추정하고, 이 속도 변화를 감지해 건물의 구조적 안정성을 평가하는 방법은 지속적인 중요 연구 주제였다. 미국 LA의 Sherman Oaks 건물에서는 1971년 Fernando 지진 발생 시의 데이터를 측정하여(Fig. 7), 외관 상으론 큰 손상이 없는 건물의 2층 기둥에서 광범위한 균열을 찾았다(Rahmani et al., 2015). 이때, 수신기는 1층과 중간층, 꼭대기 총 3개의 수신기가 설치되어 건물을 상단부와 하단부로 나누어 파의 속도를 해석하여 2층 균열이 있던 하단부에서 속도 감소가 크다는 것을 파악했다.

Fig. 7.

Distribution of structural damage along the height in Sherman Oaks 12-story office building during the San Fernando 1971 earthquake (left; drawn based on John Blume Associates) and the two-layer shear beam model to be fitted (right).

한편 García-Macías and Ubertini(2019)은 이탈리아 페루자 지구에서 석탑에 대한 탐사를 통해 석조 건물 모델을 계층화(layering)하여 손상을 정량화 하였으며, 이를 실제 손상과 비교하기 위해 ABAQUS 6.10 플랫폼을 이용해 석탑의 비선형 3D 수치 모델을 구조 도면 및 문헌을 통해 구현하였다. 그 결과 측정한 데이터를 이용해 모델에서 추정한 각 높이에서의 강성 변화는 지진으로 인한 손상과 밀접한 관련이 있었으며 지연 시간을 통해 식별한 석탑의 손상 부분은 실제 손상 위치가 일치하였다. 즉, 강성 변화 파악에 기초한 손상 영역은 충분히 정량화 할 수 있음을 확인하였다.

건물 모니터링

지진 발생일에 미국 Imperial County Services 건물에서 측정한 탄성파 데이터에 간섭법을 적용해 건물에서 전파되는 파의 속도 변화를 통해 지진 발생 시간 동안의 손상 위치를 추정하였다(Todorovska and Trifunca, 2008). 각 층에서 최대 진폭 전과 후 그리고 최대 진폭 시점까지 총 3개의 시간대에 측정된 수평 성분의 탄성파 데이터에 곱풀기 간섭법을 적용해 얻은 충격함수 반응으로 파의 속도를 측정하였다. 측정한 속도를 이용해 건물의 강성 감소로 발생하는 지연 시간을 분석하고 손상 부위를 예측하고자 했으며 기준 파형은 지진 발생 전 측정된 데이터를 사용했다. 데이터는 0.1 ~ 0.125 Hz 와 25 ~ 27 Hz 대역 통과 필터를 적용하였고 지진 발생 후 건물은 심각하게 손상되어 육안으로 그 부위를 파악할 수 있었다. 건물 전체의 강성은 약 40 ~ 80% 가 감소되는 것을 확인할 수 있고 지진 발생 시 1층에서 가장 큰 강성 감소가 발생하였다. 강성 변화는 건물의 상부에는 큰 균열이 발생하지 않았고 하부에서 대부분의 균열이 발생함을 의미하며 이는 외부에서 육안으로 관측한 당시 손상 기록과 일치했다.

이 외에도 미국 Green building에서 측정한 데이터에 간섭법을 적용하여 건물의 IRF 획득과 함께 Bayesian 모델을 함께 사용해 IRF를 더욱 건물의 특성과 관련 지었으며 이를 이용해 파의 속도를 모니터링 하고 동시에 손상을 파악하였다(Sun et al., 2017). 지진 발생 시의 데이터와 평상시 배경 잡음을 측정한 데이터를 통해 모니터링 하였으며 손상 탐지뿐만 아니라 지진 발생 후의 지속적인 모니터링도 가능했다.

결 론

탄성파 간섭법은 두 수신기에서 신호를 측정하고 기준 수신기 위치에서 생성된 가상의 송신원을 이용하며 다양한 탄성파 탐사 데이터에 적용할 수 있다. 이때 측정한 신호는 인공 송신원에 의한 신호들뿐만 아니라 지하 매질구조에서 전파된 배경 잡음, 지진으로 인한 신호, 자동차 등 인공적인 물체들에 의해 만들어진 신호까지도 포함되며 이러한 배경잡음을 이용한 간섭법이 가장 많이 사용되고 있다.

기본적인 탄성파 간섭법은 교차상관을 적용하는 방법이 대표적이며 그 외에도 곱풀기, 결맞음을 이용한 방법들이 있다. 교차상관을 사용할 경우 두 수신기 간의 공통된 경로가 삭제되고 결과적으로 첫 번째 수신기에서 시작해 지하 매질에 반사되어 두 번째 수신기로 도달하는 신호만 남게 된다. 곱풀기와 결맞음 역시 유사한 결과를 보여주며 곱풀기의 경우 특히 파의 감쇠를 추정하는 데 주로 사용된다. 결맞음 방법은 파장의 위상에 대한 정보만 남게 되어 갑작스러운 진폭 변화 발생 등의 상황에 적용할 수 있다.

반사법 탄성파 탐사 데이터에서는 탄성파 간섭법을 통해 인공 송신원 위치를 조정할 수 있어 기존의 반사파 데이터로는 확인하기 힘들었던 복잡한 지질 구조 등을 더 정확하게 파악할 수 있다. 또한, 측선 위치와 상관없이 수신기만 설치되어 있다면 새로운 측선 방향으로 정보를 얻을 수 있다. 그 외에도 굴절법, 표면파 탐사에서는 간섭법을 이용해 새로운 굴절파 데이터와 기존의 원거리 벌림거리 데이터를 합침으로써 가상 원거리 벌림거리의 데이터를 얻을 수 있으며 더 높은 신호대잡음비를 가진 데이터를 획득할 수 있다.

탄성파 간섭법은 잡음을 이용한 수동형 탐사에서도 상대적으로 높은 신호대잡음비의 데이터를 얻을 수 있다는 장점 덕분에 지속적인 능동형 탐사가 어렵거나 모니터링이 필요한 안정성 진단 분야에서 주로 사용한다. 사면의 안전성을 확인하거나 능동형 탐사가 어려운 도심지 내에서 지하구조를 규명하기 위해 교통 잡음이나 산업단지 잡음 등을 사용한다. 또한, 최근에는 도시 내 생활 잡음을 이용해 지진이나 시설 낙후로 인한 건물이나 다리의 손상을 확인하는 구조물 안전진단 분야에서 활용도가 높아지고 있다. 탄성파 간섭법은 기존의 능동형, 수동형 탄성파 탐사법에서 발생하는 공간적 혹은 비용적 한계, 복잡한 지질 구조 등으로 인한 데이터 해석 등의 문제 해결에 도움을 줄 수 있으며, 배경잡음을 이용할 수 있기 때문에 낙후된 도심지나 시설물 등 안정성 모니터링이 필요한 분야에서 효과적으로 활용할 수 있을 것으로 기대된다.