Optimization of Well Operations in a Carbonate Reservoir Using Stochastic Simplex Approximate Gradient

Byunggun Oh; Youngjoo Kim; Wonsuk Lee; Youngho Jang; Baehyun Min; Hoonyoung Jeong

doi:10.32390/ksmer.2021.58.2.119

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 30 April 2021. 119-129
https://doi.org/10.32390/ksmer.2021.58.2.119

Optimization of Well Operations in a Carbonate Reservoir Using Stochastic Simplex Approximate Gradient

StoSAG를 이용한 탄산염암 저류층의 유정 운영 최적화

Byunggun Oh¹

Youngjoo Kim²

Wonsuk Lee³

Youngho Jang⁴

Baehyun Min⁵

Hoonyoung Jeong⁶^*

오 병건¹

김 영주²

이 원석³

장 영호⁴

민 배현⁵

정 훈영⁶^*

¹Master Program, Department of Energy Systems Engineering, Seoul National University

²Integrated PhD Program, Department of Energy Systems Engineering, Seoul National University

³Principal Research Engineer, Petroleum & Marine Research Div., Korea Institute of Geoscience & Mineral Resources (KIGAM)

⁴Research Professor, Center for Climate/Environment Change Prediction Research, Ewha Womans University

⁵Associate Professor, Department of Climate and Energy Systems Engineering, Ewha Womans University

⁶Assistant Professor, Department of Energy Systems Engineering, Seoul National University

¹서울대학교 에너지시스템공학부 석사과정

²서울대학교 에너지시스템공학부 석박통합과정

³한국지질자원연구원 책임연구원

⁴이화여자대학교 기후․환경변화예측연구센터 연구교수

⁵이화여자대학교 기후․에너지시스템공학과 부교수

⁶서울대학교 에너지시스템공학부 조교수

^{*Corresponding Author}

ABSTRACT

Well operating conditions can significantly affect the economic feasibility of developing an oil and gas field. The optimal operating conditions can be calculated using gradient-based optimization algorithms. However, using the finite difference method for this calculation is significantly costly under reservoir uncertainty and complex operating conditions. Thus, stochastic simplex approximate gradient (StoSAG), which is a calculation of the gradient by perturbing decision variables randomly, is an efficient application for optimization under uncertainty . In this study, StoSAG was applied to optimize the operating conditions in a real carbonate reservoir. Compared to the initial operating conditions, the optimized model shows a 10% increase in net present value (NPV ). The results can be utilized to determine cost-efficient operating conditions for complex reservoirs.

Keywords

Optimization

Well Operation Conditions

Stochastic Gradients

StoSAG

유가스전 개발에 있어 유정 운영 조건은 개발 경제성에 큰 영향을 미친다. 경사도 기반의 최적화 기법을 이용하여 최적 유정 운영 조건을 효율적으로 탐색할 수 있다. 그러나 저류층 불확실성이 높고 많은 유정이 존재한다면 유한차분법을 이용하여 경사도를 계산하는 데 막대한 계산량이 요구된다. 최적화 변수의 미소 변화를 추계학적으로 생성하여 경사도를 계산하는 방법 중 하나인 Stochastic Simplex Approximate Gradient(StoSAG)를 이용하면 불확실성이 높고 많은 수의 유정을 가진 유정 운영 최적화 문제를 풀 수 있다. 본 연구에서는 StoSAG를 이용하여 실제 탄산염암 저류층의 생산 및 주입 조건을 최적화하였다. 최적화된 운영 조건은 초기 운영 조건에 비해 순현재가치가 약 10% 증가하였다. 본 연구결과는 불확실성이 높고 유정 개수가 많은 저류층의 유정 운영 최적화를 효율적으로 수행하는 데에 활용할 수 있다.

키워드

최적화

유정 운영 조건

추계학적 경사도

Stochastic Simplex Approximate Gradient

MAIN

서 론
추계학적 경사도 기법
대상 저류층 모델
최적화 결과
결 론

서 론

전통 유가스전 개발, 셰일가스전 개발, 이산화탄소 지중 저장, 고준위 방사성 폐기물 지하 저장, 지열 에너지, 지하수 관리 등 지하 암석층에서 유체를 생산 및 주입할 경우, 지하에 위치한 암석층에 대한 정보는 제한적이다. 제한된 정보에 기반하여 구축된 지하 암석층 모델은 높은 불확실성을 가진다. 암석층 모델의 높은 불확실성에 대한 충분한 검증과 계획 없이 개발할 경우, 지반침하, 유도지진, 핵종 유출, 지하수 오염, 주입 유체의 유출 등의 안전성 문제와 개발 사업의 수익이 현저히 감소하는 경제성 문제를 불러일으킬 수 있다. 따라서, 암석층 불확실성으로 발생하는 문제를 최소화하기 위해 지하 암석층에서의 유체 유동을 수치적으로 시뮬레이션하여 유체 생산 및 주입 운영 계획의 안전성을 검증하고 효율성 및 경제성을 위한 최적의 유정 운영 계획이 필요하다(Jeong et al., 2018).

유정 운영 조건 최적화시 사용되는 최적화 기법은 비경사도 기반과 경사도 기반으로 분류된다. 비경사도 기반 최적화 기법은 광역해를 찾는 데에는 유리하나 막대한 계산량이 소요된다는 단점이 있다(Isebor et al., 2014). 유정 운영 최적화에 Particle Swarm Optimization, Mesh Adaptive Direct Search 등의 비경사도 기반 최적화 기법이 사용된다(Kim et al., 2019). 경사도 기반 최적화 기법은 지역해에 수렴할 수 있다는 단점이 있으나 해를 비경사도 기반 최적화에 비해 신속하게 찾을 수 있다는 장점이 있다. 따라서, 지역해가 많은 유정 위치 최적화에는 비경사도 기반 기법이 사용되고 유정 운영 조건 최적화에는 경사도 기반 최적화 기법이 일반적으로 사용된다(Bellout et al., 2012).

경사도 기반 최적화가 비경사도 기반 최적화에 비해 빠르다고 하더라도 저류층 불확실성을 대표하는 저류층 모델 개수가 많고 최적화할 유정 운영 조건의 개수가 많으면 유한차분법을 이용한 경사도를 계산하는데 상당한 계산량이 요구된다. 경사도 계산에 많은 시간을 소요하여 찾은 해가 지역해일 가능성도 존재한다. 또한, 경사도 기반의 최적화를 이용할 경우 광역해를 찾기 위해서는 여러 초기 해에 대해 최적화를 수행하여야 한다. 따라서, 시도할 초기 해 개수가 많고 저류층 불확실성을 대표하는 저류층 모델 개수와 최적화할 유정 운영 조건의 개수가 많으면 유한차분법을 이용한 경사도 기반 최적화는 막대한 계산량 때문에 주어진 시간 내 만족할 만한 결과를 얻기가 어렵다. 이러한 유한차분법의 문제를 해결하기 위해 추계학적 경사도를 활용할 수 있다. 추계학적 경사도는 유한차분법에 비해 부정확하지만 빠르게 계산할 수 있으며, 초기 해 개수, 저류층 불확실성을 대표하는 저류층 모델 개수, 최적화할 유정 운영 조건의 개수가 많은 최적화 문제를 보다 효율적으로 해결할 수 있다(Jeong et al., 2020).

본 논문은 다음과 같이 구성되어 있다. 먼저, 추계학적 경사도에 대한 소개와 함께 본 연구에 사용된 기법인 StoSAG에 대해 설명한다. 다음으로 최적화 수행 대상인 실제 탄산염암 저류층 모델 및 최적화 문제 설정에 대해 설명한 후, 최적화 적용 결과와 그에 대한 분석을 수행한다. 추가적으로, 물 처리 및 주입 비용에 대한 유정 운영조건의 민감도 분석을 수행한다. 마지막으로, 본 연구를 통해 확인한 StoSAG의 적용결과를 요약한다.

추계학적 경사도 기법

(1)

\nabla f = {[\frac{\partial f}{\partial x_{1}} \frac{\partial f}{\partial x_{2}} \dots \frac{\partial f}{\partial x_{N_{x}}}]}^{T}, x = {[x_{1} x_{2} \dots x_{N_{x}}]}^{T}

경사도는 수식 (1)과 같이 나타낼 수 있다. 벡터 $x$ 는 $N_{x}$ 개의 요소를 가지는 벡터이다. 반복적으로 경사도 방향으로 벡터 $x$ 에 변화를 주면 목적함수 $f$ 가 최대 혹은 최소인 $x$ 에 도달할 수 있다. 이를 알고리즘화한 방법이 Steepest Ascent/Descent Method이다(수식 (2)).

(2)

x_{k + 1} = x_{k} \pm α_{k} \frac{\nabla f (x_{k})}{‖ \nabla f (x_{k}) ‖_{\infty}}, k = 0, 1, \dots

$\nabla f (x_{k})$ 의 - 및 + 기호는 목적함수 $f$ 를 각각 최소화 및 최대화할 경우에 해당된다. Gradient Ascent/Descent Method는 경사도와 $α$ 의 값을 각 위치에서 계산하여 다음 해를 구한다. $α$ 는 해당 위치에서 경사도 방향으로 어느 정도 이동할지 정해주는 값이며 Line Search Method(Nocedal and Wright, 2006)를 사용하여 계산한다. Gradient Ascent/ Descent Method는 수식 (2)를 이용하여 다음 x를 구하고 새로운 x로 계산한 목적함수의 값이 이전 반복의 목적함수와 비교하여 일정 수준 이하가 되는 등의 수렴 조건이 만족할 때까지 계산을 반복한다.

수식 (2)의 계산을 수행하기 위해서는 경사도를 계산해야한다. 경사도를 구하는 가장 전통적인 방법은 유한차분법(Finite Difference Method)(Sun and Sun, 2015)이다. 유한차분법은 수식 (3)과 같은 방법으로 경사도를 계산한다.

(3)

\frac{\partial f}{\partial x_{i}} = \frac{f (x_{1}, \dots, x_{i} + \partial x_{i}, \dots, x_{N_{x}}) - f (x_{1}, \dots, x_{i}, \dots, x_{N_{x}})}{\partial x_{i}}

유한차분법으로 경사도를 구할 경우, 1개의 저류층 모델에 대하여 총 $N_{x} + 1$ 개의 시뮬레이션 결과가 필요하다. 만약, 저류층의 불확실성을 대표하는 모델이 $N_{e}$ 개 있다면, 총 $N_{e} (N_{x} + 1)$ 개의 시뮬레이션 결과가 필요하다. 병렬 컴퓨팅을 이용해 여러 개의 시뮬레이션을 동시에 수행한다고 해도 상당한 계산 시간이 필요로 하며, 시뮬레이션 동시 수행을 위해서는 다수의 시뮬레이터 라이선스가 필요하다. 유한차분법을 이용한 경사도 기반 최적화 알고리즘의 단점을 완화하기 위해 다양한 추계학적 경사도 계산 기법이 연구되어 왔다. 경사도를 계산하는데 걸리는 시간을 감소시키기 위해 Chen et al.(2009)은 수식 (4), (5), (6)과 같은 앙상블 기반의 추계학적 경사도(EnOpt)를 사용하였다. ${\hat{x}}_{k, i}$ 는 k번째 반복의 해 $x_{k}$ 에 평균이 0이고 공분산 $U_{x}$ 인 무작위 교란값을 더해준 벡터이다. $N_{e}$ 는 앙상블의 개수를 뜻하며, $J (m_{i}, x_{k})$ 는 i번째 저류층 모델 $m_{i}$ 에 $x_{k}$ 를 대입했을 때의 목적함수의 값을 뜻한다.

(4)

d_{k, E n O p t} = \frac{1}{N_{e} - 1} \sum_{i = 1}^{N_{e}} ({\hat{x}}_{k, i} - \bar{{\hat{x}}_{k}}) (J (m_{i}, {\hat{x}}_{k, i}) - J \bar{(m_{i}, {\hat{x}}_{k})})

(5)

\bar{{\hat{x}}_{k}} = \frac{1}{N_{e}} \sum_{i = 1}^{N_{e}} {\hat{x}}_{k, i}

(6)

J \bar{(m_{i}, {\hat{x}}_{k})} = \frac{1}{N_{e}} \sum_{i = 1}^{N_{e}} J (m_{i}, {\hat{x}}_{k, i})

EnOpt는 유한차분법과 달리 각 원소별로 하나씩 교란을 주는 것이 아니라 모든 벡터 원소에 동시에 교란을 주고 목적함수 값의 변화를 평균하여 경사도를 근사한다. 따라서, 최적화 변수의 개수와 상관없이 $2 N_{e}$ 개의 시뮬레이션 결과만 수행하면 경사도를 계산할 수 있다. 예를 들어, 100개의 저류층 등가 모델에서 20개의 생산정의 생산조건을 최적화할 때, 경사도를 한번 계산하기 위해 유한차분법을 사용할 경우, 총 2100번의 시뮬레이션 수행이 필요하고 EnOpt를 사용할 경우, 총 200번의 시뮬레이션 수행이 필요하다. 최적해에 수렴하기 위해서는 초기 해로부터 여러 번의 경사도 계산이 필요하고 다수의 초기해에 대해 최적화를 수행해야 광역 해에 도달할 수 있다는 점을 추가로 고려한다면, EnOpt 방식의 추계학적 경사도 계산 기법이 계산 비용 측면에서 매우 효율적이라고 할 수 있다. 그러나 EnOpt는 $J (m_{i}, {\hat{x}}_{k, i})$ 의 분산이 커질수록 경사도가 부정확해지며 목적함수 값을 현저히 증가시키거나 감소시키는 것이 불가능하다는 단점이 있다(Stordal et al., 2016).

EnOpt는 Simultaneous Perturbation Stochastic Approximation(SPSA)(Spall, 1992)의 변형된 한 형태로 Bangerth et al.(2006)은 SPSA를 유정 위치 최적화에 적용하였다. SPSA는 교란을 Bernoulli 분포로부터 추출하여 $x$ 에 더해주므로 경사도 계산비용이 높은 단점이 있다. Li et al.(2013)는 SPSA를 유정 위치, 유정 운영 조건을 동시에 최적화하는 데 적용하였다. Li and Reynolds(2011)는 SPSA에서 교란을 정규 분포를 따르도록 수정한 Stochastic Gaussian Search Direction(SGSD)를 제안하였다.

Simplex Gradient(SG)(Yan and Reynolds, 2014)는 SGSD에서 교란 계수에 대해 1을 사용하여 SGSD의 형태를 수식 (7)과 같이 단순화함으로써 경사도를 보다 용이하게 계산할 수 있다.

(7)

d_{k, S G} = \frac{1}{N_{e}} \sum_{i = 1}^{N_{e}} ({\hat{x}}_{k, i} - x_{k}) (J (m_{i}, {\hat{x}}_{k, i}) - J (m_{i}, x_{k}))

Bangerth et al.(2006), Li and Reynolds(2011), Li et al. (2013), Yan and Reynolds(2014) 는 변형된 SPSA를 한 개의 저류층 모델에 대해 적용하여 저류층 모델의 불확실성을 고려하지 않았다. 본 연구에서 사용된 Stochastic Simplex Approximate Gradient(StoSAG)는 SG를 저류층 불확실성을 대표하는 다수의 저류층 모델에 적용될 수 있도록 수정하고 반복 횟수를 조정하여 정확도를 조절할 수 있는 추계학적 경사도이다(Fonseca et al., 2017). StoSAG는 SG와는 다르게 각 저류층 모델에 $N_{p}$ 개의 교란을 적용한 후, 목적함수의 값들을 평균하여 경사도 계산에 사용한다. StoSAG의 계산 방식은 수식 (8)과 같이 나타낼 수 있다.

(8)

d_{k, S t o S A G} = \frac{1}{N_{e}} \sum_{i = 1}^{N_{e}} [\frac{1}{N_{p}} \sum_{j = 1}^{N_{p}} ({\hat{x}}_{k, i, j} - x_{k}) (J (m_{i}, {\hat{x}}_{k, i, j}) - J (m_{i}, x_{k}))]

StoSAG는 하나의 경사도를 계산하기 위해 사용된 앙상블의 수가 많을수록, 각 앙상블의 목적함수 값을 계산하기 위한 교란의 수가 많을수록 경사도를 정확하게 근사한다(Fonseca et al., 2015).

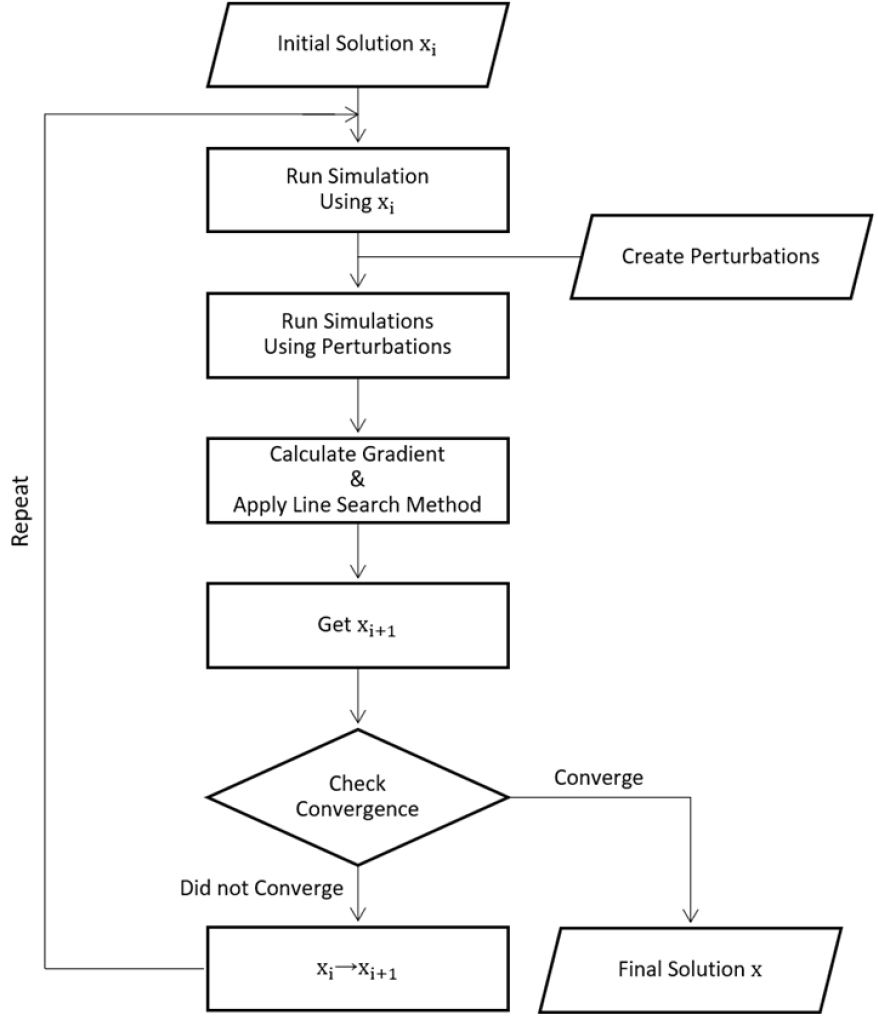
본 연구에서는 유정 운영 조건의 함수인 NPV를 최대화하기 위해 StoSAG로 경사도를 계산하여 최적 유정 운영 조건을 찾는다. StoSAG를 이용한 최적화 알고리즘의 순서도는 Fig 1과 같다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F1.jpg

Fig. 1.

Workflow of the optimization algorithm.

대상 저류층 모델

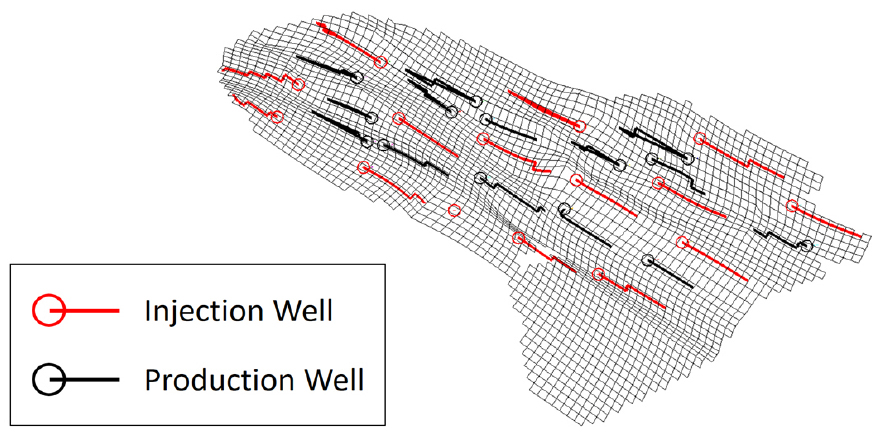
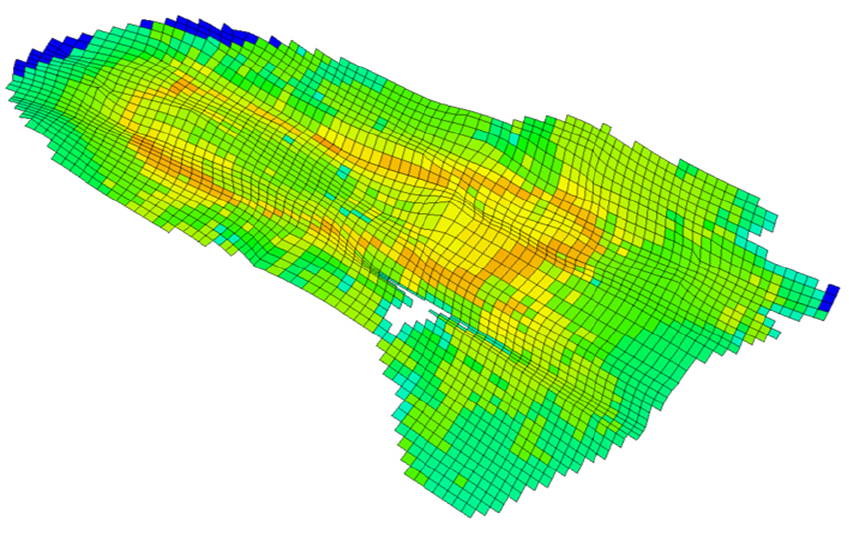
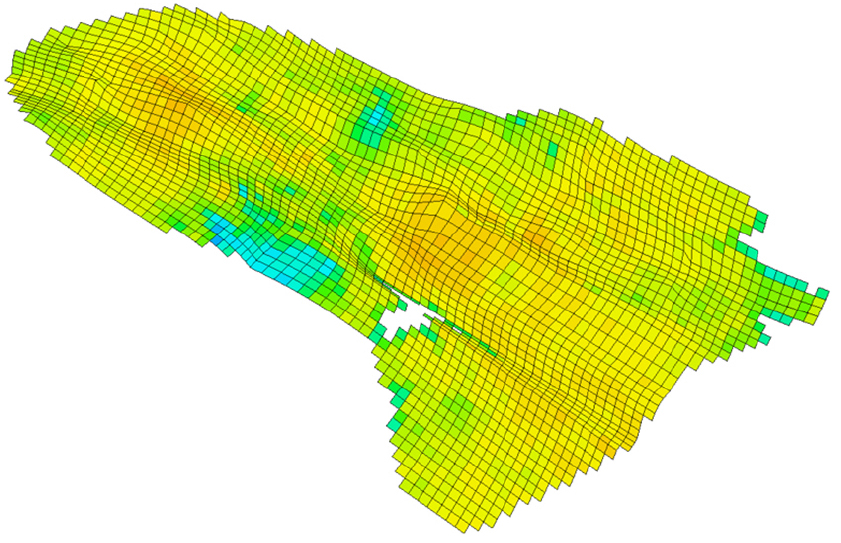
본 연구에서 사용된 저류층 모델은 총 86,213개의 셀로 이루어진 실제 탄산염암 저류층 기반의 모델이다. 저류층 전반에 걸쳐 생산정 15개와 주입정 14개가 설치되어 있으며, 설치 위치는 Fig. 2와 같다. 1개의 생산정을 제외한 모든 유정은 수평정이며, 저류층 주변부의 주입정은 물 포화도가 높은 지역에 설치되어 있고, 중심부의 주입정은 비교적 오일 포화도가 높은 지역에 설치되어 있다. 생산정과 주입정의 위치분포를 살펴보면, 주입정들이 생산정의 주변부를 감싸고 있다. Fig. 3는 해당 모델의 34개의 층 중 최상층의 오일 포화도를 나타내었다. 저류층 암석의 공극률은 층마다 비슷한 분포를 가지고 있으며, 최상층의 공극률은 Fig. 4와 같이 분포한다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F2.jpg

Fig. 2.

Locations of 14 production wells and 15 injection wells.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F3.jpg

Fig. 3.

Oil saturation of the field model on the top layer. The color legend is omitted because of confidentiality.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F4.jpg

Fig. 4.

Porosity of the field model on the top layer. The color legend is omitted because of confidentiality.

각 유정에서의 제한 조건은 Table 1과 같다. 기존 생산 운영 조건에서는 전체 목표 일일 오일 생산량이 각 오일 생산정에 같은 비율로 할당된다. 생산 기간 중에 Table 1의 유정 제한 조건을 벗어날 경우, 유정 제한 조건을 벗어나지 않는 최대의 생산량으로 생산하고 나머지 생산량을 다른 유정들이 같은 비율로 할당 받아 생산하게 된다. 주입정은 전체 주입 목표량은 없이 공저압력이 4400 psi를 유지하도록 주입하되, 1600 STB/day를 초과할 경우, 주입량이 제한된다. 전체 주입 및 생산 목표량은 기존의 생산 및 주입 계획의 생산량이 충분하다고 가정하여 설정했으며, 공저압력 목표는 지층의 파쇄압력으로 인해 제한되기 때문에 4400 psi로 설정하였다. 저류층 모델은 Schlumberger 社의 ECLIPSE 100을 이용하여 시뮬레이션을 수행하였다.

Table 1.

Well constraints in the simulation model

Production Period	28 years
Production Well Constraints	Bottomhole Pressure : 1200 psi Tubing Head Pressure Limit : 350 psi Daily Production Rate Limit : 1370 STB/day Economic Limit : 250 STB/day
Injection Well Constraints	Bottomhole Pressure : 4400 psi Daily Injection Rate Limit : 1600 STB/day

최적화 결과

본 연구의 최적화 목적은 약 28년의 생산 기간 동안 가장 높은 NPV를 달성하는 유정 운영 조건을 찾는 것이다. 최적 운영 조건을 찾기 위해 15개의 물 주입정의 물 주입 비율과 14개의 생산정의 생산 비율 그리고 생산 유량 대비 주입 유량을 나타내는 생산 대비 주입 비율(Voidage Replacement Ratio, VRR)값까지 총 30개의 값을 최적화 변수로 설정했다. 30개의 변수에 적용된 범위와 제한 조건은 Table 2와 같다. 각 유정 간 할당 비율이 전체 생산량의 백분율로 보일 수 있도록 비율의 총합은 100이 되도록 지정해주었다.

Table 2.

Search range and constraints of decision variables

	Search range	Constraints
Ratio between Producers, $q_{o, 1} \dots q_{o, 14}$ (%)	$0.01 \leq q_{o, i} \leq 100$	$\sum_{i = 1}^{14} q_{o, i} = 100$
Ratio between Injectors, $i_{w, 1} \dots i_{w, 15}$ (%)	$0.01 \leq i_{w, i} \leq 100$	$\sum_{i = 1}^{15} i_{w, i} = 100$
VRR	$0.5 \leq V R R \leq 1.5$	-

The ratios are percentages.

본 최적화의 목적함수는 NPV(Net Present Value)가 사용되었고 계산 방법은 수식 (9)와 같다. NPV에는 물 주입 및 처리 비용과 생산된 오일로 인한 수익만이 포함되었으며, 유정 운영비용은 고려되지 않았다. 목적함수인 NPV 계산에 사용된 경제성 인자들의 값은 Table 3과 같다. 최적화 결과 비교를 위해 설정된 생산정과 주입정의 기본 운영 조건에서 14개의 생산정간의 목표생산량 비율을 같게 설정되어있으며, 15개의 주입정간의 목표생산량 비율도 마찬가지로 균등하게 배분하였다. VRR은 생산된 유체 부피 대비 주입 유체의 부피 비율을 뜻하며 기본 운영 조건에서 1로 설정하였다. AP로 시작하는 변수들은 생산정간의 생산 유체 할당 비율을 뜻하며, 전체 생산량을 100이라고 가정했을 때 각 유정에 할당되는 비율을 나타낸다. AI로 시작하는 변수들은 주입정간의 주입 유체 할당 비율을 뜻하며, 전체 주입량을 100이라고 가정했을 때 각 유정에 할당되는 비율을 나타낸다. 기본 운영 조건은 생산된 유체의 부피와 같은 부피를 물 주입정을 통해 주입하며, 모든 생산정과 주입정이 같은 부피 비율로 생산/주입을 한다(Table 4). 본 연구에서는 기본 운영 조건을 대조군로 지정하였으며, 기본 운영 조건으로 생산한 결과와 비교한 각종 수치의 변화를 중심으로 최적화 결과를 분석하였다.

Table 3.

Economic parameters in equation (9)

	Value
Discount Rate $[%]$	10
Oil Price $r_{o p} [$ / S T B]$	60
Water Disposal Cost $c_{w p} [$ / S T B]$	5
Water Injection Cost $c_{w i} [$ / S T B]$	5

Table 4.

Ratios for production and injection wells. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

Production well	Ratio	Injection well	Ratio
AP2	0.07142	AI1	0.0667
AP3	0.07142	AI2	0.0667
AP4	0.07142	AI3	0.0667
AP5	0.07142	AI4	0.0667
AP6	0.07142	AI5	0.0667
AP7	0.07142	AI6	0.0667
AP9	0.07142	AI7	0.0667
AP10	0.07142	AI8	0.0667
AP11	0.07142	AI9	0.0667
AP12	0.07142	AI10	0.0667
AP13	0.07142	AI11	0.0667
AP14	0.07142	AI12	0.0667
AP15	0.07142	AI13	0.0667
AP16	0.07142	AI14	0.0667
		AI15	0.0667

광역 해를 탐색하기 위해 15개의 초기 해에 대해 최적화를 진행하였으며 15개의 초기 해는 Latin Hypercube Sampling을 활용하여 생성하였다(McKay et al., 1979). StoSAG 경사도를 구하기 위해 사용된 교란의 개수는 15개이며 이는 최적화 변수 개수의 50%이다. 수렴 조건은 목적함수 값의 변화율이 0.1%보다 작을 때, 또는 x의 Norm의 상대적 변화율이 0.001%보다 작을 때 두 가지가 설정되었으며 수식으로 표현하면 Table 5와 같다.

(9)

N P V = \sum_{n = 1}^{N_{e}} \frac{∆ t_{n}}{(1 + b)^{\frac{∆ t_{n}}{365}}} \{\sum_{j = 1}^{N_{p r o}} (r_{o p} ∙ \bar{q_{o, j}^{n}} - c_{w p} ∙ \bar{q_{w p, j}^{n}}) - \sum_{k = 1}^{N_{i n j}} c_{w i} ∙ \bar{q_{w i, j}^{n}}\}

Table 5.

Convergence criteria for the optimization

Convergence Criteria
Relative Change of Objective Function	$\frac{\|f (x_{i + 1}) - f (x_{i})\|}{f (x_{i})} ＜ 0.001$
Relative Change of x norm	$\frac{\|x_{i + 1} - x_{i}\|}{\|x_{i}\|} ＜ 0.00001$

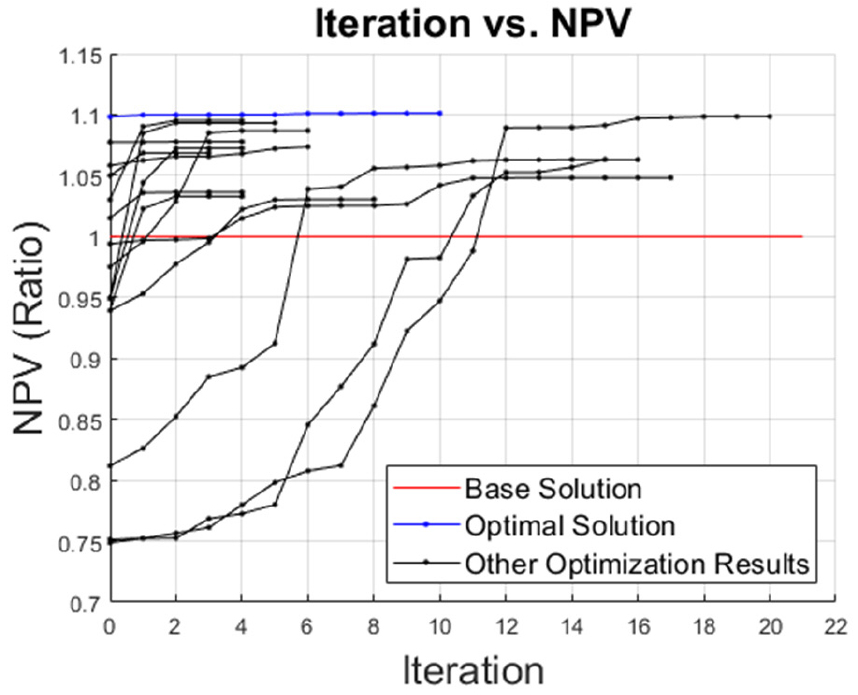
Fig. 5은 초기해 15개의 최적화 수렴과정이다. 기본 운영 조건의 NPV는 Fig. 5에서 빨간색 수평선으로 표기되었다. 수렴된 해의 NPV를 기본 운영 조건을 이용한 결과와 비교했을 때, 모든 초기 해에 대해 NPV가 증가하였다. 최종적으로 가장 높은 NPV를 달성한 최적 운영 조건은 Fig. 5의 파란색 선에 해당한다. 최적 운영 조건의 NPV는 기본 운영 조건 대비 약 10% 정도 높았다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F5.jpg

Fig. 5.

Iteration versus net present value (NPV) of 15 initial solutions. All the NPVs were divided by the NPV of the base solution because of confidentiality

NPV가 가장 높은 최적 운영 조건의 구체적인 운영 조건은 Table 6와 같다. 기존 운영 조건과 달리, 유정 간 할당량 차이가 존재하며 VRR 값이 0.8268로 기본 운영 조건보다 적게 주입되었다. 최적해는 기존 운영 조건에 비해 물 주입량을 감소시켜 물 생산량을 감소시키면서도 오일 생산량을 유지하였기 기존보다 큰 NPV를 달성하였다. 이에 대한 요인은 크게 3가지로 분석하였다.

Table 6.

Optimal ratios for production and injection wells. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

Production well	Ratio	Injection well	Ratio
AP2	0.045	AI1	0.034
AP3	0.117	AI2	0.125
AP4	0.028	AI3	0.107
AP5	0.057	AI4	0.059
AP6	0.037	AI5	0.08
AP7	0.132	AI6	0.119
AP9	0.135	AI7	0.097
AP10	0.015	AI8	0.046
AP11	0.074	AI9	0.025
AP12	0.095	AI10	0.046
AP13	0.096	AI11	0.07
AP14	0.006	AI12	0.014
AP15	0.073	AI13	0.09
AP16	0.09	AI14	0.003
		AI15	0.086

첫 번째, 최적 운영 조건은 VRR을 0.8268을 사용하여 기본 운영 조건에 비해 물 주입량을 감소시켰다. 그러나 단순히 물 주입량을 감소시킨 것만으로는 NPV를 증가시킬 수 없다. Table 7에서 주어진 것처럼 물 주입량은 기본 운영 조건 대비 34.7%로 줄임과 동시에 물 생산량을 45.16%로 줄이면서도 비슷한 수준의 오일 생산량을 유지하였다. 저류층 유체투과율 및 오일 포화도의 비균질성과 유정의 공간적 위치를 고려하였기 때문에 각 유정 생산량과 주입량 비율이 적절히 조정되어 물 생산량은 줄이고 오일 생산량을 유지하였다.

Table 7.

Comparison of production and injection cumulatives and NPV

	Base Solution	Optimal Solution	Change
Oil Production Cumulative, %	100	98.88	-1.13
Water Production Cumulative, %	100	54.85	-45.16
Water Injection Cumulative, %	100	65.33	-34.7
NPV, %	100	109.87	9.87

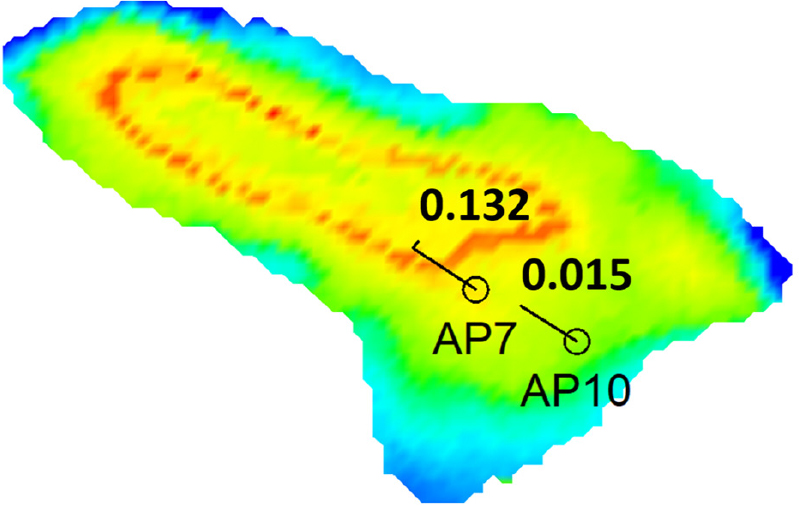
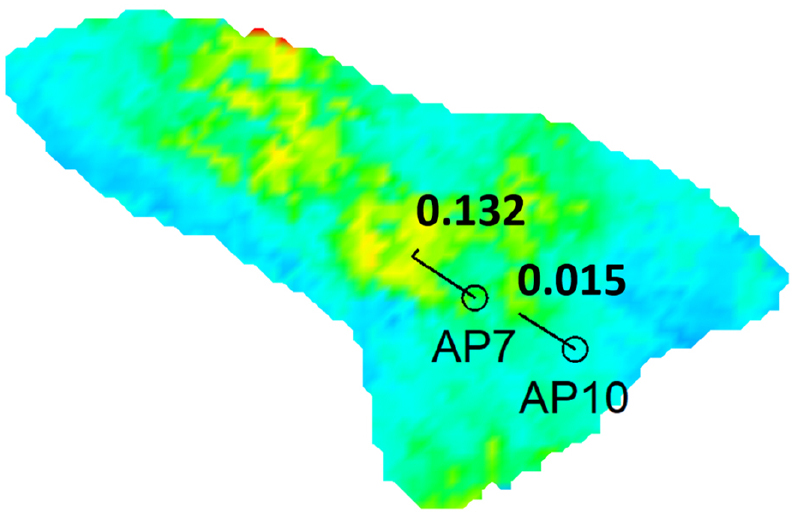
앞서 소개했듯이 사용된 저류층 모델은 중심부에 높은 유체투과율과 오일 포화도를 가지는 지역이 존재한다. 그러나 기본 운영 조건은 모든 유정에 동일한 생산량 비율이 할당되어 오일 포화도가 높지 않은 지역에서도 생산되므로 물 생산량이 크고 오일 포화도와 유체투과도가 높은 지역에서 오일을 더 생산할 수 있음에도 덜 생산되었다. 이에 반해 최적 해의 각 유정 생산량 할당 비율에는 유체투과율과 오일 포화도의 공간적 분포가 반영되었다. 예를 들어 Fig. 5과 Fig. 6 및 7에서 보여지는 것처럼 AP7은 AP10에 비해 유체투과율와 오일 포화도가 높은 지역에 위치한다. AP7과 AP10은 각각 전체 생산 할당량의 13.2%와 1.5%가 할당되었다. 여러 층의 포화도와 유체투과도 정보를 그림으로 표현하기 위해 각 위치의 특성을 수식 (10)를 이용해 평균화한 후 시각화하였다.

(10)

X_{h e i g h t a v e r a g e d} = \frac{\sum_{i = 1}^{N_{l a y e r}} h_{i} X_{i}}{\sum_{i = 1}^{N_{l a y e r}} h_{i}}

where $X$ is property

$h$ is height of each layer

$N_{l a y e r}$ is number of layers in the model

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F6.jpg

Fig. 6.

Height-averaged oil saturation and location of AP7 and AP10. The color legend is omitted because of confidentiality.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F7.jpg

Fig. 7.

Height-averaged permeability and location of AP7 and AP10. The color legend is omitted because of confidentiality.

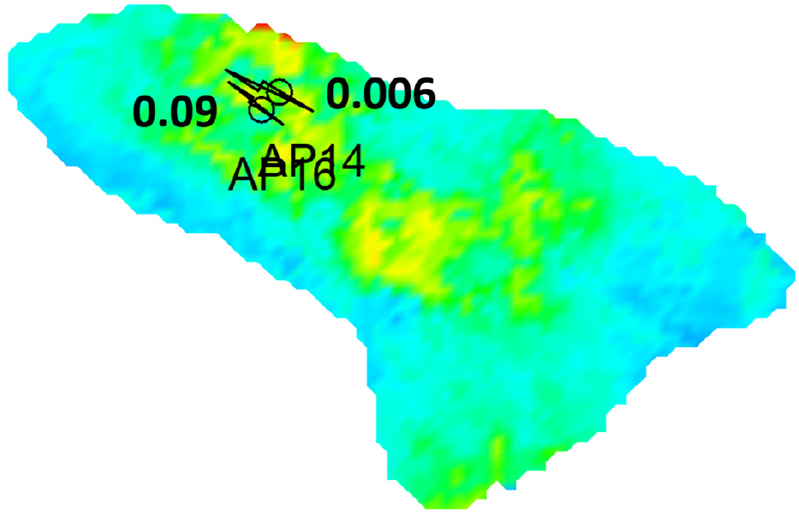
두 번째, 최적해에 유정 간의 공간적 거리가 반영되었다. Fig. 8에서 AP14와 AP16은 거리가 매우 가까워 거의 동일한 지역을 배수 지역으로 가지기 때문에 각각 0.6%와 9%의 생산량을 할당됐다. 두 유정은 기본 운영 조건 대비 48.1% 적은 물과 22% 더 많은 오일을 생산했다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F8.jpg

Fig. 8.

Height-averaged permeability and location of AP14 and AP16. The color legend is omitted because of confidentiality

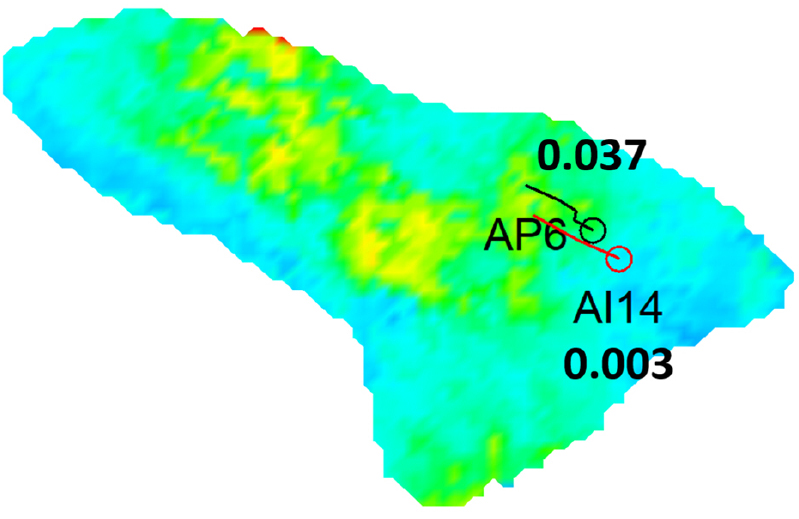
Fig. 9에서 AP6과 AI14는 가까운 거리에 있어 AI14에서 주입된 물이 AP6에서의 물 생산량 증가에 기여한다. AI14에서 주입된 물이 AP6 주변부의 물 포화도를 증가시키고 이는 오일의 상대유체투과도를 감소시켜 생산에 비효율을 초래한다. 최적 해에서는 이를 방지하고자 AI14에 전체 물 주입량의 0.3%를 할당하였다. 결과적으로, AP6은 기본 운영 조건 대비 20% 적게 물을 생산하면서 86% 많은 오일을 생산하였다.

https://static.apub.kr/journalsite/sites/ksmer/2021-058-02/N0330580204/images/ksmer_58_02_04_F9.jpg

Fig. 9.

Height-averaged permeability and location of AP6 and AI14. The color legend is omitted because of confidentiality

세 번째, VRR이 1보다 낮아 저류층 압력 감소로 인해 오일 점성도가 감소하여 오일 생산성을 높였다. 대조군 및 최적 운영 조건 모두 저류층 압력이 기포점 이상인 상태이므로 압력이 감소하면 오일 점성도가 감소한다. 최적 운영 조건에서는 대조군보다 저류층 압력이 감소하면서 저류층 내의 오일 점성도가 감소한다. Darcy 방정식에 의하면, 같은 압력 강하에서도 유체의 점성도가 낮으면 유체의 유동이 원활해진다. 또한, 중심부의 주입정의 경우 물 층이 아닌 오일 층에 물을 주입하고 있다. 물을 오일에 주입할 때, 오일의 면적 물과 오일의 상대유동비(Mobility Ratio $= \frac{k_{r w} / μ_{w}}{k_{r o} / μ_{o}}$ )에 따라 물 주입으로 인한 오일 생산성 증가의 효율이 달라진다. 일반적으로, 이 값이 작을수록 물 주입으로 인해 더 넓은 부피의 오일을 밀어낼 수 있다(Dyes et al., 1954). 점성도 감소로 인해 오일의 유동성이 증가하고, 물 주입의 효율이 증가하였기 때문에 VRR을 1보다 낮추는 최적 운영 조건이 압력이 높게 유지되는 기본 운영 조건과 같은 양의 오일을 생산할 수 있었다.

앞서 살펴 보았듯이 최적화된 운영 조건의 경제성은 물 처리 비용과 물 주입 비용의 감소에서 비롯된다. 이에 따라 핵심 경제성 인자인 물 처리 비용과 물 주입 비용의 변화에 따른 최적 조건 및 NPV의 변화를 추가로 분석하였다. 기존 최적화에서는 오일 단위 가격은 $$ 60 / STB$ , 물 단위 주입 비용 ( $c_{w i}$ )과 물 단위 처리 비용 ( $c_{w p}$ ) 각각 $$ 5 / STB$ 이 사용되었다. 경제성 인자 민감도 분석에서는 물 단위 주입/처리 비용을 50% 저렴한 $$ 2.5 / STB$ 로 설정해 최적화를 수행하였다.

최적화 수행 결과 도출된 최적 운영 조건을 이용해 생산 및 주입을 시뮬레이션한 결과는 Table 8과 같다. 물 주입/처리 비용이 50%로 줄어들었을 때는 $$ 5 / bbl$ 인 경우에 비해 더 적은 5.4%의 NPV 증가율을 보였다. 도출된 최적해의 각 변수의 값은 Table 8과 같다. 도출된 최적해는 기본 최적화 문제에서 구해진 최적해와 비교했을 때, VRR이 0.87로 증가하면서 더 많은 물을 주입하였다. 물 주입 비용이 저렴해지면서 더 많은 물 주입하고 오일 생산량을 조금이라도 증가하도록 해가 선택되었다.

Table 8.

Optimal ratios for production and injection wells when $c_{w i}$ and $c_{w p}$ are $2.5/STB. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

Production well	Ratio	Injection well	Ratio
AP2	0.118	AI1	0.04
AP3	0.047	AI2	0.12
AP4	0.11	AI3	0.071
AP5	0.012	AI4	0.073
AP6	0.1	AI5	0.02
AP7	0.033	AI6	0.037
AP9	0.053	AI7	0.055
AP10	0.041	AI8	0.194
AP11	0.126	AI9	0.039
AP12	0.079	AI10	0.057
AP13	0.055	AI11	0.032
AP14	0.066	AI12	0.034
AP15	0.059	AI13	0.101
AP16	0.068	AI14	0.058
		AI15	0.086

결 론

본 연구에서는 추계학적 경사도를 이용하여 실제 탄산염암 기반 저류층 모델에 대한 주입 및 생산 조건에 대한 최적화를 수행하였다. 본 연구의 최적화 기법과 결과에 대한 요약은 다음과 같다.

∙ 경사도를 추계학적으로 구하는 StoSAG를 사용하면 전통적인 FDM 기법보다 계산 비용 측면에서 효율적인 최적화를 수행할 수 있다. 이 효과는 최적화 문제 대상의 앙상블 개수가 많을수록, 최적화 대상 변수의 개수가 많을수록 극대화된다.

∙ StoSAG 기법을 이용해 모델의 15개의 주입정과 14개의 생산정의 최적 운영조건을 도출하였다. NPV가 목적함수로 사용되었고 단위 오일 가격, 단위 물 주입 비용, 단위 물 처리 비용은 각각 $$ 60 / STB$ , $$ 5 / STB$ , $$ 5 / STB$ 이 사용되었다. 도출된 최적 운영조건으로 광구를 운영할 경우 약 10%의 NPV 증가를 달성하였다.

∙ 기본 운영 조건 대비 최적 운영 조건에 대한 NPV가 10% 증가한 것은 크게 3가지 요인으로 분석하였다.

- 기본 운영 조건 대비 적은 양의 물을 주입하고도 동일한 수준의 오일 생산량이 생산됨.

- 유정의 공간적 위치와 저류층 유체투과율 분포를 고려하여 생산, 주입 비율이 조정됨.

- 적은 양의 물을 주입하여 저류층 압력을 낮춰 오일 점성도 감소시켜 유체의 유동성과 물 주입의 효율이 증가함.

∙ 경제성 인자인 단위 오일 가격, 단위 물 주입 비용, 단위 물 처리 비용이 각각 $$ 60 / STB$ , $$ 2 / STB$ , $$ 2 / STB$ 일 때의 최적화를 수행하여 민감도 분석을 수행하였다. 기본 운영 조건 대비 최적 운영조건은 NPV가 5.4% 정도 증가하였다.

Acknowledgements

본 연구는 한국지질자원연구원의 지원(과제번호: GP2020- 006)을 받아 수행되었습니다.

References

Bangerth, W., Klie, H., Wheeler, M.F., Stoffa, P.L., and Sen, M.K., 2006. On optimization algorithms for the reservoir oil well placement problem. Computational Geosciences, 10, p.303-319. 10.1007/s10596-006-9025-7

Bellout, M.C., Echeverría Ciaurri, D., Durlofsky, L.J., Foss, B., and Kleppe, J., 2012. Joint optimization of oil well placement and controls. Computational Geosciences, 16, 1061-1079. 10.1007/s10596-012-9303-5

Chen, Y., Oliver, D.S., and Zhang, D., 2009. Efficient ensemble-based closed-loop production optimization. SPE Journal, 14, p.634-645. 10.2118/112873-PA

Dyes, A.B., Caudle, B.H., and Erickson, R.A., 1954. Oil production after breakthrough as influenced by mobility ratio. Journal of Petroleum Technology, 6(4), p.27-32. 10.2118/309-G

Fonseca, R.M., Kahrobaei, S.S., Van-Gastel, L.J.T., Leeuwenburgh, O., and Jansen, J.D., 2015. Quantification of the impact of ensemble size on the quality of an ensemble gradient using principles of hypothesis testing. SPE Reservoir Simulation Symposium, Society of Petroleum Engineers, p.804-828. 10.2118/173236-MS

Fonseca, R.R.M., Chen, B., Jansen, J.D., and Reynolds, A., 2017. A stochastic simplex approximate gradient (StoSAG) for optimization under uncertainty. International Journal for Numerical Methods in Engineering, 109(13), p.1756-1776. 10.1002/nme.5342

Gao, G., Li, G., and Reynolds, A.C., 2007. A stochastic optimization algorithm for automatic history matching. SPE Journal, 12, p.196-208. 10.2118/90065-PA

Isebor, O.J., Echeverrı, D., and Durlofsky, L.J., 2014. Generalized field-development optimization with derivative-free procedures. SPE Journal, 19, p.891-908. 10.2118/163631-PA

Jeong, H., Sun, A.Y., Jeon, J., Min, B., and Jeong, D., 2020. Efficient ensemble-based stochastic gradient methods for optimization under geological uncertainty. Frontiers in Earth Science, 8, p.108. 10.3389/feart.2020.00108

Jeong, H., Sun, A.Y., and Zhang, X., 2018. Cost-optimal design of pressure-based monitoring networks for carbon sequestration projects, with consideration of geological uncertainty. International Journal of Greenhouse Gas Control, 71, p.278-292. 10.1016/j.ijggc.2018.02.014

Kim, J., Kang, B., Jeong, H., and Choe, J., 2019. Field development optimization using a cooperative micro-particle swarm optimization with parameter integration schemes. Journal of Petroleum Science and Engineering, 183, p.106416. 10.1016/j.petrol.2019.106416

Li, G., and Reynolds, A.C., 2011. Uncertainty quantification of reservoir performance predictions using a stochastic optimization algorithm. Computational Geosciences, 15, p.451-462. 10.1007/s10596-010-9214-2

Li, L., Jafarpour, B., and Mohammad-Khaninezhad, M.R., 2013. A simultaneous perturbation stochastic approximation algorithm for coupled well placement and control optimization under geologic uncertainty. Computational Geosciences, 17, p.167-188. 10.1007/s10596-012-9323-1

McKay, M.D., Beckman, R.J., and Conover, W.J., 1979. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 21, p.239. 10.2307/1268522

Nocedal, J. and Wright, S.J., 2006. Numerical Optimization, Springer, New York, USA.

Spall, J.C., 1992. Multivariate Stochastic Approximation Using a Simultaneous Perturbation Gradient Approximation. IEEE transactions on automatic control, 37, p.332-341. 10.1109/9.119632

Stordal, A.S., Szklarz, S.P., and Leeuwenburgh, O., 2016. A theoretical look at ensemble-based optimization in reservoir management. Mathematical Geosciences, 48(4), p.399-417. 10.1007/s11004-015-9598-6

Sun, N.-Z. and Sun, A., 2015. Model calibration and parameter estimation, Springer, New York, USA. 10.1007/978-1-4939-2323-6

Yan, X. and Reynolds, A.C., 2014. Optimization algorithms based on combining FD approximations and stochastic gradients compared with methods based only on a stochastic gradient. SPE Journal, 19, p.873-890. 10.2118/163613-PA

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Optimization of Well Operations in a Carbonate Reservoir Using Stochastic Simplex Approximate Gradient

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Fig. 1.

Workflow of the optimization algorithm.

Fig. 2.

Locations of 14 production wells and 15 injection wells.

Fig. 3.

Oil saturation of the field model on the top layer. The color legend is omitted because of confidentiality.

Fig. 4.

Porosity of the field model on the top layer. The color legend is omitted because of confidentiality.

Table 1.

Well constraints in the simulation model

Table 2.

Search range and constraints of decision variables

Table 3.

Economic parameters in equation (9)

Table 4.

Ratios for production and injection wells. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

(9)

Table 5.

Convergence criteria for the optimization

Fig. 5.

Iteration versus net present value (NPV) of 15 initial solutions. All the NPVs were divided by the NPV of the base solution because of confidentiality

Table 6.

Optimal ratios for production and injection wells. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

Table 7.

Comparison of production and injection cumulatives and NPV

(10)

Fig. 6.

Height-averaged oil saturation and location of AP7 and AP10. The color legend is omitted because of confidentiality.

Fig. 7.

Height-averaged permeability and location of AP7 and AP10. The color legend is omitted because of confidentiality.

Fig. 8.

Height-averaged permeability and location of AP14 and AP16. The color legend is omitted because of confidentiality

Fig. 9.

Height-averaged permeability and location of AP6 and AI14. The color legend is omitted because of confidentiality

Table 8.

Optimal ratios for production and injection wells when cwi and cwp are $2.5/STB. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively

Acknowledgements

References

Optimal ratios for production and injection wells when $c_{w i}$ and $c_{w p}$ are $2.5/STB. The prefixes (AP and AI) represent production and injection wells, respectively. The sums of the ratios for production and injection wells are 1, respectively