서 론

탄소중립 달성을 위하여 대기 중에 존재하는 이산화탄소(CO₂)를 포집하여 지하에 영구적으로 저장하는 CO₂ 포집 및 저장(carbon capture and storage, CCS)이 기술적 돌파구로 주목받고 있다. 지하에 영구적으로 CO₂를 저장하는 지중저장(geological storage)은 심부 염대수층(deep saline formations), 고갈 유 ‧ 가스전(depleted oil and gas fields), 석탄층(coalbed methane) 등이 대상이며, 이때 저장용량(capacity), 주입성(injectivity), 밀폐성(containment)을 통하여 안정성을 파악하여야 한다(Park and Huh, 2013; Rycroft et al., 2024). 대상 저장소 유형 중 고갈 유 ‧ 가스전은 긴 시간 동안 저류층 구조 내 탄화수소를 부존했기에 구조적인 무결성(integrity)이 존재하며, 기존의 생산 설비를 활용할 수 있어 경제성 확보 및 개발 기간 단축에 이점을 가진다(Hughes, 2009; Kim et al., 2023).

CO₂ 지중저장은 다양한 기간과 규모에 걸쳐 발생할 수 있는 물리 ‧ 화학적 포획 기작(trapping mechanism) 조합을 통하여 수행되기에 저장용량 평가 시 이를 고려하여야 한다(Bachu et al., 2007). 포획 기작은 지질학적 불균질성, 저류층의 온도, 압력, 두께 등의 매개변수에 따라 다르며, CO₂ 주입 시 저장 효율성 평가를 위하여 각 포획 기작의 CO₂ 저장용량에 대한 정량적 분석이 필요하다(Allinson et al., 2014). 특히, CO₂가 공극 공간에 갇힌 상태로 남아있는 잔류 포획(residual trapping)과 주입된 CO₂가 저류층 내 염수에 용해되는 용해 포획(solubility trapping)은 광물 포획(mineral trapping) 및 구조 포획(structural trapping)에 비하여 각각 저류층 내 반응의 신속성 및 안정성이 뛰어나기에 저장성능 분석의 효과적인 지표로 활용된다(Davoodi et al., 2023; Ismail and Gaganis, 2023).

CCS의 저류층 시뮬레이션과 관련하여 기존 연구에서는 고갈 가스전 내 잔류가스의 양이 많을 경우, 잔류 포획 형태의 저장이 주로 이루어짐을 확인하였다(Raza et al., 2017). Cao et al.(2020)은 고갈 가스전에서의 가스 회수율, 저류층 온도, 주입률(injection rate) 등이 저장용량에 미치는 영향을 분석하였으며, 저류층 온도가 낮을수록 CO₂ 저장에 유리하고 잔류 수포화율과 회수율이 높을수록 저장용량이 작아짐을 언급한 바 있다. 또한, 빠르고 신뢰할 수 있는 결과 도출을 위해 저류층 물성과 주입조건을 입력자료로 기계학습 기반의 잔류 포획 지수(residual gas trapping index, RTI) 및 용해 포획 지수(solubility gas trapping index, STI) 예측 연구가 수행되어 왔다(Kim et al., 2017; Kutz, 2017; Song et al., 2020; Safaei-Farouji et al., 2022; Vo-Thanh and Lee, 2022). 이러한 연구는 대규모 데이터 분석과 처리를 통해 지하 지질구조 내 유체 유동 문제의 복잡한 비선형 관계를 효과적으로 접근하고 저장효율지수 예측모델의 유용함을 제시하고 있다.

대부분의 지중저장 연구는 심부 염대수층을 대상으로 하였으나, 저장소에 대한 사전정보가 부족하여 탐사작업을 위한 시간과 비용이 추가적으로 요구된다. 반면 고갈 가스전의 경우, 기존의 유 ‧ 가스 생산 이력으로 유체함량 및 저류층 물성 등의 정보를 보유하고 있어 저장효율지수 예측모델 구축에 이점을 가지고 있다. 그러나 고갈 가스전을 대상으로 시뮬레이션을 사용한 저장안정성 분석과 기계학습을 활용한 저장효율지수 예측 연구는 전무한 실정이다. 이 연구에서는 고갈 가스전에서 CO₂ 저장안정성에 영향을 미치는 인자에 대하여 분석하고, 다양한 기계학습 기법의 적용을 통해 이들의 효율성 및 신뢰성을 파악하고자 한다.

고갈 가스전에서의 CO₂ 저장용량 및 효율 파악을 위한 민감도 분석

저류층 모델 구축 및 CO₂ 주입 설계

고갈 가스전에서의 CO₂ 지중저장을 모사하기 위하여 선행연구(Agartan et al., 2018; Khan, 2022; BOEM, 2023)에서 제시된 저류층 입력인자를 바탕으로 SLB社의 Petrel 및 Eclipse 300을 활용하여 저류층 내 다성분 유체 거동을 모사하였다. 저류층에는 염수와 가스만 존재한다고 가정하였으며, Peng-Robinson 상태방정식을 활용하여 고갈 가스전 내의 염수와 가스의 상평형을 정의하였다. 또한, 두 유체의 초기 포화율에 따른 상대유체투과도는 Khan(2022)의 값을 활용하였으며(Fig. 1), 경계조건의 경우 저류층 외 다른 지역의 유체 거동의 영향을 받지 않도록 no flow 조건으로 설정하였다. 고갈 가스전은 심도 2,700 m, 압력 330 bar의 조건을 적용하여 저류층 내 CO₂의 초임계 조건을 충족하도록 하였으며, 공극률과 유체투과도는 다양한 저류층 정보를 반영하기 위하여 다수의 연구가 수행된 Gulf of Mexico의 고갈 가스전 물성을 활용하였다(Table 1).

Fig. 1.

Gas/water relative permeability.

구축된 고갈 가스전 저류층 모델에 대하여 CO₂ 주입 전 단일 생산정을 통하여 10년간 가스 생산을 수행하였으며, 생산한계 공저압인 50 bar 도달 시 생산을 중단하도록 하였다. 이때 약 242 MMscf의 가스가 생산되었으며, 생산 종료 후 해당 생산정은 CO₂ 주입정으로 전환하여 활용하였다. CO₂ 주입은 15년간 진행하여 주입정의 공저압이 초기 저류층압력(initial reservoir pressure)에 도달 시 주입을 종료하였다(Table 2). 이에 CO₂ 지중저장 시 초기 주입 기간 이후 장기적인 저장안정성을 파악하기 위하여 가스 생산 및 CO₂ 주입 기간을 포함한 향후 200년의 저류층 내 유체 거동을 확인하였다.

CO₂ 저장관련인자의 민감도 분석 조건

잔류 및 용해 포획 기작과 연관된 저장효율지수인 RTI와 STI는 식 (1), (2)와 같으며(Nghiem et al., 2010), CO₂ 저장안정성 및 효율을 이해하기 위하여 활용된다. 이 연구에서는 Table 3과 같이 주입조건과 저류층 물성에 대하여 Base Case를 기준으로 변화 범위를 설정하였으며, 각 단일 변수에 대한 민감도 분석으로부터 고갈 가스전 저류층 내 CO₂ 주입 후 포획 기작에 따른 누적 저장용량 및 저장효율지수 변화를 파악하고자 한다. 또한, 기계학습 시 입력자료 구성을 위한 저장관련인자와 영향 범위를 확인하고자 한다. 민감도 분석 시 저장관련인자 값에 따라 동일한 상대유체투과도를 사용하였으며, CO₂ 주입 시작은 가스 생산 10년 후로 설정하였다. 이때 조건 별 저류층 포기 압력 도달에 따른 가스 생산 기간에는 차이가 있을 수 있다.

주입조건에 따른 CO₂ 저장용량 및 저장효율지수

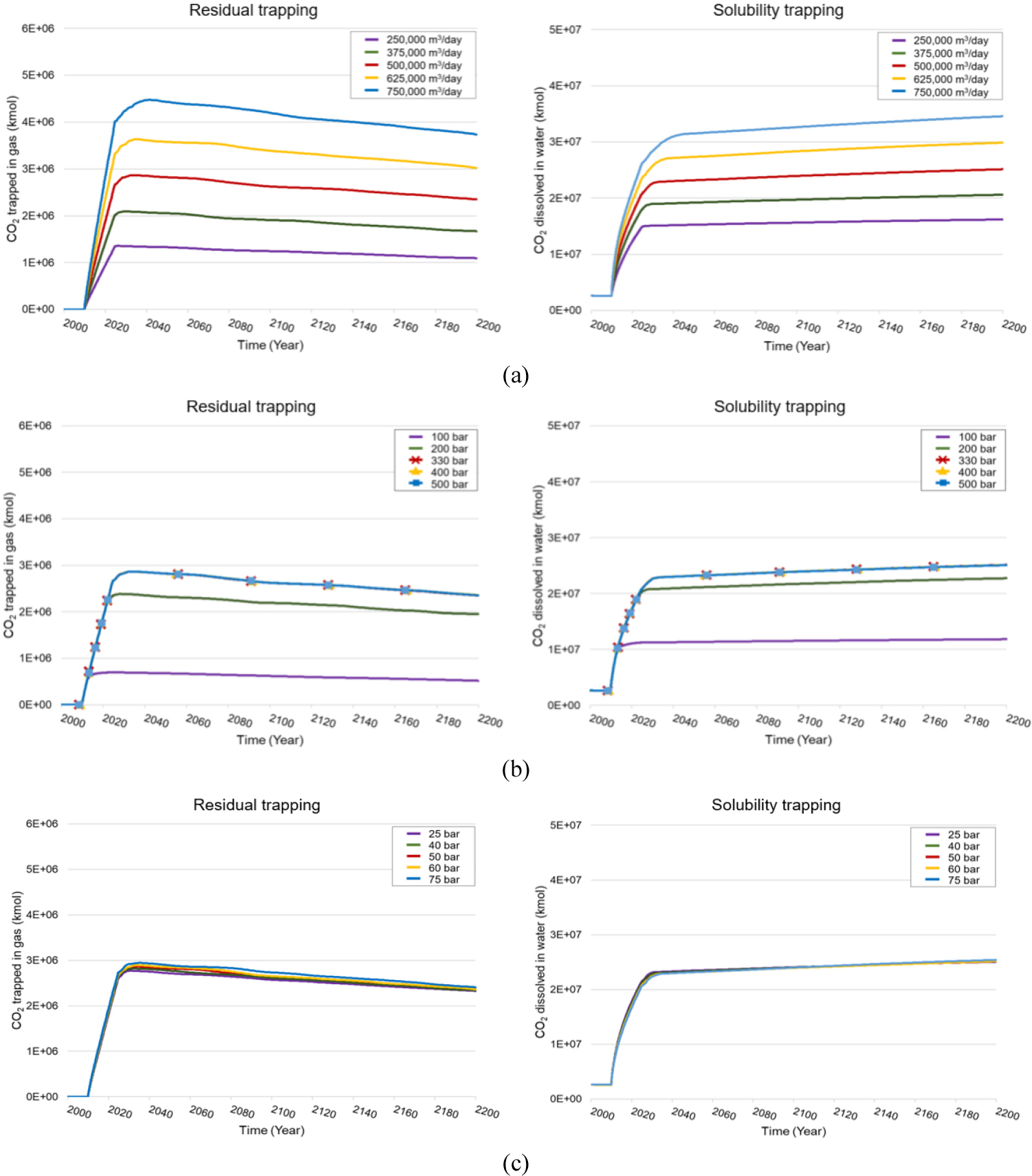
CO₂ 주입 시 주입조건에 따른 잔류 포획 및 용해 포획의 용량을 분석한 결과, CO₂ 주입률 및 최대 저류층압력이 증가할수록 잔류 및 용해 포획되는 CO₂ 저장용량은 증가하였다(Fig. 2). 그리고 일정 값 이상의 최대 저류층압력은 포획 기작에 따른 CO₂ 용량의 변화가 일어나지 않았으며, 이는 CO₂ 주입 시 저류층 압력보다 높은 공저압 값을 필요로 하기에 특정 압력 이상의 저류층에서는 CO₂ 주입 공저압이 제한되어 이와 같은 결과가 나타난 것으로 보인다. 최소공저압의 경우 값의 변화에 따른 잔류 및 용해 포획 용량의 민감도가 상대적으로 낮았다.

Fig. 2.

CO₂ storage capacity based on injection conditions: (a) injection rate, (b) maximum reservoir pressure, and (c) minimum bottom hole pressure (BHP).

Fig. 3과 같이 주입률이 증가할수록 STI가 감소하였으며, 총 저장 CO₂ 용량 대비 용해되는 CO₂ 보다 저류층 구조 내에 갇히는 CO₂ 비율이 증가하기 때문으로 판단된다. 그러나 초기 주입 기간 이후의 STI는 시간에 따라 증가하기에 잔류 포획에 비해 용해 포획의 장기적 저장안정성이 비교적 높을 것으로 생각된다. 최대 저류층압력의 가장 낮은 조건인 100 bar는 용해 포획의 양이 가장 적은 반면 STI는 가장 높았으며, 초기 저류층압력까지의 저장 제한 조건에 의하여 총 주입된 CO₂의 양이 적은 것으로 사료된다. 300 bar 이상의 조건과 저장용량에 차이를 보인 200 bar의 경우, 초기 주입 기간 이후 300 bar 이상의 조건과 저장효율지수가 유사하게 나타났다. 이는 시간에 따라 저류층 내 CO₂가 포화 상태에 도달하여 최대 저류층압력 조건의 영향이 감소하기 때문으로 보인다. 또한, 최소공저압에 따른 잔류 및 용해 포획 용량 변화는 비교적 적었으나, 저장 기간에 따른 STI의 변화보다 RTI의 민감도가 낮음을 확인하였다.

Fig. 3.

Storage efficiency index based on injection conditions: (a) injection rate, (b) maximum reservoir pressure, and (c) minimum BHP.

저류층 물성에 따른 CO₂ 저장용량 및 저장효율지수

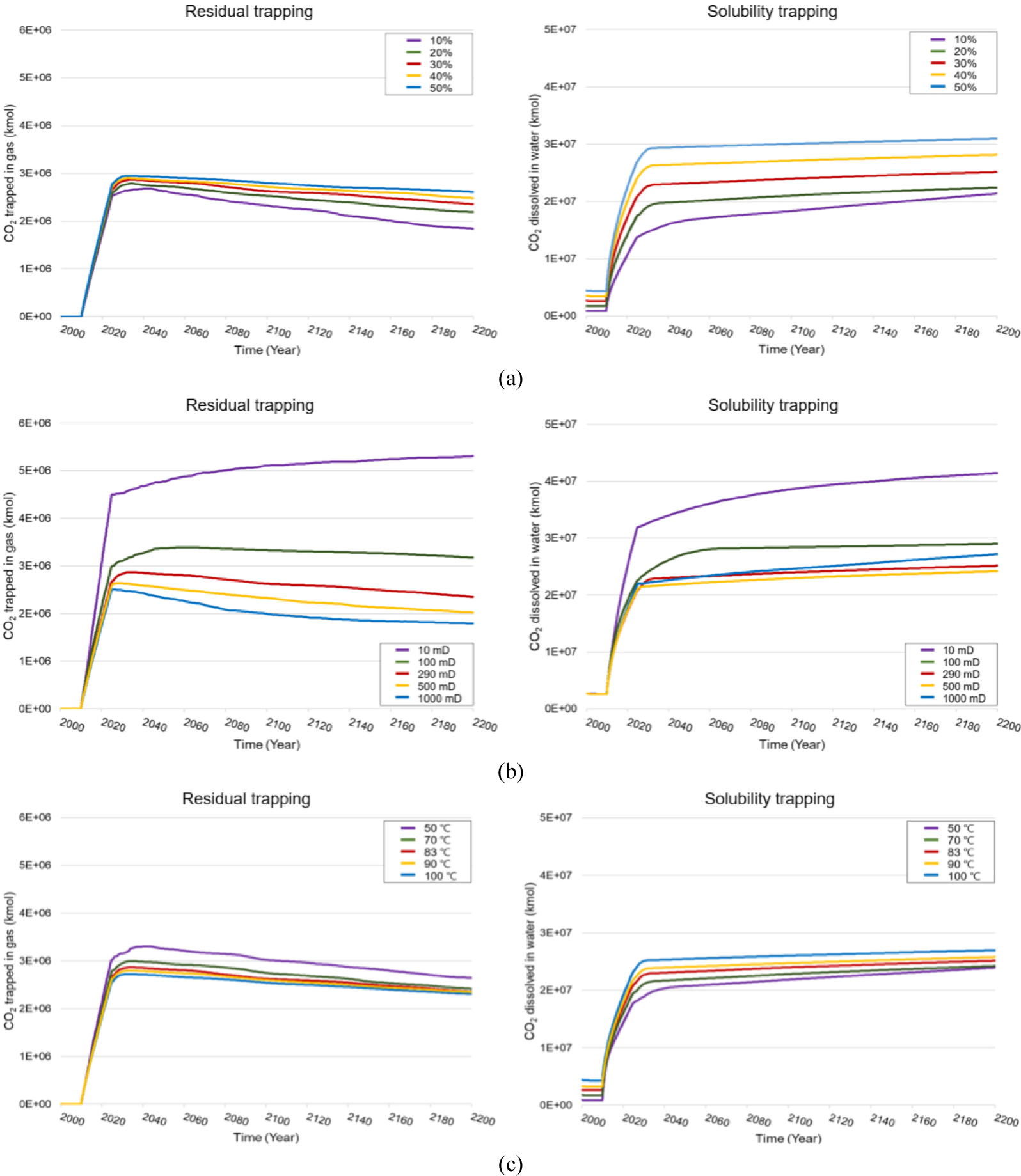
이 연구에서는 저류층 물성 인자인 공극률, 유체투과도, 온도에 대한 민감도 분석을 수행하였다(Fig. 4). 공극률이 클수록 잔류 및 용해 포획되는 CO₂ 양이 증가하였으며, 이는 CO₂가 공간에 물리적으로 존재할 수 있는 부피가 증가하기 때문이다. 반면 유체투과도의 경우 값이 작을수록 공극에서 빠져나가는 CO₂의 이동성이 저하되어 잔류 및 용해 포획의 양이 증가하였다. 또한, 온도가 낮아질수록 잔류 포획 양이 증가하고 높은 온도에서 용해 포획의 양이 증가하였다. 이는 온도 저하에 따른 CO₂ 점도 증가로 인해 이동성이 감소하고 결과적으로 공극 내 저장 가능한 CO₂의 용량 증가의 영향으로 판단된다(Iglauer, 2011). 공극률 및 온도 인자의 경우, CO₂ 주입 시 저류층 내 저장 공간 및 염수로의 용해에 대한 직접적인 영향을 미치기에 초기 주입 기간에서의 저장용량 변동성이 컸으나, 유체투과도는 CO₂의 이동성과 연관되어 장기적인 관점에서의 변화가 발생함을 확인하였다.

Fig. 4.

CO₂ storage capacity based on reservoir properties: (a) porosity, (b) permeability, and (c) temperature.

저장효율지수에 대한 민감도 분석 결과, 공극률의 증가에 따라 STI가 증가하는 경향이 나타났으며, 이는 염수와 반응하는 저류층의 표면적 증가에 의한 것으로 파악된다(Fig. 5). 유체투과도가 10 mD인 경우 시간이 지남에 따라 잔류 포획되는 CO₂의 양이 증가하며, RTI도 점진적으로 증가하는 추세를 보였다. 또한, 유체투과도가 높을수록 초기 STI가 높았으나, 장기적으로는 감소하는 경향이 나타났다. 이는 초기에는 투과성이 높은 저장소가 용해를 통한 CO₂ 저장에 유리하나 장기적으로는 투과성이 낮은 저류층이 비교적 안정적인 용해 포획 효율을 보일 수 있음을 뜻한다. 온도가 높은 경우 STI는 증가하였으며, 이는 저류층의 압력 상승과 비례하여 용해되는 CO₂ 용량 증가에 기인한 것으로 보인다. 그러나 온도에 따른 CO₂ 상변화 및 저류층 포화 조건 내 CO₂ 용해도에 대해 고려하지 않았기에 향후 관련 추가 연구가 필요할 것으로 사료된다.

Fig. 5.

Storage efficiency index based on reservoir properties: (a) porosity, (b) permeability, and (c) temperature.

기계학습 기반 CO₂ 저장효율지수 예측 및 저장관련인자 분석

저장효율지수 예측을 위한 기계학습 알고리즘

이 연구에서는 random forest(RF), support vector machine(SVM), extreme gradient boosting(XGB), convolutional neural network(CNN)를 활용하였다. RF의 개별 의사결정나무(decision tree)는 무작위로 학습되며, 생성된 많은 의사결정나무의 예측 평균으로 최종 예측 값을 도출한다(Breiman, 2001). SVM은 예측 값과 실제 값이 일정 크기 이내의 간격을 가지는 초평면(hyperplane)을 계산하며, 간격 범위 밖에 있는 오차를 최소화하는 특징이 있다(Zhang and O’Donell, 2020). Gradient boosting method의 방법론을 개선하여 빠른 학습과 높은 정확도를 제공하는 XGB는 모델의 성능을 평가하고 과적합을 방지하기 위하여 모델 내 교차검증이 내장되어 있다(Chen and Guestrin, 2016). 또한, CNN의 경우 행렬 곱셈에 의존하는 기존의 신경망과는 달리 입력자료와 필터(filter)라고 불리는 행렬을 결합하여 새로운 출력을 생성하는 수학적 연산인 convolution 기술을 사용한다(Analytics Vidhya, 2023). 이는 필터링(filtering), 다수의 convolution 층 및 pooling 층 연결을 통하여 특징을 선택하며(Moreira et al., 2021), 최종적으로 전통적인 다층 퍼셉트론과 유사한 dense 층을 통하여 출력을 생성할 수 있다.

저장효율지수 예측모델 설계

저장관련인자의 민감도 분석을 통하여 고갈 가스전의 저장효율에 영향을 미치는 주입률, 최대 저류층압력, 공극률, 온도, 유체투과도의 범위를 파악하였으며, 이를 예측모델 구축을 위한 입력자료로 설정하였다. 또한, 시간에 따른 저장효율지수의 영향을 반영하기 위하여 주입 시작일 기준 15년, 65년, 190년에 대한 값을 추가로 고려하였다. 이와 더불어 영향인자에 대한 다양한 변수 조건을 생성하기 위해 LHS(latin hypercube sampling) 기법을 활용하였으며, CO₂ 주입 시뮬레이션 결과인 RTI와 STI를 출력자료로 한 총 892개의 자료를 사용하였다(Table 4). 자료에 대한 저장효율지수의 확률분포는 Fig. 6과 같으며, 서로 다른 알고리즘을 활용하여 RTI와 STI를 각각 예측하는 모델을 구축하였다.

Fig. 6.

Relative frequency of storage efficiency index data: (a) residual trapping index (RTI) and (b) solubility trapping index (STI).

RF, XGB, SVM 기반 예측모델의 학습 및 테스트자료의 비율은 80%, 20%로 각 712개, 179개를 활용하였으며, 모델 학습 시 그리드 탐색을 통하여 하이퍼파라미터(hyperparameter)를 최적화하였다(Table 5). RF는 결정트리의 수인 number of estimators, 결정트리의 최대 깊이를 지정하는 max depth, 리프 노드가 가져야 할 최소 샘플 수인 min samples leaf, 내부 노드 분할을 위한 최소 샘플 수인 min samples split에 대한 최적화를 수행하였다. XGB의 경우 number of estimators, max depth와 더불어 학습 단계에서 모델의 가중치를 조정하는 학습률(learning rate)과 리프노드의 추가 분할 시 최소 손실 감소 값으로써 과적합을 방지하는 gamma를 고려하였다. SVM은 오류와 마진 간 균형을 제어하는 C와 커널 유형을 반영하였다.

CNN 모델의 학습 및 테스트자료는 8:2로 분할 후 학습자료에 대하여 8:2의 비율로 검증 자료를 구성하였으며, convolution, pooling, flatten, dense 층의 구조를 적용하였다. 예측을 위한 입력자료의 경우 저류층의 공극률, 유체투과도, 온도, 최대 저류층압력, 주입률, 저장 기간의 순서로 배치하였다. 예측모델이 선형 관계 이외의 입력자료를 학습할 수 있도록 활성화 함수(activation function)인 rectified linear unit을 활용하였으며, 해당 모델에서는 max pooling 기반 2×2 크기의 커널을 활용하여 출력 맵을 생성하였다. 이와 더불어 마지막 dense 층에는 회귀를 위한 단일 뉴런만 있도록 구성하였다. 그리드 탐색 기반의 하이퍼파라미터 최적화를 수행하기 위하여 convolution 층에서 활용되는 filter와 kernel size, 모델의 학습 과정에서 사용되는 batch size에 대하여 Table 4의 범위를 활용하였다. 또한, 학습 및 검증자료에 대하여 epoch에 따라 발생 가능한 평균 제곱근 오차(root mean square error, RMSE)를 표준화한 식 (3)의 NRMSE(normalized root mean square error)를 도출하여 과적합 방지를 위한 epoch의 수를 설정하였다(Fig. 7).

Fig. 7.

Normalized root mean square error (NRMSE) of the prediction model according to the epoch: (a) RTI and (b) STI.

여기서 yi는 시뮬레이션을 통해 취득한 저장효율지수, yi^는 기계학습 모델이 예측한 저장효율지수를 뜻한다.

기계학습 알고리즘 별 저장효율지수 예측결과 및 분석

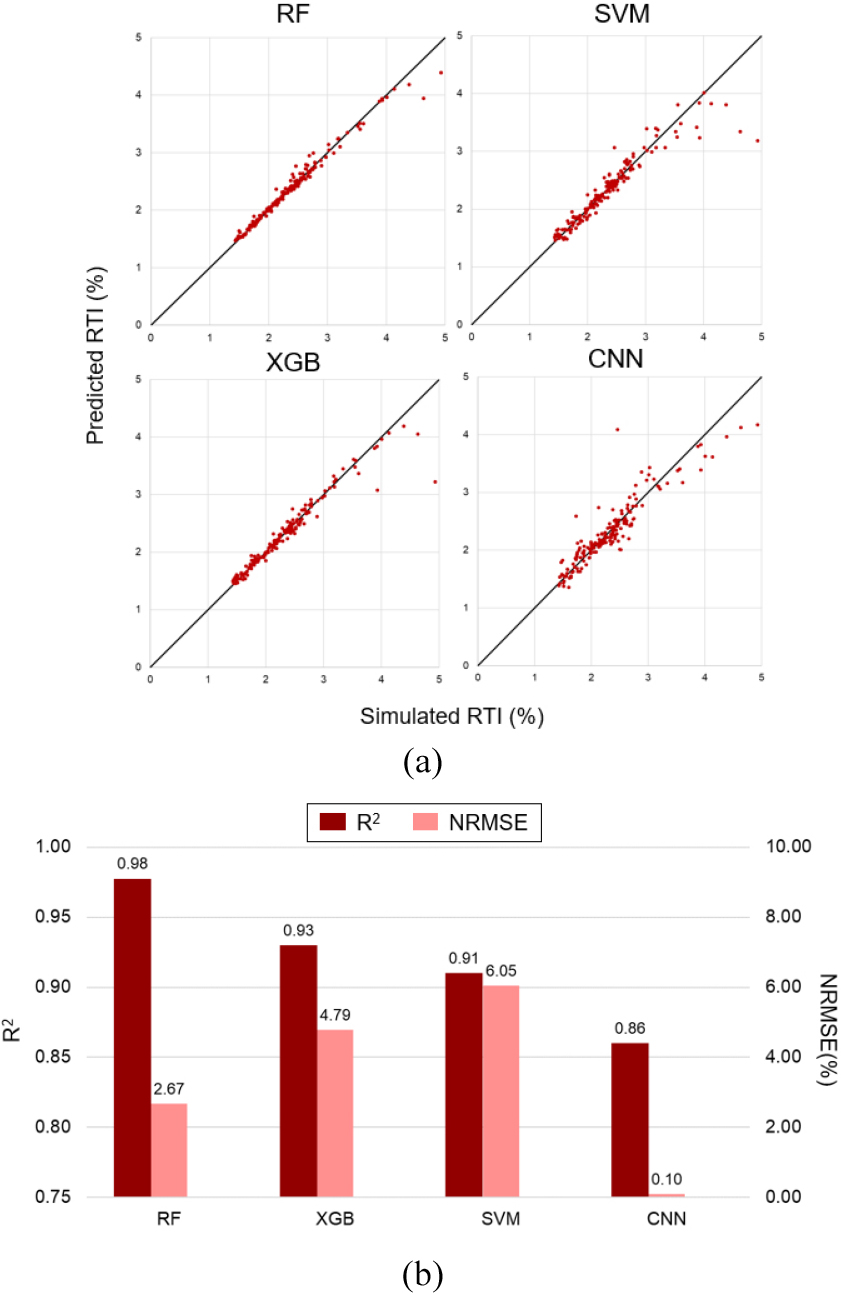
구축한 기계학습 기반 예측모델에 대한 성능 평가를 위하여 결정 계수(coefficient of determination, R²)와 NRMSE를 사용하였다. RTI 예측 시 4가지 모델의 test 결과는 약 0.8 이상의 R²을 나타냈다(Fig. 8). SVM, XGB, CNN 기반 모델의 경우, 비교적 자료의 양이 적은 3% 이상의 RTI 예측에 어려움이 있었으나 RF 예측모델은 학습자료의 개수에 대한 영향이 비교적 적음을 파악하였다. 또한, 각 모델의 성능 비교를 위하여 R²과 NRMSE를 활용한 예측 정확도를 분석하였다. RF 모델의 R²과 NRMSE는 각각 0.98 및 2.67%로, 예측모델 중 가장 우수한 성능을 확인하였다. CNN 모델의 R²은 다른 모델에 비하여 상대적으로 낮은 적합도를 보였으며, 이는 학습자료의 일부를 검증자료로 활용하였기에 CNN 모델의 학습에 어려움이 있었기 때문으로 사료된다. 반면 검증자료를 통해 모델의 과적합을 방지하고 일반화를 향상시킬 수 있어 NRMSE는 가장 낮게 나타났다. SVM과 XGB 모델은 0.9 이상의 R²을 나타내었으나, RF 모델과 비교하여 NRMSE가 상대적으로 높았다.

Fig. 8.

Results of RTI prediction model: (a) prediction results and (b) R² and NRMSE results.

기계학습 기반 STI 예측모델의 test 결과는 Fig. 9와 같으며, RF, SVM, XGB 기반 모델은 0.9 이상의 R²을 보이며 시뮬레이션 값과 유사한 예측 값을 도출하였다. CNN 모델의 경우 40% 이상의 STI를 예측하는 데 있어 비교적 어려움이 있었으며, NRMSE가 상대적으로 높았다. 또한, RF 모델의 경우 0.97의 R², 3.19%의 NRMSE를 나타내어 STI 예측에 가장 적합함을 확인하였다. 이와 더불어 학습 및 테스트 자료에 대한 모델의 성능을 파악하기 위해 예측 값과 시뮬레이션을 통한 관측 값의 차이를 상대적으로 구한 식 (4)의 상대 오차(relative error)를 활용하였다.

Fig. 9.

Results of STI prediction model: (a) prediction results and (b) R² and NRMSE results.

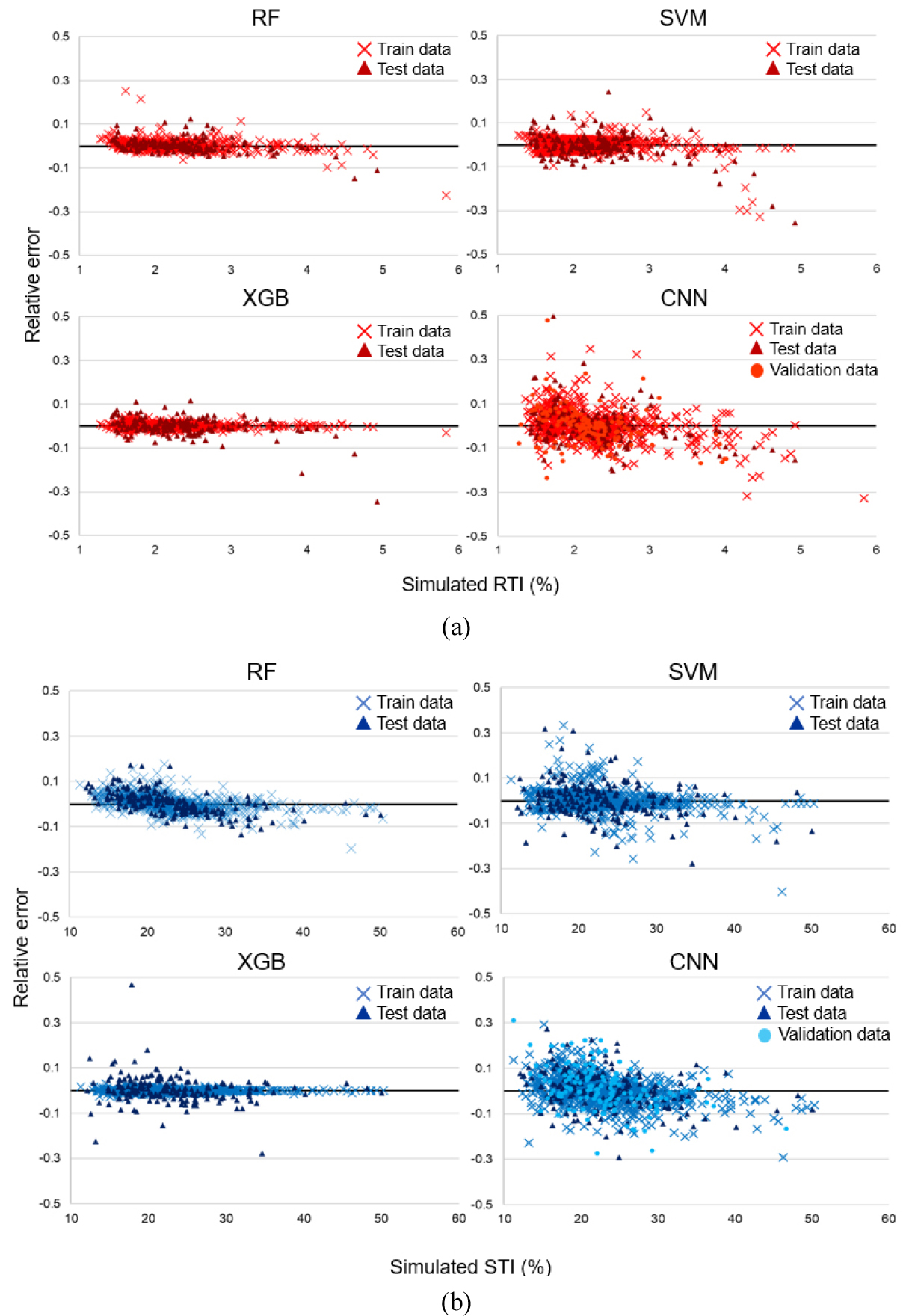
RTI 예측 시 RF 및 XGB 모델은 학습 및 테스트자료의 오차가 다른 모델에 비하여 낮았으나, XGB의 경우 학습성능에 비하여 테스트성능이 저하되는 경향을 보였다(Fig. 10). SVM은 비교적 자료의 개수가 적은 RTI에서 학습 및 테스트 오차가 매우 커지는 것을 확인하였다. 학습 및 테스트자료의 상대 오차가 가장 넓게 분포한 CNN은 해당 자료에 대하여 적합하지 않은 모델임을 파악하였으며, 이는 연구에서 활용한 학습자료가 선형적으로 종속관계 가능성이 있는 table 형태이기에 각 특성 간 상호작용이 주요한 영향을 미칠 수 있기 때문이다. CNN의 경우 이미지 형식의 자료와 같이 구조적인 패턴을 학습하도록 설계되었기에 특성 간 독립성이 강한 table 자료의 상호작용을 반영하는데 어려움이 있어 성능이 비교적 낮은 것으로 판단된다.

Fig. 10.

Relative error results of the storage efficiency index prediction model: (a) RTI and (b) STI.

또한, STI에 대한 각 모델의 상대 오차를 분석한 결과 RF는 학습 및 테스트 자료가 상대 오차 0에 밀집되어 있어 예측 시 모델에서의 과소 및 과대적합이 나타나지 않을 것으로 확인된다. XGB는 RTI와 동일하게 학습성능의 상대 오차는 가장 낮게 나타났으나 테스트자료에 대해서는 다소 성능이 감소하였으며, SVM 및 CNN 기반 STI 예측모델은 상대적으로 넓은 상대 오차 분포를 나타내었다. 이와 같이 RF 모델의 경우 학습을 위한 입력자료의 양이 비교적 적은 4% 이상의 RTI와 40% 이상의 STI에 대한 예측 시 상대 오차에 있어 성능의 저하가 발생하지 않을 뿐만 아니라 신뢰성 있는 예측이 가능한 것을 확인하였으므로 다른 기계학습 모델에 비하여 이상치에 대해 상대적으로 민감도가 낮은 것으로 사료된다.

추가적으로 시뮬레이션을 통한 관측 값과 모델에 의하여 예측된 값에 대한 차이를 뜻하는 잔차 오류(residual error)에 대하여 정규분포와 근사한 정도를 비교하였다(Fig. 11). RTI 예측을 위한 RF 모델의 잔차 오류는 평균(μ)이 0%이고, 표준편차(σ)가 0.09%로 나타났으며, 대부분의 오류가 0에 가까움을 확인하였다. SVM의 경우 넓은 오류 분포를 가졌으며, 비교적 좁은 잔차 오류 분포를 지닌 XGB는 표준편차가 상대적으로 높았다. CNN의 경우 4가지 기계학습 모델 중 가장 넓은 오류 분포를 나타내었다. STI 예측모델의 잔차 오류는 RTI 예측 오류와 유사한 경향으로 나타남을 확인하였으며, RF의 오류 분포가 상대적으로 좁고 대부분의 잔차가 0에 가까이 밀집되어 있어 안정적인 예측성능을 보였다.

Fig. 11.

Residual error results of storage efficiency index prediction model: (a) RTI and (b) STI.

이와 같이 서로 다른 알고리즘 기반의 저장효율지수 예측모델 중 RF의 잔차 오류가 가장 정규분포와 유사한 형태를 나타내었다. 해당 모델은 모든 예측 값에 대한 오류가 일정한 분산을 따르고 있기에 입력자료에 대한 과적합을 발생시키지 않은 것으로 생각된다. 또한, 값의 변동에 따른 오차의 발생이 상대적으로 적었으므로 입력자료에 대한 모델의 편향성이 낮고 일관된 예측성능을 유지할 수 있을 것으로 보인다.

저장 기간에 따른 주요 저장관련인자 분석

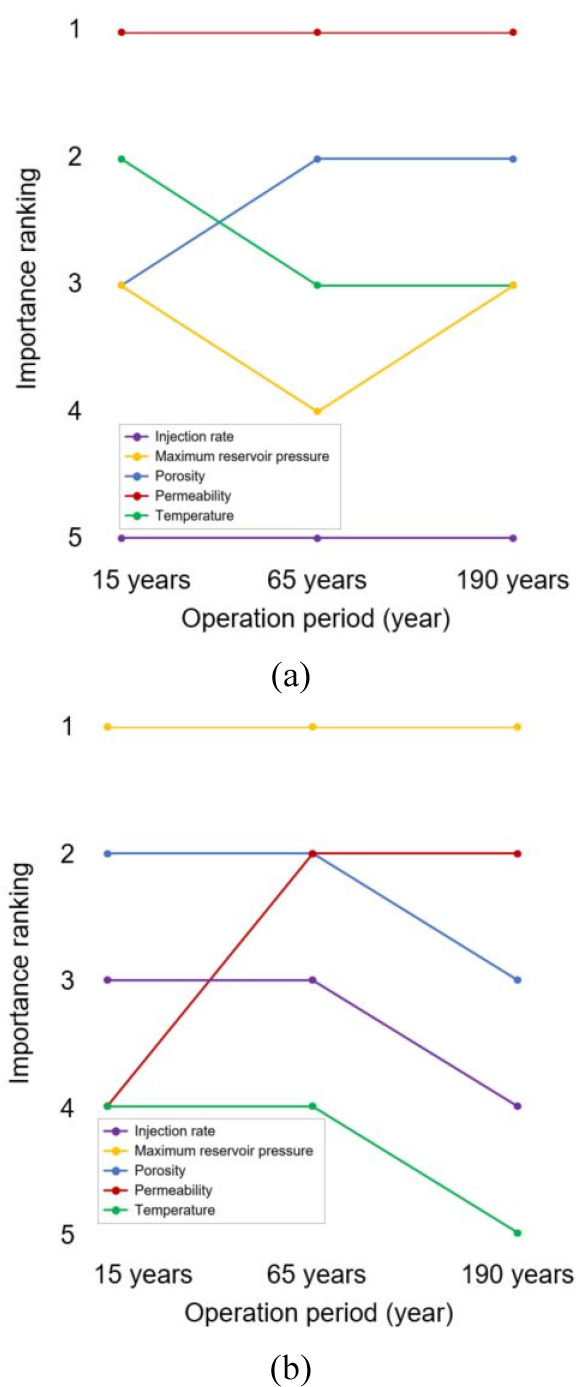
각 저장효율지수 예측모델의 테스트 결과에 대하여 저장 기간에 따른 중요도를 분석하였다(Fig. 12). 주입정 운영 기간을 기준으로 15년의 주입 완료 시점, 주입 완료 이후 50년이 지난 65년 시점, 시뮬레이션이 종료된 190년 시점에서의 RTI와 STI 값에 대하여 RF 기반의 변수 중요도 분석을 수행하였다. RTI의 경우, 주입 완료 직후 저류층 유체투과도, 온도, 공극률, 최대 저류층압력, 주입률의 순으로 중요도를 도출하였다. 주입 후 저장 기간이 지남에 따라 공극률 및 최대 저류층압력의 중요도가 상승하였으며, 저류층의 유체투과도는 기간에 관계없이 주요한 영향을 미쳤다. STI 예측 시에는 최대 저류층압력의 중요도가 상대적으로 높았으나 시뮬레이션 종료 시점에서 유체투과도의 중요도 순위가 상승함을 확인하였다. 이에 따라 잔류 포획 및 용해 포획에서 유체투과도의 중요도가 공통적으로 높음을 파악하였으며, 향후 저장효율지수 예측 시 최대 저류층압력 및 유체투과도에 대한 고려가 필요할 것으로 판단된다.

Fig. 12.

Importance analysis results for storage efficiency index prediction model: (a) RTI and (b) STI.

결 론

이 연구에서는 저류층 시뮬레이션을 활용하여 고갈 가스전에서의 CO₂ 지중저장을 위한 주입조건과 저류층 물성이 잔류 포획 및 용해 포획 용량에 미치는 영향을 분석하고, RTI 및 STI의 변화를 파악하였다. 그 결과, 낮은 주입률과 최대 저류층압력에서는 STI가 상대적으로 높게 나타났으며, 이는 높은 주입률에서 CO₂가 주로 구조적으로 포획되는 현상이 우세하고 낮은 최대 저류층압력 조건에서는 총 CO₂ 주입량이 상대적으로 적기 때문인 것으로 사료된다. 또한, 공극률의 증가는 CO₂가 공간에 물리적으로 존재할 수 있는 부피의 확대를 의미하며 이는 잔류 및 용해 포획의 양과 STI, RTI 값의 증가로 이어졌다. 한편, 유체투과도가 낮을수록 공극 내 CO₂ 이동성이 저하되어 잔류 및 용해 포획 용량이 증가하였으며 저온의 저류층에서도 이동성 저하로 잔류 포획의 용량이 증가함을 확인하였다.

이에 저장관련인자의 영향 범위에서의 시뮬레이션 값을 기계학습의 학습자료로 활용하였으며, 서로 다른 알고리즘을 기반으로 RTI, STI를 예측하였다. 본 연구에서 설정한 시스템에서는 RF 기반의 저장효율지수 예측모델이 상대적으로 더 신뢰성 있는 성능을 보였다. 또한, 저장효율지수 예측모델의 저장관련인자 민감도 분석 결과를 통해 RTI는 저류층 유체투과도, STI는 최대 저류층압력이 주요한 인자임을 확인하였다. 그러나 연구에서 활용한 저장효율지수 예측모델의 경우, 기계학습 모델의 학습자료 수집을 위한 CO₂ 주입 시뮬레이션을 필요로 하여 효율성이 저하되는 한계가 존재한다. 따라서 대량의 저류층 물성 및 주입조건에 따른 저장효율지수를 취득하여 예측모델의 적용성을 높여야 할 것이다. 향후 이 연구는 저류층 물성 및 주입조건에 대한 사전정보를 보유한 현장 고갈 가스전에서의 저장효율지수 예측을 통하여 사업 초기 단계에서의 저장안정성을 파악하기 위한 효율적인 방법으로 활용할 수 있을 것이다.