서 론
갱도의 안정성 평가 방법
안정도해법
한계곡선법
Q 시스템 활용
광주의 안정성 평가 방법
선행연구 검토
시험광산의 안정성 평가
경험적 방법에 의한 갱도 안정성 평가 결과
경험적 방법에 의한 광주의 안정성 평가 결과
전산해석에 의한 갱도 및 광주의 안정성 평가 결과
갱도 및 광주의 규격 수정 제안
채굴작업장의 안전관리 및 관리기법
최대 수평응력의 영향
미소진동 기술
갱내 LiDAR 측량
현안 및 향후 과제
채수율에 대한 고찰
채광 완료 후의 갱도 안정성 문제
결 론
서 론
1992년 국내 갱내 채굴광산의 수는 19개였으나 2017년 87개로 증가하였는데, 구체적인 전환 사유로는 환경문제와 민원이 가장 큰 요인이었고 그 외 노천채굴 대상 자원의 소진과 양질의 석회석 자원 잔존 매장량의 감소에 기인한 것으로서 광산개발은 개발환경의 다변화와 사회/환경의 규제 강화 등에 많은 영향을 받는 것으로 볼 수 있다.
2015년부터 2017년까지 매년 갱내 채굴광산 지역에 지반 함몰이 발생하였으며 지진규모로는 최대 3.5를 기록하였다. 그 후 2017년 1월에는 광산안전법이 개정 및 시행되었고 이에 따른 하위 법령도 제정되었다. 현 광산안전법의 시행으로 민간 전문가를 중심으로 한 광산안전위원회의 설치(광산안전법 제22조 2 및 시행령 제18조)와 광산안전기술과 관련된 조항들이 새로운 광산안전기술기준에 수록됨으로써 개별광산의 광산안전규정을 탄력적으로 개정할 수 있게 되었다.
세월호 사고 이후 발생된 광산지역 지반 함몰 우려에 대처하기 위해 광산별로 실시된 안전진단 결과를 분석해 보면 첫째 편과 편 사이의 수평광주와 수직광주에 대한 안정성 검토가 필요한 것으로 나타났으며, 둘째 갱도와 채굴작업장 및 광주의 안정성을 평가하기 위해서는 LiDAR 등을 이용한 갱내 3차원 측량(3D Scanning)과 3차원 도면의 작성이 요구되고 있다. 셋째 채굴 전, 채굴작업 중 및 채굴 종료 후의 채광장 및 갱도의 안전관리뿐만 아니라 설정된 채굴공동과 광주의 안정성 검증을 위하여 미소진동(AE/MS) 측정과 같은 암반거동 모니터링의 필요성을 강조하고 있다. 또한 대부분의 갱내 채굴광산에서는 계획채광의 이행이 시급한 것으로 나타났다.
국내 광산의 갱내 채굴 방식은 광체의 부존 여건에 따라 다양한데 채굴 대상 광체의 수평방향 폭이 수십 미터 이상되는 경우에는 일반적으로 주방식채광법(Room and Pillar Mining Method)을 적용하며 연직방향의 두께를 고려하여 여러 개의 편별로 동일한 채광법을 적용한다. 이때 편간 수직고의 크기에 따라 먼저 형성된 바닥 또는 천반을 대상으로 추가로 채굴하는 방식을 적용하기도 한다. 이와 같은 방식은 국내뿐만 아니라 미국의 동부 광산들에서도 적용되고 있으며 채굴 완료 후의 채굴적(갱도)의 높이는 20미터 이상에 달하기도 하는데 이 방식을 특별히 광주식채광법(Stope and Pillar Mining Method)이라 칭하며(Chung et al., 2010), 일반적으로 Fig. 1과 같은 방식으로 채광을 진행한다. 광주식채광법은 주방식채광법과 유사하며 주로 경암 광체에 적용되며 갱도는 규칙적 또는 임의의 형태로 수평방향으로 굴진되는데 미국의 경우 비석탄광의 전체 채광량의 50%를 차지하고 있다. 한편 광체의 폭이 작아서 하나의 편에서 두 개의 수평갱도를 개설하기 어려운 경우에는 굴진채광 방식을 적용하고 있다.
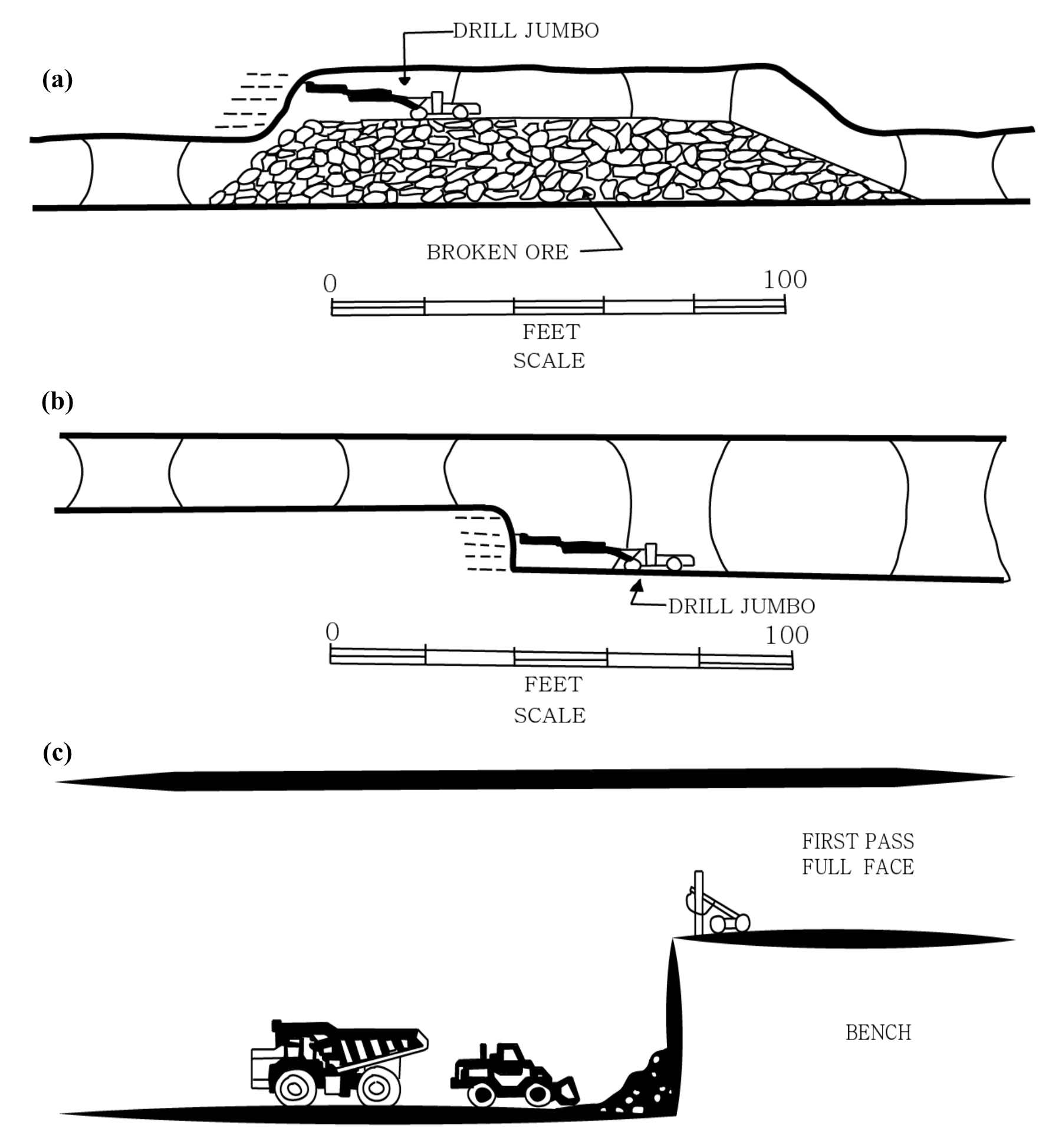
Fig. 1.
Stope- and pillar-mining method. (a) Breast stoping followed by overhand slabbing. (b) Breast stoping followed by benching (horizontal drilling). (c) Breast stoping followed by benching (vertical drilling) (based on Chung et al., 2010).
본 기고문에서는 최근 10여 년간 국내 갱내 채굴광산의 안전관리를 위해 수행된 대표적인 광산에 대한 채굴작업장, 갱도 및 광주 등의 안정성 평가 결과를 소개하고자 한다.
갱도의 안정성 평가 방법
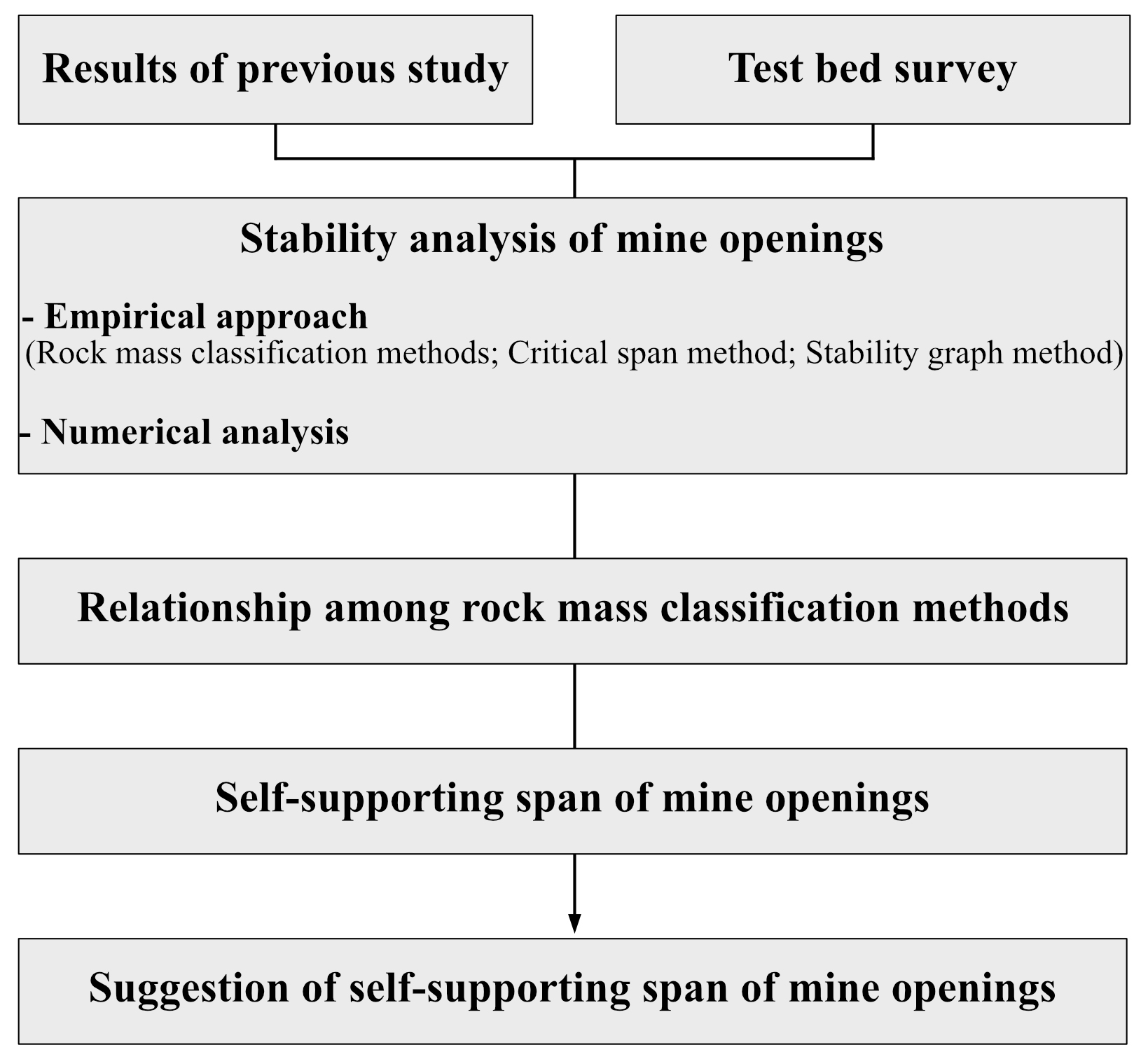
갱도 및 광주의 안정성을 평가하는 방법으로는 주로 경험적 방법에 의한 안정성 평가방법과 전산해석에 의한 방법을 사용할 수 있으며 이중 갱도 또는 채굴 공동의 안정성을 평가하는 흐름도는 Fig. 2와 같다.
안정성 평가 시 우선적으로 암반분류법을 통해 노출된 현장 암반을 평가해야 하며, 국내에서 널리 사용되는 암반분류법은 Bieniawski(1989)가 제안한 Rock Mass Rating (RMR), Barton et al.(1974)이 제안한 Q-system, Hoek (1994)이 제안한 Geological Strength Index(GSI)가 있다.
RMR 분류법과 차트에 의해 측정하는 GSI는 기본적으로 다음과 같은 공통 인자를 포함하고 있다. 즉 RMR 평가에 활용되는 인자 중 암석 코어의 암질지수인 RQD, 평균 절리 간격, 절리 상태 등 3개의 인자는 GSI 평가 지표에 제시되어 있는 불연속면의 표면상태(가로축)와 불연속면의 분포특성(세로축) 등 2개의 요소로 함축되어 평가되고 있다. 그리고 Q 시스템에서 역시 RQD, 절리군 수(Jn) 및 절리면의 충전물 또는 변질정도(Ja) 등 3개 요소가 RMR 3개 인자 및 GSI 2개 인자들과 대비되는 것으로 볼 수 있다. 경우에 따라서 현장에서 GSI 기법으로 간편하게 암반 평가를 수행할 수 있으며 그 결과를 보완하기 위해서는 지하수 상태와 암석의 강도 조건을 추가할 수 있다.
안정도해법
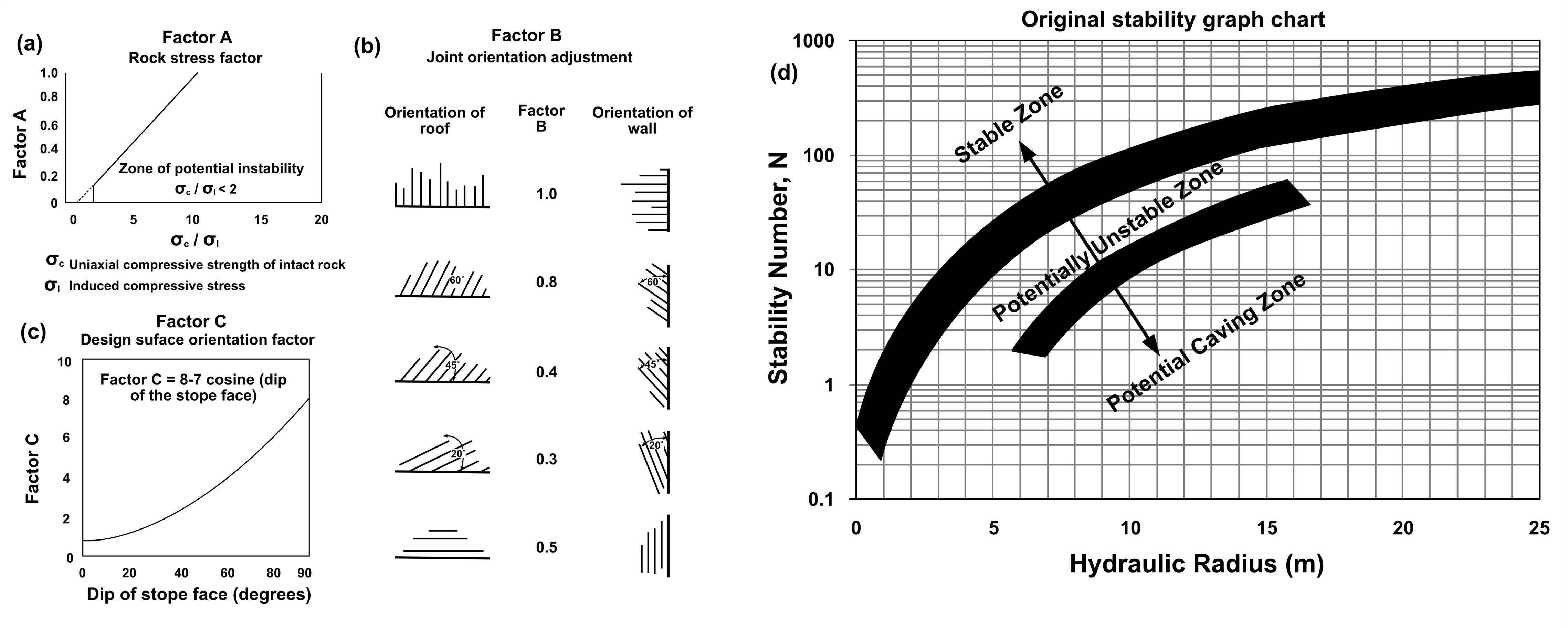
Mathews et al.(1981)이 제안한 안정도해법(Stability Graph Method)은 안정성 계수 과 채굴공동의 특정면(천반 또는 측벽)의 형상계수(HR)를 이용하여 채굴 공동의 안정성을 평가하는 방법이다. 200여 건 이상의 채굴공동(Open stope mining) 사례를 기반으로 개발된 안정도해법은 현재에도 북미 등에서 널리 사용되고 있다. Fig. 3은 안정성 계수 산정에 필요한 보정계수와 안정도해이다.
여기서, = Q 값 중 와 SRF를 1로 가정하여 계산된 값
A = 암반 응력 보정계수
B = 불연속면 위치 보정계수
C = 중력 보정계수
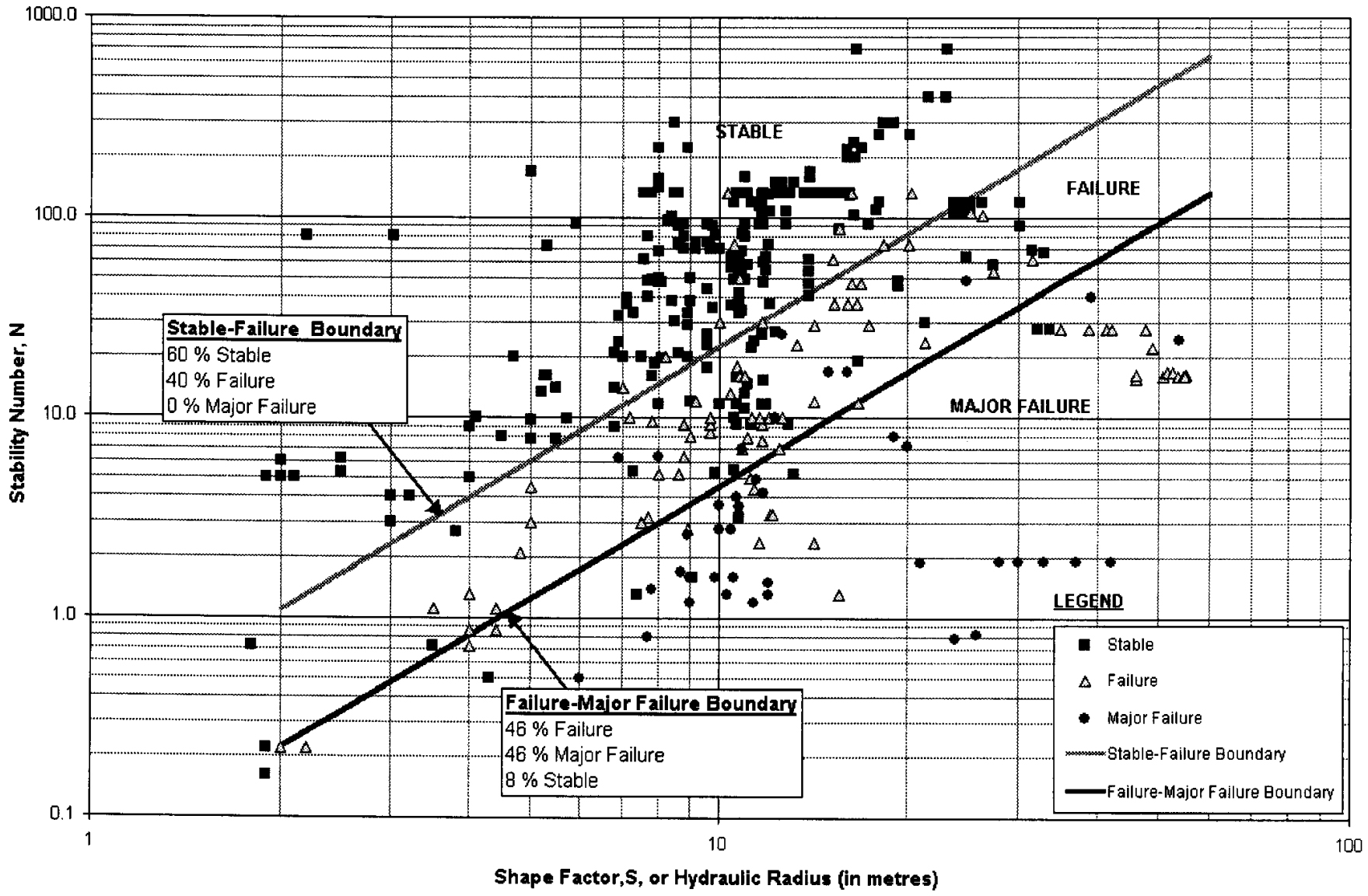
Mawdesley et al.(2001)은 로지스틱 회귀 분석을 통해 안정도해법의 구역 경계를 최적화하여 Fig. 4와 같은 형태를 제안하기도 하였다. Putra et al.(2024)는 광산 초기 설계에서 채굴공동의 최적화 알고리즘 개발을 위해 안정도해법을 적절히 활용한 바 있다.
한계곡선법
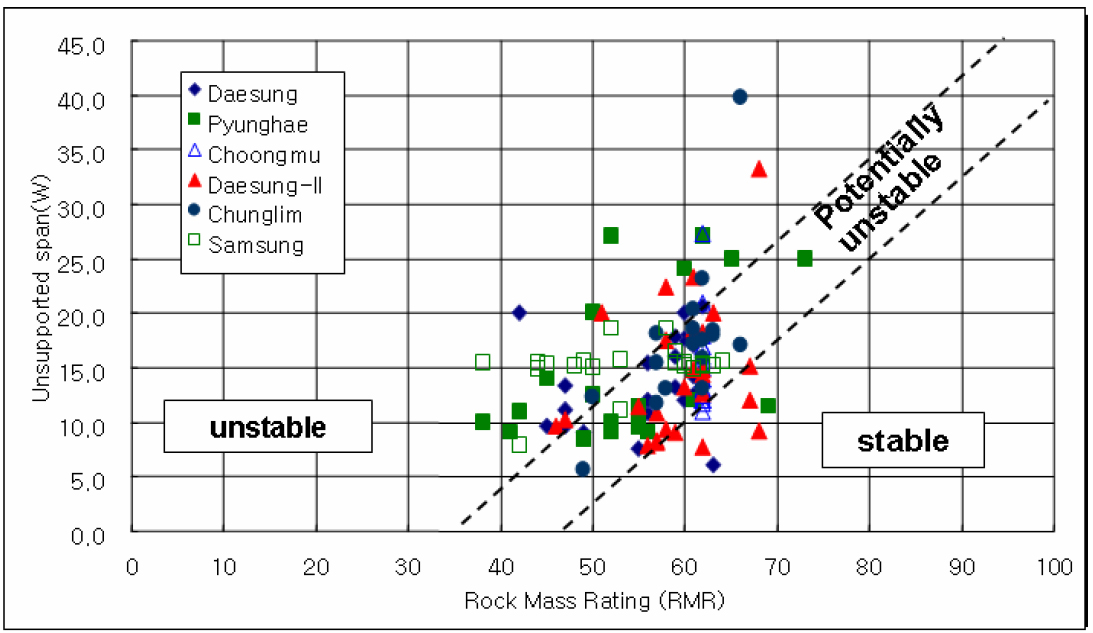
한계곡선법(Critical Span Method)은 RMR 값을 이용하여 채굴 공동(갱도)의 상태를 평가하는 방법으로서 한국지질자원연구원에서 개발한 기법이다(KIGAM, 2005). 한국지질자원연구원은 6개의 석회석 광산을 대상으로 수행된 현장조사 결과를 바탕으로 Lang et al.(1991)이 제안한 한계공동 폭 설계방법(Critical Span Design Method)을 수정하여 Fig. 5와 같이 국내 갱내 채굴광산에 적용 가능한 한계곡선을 제안하였다. 이 방법을 이용하면 RMR 값과 무지보 갱도 폭을 토대로 갱도의 상태를 불안정(Unstable), 잠재적 불안정(Potentially Unstable) 및 안정(Stable)으로 쉽게 평가할 수 있다.
Koo et al.(2008)은 국내 석회석 광산의 무지보 갱도 폭을 결정하기 위해 한계곡선법을 적용하였으며, 그 적절성을 확인한 바 있다.
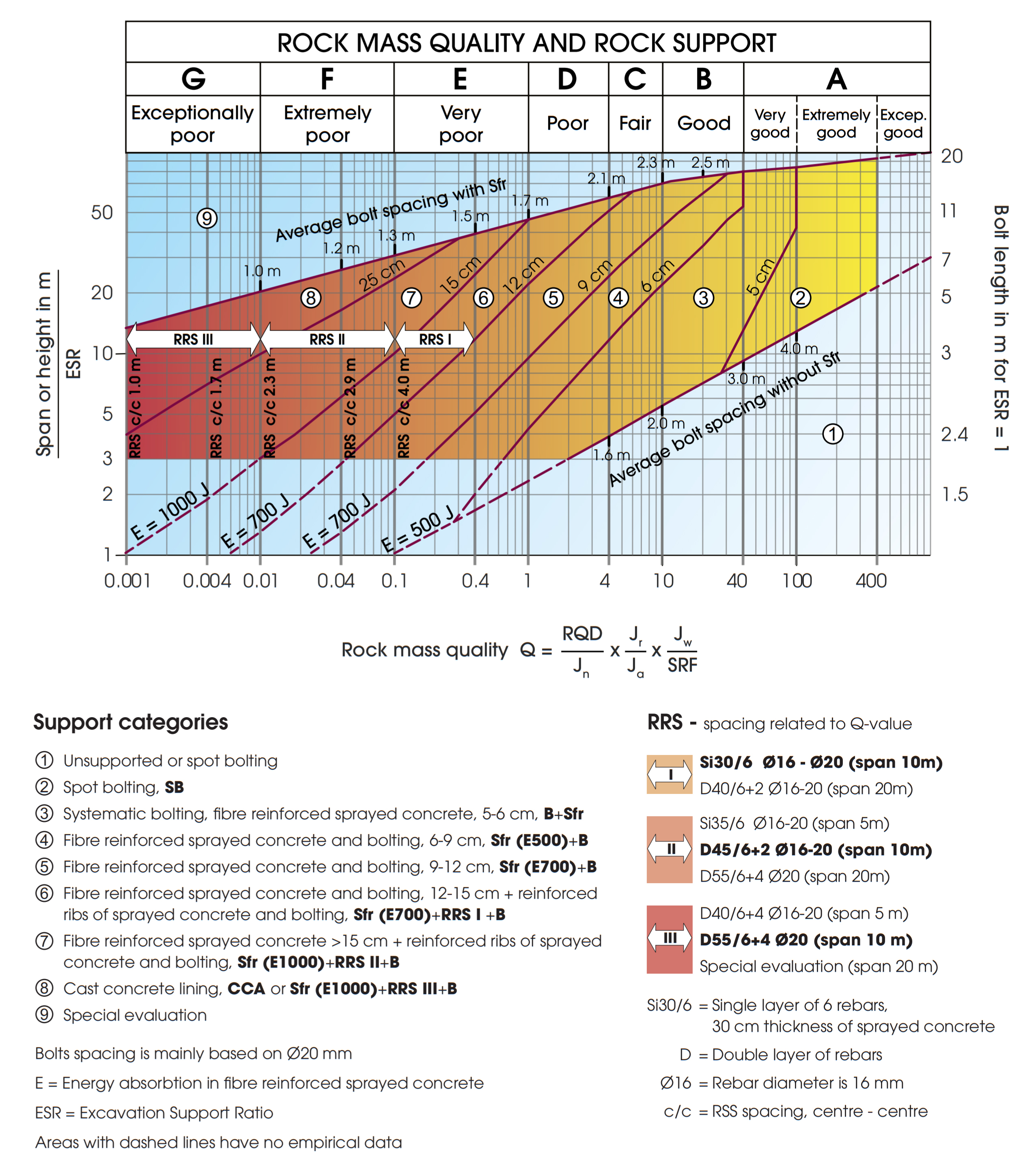
Q 시스템 활용
Q 시스템은 암반의 Q 값(최소, 평균 및 최댓값)에 대응하는 등가굴착지수()를 도표에 도시하는 방법으로 Fig. 6과 같이 9개의 지보 범주를 제시하고 있다.
광주의 안정성 평가 방법
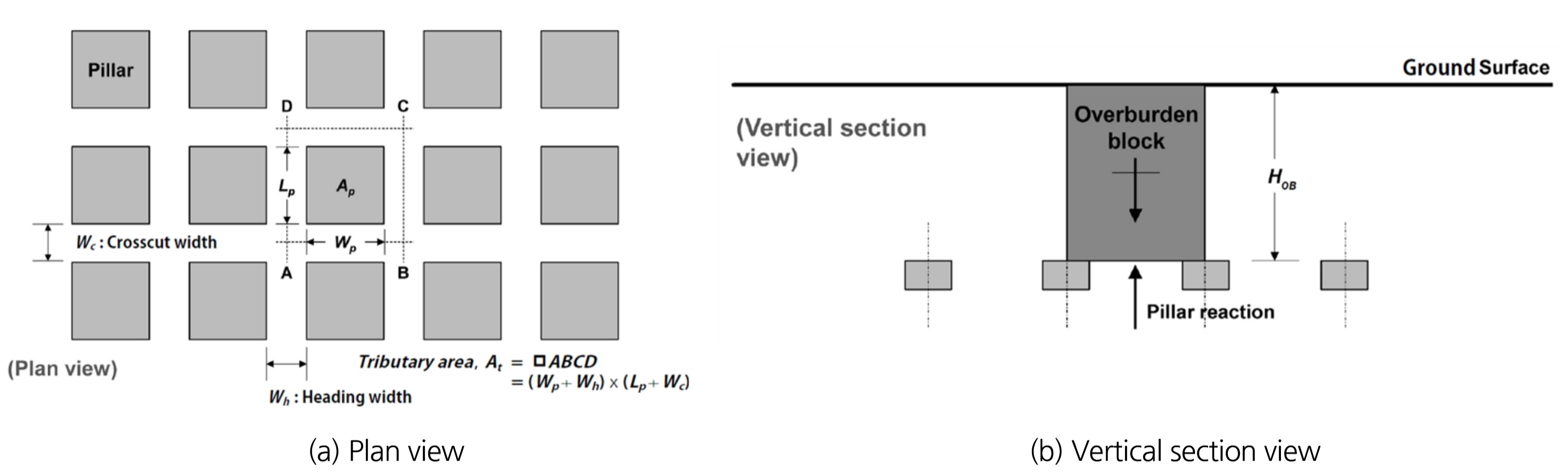
안전율(FOS; Factor Of Safety=광주의 강도/광주 내에 작용하는 평균 응력)을 계산하여 광주의 안정성을 판단하는 기법은 NIOSH(2011)에 의해 제안된 바 있다. 이 기법에서 광주에 작용하는 평균 응력은 지류론(Tributary area theory)에 근거하고 있다. 지류론은 광주에 작용하는 연직응력을 추정하기 위해 일반적으로 사용하는 간단한 방법으로 광주의 안정성 평가, 설계 등에 폭넓게 사용되고 있다(Jang, 2018; Yoon and Song, 2020; Monsalve et al., 2022). 지류론은 광주의 상부하중을 모든 광주가 동일하게 지지한다는 것을 전제로 하며, Fig. 7은 광주가 부담하는 상부하중 작용 면적(Tributary area, )과 광주와의 관계를 보여준다.
지류론에 의해 광주에 작용하는 연직응력 는 다음과 같이 계산될 수 있다.
여기서 는 상부하중 작용 면적(m2), 는 광주 면적(m2), 𝛾는 암반의 단위중량(kN/m3), 는 상부하중 작용 심도(m)이다.
광주의 역학적 특성은 복잡하기 때문에 경험적으로 광주의 강도를 계산하는 식이 사용되는데, 광주의 강도 계산식은 아래와 같다(NIOSH, 2011). 이 경우에 광주의 길이나 대규모 불연속면은 고려하지 않는다.
여기서 는 암석의 일축압축강도(MPa), 는 지표로부터의 심도(m), 는 광주의 폭(m)이다.
그런데 광주의 길이가 길어지면 광주의 강도가 더 커지는 점을 고려하여 다음과 같이 개선된 식이 도출되었다.
여기서 는 등가 폭(m), 는 광주의 폭(m), 는 광주의 단면적(m2), 는 광주의 둘레(m), (Length Benefit Ratio)은 길이 효과 보정계수이다.
Table 1은 광주 종횡비에 따른 LBR 값이다.
Table 1.
Values of the length benefit ratio (LBR) for rectangular pillars with various width-to-height ratios (NIOSH, 2011)
| Width-to-height ratio | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 |
| LBR | 0.00 | 0.06 | 0.22 | 0.20 | 0.76 | 0.89 | 0.96 | 0.98 | 0.99 | 1.00 |
따라서 광주의 강도는 다음과 같은 식으로 다시 표현될 수 있다.
불연속면이 광주 전체를 지나가는 경우(관통절리) 광주의 안정성에 큰 영향을 줄 수 있으므로 광주의 강도 계산 시에 이를 다음과 같이 고려하여야 한다.
여기서 (Large Discontinuity Factor)는 불연속면 보정계수, (Discontinuity Dip Factor)는 불연속면 계수, (Frequency Factor)는 불연속면이 광주와 교차하는 빈도수의 계수이다.
위 식은 다음과 같이 표현된다.
Table 2는 광주 종횡비와 불연속면 경사에 따른 DDF 값이며, Table 3은 불연속면이 광주와 교차하는 빈도수에 따른 FF 값이다.
Table 2.
Discontinuity dip factor (DDF) representing the strength reduction caused by a single discontinuity (NIOSH, 2011)
Table 3.
Frequency factor (FF) used to account for large discontinuities (NIOSH, 2011)
| Average frequency of large discontinuities per pillar | 0.0 | 0.1 | 0.2 | 0.3 | 0.5 | 1.0 | 2.0 | 3.0 | >3.0 |
| Fraquency factor (FF) | 0 | 0.1 | 0.18 | 0.26 | 0.39 | 0.63 | 0.86 | 0.95 | 1.0 |
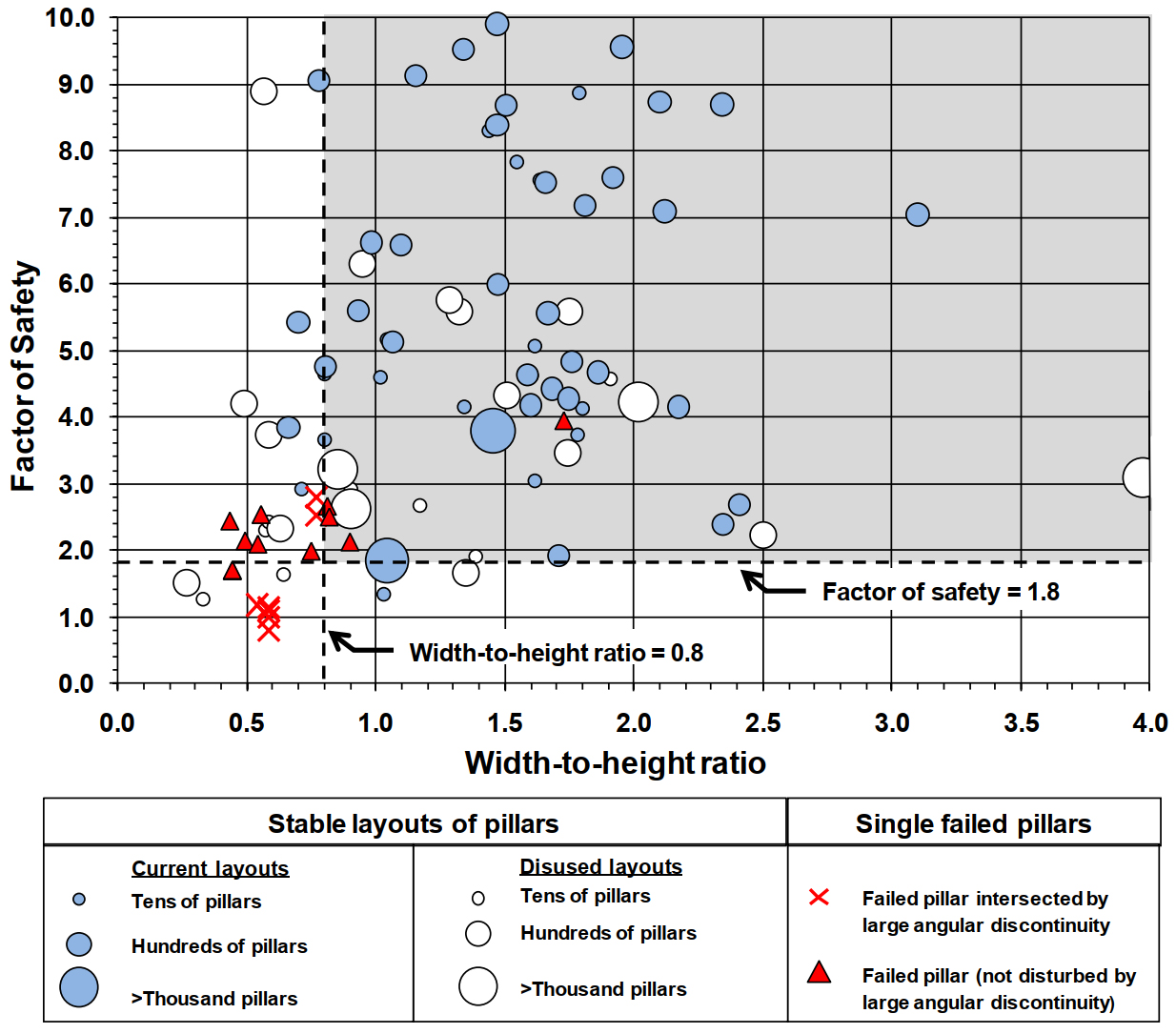
NIOSH(2011)는 미국 동부의 34개 석회석 광산의 광주를 조사한 결과를 이용하여 Fig. 8과 같은 광주 설계 차트를 제안하였다. 도표에서 보는 바와 같이 광주의 안정성이 확보되는 구간은 점선으로 구분된 1사분면 내에 속해야 하며 이때의 안전율은 최소 1.8이 되어야 하고 폭과 높이의 비 즉 종횡비는 0.8 이상이 되도록 한다. 이와 같이 안전율을 1보다 크게 설정하는 이유는 불확실성을 고려하였기 때문이다.
지류론에 의해 광주에 작용하는 응력을 구하는 방법은 간단하긴 하지만, 계산된 응력 수준이 과대 평가될 수 있고(Yoon and Song, 2020; Monsalve et al., 2022; Vlachogiannis and Benardos, 2024), 이로 인해 광주의 안전율이 과소 평가될 수 있다. Fig. 9는 주방식채광법을 적용한 갱내 채굴광산의 광주에 작용하는 응력을 지류론과 전산해석을 이용하여 계산한 결과를 비교한 것이다. 측압에 따라 응력 수준이 변하긴 하지만, 지류론을 이용하여 계산된 응력의 수준이 가장 높다는 것을 알 수 있다.
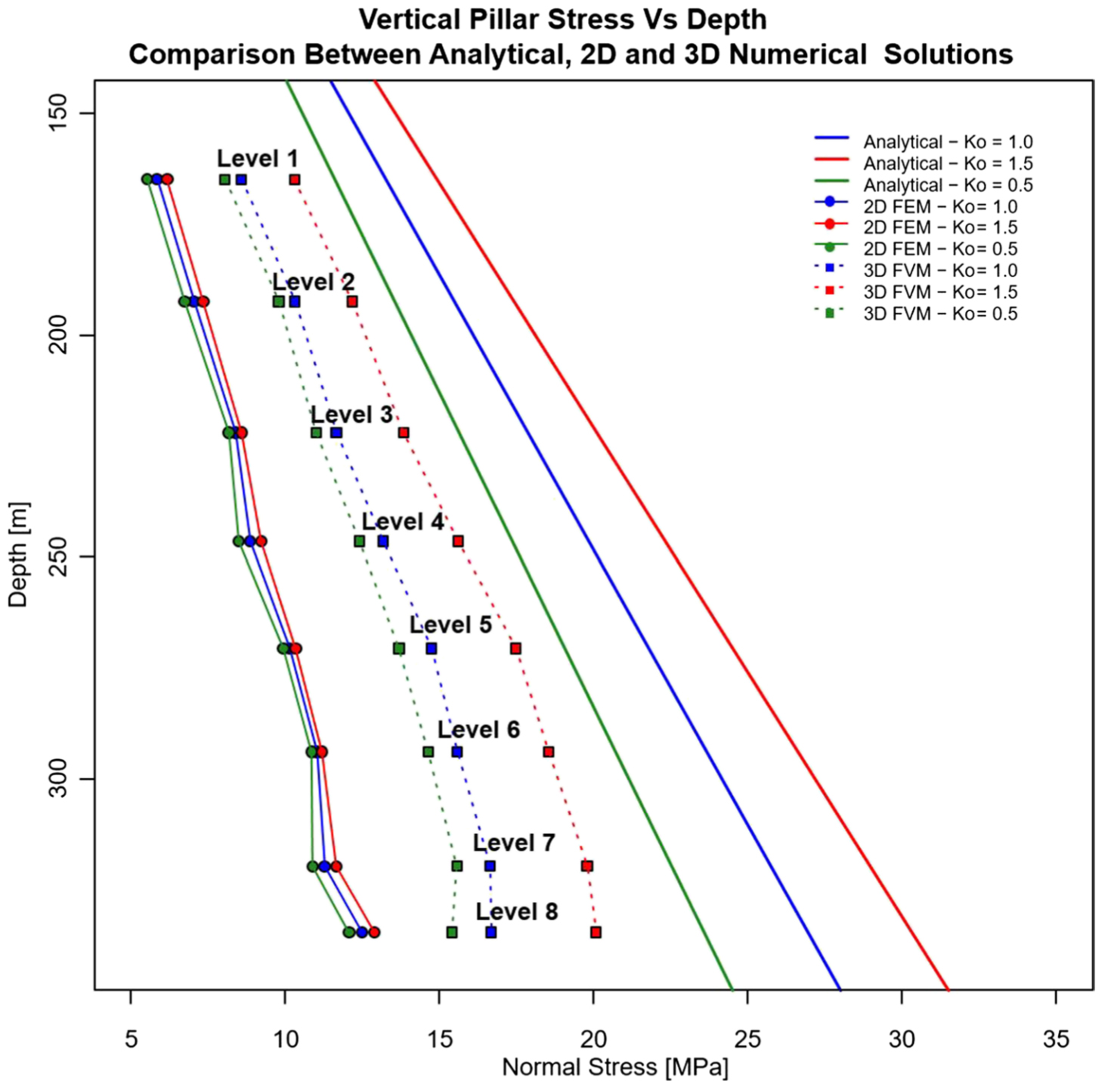
Fig. 9.
Analytical vs. 2D and 3D numerical normal stress estimation on the case study mine pillars (Monsalve et al., 2022).
선행연구 검토
지금까지 갱도 및 광주의 안정성 평가를 목적으로 4개 기관에서 연구가 수행되었으며 결과를 기관별로 요약하면 다음과 같다.
KIGAM(2021)은 심부화되고 있는 갱내 채굴광산의 안전을 제고하기 위하여 갱도의 안전설계 표준 가이드라인을 제시하였다. 해당 연구에서는 NIOSH(2011)가 제안한 갱도 설계지침을 기초로 하되 보다 정밀한 광주의 안정성을 평가하기 위하여 절리 정량화 기법을 개발하였다. 또한 지류론에 의한 연직응력 추정의 오차를 고려하여 갱내 채굴 광산에서 보편적으로 사용할 수 있는 광주 및 갱도 설계 가이드라인을 도출하였다. 이 가이드라인은 신선암의 일축압축강도 값이 45 MPa 이상, RMR 값이 60을 초과하고 연약대와 연화대 등을 포함하지 않는 양호한 등급 이상의 비금속광 암반 내에 갱도 설계 시 적용 가능한 지침으로 초기 설계, 설계 변경, 주의 사항, 부록 등의 항목으로 구성되어 있다. 갱도 및 광주의 설계지침에서는 첫째 초기 설계 시 안정성을 고려하여 갱도 천반의 폭을 최대 12 m 이내로 설계할 것을 권장하며, 둘째 비금속 광산에서 사용되는 대형 채광장비의 규격 및 채광 작업의 효율을 고려할 경우 채광장의 규격은 13.5 m의 폭과 7.5 m의 높이를 유지할 수 있을 것으로 보았다. 또한 광주 설계 시 광주에 작용하는 연직응력 평균 값을 일축압축강도 값의 25% 미만으로 설계하고 안전율 1.8 이상, 종횡비(광주의 폭/높이) 최소 0.8 이상을 유지할 것을 제안하였다.
KIGAM(2005)에서는 자체 개발한 한계곡선법에 의해 무지보 갱도의 규격을 제시하였으며, 비교적 불량한 암반조건(GSI 30)을 대상으로 단일편 갱도 및 복수편 갱도에서의 갱도 폭 변화에 따른 갱도 및 광주의 안정성 해석을 수행하였다. 연구 결과를 살펴보면 갱도 높이 8 m인 일반적인 갱내 채굴 석회석 광산의 복수편 갱도를 굴착할 경우 갱도의 폭이 16 m를 초과하지 않아야 하며 수평광주의 두께를 갱도의 높이보다 크게 유지할 것을 제안하고 있다.
IMER(2020)은 갱내 채굴광산의 낙반붕락재해 예방을 목적으로 갱도 및 광주의 안전규격 제시를 위한 연구를 전국 가행 광산 중 수평 및 수직광주를 유지하고 있는 25개 광산을 대상으로 실시하였으며, 해당 연구에서는 경험적인 방법과 수치해석적 접근을 통하여 갱도 및 광주의 안전규격을 산출하였다. 이들 25개 광산의 상부편 바닥 하부 수평광주(Sill pillar)와 하부편의 천반 수평광주(Crown pillar)가 동일한 구역이 연구대상으로 선정되었다. 경험적 방법을 이용한 결과 평균적인 암반(RMR 64, UCS 100 MPa) 및 갱도의 폭 12 m인 경우 안정성이 충분히 확보되는 것으로 나타났으며 NIOSH(2011)가 제안한 안정성 평가방법을 이용하여 심도별(100 m로부터 250 m까지)로 폭과 높이가 각각 12 m 및 7 m인 갱도와 광주의 안정성을 평가한 결과 심도가 250 m 미만에서는 권고 안전율인 1.8을 확보하는 것으로 분석되었다. 또한 심도별(100 m로부터 250 m까지)로 갱도규격 13 m × 8 m, 폭 11 m의 수직광주로 채굴작업장을 구성할 때 수평광주 두께의 변화에 따른 암반거동 해석을 하였는데 이때 한계변형률법(Critical strain)을 이용하여 안정성을 분석한 결과 수평광주 두께 13 m 이상의 조건에서는 안정성이 확보되는 것으로 나타났다.
KORES(2019)는 갱내 채굴광산의 갱도 및 광주의 안전규격을 제시하기 위하여 광산 현장에서 측정한 암석물성 또는 기본 제공 물성을 활용하고 이를 인공신경망 기법(Neural Network)의 연약암반 조건에 조합시킴으로써 무지보 갱도의 폭과 높이 선정이 가능한 설계용 도표를 제안하였다. 도출된 결과물로는 Q값을 기초로 무지보 갱도의 폭, 안정도해법(Stability Graph Method)을 이용한 무지보 갱도의 높이 그리고 지류론과 경험적 방법(NIOSH, 2011)을 바탕으로 한 기둥형 광주 및 수평광주 안정성 평가 등이 있다. 또한 석회석 부존 층별 물리역학적 특성 및 암반분류값에 대한 통계처리 후 제시된 대푯값을 이용하여 설계 절차를 검증하였다. 지류론 및 강도 경험식을 적용하여 수직광주(기둥형)와 수평광주의 안정성을 평가하였고 NIOSH(2011)가 제안한 광주 종횡비 0.8 이상, 기준안전율 1.8 이상을 준용하였다. 암석의 일축압축강도 값 60 MPa 및 80 MPa인 암반 내, 지표로부터 심도 100 m 지점의 채굴 공동(폭 12 m, 높이 8 m) 개설 시 수직광주 및 수평광주의 안정성 평가 차트에서는 일축압축강도 값이 클 경우 수직 및 수평광주의 두께를 작게 설치하여도 안정성의 확보가 가능한 것으로 나타났다.
시험광산의 안정성 평가
IMER(2021)은 이상의 4개 기관 선행 연구결과를 바탕으로 하여 국내 석회석 광산에서의 갱도와 광주의 규격 설정에 대한 적합성을 검증하였다. 해당 연구에서는 국내 석회석 광산을 풍촌층, 갑산층 및 옥천층군 등 층군별로 구분하여 5개 시험광산을 선정하고 이들 가행 중인 광산의 현재 채광작업장 인근 갱도 및 광주 25개를 대상으로 안정성 평가를 수행하였다.
현장 실측결과 이들 광산의 갱도 폭은 최소 10 m 이상 최대 18 m까지로 측정되었으며 갱도와 광주의 높이는 최소 6.5 m로부터 최대 7.5 m까지로 나타났다. 갱도와 광주의 측벽을 이루는 암반에 대한 평가 결과 RMR 값은 최소 66.2로부터 최대 77.6으로 산출되었으며 GSI 값은 최소 50으로부터 최대 75까지로 나타났다. Q 값은 최소 8.2로부터 최대 21.8까지로 측정되었다.
경험적 방법에 의한 갱도 안정성 평가 결과
IMER(2021)에서 5개 시험광산을 대상으로 경험적 방법에 의한 갱도 안정성 평가 결과를 요약하면 다음과 같다.
한계곡선법의 적용:
각 광산 측정 자료의 평균값(RMR 및 갱도폭)을 한계곡선상에 도시한 결과 5개 시험광산의 조사 갱도 및 광주는 안정한 상태로 평가되었는데 이는 지보 없이 갱도가 안정한 상태로 유지됨을 의미한다. 무지보 갱도 폭을 산정한 결과 최대 27 m까지로 분석되었다. 6개 석회석 광산을 대상으로 적용된 한계곡선법(KIGAM, 2005)은 확장안정도해법(Mawdesley et al., 2001)과 한계공동폭(Lang et al., 1991)을 이용하여 개발된 갱도 안정성 평가방법으로서 국내 광산 조사자료를 기반으로 구축되었다는 점에서 그 활용도가 높은 것으로 평가된다.
안정도해법의 적용:
5개 시험광산의 현장 조사자료를 바탕으로 (안정성계수)와 HR(수리반경 또는 형상계수)를 산정하고 응력보정계수(A), 불연속면의 위치 보정계수(B) 및 중력보정계수(C)를 각각 1, 0.2 및 1로 적용하였으며 갱도의 높이에 비해 갱도의 폭이 큰 국내 광산을 기준으로 하여 천반의 상태를 분석한 결과 조사한 모든 갱도와 광주는 안정한 영역(Stable zone)에 속하는 것으로 나타났다. 현장조사 결과 국내 광산의 갱도 높이는 6.5 m로부터 7.2 m 정도의 규격으로 개설되는 특징을 가지고 있어 갱도 폭의 변화는 수리반경(HR) 값에 큰 영향을 미치지 않고 있으며 안정성계수()는 Q 값에 의해 결정되는 것으로 나타났다.
Q 시스템의 적용:
5개의 시험광산 내 25개의 현장 조사 갱도 및 광주 모두 무지보 유지가 가능한 범주 내에 포함되고 있다. Q 시스템은 토목용 건설 사례를 데이터베이스로 하여 개발된 암반 내 공동 설계지침으로 주로 영구적인 터널을 대상으로 하고 있어 임시적인 광산 갱도에 적용할 경우 지나치게 보수적인 결과를 보여 주는 것으로 평가되었다.
도출된 갱도 및 광주 안전규격의 제안식 선정을 위해 한계곡선법, 안정도해법 및 Q 시스템을 활용하여 안정성 평가를 수행한 결과 5개의 시험광산 25개의 갱도 및 광주가 안정한 상태로 평가되었다.
IMER(2021)은 또한 KIGAM(2005)에서 활용한 6개 광산자료와 5개의 시험광산에서 취득한 자료를 모두 활용하여 갱도 및 광주에 대한 안전규격을 제시하였다. 대부분의 갱내 채굴 석회석 광산의 경우 일축압축강도 값이 100 MPa 내외의 범위를 가지며 지하수 상태는 건조 상태인 점을 고려하면 현장 기술자가 GSI를 손쉽게 평가함으로써 RMR 값을 추정할 수 있다.
이들 11개 광산은 갱도 폭 15 m 이하로 개설되는 특징을 보이며 GSI의 범위는 60으로부터 64까지로 나타났다. 예외적으로 GSI 값이 70 이상을 보이는 광산에서는 폭 22 m의 갱도를 무지보 상태로 유지하고 있는 것으로 관측되었다. 일축압축강도 값이 45 MPa 이하의 연암인 경우와 지하수 상태가 ‘젖음’으로 판정될 경우 측정된 GSI 값보다 상대적으로 작은 RMR 값을 보여 주며 이러한 현상은 일축압축강도 값이 81 MPa인 보통암인 경우일지라도 지하수 상태가 ‘젖음’으로 평가될 때에 나타나게 된다. 그러므로 GSI 값이 50 이상의 비교적 양호한 암반의 경우에도 일축압축강도 값이 50 MPa 이하의 연암 또는 지하수 상태가 ‘젖음’보다 불리한 상태일 때에는 RMR 값이 작게 평가되는 점에 유의해야 한다.
이상과 같은 경험적 방법에 의한 갱도 및 광주의 안전규격은 다음과 같이 제안되었다.
• GSI 값이 50 이상인 암반 내에서는 갱도 폭 12 m까지 무지보로 유지할 수 있으며
• GSI 값이 60 이상인 암반 내에서는 갱도 폭 15 m까지 무지보로 유지할 수 있다.
• 암반 내에 지하수가 유입되는 경우 또는 일축압축강도 값이 50 MPa 이하인 암반의 경우에는 보수적인 안정성 평가가 필요하며,
• GSI 값이 50 미만이거나 갱도 폭을 12 m 이상으로 유지하고자 하는 경우에는 전문기관에 의한 별도의 안정성 평가가 필요하다.
경험적 방법에 의한 광주의 안정성 평가 결과
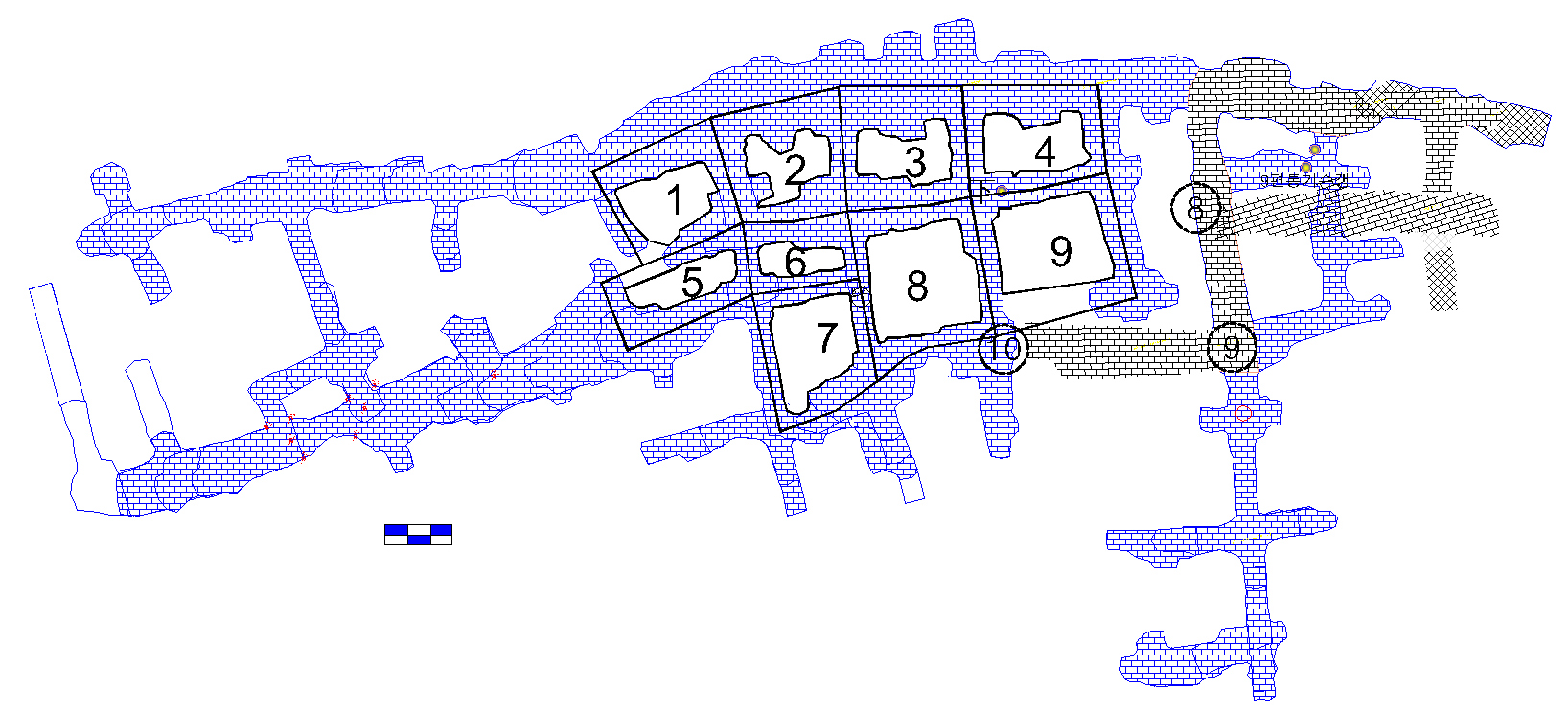
IMER(2020)에서는 NIOSH(2011)이 제안한 광주 설계 지침을 활용하여 국내 K광산에 존재하는 광주의 안정성 평가를 수행하였으며, Fig. 10은 K광산 9편의 갱내도이다. 해당 갱도에 존재하는 광주를 대상으로 관통절리가 없는 경우, 하나의 관통절리가 있는 경우(55° 및 80°)에 대한 안전율 분석결과는 Fig. 11과 같다. 불연속면에 의한 영향을 고려한다면, 2번과 3번 및 6번 광주의 안정성이 상대적으로 낮은 것으로 판단되었다.
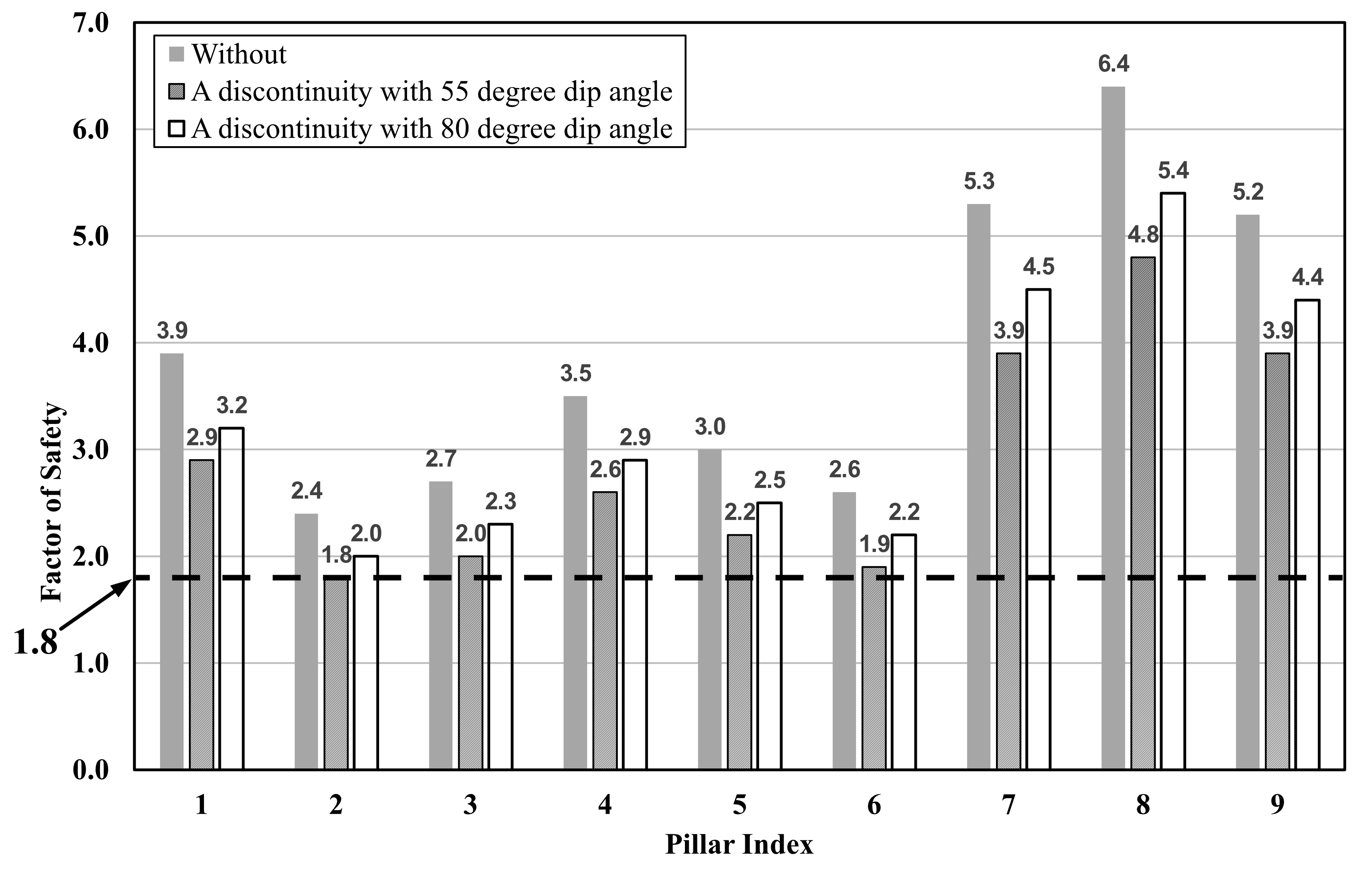
Fig. 11.
Stability analysis results based on the NIOSH method without discontinuity, with 55-degree and 80-degree dip-angle discontinuities (IMER, 2020).
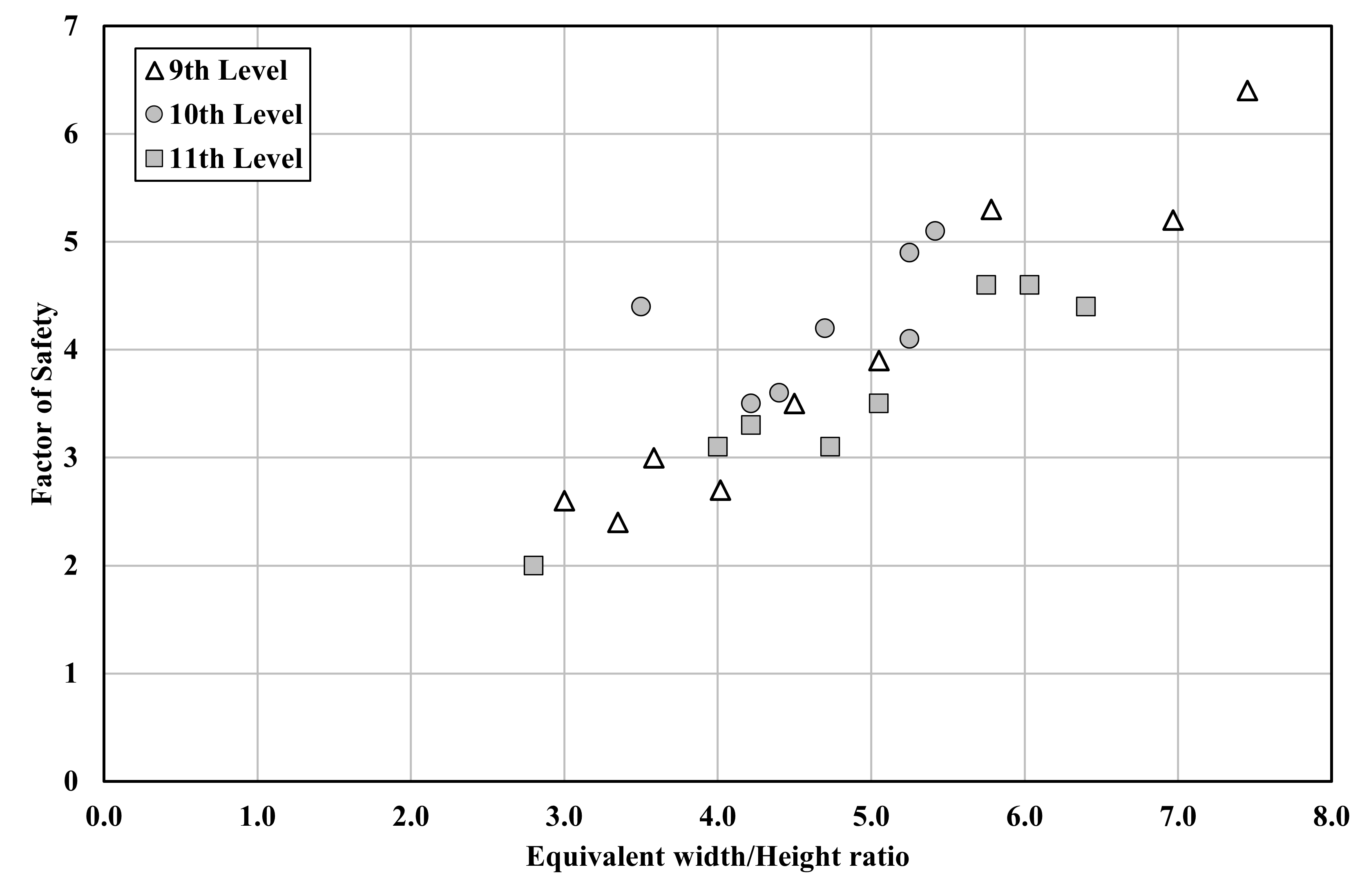
Fig. 12는 K광산 9편~11편에 존재하는 광주에 대한 유효 종횡비(등가폭/높이)와 안전율 관계를 나타내는데, 유효 종횡비가 커질수록 안전율이 증가하는 것을 볼 수 있다. 광주의 종횡비는 광주의 강도에 영향을 미치며 특히 관통절리에 의해 광주의 강도가 저하될 수 있으며, Fig. 13과 같이 관통절리를 따라 광주가 파괴되는 사례가 보고되기도 한다. K광산의 평균 광주 종횡비는 4.3으로 상당히 높은 편이며 광주의 길이 증가로 인해 종횡비가 두 배로 늘어나면 광주의 강도가 약 35% 증가하는 것으로 나타났다.
전산해석에 의한 갱도 및 광주의 안정성 평가 결과
IMER(2021)은 RS3(Rocscience, 2024)을 이용한 전산해석과 한계변형률법(Critical strain)을 활용하여 갱도 및 광주의 규격, GSI 값, 심도 등의 변수에 따른 갱도와 광주의 3차원 거동 분석과 안정성 해석을 수행하였다.
한계변형률은 굴착 중인 터널(갱도) 내에서 계측되는 변위를 토대로 터널의 안정성을 평가하기 위해 Sakurai(1982)가 제안한 개념으로서 갱도 굴착 후 갱도 주위 암반 내에서 발생하는 변형률(변위/갱도반경)을 산출하고 해당 암반의 한계변형률과 비교함으로써 굴착된 갱도의 안정성 여부를 판단할 수 있다.
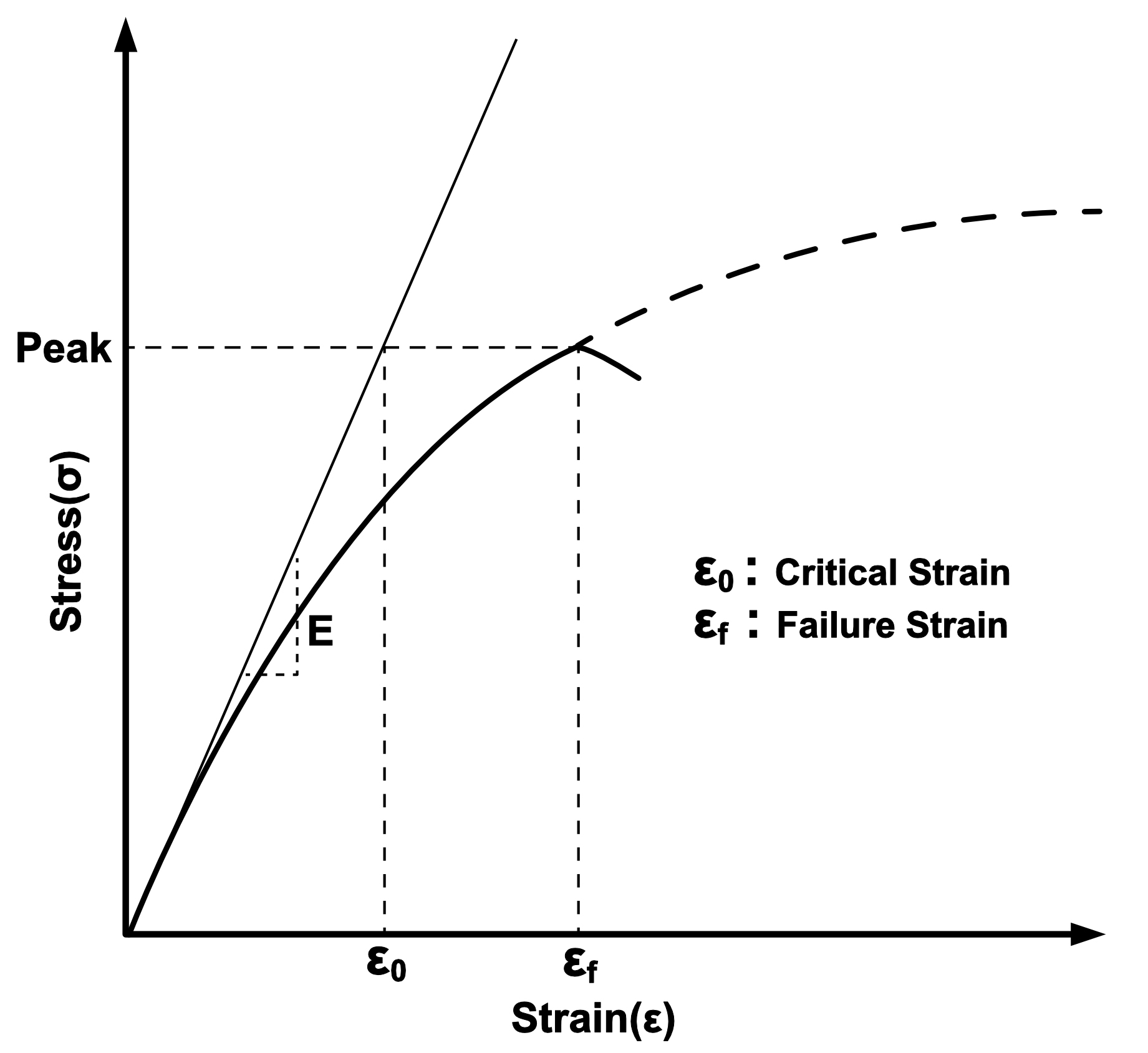
Fig. 14는 응력-변형률곡선에서의 한계변형률과 파괴 변형률을 보여주며, 암석의 한계변형률 는 일축압축시험을 통해 결정할 수 있다.
여기서 는 암석의 일축압축강도, 는 암석의 탄성계수 이다.
암반의 일축압축강도와 변형계수는 암석의 값보다 작으므로, 암반의 한계변형률 는 암석의 한계변형률 보다 작다. 따라서, 암반의 한계변형률 결정을 위해 다음 식과 같이 결정된다.
여기서 은 암반의 일축압축강도, 는 암반의 변형계수, 는 감쇠지수이다.
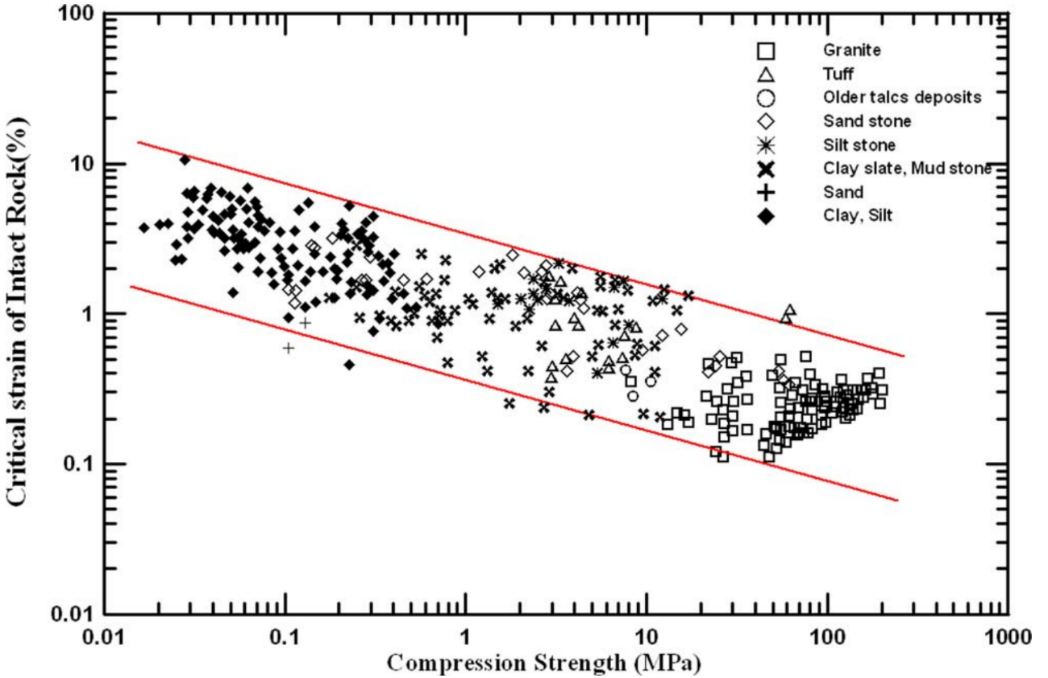
Sakurai(1983)은 암석과 암반을 대상으로 실내시험과 현장시험을 수행하였으며, 감쇠지수 가 1~3의 범위의 값을 가짐을 확인하였다. Fig. 15는 암석과 한계변형률 사이의 관계를 도시한 것으로, 감쇠지수 의 값을 고려했을 때 암석의 한계변형률과 일축압축강도와의 관계를 암반에 적용할 수 있다.
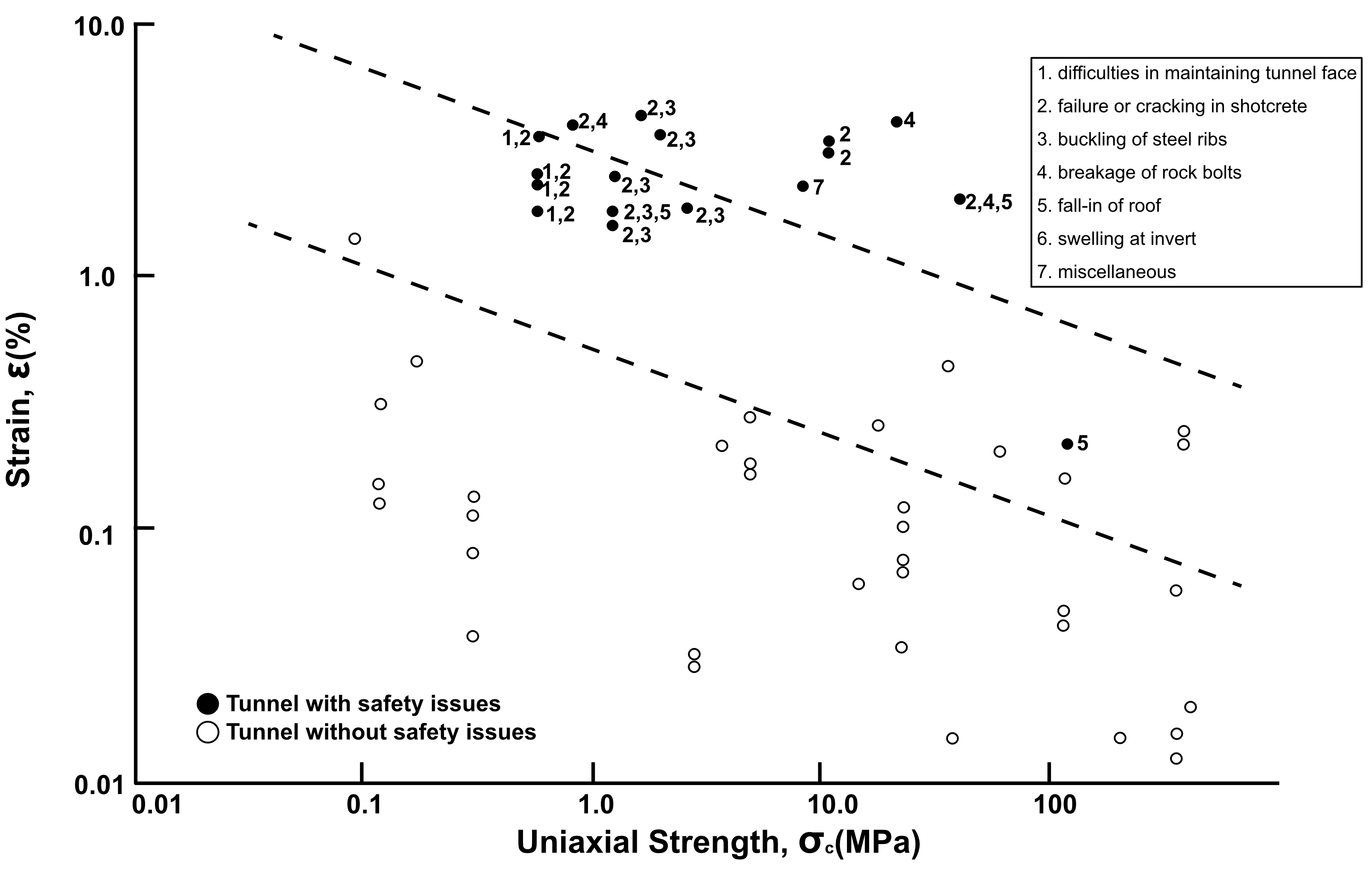
Sakurai(1997)는 Fig. 16과 같이 실제 터널 계측 자료를 한계변형률 도표에 도시한 결과 관측된 데이터가 한계변형률 상한 경계에 가까울수록 안정성 문제가 발생되는 것에 착안하여 터널 관리 단계를 설정함으로써 터널의 위험 관리를 위한 기준 마련에 활용하였다.
전산해석은 한계곡선법에 의해 제시된 갱도 규격과 GSI 값을 기준으로 9개의 해석 조건별로 수행되었으며(IMER, 2021), Table 4와 Table 5는 해석조건과 입력변수이다. 갱도의 폭과 수직광주 폭의 비는 1:1로 하였고 지표로부터 갱도까지의 심도를 고려하였다. 해석모델인 채굴작업장의 골격은 3개 편으로 이루어져 있으며 주갱도 3개, 크로스 갱도 4개로 구성하였다. 암반의 강도, 갱도 및 광주의 규격, 토피고의 변화를 고려한 대표적인 해석 결과를 소개하면 다음과 같으며, Fig. 17은 수치해석 결과를 바탕으로 계산된 한계변형율 분석 결과이다.
Table 4.
GSI and geometrical parameters of the underground mine stope for numerical analysis (IMER, 2021)
| Case1 | Case2 | Case3 | Case4 | Case5 | Case6 | Case7 | Case8 | Case9 | |
| GSI | 45 | 45 | 45 | 50 | 50 | 50 | 60 | 60 | 60 |
| Depth (m) | 100 | 200 | 300 | 100 | 200 | 300 | 100 | 200 | 300 |
| Width or pillar/opening (m) | 12 | 12 | 12 | 12 | 12 | 12 | 15 | 15 | 15 |
Table 5.
Input parameters for numerical analysis (IMER, 2021)
|
Unit weight (kN/m3) |
UCS (MPa) |
Em (GPa) | Poisson’s ratio | K value | mb | s | a |
| 27.7 | 100 | 8.74 | 0.22 | 1 | 1.68 | 0.0022 | 0.508 |
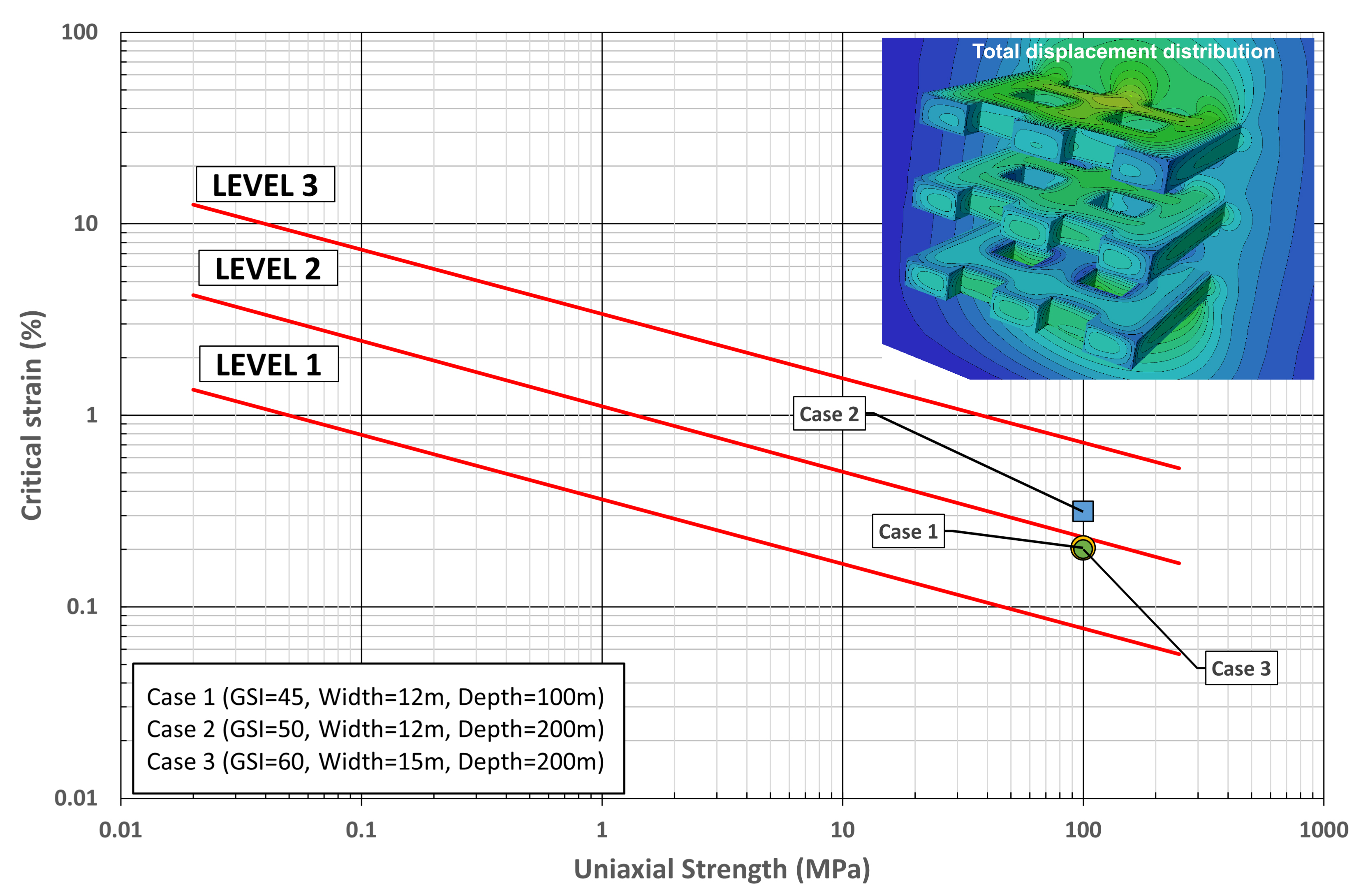
Fig. 17.
Application of critical strain method using numerical analysis for 12 and 15 m wide opening and pillar (modified from IMER, 2021).
첫째, GSI 값이 45이고 갱도 및 광주의 폭이 12 m 그리고 토피고가 100 m인 경우 3개 편의 변형률이 0.2% 이하로서, 이는 “Level1”에 해당되어 채광장 내 갱도 및 광주의 안정성이 확보되는 것으로 나타났다.
둘째, GSI 값이 50이고 갱도 및 광주의 폭이 12 m 그리고 토피고가 200 m일 때 한계변형률은 “Level 2” 하단에 포함되여 안정성이 확보될 수 있는 것으로 판단된다.
셋째, GSI 값이 60이고 갱도 및 광주의 폭이 15 m 그리고 토피고가 200 m일 때 각 편의 변형률 값은 “Level 1”에 포함되어 안정성이 확보될 수 있는 것으로 판단된다.
끝으로 GSI 값이 60이고 갱도 및 광주의 폭이 15 m 그리고 토피고가 300 m일 때는 전산해석 과정이 수렴하지 않는데 이는 채굴 후 암반의 변형이 지속되기 때문인 것으로 볼 수 있어 안정성이 확보되지 않는 것으로 평가된다.
결론적으로 갱도 폭 12 m, GSI 45, 토피고 100 m 이하의 조건을 비롯하여 갱도 폭 12 m, GSI 50, 토피고 200 m 미만 조건과 갱도 폭 15 m, GSI 60, 토피고 300 m 미만인 조건에서는 갱도 및 광주의 안정성이 확보되는 것으로 볼 수 있다.
해석 모델(주갱도 3개)과 유사한 갱도 구성을 갖는 광산의 경우 채굴 심도가 증가할 때에는 채굴작업장 중앙부에 위치한 주갱도의 거동을 중점적으로 모니터링할 필요가 있다.
갱도 및 광주의 규격 수정 제안
이상과 같은 연구를 통하여 무지보 갱도 및 광주의 규격을 다음과 같이 제안하였다.
• 갱도의 폭은 12 m~15 m 이내로 하고 수직광주의 폭은 최소한 갱도의 폭과 같게 유지
• 갱도 및 수직광주의 높이는 7 m~9 m를 권고
• 여러 편 개발 시 편간 수직고를 20 m 이상으로 하고 수평광주의 두께는 13 m 이상 유지
위의 기준에 벗어나는 경우 특히 암반 내 지하수가 유입(지하수 상태가 ‘젖음’보다 불리한 상태)되거나 암석의 일축압축강도 값이 50 MPa이하일 경우와 연속성이 큰 불연속면(예: 관통절리)을 포함하거나 암반의 GSI 값이 50미만인 경우에는 전문기관의 안정성 평가가 요구되는 것으로 판단되며 안정성 평가 시에는 초기응력의 측정이 필요하다.
채굴작업장의 안전관리 및 관리기법
최대 수평응력의 영향
응력에 의해 유발된 균열 또는 낙반이 최대 수평응력과 직교하는 방향으로 전파되는 사례가 보고되기도 한다(NIOSH, 2011). 이는 천반의 불안정성을 증가시킬 수 있는데, 갱도의 심도와 관계 없이 발생하기도 한다(Esterhuizen et al., 2007). 이러한 경우에는 주운반갱도의 굴진 방향은 최대 수평응력이 작용하는 방향과 나란하게 설정하는 것이 안정성 확보에 유리하고 크로스 갱도는 엇갈리게(Offset) 개설하여 최대 수평응력이 작용하는 방향과 직교하는 방향으로 개설된 갱도의 길이를 최소화하도록 하는 것이 바람직하다. 또한 주운반갱도보다 크로스 갱도의 폭을 좁게 하는 것이 천반 붕락 가능성을 낮출 수 있다. Fig. 18은 이와 관련된 실제 사례를 보여준다.
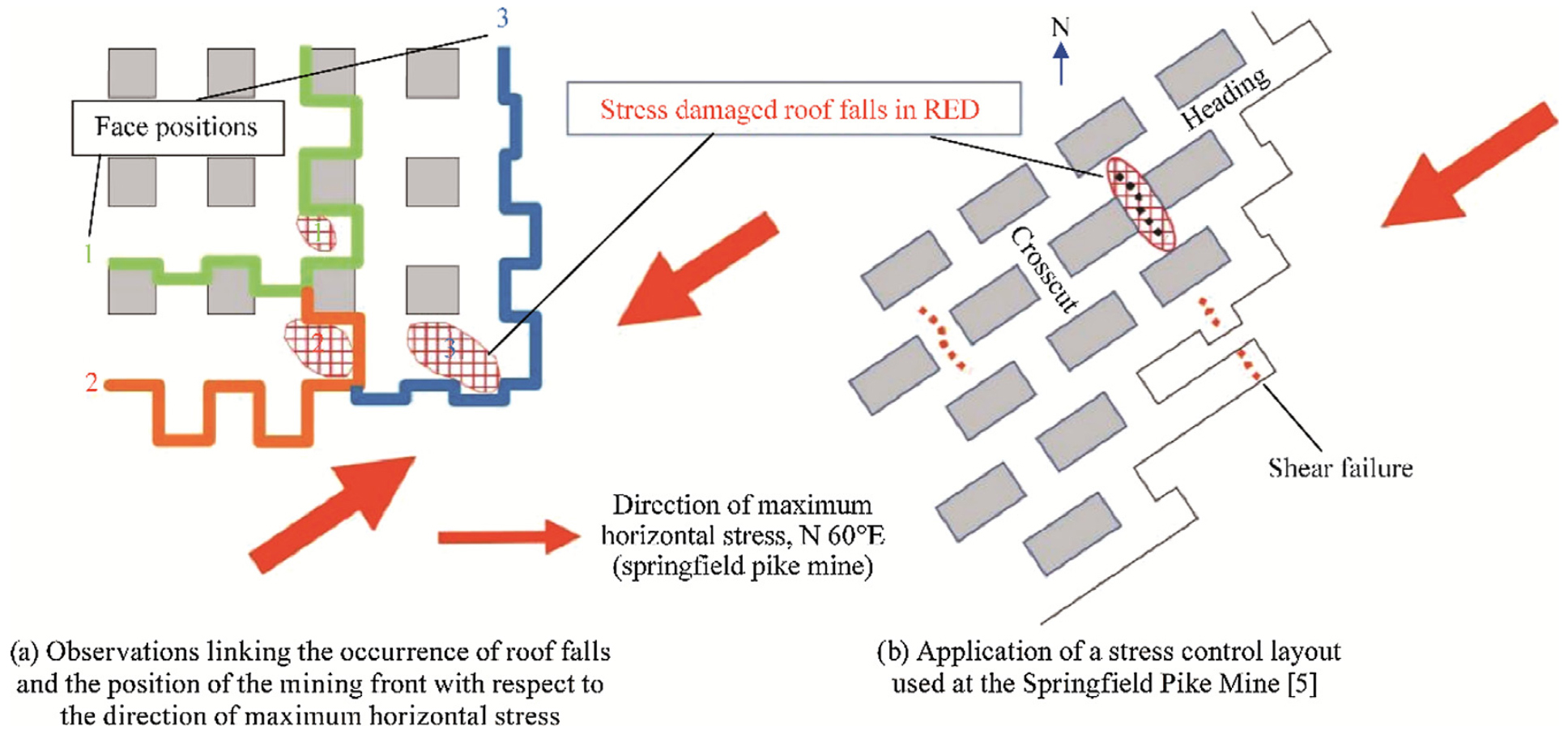
Fig. 18.
Examples of how mine layout orientation can influence roof fall characteristics (Iannacchione et al., 2020).
이러한 방식으로 광산의 layout을 변경하는 것은 응력과 관련된 모든 안정성 문제를 해결할 수 있는 건 아니지만, 불안정성을 상당히 저감할 수 있다(Kuhnhein and Ramer, 2004). 다만, 장비의 이동 및 운반 등의 용이성도 함께 고려되야 한다.
앞서 언급한 K광산의 경우 9편으로부터 11편까지 주운반갱도의 방향이 최대 수평응력이 작용하는 방향과 거의 일치하고 있어 주운반갱도의 개설 방향은 적절한 것으로 보이나 크로스 갱도의 경우 십(十)자형으로 개설되어 있어 차후에는 엇갈리게 개설하는 것을 고려해 볼 필요가 있다(IMER, 2020). 만약 저각의 직상반(Immediate roof) 보의 두께가 1.2 m 이하가 되면 천반 지보 시공이 필요하다.
한편 수치해석을 통해 채굴작업 과정의 응력 이력을 사전에 파악하면 채굴 과정에 발생될 수 있는 잠재적인 불안정성 요인을 극복할 수 있고 모니터링을 통하여 이 시기의 안정성을 확인할 수 있다.
미소진동 기술
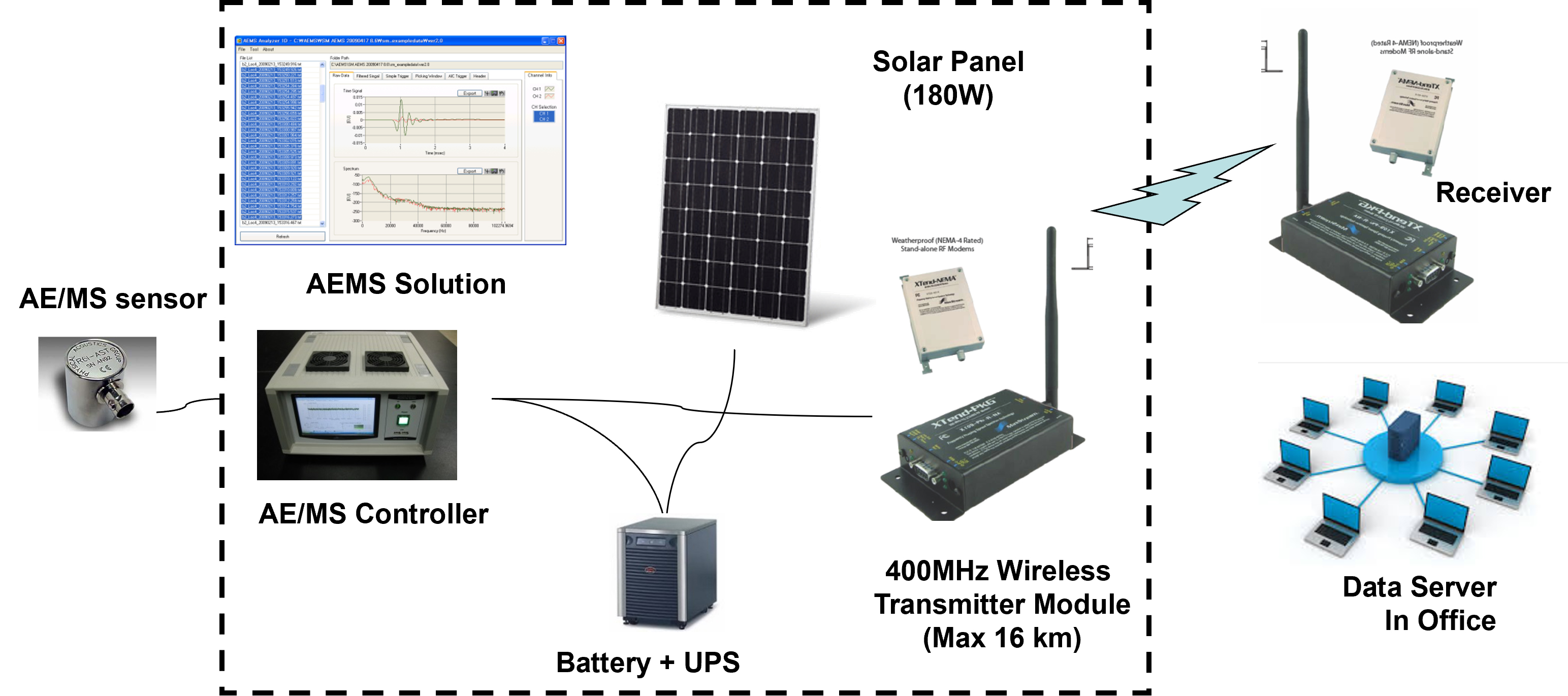
암석 시편에 축방향의 하중이 가해지는 압축시험 과정을 통해 Fig. 19와 같은 응력-변형률 그래프를 얻을 수 있다. 이 과정에 시편 내에 미소진동이 발생되는 것을 관찰할 수 있으며 미소진동은 작용되는 하중이 시편 강도 값의 40~60%일 때 발생되기 시작하며 서서히 발생 빈도가 증가하다가 하중 값이 시편 강도의 70% 이상이 되면 발생 빈도가 급격히 증가하며 파괴가 일어나기 직전까지 진행되는 메커니즘을 가진다. 일반적으로 암석 내에서 발생되는 미소진동은 인간의 가청영역에 해당하는 수백~수천 Hz 영역에 해당하며, 그보다 낮은 주파수의 영역도 광산 안전의 목적으로 모니터링 대상이 되고 있다. Fig. 20은 한국지질자원연구원에서 개발한 시스템의 개요도로서 관측 대상 암반 내 시추공 속에 센서를 매립하고 센서와 컨트롤러가 내장된 컴퓨터가 계측선으로 연결되어 갱내에서 자료를 취득할 수 있으며 과거에는 취득된 자료를 갱내에 설치된 컴퓨터로부터 외장 기억장치(USB 등)에 옮겨 갱외 사무실에서 분석하는 과정을 거쳤다.
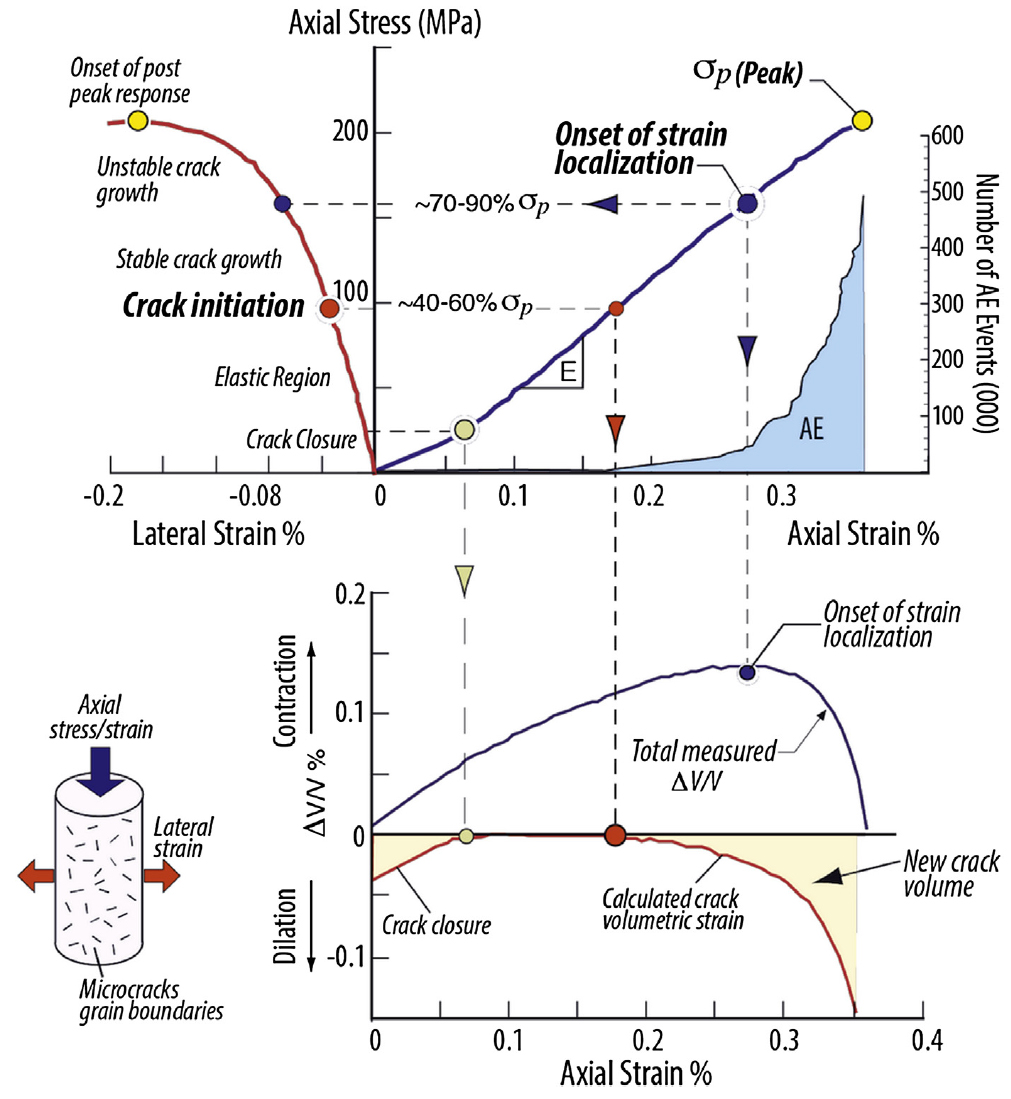
Fig. 19.
Stages in the progressive failure of rock specimens subjected to compressive loading (Hoek and Martin, 2014).
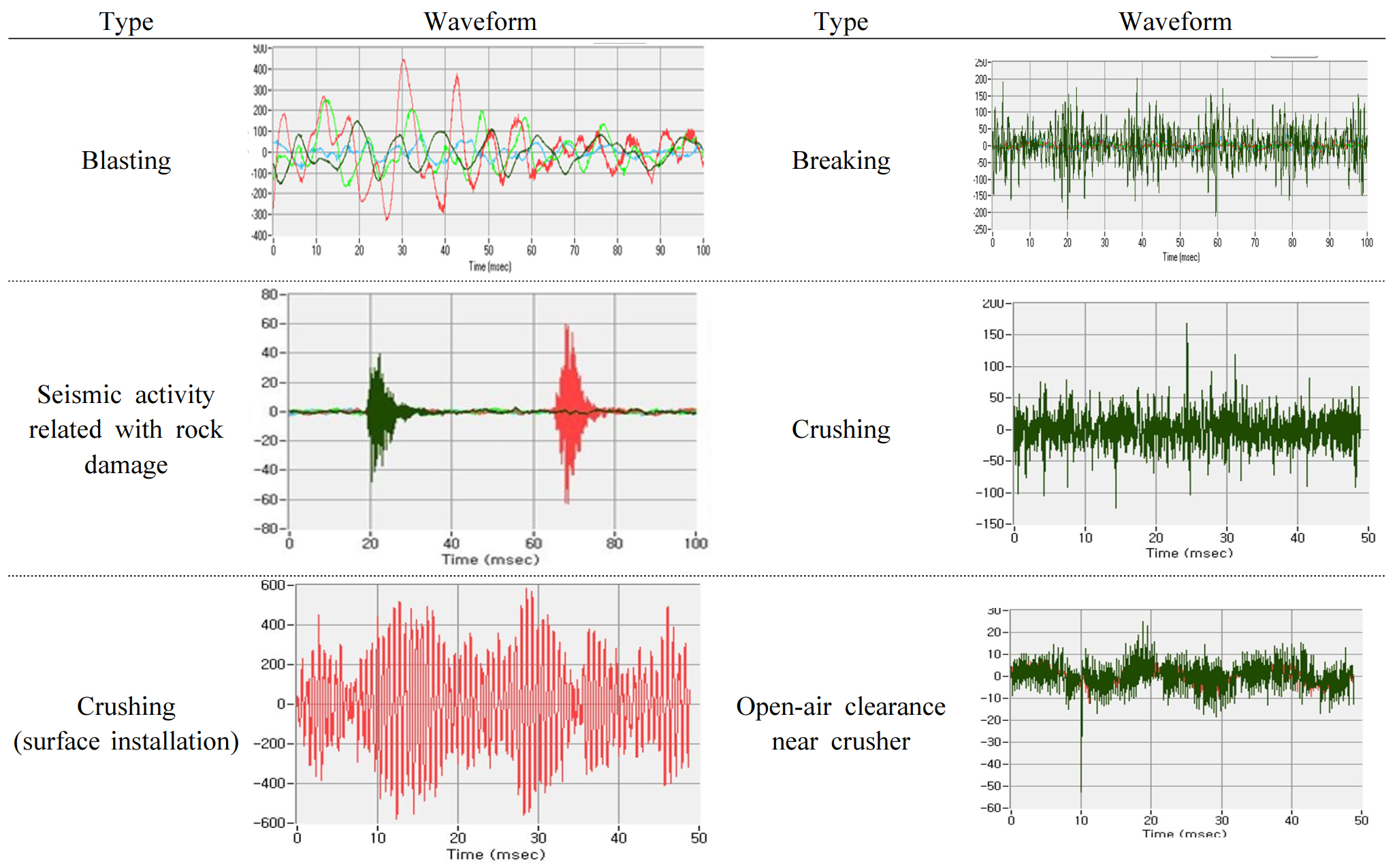
미소진동 모니터링 시스템은 설치 목적 및 계측 대상에 따라 1축(성분) 센서와 3축(성분) 센서로 나뉠 수 있는데 1축 센서는 주로 진원의 위치를 파악하는 데 이용되고 3축 센서는 진원의 에너지, 지진 모멘트 및 크기를 파악하는 데 적합하다(Xiao et al., 2016). 관측 대상 영역의 주위를 3차원적으로 감싸도록 센서가 배치되어야 하며 하나의 관측 지점 주위에 최소한 4개 이상의 센서가 배치되도록 하는 것이 바람직하다. 최근에는 취득된 자료를 광케이블에 의해 갱외로 송출하고 스마트폰 어플리케이션 상에서 실시간으로 모니터링할 수 있게 되었다. 취득되는 파형은 갱내에서 수행되는 작업의 유형에 따라 다른 양상을 보이며 암반 손상으로 추정되는 파형은 발파나 천공 작업 또는 전기잡음과 대비하여 서로 다른 고유의 형태를 보인다(Cheon et al., 2014).
S광산 시험채광 과정에 인접한 제3의 작업장에서 발생된 천반 붕락 현상을 시험 과정에 설치한 미소진동 모니터링 시스템으로 관측할 수 있었는데 관측 시점이 암반 붕락 시점보다 2~3일 먼저 기록되었던 것으로 보아 미소진동 계측 시스템에 의해 암반 붕락 현상을 사전에 충분히 감지할 수 있는 것으로 보이며 본 시스템이 갱내 광산의 안전관리에 적절히 활용될 수 있을 것으로 판단된다. Fig. 21은 갱내 채굴광산에서 채광 및 분쇄 작업 중에 계측된 미소진동 파형의 사례이다.
갱내 LiDAR 측량
LiDAR(Light Detection And Ranging)는 내장된 제어장치와 GPS 및 카메라에 의해 대상 구조물 표면의 3차원 점군(Point Cloud) 자료를 생성시킴으로써 그 결과물이 구조물의 3차원 모델링에 활용된다. 본 시스템은 노천채광장뿐만 아니라 갱내 채굴 공동과 갱내 구조물 측량에도 활용될 수 있다. Fig. 22는 갱내 채굴광산의 3차원 계측에 활용된 예로서 천반 및 측벽을 가로지르는 파쇄대의 확인과 수평광주의 두께의 확인 그리고 정확한 광주의 형상을 확인하는 데 활용된 사례이며 이들 자료가 수치해석에서 채광장 모델링 자료로 이용된다.
현안 및 향후 과제
채수율에 대한 고찰
채광의 운영 효율성에 영향을 미치지 않으면서 광산의 수익성을 최적화하는 것을 전제로 갱도 및 광주의 안전한 규격을 결정해야 하는데, 현재 대부분의 국내 광산 채수율은 Table 6과 같이 25% 이내의 수준에 머무르고 있어, 70~80%에 해당되는 고품위 부존 자원이 사장되고 있다. 이는 국내의 경우 지표침하로 인한 산지 훼손 문제 등이 채수율을 향상시키는 데 큰 장애 요인으로 작용하고 있기 때문인 것으로 볼 수 있다. 유사한 채광법을 적용하는 외국 광산의 경우에는 50~80%의 채수율을 보이고 있는 상황을 고려할 때(Darling, 2011), 국내 광산의 채수율 향상을 위한 대책 마련이 절실하다.
Table 6.
Calculated recovery rates of domestic underground limestone mines
채광 완료 후의 갱도 안정성 문제
지금까지 본 기고문에서 계획채광에 따라 안정성과 경제성이 확보되는 적정 채광법을 적용하는 과정에 경험적인 방법과 수치해석적인 안정성 평가 방법을 활용하고 이를 검증하기 위하여 LiDAR와 미소진동 모니터링을 이용하는 방법에 대해 다루었다. 외국의 사례에서 볼 수 있듯이 안전관리가 잘 수행되었던 광산의 경우에도 채굴 완료 후 30여년 이상 경과되면 시간과 관련된 두 가지의 지반안전 문제가 발생될 수 있다. 첫 번째 문제는 강도 값보다 낮은 수준의 하중(채광작업 이전/채광작업 중)일지라도 장기간 지속적으로 작용하게 되면 암반이 결국 파괴되는 현상(Creep)으로서 국내 광산의 경우도 이에 대비할 필요가 있다.
두 번째로 일반광에서는 드문 경우이기는 하지만 채수율이 높은 석탄광의 경우에 Fig. 23에서 보는 바와 같이 전체 채굴 폭 대 채굴 심도의 비가 1.2 이상이 되는 조건에서 최대 지반침하가 발생됨으로 인해 지상의 구조물에 영향을 미칠 수 있는 문제로서(Darling, 2011), 이미 채굴 완료된 광산 지역의 지상을 개발할 때에 확인되어야 할 것으로 본다.
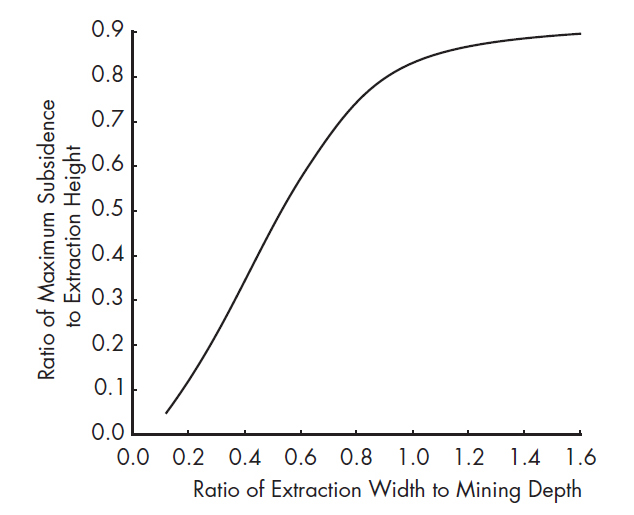
Fig. 23.
Simplified relation between the maximum subsidence and extraction height, extraction width, and mining depth (Darling, 2011).
결 론
국내 비금속 갱내 채굴광산은 편별 주방식채광법과 일부 광주식채광법이 적용되고 있으며 그 외 광산에서는 굴진채광법이 적용되고 있다. 갱도 및 광주에 대한 안정성 평가에는 한계곡선법, 안정도해법, Q 시스템 및 NIOSH가 제안한 방법과 같은 경험적 방법과 수치해석적 접근이 주로 활용되고 있으며 이에 따라 기관별 수행 연구와 시험광산 연구를 통하여 안전규격이 제안되었다.
선행연구에서는 갱도의 안전규격이 폭 12 m, 높이 7~8 m로 제안된 바 있으며 자원산업연구원(IMER)에서 수행한 경험적 방법 및 수치해석과 한계변형률법의 적용 연구에서는 갱도의 폭을 12~15 m, 갱도 및 수직광주의 높이 7~9 m, 편간수직고(복수편 개발 시) 20 m 이상으로 수정 제안되었다.
개별 광산에 대한 연구결과 광주의 종횡비(광주의 폭/높이의 비)가 클수록 안전율이 증가하는 것으로 나타났다. 주운반갱도를 최대 수평응력이 작용하는 방향과 나란하게 그리고 크로스 갱도는 엇갈리게 개설하는 것이 유리하며, 저각의 직상반 보의 두께가 1.2 m 이하일 때에는 천반지보를 시공하여야 하는 것으로 분석되었다.
최근 10여 년간 우리나라 갱내 채굴광산의 안전관리를 위해 수행된 채굴작업장, 갱도 및 광주 등의 안정성 평가와 연구 결과는 갱내 채굴광산의 안전관리 현황과 과제를 동시에 보여 주고 있다. 갱내 채굴광산의 안전을 확보하기 위하여 먼저 계획채광 이행의 시급성과 LiDAR 등을 이용한 갱내 3차원 측량과 미소진동 모니터링시스템의 확대 보급에 대한 필요성을 강조하고 있다.
또한 채굴과정에 발생되는 응력 이력을 파악하게 되면 모니터링 방안과 잠재적 불안정성 요인에 대한 대처가 가능하다. 미소진동 모니터링은 암반 붕락 현상의 사전 감시 및 예방 차원에서 국내 광산에 확대 보급이 필요하다. 이와 더불어 3차원 측량(LiDAR 3D Scanning)으로 암반 내 취약대의 파악뿐만 아니라 광주의 규격 및 형상을 확인하고 나아가 계획채광을 구현하는데 활용할 것을 제안한다. 자원 선진국들에 비해 극히 저조한 채수율을 증대시키기 위한 방안 마련을 통해 부존 자원의 활용을 극대화할 수 있는 정책 수립 역시 요구된다.
앞으로 채광 종료 후 발생이 예상되는 암반의 Creep 현상과 광산지역 지반침하 문제에 대해서도 심화연구를 통한 대책 마련이 필요하다.