Seismic Velocity Modeling Building Using Depthwise Separable Convolutional Neural Network

Jun Hyeon Jo; Wansoo Ha

doi:10.32390/ksmer.2022.59.2.148

Preview

Research Paper

Journal of the Korean Society of Mineral and Energy Resources Engineers. 30 April 2022. 148-160
https://doi.org/10.32390/ksmer.2022.59.2.148

Seismic Velocity Modeling Building Using Depthwise Separable Convolutional Neural Network

깊이별 분리 합성곱 신경망을 이용한 탄성파 속도 모델 구축

Jun Hyeon Jo¹

Wansoo Ha²^*

조 준현¹

하 완수²^*

¹Postgraduate Student, Department of Energy Resources Engineering, Pukyong National University, Busan, Korea

²Professor, Department of Energy Resources Engineering, Pukyong National University, Busan, Korea

¹부경대학교 에너지자원공학과 박사과정

²부경대학교 에너지자원공학과 교수

^{*Corresponding Author}

ABSTRACT

The construction of an accurate velocity model is one of the most important tasks in seismic data processing for hydrocarbon exploration. Because deep neural networks have garnered significant attention in the field of geophysics recently, studies have been performed to predict velocity models using regular convolutional neural networks. Herein, we propose a neural network with depthwise separable convolutional layers and an encoder–decoder structure to construct a velocity model. This network is trained using a supervised learning approach, and we predict P-wave velocity models from time-domain wavefields. In this network structure, depthwise separable convolutions perform spatial-oriented convolutions independently for each input channel. These depthwise separable convolutions can improve network performance while significantly reducing the number of model parameters as compared with regular convolutions. Synthetic velocity models generated for training contain various geological features, including folds, faults, and salt-dome structures. We compare a network with depthwise separable convolutions and a network with regular convolutions based on the same training conditions and hyperparameters. Experiments demonstrate that the network with depthwise separable convolutions is more efficient than the network with regular convolutions for constructing a seismic velocity model.

Keywords

deep neural networks

depthwise separable convolutions

velocity model building

정확한 속도 모델 구축은 석유 가스 탐사를 위한 탄성파 자료처리에서 가장 중요한 작업 중 하나이다. 최근 심층 신경망 기법이 지구물리학 분야에서 큰 인기를 얻으면서, 일반 합성곱 신경망을 이용하여 속도 모델을 예측하는 연구들이 출판되고 있다. 본 연구에서는 속도 모델 구축을 위해 깊이별 분리 합성곱 층과 인코더-디코더 구조를 가진 신경망을 제안하였다. 이 신경망은 지도 학습 방식으로 훈련되며 시간 영역 파동장으로부터 P파 속도 모델을 예측한다. 이 신경망 구조의 핵심 부분인 깊이별 분리 합성곱은 입력 채널 별로 독립적으로 공간 방향의 합성곱을 수행한다. 깊이별 분리 합성곱을 이용하면 일반 합성곱에 비해 모델 매개변수 수를 크게 줄이면서 신경망의 성능을 개선할 수 있다. 훈련을 위해 생성한 합성 속도 모델들은 습곡, 단층 및 암염 구조 등 다양한 지질학적 특징을 포함한다. 깊이별 분리 합성곱을 이용한 신경망과 일반 합성곱을 이용한 신경망을 동일한 하이퍼파라미터 및 훈련 조건으로 비교 분석하였다. 실험 결과 깊이별 분리 합성곱 신경망이 일반 합성곱 신경망보다 속도 모델 구축 문제에서 더 효율적인 것으로 나타났다.

키워드

심층 신경망

깊이별 분리 합성곱

속도 모델 구축

MAIN

서 론
이 론
깊이별 분리 합성곱
Tomography_CNN
합성 데이터 생성
탄성파 속도 모델
시간 영역 파동장
신경망 훈련
결 과
잡음 예제
토 의
결 론

서 론

정확한 속도 모델 구축은 탄성파 탐사 자료처리에서 가장 중요한 작업 중 하나이다. 속도 모델의 품질은 역시간 구조보정(Baysal et al., 1983) 및 기타 탄성파 영상화 기법(Bunks et al., 1995)에 큰 영향을 끼친다. 심해저 석유 가스 탄성파 탐사가 증가함에 따라 복잡한 지질 구조를 해석해야 하는 사례가 점점 많아지고 있다. 이는 탄화수소 탐사의 조건을 더욱 까다롭게 만드는 요인 중 하나이며, 정확한 탄성파 이미지를 얻기 위해서는 높은 품질의 속도 모델이 요구된다. 이러한 속도 모델을 얻기 위한 기존 방법에는 대표적으로 속도분석, 구조보정 속도분석, 주시 토모그래피, 전파형 역산(Tarantola, 1984) 등이 있다. 석유 가스 탐사에 주로 사용하는 지표면 주시 토모그래피는 크게 굴절주시 토모그래피와 반사주시 토모그래피로 구분할 수 있으며(Zhang et al., 1998), 전파형 역산은 시간 영역(Tarantola, 1984; Gauthier et al., 1986; Mora, 1987), 주파수 영역(Pratt and Worthington, 1990; Pratt et al., 1998) 및 라플라스 영역(Shin and Cha, 2008) 역산 등으로 구분할 수 있다. 탄성파 탐사 자료의 주시 정보만 이용하는 주시 토모그래피와 달리, 전파형 역산은 탐사 자료의 진폭과 주시를 함께 이용한다. 그러나 주시 토모그래피 및 전파형 역산 모두 하나의 속도 모델을 계산하는 데 시간이 오래 걸리고, 불량 조건(ill-posed)을 가진 역해석 문제에 해당하며, 역산 결과가 초기 속도 모델에 따라 참 속도 모델에 수렴하지 못할 수 있다는 한계점이 존재한다(Virieux and Operto, 2009).

최근 심층 신경망 기법이 다양한 분야에서 복잡하고 비선형적인 문제를 성공적으로 해결하는 사례가 많아짐에 따라 지구물리학 분야에서도 큰 인기를 얻고 있다. 심층 신경망이란 입력층과 출력층 사이에 비선형 변환을 수행하는 여러 은닉층을 쌓은 인공 신경망으로 심층 신경망을 이용하면 높은 수준의 유용한 표현을 학습할 수 있다. 보편적 근사치 정리(universal approximation theorem)에 따르면 단 하나의 은닉층을 가진 다층 피드포워드(feedforward) 신경망이라도 은닉층의 유닛 수가 충분히 많다면 임의의 연속적인 함수를 근사할 수 있다(Hornik et al., 1990). 이러한 점에 영감을 받아 탄성파 속도 모델 구축 문제에도 심층 신경망 기법을 적용하는 연구들이 출판되어 왔다. Yang and Ma (2019)는 UNet 구조에서 탄성파 자료에 맞게 수정한 신경망을 사용하였으며, Wu and Lin(2019)은 인코더-디코더(encoder-decoder) 구조를 가진 합성곱 신경망에 CRF (conditional random field)을 추가하여 역산 성능을 향상시켰다. Wang and Ma(2020)는 대량의 자연 이미지를 속도 모델로 변환하여 파동 방정식을 학습하도록 유도한 VMB_Net을 제안하였으며, Li et al.(2020)은 인코더-디코더 구조에 특성 생성기(feature generator)를 추가한 SeisInvNet을 제안하였다. Liu et al.(2021)은 대량의 합성 속도 모델을 자동으로 생성하는 알고리즘을 소개하며 기존 SeisInvNet을 개선하였다. 이 연구들은 이미지 처리에 널리 사용하는 합성곱 신경망을 통해 시간 영역 파동장으로부터 직접 속도 모델을 구축하였다(Yang and Ma, 2019; Wu and Lin, 2019; Wang and Ma 2020; Li et al., 2020; Liu et al., 2021).

본 연구에서는 탄성파 속도 모델 구축을 위해 인코더-디코더 구조를 가진 Tomography_CNN을 제안한다. 이 신경망에서는 일반 합성곱을 사용한 기존 연구들과 달리 깊이별 분리 합성곱을 사용하였다. 이 신경망 구조의 핵심 부분인 깊이별 분리 합성곱은 입력 채널 별로 독립적으로 공간 방향의 합성곱을 수행한다. 깊이별 분리 합성곱을 이용하면 일반 합성곱보다 모델 매개변수 수와 연산 횟수를 크게 줄임으로써 효율적인 계산이 가능해진다. 신경망 훈련시 다양한 지질학적 특징을 학습할 수 있도록 습곡, 단층 및 암염 구조를 가진 합성 속도 모델을 대량으로 생성하였다. 그런 다음, 생성된 합성 속도 모델을 이용해 인공 수치 모델링을 수행하여 시간 영역 파동장을 얻었다. 탄성파 속도 모델 구축 문제에 깊이별 분리 합성곱이 어떠한 이점이 있는지 알아보기 위해 동일한 하이퍼파라미터 및 훈련 조건을 가지고 깊이별 분리 합성곱으로 구축한 신경망과 일반 합성곱 신경망으로 구축한 신경망으로부터 얻은 결과를 비교 분석하였다.

이 론

일반적으로 탄성파 탐사에서 지표면 아래 지질 정보를 얻기 위해서는 탄성파 송신원을 통해 인공 지진파를 일으키고 수신기를 통해 탄성파 기록을 취득한다. 본 논문에서는 일정한 밀도를 가진 시간 영역 2차원 음향파 파동 방정식을 사용하여 데이터를 생성하였다.

(1)

\frac{1}{c^{2}} \frac{\partial^{2} u}{\partial t^{2}} = \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial z^{2}} + f,

위 식에서 $c$ 는 P파 속도이며, $u$ 는 파동장, $f$ 는 탄성파 송신원이다. 심층 신경망 기법을 이용한 속도 모델 구축 문제는 다음과 같이 나타낼 수 있다.

(2)

\bar{V} = N (D; Θ),

위 식에서 $\bar{V}$ 는 예측한 속도 모델을 나타내며, $N$ 은 비선형 연산자의 역할을 수행하는 심층 신경망, $D$ 는 입력 탄성파 기록, $Θ$ 는 모델 매개변수인 신경망의 가중치를 나타낸다. 훈련이 완료된, 또는 모델 매개변수가 최적화된 신경망에 탄성파 기록을 입력하면 속도 모델을 출력한다. 완전 파형 역산의 경우 실제 탐사로 얻은 데이터와 수치 모델링을 통해 얻은 데이터의 오차를 이용해 목적 함수를 정의하고, 목적 함수가 감소하는 방향으로 속도 모델을 반복적으로 갱신함으로써 최적화한다. 이와 달리, 심층 신경망은 참 속도 모델과 예측한 속도 모델의 오차를 손실 함수로 정의하고, 손실 함수가 감소하는 방향으로 모델 매개변수를 반복적으로 갱신함으로써 신경망 가중치를 최적화한다. 따라서 완전 파형 역산은 초기 속도 모델이 필요하지만 심층 신경망 기법은 대량의 데이터 세트 및 적절한 신경망 설계가 필요하다.

본 논문에서는 손실 함수(loss function)를 정의하기 위해 평균 절대 오차(mean absolute error, MAE), 평균 제곱 오차(mean square error, MSE) 및 구조 유사성 지수(Structural Similarity Index, SSIM)을 도입하였다. 먼저 MAE는 다음과 같이 나타낼 수 있다.

(3)

L_{M A E} = \frac{1}{N} \sum_{i = 1}^{N} | {\bar{V}}^{i} - V^{i} |,

$V^{i}$ 는 i번째 참 속도 모델이며, ${\bar{V}}^{i}$ 는 i번째 예측된 속도 모델이다. 그리고 MSE는 다음과 같이 나타낼 수 있다.

(4)

L_{M S E} = \frac{1}{N} \sum_{i = 1}^{N} | {\bar{V}}^{i} - V^{i} |^{2},

이미지 재구성 문제에서 MAE 및 MSE은 대표적인 손실함수로 사용되지만 이러한 평가 지표들은 이미지의 각 위치를 개별적으로 처리하므로 이미지의 지역 구조 및 세부 사항을 포착하기 어렵다. 이러한 점을 고려하여 이미지의 지역 구조 및 세부 사항을 포착할 수 있는 SSIM을 도입하였다(Wang et al., 2004).

(5)

S S I M (x, y) = \frac{(2 μ_{x} μ_{y} + C_{1}) (2 σ_{x} y + C_{2})}{(μ_{x}^{2} + μ_{y}^{2} + C_{1}) (σ_{x}^{2} + σ_{y}^{2} + C_{2})},

여기서 $x$ 와 $y$ 는 각각 두 이미지 내의 윈도우(window)를 의미하고 $μ_{x}$ 와 $μ_{y}$ 는 $x$ 및 $y$ 윈도우의 국소 평균, $σ_{x}$ 와 $σ_{y}$ 는 표준편차, $σ_{x y}$ 는 $x$ 와 $x$ 의 교차 공분산을 나타낸다. 이 평가 지표는 추출한 두 이미지 윈도우 사이의 유사성을 측정한다. SSIM 값의 범위는 0부터 1까지이며 1에 가까울수록 유사성이 높다. SSIM의 경우 손실 함수 값이 감소하는 방향으로 모델 매개변수를 갱신하도록 다음과 같이 손실 함수를 정의하였다.

(6)

L_{s s i m} = 1 - \frac{1}{N} \sum_{i = 1}^{N} S S I M ({\bar{V}}_{x}^{i}, V_{y}^{i}),

최종 손실 함수는 다음과 같이 정의하였다(Zhang and Lin, 2020; Liu et al., 2021).

(7)

L_{s u m} = L_{M A E} + L_{M S E} + L_{s s i m},

깊이별 분리 합성곱

일반 합성곱과 깊이별 분리 합성곱(depthwise separable convolutions) 연산은 다음과 같다(Kaiser et al., 2017).

(8)

C o n v (W, y)_{(i, j)} = \sum_{k, l, m}^{K, L, M} W_{(k, l, m)} ․ y_{(i + k, j + l, m)},

(9)

P o i n t w i s e C o n v (W, y)_{(i, j)} = \sum_{m}^{M} W_{(m)} ․ y_{(i, j, m)},

(10)

D e p t h w i s e C o n v (W, y)_{(i, j)} = \sum_{k, l}^{K, L} W_{(k . l)} ⊙ y_{(i + k, j + l)},

(11)

S e p C o n v (W_{p}, W_{d}, y)_{(i, j)} = P o i n t w i s e C o n v_{(i, j)} (W_{p}, D e p t h w i s e C o n v_{(i, j)} (W_{d}, y)),

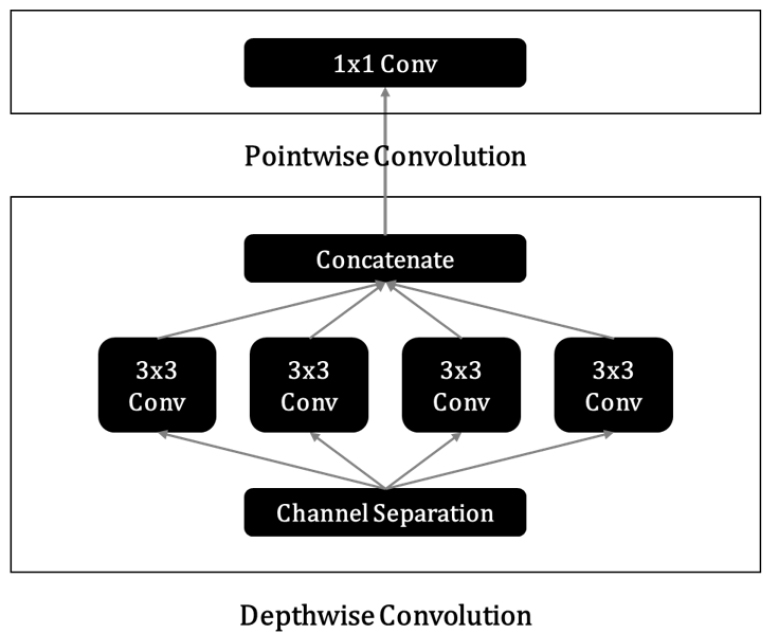
위 식에서 $W$ 는 가중치의 집합, $y$ 는 출력, $K$ 는 커널의 크기, $L$ 은 입력의 채널, $M$ 은 출력의 채널, $i$ 는 입력의 높이, $j$ 는 입력의 너비, $⊙$ 는 원소별 곱을 나타낸다. 식 (8)은 일반 합성곱, 식 (9)은 점별 합성곱, 식 (10)은 깊이별 합성곱, 식 (11)은 깊이별 분리 합성곱을 나타낸다. 식 (11)에서 볼 수 있듯이, 깊이별 분리 합성곱은 깊이별 합성곱 및 점별 합성곱의 조합이다. 이 연산은 먼저 입력 채널별로 공간 방향의 합성곱을 수행한 다음, 점별 합성곱을 통해 출력 채널을 합친다. 이를 통해 공간 방향 특성의 학습과 채널 방향 특성의 학습을 서로 분리하는 효과를 얻을 수 있다. 따라서 깊이별 분리 합성곱을 사용하면 일반 합성곱보다 모델 매개변수 수와 연산 횟수를 크게 줄여 효율적인 계산이 가능해진다. Fig. 1에 4개의 입력 채널을 가진 3 × 3 크기의 깊이별 분리 합성곱 연산 예시를 보였다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F1.jpg

Fig. 1.

Example of depthwise separable convolution operation with four input channels and 3 × 3 separable convolution. Depthwise separable convolutions comprise depthwise and pointwise convolutions.

Tomography_CNN

탄성파 탐사 자료로부터 바로 P파 속도 모델을 구축하기 위해 깊이별 분리 합성곱 신경망인 Tomography_CNN을 설계하였다. 이 신경망의 구조는 앞선 사례들(Yang and Ma, 2019; Wu and Lin, 2019; Wang and Ma 2020; Li et al., 2020; Liu et al., 2021)과 마찬가지로 인코더-디코더 구조를 따른다. 먼저 인코더는 탄성파 자료에 대한 효율적인 압축을 통해 추상적인 표현을 학습하면서 특성(features)을 추출할 수 있다. 그런 다음, 디코더가 추출된 특성으로부터 지표면 아래 속도 모델을 재구성한다.

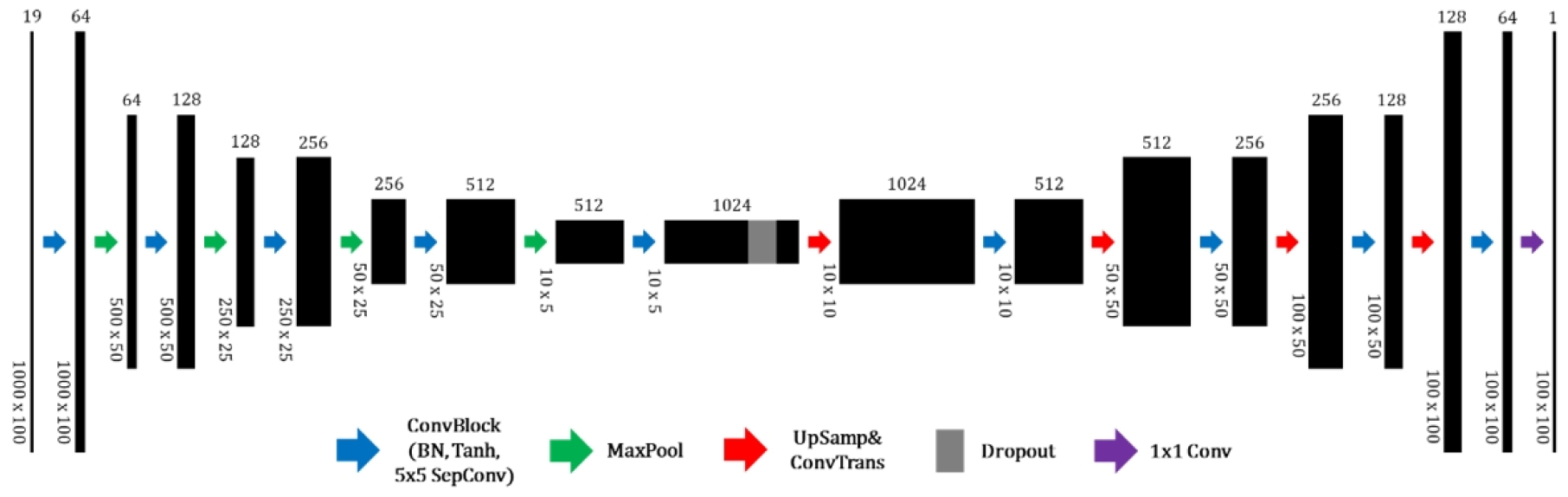
이 신경망의 구조를 자세히 살펴보면, 먼저 인코더의 경우 맥스풀링(maxpooling)을 통해 입력 자료 크기를 점차 감소시키면서 채널의 수를 64개, 128개, 256개, 512개, 1024개로 증가시킨다. 이는 자료를 압축함으로써 계산량을 줄이면서 동시에 유용한 특성을 최대한 많이 추출하기 위함이다. 인코더 마지막 층에는 무작위로 특성을 20% 만큼 버리는 드롭아웃(dropout)을 추가하였다. 디코더에서는 압축된 자료 크기를 최종적으로 속도 모델 크기가 되도록 점차 증가시키면서 채널의 수를 1024개, 512개, 256개, 128개, 64개로 감소시킨다. 이 때 전치 합성곱(transposed convolution) 및 업샘플링(upsampling)의 조합을 사용함으로써 체커보드 문제(checkerboard artifacts)를 완화하였다(Odena et al., 2016). 마지막 층에서는 1 × 1 크기의 커널을 가진 일반 합성곱 층을 통해 채널의 크기가 1인 속도 모델을 출력하도록 설계하였다.

이 신경망에는 총 9개의 합성곱 블록과 4개의 전치 합성곱 층이 사용되었으며, 각 합성곱 블록에는 5 × 5 크기의 깊이별 분리 합성곱 및 쌍곡탄젠트(hyperbolic tangent) 활성화 함수, 그리고 신경망의 입력과 출력의 분포를 일정하게 유지하도록 도와줌으로써 그래디언트 문제를 완화할 수 있는 배치 정규화(Loffe and Szegedy, 2015) 기법을 적용하였다. 하나의 블록 내에는 배치 정규화, 활성화 함수 및 합성곱 층을 배치하였으며 하나의 블록마다 총 세 번의 합성곱 연산을 수행하도록 설계하였다. 신경망의 가중치 초기화는 쌍곡탄젠트 활성화 함수에 적합하다고 알려진 Xavier Glorot 초기화를 사용하였다(Glorot and Bengio, 2010).

탄성파 속도 모델 구축 문제는 일반적인 의미 분할(semantic segmentation) 문제에 활용되는 이미지 간 번역(translation) 모델과 달리 입력 이미지와 출력 이미지의 영역이 서로 다르다. 속도 모델 구축의 경우 탄성파 자료 영역에서 속도 모델 영역으로 영역 변환을 수행해야 하며 입력과 출력 이미지 크기가 서로 다르다. 따라서 신경망을 입력 및 출력 이미지 크기에 맞게 유연하게 구축할 수 있도록 설계할 필요가 있다. 이러한 점을 고려하여, 입력 이미지의 크기를 10 × 5까지 압축함으로써 입력 이미지 크기와 출력 이미지 크기가 서로 다르더라도 사용할 수 있도록 신경망을 설계하였다. 맥스풀링과 업샘플링의 매개변수만 조정하면 입력 또는 출력 이미지 크기가 변경되어도 그에 맞춰 신경망을 사용할 수 있다. Tomography_CNN의 구조는 Fig. 2에서 볼 수 있으며, 같은 신경망 구조에서 깊이별 분리 합성곱을 일반 합성곱으로 대체한 심층 신경망을 Tomography_nCNN이라고 명명하였다. 일반 합성곱으로 구축한 Tomography_ nCNN의 총 모델 매개변수 수는 134,653,351개이지만 깊이별 분리 합성곱으로 구축한 Tomography_CNN의 총 모델 매개변수 수는 17,674,261개이다. 이러한 감소 정도는 합성곱의 커널 크기, 합성곱 층의 개수 등에 따라 달라질 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F2.jpg

Fig. 2.

Architecture of Tomography_CNN. ConvBlock performs three convolution operations, i.e., batch normalization, hyperbolic tangent activation, and depthwise separable convolutions.

합성 데이터 생성

심층 신경망의 성능에 큰 영향을 미치는 요인 중 하나는 훈련 데이터 세트의 양과 품질이다. 이상적으로는 대량의 실제 탄성파 탐사 자료를 가지고 신경망을 훈련할 경우 최고의 성능을 발휘할 수 있다. 그러나 실제 탐사 자료를 대량으로 얻는 것은 한계가 있으며, 수동으로 레이블링을 수행할 경우 시간도 오래 걸릴 뿐 아니라 부정확한 레이블을 신경망에 주입할 수 있는 위험이 있다. 이는 매우 비효율적이며 훈련 데이터의 품질도 보장할 수 없다. 따라서 다양한 지질학적 특징을 포함하는 합성 속도 모델을 직접 생성하였으며, 인공 수치 모델링을 통해 그에 해당하는 시간 영역 파동장을 얻음으로써 훈련 데이터 세트를 구축하였다. 본 연구에서는 균일한 밀도를 가진 등방성 2차원 속도 모델에 초점을 맞추었으며 시간 영역 파동장은 2차원 음향파 파동 방정식을 이용해 생성하였다.

탄성파 속도 모델

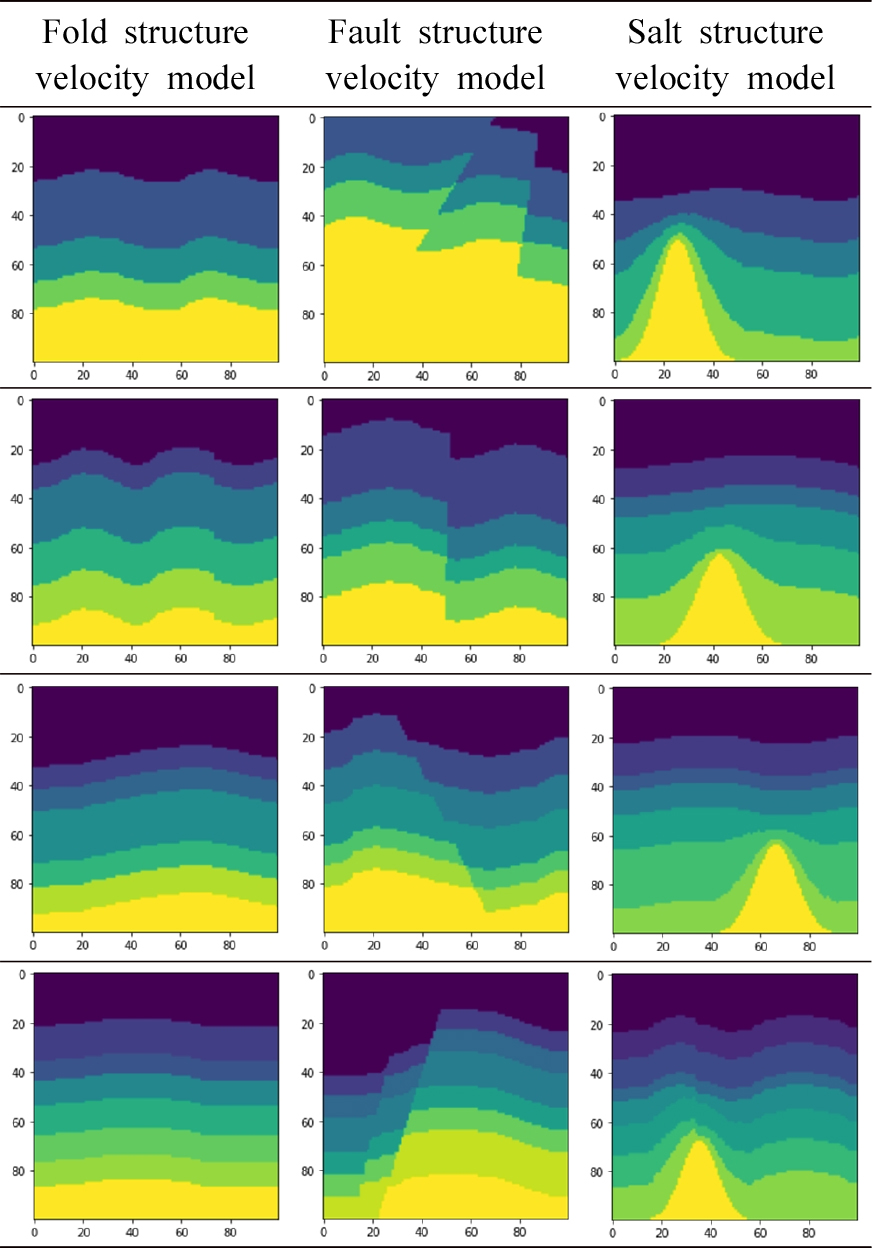
합성 속도 모델에 최대한 다양한 지질학적 특징을 포함하기 위해 습곡, 단층 및 암염 구조 모델을 가지는 총 12개의 클래스를 가진 합성 데이터 세트를 생성하였다. 각 구조 모델마다 4 ~ 7개의 경계면을 가지며 각 클래스마다 3,000개의 속도 모델을 포함하도록 설계하였다. 총 36,000개의 인공 속도 모델을 생성하였으며 속도 모델의 층 수는 5 ~ 8개가 된다. 습곡 구조 모델의 경우 코사인 함수를 사용하여 층 인터페이스의 굴곡을 무작위로 생성하도록 설계하였으며 단층 및 암염 구조 모델은 생성된 습곡 구조 모델을 기반으로 단층을 추가하거나 암염을 추가하였다. 단층면은 평면으로 가정하여 한 개 또는 두 개의 단층을 임의의 위치와 기울기를 가지도록 추가하였으며 암염의 모양은 가우스 함수를 사용하여 정의한 뒤, 모델 하부로부터 상부층을 위로 밀어내는 형태로 임의의 위치에서 생성하도록 설계하였다. Fig. 3에 생성된 인공 속도 모델의 예시를 보였다. 모든 속도 모델은 격자 간격이 10 m로, 너비가 1 km, 깊이가 1 km인 100 × 100 크기의 격자를 가진다. 배경 속도 값은 층이 깊어질수록 1.5 km/s에서 최대 4 km/s 까지 증가하며 속도 모델을 생성할 때마다 해저 층 속도에 무작위로 변동을 주었다. 암염에서의 P파 속도는 4.5 km/s이다. 서로 인접한 경계면은 최소 8개의 격자 이상 떨어져 있으며 인접한 층 사이의 속도 차이는 최소 300 m/s이상이 되도록 설정하였다. 출력 데이터로 사용되는 속도 모델의 크기는 1 × 100 × 100 (속도 모델 채널 × 너비 격자 개수 × 깊이 격자 개수)이 된다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F3.jpg

Fig. 3.

Examples of velocity models in training data; 36,000 synthetic velocity models can be classified into 12 classes, and each class contains 3,000 velocity models.

시간 영역 파동장

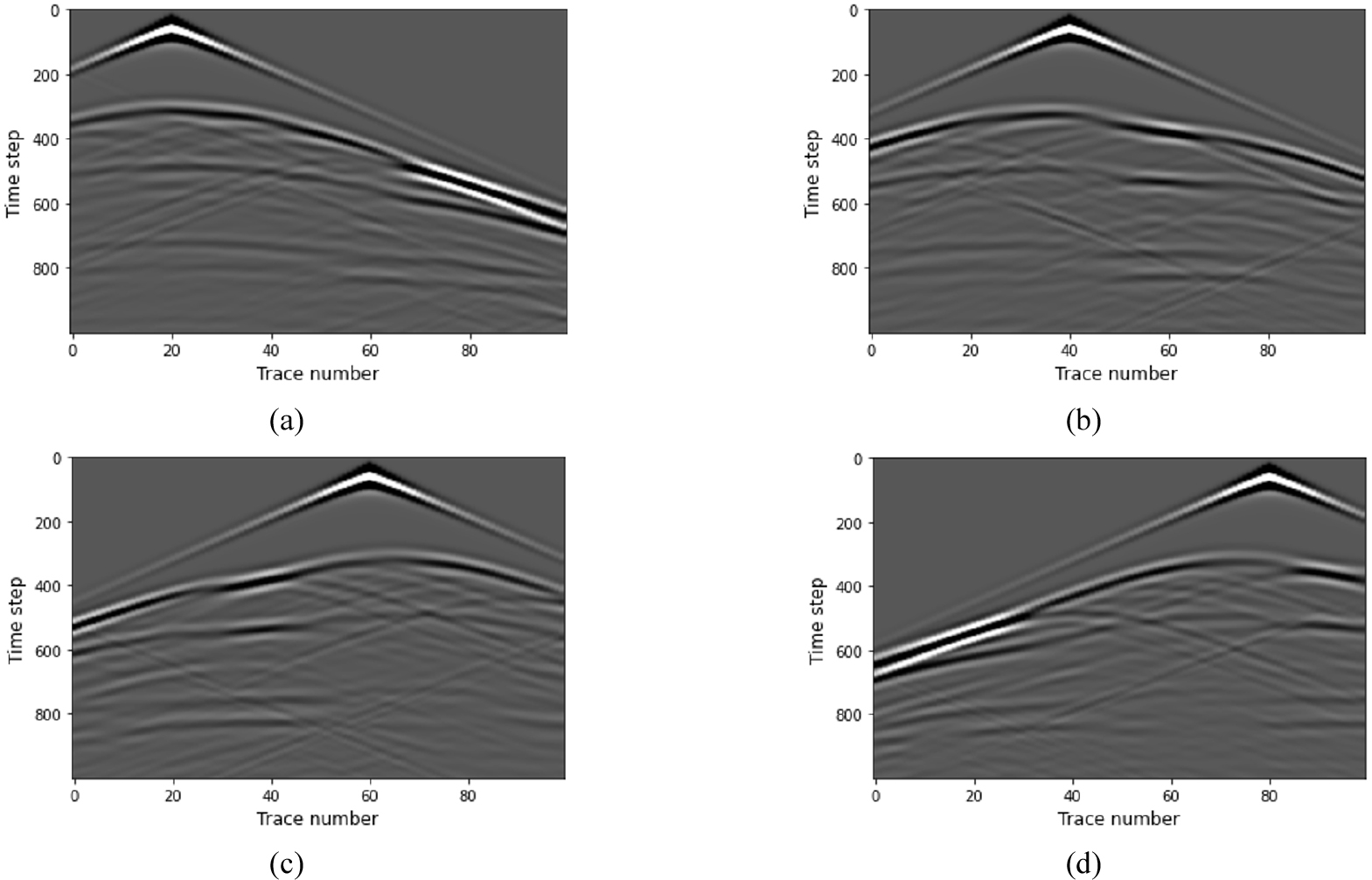
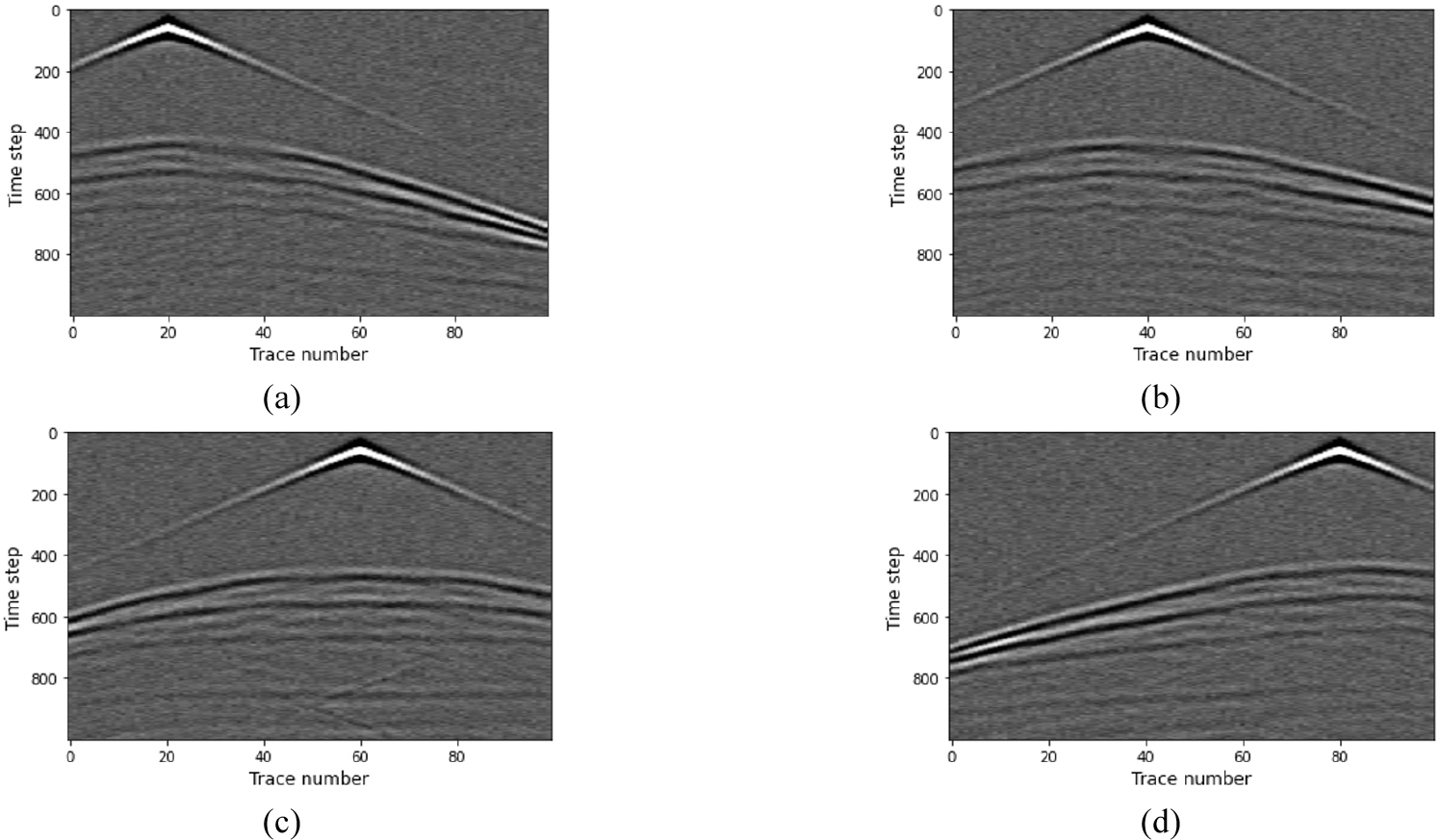
시간 영역 파동장은 식 (1)을 이용해 시간 2차 공간 8차 유한 차분법을 사용하여 계산하였다. 총 기록 시간은 1 s, 샘플링 간격은 1 ms, 송신원 파형은 최대 주파수가 40 Hz인 리커 파형(Ricker wavelet), 경계 조건은 Keys 경계 조건(Keys, 1985)이다. 인공 수치 모델링을 수행한 결과는 Fig. 4에 나타내었다. 하나의 속도 모델마다 50 m 간격으로 19개의 공통송신원모음을 생성하였으며 지표면의 수신기는 10 m간격으로 배치하였다. 따라서 시간 영역 파동장을 사용하는 입력 데이터의 크기는 19 × 1,000 × 100(송신원 개수 × 시간 샘플 개수 × 수신기 개수)이 된다. 각 입력 채널에 각각의 공통송신원모음을 할당하였고, 각각의 공통송신원모음은 서로 독립적이므로 각 채널별로 공간 합성곱을 수행하는 깊이별 분리 합성곱이 적절할 것이라 예상할 수 있다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F4.jpg

Fig. 4.

Example of shot gathers excited at offsets of (a) 200 m, (b) 400 m, (c) 600 m, and (d) 800 m.

신경망 훈련

본 절에서는 Tomography_CNN과 Tomography_nCNN의 훈련 조건 및 하이퍼파라미터(hyper-parameter)에 대해 설명한다. 깊이별 분리 합성곱으로 구축한 신경망과 일반 합성곱으로 구축한 신경망의 비교 분석을 위해 합성 데이터 세트 및 하이퍼파라미터는 서로 동일하게 설정하였다. 동일한 합성 데이터 세트를 각각 훈련 데이터 세트에 80%, 검증 데이터 세트에 10%, 테스트 데이터 세트에 10%만큼 균등하게 할당함으로써 신경망이 특정 유형의 속도 모델에 대해서만 훈련되지 않도록 분배하였다. 신경망에 주입될 훈련 데이터 세트는 28,800쌍, 검증 및 테스트 데이터 세트는 각각 3,600쌍이 되며, 시간 영역 파동장에 표준화를 적용하여 입력 데이터 분포를 평균 0, 표준 편차 1의 값을 갖도록 조정하였다. 하이퍼파라미터의 경우 초기 학습률이 0.0005인 아담(Adam) 옵티마이저(Kingma and Ba, 2015)를 사용하였으며, 배치 크기는 20으로 총 50번의 에포크(epochs)를 가지고 두 신경망을 훈련하였다. 모든 에포크 중 가장 낮은 검증 손실을 가진 모델을 저장하였으며 에포크가 진행될 때마다 학습률을 3%씩 감소시키는 학습률 스케줄러를 사용하였다. 실험은 Nvidia Geforce RTX 3090 GPU 한 장을 이용해 수행하였으며 심층 학습에 사용된 코드는 PyTorch 1.8.1 버전 환경에서 실행하였다.

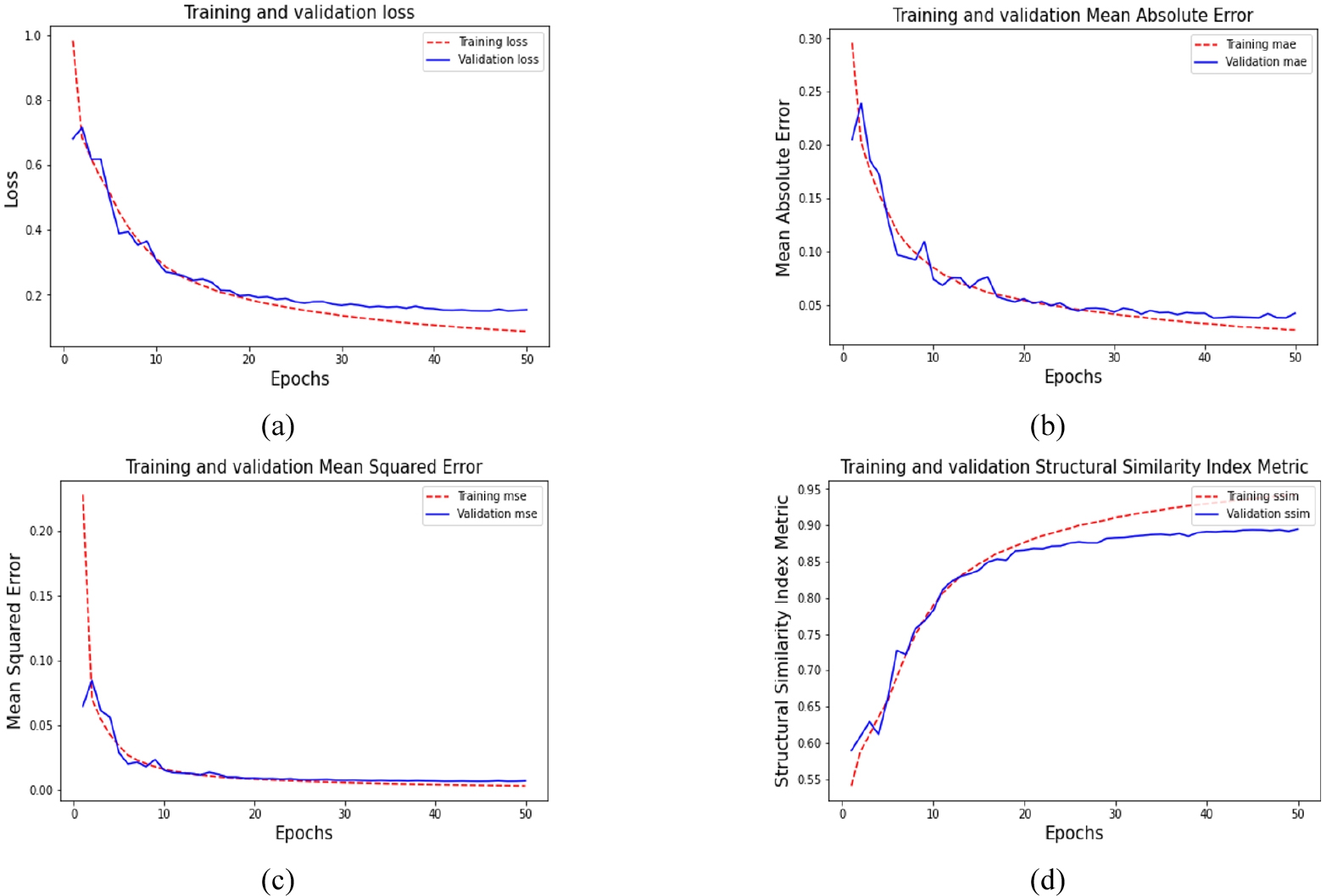
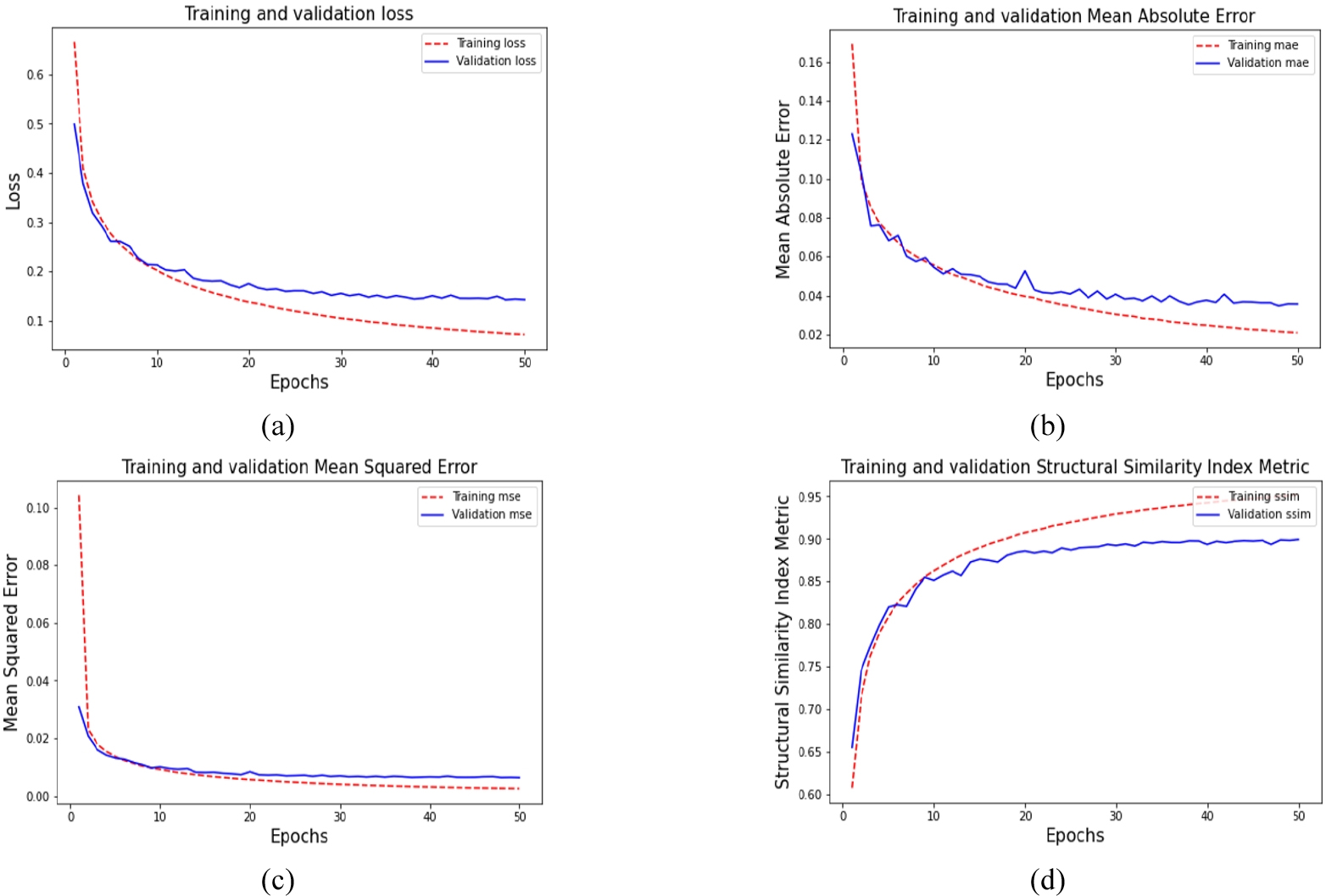
신경망 훈련 결과, 일반 합성곱을 사용한 Tomography_ nCNN의 훈련 시간은 에포크 당 약 20분 7초가 소요되었다. 훈련 및 검증 손실 함수 그래프는 Fig. 5(a)에 나타내었다. 훈련 및 검증 MAE, MSE, SSIM 그래프는 각각 Fig. 5(b), (c), (d)에 나타내었다. 가장 낮은 검증 손실을 가진 모델을 저장하였고, 해당 손실 및 정량적 평가 지표 값들은 Table 1에 정리하였다. 이에 반해, 깊이별 분리 합성곱을 사용한 Tomography_CNN의 훈련 시간은 에포크 당 약 8분 33초가 소요되었다. 훈련 손실은 Tomography_nCNN의 결과보다 약간 더 작은 값으로 수렴하였으며 해당 손실 함수 그래프는 Fig. 6에 나타내었다. 가장 낮은 검증 손실을 가진 모델을 저장하였으며, 해당 손실 및 정량적 평가 지표 값들은 Table 2에 정리하였다. 깊이별 분리 합성곱을 이용한 경우 일반 합성곱을 사용한 경우에 비해 훈련 시간은 절반 이하이고 최종 손실 값도 더 작은 것을 알 수 있다. 깊이별 분리 합성곱을 사용하면 총 모델 매개변수 수가 134,653,351개에서 17,674,261개로 감소하여 신경망의 수용력(capacity)이 나빠질 수 있다고 생각할 수도 있지만, 일반 합성곱보다 모델 매개변수를 더 효율적으로 사용하기 때문에 일반적으로 유사한 결과를 얻을 수 있다(Chollet, 2017a).

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F5.jpg

Fig. 5.

Training and validation loss curves of Tomography_nCNN with regular convolutions: (a) loss, (b) mean absolute error, (c) mean squared error, and (d) structural similarity index.

Table 1.

Results of Tomography_nCNN with regular convolutions after training

Train loss	0.0905	Validation loss	0.1506
Train MAE	0.0273	Validation MAE	0.0378
Train MSE	0.0034	Validation MSE	0.0066
Train SSIM	0.9401	Validation SSIM	0.8938

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F6.jpg

Fig. 6.

Training and validation curves of Tomography_CNN with depthwise separable convolutions: (a) loss, (b) mean absolute error, (c) mean squared error, and (d) structural similarity index.

Table 2.

Results of Tomography_CNN with depthwise separable convolutions after training

Train loss	0.0738	Validation loss	0.1423
Train MAE	0.0215	Validation MAE	0.0347
Train MSE	0.0026	Validation MSE	0.0064
Train SSIM	0.9503	Validation SSIM	0.8988

결 과

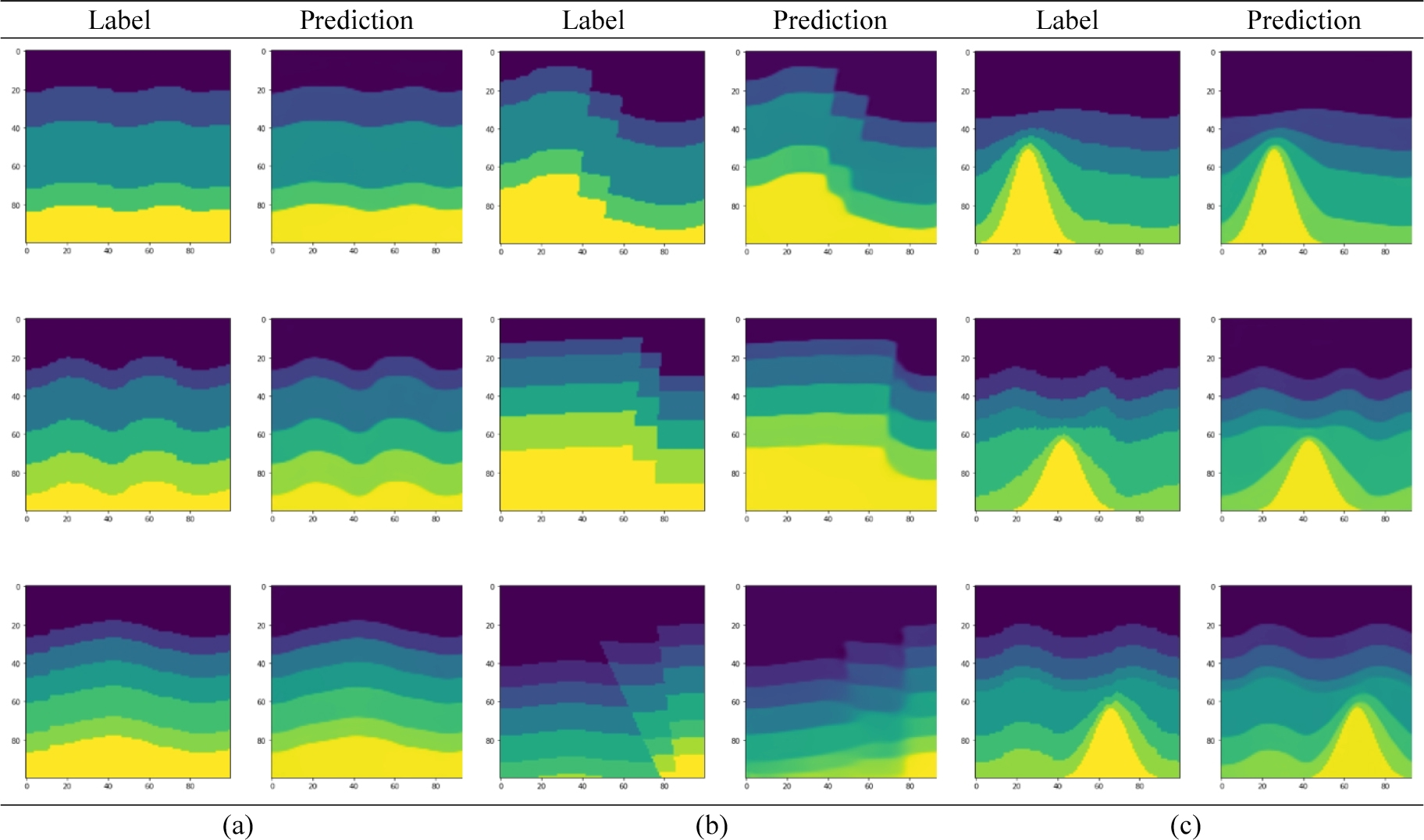
훈련된 두 신경망 중 먼저 일반 합성곱을 이용한 Tomography_nCNN을 사용하여 테스트 데이터 세트에서 속도 모델을 예측하였다. 테스트 손실은 0.1524가 나왔으며, 테스트 MAE는 0.0383, MSE는 0.0068, SSIM은 0.8927가 나왔다. 예측한 속도 모델은 Fig. 7에 제시하였다. 그림에서 참 속도 모델과 유사한 예측 결과를 볼 수 있다. 층의 개수 및 인터페이스 형태, 암염의 위치 및 형태 등은 정확하지만 상대적으로 매끄럽게 구축하는 것을 확인할 수 있었다. 이는 참 속도 모델은 불연속적인 값으로 할당되어 있는 반면에 신경망은 연속적인 값으로 예측하기 때문이다. 단층의 경우 신경망이 다소 흐릿하게 예측하는 것을 볼 수 있는데, 이 부분은 단층을 포함한 훈련 데이터 쌍을 증가시키거나 심층 신경망 설계를 개선할 필요가 있어 보인다. 테스트 데이터에서 하나의 속도 모델을 예측하는 시간은 약 11 ms가 걸렸다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F7.jpg

Fig. 7.

Prediction results of test data: left column, label; right column, prediction by Tomography_nCNN with regular convolutions. Velocity models with (a) fold, (b) fault, and (c) salt structures.

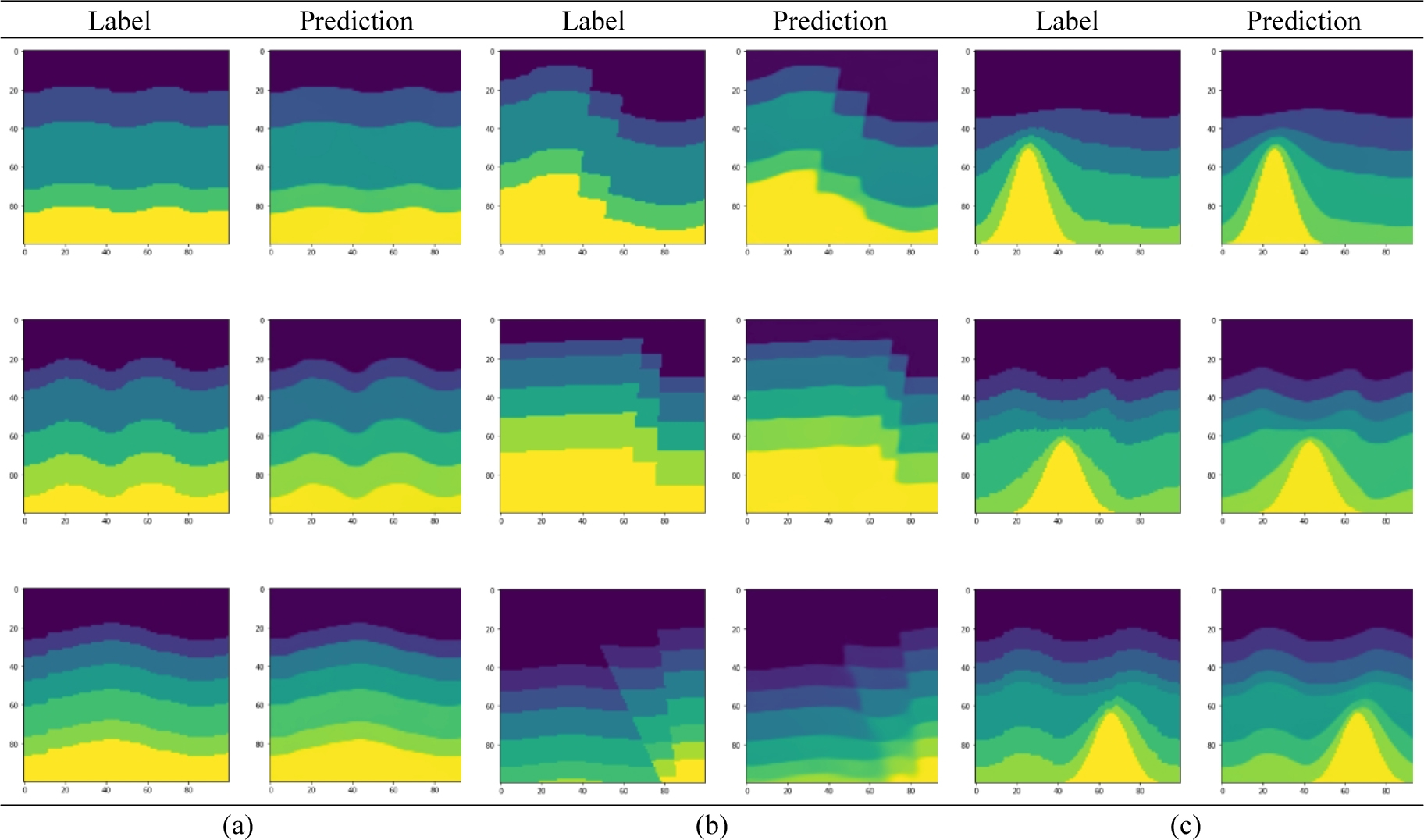
다음으로, 깊이별 분리 합성곱을 사용한 Tomography_ CNN을 가지고 테스트 데이터 세트에서 속도 모델을 예측하였다. 그 결과, 테스트 손실은 0.1437로 상대적으로 더 작은 값을 보여주었으며 테스트 MAE는 0.0351, MSE는 0.0065, SSIM은 0.8979가 나왔다. 예측한 속도 모델은 Fig. 8에서 볼 수 있다. 일부 단층 예측 결과가 향상된 것을 볼 수 있지만 전체적으로 결과에 큰 차이는 없었다. 테스트 데이터에서 하나의 속도 모델을 예측하는 시간은 약 7 ms가 걸렸다. 두 신경망의 테스트 손실 및 정량적 평가 지표 값들은 Table 3에 함께 정리하였다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F8.jpg

Fig. 8.

Prediction results of test data: left column, label; right column, prediction by Tomography_CNN with depthwise separable convolutions. Velocity models with (a) fold, (b) fault, and (c) salt structures.

Table 3.

Results of Tomography_nCNN and Tomography_CNN from test dataset.

Tomography_nCNN		Tomography_CNN
Test loss	0.1524	Test loss	0.1437
Test MAE	0.0383	Test MAE	0.0351
Test MSE	0.0068	Test MSE	0.0065
Test SSIM	0.8927	Test SSIM	0.8979

잡음 예제

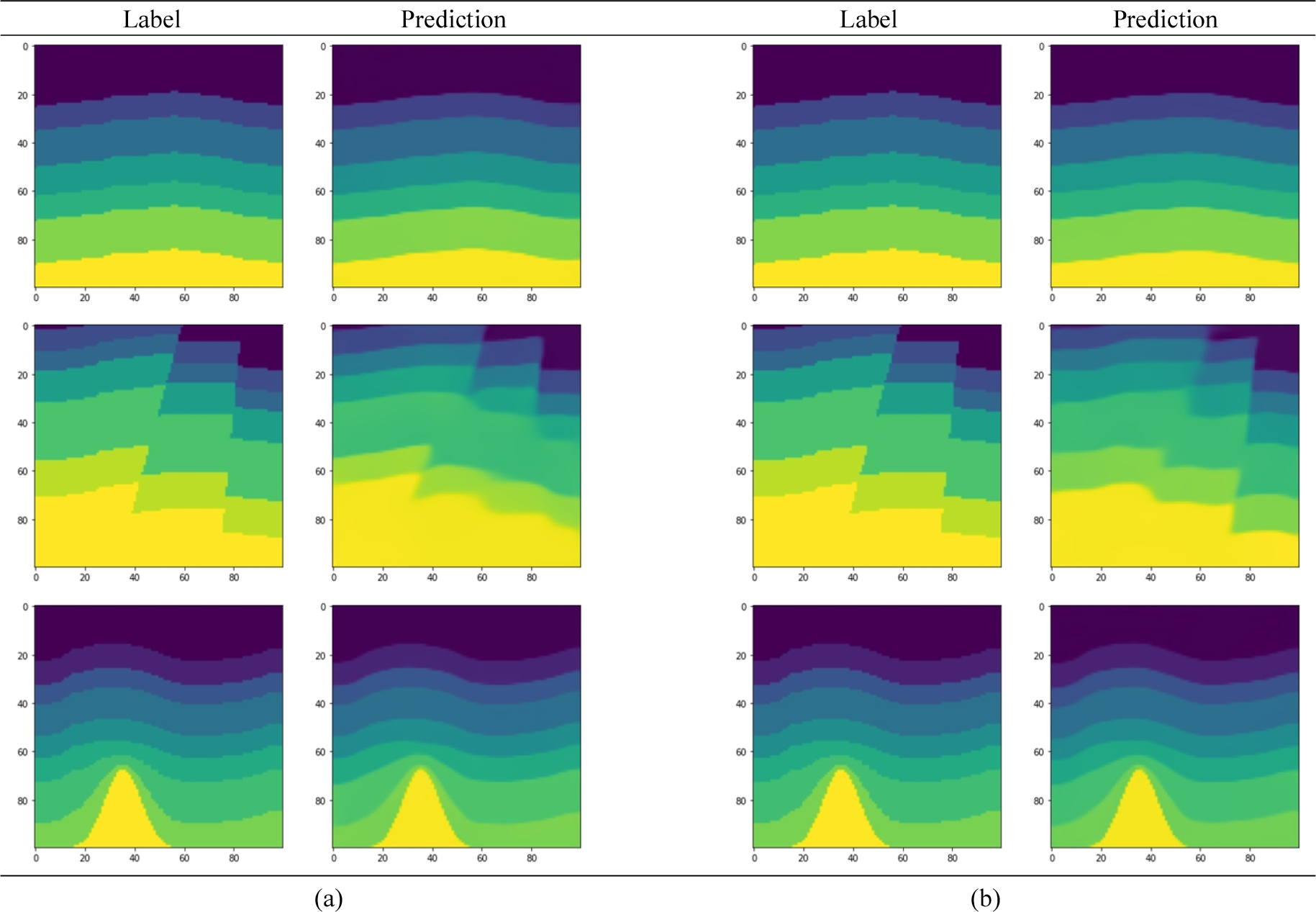
앞의 테스트는 모두 인공 합성 자료를 이용해 수행한 것으로, 실제 자료에 포함된 잡음의 영향이 배제되어 있다. 신경망의 잡음에 대한 견고성을 검증하기 위해 잡음이 포함된 자료에 대한 실험을 전이학습(transfer learning)을 이용해 수행하였다. 먼저 속도 모델의 경우 3.1절에서 설명한 내용과 같은 조건을 가지고 총 3,600개를 생성하였으며, 이에 해당하는 시간 영역 파동장은 3.2절의 조건에 따라 생성하였다. 이를 통해 생성한 시간 영역 파동장에 신호대 잡음비(signal to noise ratio)가 5인 무작위 잡음을 추가하였다(Fig. 9). 전이 학습을 위한 훈련 데이터 세트는 2,880쌍, 검증 및 테스트 데이터 세트는 각각 360쌍으로 나눴으며, 잡음이 있는 시간 영역 파동장에 표준화를 적용하였다. 초기 학습률만 5×10^-5로 수정하였으며 나머지 하이퍼파라미터는 잡음이 없는 경우와 같은 값을 가지고 전이 학습을 수행하였다. 훈련이 끝난 뒤, 테스트 데이터 세트에서 속도 모델을 예측한 두 신경망의 결과는 Fig. 10에 나란히 제시하였다. Fig. 10에서 볼 수 있듯이 두 신경망 모두 무작위 잡음에 대해 학습을 성공적으로 한 것을 확인할 수 있으며, 잡음이 없는 경우보다는 정확도가 약간 떨어지는 결과를 얻을 수 있었다. 일반 합성곱을 사용한 Tomography_nCNN의 경우 테스트 손실은 0.1644가 나왔으며, 테스트 MAE는 0.0392, MSE는 0.0073, SSIM은 0.8821가 나왔다. 깊이별 분리 합성곱을 사용한 Tomography_CNN의 경우 테스트 손실이 0.1605, 테스트 MAE는 0.0379, MSE는 0.0071, SSIM은 0.8845가 나왔다. 해당 테스트 손실 및 정량적 평가 지표 값들은 Table 4에 함께 정리하였다.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F9.jpg

Fig. 9.

Example of noisy shot gathers excited at offsets of (a) 200 m, (b) 400 m, (c) 600 m, and (d) 800 m. Noisy data with SNR (signal to noise ratio) is approximately 5 dB.

https://static.apub.kr/journalsite/sites/ksmer/2022-059-02/N0330590203/images/ksmer_59_02_03_F10.jpg

Fig. 10.

Prediction results of noisy test data: left column, label; right column, prediction by (a) Tomography_nCNN with regular convolutions and (b) Tomography_CNN with depthwise separable convolutions.

Table 4.

Results of Tomography_nCNN and Tomography_CNN from noisy test dataset.

Tomography_nCNN		Tomography_CNN
Test loss	0.1644	Test loss	0.1605
Test MAE	0.0392	Test MAE	0.0379
Test MSE	0.0073	Test MSE	0.0071
Test SSIM	0.8821	Test SSIM	0.8845

토 의

훈련된 심층 신경망을 이용한 속도 모델 구축의 경우 기존의 역산 방법들과 달리 사전 지식이나 지구물리학적 모델을 사용할 필요가 없다. 부정확한 초기 속도 모델로 인한 지역 최소값(local minima) 수렴 문제도 없으며 일단 신경망 훈련만 완료되면 하나의 속도 모델을 예측하는 비용은 무시할 수 있다. 이러한 장점에도 불구하고 신경망 훈련 비용은 훈련 데이터 세트의 크기 및 모델 매개변수 수에 크게 영향을 받게 되므로 훈련 비용 또한 심층 학습시 중요하게 고려해야 할 부분이다. 본 연구에서 깊이별 분리 합성곱으로 구축한 신경망이 일반 합성곱으로 구축한 신경망보다 훈련 비용을 절약할 뿐 아니라 테스트 데이터에서도 유사한 성능을 보여주었다. 탄성파 이미지는 RGB 채널을 가지는 자연 이미지와 달리 입력 채널(송신원 개수)별로 독립적이다. 따라서 일반 합성곱보다 입력 채널 별로 공간 방향의 합성곱을 수행하는 깊이별 분리 합성곱의 사용이 합리적이며, Chollet(2017b) 또한 입력 이미지가 공간상의 위치는 상관관계가 크지만 채널 별로는 매우 독립적인 경우 깊이별 분리 합성곱을 사용하는 것이 타당하다고 언급하였다.

잡음 예제의 경우 상대적으로 적은 양의 데이터를 가지고도 전이 학습을 통해 성공적으로 잡음을 학습할 수 있음을 보여주었다. 그러나, 예측 결과로부터 잡음이 신경망 성능에 영향을 미치는 것을 알 수 있었으며 앞으로 잡음에 대한 민감도 연구가 필요하다.

심층 신경망 훈련에 사용되는 합성 속도 모델은 실제 속도 모델보다 단순하고 지질학적 특징이 덜 풍부하다는 단점이 있다. 예를 들어, 본 연구에 사용한 인공 속도 모델은 균일한 밀도를 가진 등방성 2차원 속도 모델로 한정하였으며 해당 시간 영역 파동장은 음향파 파동 방정식에 기반하여 생성하였다. 실제 자료는 3차원이며 이방성 및 밀도 등 매질의 여러 가지 물성도 영향을 미친다. 본 연구에 사용한 속도 모델은 최대 2개의 단층만 포함하며 층 인터페이스 구조 및 암염 형태도 제한적이다. 그럼에도 불구하고 지도 학습 방식으로 훈련되는 신경망의 특징을 고려하면 인공 합성 자료는 자동으로 대량 생성할 수 있다는 장점이 있다. 따라서 앞으로 실제 지질 구조와 더 유사한 인공 속도 모델을 생성하는 방법을 고안하는 것이 중요하다.

본 연구에서 훈련된 신경망을 현장 자료에 바로 적용하기에는 아직 해결해야 할 부분이 많다. 먼저 훈련에 사용한 인공 속도 모델은 1 km × 1 km 크기를 가진다. 현장 자료의 크기를 가지는 합성 속도 모델을 가지고 시간 영역 파동장을 생성하는 경우, 송신원 개수, 기록 시간 및 샘플링 간격 등에 따라 입력 데이터의 크기가 상당히 증가하게 된다. 이는 대량의 데이터를 가지고 훈련하는 심층 학습에 큰 제약이 된다. 따라서 시간 영역 파동장이 아닌 다른 형태의 탄성파 자료를 입력으로 사용하는 방법도 고려해 볼 필요가 있다. 또한, 현장 자료에서의 송수신기 배열 정보도 중요한데 본 연구에서는 수신기 배열을 고정하고 신경망을 훈련하였으므로 해당 정보는 학습되지 않았다. 앞으로는 송수신기 배열 정보가 포함된 훈련 데이터 세트 준비 및 해당 정보를 학습할 수 있는 신경망 구조 설계가 필요하다.

본 연구에서는 비교를 위해 한 장의 GPU 카드만 이용해 신경망 훈련을 수행한 경우의 시간을 제시하였는데, 여러 장의 GPU 카드를 이용해 병렬로 훈련을 수행하면 더 빠르게 신경망을 훈련시킬 수 있다. 컴퓨터 하드웨어 성능은 나날이 발전하고 있으므로 향후 같은 심층 신경망도 더 빠른 GPU와 더 많은 데이터를 이용해 훈련하여 성능을 향상시킬 수 있을 것이다. 본 연구에서는 기존 연구들과 마찬가지로 2차원 속도 모델 구축 문제만 다루었는데, 이는 대량의 3차원 속도 모델을 가지고 신경망을 훈련하기에는 아직 GPU 성능이 부족하기 때문이다. 3차원 적용은 앞으로 수년 내에 가능할 것으로 보이며, 이를 위해서는 2차원 문제에 대한 연구를 먼저 수행할 필요가 있다.

결 론

속도 모델을 얻는 기존 역산 방법들은 하나의 속도 모델을 예측하는 데 계산 시간이 오래 걸리며 초기 속도 모델에 따라 역산이 실패할 수 있다는 단점이 있다. 심층 신경망 기법을 이용한 속도 모델 구축은 초기 속도 모델을 필요로 하지 않으며, 훈련이 완료되면 하나의 속도 모델을 예측하는 비용은 무시할 수 있다. 본 연구에서는 탄성파 속도 모델 구축을 위해 깊이별 분리 합성곱을 사용하고 인코더-디코더 구조를 가진 Tomography_CNN을 제안하였다. 일반 합성곱을 사용한 경우와 달리 깊이별 분리 합성곱을 사용한 결과, 출력 속도 모델의 품질을 유지하면서도 총 매개변수 수를 크게 줄임으로써 신경망 훈련 비용을 감소시킬 수 있었다. 추후 연구에서 심층 학습을 이용한 탄성파 속도 모델 구축 기법의 현장 자료 적용을 위해서는 더 많고 다양한 훈련 자료 및 그에 따른 대량의 연산이 필요한데, 깊이별 분리 합성곱을 이용해 훈련 시간을 단축시킬 수 있을 것이다. 단, 심층 신경망을 현장 자료에 적용하기 위해서는 송수신기 배열 변화, 잡음 민감도, 복잡한 훈련 속도 모델, 현장 자료 크기의 훈련 데이터 등 실제 자료의 특징을 고려한 추가 연구를 수행할 필요가 있다.

Acknowledgements

이 성과는 2021년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2021R1F1A1064432).

References

Baysal, E., Kosloff, D.D., and Sherwood, W.C., 1983. Reverse time migration, Geophysics, 48, p.1514-1524. 10.1190/1.1441434

Bunks, C., Saleck, F.M., Zaleski, S., and Chavent, G., 1995. Multiscale seismic waveform inversion, Geophysics, 60, p.1457-1473. 10.1190/1.1443880

Chollet, F., 2017a. Xception: Deep learning with depthwise separable convolutions, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, p.1251-1258. 10.1109/CVPR.2017.195

Chollet, F., 2017b. Deep Learning with Python, Manning, New York, USA, p.261-263.

Gauthier, O., Virieux, J., and Tarantola, A., 1986. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results, Geophysics, 51, p.1387-1403. 10.1190/1.1442188

Glorot, X. and Bengio, Y., 2010. Understanding the difficulty of training deep feedforward neural networks, Proceedings of Machine Learning Research, 9, p.249-256.

Hornik, K., Stinchcombe, M., and White, H., 1990. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks, Neural Networks, 3, p.551-560. 10.1016/0893-6080(90)90005-6

Kaiser, L., Gomez, A.N., and Chollet, F., 2017. Depthwise separable convolutions for neural machine translation, Computation and Language, arXiv:1706.03059v2.

Keys, R.G., 1985. Absorbing boundary conditions for acoustic media, Geophysics, 50, p.892-902. 10.1190/1.1441969

Kingma, D.P. and Ba, J., 2015. Adam: A method for stochastic optimization, 3rd International Conference on Learning Representations, p.1-15.

Li, S., Liu, B., Ren, Y., Chen, Y., Yang, S., Wang, Y., and Jiang, P., 2020. Deep-learning inversion of seismic data, IEEE Transactions on Geoscience and Remote Sensing, 58, p.2135-2149. 10.1109/TGRS.2019.2953473

Liu, B., Yang, S., Ren, Y., Xu, X., Jiang, P., and Chen., Y., 2021. Deep-learning seismic full-waveform inversion for realistic structural models, Geophysics, 86, p.R31-R44. 10.1190/geo2019-0435.1

Loffe, S. and Szegedy, C., 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift, Proceedings of the 32nd International Conference on Machine Learning, 37, p.448-456.

Mora, P., 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data, Geophysics, 52, p.1211-1228. 10.1190/1.1442384

Odena, A., Dumoulin, V., and Olah, C., 2016. Deconvolution and checkerboard artifacts. Distill, 1(10), e3. 10.23915/distill.00003

Pratt, R.G. and Worthington, M.H., 1990. Inverse theory applied to multi-source cross-hole tomography. Part 1: acoustic wave-equation method, Geophysical Prospecting, 38, p.287-310. 10.1111/j.1365-2478.1990.tb01846.x

Pratt, R.G., Shin, C., and Hicks, G.J., 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion, Geophysical Journal International, 133, p.341-362. 10.1046/j.1365-246X.1998.00498.x

Shin, C. and Cha, Y., 2008. Waveform inversion in the Laplace domain, Geophysical Journal International, 173, p.922-931. 10.1111/j.1365-246X.2008.03768.x

Tarantola, A., 1984. Inversion of seismic reflection data in the acoustic approximation, Geophysics, 49, p.1259-1266. 10.1190/1.1441754

Virieux, J. and Operto, S., 2009. An overview of full-waveform inversion in exploration geophysics, Geophysics, 74, p.WCC1-WCC26. 10.1190/1.3238367

Wang, W. and Ma, J., 2020. Velocity model building in a crosswell acquisition geometry with image-trained artificial neural networks, Geophysics, 85, p.U31-U46. 10.1190/geo2018-0591.1

Wang, Z., Bovik, A.C., Sheikh, H.R., and Simoncelli, E.P., 2004. Image quality assessment: from error visibility to structural similarity, IEEE Transactions on Image Processing, 13, p.600-612. 10.1109/TIP.2003.81986115376593

Wu, Y. and Lin, Y., 2019. InversionNet: A real-time and accurate full waveform inversion with CNNs and continuous CRFs, Signal Processing, arXiv:1811.07875v2.

Yang, F. and Ma, J., 2019. Deep-learning inversion: A next-generation seismic velocity model building method, Geophysics, 84, p.R583-R599. 10.1190/geo2018-0249.1

Zhang, J., Brink, U.S., and Toksoz, M.N., 1998. Nonlinear refraction and reflection travel time tomography, Journal of Geophysical Research Solid Earth, 103, p.29743-29757. 10.1029/98JB01981

Zhang, Z. and Lin, Y., 2020. Data-driven seismic waveform inversion: A study on the robustness and generalization, IEEE Transactions on Geoscience and Remote Sensing, 58, p.6900-6913. 10.1109/TGRS.2020.2977635

Journal of the Korean Society of Mineral and Energy Resources Engineers ISSN:2288-0291(Print) 2288-2790(Online) 한국자원공학회지

Preview

Seismic Velocity Modeling Building Using Depthwise Separable Convolutional Neural Network

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Fig. 1.

Example of depthwise separable convolution operation with four input channels and 3 × 3 separable convolution. Depthwise separable convolutions comprise depthwise and pointwise convolutions.

Fig. 2.

Architecture of Tomography_CNN. ConvBlock performs three convolution operations, i.e., batch normalization, hyperbolic tangent activation, and depthwise separable convolutions.

Fig. 3.

Examples of velocity models in training data; 36,000 synthetic velocity models can be classified into 12 classes, and each class contains 3,000 velocity models.

Fig. 4.

Example of shot gathers excited at offsets of (a) 200 m, (b) 400 m, (c) 600 m, and (d) 800 m.

Fig. 5.

Training and validation loss curves of Tomography_nCNN with regular convolutions: (a) loss, (b) mean absolute error, (c) mean squared error, and (d) structural similarity index.

Table 1.

Results of Tomography_nCNN with regular convolutions after training

Fig. 6.

Training and validation curves of Tomography_CNN with depthwise separable convolutions: (a) loss, (b) mean absolute error, (c) mean squared error, and (d) structural similarity index.

Table 2.

Results of Tomography_CNN with depthwise separable convolutions after training

Fig. 7.

Prediction results of test data: left column, label; right column, prediction by Tomography_nCNN with regular convolutions. Velocity models with (a) fold, (b) fault, and (c) salt structures.

Fig. 8.

Prediction results of test data: left column, label; right column, prediction by Tomography_CNN with depthwise separable convolutions. Velocity models with (a) fold, (b) fault, and (c) salt structures.

Table 3.

Results of Tomography_nCNN and Tomography_CNN from test dataset.

Fig. 9.

Example of noisy shot gathers excited at offsets of (a) 200 m, (b) 400 m, (c) 600 m, and (d) 800 m. Noisy data with SNR (signal to noise ratio) is approximately 5 dB.

Fig. 10.

Prediction results of noisy test data: left column, label; right column, prediction by (a) Tomography_nCNN with regular convolutions and (b) Tomography_CNN with depthwise separable convolutions.

Table 4.

Results of Tomography_nCNN and Tomography_CNN from noisy test dataset.

Acknowledgements

References